Abstract
There are many instances where it is desirable to determine, at a distance, whether a subject is carrying a hidden load. Automated detection systems based on gait analysis have been proposed to detect subjects that carry hidden loads. However, very little baseline gait kinematic analysis has been performed to determine the load carriage effect while ambulating with evenly distributed (front to back) loads on human gait. The work in this paper establishes, via high resolution motion capture trials, the baseline separability of load carriage conditions into loaded and unloaded categories using several standard lower body kinematic parameters. A total of 23 participants (19 for training and 4 for testing) were studied. Satisfactory classification of participants into the correct loading condition was achieved by employing linear discriminant analysis (LDA). Six lower body kinematic parameters including ranges of motion and path lengths from the phase portraits were used to train the LDA to discriminate loaded and unloaded walking conditions. Baseline performance from 4 participants who were not included in training data sets show that the use of LDA provides a 92.5% correct classification over two loaded and unloaded walking conditions. The results suggest that there are gait pattern changes due to external loads, and LDA could be applied successfully to classify the gait patterns with an unknown load condition.
Keywords: Locomotion, Gait analysis, External loads, Linear discriminant analysis
1. Introduction
There are many instances where it is desirable to determine, at a distance, whether a subject is carrying a hidden load. Several sensor modalities (e.g., imaging and radar) have been considered for this application. Many of these proposed methods rely on the assumption that a subject’s gait is altered in a detectable way due to the load. The work in this paper establishes, via high resolution motion capture trials with 19 participants for training and 4 participants for validation, the separability of participants into loaded and unloaded categories utilizing several lower body kinematic variables. Any practical hidden load detection system based on gait analysis, such as video, will have poorer performance than that established in this paper because any “real world” system will extract noisier kinematic variables than motion capture systems. Even using motion capture, it is difficult to correctly classify loading condition based on lower body kinematics when the load is distributed evenly from front to back. However, satisfactory classification of participants into the correct loading condition was achieved by employing linear discriminant analysis (LDA). Many researchers have widely used discriminant analysis for image-processing (Boulgouris & Chi, 2007; Han & Bhanu, 2006) and face recognition (Yu & Yang, 2001). In the present study, we explore the applicability of LDA to gait pattern classification. The LDA classifier developed here establishes a 92.5% correct classification (loaded vs. unloaded) for baseline performance for any detection system that uses the same kinematic variables as those used in this paper.
There are many previous studies that characterize the nature of gait and the effects of various factors (such as loading condition) on gait patterns. One such study showed that the duration of the double stance increased as loads were heavier, but single stance duration decreased in 10 healthy males (Kinoshita, 1985) and in 15 boys (Hong & Brueggemann, 2000). Also, it was shown that the normal walking pattern was significantly modified by external load conditions: backpack or double-pack (Kinoshita, 1985). Backpack loading has a more significant effect on gait pattern than double-pack loading. For example, forward leaning of the trunk is a natural behavior to help keep the whole body center-of-mass (COM) over the feet with backpacking (Harman, Han, Frykman, & Pandorf, 2000; Hong & Brueggemann, 2000; Knapik, Harman, & Reynolds, 1996). There is, however, no forward leaning when ambulating with an evenly distributed front-to-back load carriage system (Kinoshita, 1985). It was found that forward inclination considerably increased as weight increased in order to minimize energy cost (Inman, Ralston, & Todd, 1981; Luttgens & Wells, 1982). This minimized energy expenditure resulted in the decrease of vertical positions at the knee and ankle with added weight (Wittman, Ward, & Flynn, 2005). Several published studies indicated that ankle rotation increased in the sagittal plane under loaded conditions (Kinoshita, 1985; Knapik et al., 1996). These studies also showed that knee flexion after impact was greater when carrying loads in order to absorb increased impact forces.
The use of a phase portrait is a way to describe human locomotion (Winstein & Garfinkel, 1989) and to show dynamic explanation of joint movements (Burgess-Limerick, Abernethy, & Neal, 1993). It provides a system’s position and rate of position changes in a two-dimensional plane. The path length of the phase portrait can be used to determine the effectiveness of the postural system in controlling the lower body stability and steadiness similar to distance measures of center-of-pressure (COP) in sway balance control tests (Prieto, Myklebust, Hoffmann, Lovett, & Myklebust, 1996). Previous studies neither analyzed these quantities for walkers with and without an evenly distributed load nor did they establish the baseline performance of classification methods for determining loaded vs. unloaded walking.
BenAbdelkader and Davis (2002) used video as a sensing modality to differentiate between loaded vs. unloaded participants. This work used variables that measured swinging periodicity of legs and arms. Another variable to differentiate carrying vs. not carrying an object were the medians of the time series for lower parts of body. The study used a simple “and” type classifier that classified as natural walking if all criteria were met. If any of the criteria was violated, then the state was classified as loaded walking. A significant difference between the work of BenAbdelkader and Davis and the present study is that the loads in the study of BenAbdelkader and Davis study were not evenly distributed.
Although much has been learned over the last few decades about external load effects on gait patterns, development of discriminant techniques to classify evenly distributed external loads is lacking. As such, the two primary goals of this study were: (1) To establish the upper bound on performance of classification of loading condition using LDA. (2) Provide pre- and post-loading analysis of several common gait kinematic discriminants that also serve as inputs to the LDA classifier. It was hypothesized that there are significant differences in lower body joint kinematic quantities while carrying an evenly distributed load, and classification of an unknown participant’s loading condition is possible based on the these quantities.
2. Methods
2.1. Participants and experimental setup
Twenty-three participants, 14 male and 9 female (mean age ± SD = 22.52 ± 3.84 years), participated in the study. They were randomly grouped to 19 (12 male and 7 female) participants for model training and 4 (2 male and 2 female) participants for model validation. All participants gave their informed consent prior to participation as defined by the Committee for Participants of Investigative Projects at the Virginia Polytechnic Institute and State University. The participants’ mean body heights and weights were 175.11 ± 8.48 cm, 73.50 ± 16.22 kg for the training group, and 171.25 ± 3.77 cm, 70.88 ± 12.44 kg for the testing group, respectively. To determine a participant’s preferred walking speed, the treadmill was started and the velocity gradually increased so as to achieve a participant’s most comfortable walking speed. The same preferred walking speed was used for both loading conditions to control any speed-related changes such as dynamic stability (England & Granata, 2007), metabolic costs (Griffin, Roberts, & Kram, 2002), and so on.
A total of 23 reflective markers (Chow et al., 2005; Kim, Lockhart, & Yoon, 2003) were attached to the participants’ anthropometric landmarks (top of the head, base of second toe, malleolus, epicondyle, greater trochanter, clavicle, styloid process of ulna, lateral epicondyle of humerus, greater tubercle, acromion, anterior portion of temporal bone, and center of the calcaneus) to capture participants’ 3D motion using a ProReflex system (Qualisys, Gothenburg, Sweden) at the sampling rate of 120 Hz. Only data for lower body markers were analyzed to focus on changes of lower body kinematics. Treadmill walking was performed for 30-s sessions with participants without any external load (unloaded walking) and while wearing a vest with a mass of 12.5 kg. A single 12.5 kg weight was selected in order to investigate the effects of one fixed weight for people with different height and weight. Also, it is about 10 to 20% of subjects’ body mass which is a suitable load for individuals when considering evenly distributed load carriage. More importantly, the weight was selected to fall within the range of masses normally tested in load-effect experiments (Harman et al., 2000; Hong & Brueggemann, 2000; Kinoshita, 1985; Wang, Pascoe, & Wimar, 2001). The vest was attached to the participant’s body using two shoulder straps and three side straps so that it did not obstruct any upper or lower body movements. Five trials were repeated in each load condition and the order of external load conditions in each subject was completely randomized to reduce any order effects.
2.2. Analysis
Consecutive left heel contacts determined the period of one stride in this study. Thus, one stride included both a left and a right step. Left heel contacts were determined using the vertical velocity changes of heel markers to identify gait periods (Mickelborough, van der Linden, Richards, & Ennos, 2000). Two consecutive left strides were averaged for the analysis. The kinematic data were smoothed using a 61-point fourth-order Savitzky-Golay filter (Thomas, Corcos, & Hasan, 2003) and then derived for the angular position to determine angular velocity. All following angles were measured in the sagittal plane. Hip angles were defined from the horizontal to the thigh segment. Knee angles were determined between the thigh segment and the shank segment, and ankle angles were between the shank segment and the foot (Harman et al., 2000). Then, sagittal plane joint ranges of motion (ROM) were calculated as the difference between peak flexion and peak extension (LaFiandra, Wagenaar, Holt, & Obusek, 2002) at hip, knee, and ankle joints (Hip ROM, Knee ROM, and Ankle ROM). These values were used to quantify the magnitude of joint angular movement over the gait cycle.
2.3. Phase portrait path length (PL)
The phase portraits (Fig. 1) used in this study were determined from the angular position (θ) vs. angular velocity (θ̇). Segmental angular velocities were calculated from the sagittal plane angles. Angular velocities were then multiplied by the total duration for path length calculations. From the resulting phase-planes, path length (Eq. (1)) is estimated as the sum of the straight line distances between consecutive points for hip, knee, and ankle angles (PLHip, PLKnee and PLAnkle). These values were used to quantify the magnitude and velocity of joint angular movement as a function of time over a gait cycle,
| (1) |
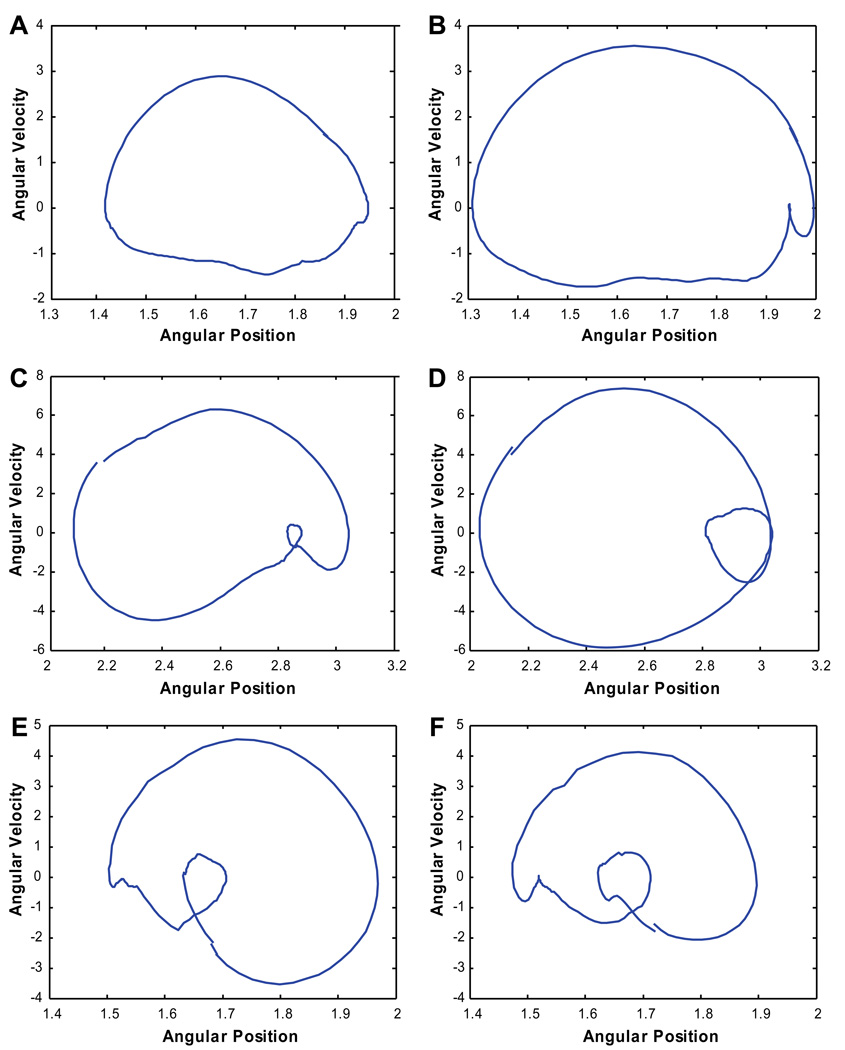
Fig. 1.
Phase portraits of hip, knee, and ankle angles from one typical participant (A) hip phase in unloaded walking condition, (B) hip phase in loaded condition, (C) knee phase in unloaded walking, (D) knee phase in loaded walking, (E) ankle phase in unloaded walking, and (F) ankle phase in loaded walking.
2.4. Statistics and linear discriminant analysis (LDA)
Analysis of variance (ANOVA) was used to test for the main effects of load condition (2 levels) on the dependent variables (Hip ROM, Knee ROM, Ankle ROM, PLHip, PLKnee, and PLAnkle). A p value less than .05 indicates a statistically significant difference between loaded and unloaded walking for a given variable. Results showed that three variables (Hip ROM, PLHip, and PLKnee) indicated statistically significant differences between unloaded and loaded walking (Table 1). Therefore, only these variables were used as inputs to the LDA classifier, and the other three variables (Knee ROM, Ankle ROM, and PLKnee) were not used.
Table 1.
The averages and SD of joint ranges of motion in the sagittal plane and path lengths under two loading conditions (unloaded and 12.5 kg loaded) from 19 training participants. Bolded values indicate a statistically significant load effect – ANOVA.
| Variable | Unloaded | Loaded | p Values |
|---|---|---|---|
| Hip ROM (°) | 38.389 ± 3.882 | 41.371 ± 3.409 | < .01 |
| Knee ROM (°) | 62.706 ± 5.498 | 62.236 ± 4.797 | .490 |
| Ankle ROM (°) | 27.092 ± 7.757 | 27.750 ± 5.304 | .453 |
| PLHip | 1.339 ± 0.137 | 1.456 ± 0.122 | < .01 |
| PLKnee | 2.471 ± 0.242 | 2.556 ± 0.234 | < .01 |
| PLAnkle | 1.178 ± 0.733 | 1.151 ± 0.180 | .708 |
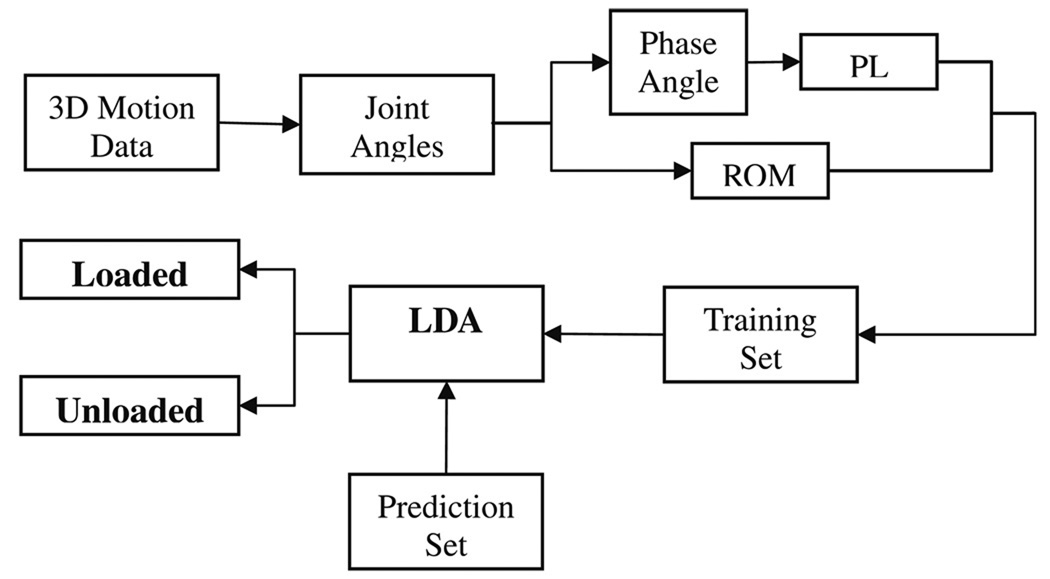
For this study, linear discriminant analysis (LDA) was implemented to find a classification boundary between loaded and unloaded conditions using three kinematic variables. LDA is closely related to ANOVA and regression analysis. These methods also attempt to express a dependent variable as a linear combination of other variables (Sharm, 1996). More information on LDA and its application can be found in Yu and Yang (2001) and Boulgouris and Chi (2007). For the classification, LDA is trained using 19 subjects’ experimental data. The effectiveness of this analysis is then determined using the untrained trials from the sequestered 4 subjects. The overall processing flow is shown in Fig. 2.
Fig. 2.
A summarized processing flow to classify loaded or unloaded walking conditions.
To validate the quality of LDA, principal component analysis (PCA) was conducted for gait waveform data using hip, knee, and ankle angles. Detailed information to perform PCA can be found in Deluzio, Wyss, Zee, Costigan, and Sorbie (1997), Deluzio, Wyss, Costigan, Sorbie, and Zee (1999), and Deluzio and Astephen (2007). PC scores from the first and second principal components (PCs) were generated for each participant for both unloaded and loaded conditions. Student’s t test was applied to PC scores if there were statistically significant differences between the two loading conditions. Twenty-three participants with two loading conditions for PCA summed to 46 trials. For the LDA classification, 38 trials from 19 participants were used for training, and 8 trials from the untrained 4 participants were used for testing LDA.
3. Results
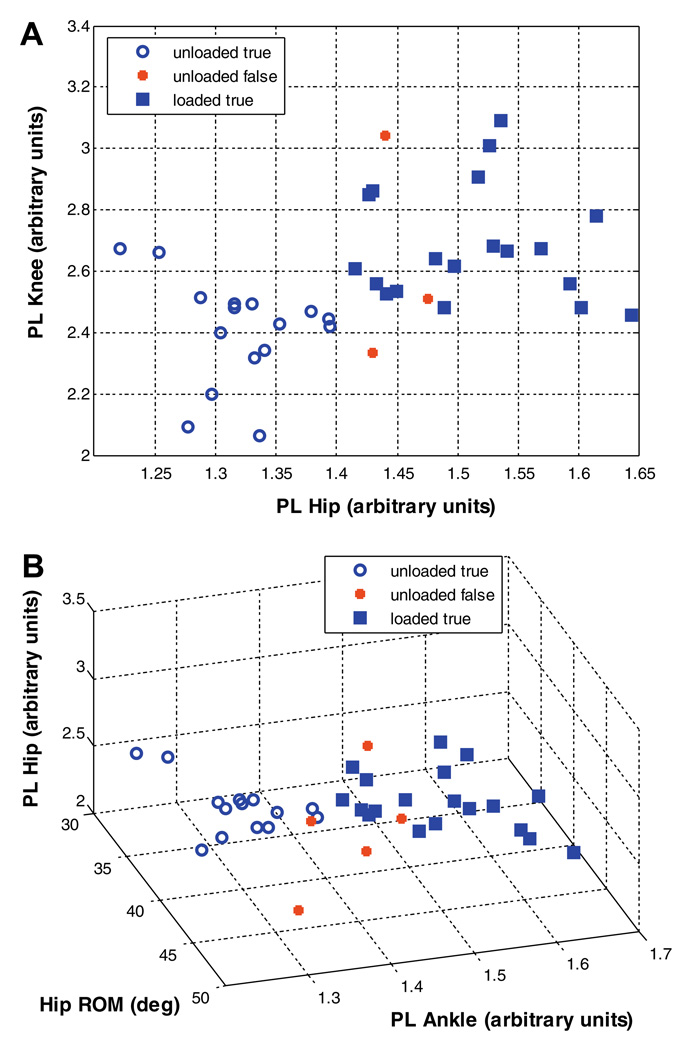
There were statistically significant differences for Hip ROM, PLHip, and PLknee; the other dependent variables did not show significant differences. Carrying an evenly distributed load resulted in increased hip ROM and path lengths of the hip and knee (Table 1). The LDA classifier was trained using 19 participants. The performance of the classifier was tested using 40 trials from 4 participants that were not used for training. The LDA classifier achieved a 92.5% correct classification rate (37 out of 40) with inputs of PLHip and PLknee. This indicates that 92.5% of the unknown load conditions were assigned to the correct category (Fig. 3A and Table 2). The false alarm rate, which is the rate that classifies unloaded walking as loaded, was 7.5% (3 out of 40). Other combinations of variables showed an 87.5% correct classification (Fig. 3B and Table 2). Using two path length variables (PLHip, and PLknee) led to the best classification. A lower classification rate was achieved using the two hip joint variables (Hip ROM and PLHip). This indicates that these two variables were correlated, so they provided less information for classification than using the two PL variables (Fig. 3B).
Fig. 3.
Scatter plots of load classification after linear discriminant analysis (LDA). (A) A 92.5% (37 out of 40) correct classification rate was achieved when using two path length variables. (B) A 87.5% (35 out of 40) correct classification rate was achieved when using three path length variables. True is the correct classification and false is the incorrect classification after linear discriminant analysis.
Table 2.
Classification rate results with various combinations of kinematic input variables.
| Input variables | Classification rate (%) |
|---|---|
| Hip ROM + Hip PL + Knee PL | 87.5 |
| Hip PL + Knee PL | 92.5 |
| Hip ROM + Knee PL | 87.5 |
| Hip ROM + Hip PL | 87.5 |
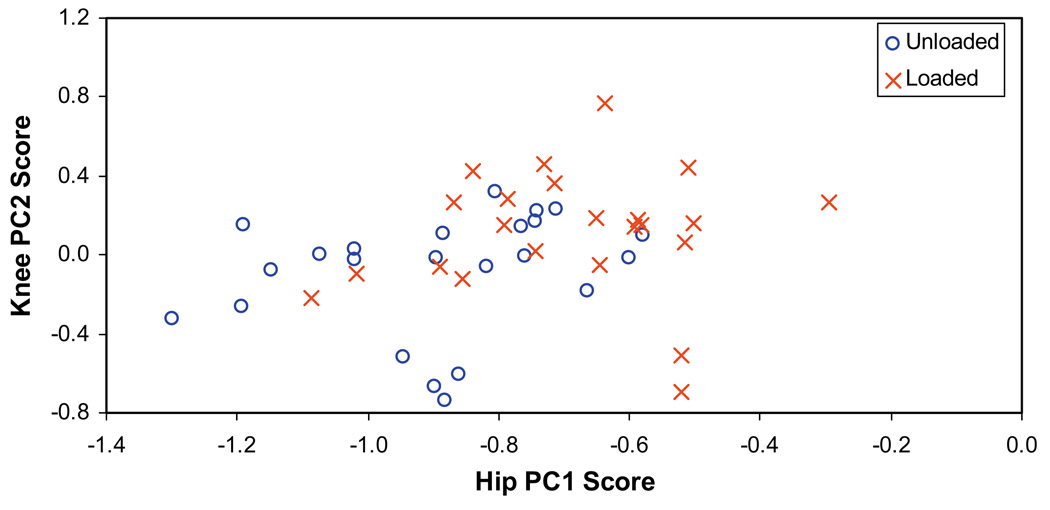
The PCA results showed that 90% of the data variation was captured in the first two PCs. There were statistically significant differences (p < .05) in the first principal component score for the hip and the second principal component score for the knee angle waveform data (Table 3). A scatter plot (Fig. 4) of the two PC scores showed the discriminatory ability of each PC. It also demonstrated that a smaller PC score was associated with unloaded walking.
Table 3.
A summary of Student’s t test results (mean ± SD) comparing the PC scores between unloaded and loaded walking conditions. Bolded values indicate statistically significant differences (p < .05) between the two groups.
| Angle | PC | Unloaded | Loaded | p Value |
|---|---|---|---|---|
| Hip | PC1 | −0.89 ± 0.19 | −0.69 ± 0.19 | < .05 |
| PC2 | −0.06 ± 0.30 | 0.06 ± 0.28 | .177 | |
| Knee | PC1 | 0.34 ± 0.32 | 0.32 ± 0.30 | .835 |
| PC2 | −0.09 ± 0.30 | 0.11 ± 0.32 | < .05 | |
| Ankle | PC1 | −1.91 ± 0.18 | −1.84 ± 0.24 | .26 |
| PC2 | −0.01 ± 0.31 | 0.04 ± 0.29 | .55 |
Fig. 4.
A scatter plot of the first hip and second knee principal component scores for 23 participants with unloaded and loaded walking. The unloaded walking is coded as “○” and the loaded walking is coded as “×”.
The LDA classifier achieved an 87.5% correct classification rate (7 out of 8) with inputs of hip and knee PC scores and knee and ankle PC scores. This indicates that 87.5% of the unknown load conditions were assigned to the correct category (Table 4). Other combinations of variables showed a 75% correct classification rate (6 out of 8) as shown in Table 2.
Table 4.
Classification rate results with various combinations of input PC scores.
| Input variables | Classification rate (%) |
|---|---|
| Hip + Knee + Ankle PC scores | 75.0 |
| Hip + Knee PC scores | 87.5 |
| Knee + Ankle PC scores | 87.5 |
| Hip + Ankle PC scores | 75.0 |
4. Discussion
We presented classification results (loaded/unloaded) with a simple linear discriminant analysis classifier that analyzed the motion capture data as training data sets from 19 participants. The classifier in question gave a baseline performance of 92.5% correct classification from 4 untrained participants of loaded vs. unloaded walking conditions when load was evenly distributed on the upper body. These results confirm that a measurable difference exists between loaded and unloaded walking conditions using the gait kinematics. It is important to note that any real world system that non-invasively measures the same variables used in this paper should have poorer performance than our results. It may not even be practical to obtain these types of variables in real world settings utilizing video capture systems.
The kinematic variables in Fig. 3 illustrate the possibility of gait pattern separation for participants not included in the training data sets. The differences between unloaded and loaded walking are noticeable, which indicates that these three variables would be sufficient to classify the conditions on a statistical basis. Thus, the results suggest that the use of kinematic variables in a video camera system (if at all possible) may also lead to the advanced real-time classification.
All joint ranges of motions were similar to previous studies (Chow et al., 2005; Harman et al., 2000; Kerrigan, Todd, & Croce, 1998; LaFiandra et al., 2002). It was found that the gait adaptation of external loads would result in angular changes of hip and knee joints (Table 1). Several studies (Chow et al., 2005; Harman et al., 2000; LaFiandra et al., 2002) also reported that increased hip ROM was to generate power and absorb impact when carrying a load. PCA results also support the kinematic changes in the hip and knee joints (Table 3). No significant changes in ankle kinematics were found in this study as also shown in Chow et al. (2005) with up to 15% of body weight. It was also found that the increased path lengths of hip and knee joints (Table 1) would indicate more angular displacement and velocity changes due to external loads. It may support the shorter single stance time (Chow et al., 2005; Hong & Brueggemann, 2000; Kinoshita, 1985; Wang et al., 2001) and the faster cadence in previous studies (Harman et al., 2000; LaFiandra et al., 2002). This results in decreased transversal pelvic rotation (LaFiandra et al., 2002). However, this study is limited to an investigation of sagittal plane kinematics.
When the two path length variables (PLHip, and PLknee) were used as an input, the accuracy of the LDA was the highest among many input variable combinations (Fig. 3A and Table 2). In other words, when hip ROM was used with other variables, it reduced the discrimination ability in LDA (Fig. 3B and Table 2). In addition, using LDA with PL variables showed better separated regions than PCA with lower body joint angles when comparing Figs. 3 and 4. According to Tables 2 and 4, LDA using kinematic variables provides better classification of unloaded and loaded conditions than using PC scores. In short, LDA is a simple but very effective tool for classification of gait data in this study.
The same treadmill speed was used (set for each participant’s normal walking speed) for both loaded and unloaded conditions. This ensures that both walking conditions were close to identical due to the same normal walking speed (i.e., nearly constant stride frequency at a given speed). Further studies would be necessary to find the effects of walking speed by having each participant walk at a normal walking speed for each load condition over ground vs. treadmill walking. Another important result found in this study is that it is not required to have a priori knowledge of an individual’s gait kinematics to correctly classify loaded vs. unloaded walking conditions assuming the “real world” system can extract the kinematic quantities with high enough fidelity and enough training data exists.
Acknowledgments
The work described in this paper was fully supported by a grant from The Office of Naval Research and The Applied Research Laboratory, Penn State University.
Footnotes
Author agreement
All authors contributed to the development and analyses of the data. Each of the authors has read and concurs with the content in the final manuscript. The material within has not been and will not be submitted for publication elsewhere except as an abstract.
Conflict of interest statement
There is no conflict of interest.
References
- BenAbdelkader C, Davis L. Detection of people carrying objects: A motion-based recognition approach. Proceedings FGR. 2002:363–368. [Google Scholar]
- Boulgouris N, Chi Z. Gait recognition using radon transform and linear discriminant analysis. IEEE Transactions on Image Processing. 2007;16:731–740. doi: 10.1109/tip.2007.891157. [DOI] [PubMed] [Google Scholar]
- Burgess-Limerick R, Abernethy B, Neal RJ. Relative phase quantifies interjoint coordination. Journal of Biomechanics. 1993;26:91–94. doi: 10.1016/0021-9290(93)90617-n. [DOI] [PubMed] [Google Scholar]
- Chow DHK, Kwok MLY, Au-Yang ACK, Holmes AD, Cheng JCY, Yao FYD, et al. The effect of backpack load on the gait of normal adolescent girls. Ergonomics. 2005;48:642–656. doi: 10.1080/00140130500070921. [DOI] [PubMed] [Google Scholar]
- Deluzio KJ, Astephen JL. Biomechanical features of gait waveform data associated with knee osteoarthritis: An application of principal component analysis. Gait and Posture. 2007;25:86–93. doi: 10.1016/j.gaitpost.2006.01.007. [DOI] [PubMed] [Google Scholar]
- Deluzio KJ, Wyss UP, Costigan PA, Sorbie C, Zee B. Gait assessment in unicompartmental knee arthroplasty patients: Principal component modeling of gait waveforms and clinical status. Human Movement Science. 1999;18:701–711. [Google Scholar]
- Deluzio KJ, Wyss UP, Zee B, Costigan PA, Sorbie C. Principal component models knee kinematics and kinetics: Normal vs. pathological gait patterns. Human Movement Science. 1997;16:201–217. [Google Scholar]
- England SA, Granata KP. The influence of gait speed on local dynamic stability of walking. Gait and Posture. 2007;25:172–178. doi: 10.1016/j.gaitpost.2006.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin TM, Roberts TJ, Kram R. Metabolic cost of generating muscular force in human walking: Insights from loadcarrying and speed experiments. Journal of Applied Physiology. 2002;95:172–183. doi: 10.1152/japplphysiol.00944.2002. [DOI] [PubMed] [Google Scholar]
- Han J, Bhanu B. Individual recognition using gait energy image. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2006;28:316–322. doi: 10.1109/TPAMI.2006.38. [DOI] [PubMed] [Google Scholar]
- Harman E, Han KH, Frykman P, Pandorf C. The effects of backpack weight on the biomechanics of load carriage. Natick, MA: US Army Research Institute of Environmental Medicine Military Performance Division Technical Report, T-00-17; 2000. [Google Scholar]
- Hong Y, Brueggemann GP. Changes in gait patterns in 10-year-old boys with increasing loads when walking on a treadmill. Gait and Posture. 2000;11:254–259. doi: 10.1016/s0966-6362(00)00055-2. [DOI] [PubMed] [Google Scholar]
- Inman V, Ralston HJ, Todd F. Human walking. Williams and Wilkins; 1981. [Google Scholar]
- Kerrigan DC, Todd MK, Croce UD. Gender differences in joint biomechanics during walking. American Journal of Physical Medicine and Rehabilitation. 1998;77:2–7. doi: 10.1097/00002060-199801000-00002. [DOI] [PubMed] [Google Scholar]
- Kim S, Lockhart T, Yoon HY. Relationship between age-related gait adaptations and required coefficient of friction. Safety Science. 2003;43:425–436. doi: 10.1016/j.ssci.2005.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinoshita H. Effects of different loads and carrying systems on selected biomechanical parameters describing walking gait. Ergonomics. 1985;28:1347–1362. doi: 10.1080/00140138508963251. [DOI] [PubMed] [Google Scholar]
- Knapik J, Harman E, Reynolds K. Load carriage using packs: A review of physiological, biomechanical and medical aspects. Applied Ergonomics. 1996;27:207–216. doi: 10.1016/0003-6870(96)00013-0. [DOI] [PubMed] [Google Scholar]
- LaFiandra M, Wagenaar RC, Holt KG, Obusek JP. How do load carriage and walking speed influence trunk coordination and stride parameters? Journal of Biomechanics. 2002;36:87–95. doi: 10.1016/s0021-9290(02)00243-9. [DOI] [PubMed] [Google Scholar]
- Luttgens K, Wells K. Kinesiology: Scientific basis of human motion. 7th ed. Philadelphia: Saunders College Publishing; 1982. [Google Scholar]
- Mickelborough J, van der Linden ML, Richards J, Ennos AR. Validity and reliability of a kinematic protocol for determining foot contact events. Gait and Posture. 2000;11:32–37. doi: 10.1016/s0966-6362(99)00050-8. [DOI] [PubMed] [Google Scholar]
- Prieto TE, Myklebust JB, Hoffmann RG, Lovett EG, Myklebust BM. Measures of postural steadiness: Differences between healthy young and elderly adults. IEEE Transactions on Biomedical Engineering. 1996;43:956–966. doi: 10.1109/10.532130. [DOI] [PubMed] [Google Scholar]
- Sharm S. Applied multivariate techniques. New York: John Wiley and Sons, Inc; 1996. [Google Scholar]
- Thomas JS, Corcos DM, Hasan Z. Effect of movement speed on limb segment motions for reaching from a standing position. Experimental Brain Research. 2003;148:377–387. doi: 10.1007/s00221-002-1287-2. [DOI] [PubMed] [Google Scholar]
- Wang Y, Pascoe DD, Wimar W. Evaluation of book backpack load using walking. Ergonomics. 2001;44:858–869. doi: 10.1080/00140130118572. [DOI] [PubMed] [Google Scholar]
- Winstein CJ, Garfinkel A. Qualitative dynamics of disordered human locomotion: A preliminary investigation. Journal of Motor Behavior. 1989;21:373–391. doi: 10.1080/00222895.1989.10735490. [DOI] [PubMed] [Google Scholar]
- Wittman MG, Ward JM, Flynn PJ. Visual analysis of the effects of load carriage on gait. Proceedings of SPIE. 2005;5779:15–22. [Google Scholar]
- Yu H, Yang J. A direct LDA algorithm for high-dimensional data – with application to face recognition. Pattern Recognition. 2001;34:2067–2070. [Google Scholar]