Emergent bistability by a growth-modulating positive feedback circuit

Abstract

A synthetic gene circuit is often engineered by considering the host cell as an invariable “chassis”. Circuit activation, however, may modulate host physiology, which in turn can drastically impact circuit behavior. We illustrate this point by a simple circuit consisting of mutant T7 RNA polymerase (T7 RNAP*) that activates its own expression in bacterium Escherichia coli. Although activation by the T7 RNAP* is noncooperative, the circuit caused bistable gene expression. This counterintuitive observation can be explained by growth retardation caused by circuit activation, which resulted in nonlinear dilution of T7 RNAP* in individual bacteria. Predictions made by models accounting for such effects were verified by further experimental measurements. Our results reveal a novel mechanism of generating bistability and underscore the need to account for host physiology modulation when engineering gene circuits.

Introduction

A central challenge in synthetic biology is to construct reliable and useful biological systems in a predictable manner ^1–4. A typical design process entails multiple rounds of gene circuit modeling, construction, and optimization. This process is often carried out by considering the host cell as an invariable “chassis”, or assuming a well-defined interface with the circuit. This circuit-centric view of gene circuit engineering has been implied in efforts to standardize synthetic biological parts ⁵.

As has been noted, however, a circuit is functional only in the context of its host and its activation may invoke unintended interactions with the host ^2,6,7. These interactions may be local: there may be cross-talk between circuit components and endogenous host proteins. They may be global: expression of circuit components may be detrimental or beneficial to the host cell, leading to modulation of cell physiology. In general, unintended interactions have been neglected in engineering and characterizing synthetic gene circuits. This practice is advantageous in that it can drastically simplify the design process. To date, it appears to be well-justified in published examples ^8–17, where the dominant observed dynamics can be explained by the intended circuit design.

However, it has been recognized that interactions between a cellular network and its host may significantly modulate the network dynamics. For example, bacterial physiology can modulate noise and dynamics of gene expression ¹⁸ and profoundly affect dynamics of phage infection^19,20. Theoretical studies have also suggested that lactose metabolism and its impact on bacterial growth can significantly affect activation dynamics of the lac operon, particularly its ability to generate bistability ^21–23. In higher organisms, cellular geometry has been shown to modulate intracellular dynamics of the MAPK pathway in neurons during synapse activation²⁴.

In efforts to engineer gene circuits to date, however, little attention has been paid to the impact of unintended circuit-host interactions. Specifically, it remains elusive as to how such interactions modulate nonlinear dynamics of gene circuits. A better understanding of this question would have profound implications for exploring design strategies of cellular networks ², for standardizing biological parts and systems ^3,5, and for engineering cells as computing units ²⁵.

In this work, we show that circuit-mediated modulation of host physiology can lead to the emergence of complex yet predictable dynamics beyond the capacity of the circuit itself. In particular, we analyze a minimal gene circuit consisting of an auto-activating mutant T7 RNA polymerase (T7 RNAP*) in bacterium Escherichia coli. Although activation by T7 RNAP* is noncooperative, the circuit can generate bistable gene expression. This counterintuitive observation can be explained, however, by accounting for circuit-induced growth retardation in addition to the feedback regulation. Based on this notion, we develop simple mathematical models to predict how the bistability can be modulated by varying the circuit induction level and the cell growth rate. The model predictions are validated by further experiments conducted at both single-cell and population levels.

Results

Persistent bimodal gene expression by a minimal positive-feedback circuit

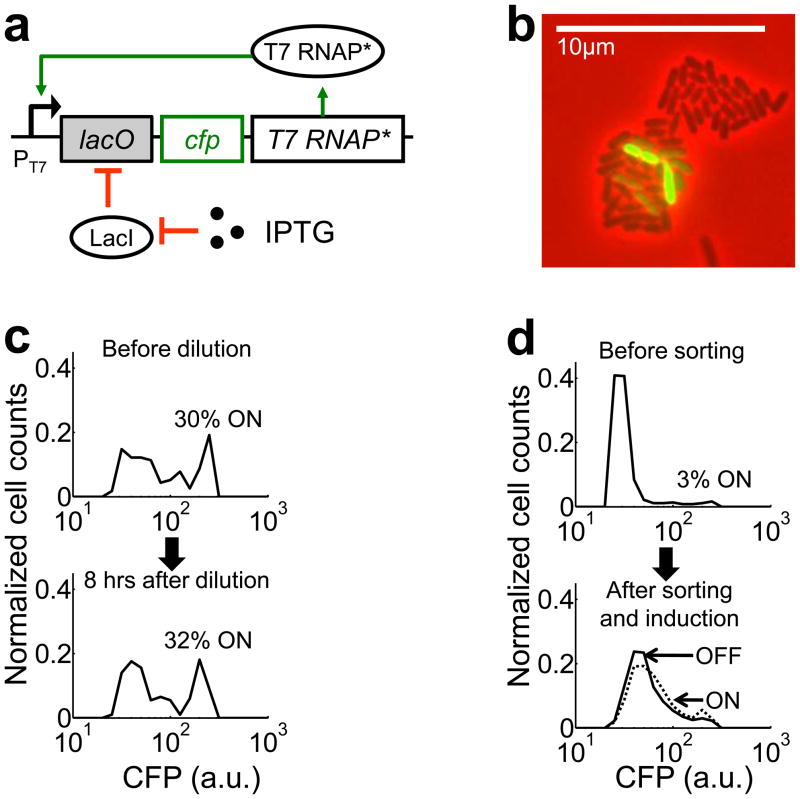
Our analysis focused on a positive feedback circuit that consists of a mutant T7 RNAP* activating its own expression from a T7 promoter (P_T7) (Figs. 1a and S1a). The mutant gene has a single deletion at the 186^th base pair, but it was expressed into functional T7 RNAP* (see Supplementary Results and Fig. S2), likely by programmed translational frameshift ²⁶. The P_T7 promoter carries a lac operator site (lacO) and it is repressed in E. coli strains expressing LacI. In these strains, the circuit can be induced by isopropyl-β-D-thiogalactopyranoside (IPTG, 1). A cyan fluorescent protein (CFP) is co-expressed with T7 RNAP* as circuit readout. Despite its simplicity, the circuit regularly generated bimodal CFP expression in MC4100Z1 cells upon full induction (1000μM IPTG): each culture consisted of two distinct subpopulations with either low (OFF) or high (ON) CFP expression (Fig. 1b, Supplementary Movies 1 and 2).

Figure 1. Bistability induced by a T7 RNAP* positive-feedback circuit.

(a) The circuit consists of T7 RNAP* regulated by its own promoter (P_T7lac). IPTG activates the circuit. CFP serves as the circuit readout.

(b) A microcolony of MC4100Z1 cells carrying the circuit, induced with 1000μM IPTG. The colony exhibited bimodal CFP expression. The corresponding movie is included as Supplementary Movie 1.

(c) The bimodal expression represented steady state behavior. The cell culture gave rise to ~31% ON cells both before dilution and 8 hours after dilution.

(d) The OFF subpopulation (solid line) could be induced to generate a similar distribution as the ON subpopulation (dotted line). The results in (c) and (d) are representative data from three replicates (Figs. S3 and S4). Cell counts were normalized by total number of cells in each sample. The percentages of ON cells were different in (c) and (d) due to different experiment protocols (see Materials and Methods).

(e) Time series of sample OFF, INT, and ON colonies (see Fig. S5 for additional data).

Several mechanisms could cause the bimodal CFP expression. The OFF cells might have been in the process of switching ON. To test this possibility, we incubated cell cultures for eight hours with full induction. We then diluted each culture 100-fold into fresh medium to allow for additional eight hours of growth with full induction. We observed that each population after the second cycle of growth contained a similar percentage of ON cells as its seeding culture before the dilution (Figs. 1c & S3). Therefore, the bimodal CFP distribution before the dilution was likely at steady state.

Alternatively, the OFF cells might have lost circuit function and were unable to express CFP at high levels. To test this possibility, we sorted a bimodal population into an OFF and an ON subpopulations. Both subpopulations were diluted into fresh medium and incubated without induction for four hours to allow the CFP level of the ON subpopulation to converge to that of the OFF subpopulation. Cells were then incubated for additional eight hours with full induction. At this time, both the OFF and ON subpopulations showed similar percentage of ON cells (Figs. 1d & S4). This result indicated that the circuit in the OFF subpopulation was functional. In addition to the functional tests, DNA sequencing confirmed that the circuit in the OFF subpopulation was indeed intact.

Hysteresis at the single-cell level

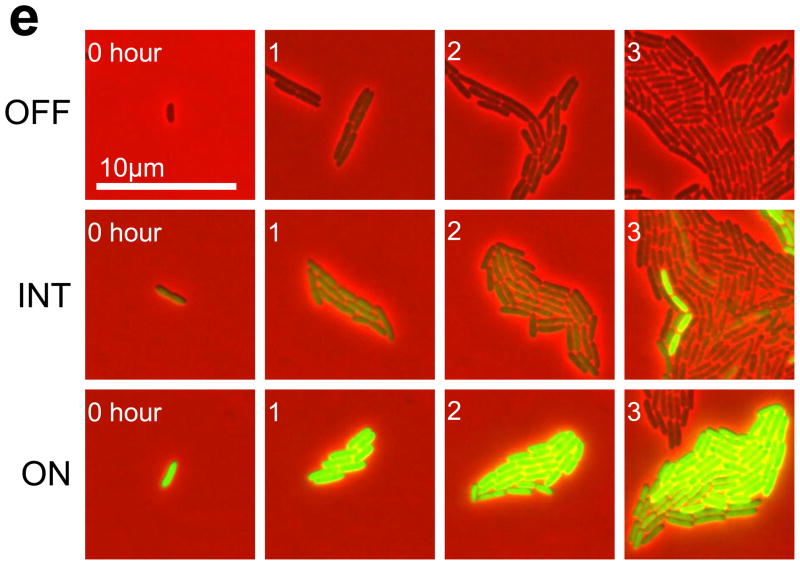
As bimodality is a hallmark of bistable switches ^{9,10,15,27–31}, we hypothesized that the circuit was bistable in these cells. If so, the cell state would be inheritable as a cell divides: an OFF cell would likely generate an OFF colony; an ON cell would likely generate an ON colony; a cell with an intermediate state (INT) would generate a mixed colony. To test this notion, we tracked the growth of microcolonies initiated with cells in different states. These colonies were fully induced during the observation (three to six hours). Each colony was classified as ON, OFF, or INT according to the CFP intensity of its seeding cells (see Materials and Methods). Fig. 1e shows sample time series of an OFF colony, an INT colony, and an ON colony (see Fig. S5 for additional data). Our results showed that the initial state of a colony governed the final distribution of cell states. A colony initiated with OFF cells largely stayed OFF; a colony initiated with ON cells almost always stayed ON (Figs. 1e & S5). Occasionally, a subpopulation of cells within an OFF colony switched ON spontaneously (Fig. S5a, colony 5). Spontaneous switching-OFF within an ON colony also occurred, but rarely (results not shown). A colony with an initial INT state could bifurcate into a population with both ON and OFF cells (Fig. 1e), or gave rise to a colony with only OFF cells or one with only ON cells (Fig. S5b). Such a colony might be around an unstable steady state. It would switch either to an ON state or an OFF state, depending on the effects of cellular noise, as well as which stable state was closer to its initial state. Taken together, these single-cell measurements supported the notion that the circuit was bistable.

Growth inhibition by circuit activation

The observation of hysteresis was counterintuitive, however, because the positive feedback circuit lacks cooperativity to generate bistability ³². It has been established experimentally that T7 RNAP transcription activity increases linearly with concentration of T7 RNAP and lacks cooperativity ^33–35. In addition, T7 RNAP does not require accessory proteins for its activities, including initiation, elongation, and termination of transcription ³⁶. This is also consistent with structural studies, which showed that T7 RNAP binds to its promoter as a monomer ³⁷. To test if the mutant T7 RNAP* also lacked cooperativity, we constructed a linear gene cascade (Fig. S6). T7 RNAP* is co-expressed with an enhanced yellow fluorescent protein (EYFP). It binds to a P_T7Lac promoter and transcribes CFP. We induced the circuit with varying anhydrous tetracycline (aTc, 2) concentrations (0–100ng/ml) and a constant IPTG concentration (1mM). Next, we measured both EYFP and CFP expression in single cells using microscopy. Our results showed that CFP exhibited a Hill’s coefficient of ~0.99 with respect to EYFP (Fig. S6), confirming the lack of cooperativity in T7RNAP* transcriptional activity. Therefore, some other mechanisms must have contributed to the bistable circuit activation.

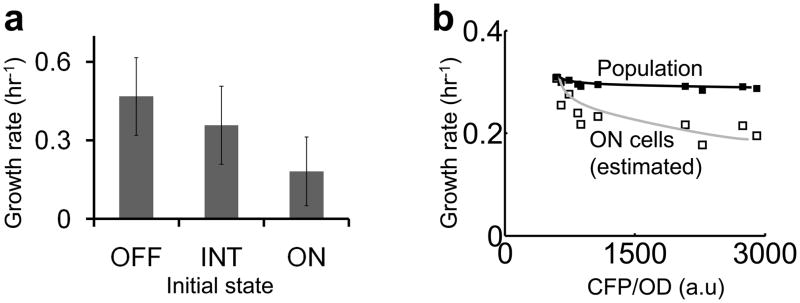
In single-cell experiments, we noticed that ON cells on average grew more slowly than OFF cells (Fig. 2a). To quantify this difference, we tracked microcolonies with OFF, INT, or ON initial states and calculated average growth rates of each initial state (Supplementary Methods). The growth rates were 0.47/hr for OFF cells, 0.36/hr for INT cells, and 0.18/hr for ON cells. At the population level, the growth rates also decreased with increasing CFP expression (Fig. 2b, filled squares & black line). The observed reduction was likely an underestimate due to the bimodal circuit activation in each population, where the OFF cells constituted most of the biomass and masked growth retardation in the ON cells. Assuming that each population consisted of 30% ON cells, the estimated growth rates of the ON cells (Supplementary Methods) showed more drastic growth reduction (Fig. 2b, open squares & grey line). Note that the growth rates and the extent of growth retardation were different in Fig. 2a and Fig. 2b due to different experimental conditions. In addition, we further tested the impact on cell growth by expressing the T7 RNAP* gene that was fused to an eyfp gene using a P_Tet promoter. Fig. S7 shows that the induction of this plasmid (reported by EYFP expression) reduced bacterial growth. In all, both single-cell and population measurements indicated growth retardation due to circuit activation, which may deplete cellular resources for growth ^38,39.

Figure 2. Circuit activation reduces bacterial growth rates.

(a) In microcolonies, increasing CFP expression reduced the growth rate. Error bars indicate the standard deviation of 65 OFF colonies, 12 INT colonies, and 16 ON colonies respectively. One-way analysis of variance shows that the growth rates of OFF, INT, and ON colonies are significantly different (p-value~1×10⁻⁹). A multiple comparison test using 95% confidence interval shows that INT colonies grew slower than OFF colonies, ON colonies grew slower than INT colonies, and ON colonies grew slower than OFF colonies.

(b) At the population level, increasing CFP expression also reduced the growth rate. Under each condition, the growth rate of ON cells (open squares, grey line) was estimated by assuming 30% ON cells in each population (Supplementary Methods).

Modeling the emergent bistability due to circuit-host interaction

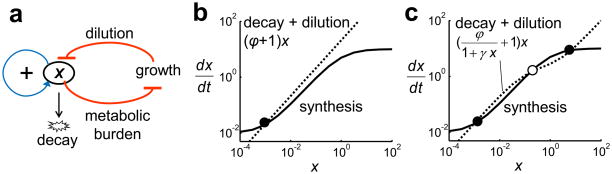
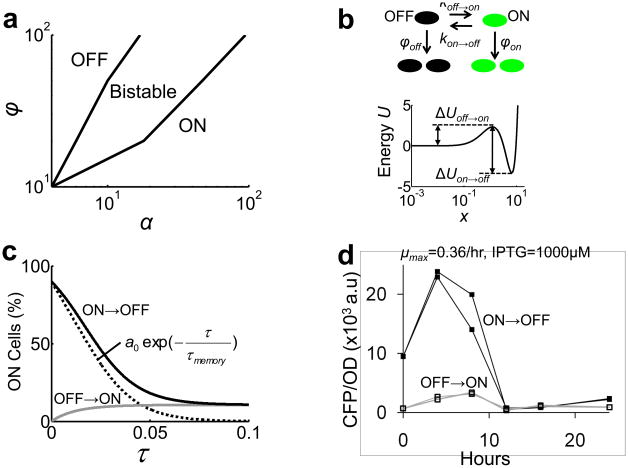
Based on these observations, we hypothesized that the interplay between the T7 RNAP* positive feedback loop and the growth modulation together constituted a bistable switch (Fig. 3a). Cellular noise generates cell-cell variations in T7 RNAP* expression ^40,41. These variations are amplified by the positive feedback loop or by circuit-induced growth retardation. Cells expressing more T7 RNAP* grow slower, resulting in slower T7 RNAP* dilution. Therefore, T7 RNAP* is effectively regulated by two positive feedback loops, which can be described by an ordinary differential equation (see Supplementary Methods).

Figure 3. Interplay between growth modulation and the positive feedback loop can lead to bistability.

(a) T7 RNAP* (X) expression reduces the growth rate, which reduces dilution rate of T7 RNAP*. The two steps of negative regulation (red lines) form a positive feedback loop. Furthermore, T7 RNAP* activates its own expression (blue line). T7 RNAP* is thus regulated by two positive feedback loops.

Phase planes of the basic circuit model (Eq. 2) (b) without (γ=0) and (c) with growth retardation (γ=10). Filled circles indicate stable steady states and open circles indicate unstable steady states. The nullclines were calculated by using δ=0.01, α=10, and ϕ=20. See Supplementary Methods for detailed model derivation (Eqs. S3–S11).

$$\frac{d[X]}{dt}=\frac{k_0+V_m[X]}{K_d+[X]}-\frac{{\mu }_{max}[X]}{1+\theta [X]}-d_{x0}[X]$$ [1]

where X represents T7 RNAP* (nM), k₀ (nM²/hr) accounts for the leaky expression of T7 RNAP*, V_m (nM/hr) accounts for the induced synthesis of T7 RNAP*, K_d (nM) is the dissociation constant of the T7 RNAP*-P_T7Lac complex, μ_max is the maximum growth rate, θ is the metabolic burden due to T7 RNAP* expression, and d_x0 is the T7 RNAP* natural decay rate constant (1/hr).

Eq. 1 can be non-dimensionalized to yield the following equation (see Supplementary Methods).

$$\frac{dx}{d\tau }=\frac{\delta +\alpha x}{1+x}-\frac{\varphi x}{1+\gamma x}-x$$ [2]

where x is the [T7 RNAP*]; δ is the basal expression level of T7 RNAP*; α is the effective synthesis rate constant of T7 RNAP*; ϕ is the maximum growth rate; and γ is the metabolic burden due to expression of T7 RNAP*. Each dimensionless parameter lumps the effects of multiple processes.

The first term on the right hand side (RHS) models the positive feedback loop (Eq. 2). The second RHS term represents the T7 RNAP* dilution due to bacterial growth. If γ=0, bacteria always divide at ϕ. If γ > 0, expression of T7 RNAP* reduces the effective growth rate. The last RHS term represents intracellular decay of T7 RNAP*. Here, we assume that the impact of metabolic burden on growth has no cooperativity. This assumption is consistent with our experimental observations (Fig. 2) and existing literature ^38,42. If growth inhibition due to a protein is nonlinear, even constitutive expression of the protein can lead to bistability.

Figs. 3b and 3c show nullclines of Eq. 2. The synthesis nullcline (solid line) represents the first RHS term of Eq. 2. The decay nullcline (dotted line) represents the second and the third RHS terms. Without growth retardation (γ = 0), the nullclines intersect at a globally stable fixed point (Fig. 3b). With growth retardation (γ > 0), the decay nullcline becomes nonlinear and may intersect the synthesis nullcline at three fixed points, with two being stable and the other unstable (Fig. 3c). Although the T7 RNAP* positive feedback loop is noncooperative, its coupling with growth retardation can thus induce bistability. We note that both the positive feedback loop and the growth retardation are critical for generating bistability. Without the positive feedback loop, the circuit was monostable as long as the growth rates decreased monotonically with increasing [T7 RNAP] (Fig. S8).

Modeling-guided modulation of circuit dynamics

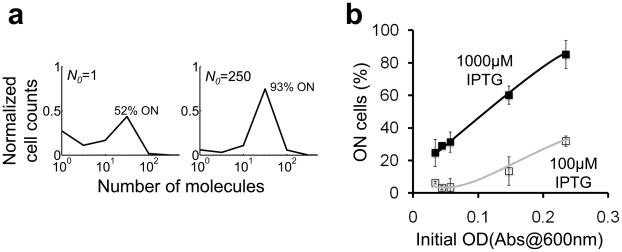
The coupling between the T7 RNAP* positive feedback loop and growth retardation would profoundly affect transient circuit dynamics as cultures shift from exponential growth phase to stationary phase. The stochastic, single cell dynamics can be modeled by accounting for bacterial growth using a logistic equation (Supplementary Methods; Table S1 & Eq. S15). The model predicts that as a culture shifts into stationary phase (as culture density approaches the carrying capacity), the percentage of ON bacteria would increase with the initial number of cells at which the circuit is induced (Fig. 4a). The model prediction was confirmed by our experiments carried out at two IPTG induction levels. At each induction level, the percentage of ON cells increased with initial optical density (OD). The percentage of ON cells at 100μM IPTG (Fig. 4b, open squares & grey line) increased more slowly with increasing initial OD than that at 1000μM IPTG (Fig. 4b, filled squares & black line). At 100μM IPTG, increasing initial OD from 0.03 to 0.23 increased the percentage of ON cells from 0% to approximately 30% (Fig. S9a). At 1000μM IPTG, increasing initial OD increased the percentage of ON cells from 30% to 90% (Fig. S9b).

Figure 4. Modulation of circuit dynamics by initial culture density.

(a) Stochastic simulations show that the percentage of ON cells would increase with increasing N₀ (the initial number of cells per population). See Supplementary Methods for modeling details (Table S1 & Eq. S15).

(b) Experimental validation of (a): the percentage of ON cells increased with OD and [IPTG] (see Fig. S9 for the corresponding CFP distributions). The lines are drawn as a guide for the eyes. Each error bar indicates the standard deviation of four replicates collected from two independent experiments.

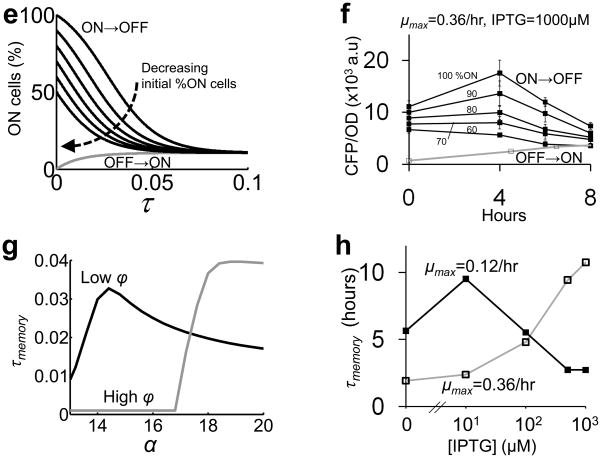
In addition, our model suggests a way to modulate circuit dynamics by growth rates and induction conditions. To this end, we performed bifurcation analysis of Eq. 2 in terms of two experimentally controllable parameters α and ϕ (Fig. 5a), where α, the T7 RNAP* synthesis rate constant, increases with [IPTG] and ϕ increases with the maximum growth rate (μ_max). Our model predicts that increasing α and decreasing ϕ would shift a population from a monomodal OFF state, across a bistable state, to a monomodal ON state (Fig. 5a).

Figure 5. Modulation of circuit dynamics.

(a) A bifurcation diagram obtained by solving Eq. 2 (δ=0.01; γ=10) analytically with standard methods ⁵⁰.

(b) Modeling stochastic switching between the OFF and ON cells and their differential growth. See Supplementary Methods for detailed model description (Eqs. S12–S14).

(c) The simulated time series of ON cells percentage in an OFF → ON culture (grey line) and an ON → OFF culture (black line) (α=19 and ϕ=100). The difference between the two (black dotted line) was fitted to a₀exp(−τ/τ_memory) to obtain τ_memory.

(d) The CFP level of ON → OFF cell cultures (black lines, filled squares) eventually converged to that of the OFF → ON cultures (grey lines, open squares) at the twelfth hour.

(e) Simulations predict that decreasing initial percentage of ON cells reduced memory.

(f) ON → OFF cultures (black lines, filled squares) were prepared by mixing varying ratios of ON cultures and OFF cultures (as indicated). Consistent with the model predictions (e), the CFP levels of ON → OFF cultures converged faster to that of the OFF → ON culture (grey line, open squares) with decreasing initial ON culture percentage. Each error bar indicates the standard deviation of three replicates.

(g) The maximal τ_memory is predicted to occur at low α for a low ϕ (=60) and at high α for a high ϕ ( = 90).

(h) Experimental validation of (g). The τ_memory was calculated by using average time series of at least four replicates (Fig. S11).

However, this prediction only applies to the dynamics of an “average” cell. In a population, the circuit dynamics are further modulated by the different growth rates of OFF and ON cells and stochastic switching between the two states. This aspect can be accounted for by using a simplified population model (Fig. 5b; Eqs. S12–S14). The transition rates between the ON and OFF states are proportional to exp(−ΔU) ²⁹, where the energy barrier ΔU (Fig. 5b) can be calculated from Eq. 2 (Supplementary Methods; Eq. S14). This model indicates that a culture with ON history and one with OFF history would eventually approach the same steady-state distribution, primarily due to faster OFF cell growth (Fig. 5c).

We next measured circuit dynamics by modulating both μ_max and [IPTG]. A low μ_max (0.12/hr) was achieved by using minimal M9 media supplemented with 0.1% succinate (Fig. S10a); a high μ_max (0.36/hr) was achieved by using minimal M9 media supplemented with 0.4% glucose and 0.1% casamino acids (Fig. S10b). We inoculated fresh media containing varying [IPTG] with cells with either ON or OFF history by diluting overnight cultures 100-fold (see Materials and Methods). Next, the cultures were incubated for eight hours in the high μ_max media and 12 hours in the low μ_max media. In each culture, we measured CFP at the population level to estimate the ON cell percentage.

Consistent with the model predictions (Fig. 5c), we observed transient hysteresis at the population level (Fig. S11). This aspect was more evident in a periodic-dilution experiment at a longer time scale (Fig. 5d). Here, ON → OFF cell cultures (Fig. 5d, black lines, filled squares) were diluted periodically at eight hour intervals into fresh M9 media supplemented with 0.4% glucose, 0.1% casamino acid, and 1mM IPTG. The CFP level of ON → OFF cell cultures eventually converged to that of the OFF → ON cultures (Fig. 5d, grey lines, open squares) at the twelfth hour. This convergence was unlikely due to mutants because the OFF cells were functional (Figs. 1d & S4).

The variability among replicate cultures for each condition (Fig. S11), particularly in the ON → OFF cultures (filled squares), was likely due to the variation in the initial percentage of ON cells in these cultures, which were derived from different clones. Indeed, both modeling and experimental results showed that the temporal circuit dynamics were sensitive to the initial percentage of ON cells (Fig. 5e & f). On the other hand, the hysteresis observed at the single cell level was less variable due to the homogeneous ON state of the seeding cells (Fig. S5c).

To quantify hysteresis, we use the difference in the percentage of ON cells between an OFF→ON culture and an ON→OFF culture, which can be approximated by an exponential function (Fig. 5c). We then define the memory (τ_memory) as the relaxation time of this function. Fig. 5g shows τ_memory at varying α for a low ϕ and a high ϕ. According to this result, the maximal τ_memory occurs at low [IPTG] for a slow maximum growth rate, and shifts to high [IPTG] for a fast maximum growth rate. The maximal τ_memory would also occur in the bistable region (Fig. 5a). This makes intuitive sense because in the bistable region, the energy barrier between the two states would decrease the stochastic switching between the two states (Fig. 5b), hence τ_memory increases. In monostable regions, a cell would switch to the only stable state without inhibition by the energy barrier, hence τ_memory decreases. Despite the observed variability (Fig. S11), the dependence of τ_memory on the growth rates and the induction levels agreed well with the model predictions (Fig. 5g). At μ_max = 0.1/hr, the τ_memory peaked at 10μM [IPTG] (Fig. 5h). In contrast, the maximal τ_memory was shifted to higher [IPTG] at μ_max = 0.36/hr (Fig. 5h).

In our analysis, we have focused on using a parsimonious model (Eq. 2) to capture the dominant circuit dynamics. We have thus omitted the potential impact of the growth rate on model parameters other than the protein dilution rate, such as synthesis rates of RNA and proteins ^43,44. Despite these simplifications, predictions from both our base model and the more complex models derived from it were validated by experiments. Furthermore, we note that these simplifications are well justified. First, the transcription in our system is regulated by T7 RNAP* and is decoupled from transcription by the host RNAP. Second, evidence suggests that the translation rate is not strongly affected by the growth rate. For instance, a previous study showed that the translation rate of LacZ mRNA does not change significantly with growth rates ⁴⁵. Finally, unless there is very strong coupling between the growth rate and the protein synthesis rate, our conclusions still hold. To illustrate this point, we extend the base model (Fig. 3a and Eq. 2) by considering the reduction of protein synthesis rate due to growth retardation (Fig. S12a). As shown by the phase diagrams, as long as the negative impact on the protein synthesis rate is relatively small, the circuit can still exhibit bistability (Figs. S12b&c).

Discussion

In summary, we have shown that unintended interactions between a simple circuit and its host can lead to complex, yet predictable behavior. Our results establish a hereto-unknown mechanism by which bistability arises from the interplay between a noncooperative positive feedback circuit and circuit-induced growth retardation. This mechanism is fundamentally distinct from generation of bistability by intrinsically nonlinear positive feedback regulation, such as protein dimerization ^8–10,17,27 and cooperative formation of heterodimers ⁴⁶. On one hand, growth retardation can act synergistically with the intrinsic nonlinearity in positive feedback loops: it can increase bistable region of a switch that consists of a cooperative positive feedback loop. On the other hand, growth retardation can impact hysteresis at the population level (Figs. 5b–h). It would be interesting to explore whether such a mechanism contributed to the bistability of natural or synthetic switches previously characterized ^8,28,29. This unique mechanism to generate bistability may also be important for dynamics of natural circuits whose activation involves a growth modulating positive feedback loop. For instance, CadC is a transcriptional factor that regulates weak organic acid resistance in E. coli. It forms a positive feedback loop by activating its own transcription. Upon activation, it activates a downstream gene (cadA) that inhibits cell growth by an unknown mechanism ⁴⁷. Similarly, CsgD is a positively autoregulated transcription activator in E. coli. Its activation induces formation of biofilms, where bacteria grow slower than in a planktonic state ⁴⁸. Both examples share the same architecture as our circuit (Fig. 3a); as such, growth modulation may facilitate the generation of bistability in each case.

Materials and methods

Plasmids construction

The pCFP plasmid (ColE1 origin, ampicilin resistant, Fig. S1b) was constructed by inserting a polymerase chain reaction (PCR)-amplified CFP from a pZE12CFPLite plasmid (from Michael Elowitz) into a pET15b vector (Clontech), downstream of a P_T7lac promoter. Without T7 RNAP, pCFP did not express any CFP when induced with 1000μM IPTG (Fig. S1c). The pCFPT7 plasmid (ColE1 origin, ampicilin resistant) was constructed by inserting a PCR-amplified T7 RNA Polymerase (T7 RNAP) from a pAR1219 plasmid (from Yohei Yokobayashi) into the pCFP plasmid, downstream of the CFP gene (Fig. S1a). Here, we used a mutant T7 RNAP* gene that has a single base pair deletion at the 186^th bp. The mutant gene is translated into functional T7 RNAP* (Supplementary Results).

Strains, growth conditions, and media

Unless otherwise noted, MC4100z1 cells (from Michael Elowitz) were used throughout this study. The MC4100Z1 strain was constructed by inserting a cassette containing lacIq, tetR, and spect(R) genes into the chromosome of the MC4100 strain (genotype: araD139 (argF-lac)205 flb-5301 pstF25 rpsL150 deoC1 relA1). For each cell strain, a single frozen stock was used throughout the experiment. We plated the frozen stock on LB agar plates (supplemented with appropriate antibiotics) and then randomly picked cell colonies for experiments. LB media were used to prepare overnight cultures. Unless otherwise noted, minimal media M9, supplemented with 0.4% glucose and 0.1% Casamino acids was used for cell growth. Overnight cultures were spun down and washed with sterile water before diluting them into fresh media. The pCFP and pCFPT7 plasmids were maintained by using 75μg/ml of carbenicilin. All liquid cultures were grown in 15ml culture tubes at 37°C and 250 rotations per minute.

Fluorescence microscopy

10ml of 1.5% M9 melted agar (supplemented with 75μg/ml carbenicilin) was poured into a custom agar plate. Immediately after the agar solidified, 1μl cell culture was pipetted onto the agar and covered with a glass cover slip. Images were taken using a Leica DMI6000B fluorescence microscope (Leica, Bannockburn, IL) with a mercury excitation lamp. CFP was taken using a 436±10nm excitation filter and a 480 ± 20nm emission filter. YFP was taken using a 500±10nm excitation filter and a 535±15nm emission filter. Phase and fluorescent images were collected by using a 100X oil-immersion lens. For each image, phase intensities were recorded in a red channel and fluorescent intensities were recorded in a green channel. Microscope chamber was maintained at 37°C. When measuring CFP distribution (Figs. 1, 4, S1, S3, S4, S6, S8, and S9), at least 10 images were taken for each sample to obtain representative statistics. Original images were analyzed directly using the CellC program to obtain the area and the CFP intensity of each cell ⁴⁹. The CFP intensity was normalized by the corresponding cell area.

Flow cytometry

For experiments in Figs. 1d and S4, 3μl uninduced overnight culture was diluted into 3ml fresh M9 medium and induced with 1000μM IPTG for 12 hours. Each resulting culture was diluted 10-fold into phosphate-buffered saline (137mM NaCl, 2.7mM KCL, 10mM Na₂HPO₄, 2mM KH₂PO₄), and sorted into fresh M9 media according to CFP expression by using a FACStar Plus (Becton Dickinson, San Jose, CA) flow cytometer with a 457nm argon excitation laser and a 485 ± 22nm CFP emission filter. At least 100,000 cells were obtained for each subpopulation (Figs. 1d & S4). After sorting, cells in each subpopulation were spun down and resuspended in 3ml fresh M9 medium. The resulting cultures were incubated until their OD reached ~0.1, before being induced with 1000μM IPTG and incubated for additional eight hours.

Hysteresis experiments at the single-cell level

For experiments in Figs. 1e and S5, 300μl uninduced overnight culture was diluted into 3ml fresh M9 medium and induced with 1000μM IPTG for at least one hour. Next, samples were prepared following methods described in the section “Fluorescence Microscopy”. M9 agar was supplemented with 1000μM IPTG and 75μg/ml of carbenicilin. We tracked at least 20 frames in each experiment. Microscope images were recorded for each cell lineage at one hour interval for at least three hours (Figs. 1e & S5). Beyond three hours, some frames were saturated with overlapping cells, thus making it impossible to analyze the images (results not shown). We classified each lineage based on the CFP intensity of its seeding cell: OFF state (CFP ≤ 85); INT (85 < CFP ≤ 170); and ON state (170 < CFP ≤ 255). Note that 255 is the saturating level.

Hysteresis experiments at the population level

For OFF → ON experiments (Fig. S11), 30μl uninduced overnight culture was diluted into 3ml fresh media and induced with varying [IPTG]. For ON → OFF experiments (Fig. S11), 400μl uninduced overnight culture was first diluted into 1.6ml fresh M9 medium supplemented with 0.4% glucose (or 0.1% succinate), 0.1% Casamino acids, and 1000μM [IPTG] and incubated for at least eight hours. The resulting cultures were spun down and washed twice with fresh media, and then diluted 100-fold into 3ml fresh media containing varying [IPTG]. For each sample, both optical density (OD) and fluorescence were measured by using 200μl culture in a 96-well plate with a Victor (PerkinElmer, Shelton, CT) plate reader. OD was measured by using absorbance at 600nm. CFP was measured by using a 450nm excitation filter and a 500nm emission filter. YFP was measured by using a 490nm excitation filter and a 535nm emission filter.

Statistical analysis

All statistical analysis was performed using standard Matlab functions. A one-way analysis of variance was performed by using the function ‘anova1’ and a multiple comparison test was performed using the function ‘multcompare’.