Phage Mu transposition immunity: protein pattern formation along DNA by a diffusion-ratchet mechanism

Summary

DNA transposons integrate into host chromosomes with limited target sequence-specificity. Without mechanisms to avoid insertion into themselves, transposons risk self-destruction. Phage Mu avoids this problem by transposition immunity, involving MuA-transposase and MuB ATP-dependent DNA-binding protein. MuB-bound DNA acts as an efficient transposition target, but MuA clusters bound to Mu DNA ends activate the MuB-ATPase and dissociate MuB from their neighborhood before target site commitment, making the regions near Mu ends a poor target. This MuA-cluster-MuB interaction requires formation of DNA loops between the MuA- and the MuB-bound DNA sites. At early times, MuB clusters are disassembled via loops with smaller average size and at later times, MuA clusters find distantly located MuB clusters by forming loops with larger average sizes. We demonstrate that iterative loop formation/disruption cycles with intervening diffusional steps result in larger DNA-loops, leading to preferential insertion of the transposon at sites distant from the transposon ends.

Introduction

Transposons are mobile genetic elements that translocate from one site within a genome to another. Most of these elements exhibit practically no target sequence specificity, although some elements display specific site targeting capabilities. Bacteriophage Mu is one of the transposon family members whose transposition mechanism is well studied. Assembly of highly specific protein-DNA complexes is required before the DNA cleavages and joining steps of transposition (Mizuuchi et al., 1992). Only two Mu encoded proteins, MuA and MuB are required for these reaction steps (Mizuuchi, 1992).

First, the MuA transposase binds to three sites at each end of the Mu genome and then bridges two ends together to form the Stable Synaptic Complex (SSC). In this complex, two Mu DNA ends are synapsed by a stably bound MuA tetramer. MuA introduces a single-strand nick at each 3′-end of Mu genome, forming the Cleaved Donor Complex (CDC). The exposed 3′-hydroxyl groups act as nucleophiles for strand transfer to insert the Mu DNA to a new target DNA site, resulting in the formation of the Strand Transfer Complex (STC) (Mizuuchi, 1992). The very stable transposase-transposon end complexes, such as the SSC, CDC, and STC are collectively called transpososomes, and the general architecture of the complex is thought to be conserved through the reaction steps. How the CDC chooses a new target DNA site has been a puzzle in the case of some transposons. In the absence of a target site selection mechanism, DNA sites proximal to the donor transposon ends would have a high probability of becoming the new target sites, risking self-destructive autointegration into its own genome. Physiologically, this may not be a problem for simple parasitic transposons, but transposing phages such as Mu, which replicate their genome via multiple rounds of transposition, must minimize the risk of auto-integration or transposition into another copy of Mu genome during the replication cycle. MuB protein plays a central role in the target site selection for Mu transposition (Adzuma and Mizuuchi, 1988).

MuB is an ATP-dependent DNA binding protein, which in the presence of ATP, assembles into oligomeric clusters on DNA with limited sequence specificity, making nearby DNA sites an efficient transposition target by activating the CDC for strand transfer (Baker et al., 1991; Surette and Chaconas, 1991). On the other hand, MuA stimulates the ATPase activity of MuB, resulting in dissociation of MuB from DNA (Adzuma and Mizuuchi, 1988; Maxwell et al., 1987). Therefore, MuB accumulates on DNA sites distal to bound MuA at the Mu ends, resulting in a strong preference for transposition to occur at DNA sites at least several kbp away from MuA-bound ends (Adzuma and Mizuuchi, 1988, 1989). This phenomenon is called target immunity and is thought to prevent destruction of the Mu genome by autointegration. One Mu end sequence with three MuA binding sites efficiently protects nearby DNA sites (immune target) from Mu insertion in the presence of MuA, and so do the MuA tetramers assembled in the form of transpososomes (Adzuma and Mizuuchi, 1988; Greene and Mizuuchi, 2002c). Thus, a cluster of multiple MuA molecules bound on DNA confers immunity to nearby DNA sites irrespective of the specific arrangement of the complex. While an immune target is disfavored as a transposition target, discrimination between immune and non-immune targets (distant DNA sites from Mu end sequences) diminishes at higher than optimal concentrations of MuB, and saturation of the target DNA by MuB strongly inhibits transposition (Y. Wang, M. Mizuuchi and K. Mizuuchi, unpublished observation). Under physiological in vivo conditions for Mu growth, only a small percentage of the DNA length is expected to be covered by MuB. There are two outcomes of the MuA-MuB interaction in the course of Mu transposition; MuA mediated MuB dissociation from DNA by the ATPase activation during target immunity establishment, and MuB activation of the transpososome for target DNA insertion. It has been puzzling how these two contrasting processes are balanced to avoid autointegration, yet at the same time allow efficient integration into appropriate targets. We discuss how appropriate temporal orchestration of these processes can assure a physiologically sensible outcome.

We have studied the dynamics of MuB-DNA interaction under a variety of conditions by making use of fluorescently labeled MuB and total internal reflection fluorescence (TIRF) microscopy (Greene and Mizuuchi, 2002c, 2004). In these studies we monitored the association and dissociation of enhanced green fluorescent protein-MuB fusion (EGFP-MuB) with single DNA molecules immobilized onto a slide glass surface. These previous studies showed that at MuB concentrations that result in 5 to 10 % of DNA being covered by MuB, MuB assembles on DNA starting from smaller oligomers into clusters consisting of up to roughly 100 or so monomers. Efficient MuB disassembly by the tetrameric form of MuA assembled as transpososomes occurs when DNA is allowed to engage in free Brownian motion for several minutes in the absence of the buffer flow. When the buffer flow was resumed to restretch the DNA, we observed that concomitant with the decrease of DNA-bound MuB, large DNA loops had formed in the absence of buffer flow. These DNA loops, with an average size of 6 to 7 kbp, lasted many seconds after the restart of buffer flow. Loop formation and efficient MuB disassembly depended on the target DNA binding ability of the transpososome and the presence of the MuB-interacting domain on the MuA molecules in the transpososome. We concluded that the observed DNA loops were held through interactions between the transpososome and MuB, both bound to the same DNA at different locations. We also concluded that the relative stability of the loops and the efficiency of MuB disassembly were based on the stability of the interaction between multiple MuA molecules and the MuB cluster.

The observed average loop size appeared sufficiently large to explain the distance of influence of the Mu target immunity of more than several kbp, but it was much larger than expected from the random DNA looping based on the DNA chain dynamics (Ringrose et al., 1999; Shore et al., 1981). Thus, the following puzzling questions remained. Do large loops form from the beginning, although it is unclear how relatively low occupancy of the DNA by MuB could dramatically influence the DNA chain dynamics? Alternatively, are initial loop sizes smaller and then expand continually by a long-range processive mechanism? Or, do individual loop sizes expand discontinuously in a stepwise fashion, and if so, how is this accomplished? In the previous study, the MuA clusters were not fluorescently labeled and also were not covalently anchored to defined sites along the DNA. Therefore, it was not possible to monitor the time-dependent evolution of DNA looping dynamics around the location of individual MuA clusters to investigate how the relatively large average loop size of 6-7 kbp was attained during the reaction.

In this study, we constructed a fluorescently labeled truncated form of transpososomes and allowed them to covalently insert into λ DNA as a stable form of MuA cluster for monitoring their interaction dynamics with MuB clusters bound to the same DNA (Fig. 1). In other words, the transpososome (STC), which cannot interact with a new target site, was used as a reagent to represent not only the entity that protects the Mu genome at the stage of the STC from secondary Mu insertion, but also to represent other forms of the Mu end-bound MuA clusters that occur during the course of Mu transposition. Therefore, we call this truncated form of STC a “MuA cluster” in this report. Using TIRF microscopy, we then visualized the dynamic behavior of MuB-DNA complexes flanking this form of the DNA-bound MuA cluster. We followed the population-averaged changes in the DNA loop size distribution as a function of the time during which the DNA was allowed to undergo free Brownian motion. The average DNA loop size grew larger as the duration of the free Brownian motion for loop formation was extended. However, there was no indication of continuous loop size expansion, and iterative cycles of loop formation and disruption appeared to be involved in the process. Based on these results, we propose a diffusion-ratchet mechanism, which could be considered a subclass of reaction-diffusion type mechanisms, for transposition target immunity. We also discuss the mechanistic relationship between this reaction and chromosome partitioning in bacteria, and propose a functional history of transposition target immunity among different transposons.

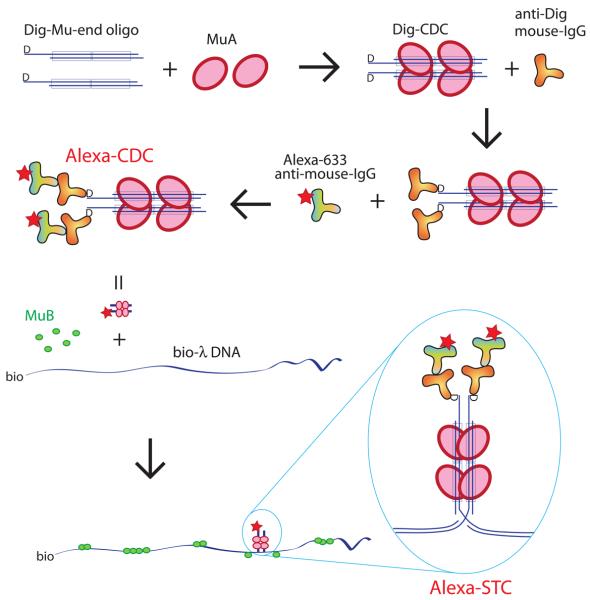
Figure 1.

Assembly of the λ DNA substrate with fluorescently labeled MuA cluster (STC). DIG-labeled Mu-end DNA fragments were assembled with MuA to generate DIG-labeled CDCs, which were sequentially decorated by anti-DIG mouse IgG and Alexa-633-anti-mouse IgG to form Alexa-lebeled CDCs. Labeled CDCs were inserted into biotin-tagged λ DNA to form the substrate DNA containing Alexa-STC. The DNA strands are disrupted at the site of insertion, but they are held together by the stably bound MuA tetramer. See Experimental Procedures for details.

Results

Simultaneous Observation of MuB Clusters and MuA clusters

We constructed a system to simultaneously observe the dynamic behavior of MuA clusters at fixed locations along λ DNA and EGFP-MuB bound to the same DNA (Fig. 2A). Fluorescently labeled transpososomes used as a model reagent to represent Mu end-bound MuA clusters were constructed from DIG-modified Mu-end DNA fragments, anti-DIG mouse-antibody and Alexa-633 conjugated anti-mouse-IgG antibody (Fig. 1), and characterized as described in the Supplemental Data. The fluorescence-labeled CDCs were transposed into λ DNA biotinylated at the right end, and immobilized on the slide glass surface of the flow cell essentially as described for regular biotin-tagged λ DNA (Greene and Mizuuchi, 2002a), with modifications as described in the Experimental Procedures. After flushing out free MuA clusters and unattached DNA with washing buffer, we infused 25 nM EGFP-MuB in the presence of ATP to observe the locations of the MuA clusters and MuB distribution along the DNA simultaneously in two separate channels as shown in Fig. 2B and Movie S1. At this MuB concentration, roughly 5-10% of the DNA was covered with EGFP-MuB. The fluorescent signal for EGFP-MuB is shown in the top panel and that for the Alexa-633 marking the MuA cluster locations is shown in the bottom panel with the molecules stretched by the buffer flow. Fluorescent spots of Alexa-633 non-specifically attached on the slide glass surface that remained immobile irrespective of the buffer flow status were ignored. The typical average number of MuA clusters detected per λ DNA in the experiments was 3.4 and most of the λ DNA had a fluorescence-marked MuA cluster (Table S1).

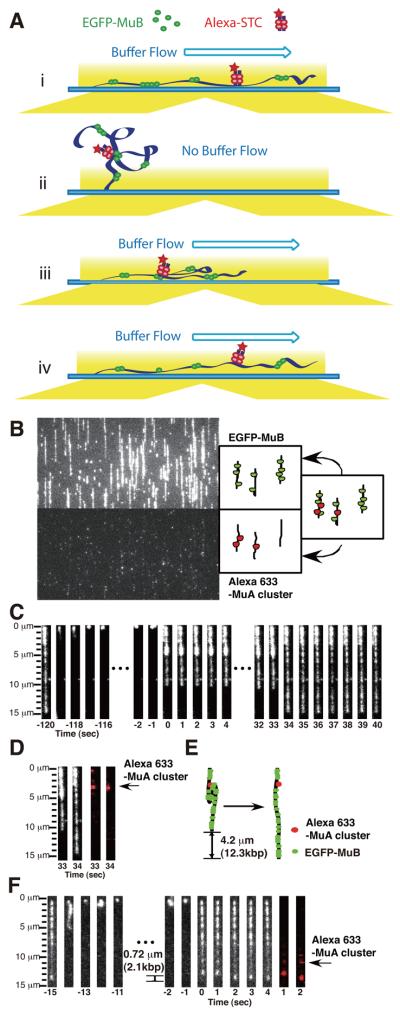
Figure 2.

Simultaneous observation of MuB-target DNA complexes and MuA clusters. (A) Schematic representation of the experimental steps. Bio-λ DNA with fluorescent marked MuA clusters (Alexa-STCs) was tethered to a flow cell. The buffer containing EGFP-MuB was infused. (i) With constant flow of the EGFP-MuB solution, stretched λ DNA containing MuA clusters accumulates a steady state level of MuB clusters without the influence of the MuA clusters through DNA looping. (ii) During the buffer flow interruption, free Brownian motion of the DNA allows looping interaction between MuA clusters and nearby MuB clusters. (iii) When the buffer flow is resumed, molecules engaged in looping interactions extend only partially. (iv) After a short period, the loop is disrupted and one-step extension to the original DNA length takes place. (B) A snap shot image shows the MuA cluster locations (bottom) and EGFP-MuB (top) during the initial buffer flow period. (C) Image sequences of DNA loop formation and disruption of EGFP-MuB target complexes. Buffer flow was interrupted for 2 min and restarted at time 0. The loop disruption took place between 33 and 34 sec. (D) Pair-wise images before (33 sec) and after (34 sec) loop disruption for the EGFP-MuB channel and Alexa-633 channel are shown with a schematic interpretation (E). (F) An example of loop disruption of EGFP-MuB target complexes and the positions of Alexa-Fluor-633 marked MuA clusters after 15 sec buffer flow interruption.

A MuA cluster is located at one end of a loop of MuB-bound DNA

As described previously (Greene and Mizuuchi, 2002c), to initiate DNA loop formation, buffer flow was interrupted, allowing free Brownian motion of the DNA (Fig. 2Aii). The entire length of DNA (monitored by the bound MuB clusters) except for the tethered end disappeared from the evanescent illumination field within one second. The buffer flow was then restarted to observe the result of the interactions that took place during the period of free Brownian motion (Fig. 2Aiii). Extension of the DNA molecules by the flow took about one second after the flow restart. As expected, some of the DNA returned to full-length immediately, but others only partially stretched initially and returned to the full-length a short period later, indicating that DNA loops were formed during the buffer flow interruption as reported previously (Movie S2). The length difference immediately before and after a loop disruption was taken as the DNA loop size. Individual loops extended in one step. Because of the small number of MuA clusters per λ DNA, most DNA molecules had one or no loop; only a small fraction of molecules had more than two loops. A few examples are shown in Figure 2 and Movies S3. After resuming buffer flow, the molecule in Fig. 2C-E extended to a length 4.2 μm shorter than the full-length and a dense cluster of EGFP-MuB was observed between 3.2 and 5.3 μm from the immobilized end of the molecule prior to loop disruption. The molecule returned to the original length at 34 sec after restart of buffer flow. The fluorescent signal of Alexa-633 marking the MuA cluster was observed at the top edge of the loop and it did not move when the loop was opened. Thus, this molecule had a MuA cluster located at 3.2 μm (~9.5 kbp) from the right end of the λ DNA, which was interacting with the MuB cluster located 4.2 μ (~12.5 kbp) downstream at the moment the buffer flow was resumed. In the case of the molecule in Fig. 2F, a shorter loop located closer to the unanchored end opened between 1 and 2 seconds after buffer flow restart.

About 25% of the fluorescently labeled MuA clusters were engaged in detectable DNA looping at the time of the buffer flow restart irrespective of the duration of the buffer flow interruption, which ranged from 15 sec to 120 sec (Table S2). In this study, 90% of DNA loops were formed between a single MuA cluster and a MuB cluster as shown in Figure 2C and 2F. For the remaining 10%, no fluorescence signal from the MuA cluster was detected at the ends of the DNA loop. This could be either because there was a MuA cluster involved, but it did not contain Alexa-633-IgG, or they were caused by interactions between MuB clusters at separate locations without involving a MuA cluster. We suspect the latter possibility; when higher concentrations of MuB than our standard conditions were used, or with a significantly longer duration of the flow interruption, looping of MuB-bound DNA in the absence of MuA clusters has been observed due to aggregation of DNA-bound MuB clusters. Therefore, loops without accompanying Alexa-633 signal were not considered for further analysis. No DNA loops were observed with Alexa-633 signal at both ends, arguing against the possibility of interaction between multiple MuA clusters.

Length of the DNA loop increases with the duration of free Brownian motion of the DNA

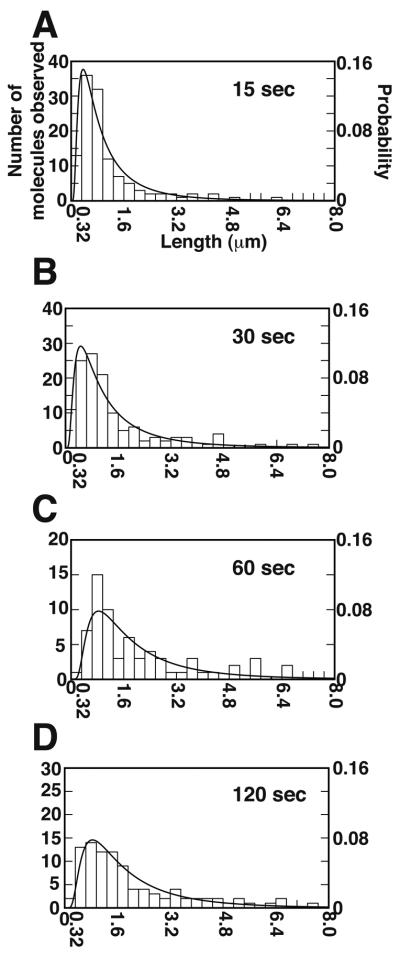
Next, we measured the size and lifetime of observable DNA loops after different durations of buffer flow interruption, with the caveat that loops much shorter than 1 kbp (~0.3 μm), or those which persist less than one second after the restart of buffer flow, would be difficult to detect with our current method. After 15 seconds of buffer flow interruption, two thirds of the observable loops were less than 0.8 μm (~2.4 kbp) and the average DNA loop size was 0.99 μm (~3 kbp) (Fig. 3A). After longer periods of Brownian motion, the MuA clusters start to interact more frequently with MuB clusters located at further distance. For example, 30 seconds after buffer flow interruption, the average DNA loop size grew to 1.43 μm (Fig. 3B). At 15 or 30 seconds of buffer flow interruption, about 10% of the observable loops were less than 0.32 μm. Over time, the size distribution of the observable loops broadened and the average size of the loops reached a near maximum of 2 μm (~6 kbp) after 60 seconds. After 60 and 120 seconds of buffer flow interruption, only about 2% of the observable loops were less than 0.32 μm (Fig. 3C and D). These observations clearly indicate that at earlier times during the free Brownian motion of the DNA, the MuA clusters form DNA loops by capturing the MuB clusters bound at a relatively close location along the DNA molecule.

Figure 3.

DNA loop size distributions after different flow interruption durations. Panels A, B, C and D show the results with the buffer flow interruption times of 15, 30, 60 and 120 second, respectively. All data are fitted to an inverse Gaussian distribution with the fitting parameters as described in Table S3.

Typical loops lasted 5 sec or less after the buffer flow was resumed while some loops lasted 1 min or longer (Fig. S2). After 15 sec of free Brownian motion, loops with shorter lifetimes were dominant, but with extended periods of flow interruption, proportion of loops with longer lifetime increased.

To confirm that the DNA looping dynamics observed above using EGFP-MuB are not dramatically different from that with wt-MuB, we repeated the experiments using a mixture of 22.5 nM wt-MuB and 2.5 nM EGFP-MuB. The results were essentially similar, except that the average loop lifetime was slightly longer (Figure S3).

Removal of MuB from regions around MuA clusters

A defining feature of the target immunity mechanism is that the MuA-MuB interaction should result in local dissociation of MuB from DNA. Therefore, we measured the intensity change of the EGFP-MuB signal around MuA clusters after flow interruption. First, the EGFP signal was measured for 1.6 μm (5 kbp) regions centered around individual MuA clusters after 30 min of steady flow of the buffer containing EGFP-MuB. After a period of flow interruption during which samples were not illuminated, the buffer flow and data collection were resumed and most of the loop disruption took place after 2 min. At the end of this period, the EGFP signal of the corresponding 1.6 μm regions was measured. The distribution of the ratios of the EGFP signal after and before the free Brownian motion around individual MuA clusters is shown in Figure 4A. These data represent both molecules for which loop formation was detected and those that did not exhibit looping at the time of flow restart. The distributions of the EGFP-MuB signal ratio for those two categories of molecules were not noticeably different (data not shown).

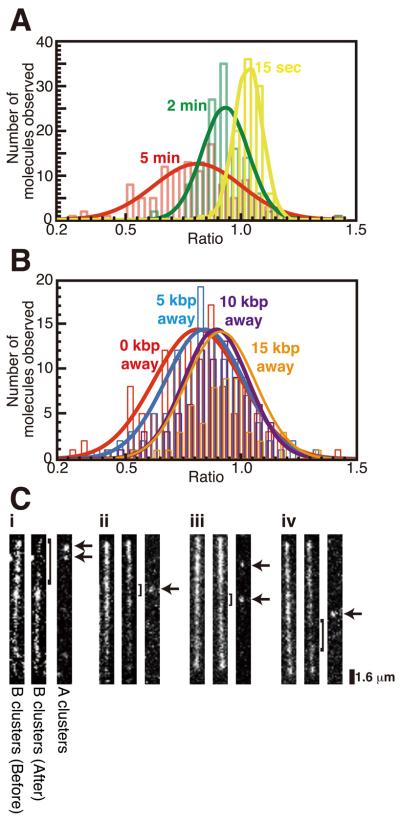
Figure 4.

EGFP-MuB dissociation from the target complex. (A) EGFP signal intensities of 5 kbp (1.6 μm) segments surrounding the locations of MuA clusters were measured before and after buffer flow interruption and the intensity ratio (After/Before) was calculated for each MuA cluster. Distributions of the ratio after buffer flow interruption of 15 sec (yellow), 2 min (green) and 5 min (red) are shown with a Gaussian fit. (B) The intensity ratio distribution was also measured for locations at 5 (blue), 10 (purple) or 15 (orange) kbp away from MuA clusters (center distance of 5 kbp windows) after 5 min buffer flow interruption and compared to the 5 min data in (A) (red). Gaussian fitted curves were normalized relative to the peak value. (C) Representative fluorescence image pairs of individual EGFP-MuB target complexes before (left) and after (center) buffer flow interruption and Alexa-633 marked MuA clusters (right). Arrows indicate the positions of the MuA clusters involved. Brackets indicate the region where EGFP-MuBs were dissociated during buffer flow interruption.

After 15 sec interruption of the buffer flow, no significant changes of the bound EGFP-MuB in the 5 kbp window at individual MuA clusters were detected as judged by the distribution of the after/before ratio of 1.03 ± 0.06 (mean ± σ). This 6% spread of the distribution reflects both the intrinsic fluctuation of MuB clusters that takes place between the two measurement times and the quantitation error. After 2 min of flow interruption, an average 7% EGFP-MuB depletion was observed within the 5 kbp window (after/before ratio; 0.93 ± 0.10). After 5 min of flow interruption, about 19% reduction of the EGFP-MuB concentration was detected (after/before ratio; 0.81 ± 0.19). With an extended period of flow interruption, the distribution of after/before EGFP signal ratio significantly broadened, and there remained a substantial fraction of MuA clusters for which the MuB concentration near the MuA cluster did not change significantly. Several examples of significant EGFP-MuB signal reduction around a MuA cluster are shown in Figure 4C. The extent of local MuB concentration reduction represented by the mean value of the after/before ratio distribution at sites away from MuA clusters after 5 min of free Brownian motion decreased with the distance from a MuA cluster, but only very gradually. At locations 5, 10, and 15 kbp away from MuA clusters, the mean fluorescence intensity ratio was 0.84, 0.89, and 0.91 compared to 0.81 for the area surrounding the MuA cluster (Fig. 4B).

We also noticed that some molecules displayed regions of significant EGFP-MuB signal reduction at some distance away from the positions of MuA clusters. While it is difficult to rule out possible involvement of MuA clusters that were not fluorescently-labeled, it is tempting to speculate that some MuA clusters captured a MuB cluster at some distance early during the free Brownian motion period and spent a substantial time disassembling the clusters near this site, instead of first disassembling MuB clusters closer along the DNA to the MuA cluster (see Fig. 2C and 4C-iv for possible examples). These observations, combined with the broad distribution of the MuB removal efficiency near individual MuA clusters, and the detectable but only weak dependence of the MuB removal efficiency on the distance to the MuA clusters highlight the highly stochastic nature of the process studied here. In other words, while in the population average, we expect MuB clusters proximal to MuA clusters to experience earlier removal than distal MuB clusters, in individual cases, the time sequence of MuB cluster removal may not necessarily be spatially ordered. On the other hand, observed depletion of very short loops (< 1 kbp) after longer durations of free Brownian motion (Fig. 3) suggests that MuB clusters very close to a MuA cluster are more efficiently depleted within a few minutes. However, direct confirmation of highly localized MuB depletion requires further technical improvements of the quantitation method.

How quickly does MuB bind DNA?

For the consideration of the mechanism of both loop-size expansion and MuB depletion from the neighborhood of a MuA cluster, knowledge of how MuB molecules reoccupy the region from which they have dissociated is critical. The MuB molecules that reoccupy the evacuated DNA region can come from two sources. One source is a fraction of the MuB molecules in the buffer that are ATP-bound and already in the DNA binding competent state. Previous study of MuB binding kinetics under similar conditions showed that it takes about 15 minutes or longer for the binding to reach an apparent steady state at 25 nM MuB (Greene and Mizuuchi, 2004). Another contributing source of MuB for reoccupation of the depleted DNA region are the newly dissociated molecules that join the pool in the solution. These molecules are already located very close to the original DNA site for rebinding, and therefore if there were no significant time delay for regaining the competence for DNA binding after their release, they would likely contribute to the rebinding to the DNA region from where they dissociate. Therefore, we were interested in finding out how quickly these molecules regain the ability to bind DNA. While we do not know in which nucleotide-state MuB is released, we could ask how long it would take, once MuB gets to the nucleotide-free state, for it to reacquire ATP, engage in necessary conformational changes, and bind DNA.

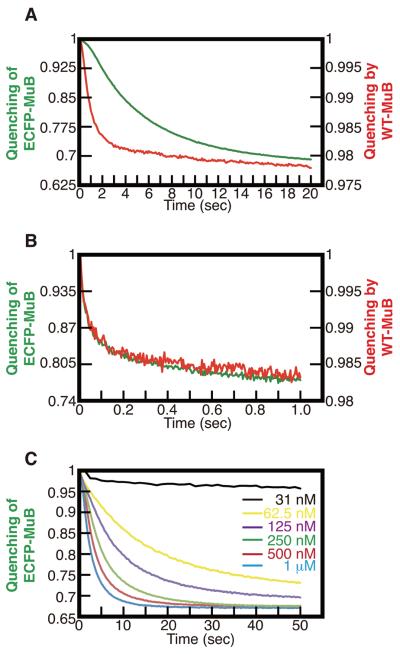
MuB-DNA binding kinetics were measured by stopped-flow experiments. We developed a fluorescence-based real-time nonspecific DNA-protein binding assay, using Alexa-514 labeled DNA and FRET measurement or fluorescence quenching measurements as described in Supplemental Experimental Procedures. ECFP-MuB DNA binding kinetics were measured as donor fluorescence emission decrease after rapid mixing of equal volumes of 20 μg/ml Alexa-514-DNA solution containing ATP, and 2 μM protein solution without ATP (Fig. 5A). The reaction time course showed sigmoidal kinetics indicating two distinct phases, a short lag-phase of 1-2 s followed by an accelerated reaction rate to reach near steady state DNA binding after 15 seconds. The half maximum binding point was around 4 seconds. Therefore, even at the relatively high concentration of 1 μM, it takes several seconds for MuB to gain DNA binding activity after ATP addition. When ECFP-MuB was preincubated with ATP first and then rapidly mixed with Alexa-514-DNA, no lag time was detected and the binding was mostly complete after 0.1 sec, indicating that the DNA-binding competent form of MuB was generated during the preincubation with ATP (Fig. 5B).

Figure 5.

MuB-DNA binding kinetics. (A) DNA binding was monitored after mixing ECFP-MuB or wild type MuB with Alexa-514 labeled dsDNA and ATP. Green and red lines indicate ECFP-MuB and wild type MuB, respectively. (B) DNA binding of the ATP pre-activated MuB was monitored by mixing ECFP-MuB or wild type MuB, preincubated with ATP for 10 min at 25 °C, with Alexa-514 labeled dsDNA. (C) The same experiment as in A was carried out at different concentrations of ECFP-MuB as indicated. Irrespective of the protein concentration, ECFP-MuB fluorescence quenching of about 1.5% was observed in several seconds following addition of ATP independent of DNA, as more clearly seen at a low protein concentration here. The final concentrations of reaction components in A and B were: 1 μM ECFP-MuB or wild type MuB, 10 ng/μl Alexa-514 labeled dsDNA and 2 mM ATP. All data are plotted as the ratio of fluorescent intensity at each time point to that at the first time point.

In a biochemical assay to detect transposition target immunity, EGFP-MuB exhibited the ability to support target immunity, but the efficiency of target immunity in the presence of EGFP-MuB was somewhat compromised compared to reactions in the presence of unmodified MuB (Greene and Mizuuchi, 2002b). Therefore, we also measured the DNA binding kinetics of the unmodified MuB. The fluorescence quenching of Alexa-514-DNA by MuB binding was used for this assay. The DNA binding kinetics of unmodified MuB after addition of ATP were qualitatively similar, but about 4 times faster compared to that of ECFP-MuB (Fig. 5A). However, after pre-incubation with ATP, the DNA binding kinetics of unmodified MuB were indistinguishable from that of ECFP-MuB (Fig. 5B).

Previous studies of the ATP-induced MuB oligomerization kinetics based on the FRET signal between ECFP-MuB and EYFP-MuB showed a similar initial lag phase and pre-incubating MuB with ATP eliminated the lag (Greene and Mizuuchi, 2002b). Thus, we propose that the DNA binding time delay is caused by the prerequisite MuB oligomerization step. As expected from this proposal, the delay time for reacquisition of DNA binding ability is longer at lower MuB concentrations (Fig. 5C). The DNA binding delay time would allow sufficient MuB diffusion away from the site of DNA dissociation. Thus, the localized rebinding of the dissociated MuB molecules to DNA sites from where they dissociate would have little impact on the local depletion of the DNA-bound MuB by MuA clusters.

Discussion

Phage Mu transposition target immunity depends on the interaction dynamics among MuA transposase, MuB ATPase and DNA molecules. MuA not only first has to assemble into a transpososome with the Mu end DNA segments, but it also must be activated by MuB in order to efficiently carry out the strand transfer reaction to insert the Mu DNA into chromosomal DNA to initiate DNA replication. MuB is an ATP-dependent non-specific DNA binding protein that on its own binds essentially at any DNA site (Greene and Mizuuchi, 2002a; Maxwell et al., 1987). MuA activates MuB ATPase, causing it to dissociate from DNA. For this MuA-MuB interaction to remove MuB from the neighborhood of Mu ends where MuA is bound, DNA looping between the sites of binding of the two proteins must be involved (Adzuma and Mizuuchi, 1989; Greene and Mizuuchi, 2002c). However, a naïve model of looping-mediated removal of MuB from the MuA-bound Mu end neighborhood may predict that the reach of target immunity is limited by the distance of the equilibrium DNA looping size distribution that is governed by the physical properties of DNA. However, the range of transposition target immunity of more than several kbp (Adzuma and Mizuuchi, 1988; Resibois et al., 1984) extends further than this prediction. How does the involvement of ATP hydrolysis by MuB help the establishment of the MuB distribution pattern along DNA with a depleted area around Mu ends beyond the expected most frequent DNA looping distance, while resisting the neutralizing effect of rebinding of the dissociated protein to the depleted area?

One possibility might be that the mechanical properties of DNA, even with relatively low MuB binding density at which the physiological reaction takes place, differ from naked DNA, favoring larger than expected loop sizes. The results reported here do not support this possibility; a relatively small average loop size was observed earlier during the free Brownian motion period. The longer the duration of free Brownian motion of the DNA, the larger the average DNA loop size became. After 15 seconds of buffer flow interruption, the average loop size was about 3 kbp, which was already larger than the predicted distance of less than 1 kbp based on the inter-segmental collision probability distribution of DNA by itself (Ringrose et al., 1999; Shore et al., 1981). The average size of the DNA loops reached near the maximum, about 6 kbp, in roughly 60 seconds, although it appeared to take longer for the MuB distribution pattern to reach a steady state. How does the loop size get larger with the extended time for free Brownian motion of the DNA?

Another possibility is the continuous growth of the loop size without loop disruption. We believe this is not the case for the following reasons. Firstly, after the restart of the buffer flow, we never observed any detectable change of individual loop size before loop disruption even with loops that persisted for sufficiently long periods that we should have observed loop size change if the overall process were processive. Secondly, the average observable loop lifetime was much shorter than the free Brownian motion period needed to reach the maximum steady state size, with a caveat that the small tensile force caused by the buffer flow might have accelerated the loop disruption rate. Thirdly, only about 1/4 of the MuA clusters appeared to be engaged in MuB cluster interaction via detectable looping at the moment the buffer flow was restarted (Table S2) and yet, irrespective of the loop detection, the neighboring area of MuA clusters had a reduced concentration of MuB after several minutes compared to before the buffer flow interruption. Therefore, we propose that the average loop size expansion takes place through repeated rounds of loop formation and disruption. This is consistent with the MuB polymer distribution and MuB-DNA association/dissociation dynamics. In this study, less than 10% of the total DNA length was covered by EGFP-MuB, corresponding to at most 1500 EGFP-MuB monomers per λ DNA, or less than 150 monomers per 5 kbp. If one assumes, for the sake of discussion, an average MuB polymer size of 30 monomers, then the clusters would be separated by gaps of near 1 kbp. This is difficult to reconcile with a model involving continuous loop expansion. Therefore, processive removal of multiple MuB molecules within one cluster by a MuA cluster is unlikely to extend to an overall processive mechanism of loop size expansion at a physiological MuB-DNA ratio. The DNA association rate at the MuB concentration used would be too slow to entertain a model involving an oriented MuB chain tread-milling along DNA promoted by MuA, generating MuB clearing in its wake; such complete MuB clearing behind each MuA cluster was also not generally observed. Further, the expected speed of such an obligatorily processive motion would be too slow to account for the average loop size expansion rate. In addition, any continuously processive model for loop expansion suffers from the difficulty to explain the origin of the directionality of the net movement, namely choice between loop expansion vs contraction. Therefore, we propose that individual DNA loops are disrupted either after partial or complete disassembly of a MuB cluster. Then, why are larger loops favored after longer durations of free Brownian motion?

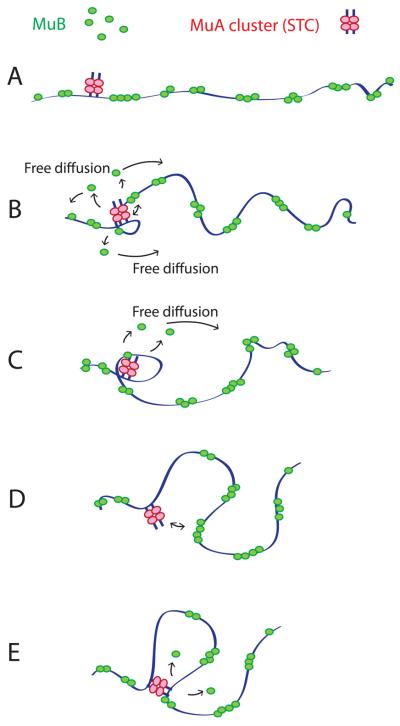
The local concentration of DNA-bound MuB near MuA clusters was reduced during the period of buffer flow interruption. The observed extent of reduction was on average roughly 20 % after 5 min of the buffer flow interruption for the 5 kbp surrounding MuA clusters. There was a wide distribution in the extent of MuB depletion around each MuA cluster. Although the extent of MuB depletion observed was only modest and a longer duration of free DNA Brownian motion appeared to be needed for further MuB depletion under the experimental conditions used, we believe that MuB depletion very close to MuA clusters must have been more significant. We argue that the depletion of very short loops observed at later times took place because of the MuB depletion very close to MuA clusters. The actual fraction of the very short loops among all loops at 15 sec of free Brownian motion might have been even larger than observed, especially if one assumes that some loops shorter than 1 kbp could have escaped detection. Considering that at 15 sec of free Brownian motion many of the loops observed would have been in the second or more round of the looping cycle, judged by the observed loop lifetime, the proportion of small loops would have been even higher initially than observed at 15 sec. Redistribution of these small loops, which were more abundant at the beginning of free Brownian motion, explains the gradual average loop size expansion. We argue that depletion of nearby MuB clusters drives MuA clusters to a further distance away (Fig. 6).

Figure 6.

Model. (A) Without MuA-MuB interactions that involve DNA looping, MuB cluster distribution along the DNA would be essentially random. (B) DNA Brownian motion allows DNA looping-dependent MuA-MuB interactions. A MuB cluster near the MuA cluster is disassembled via small DNA loop formation. MuB molecules dissociate via MuA-stimulated ATP hydrolysis, diffuse away, regain DNA binding ability after a time delay and join MuB clusters at a distance. (C) Individual MuB cluster disassembly may involve processive change of the loop size, which is limited by the cluster size. (D) The DNA loop is disrupted as each MuB cluster is disassembled and a new loop forms involving a remaining MuB cluster. (E) Depletion of MuB clusters near the MuA cluster encourages larger DNA loop formation.

However, we believe that the MuB distribution pattern observed here has not reached a steady state within 5 min, and we were unable to examine the outcome after longer free Brownian motion periods because MuA-independent looping by inter MuB cluster aggregation under the conditions used became significant with extended periods of buffer flow interruption. The 20% reduction of the local MuB concentration observed here is insufficient to explain the target immunity. Under standard in vitro transposition reaction conditions, depletion of MuB from a small immune plasmid DNA in the presence of MuA is essentially complete within 15 min, or earlier (Adzuma and Mizuuchi, 1988). We believe that the apparently less efficient MuB removal from larger regions observed here compared to biochemical experiments stems from the technical constraints of TIRF microscopy, which requires a different buffer compared to the standard transposition reaction conditions, and also in part from the use of the EGFP-MuB instead of wt-MuB.

How could the MuB removal near the Mu end sequences that are about to engage in transposition be established prior to the time when each transposon copy is ready to commit to a new target site? During Mu phage growth inside a cell, removal of MuB from near a copy of Mu end sequence takes place well before a transpososome is assembled. Plasmid DNA molecules that contain one Mu end sequence with three MuA binding sites exhibit target immunity (Adzuma and Mizuuchi, 1988), indicating that three MuA monomers occupying one Mu end can interact with neighboring MuB clusters via DNA looping to dissociate them even before two ends are synapsed to form the SSC with a stable MuA tetramer. Local MuB cluster disassembly would continue as the transpososome is assembled. By the time the CDC is formed and ready for target site commitment to carry out strand transfer, the MuB would have been removed from the neighborhood of this CDC, which would be interacting with a MuB cluster located at a significant distance away from itself along the DNA to be ready to insert into DNA at this location. After completion of target DNA insertion, the STC would continue to remove MuB from its neighborhood to protect the Mu genome. Thus, we believe that qualitatively the same mechanism of MuB removal by the truncated STC used in this study operates with all forms of the Mu end-MuA complexes and maintains MuB depletion around Mu ends throughout the phage growth period. Therefore, whenever a CDC is assembled and ready for target site commitment, proper MuB distribution in the neighborhood is already established.

In this discussion, we have focused on the disassembly of MuB clusters from the DNA region near where MuA cluster is bound, resulting in a non-equilibrium MuB distribution pattern along the DNA. The process could equally well be viewed as transportation of transposon ends to distant locations along the DNA. However, this transportation process differs from those involving classical motor proteins; the MuA-bound Mu end does not processively track along the DNA. Instead, multiple dissociation association cycles with intervening Brownian dynamics are critical parts of the mechanism, which stochastically brings about net average transportation of the MuA cluster along the DNA. Because the MuA cluster has affinity to the MuB clusters bound to DNA, it ends up where the local density of MuB is higher, but because it disassembles the MuB clusters as the interaction is established, a dynamic instability results until a steady state is reached later. One might call this type of mechanism a “diffusion-ratchet”, which may be considered a special class of reaction-diffusion pattern formation mechanism (Turing, 1952). Because MuB clusters are removed from the neighborhood of one MuA cluster, this region is avoided by other MuA clusters as well. Thus, the mechanism manifests itself as a spatial interference among multiple MuA clusters. Mu and other transposons avoid target sites near preexisting (ends of) transposons of the same kind, an observation which led to the term “transposition target immunity” (Lee et al., 1983).

We recognize certain similarities between the reaction discussed here and a class of ParA/B family of chromosome partition systems in prokaryotes, which we believe function by a similar mechanism (A. Vecchiarelli, et at., submitted): each of these systems involves an ATP-dependent nonspecific DNA binding protein and a partner protein that binds a specific DNA site and stimulates the cognate ATPase activity in the presence of DNA. Another example of systems that has been proposed to operate by a reaction-diffusion-type mechanism is the MinD/MinE system in bacteria, which is involved in the mid-cell localization of the cell division septum (Meinhardt and deBoer, 2001). MinD is an ATP-dependent membrane binding protein, and MinE is a stimulator of MinD ATPase. MinD also belong to ParA (type I) family of partition ATPases (Gerdes et al., 2000; Motallebi-Veshareh et al., 1990). Like MuB, ParA binds DNA in the presence of ATP, and like MuA, ParB, which binds to specific sites on its cognate plasmid/chromosome is a stimulator of ParA ATPase in the presence of DNA. The common key ingredients among these systems are the nucleotide state dependent shift of the ATPase molecules between a high-diffusion state in the cytosol and a low diffusion state bound to a “matrix”, a large structural element such as nucleoid DNA or membrane. The ATP-dependent conformational change, which involves protein oligomerization, is controlled by the partner protein, which perhaps also assembles into oligomeric forms. The partner protein may bind to its cargo for transportation, such as plasmid DNA for segregation, and form a higher order protein-DNA complex. These systems generate ATP-driven collective molecular movements or molecular patterning inside a cell. If a large number of the ATPase-stimulator molecules is bound to the DNA cargo, such as the plasmid DNA for partition or transposon ends for the target immunity, it is not difficult to imagine that the overall motion could become more processive, as observed for the intracellular oscillation of plasmid DNA prior to segregation (Ebersbach and Gerdes, 2004; Hatano et al., 2007; Pratto et al., 2008). Then, as demonstrated in this study, local Brownian dynamics of the DNA chain is expected to play one of the key roles for this class of chromosome partition reaction as well.

The mechanism we propose here would, with an additional protein participant that also controls the dynamics of the ATP-dependent DNA binding protein, easily explain other puzzles concerning related phenomena. Certain transposons such as Tn7 and Tn3, which are either known to or thought to use unique target locations, exhibit target immunity that extends much further than that of Mu (Craig, 2002; Lee et al., 1983). This has not only been difficult to explain from mechanistic point of view, but the physiological benefit of target immunity for these parasitic elements has been obscure. Here, as an extension of our mechanistic model, we offer a rational solution to these puzzles. Let's suppose that this additional protein component binds to a specific target DNA site, and inhibits the disassembly of the ATPase in its neighborhood, for example by inhibiting the ATPase activity. This additional participant could then generate a long range targeting mechanism for the cargo to be transported to the site marked by this protein. This would be an attractive biological function of the “target immunity” for a site-specific and structure-specific targeting transposon such as Tn7 (Craig, 2002) to assist the target search process. TnsD protein of Tn7 is known to bind next to a specific target DNA site called att-Tn7 to direct transposition targeted to att-Tn7, and in another pathway, TnsE directs transposition to near specific DNA structures of replication intermediate (Craig, 2002). The target immunity of the Tn3 family of transposons might also function as a special DNA structure targeting mechanism similar to the TnsE pathway of Tn7. For Tn7 target immunity, TnsC and TnsB are thought to play similar roles to MuB and MuA (Craig, 2002). Then, the role of TnsD and TnsE would be to stabilize the TnsC-DNA complex in close proximity to their cognate target sites, making it resistant to the TnsB mediated disassembly. This type of target search could greatly accelerate the search by changing the very short step-size of the unassisted diffusional random walk to an ATP-assisted random walk with a much larger effective step-size. This would reduce the over-sampling of the search sites away from the intended target location. As the target site gets close, an attractive force toward the target would develop because of the presence of the “un-removable” TnsC clusters, resulting also in a greatly increased targeting specificity compared to the conventional passive diffusion-based target search. Such a mechanism could easily explain the physiological reason for the long range of the target immunity exhibited by Tn7 and Tn3 that extends beyond 100 kbp away from a preexisting transposon end sequence (Craig, 2002; Lee et al., 1983). Considering the limited but recognizable similarities of the amino acid sequence and predicted secondary structures of MuB and TnsC (P. Rice, personal communication), it would be reasonable to speculate that the Mu transposition target immunity system may have evolved from a Tn7 type target site search system by preserving the “interference” aspect of the reaction while losing the specific site targeting function.

Experimental Procedures

DNAs and Proteins

Biotinylated λ DNA, MuA, MuB, EGFP-MuB and ECFP-MuB were prepared as described (Greene and Mizuuchi, 2002a, b). Oligonucleotides used are listed in the Supplemental Experimental Procedures.

Construction of fluorescent labeled Strand Transfer Complex

Transpososomes were first formed by mixing MuA and DIG-labeled Mu-end DNA fragment with MuA binding sites (R1 and R2) as described previously (Savilahti et al., 1995) (Figure S1A, lane 1). Briefly, transpososomes were assembled in Buffer A (25 mM Hepes pH 7.6, 7.5% glycerol, 15% DMSO, 0.04% Triton, 10 mM MgCl₂, and 200 mM NaCl) containing 200 nM donor dsDNA and 1 μM MuA. The anti-DIG mouse-IgG (Roche) was then added and incubated at 30 °C for 20 min. More than 95 % of the transpososome was converted to the anti-DIG antibody-bound complex (Figure S1A, lane 2). Alexa-633-conjugated anti-mouse-IgG antibody (Invitrogen) was added to the mixture of the transpososome-anti-DIG antibody complex and incubated at 30 °C for additional 20 min. At higher concentrations of Alexa-conjugated antibody, the complex migrated slower, indicating that many Alexa-633 conjugated antibody molecules could bind to the complex (Figure S1A). In this study, we mixed the transpososomes assembled from 40 nM Mu end DNA and 200 nM MuA with anti-DIG antibody and Alexa-633 conjugated antibody at concentrations of 12 μg/ml and 16 μg/ml, respectively. The antibody-decorated transpososome preparation showed similar DNA strand transfer activity to the transpososome preparation prior to antibody decoration (Figure S1B).

The fluorescent transpososomes were used for assembly of strand transfer complexes (STCs) without any purification. STCs were assembled in reaction mixture containing 25 mM Hepes pH 7.6, 7.5% glycerol, 10 mM MgCl2, 150 mM NaCl, 2 mM ATP, 100 pM biotinylated λ DNA, 100 nM MuB and 5 nM transpososomes. The reaction mixture was incubated 30 min at 30 °C. The STCs were used for the single-molecule experiments without any purification. The transpososome concentrations are given based on the amount of the Mu end DNA fragment used, without correction for assembly efficiency.

Total Internal Reflection Fluorescence Microscopy

The TIRF microscopy experiments were carried out essentially as described previously (Greene and Mizuuchi, 2002c) with following modifications. The TIRF microscope was built around a Nikon TE 2000 E Eclipse frame (Nikon). A 488-nm diode-pumped, solid-state laser (Coherent) and a 633-nm HeNe Laser (Research Electro-Optics) were focused through a fused silica prism onto a flow cell containing the immobilized target complexes. Fluorescent images were formed through an objective lens (100x Plan Apo VC, NA 1.4, Nikon) and a tube lens and captured by a CCD (Cascade II 512, Roper Scientific) through notch filters (NF-01-488/532/635-25×5.0, Semrock) using Metamorph 6 imaging software (Molecular Devices). A Dual-View (Optical Insights) containing a 630 nm dichroic mirror (630 DCXR, Chroma Technologies) was located between the microscope body and the CCD to separate fluorescent images of EGFP and Alexa-633.

The flow cells were assembled as described previously (Tan et al., 2007). Before use, the flow cells were first incubated for 30 min at room temperature with Buffer TN100 (10 mM Tris-HCl pH 8.0, 100 mM NaCl) containing 1 mg/mL Liposome (SUV was prepared by sonication of multilamellar vesicles prepared with DOPC mixed with 1% biotin-PE; Avanti Polar Lipids), then rinsed with Buffer TN100, followed by incubation for 30 min at room temperature with Buffer TN100 containing 1 mg/ml Neutravidin (Pierce). The flow cells were then rinsed with Buffer B (25 mM Tris-HCl pH 8.9, 10 % glycerol, 150 mM NaCl, 10 mM MgCl₂, and 2 mM dithiothreitol (DTT)) containing 2 mg/ml α-casein to ensure blocking of the exposed glass/fused silica surfaces. The biotinylated DNA assembly was infused into the flow cells using a syringe pump at 50 μL/min for 10 min and incubated for an additional 10 min to immobilize the DNA. Buffer B was pumped into the flow cell at 50 μL/min for 10 min to wash out unimmobilized DNA. MuB solution was made in Buffer B containing 2 mM ATP, 25 nM EGFP-MuB, 6% glucose, 0.1 mg/mL glucose oxidase, 0.025 mg/ml catalase and 0.1 mg/ml α-casein, and infused to the flow cell at 50 μl/min for 30 min. Flow was interrupted with a remote switch valve.

DNA binding assay

Alexa-Fluor-514 labeled DNA containing the dye at every 11 bp was used for stopped flow binding kinetics measurements. Alexa-Fluor-514 fluorescence quenching by unmodified MuB binding, or fluorescence signal decrease of ECFP-MuB binding to the Alexa-Fluor-514 labeled DNA by FRET was measured as described in the Supplemental Experimental Procedures.

Highlights.

Dynamic behavior of MuA and MuB bound to the same DNA was observed simultaneously

DNA loops are formed between a single MuA cluster and a MuB cluster

Length of the DNA loop increases with the duration of free Brownian motion of the DNA

Iterative loop formation/disruption cycles result in larger DNA-loops formation