Recognizing Protein Substructure Similarity Using Segmental Threading

Summary

Protein template identification is essential to protein structure and function predictions. However, conventional whole-chain threading approaches often fail to recognize conserved substructure motifs when the target and templates do not share the same fold. We develop a new approach, SEGMER, for identifying protein substructure similarities by segmental threading. The target sequence is split into segments of 2–4 consecutive or non-consecutive secondary structural elements, which are then threaded through PDB to identify appropriate substructure motifs. SEGMER is tested on 144 non-redundant hard proteins. When combined with whole-chain threading, the TM-score of alignments and accuracy of spatial restraints of SEGMER increase by 16% and 25%, respectively, compared to that by the whole-chain threading methods only. When tested on 12 Free Modeling targets from CASP8, SEGMER increases the TM-score and contact accuracy by 28% and 48%, respectively. This significant improvement should have important impact on protein structure modeling and functional inference.

Introduction

It has been well established that the number of folds in the protein universe is limited (Chothia, 1992; Levitt, 2009; Orengo et al., 1994). Analysis of known sequences and structures suggests that the total number of protein folds in nature is one to several thousand (Chothia, 1992; Orengo et al., 1994; Zhang and Skolnick, 2005b). Accordingly, the solved proteins in the PDB library have been classified into hierarchical families in a variety of structural databases such as SCOP (Murzin et al., 1995) and CATH (Orengo et al., 1997). The inherent discrete characteristics of protein folding space lays down the cornerstone for the widely used threading methods for protein structure prediction (Bowie et al., 1991; Jones et al., 1992), which are designed to detect homologous/analogous protein templates by matching the whole-chain sequences of target proteins to solved protein structures. Threading is by far the most reliable and accurate approach to protein structure and function prediction when close homologous templates are not available (Kopp et al., 2007; Wang et al., 2005; Zhang, 2008), i.e. for the targets in “twilight-zone” (Rost, 1999).

In addition to the property of discreteness, it has been recently demonstrated that the protein structure space may be considered as continuous in that the supersecondary structure motifs can be used to link neighboring fold groups (Harrison et al., 2002; Sadreyev et al., 2009; Skolnick et al., 2009; Yang and Honig, 2000; Zhang et al., 2006; Zhang and Skolnick, 2005a). Harrison et al. (Harrison et al., 2002) showed that most proteins in the PDB have a significant structure overlap (spanning ~4–5 secondary structure elements) with around 10% of other protein folds which the authors called “gregarious proteins”, while alpha/beta-proteins usually share substructure motifs with >20% of other protein folds. The common substructure motifs among different protein folds are of critical importance for protein 3D structure modeling and biological function predictions. First, the conserved structure pieces excised from different protein structures can be directly used to assemble new protein structure models in approaches such as ROSETTA (Simons et al., 1997) and TASSER/I-TASSER (Wu et al., 2007; Zhang and Skolnick, 2004a). Second, spatial restraints extracted from the substructure motifs can be used to constrain the modeling simulations (Sali and Blundell, 1993; Zhang et al., 2003). Moreover, since the gregarious proteins have usually different global folds, the conserved substructure motifs may reflect ancient evolutionary relationships and therefore are associated with special functional consequences (Harrison et al., 2002; Todd et al., 2001). In a very recent work (Roy et al., 2010), Roy et al. threaded the supersecondary structure motifs in the I-TASSER models through the protein structure library which has known functions. It is found that the biological functions (including ligand binding sites, Enzyme Commission numbers and Gene Ontology terms) of a substantial number of protein targets were correctly identified by pure structural comparisons of the basic building blocks of proteins, which otherwise could not have been inferred from sequence or profile-based searches.

The substructure motifs conserved between proteins of different global folds, however, cannot be easily detected by traditional whole-chain threading algorithms, because the alignment score is usually confounded by the structurally irrelevant regions. To partly address the problem, several fragment-based methods have been proposed in protein structure modeling. For example, ROSETTA (Das et al., 2007; Simons et al., 1997) tries to identify a set of fragments (3 or 9 continuous residues) from templates which are then used to assemble the global topology of full-length structures. TASSER (Zhang and Skolnick, 2004a) and I-TASSER (Wu et al., 2007; Zhang, 2009) excise continuously-aligned structural fragments (~21 residues on average) from threading templates which are then reassembled by Monte Carlo simulations with the purpose of refining the template structures. Chuck-TASSER (Zhou and Skolnick, 2007) tries to use a ROSETTA-like procedure to build ab intio models for fragments consisting of 3 consecutive secondary structures, which are then used to guide TASSER assembly of full-length models. In a recent work, Hvidsten et al. (Hvidsten et al., 2009) built a library of local substructure descriptors which are selected to have structural element in contact. Residue contacts are then predicted based on hidden Markov model training on the substructure library (Bjorkholm et al., 2009).

Here, we develop a new segmental threading algorithm, called SEGMER, which splits the target sequence into a number of segments (short subsequences) and then threads them through the solved protein structure library. The purpose here is to remove the irrelevant fragments from target sequence in order to increase the sensitivity of the threading algorithm in identifying the specific substructures. We want to note that despite the similar principle, i.e. attacking the structure prediction problem using substructure motifs, the SEGMER algorithm is essentially different from the above-mentioned algorithms. In ROSETTA (Das et al., 2007; Simons et al., 1997), the fragment has a fixed short size (3 or 9 continuous residues), which cannot constitute a meaningful topology of substructures. In SEGMER, however, we have target segments spanning several secondary structures and focus on identifying the conserved and probably structurally stable substructure domains. Therefore the substructure identified by SEGMER should be more reliable in terms of topological similarity. In TASSER/I-TASSER (Wu et al., 2007; Zhang, 2009; Zhang and Skolnick, 2004a), the substructures are directly adopted from whole-chain threading alignments, which do not intend to remove the irrelevant sequence segments, while SEGMER directly aligns isolated segmental sequences with structural templates which help avoid side effect of irrelevant sequence regions. In chunk-TASSER (Zhou and Skolnick, 2007), since the ‘hunk-structure’ is built by ab initio simulation, it does not involve the procedure of threading sequence segments through structure databases. SEGMER, however, takes the advantage of templates when a suitable substructure is available in template library. In the work by Hvidsten et al. (Bjorkholm et al., 2009; Hvidsten et al., 2009), the mapping direction is from the whole-chain query sequence to a preselected substructure. SEGMER does a reverse mapping by aligning consecutive/non-consecutive segmental query sequences to the whole-chain templates and pick up the substructures that match best with the segmental sequences; this allows more flexibility in the substructure identifications because it is usually unknown what boundaries the substructures should be spliced at before analyzing the sequence information. In SEGMER, a pre-determined substructure library is not needed and the structural boundaries of the substructures are automatically decided by the sequence-template alignments. Moreover, the identified substructures do not necessarily have the secondary structure elements in contact that is requested by the Hvidsten et al. algorithm (Bjorkholm et al., 2009; Hvidsten et al., 2009). In summary, the novelty of SEGMER is that it focuses on identifying conserved and probably stable substructures from template proteins by removing the side effect of irrelevant residues, where other fragment-based methods in literature aim at collecting small structural pieces as building block of ab initio modeling (Das et al., 2007; Simons et al., 1997), or excising structural fragments from whole-chain threading alignments (Wu et al., 2007; Zhang, 2009; Zhang and Skolnick, 2004a), or constructing substructures by ab initio modeling (Zhou and Skolnick, 2007), or threading sequences from a pre-determined substructure library (Bjorkholm et al., 2009; Hvidsten et al., 2009).

One of the critical issues in SEGMER is the decision on the sizes and locations of the sequence segments selected for segmental threading, as well as whether the segments are consecutive in sequence order. We will investigate the algorithms using subsequences with various numbers of secondary structure elements, distributed consecutively or non-consecutively. The performance of segmental threading will be systematically benchmarked along with state-of-the-art whole-chain threading algorithms.

Definition of segments

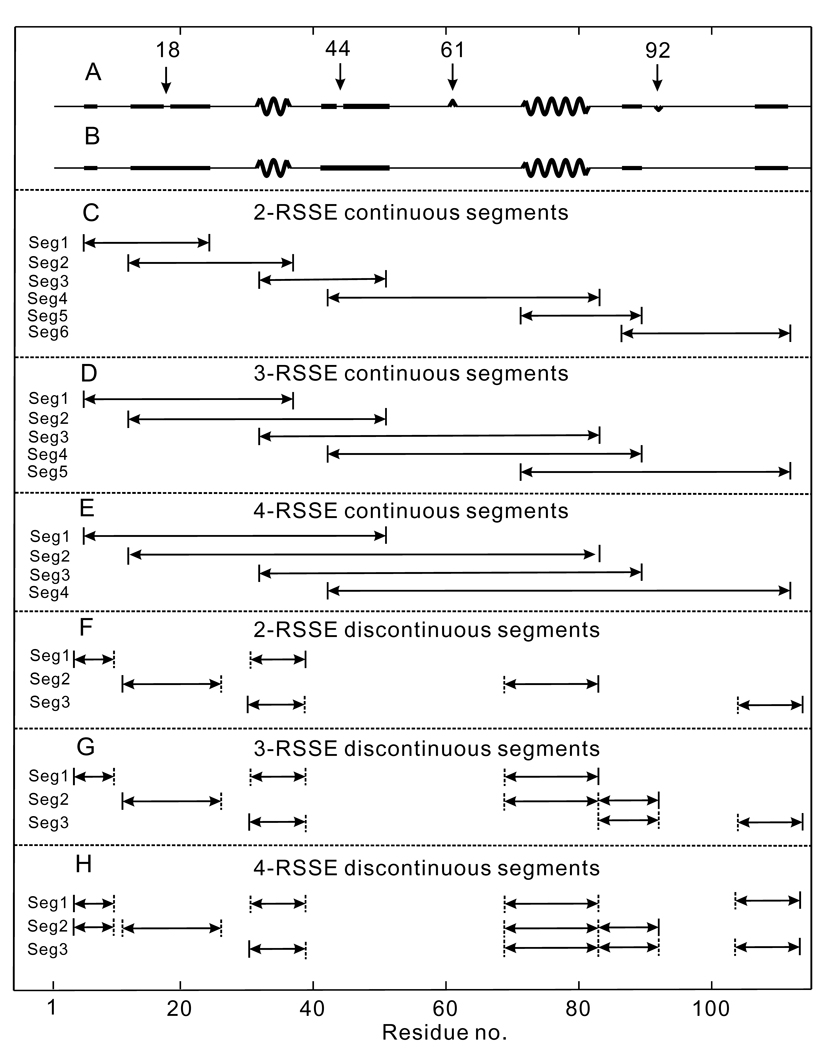
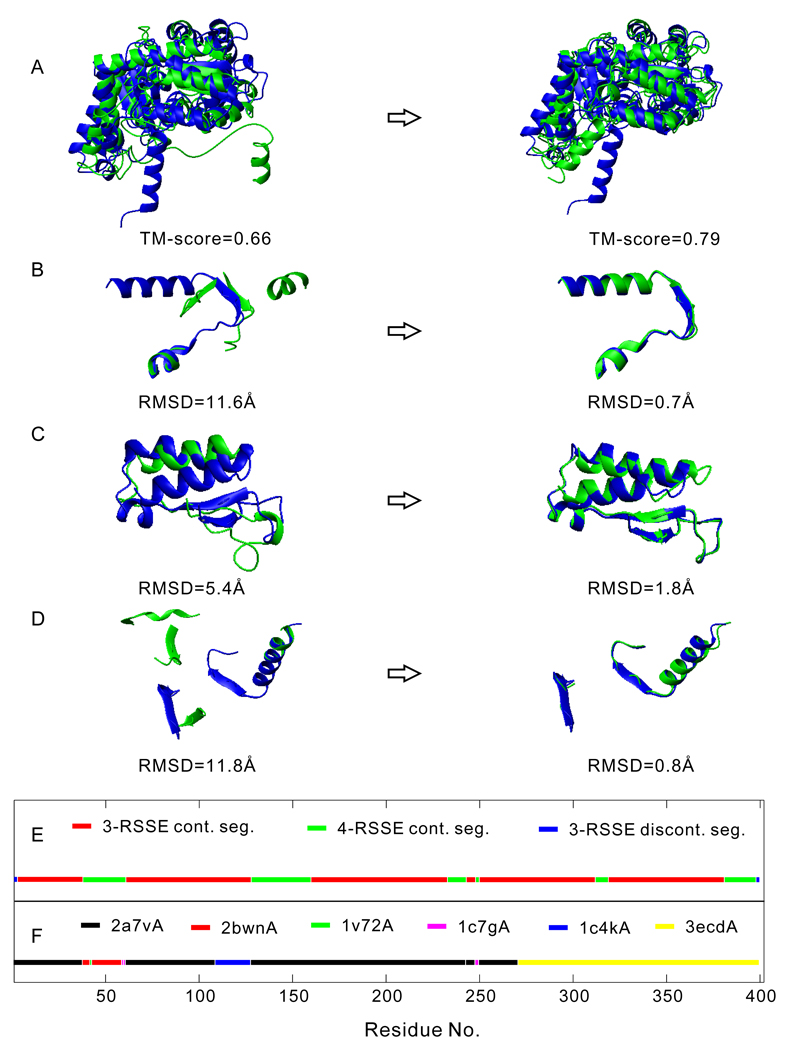
For a given protein, we first divide the query sequence into segments with subsequences; here, a segment is defined as a piece of sequence consisting of several regular secondary structure elements (RSSEs) which include α-helices and β-strands. The secondary structure is predicted from the sequence using PSI-PRED (Jones, 1999). The RSSEs are further smoothened to generate well-defined segments: First, an “island” RSSE of only one residue is converted to coil; second, if a single coil residue is sandwiched between two RSSEs, the two RSSEs and the coil residue are merged into one longer RSSE. Figures 1A and 1B illustrate this smoothing process for the sequence of the Melampsora lini avirulence protein (PDB ID: 2opcA). SEGMER considers two types of segments, covering short- to long-range residue interactions: (1) segments comprising consecutive RSSEs (no RSSEs are excluded between neighboring RSSEs in the segment, see Figs. 1C–1E; (2) discontinuous segments comprising non-consecutive RSSEs (i.e. at least one RSSE is excluded between neighboring RSSEs in the segment, see Figs. 1F–1H). Each segment type includes variable segment lengths, covering 2–4 RSSEs for query sequences.

Figure 1.

Illustration of secondary structure elements and the segments used in SEGMER. The sequence is from the protein with PDB ID 2opcA. (A) Original secondary structure prediction by PSI-PRED; alpha-helices, beta-strands and coils are represented by thick waves, thick solid lines and thin solid lines, respectively. (B) In the smoothening process, residues 18 and 44 are merged into the neighboring RSSEs while residues 61 and 92 are removed from the set of RSSEs. (C–E) Continuous segments with 2–4 RSSEs. (F–H) Examples of discontinuous segments with 2–4 RSSEs.

Data sets

We downloaded a list of non-homologous proteins from the PISCES server (Wang and Dunbrack, 2003), which contains proteins from the PDB with a sequence identity cutoff of 20%, a resolution cutoff of 1.6Å and an R factor cutoff of 0.25. From these proteins, we selected a set of 474 proteins with ≤1,000 residues and ≥5 RSSEs. We have excluded small proteins with 2–4 RSSEs because segmental threading should produce very much the same results for these proteins as conventional whole-chain threading. The proteins are randomly divided into three sets, namely, 100 training, 80 validation and 294 testing proteins. Of the 294 testing proteins, 150 are easy and 144 are hard targets. Here, the categories “easy” and “hard” are defined by the whole-chain threading program MUSTER (Wu and Zhang, 2008b): if the Z-score of the alignments is >7.5, the topology of the template is usually correct and the target is labeled as “easy”; if Z-score<7.5, the target is “hard”. A list of the proteins can be downloaded from http://zhanglab.ccmb.med.umich.edu/SEGMER/output/list.txt.

Scoring function

The scoring function for matching the query-template pairs in segmental threading includes terms for both sequence- and structure-based information. It contains sequence-based profile-profile alignment, structure profile-profile alignment, secondary structure, solvent accessibility, torsion angle and hydrophobic residue matches. A detailed description of the scoring function and the parameter optimization is given in Methods. The best match for both continuous and discontinuous segments is identified by a modified dynamic programming algorithm (see Figure 6 and discussion in Methods). The raw alignment score for each template is then transformed to Z-scores. The final templates are selected based on the Z-score.

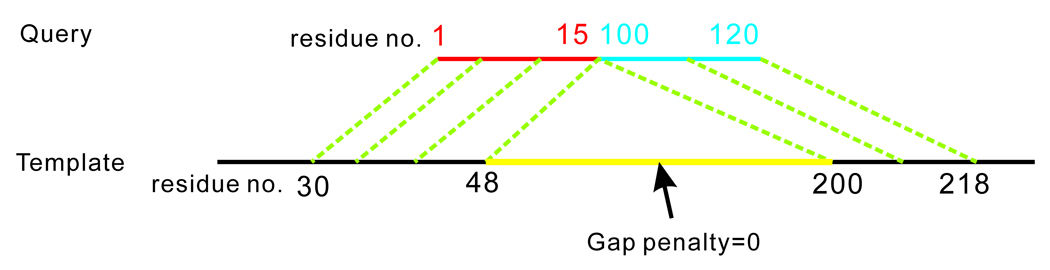
Figure 6.

Illustration of the SEGMER alignment of a discontinuous query segment with discontinuous segments of the template. Residues 1–15 in the query belong to the first RSSE (red) and residues 100–120 belong to the 5th RSSE (blue). When the two query RSSEs are aligned with residues 30–48 and 200–218 of the template, the gap penalty is set to zero in the 49 to 199 residue range (yellow). This enables the non-consecutive RSSEs of the query to align with residues in regions that are far apart in the template structures.

Evaluation criteria

We evaluate the threading results mainly based on TM-score (Zhang and Skolnick, 2004b), which has been defined to combine alignment accuracy and coverage, and to assess the quality of threading alignments by a single score value, i.e.

$$\text{TM}-\text{score}=\frac{1}{L}{\displaystyle \sum _{i=1}^{L_{\mathit{\text{a l i}}}}\frac{1}{1+\frac{d_i^2}{{\left(1.24\sqrt[3]{L-15}-1.8\right)}^2}}}$$ (1)

where d_i is the distance of the ith pair of residues after an optimal superposition of template and target. In the case of segmental threading, L is the length of the target segmental sequence and L_ali is the number of aligned residues. Because TM-score is scaled in a way to keep the score value of random structures independent of the protein size, the TM-score of small proteins (e.g. the segments in this study) is on average smaller than the TM-score of large proteins for the same range of RMSD error.

Results

We first test SEGMER on the 144 hard targets. To reduce the contamination from homology, all homologous proteins with a sequence identity >30% were excluded from our template library. Counting all possible continuous and discontinuous segments, the average number of segments that could be defined is 6,848 per protein for the proteins in our data sets, with an average segment length of 41 residues. This number, mainly due to the large number of possible discontinuous segments comprising 4 RSSEs (5,799 segments per protein), is too large for current computing power. To speed up the procedure, we only used up to 100 segments in each segment category, selecting segments that produce no or only weak whole-chain threading alignments in MUSTER. The average number of segments used in SEGMER threading is 144 per protein target.

Overall result

The average TM-score of first alignment for all the 144 proteins is 0.380, with an average RMSD to native =8.7Å. If we consider the “best in top five” alignments, the TM-score increases to 0.414. Having in mind that these proteins are hard targets and the results are mainly from the regions lacking a strong template and alignments, this result is promising since the obtained TM-score is significantly higher than that expected for random matches (TM-score=0.17) (Zhang and Skolnick, 2004b). In fact, 26% of the segments has an alignment with a RMSD <2Å or TM-score >0.5.

In Table S1 of Supplemental Information, we list the TM-score results from SEGMER in each segment category. We observe two tendencies: First, there is no clear relationship between SEGMER quality and segment length. Although the average RMSD is lower for 2-RSSE segments than for 3- or 4-RSSE segments, which is because of the well-known length effect of RMSD (i.e. random pairs of bigger proteins tend to have a higher RMSD (Zhang and Skolnick, 2004b)), the average TM-score of the longer segments tends to be higher, which indicates that the alignments of longer segments are statistically more significant. Second, for the same segment sizes, the average TM-score for continuous segments is higher than that for discontinuous ones. This demonstrates that long-range structures are more difficult to recognize in threading.

Comparison with MUSTER and HHpred

The performance of SEGMER can be most objectively judged by comparing it with conventional whole-chain threading. (Although the SEGMER alignments can also be compared with the data obtained by assembly of multiple templates, results of the latter vary remarkably depending on different ways of template selections and fragment combinations (Cheng, 2008; Fischer, 2003; Sali and Blundell, 1993; Wu and Zhang, 2007; Zhang, 2009), on which the discussion is not the focus of this work). For this purpose, we select two state-of-the-art threading programs, HHpred (Soding et al., 2005) and MUSTER (Wu and Zhang, 2008b), which were ranked as the first and the second best single threading programs in CASP8 based on the cumulative TM-score or GDT-score. MUSTER uses a composite scoring function similar to SEGMER’s for the whole-chain threading, while HHpred employs a Hidden Markov Model (HMM) based profile-profile alignment algorithm.

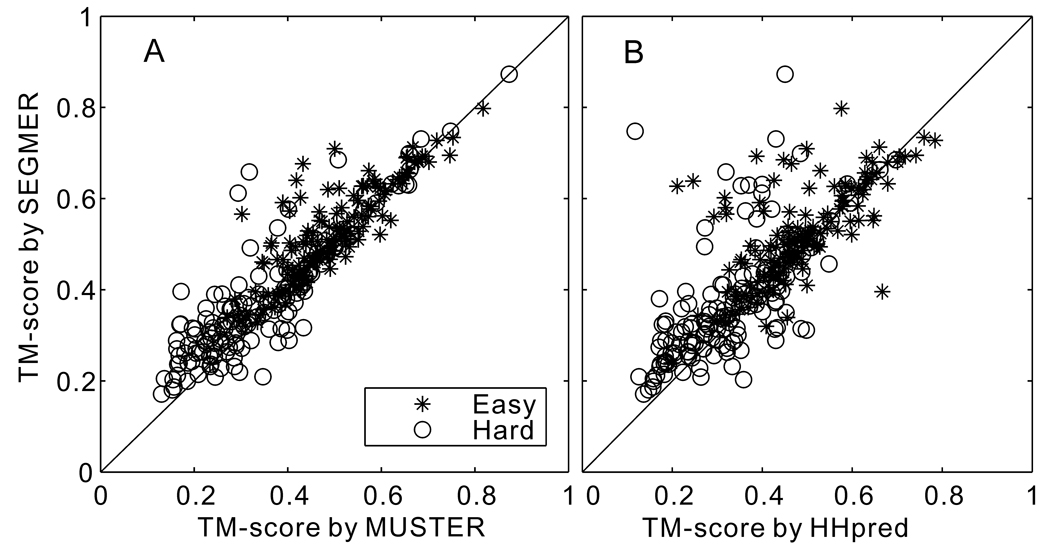
In Table 1 (Rows 2–5), we show a summary of the average TM-scores over the segment regions where all three programs (SEGMER, MUSTER and HHpred) have common alignments. There are 141 hard targets having on average 41 such segments in each protein. The average TM-score of SEGMER (0.377) is 16.0% higher than that of MUSTER and 16.4% higher than that of HHpred. The statistical significance of the higher performance of SEGMER is tested by t-test with a p-value <1×10⁻⁸ over MUSTER and HHpred. Figure 2 shows a head-to-head TM-score comparison of SEGMER with MUSTER and HHpred (see circle symbols for the hard targets). For each protein, the average TM-score of all segments in the protein is presented as one point in the figure. Out of the 141 targets, 95 (or 99) proteins appear in the upper-left region where SEGMER outperforms MUSTER (or HHpred). In 50 (or 54) cases, the absolute TM-score improvement by SEGMER over MUSTER (or HHpred) is >0.05.

Table 1.

Average TM-score of the substructures predicted by MUSTER, HHpred, and SEGMER (bold numbers show the best result in each category).

	Segments*	Methods	First	Best in Top 5
144 hard targets	Common	SEGMER	0.377	0.415
		MUSTER	0.325	0.385
		HHpred	0.324	0.369
	Unaligned	SEGMER	0.448	0.480
150 easy targets	Common	SEGMER	0.521	0.567
		MUSTER	0.489	0.549
		HHpred	0.487	0.535
	Unaligned	SEGMER	0.486	0.529
12 CASP8 FM targets	Common	SEGMER	0.384	0.420
		MUSTER	0.300	0.365
		HHpred	0.259	0.295
	Unaligned	SEGMER	0.315	0.373

^*‘Common’: segments that have alignments by all three algorithms; ‘Unaligned’: segments that have no alignments by the whole-chain threading algorithm MUSTER.

Figure 2.

Average TM-score of the first threading alignments for each protein of 144 hard targets with substructures identified by SEGMER versus that by MUSTER (A) and HHpred (B).

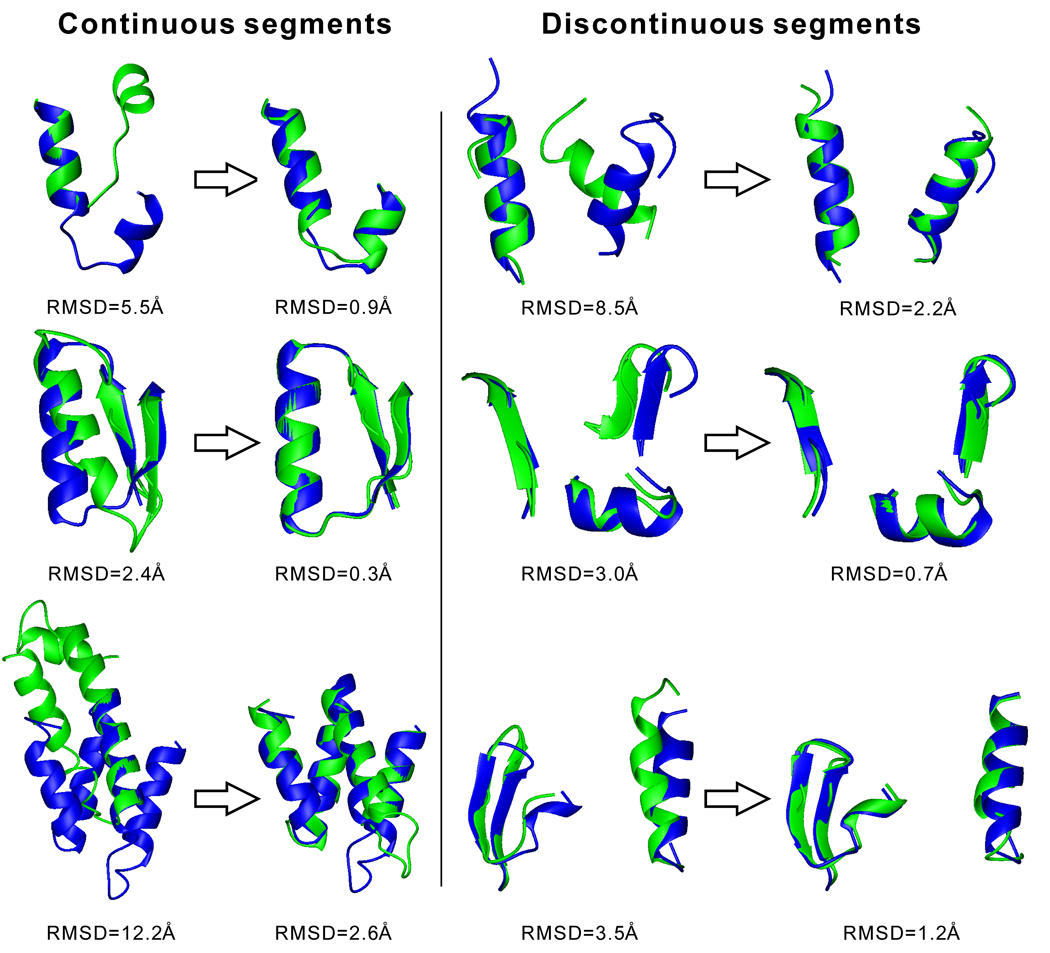
One reason for the TM-score improvement is an increase in alignment coverage, from 0.80 (HHpred) or 0.87 (MUSTER) to 0.98 (SEGMER), meaning that segmental threading can identify more complete alignments by focusing directly on the target segmental sequences. The second reason is an improvement of the alignment accuracy. In 31% of the segments, the RMSD of the alignment by SEGMER is lower than that by MUSTER while SEGMER’s alignment coverage is higher. If we consider the 2-RSSE segments with an identical number of aligned residues in SEGMER and MUSTER, the RMSD of the SEGMER alignments is 0.31Å lower than that of the MUSTER alignments. This demonstrates that by focusing on more specific sequence regions and excluding the interferences from irrelevant structure regions, segmental threading can help improve the alignment accuracy. In Figure 3, we present representative examples in various segment categories, which show the advantage of SEGMER in both alignment coverage and accuracy over the whole-chain threading algorithms.

Figure 3.

Representative examples of substructure motifs identified by whole-chain threading (MUSTER, the left-side of arrows) and segmental threading (SEGMER, the right-side of arrows) for different types of segmental sequences. The template structures from threading and the native structure are represented by green and blue cartoons, respectively. Rows 1, 2 and 3 are for 2-, 3-, 4-RSSE segments, respectively.

In Figure 4, we show an illustrative example of full-length structure construction using the structure motifs identified by SEGMER. To do this, we first sort all the SEGMER substructure templates by a W-score (=Z-score+2.5*TM-score_SM), and then superimpose the substructures in the order of their W-scores onto the first template identified by MUSTER. Here, TM-score_SM is the TM-score between the SEGMER substructure and the MUSTER template. The superimposed structural motifs are merged into the full-length model while the regions overlapping with the previously superimposed substructures are neglected. In this example (PDB ID: 2dkjA, a serine hydroxymethyltransferase), the best template from MUSTER has a TM-score=0.655 (Figure 4A, Left panel), while the new model constructed by the simple superimposition has a TM-score =0.789 (Figure 4A, Right panel). This significant improvement in TM-score is mainly due to the better local structures identified by SEGMER (see examples in Figures 4B–D), which are taken from a number of different segments and templates as selected by the W-scores (Figures 4E and 4F).

Figure 4.

An illustrative example of constructing a full-length model for the protein 2dkjA using segments identified by SEGMER. Model and experimental structures are represented by green and blue cartoons, respectively. (A) Left: the best template identified by MUSTER superimposed on the native structure. Right: the full-length model constructed by superimposing the SEGMER segments on the MUSTER template. (B–D) Representative examples of MUSTER (left) and SEGMER (right) segments as compared with the native structure. (E) Distribution of different types of segments along the combined model (each segment with the same color can be a combination of several RSSEs). (F) Distribution of different templates along the combined model.

Besides the segments aligned in common, SEGMER also generates alignments for the segments for which the whole-chain threading algorithms do not. There are 5,162 such segments which are distributed in 103 hard protein targets. Surprisingly, the average TM-score of the unaligned region (TM-score=0.448) by SEGMER is considerably higher than that of other regions (TM-score=0.377). This is probably because the commonly aligned regions in hard proteins have, by definition, weak alignment scores in the whole-chain threading programs which tend to have low-quality templates; but the unaligned regions in the whole-chain threading have on average better templates compared with the weakly-aligned regions. We have further compared the best templates identified by the structural alignment program TM-align (Zhang and Skolnick, 2005b) and found that the TM-score of the unaligned regions is indeed slightly higher than that of the weakly aligned regions.

Finally, we compare the performance of the three programs in the various specific categories of segments, namely, continuous and discontinuous, with 2, 3, or 4 RSSEs, as listed in Tables S2 to S7 in the Supplemental Information. SEGMER consistently outperforms MUSTER and HHpred in all these categories, as demonstrated by the significantly improved TM-score values.

Dependence of the improvement on protein size

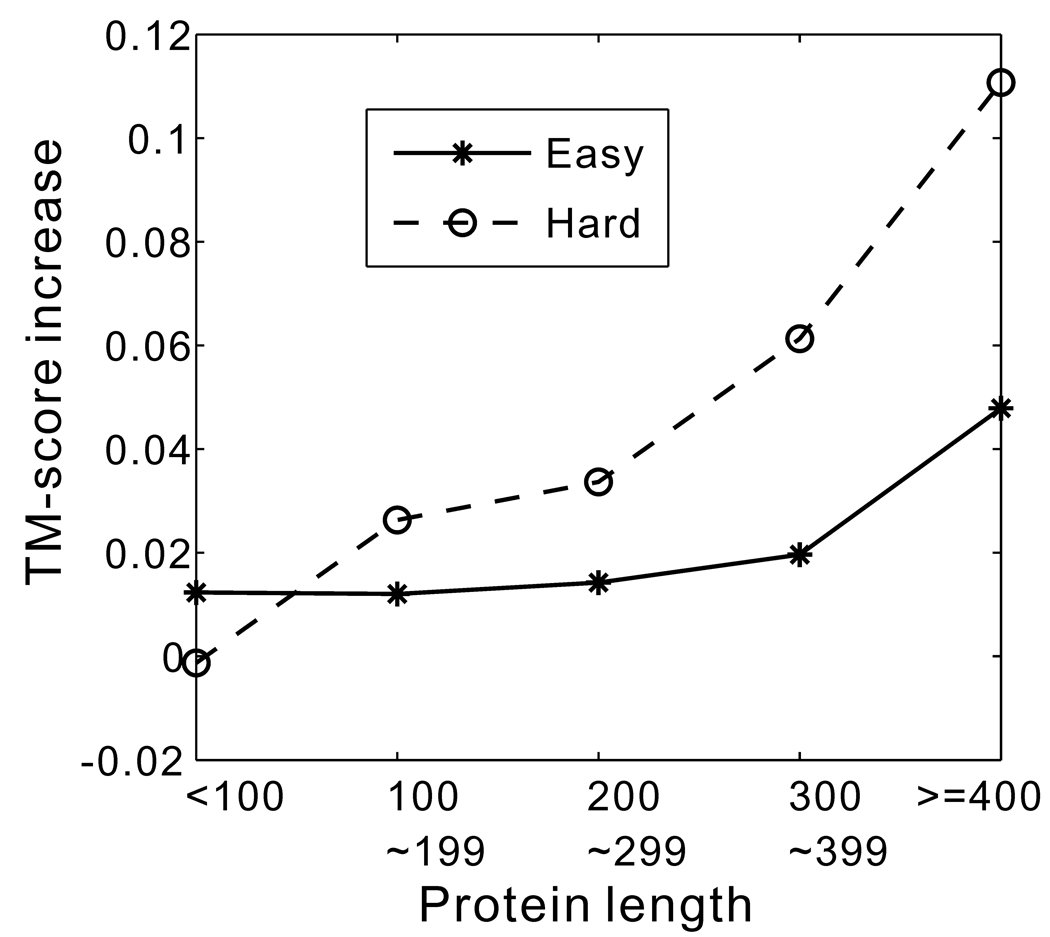
The improvement of substructure identification by SEGMER depends on the size of the target proteins. For small proteins, because the size of the protein is close to that of the segmental sequences, the procedure and the result of segmental threading are similar to that of the whole-chain threading. But for larger proteins, a large variety of segments is available for selection, which allows identifying good substructure cores that are missed by the whole-chain threading algorithms. Figure 5 shows the dependence of the average absolute TM-score increase by SEGMER over MUSTER on the protein size. Here, the TM-score is first calculated as an average of all segments in each protein, which is then averaged for all proteins in each chain-length range. There is an obvious increase in TM-score improvement as protein size increases. Also, the improvement is more pronounced in hard than in easy targets. Therefore, the application of SEGMER will yield the largest benefit in the case of large and remotely homologous targets.

Figure 5.

Absolute TM-score increase achieved by SEGMER relative to MUSTER on common segments as a function of protein length. The protein lengths have been divided into five bins: (1~99, 100~199, 200~299, 300~399, 400~1000).

Test on easy targets

Although the major purpose of developing SEGMER is to improve the threading alignments for hard targets, it is of interest to examine how SEGMER performs on easy targets because the alignments of easy targets often have some weakly aligned local segments and gaps. We need to mention that “easy target” does not mean a high sequence identity between target and template because all homologous templates with a sequence identity >30% have been excluded.

There are 42,010 segments in 150 easy targets which result in an average 280 segments per target. We repeat the SEGMER procedure for the 150 easy targets without further tuning the parameters. The TM-score results for the easy targets are listed in the middle rows of Table 1 and Tables S1–S7. A similar tendency to the one seen for the hard targets is observed, i.e. SEGMER could identify substructures of better quality than whole-chain threading in all segment categories. The average TM-score of the first template hit by SEGMER is 0.521, which is 6.5% higher than that from MUSTER (or 7.0% higher than that from HHpred). Figure 2 shows a head-to-head TM-score comparison of SEGMER with MUSTER and HHpred (see star symbols). The increase is slightly lower than that found for hard targets, partly because the substructures of easy targets have a better quality and TM-score, and therefore there is less room for further improvement. Nevertheless, the TM-score improvement is statistically significant, having a p-value ρ×10⁻⁵ over MUSTER and HHpred according to t-test. The average TM-score of the unaligned segments (0.486) is still slightly lower than that of the commonly aligned regions for the easy targets because better templates are available in the threading-aligned regions.

Test on CASP8 Free Modeling targets

In the above tests, a sequence identity cutoff <30% has been conducted for excluding homologous templates. But there may still be good templates left, which have similar global fold to the target, especially for the Easy targets. Here, we test SEGMER on 12 Free Modeling (FM) targets/domains in the 8^th Critical Assessment of Techniques for Protein Structure Prediction (CASP8) hold in the summer of 2008. These FM domains were defined by the CASP8 assessors as the targets which have no templates of similar global topology in the PDB. To mimic the CASP8 condition, we exclude all the proteins from our structure library which were released after May, 2008.

The performance of SEGMER, MUSTER and HHpred are listed in the lower part of Table 1 and Tables S2–S7. The performance of SEGMER, MUSTER and HHpred are listed in the lower part of Table 1 and Tables S2–S7. SEGMER results are obtained based on the truncated library with new proteins solved after May of 2008 excluded; the MUSTER and HHpred threading results were generated during the CASP8 experiment. For the commonly aligned segments, SEGMER achieves an average TM-score=0.384 for the first model, which is 28% (or 48%) higher than that by MUSTER (or HHpred). For the best in top 5 models, the improvement by SEGMER is >15% in both cases. Although the sample size (=12, here) may be too small to attain a solid conclusion, the significant structural improvement demonstrates the potential usefulness of SEGMER on assembling structures of these real hard targets.

Spatial restraints

Full-length protein structure models in comparative modeling can be constructed by satisfying the spatial restraints extracted from template structures (Sali and Blundell, 1993). The sparse contact and distance maps can also be used as restraints to guide the ab initio protein structure simulations when template structural information is limited (Misura et al., 2006; Zhang, 2007; Zhang et al., 2003). Four types of spatial restraints are often used in protein structure prediction (Wu and Zhang, 2007): (1) side-chain contacts; (2) C_α atom contacts; (3) short-range C_α-distance maps (|i−j|≤6); (4) long-range C_α-distance maps (|i−j|>6).

Here, we examine the spatial restraints extracted from the SEGMER threading alignments in comparison with those extracted from the MUSTER alignments. For the restraints from MUSTER, we follow the procedure used in I-TASSER (Wu et al., 2007; Zhang, 2007), i.e. we collected the contact restraints and short-range distances from the top 50 (or 20) templates for the hard (or easy) targets, selecting the contacts based on their frequency of occurrence in the template structures. The long-range distance restraints are taken from the first four templates with an average error as reported earlier (Wu and Zhang, 2007). To obtain restraints from SEGMER alignments, we use the same voting procedure as in MUSTER but all segmental alignments with a Z-score >3 are used for collecting contacts, and the first four templates at each position are used to obtain long-range distance maps.

In Table 2, we show the accuracies and errors of contact prediction when L/2 contacts are predicted for proteins of length L. The accuracy of contact prediction is defined as the number of correctly predicted contacts divided by the number of all predicted contacts (L/2). It is worth mentioning that the restraints from MUSTER are collected from the whole sequence while the restraints from SEGMER in our procedure are from those regions where the MUSTER threading has a weak alignment. Nevertheless, the overall accuracy of the contacts from SEGMER is still comparable or even better than that from MUSTER. For hard targets, the accuracy of contacts from SEGMER is higher than from MUSTER for both C_α and side-chain contacts, while for easy targets, the contact prediction accuracy of SEGMER is higher for C_α but lower for side-chain contacts than that of MUSTER. Remarkably, when we combine the contacts from SEGMER and MUSTER alignments, i.e. collect contacts from a combined set of SEGMER and MUSTER alignments by using the same voting procedure, the contact accuracy is significantly higher than when using either MUSTER or SEGMER alone, which shows that these two types of alignments and contact predictions are complementary to each other. Overall, the accuracy of SEGMER+MUSTER predictions, including both C_α and side-chain center based contacts, is about 25% (8%) higher than that from MUSTER for hard (easy) targets.

Table 2.

The accuracy and error of spatial restraints extracted from MUSTER, SEGMER, and a combination of SEGMER and MUSTER alignments (bold numbers show the best result in each category).

		MUSTER	SEGMER	SEGMER+MUSTER
144 hard targets	ACCCα*	0.286	0.336	0.362
	ACCSG†	0.374	0.407	0.463
	ERRshort(# of pairs)§	1.40(1009)	0.95(570)	1.24(1012)
	ERRlong/(# of pairs)¶	2.83(2610)	5.19(1082)	2.46(2612)
150 easy targets	ACCCα_all*	0.628	0.653	0.692
	ACCSG_all†	0.753	0.739	0.793
	ERRshort(# of pairs)§	0.95(1168)	0.52(700)	0.82(1205)
	ERRlong/(# of pairs)¶	1.53(3504)	2.36(2406)	1.33(3513)
12 CASP8 FM targets	ACCCα_all*	0.131	0.138	0.146
	ACCSG_all†	0.141	0.187	0.209
	ERRshort(# of pairs)§	2.495(437)	1.949(286)	2.294(461)
	ERRlong/(# of pairs)¶	4.28(527)	7.96(342)	3.70(528)

^*Average accuracy for C_α contact prediction

^†Average accuracy for side-chain contact prediction

^§Average error in Å of the short-range distance predictions

^¶Average error in Å of the long-range distance predictions

In Table S8 in the Supplemental Information, we divide the contact predictions into 3 categories based on the sequence separation of the predicted contacts: (1) short-range (6≤|i−j|<12); (2) medium-range (12≤|i−j|<24); (3) long-range (|i−j|≥24). For each target, we select the top L/5 predictions. Again, we observe that the accuracy of contacts predicted by SEGMER+MUSTER is significantly higher than that from MUSTER alone. For side-chain contact, for example, accuracy of the short/medium/long-range predictions by SEGMER+MUSTER are 46%/42%/42% compared to 36%/31%/35% by MUSTER, respectively. The most important long-range contact predictions have been improved by 21% compared with MUSTER, which is mainly due to the contribution from the alignments of the discontinuous segments. In an earlier structure prediction experiment, we showed that contact predictions with an accuracy >22% almost always generate positive contribution to the ab initio structures modeling (Zhang et al., 2003). As Table S8 shows, the contact prediction accuracy by SEGMER+MUSTER is higher than 30% in all sequence separation ranges for both C_α and side-chain based contacts. Because all homologous templates are excluded, this finding demonstrates again the possible usefulness of the SEGMER prediction in guiding ab initio structural simulations.

The accuracy of the predicted C_α distance maps is also shown in Table 2 (rows 4, 5, 8, 9, 12 and 13) for the hard, easy, and CASP8 FM targets. In the hard targets, the short-range distance prediction by SEGMER is obviously more accurate (error=0.95Å) than that by MUSTER (error=1.40Å) because SEGMER identifies better local secondary structures. But for long-range distance restraints, the distance error of the SEGMER predictions is larger than that from MUSTER. This is because the SEGMER predictions are mainly concentrated on the weakly aligned regions while MUSTER predictions span the whole sequence. Due to the complementarity of these two algorithms, the distance map prediction from SEGMER+MUSTER again outperforms that from MUSTER alone by 0.37 Å. For the easy and CASP8 FM targets, the improvements on the distance map prediction are 0.20 Å and 0.58 Å, respectively.

Discussion

We have developed a new divide-and-conquer type threading algorithm, SEGMER, for identifying substructure motifs from non-homologous protein templates. This endeavor is mainly motivated by the observation that non-homologous protein pairs often share common substructures even though the global folds are different (Harrison et al., 2002; Sadreyev et al., 2009; Yang and Honig, 2000; Zhang et al., 2006; Zhang and Skolnick, 2005a). These analogous substructure pairs could not be efficiently identified by conventional whole-chain threading algorithms because the scoring functions of these algorithms are designed for recognizing the global folds and the structurally irrelevant regions may confound the efficiency of the global alignments. The advantage of SEGMER is that the irrelevant parts of the target and template structures are excluded from the alignment, which allows for better scoring and sharper selection of the specific substructure templates. An on-line server of SEGMER is set up at http://zhanglab.ccmb.med.umich.edu/SEGMER. The SEGMER source programs are freely downloadable at the same website.

Testing the new method on 144 non-homologous hard protein targets whose global fold cannot be correctly identified by whole-chain threading algorithms, we find that SEGMER identifies significantly better substructures than the whole-chain threading algorithms (HHpred and MUSTER), with an average TM-score increase of 16%. When combined with the whole-chain threading templates, the accuracy of the spatial restraints of C_α and side-chain center contacts increases by about 25% while the error of long-range distance map predictions reduces by 0.37 Å on average. When applying SEGMER to 12 Free Modeling (FM) targets from CASP8, the TM-score of the identified template segments has an improvement by 28%, the contact accuracy (when combined with the whole-chain threading) is increased by 48%, and the error of the distance map from the combined segment predictions is reduced by 0.58 Å.

It is worth mentioning that the purpose of developing the segmental threading method is not to fully replace whole-chain threading, and whole-chain threading remains an efficient approach to recognize the global topology. The best results in terms of predicted spatial restraints and assembled structures are obtained by combining the segmental and whole-chain threading alignments (see Table 2 and Figure 4). Nevertheless, the significant improvement in the sensitivity of substructure detection produced by SEGMER will have an important impact on motif-based function annotation and segment-based full-length protein structure assembly, especially for those proteins that lack homologous or analogous templates. In fact, we have used the results of SEGMER threading to guide I-TASSER structure assembly simulations, and obtained very promising preliminary results in the modeling of ab initio protein targets. This study is still in progress while the current paper is being prepared. A study on the impact of segmental threading to the biological function annotation of proteins is also in progress.

Experimental Procedures

Alignment scoring function

The scoring function for segmental threading includes eight terms. The score of matching the ith residue of a segmental query sequence to the jth residue of a template is

$$\begin{array}{c}\text{Score}(i,j)={\mathrm{E}}_{\text{seq}\_\text{prof}}+{\mathrm{E}}_{\text{sec}}+{\mathrm{E}}_{\text{struc}\_\text{prof}}+{\mathrm{E}}_{\text{sa}}+{\mathrm{E}}_{\text{phi}}+{\mathrm{E}}_{\text{psi}}+{\mathrm{E}}_{\text{hydro}}+{\mathrm{E}}_{\text{shift}}\hfill \\ ={\displaystyle {\sum }_{k=1}^{20}({\text{Fc}}_{\mathrm{q}}(i,k)+{\text{Fd}}_{\mathrm{q}}(i,k)){\mathrm{L}}_{\mathrm{t}}(j,k)/2+c_1\delta (s_{\mathrm{q}}(i),s_{\mathrm{t}}(j))}\hfill \\ +{\mathrm{c}}_2{\displaystyle {\sum }_{k=1}^{20}{\text{Fs}}_{\mathrm{t}}(j,k){\mathrm{L}}_{\mathrm{q}}(i,k)+{\mathrm{c}}_3(1-2|{\text{SA}}_{\mathrm{q}}(i)-}{\text{SA}}_{\mathrm{t}}(j)|)\hfill \\ +c_4(1-2|{\phi }_{\mathrm{q}}(i)-{\phi }_{\mathrm{t}}(j)|)+c_5(1-2|{\varphi }_{\mathrm{q}}(i)-{\varphi }_{\mathrm{t}}(j)|)\hfill \\ +c_6\mathrm{M}({\mathit{\text{AA}}}_{\mathrm{q}}(i),{\mathit{\text{AA}}}_{\mathrm{t}}(j))+c_7\hfill \end{array}$$ (2)

where ‘q’stands for the query and ‘t’ for the template protein.

The first term E_{seq_prof} in Equation 2 is for the sequence profile-profile alignment. Fc_q(i, k) and Fd_q(i, k) are the frequencies of the kth amino acid at the ith query position in a multiple sequence alignment (MSA) obtained by PSI-BLAST (Altschul et al., 1997) run against the non-redundant sequence database nr (ftp://ftp.ncbi.nih.gov/blast/db) for closely (E-value cutoff=0.001) and remotely homologous (E-value cutoff=1.0) sequences, respectively. Equal weights for the close and remote sequence profiles are the parameters best-tuned for the performance based on the validation data. For generating frequency profiles, the redundancy of sequences in the MSA is accounted for by Henikoff weights (Henikoff and Henikoff, 1994); in addition, a higher weight is given to the sequences with a lower E-value (Wu and Zhang, 2008b). L_t(j, k) is the log-odds profile value (Position-Specific Substitution Matrix in PSI-BLAST with an E-value cutoff=0.001) of the kth amino acid at the jth position of the template sequence.

The second term E_sec computes the match between the predicted secondary structure s_q(i) of the ith query position and the actual secondary structure s_t(j) of the jth position of template structures. δ(s_q(i),s_t(j)) equals 1 if s_q(i)=s_t(j) and −1 otherwise. s_q(i) is predicted by PSI-PRED (Jones, 1999) while s_t(j) is generated by STRIDE (Frishman and Argos, 1995). Both s_q(i) and s_t(j) have three discrete states: alpha helix, beta strand, and loop.

The third term E_{struc_prof} is the score of matching the structure-derived profiles (frequency) Fs_t(j, k) of the kth amino acid at the jth position of the template (Wu and Zhang, 2008b) to the sequence profile (log-odds) L_q(i, k) of the kth amino acid at the ith position of the query. To construct the structure profile for templates, we compare a 9-residue fragment from each template with 9-residue fragments from all proteins in a non-redundant protein database selected by PISCES (Wang and Dunbrack, 2003). The top 25 closest fragments for each template fragment are selected based on a similarity score combining RMSD and the fragment depth similarity (Chakravarty and Varadarajan, 1999; Wu and Zhang, 2008b). For the jth position of the template structure, there are 25*9=225 aligned residues to construct the frequency profile Fs_t(j, k). L(i, k) is the log-odds profile for the kth amino acid at the ith position of the query sequence from the PSI-BLAST search with an E-value cutoff =0.001.

The forth term E_sa accounts for the difference between the predicted solvent accessibility SA_q(i) of the ith position of the query and the actual solvent accessibility SA_t(j) of the jth position of template structures. The experimental SA_t(j) for the template is generated by STRIDE (Frishman and Argos, 1995). The values of SA_q(i) for query are predicted by an artificial neural network (Chen and Zhou, 2005; Wu et al., 2007), which has a higher correlation coefficient (CC=0.71) with the actual SAs than the widely-used Hopp-Woods (Hopp and Woods, 1981) (CC=0.42) and Kyte-Doolittle (Kyte and Doolittle, 1982) (CC=0.39) hydrophobicity indices based on 2,234 non-homologous testing proteins (Wu et al., 2007).

The fifth and sixth terms (E_phi and E_psi) calculate the match between the predicted torsion angles φ_q(i) and ψ_q(i) of the ith position of the query and the actual torsion angles φ_t(j) and ψ_t(j) of the jth position of the template structures. φ_t(j) and ψ_t(j) for the template are calculated by STRIDE (Frishman and Argos, 1995). φ_q(i) and ψ_q(i) for the query are predicted by a newly developed machine-learning tool called ANGLOR (Wu and Zhang, 2008a).

The seventh term E_hydro is from a hydrophobicity scoring matrix (Silva, 2008) which encourages the hydrophobic residues (V, I, L, F, Y, W, M) to be matched in the query and the template. For segmental threading, if both the residue AA_q(i) at the ith position of the query and the residue AA_t(j) at the jth position of the template are hydrophobic, M(AA_q(i),AA_t(j))=1; if AA_q(i) and AA_t(j) are identical, M(AA_q(i),AA_t(j))=0.7; for all other cases, M(AA_q(i), AA_t(j))=0.

Finally, the last term E_shift is a constant, c₇, which is introduced to avoid the alignment of unrelated residues in the local regions.

For the best performance, the sequence profile, structure profile, predicted secondary structure, solvent accessibility and torsion angles of the query sequence are first generated using the whole-chain sequence, and then fragments are excised from them for use in each segment.

Determining parameters for SEGMER

We first examine the contribution of each of seven energy terms in Eq. 2 to the performance of the SEGMER threading result. We find that that all the terms have a positive contribution to the final threading results in the sense that the average TM-score will decrease when we drop any one of the energy terms (data not shown). For tuning the weighting factors of the seven energy terms and the two gap penalty parameters, we used a grid search technique, i.e. we divided the 9-dimensional parameter space into a grid and ran SEGMER on the validation proteins using the parameters corresponding to each grid cell. As a result, the optimized parameters for the global dynamic programming are c₁=0.66, c₂=0.39, c₃=1.60, c₄=0.19, c₅=0.19, c₆=0.31, c₇=0.99, g_o=7.01, g_e=0.55 for segments with 2 and 4 RSSEs; c₁=0.66, c₂=0.30, c₃=0.50, c₄=0.19, c₅=0.19, c₆=0.20, c₇=0.99, g_o=7.01, g_e=0.55 for segments with 3 RSSEs.

Dynamic programming

We use the Needleman-Wunsch (NW) global dynamic programming algorithm (Needleman and Wunsch, 1970) to identify the best match between a query sequence segment and the templates. A position-specific gap penalty is employed, i.e. no gap is allowed inside an RSSE; gap opening and gap extension penalties apply to other regions; the end gap penalty is neglected. For discontinuous segments, to enable the alignment of query RSSEs with template RSSEs at different locations with a large sequence separation, the original dynamic programming algorithm is modified so that no gap penalty is imposed between RSSEs. An illustrative example of a discontinuous segment sequence threaded onto a template protein is shown in Figure 6.

One of the important advantages of SEGMER over MUSTER is that SEGMER is able to specifically identify the protein templates that only have local structural similarity to the target. Because MUSTER has been optimized based on global NW dynamic programming, an interesting question is whether we could extend MUSTER by using local dynamic programming for identifying substructure similarities. For this purpose, we tried the optimized parameters of MUSTER with local dynamic programming based on the Smith-Waterman (SW) algorithm (Smith and Waterman, 1981). When we apply the local-alignment version of MUSTER to the 144 hard protein targets in our testing set, the average TM-score is found to be about the same as that from the global alignment version of MUSTER on the substructure motifs (i.e. TM-score=0.37). This means that identifying good local structural motifs cannot simply be achieved by using local rather than global dynamic programming because both alignments are essentially based on the whole-chain sequences.

Template ranking and Z-score

The whole-chain threading alignments are usually ranked by the raw alignment score normalized by the length of the full alignment (including query and template end gaps) (Wu and Zhang, 2008b). In the case of segmental threading with a given number of RSSEs, the alignment length is almost constant because the segmental alignments usually contain very few gaps. In fact, we found by analyzing the validation data that the raw alignment score is more sensitive to the alignment quality than the normalized score. Therefore, we use the raw alignment score R_score to rank the alignments. The corresponding Z-score is calculated by

$$\mathrm{Z}-\text{score}=\frac{R_{\mathit{\text{score}}}-\langle R_{\mathit{\text{score}}}\rangle }{\sqrt{\langle R_{\mathit{\text{score}}}^2\rangle -{\langle R_{\mathit{\text{score}}}\rangle }^2}},$$ (3)

where 〈…〉 denotes the average over all templates in the library.