Asymmetric Switch Costs as Sequential Difficulty Effects

Abstract

When switching between tasks of unequal difficulty, there is often a larger switch cost for the easy task than for the difficult task. The authors propose a new account of these asymmetric switch costs based on sequential difficulty effects. They argue that the asymmetry arises from impaired performance after a difficult trial regardless of whether the task switches or repeats. Empirical support for this idea is provided in two experiments on arithmetic task switching in which asymmetries are observed for secondary difficulty manipulations, even in the context of arithmetic task repetitions. The authors discuss how their sequential difficulty account might explain asymmetric restart costs in addition to asymmetric switch costs and how sequential difficulty effects might be explained by resource depletion involving executive control or working memory.

People are slower at switching than repeating tasks. This switch cost is a robust phenomenon (for a review, see Monsell, 2003), but it is often not symmetric when switching between tasks of unequal difficulty. For example, word reading is generally easier (i.e., faster and less error-prone) than color naming with Stroop stimuli (e.g., the word RED printed in blue; see MacLeod, 1991; Stroop, 1935), but when switching between those tasks, word reading is associated with a larger switch cost than color naming (Allport, Styles, & Hsieh, 1994). This switch cost asymmetry—a larger switch cost for the easier task—has been observed in studies with a variety of tasks (e.g., Allport & Wylie, 2000; Campbell, 2005; Cherkasova, Manoach, Intriligator, & Barton, 2002; Ellefson, Shapiro, & Chater, 2006; Koch, Prinz, & Allport, 2005; Leboe, Whittlesea, & Milliken, 2005; Lemaire & Lecacheur, in press; Meuter & Allport, 1999; but see Monsell, Yeung, & Azuma, 2000) and it has been addressed in some models of task switching (Gilbert & Shallice, 2002; Yeung & Monsell, 2003). As described below, these models explain asymmetric switch costs in terms of differential task priming and control input across trials, ultimately construing them as task switching effects.

In this article, we propose a new account of asymmetric switch costs. We suggest that asymmetric switch costs may not be pure task switching effects. Instead, we argue that the asymmetry may arise from impaired performance after a difficult trial regardless of whether the task switches or repeats. In what follows, we review existing models of asymmetric switch costs and introduce our sequential difficulty account. We then provide empirical support for our account with two experiments involving secondary difficulty manipulations. We conclude the article by discussing explanations of asymmetries in task switching and sequential difficulty effects.

Models of Asymmetric Switch Costs

There are few accounts of asymmetric switch costs in the literature. An early account (Allport et al., 1994) attributed the asymmetry to differential positive and negative priming of easy and difficult tasks, with stronger positive priming (or activation) of the difficult task and stronger negative priming (or inhibition) of the easy task. A switch from the difficult task to the easy task involved counteracting strong positive priming of the irrelevant task and strong negative priming of the relevant task, whereas a switch in the reverse direction involved counteracting weaker priming effects, resulting in a larger switch cost for the easy task. Although this account is interesting, the idea that the easy task is inhibited has received skepticism (e.g., Monsell et al., 2000; Wong & Leboe, 2009; Yeung & Monsell, 2003; but see Arbuthnott, 2008). Furthermore, computational models of task switching have been developed that explain asymmetric switch costs solely in terms of relative differences in activation, without inhibition of the easy task (Gilbert & Shallice, 2002; Yeung & Monsell, 2003).

The models of Gilbert and Shallice (2002) and Yeung and Monsell (2003) differ in many respects, but they capture asymmetric switch costs in similar ways. The asymmetry primarily reflects a combination of two things in each model: task priming and control input. Task priming is a transient bias in activation toward the task performed most recently. It is a major source of the switch cost produced by each model because task switches are impaired by priming of the irrelevant task and task repetitions are facilitated by priming of the relevant task. Control input is top-down activation of the currently relevant task. In both models, more control input is required to perform the difficult task than the easy task because the latter is assumed to have higher base-level activation than the former. In Gilbert and Shallice’s model, the activation pattern produced by this differential control input carries over from one trial to the next as a form of task priming that is more pronounced for the difficult task than for the easy task. In Yeung and Monsell’s model, task priming is separate from control input and it has a stronger effect on the activation of the difficult task than the easy task because of the form of the activation function in the model.

Asymmetric switch costs arise because task priming makes the difficult task a strong competitor when switching to the easy task. This competition prolongs the performance of an easy task switch relative to an easy task repetition, resulting in a large switch cost for the easy task. In contrast, regardless of whether it is primed, the easy task is always a strong competitor to the difficult task because of its high base-level activation. This competition is attenuated by high control input for a difficult task switch and by the combination of high control input and task priming for a difficult task repetition, resulting in a relatively small or null switch cost for the difficult task. The interested reader is referred to Gilbert and Shallice (2002) and Yeung and Monsell (2003) for further details concerning their models and for simulation results demonstrating that the models can produce asymmetric switch costs and even their reversal under certain circumstances.

Despite these successes in modeling asymmetric switch costs, there is some suggestion in the literature that the models of Gilbert and Shallice (2002) and Yeung and Monsell (2003) may not capture the true source of the asymmetry. As noted by Bryck and Mayr (2008), the asymmetry is linked to the act of task switching in each model, implying that actual task switches are necessary for observing it. However, this notion is challenged by work on restart costs, which are performance decrements that follow delays or interruptions that do not involve task switches (Allport & Wylie, 2000; Altmann & Gray, 2002; Gopher, Armony, & Greenshpan, 2000). Restart costs can be asymmetric in much the same way as switch costs (i.e., a larger restart cost for the easier task), indicating that the asymmetry is not contingent on task switching (Allport & Wylie, 2000; Bryck & Mayr, 2008). We arrive at a similar conclusion in the present study, but from a reinterpretation of asymmetric switch costs as sequential difficulty effects.

A Sequential Difficulty Account

Our account was motivated by the observation that switching from a difficult task to an easy task (or vice versa) involves not just a change of task, but also a change in difficulty. For ease of exposition, we will use a non-sequential, performance-based definition of difficulty: An easy task is defined as easy because it yields shorter response times (RTs) and lower error rates (ERs) than a difficult task, irrespective of the preceding task.¹ By this definition, it is possible to distinguish between task transitions and difficulty transitions. A task transition is a nominal change of task that may or may not involve a change in difficulty (i.e., two tasks could yield equivalent performance measures). A difficulty transition is a change in difficulty that may or may not involve a change of task (i.e., two same-task conditions could yield different levels of performance; e.g., incongruent and congruent Stroop color naming). Thus, in principle, task transitions and difficulty transitions can be treated orthogonally. However, in task switching situations involving tasks of unequal difficulty, the two types of transitions are confounded because task switches always involve difficulty switches and task repetitions always involve difficulty repetitions. Our observation of this confound led us to hypothesize that asymmetric switch costs may reflect a combination of two sequential effects, one associated with task transitions and one associated with difficulty transitions.² For task transitions, we noted earlier that switch costs have been modeled as priming effects across trials (Gilbert & Shallice, 2002; Yeung & Monsell, 2003; see also Logan & Schneider, 2006; Schneider & Logan, 2005, 2006). For difficulty transitions, we suggest that performance on the current trial—regardless of whether it involves an easy or difficult task, or even a task switch—may be affected by the difficulty of the task on the preceding trial. More specifically, we hypothesize that RT may become longer and ER may increase after a difficult trial. Although this is an experimental hypothesis, the theoretical basis of sequential difficulty effects will be considered later. At this point, our objective is to establish the possibility of sequential difficulty effects and describe how such effects could lead to asymmetric switch costs.

Research on sequential difficulty effects has been motivated by the finding of mixing costs, which are performance decrements for easy stimuli in mixed blocks (consisting of easy and difficult stimuli for the same task) compared with pure blocks (consisting of easy stimuli only). Mixing costs have been observed in a wide range of studies (e.g., Campbell & Arbuthnott, in press; Kiger & Glass, 1981; Lupker, Brown, & Colombo, 1997; Lupker, Kinoshita, Coltheart, & Taylor, 2003; Monsell, Patterson, Graham, Hughes, & Milroy, 1992; Strayer & Kramer, 1994a, 1994b; for a review, see Los, 1996; for work on task mixing costs, see Rubin & Meiran, 2005) and interpreted as evidence for contextual effects on performance, with difficult stimuli affecting the way that easy stimuli are processed. To determine whether mixing costs reflect global (i.e., block-wise) or local (i.e., trial-wise) effects, some researchers have looked for trial-to-trial sequential effects involving easy and difficult stimuli, leading to the finding of impaired performance following a difficult trial (e.g., Kiger & Glass, 1981; Taylor & Lupker, 2001; see also Campbell & Metcalfe, 2008). For example, Kiger and Glass found that subjects were slower to verify an arithmetic problem when it followed a difficult arithmetic problem than when it preceded the problem. Taylor and Lupker found that naming latencies were longer for various kinds of word and nonword stimuli when they followed difficult stimuli than when they followed easy stimuli.

There are three important things to note about the sequential difficulty effects observed in past research. First, they were observed across trials that did not involve task switching (though they were also observed for task switches; see Kiger & Glass, 1981), reinforcing our distinction between task transitions and difficulty transitions. Second, the effects were observed following correct trials, so they cannot be attributed to post-error slowing (e.g., Jentzsch & Dudschig, 2009; Rabbitt, 1966). Third, the effects were not associated with different congruency relations across trials, so they cannot be attributed to conflict adaptation (e.g., Botvinick, Braver, Barch, Carter, & Cohen, 2001; Brown, Reynolds, & Braver, 2007). We propose that sequential difficulty effects of this sort may be present when switching between tasks of unequal difficulty.

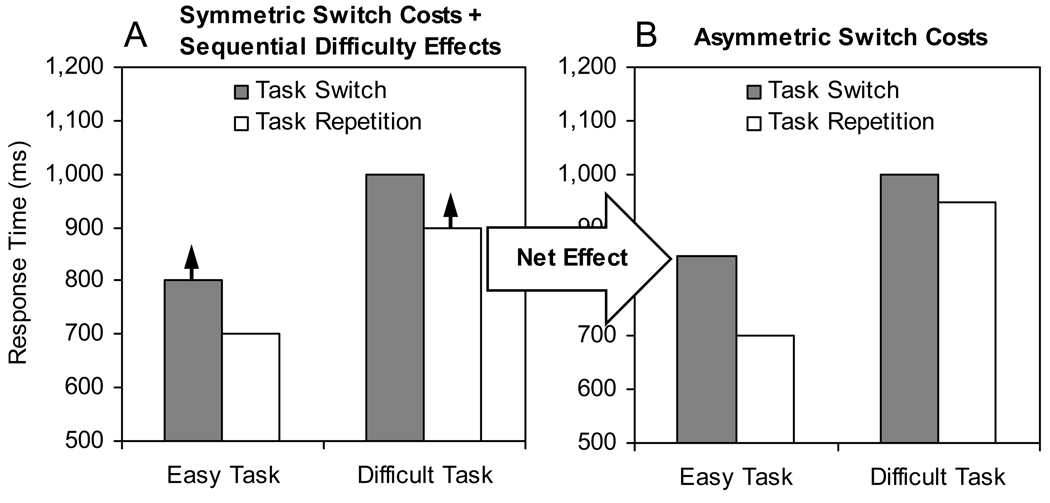
Consider a situation in which subjects are switching between easy and difficult tasks. For the sake of argument, assume that the true switch costs (uncontaminated by any other effects) are symmetric across tasks, as depicted in Figure 1A. Now imagine that sequential difficulty effects are present, with longer RTs after difficult trials regardless of the difficulty of the current trial. These effects would be manifest on switches to the easy task and on repetitions of the difficult task, as indicated by the solid arrows in Figure 1A. The symmetric switch costs and sequential difficulty effects, when combined, would yield the asymmetric switch costs depicted in Figure 1B. By this account, asymmetric switch costs reflect a combination of two sequential effects, with the true switch costs being either symmetric (as in Figure 1A) or asymmetric in either direction (note that the typical asymmetry can arise from the reverse asymmetry if the sequential difficulty effects are large enough).

Figure 1.

Illustration of how sequential difficulty effects (i.e., slowing down after a difficult trial, as indicated by solid arrows) can combine with symmetric switch costs (panel A) to produce asymmetric switch costs (panel B).

This sequential difficulty account differs markedly from the explanations provided by existing models of task switching (Gilbert & Shallice, 2002; Yeung & Monsell, 2003) because it implies that asymmetric switch costs are not pure task switching effects. A related implication is that switch costs are not pure measures of the duration of task switching processes, at least when switching between tasks of unequal difficulty (for analogous views, see Allport et al., 1994; Allport & Wylie, 2000; Logan & Bundesen, 2003; Logan et al., 2007; Schneider & Logan, 2005). Given these important implications, the goal of the present study was to investigate the possible role of sequential difficulty effects in task switching performance.

Our experimental approach involved comparing the effects of different difficulty manipulations in the same context. The motivating hypothesis was that if asymmetric switch costs in task switching reflect sequential difficulty effects, then similar asymmetries should be observed with secondary difficulty manipulations that do not necessarily involve task switching. The primary difficulty manipulation that was common to both experiments was the choice of basic tasks: verification of double-digit addition and subtraction problems. We chose these arithmetic tasks for three reasons. First, addition and subtraction have been studied previously in task switching contexts (e.g., Baddeley, Chincotta, & Adlam, 2001; Biederman, 1973; Buchler, Hoyer, & Cerella, 2008; Derakshan, Smyth, & Eysenck, 2009; Ellefson et al., 2006; Jersild, 1927; Rubinstein, Meyer, & Evans, 2001; Spector & Biederman, 1976; see also Koch et al., 2005). Second, there is evidence that subtraction is slower and more error-prone—in other words, more difficult—than addition (e.g., Campbell, 2008; Campbell & Xue, 2001; Ellefson et al., 2006; Rubinstein et al., 2001). On this basis, we predicted asymmetric switch costs, with a larger switch cost for addition than for subtraction (see Ellefson et al., 2006, for evidence of this asymmetry in children, and Campbell & Arbuthnott, in press, for an asymmetry involving addition and multiplication; but see also Rubinstein et al., 2001). Third, arithmetic tasks afford a number of secondary difficulty manipulations. We will discuss each of these manipulations in the context of specific experiments.

In each experiment, the question of interest was whether the switch costs associated with the secondary difficulty manipulation (even in the context of an arithmetic task repetition) would be similar to the asymmetric switch costs predicted for addition and subtraction.³ More specifically, we will interpret asymmetric switch costs as similar if there is a larger switch cost in the easy condition than in the difficult condition. Whether there is a small, null, or reversed switch cost in the difficult condition depends on the magnitude of the sequential difficulty effect relative to the switch cost. As can be inferred from Figure 1, as the magnitude of the sequential difficulty effect increases (i.e., the solid arrows become longer), the switch cost in the difficult condition can go from small to null to reversed. Given that we have no a priori knowledge of the relative magnitudes of sequential difficulty effects for addition and subtraction compared with our secondary difficulty manipulations, it is not possible to predict the exact form of the asymmetries. Nevertheless, observing similar asymmetries across difficulty manipulations would suggest that sequential difficulty effects contribute to asymmetric switch costs in task switching.

Experiment 1

The secondary difficulty manipulation in Experiment 1 was whether the arithmetic problems involved no carrying and no borrowing (simple problems) or involved carrying and borrowing (complex problems). Problems that involve carrying and borrowing have been shown to elicit slower and more error-prone performance than problems that do not involve such operations (e.g., Fürst & Hitch, 2000; Geary, Frensch, & Wiley, 1993; Imbo & LeFevre, in press; Imbo, Vandierendonck, & Vergauwe, 2007; for a review, see Imbo, De Rammelaere, & Vandierendonck, 2005). Therefore, by our performance-based definition of difficulty, complex problems are more difficult than simple problems. The question of interest was whether switching between simple and complex problem categories would produce an asymmetry similar to that predicted for switching between addition and subtraction, as our sequential difficulty account suggests. Consequently, we looked for asymmetric category switch costs, with a larger category switch cost for simple problems than for complex problems, even in the context of arithmetic task repetitions.

Method

Subjects

There were 30 students from Carnegie Mellon University who completed the experiment for course credit.

Apparatus

The experiment was conducted using Tscope (Stevens, Lammertyn, Verbruggen, & Vandierendonck, 2006) on computers that displayed stimuli on monitors and registered responses from QWERTY keyboards.

Stimuli

There were four types of arithmetic problems in the experiment: no-carry addition (e.g., 31 + 27 = 58), carry addition (e.g., 29 + 34 = 63), no-borrow subtraction (e.g., 47 ‒ 22 = 25), and borrow subtraction (e.g., 51 ‒ 35 = 16). For each problem type, the set of all possible problems for which all three terms in a problem were double-digit numbers was determined, resulting in sets of 1,980 problems for no-carry addition and no-borrow subtraction and sets of 1,260 problems for carry addition and borrow subtraction. Each subject received a unique random subset of the problems from each set; therefore, it was possible for a given double-digit number to be associated with more than one problem type, meaning that most (if not all) numbers were multivalent in the experiment.

Half of the problems that subjects verified were true and half were false. False problems were constructed by changing the answers to true problems such that they were incremented or decremented by either 2 or 10. The specific change for a false problem was determined randomly except for the constraint that the answer had to be a double-digit number. This approach to constructing false problems had three advantages. First, all answers were double-digit numbers regardless of whether they were true or false. Second, false answers preserved the parity (odd or even status) of true answers, thereby preventing fast rejection based on parity mismatches (Krueger & Hallford, 1984). Third, subjects could not focus exclusively on either the tens digits or the ones digits to verify a problem.

Procedure

Subjects were seated at computers in private testing rooms after providing informed consent. Written instructions were presented to subjects and explained by the experimenter. Subjects completed blocks of 65 trials in which they had to verify arithmetic problems. The problem type for the first trial was selected randomly and the problem types for the remaining 64 trials were selected pseudo-randomly such that each problem type and transition between problem types occurred equally often. Within the set of 64 trials, half of the problems were selected randomly and changed to have false answers as described above.

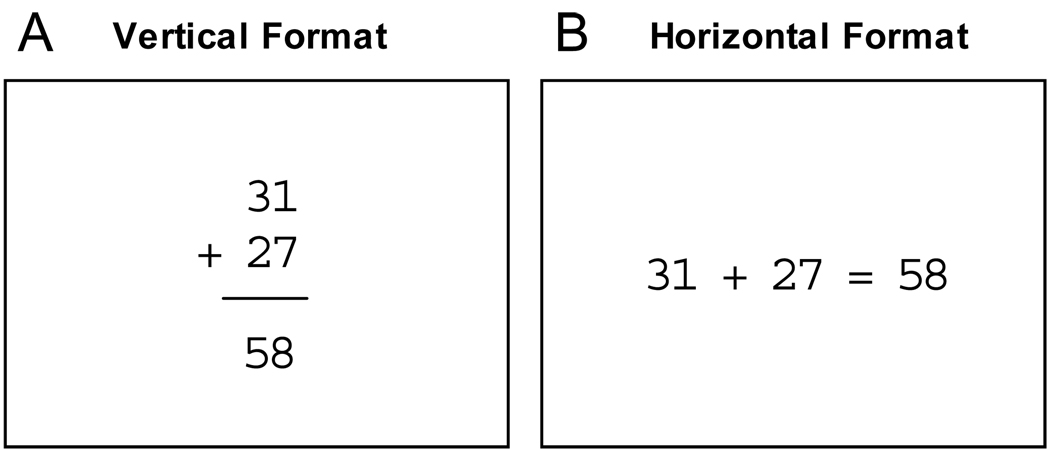
On each trial, a single problem was presented in a vertical format (see Figure 2A) in white Courier font in the center of a black screen. Subjects had to verify whether the problem was true or false by pressing one of two keys (S or L), with response mappings posted at the bottom of the screen and counterbalanced across subjects. Subjects were instructed to respond quickly and accurately. RT was measured from problem onset to the registration of the keypress response. After a response, the screen was cleared and the next trial commenced after 500 ms. Subjects completed 9 blocks of 65 trials for a total of 585 problems, with the first block as practice. Breaks were allowed between blocks.

Figure 2.

Example of an arithmetic problem presented in vertical and horizontal formats (panels A and B, respectively). Experiment 1 involved only the vertical format. Experiment 2 involved both formats.

Results and Discussion

The first trial of each block and trials with RTs exceeding three standard deviations of a subject’s cell mean in the experimental design (1.4% of trials) were excluded from analysis. Only correct trials were included in the RT analysis. Excluding trials that were immediately preceded by errors did not change the data pattern, so those trials remained in all analyses. Trials were categorized by task (addition or subtraction), task transition (task switch or task repetition from trial n − 1 to n), category (simple or complex), and category transition (category switch or category repetition from trial n − 1 to n). Mean RT and ER data were submitted to repeated-measures analyses of variance (ANOVAs) with these four variables as factors. All significant (p < .05) and marginally significant effects from the ANOVAs are reported below. Note that the problems in each block were randomized such that each of the 16 conditions in the design occurred equally often.

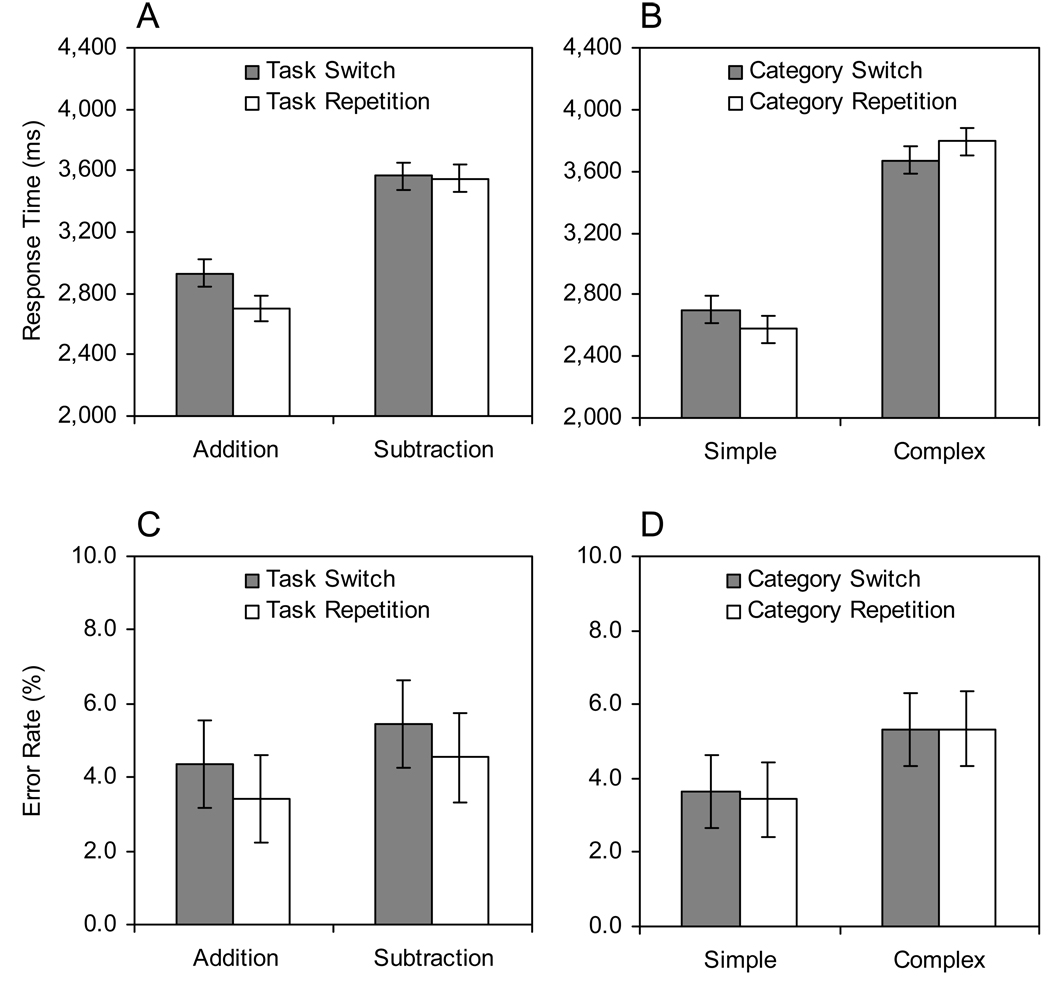
The data are summarized in Figure 3 (see Appendix A for all condition means). The RT analysis revealed that subtraction (3,556 ms) was slower than addition (2,817 ms), F(1,29) = 82.88, MSE = 790,017.16, p < .001, η_p² = .74, and task switches (3,248 ms) were slower than task repetitions (3,125 ms), F(1,29) = 10.86, MSE = 165,264.41, p < .01, η_p² = .27. As shown in Figure 3A, task and task transition interacted to produce asymmetric switch costs, F(1,29) = 12.67, MSE = 111,161.37, p < .01, η_p² = .30. There was a sizable switch cost for addition (231 ms) but not for subtraction (14 ms). These results indicate that the asymmetry observed in past research (e.g., Allport et al., 1994) can be replicated with arithmetic tasks (see also Ellefson et al., 2006).

Figure 3.

Mean response times (panels A and B) and error rates (panels C and D) from Experiment 1. Error bars represent 95% confidence intervals.

The asymmetry was not limited to task switching. Complex problems (3,733 ms) were verified more slowly than simple problems (2,640 ms), F(1,29) = 116.58, MSE = 1,228,586.08, p < .001, η_p² = .80, although category switches (3,187 ms) were not slower than category repetitions (3,186 ms), F < 1. As shown in Figure 3B, category and category transition interacted to produce asymmetric category switch costs, F(1,29) = 16.32, MSE = 110,581.54, p < .001, η_p² = .36. There was a category switch cost for simple problems (124 ms) but a reversed category switch cost for complex problems (−121 ms). This asymmetry was present even for arithmetic task repetitions (the three-way interaction involving category, category transition, and task transition was not significant, F < 1), with category switch costs of 143 ms and −111 ms for simple and complex problems, respectively, consistent with a significant interaction between category and category transition obtained in a separate ANOVA that excluded arithmetic task switches, F(1,29) = 17.16, MSE = 56,611.78, p < .001, η_p² = .37. These results indicate that asymmetric switch costs can be found with a secondary difficulty manipulation, even in the context of task repetitions. The difference in the asymmetries (viz., a null switch cost for subtraction but a reversed category switch cost for complex problems) may reflect a difference in the magnitudes of the sequential difficulty effects induced by subtraction and complex problems, a possibility that we alluded to at the end of the Introduction.

The only remaining significant effect in the RT analysis was an interaction between task and category such that the difference between complex and simple problems was larger for subtraction (1,290 ms) than for addition (895 ms), F(1,29) = 14.89, MSE = 314,570.36, p < .01, η_p² = .34.

The mean ER was 4.4%. As shown in Figure 3C, subtraction (5.0%) tended to be more error-prone than addition (3.9%), F(1,29) = 4.15, MSE = 34.72, p = .051, η_p² = .13, and task switches (4.9%) were more error-prone than task repetitions (4.0%), F(1,29) = 6.61, MSE = 15.43, p < .05, η_p² = .19. Task and task transition did not interact, F < 1. As shown in Figure 3D, complex problems (5.3%) were more error-prone than simple problems (3.5%), F(1,29) = 18.45, MSE = 20.74, p < .001, η_p² = .39, but there was no effect of category transition and no interaction between category and category transition, both Fs < 1. There were no other significant effects in the ER analysis.

In summary, asymmetric switch costs were found not only when switching between addition and subtraction (see Figure 3A), but also when switching between simple and complex problem categories (see Figure 3B), even when the arithmetic task repeated. These results are consistent with the proposal that the asymmetries reflect sequential difficulty effects. The goal of Experiment 2 was to generalize these findings to another secondary difficulty manipulation.

Experiment 2

The secondary difficulty manipulation in Experiment 2 was chosen to be very different from the manipulation in Experiment 1. None of the problems in Experiment 2 involved carrying or borrowing. Instead, we manipulated the spatial format in which each problem was presented. Some problems were presented in a vertical format with the tens and ones digits of all terms aligned in columns (see Figure 2A). Other problems were presented in a horizontal format with no spatial alignment of specific digits (see Figure 2B). Research by LeFevre and colleagues (Imbo & LeFevre, in press; Trbovich & LeFevre, 2003) indicates that horizontal problems take longer to solve and may be more error-prone than vertical problems. Therefore, by our performance-based definition of difficulty, horizontal problems are more difficult than vertical problems. The question of interest was whether switching between vertical and horizontal formats would produce an asymmetry similar to that predicted for switching between addition and subtraction, as our sequential difficulty account suggests. Consequently, we looked for asymmetric format switch costs, with a larger format switch cost for vertical problems than for horizontal problems, even in the context of arithmetic task repetitions.

Method

Subjects

There were 38 students from Carnegie Mellon University who completed the experiment for course credit. None of the subjects were in Experiment 1.

Apparatus

Same as in Experiment 1.

Stimuli

Only the no-carry addition and no-borrow subtraction problems from Experiment 1 were used. The problem sets and method of constructing false problems were identical to Experiment 1.

Procedure

The procedure was similar to that of Experiment 1 except for changes related to the format manipulation. Each problem was presented in either a vertical format or a horizontal format on each trial (see Figure 2). The problem type and format for the first trial in each block were selected randomly and the problem types and formats for the remaining 64 trials were selected pseudo-randomly such that each problem type, format, and transition between problem types and formats occurred equally often. As in Experiment 1, subjects completed 9 blocks of 65 trials for a total of 585 problems, with the first block as practice. After the experiment, subjects completed a written questionnaire in which they rated how difficult it was to solve problems presented in each format on a 9-point scale ranging from 1 (“very easy”) to 9 (“very hard”). Separate ratings were obtained for vertical and horizontal formats and the order in which the formats were rated was counterbalanced across subjects.

Results and Discussion

The first trial of each block and trials with RTs exceeding three standard deviations of a subject’s cell mean in the experimental design (1.6% of trials) were excluded from analysis. Only correct trials were included in the RT analysis. Excluding trials that were immediately preceded by errors did not change the data pattern, so those trials remained in all analyses. Trials were categorized by task (addition or subtraction), task transition (task switch or task repetition from trial n − 1 to n), format (vertical or horizontal), and format transition (format switch or format repetition from trial n − 1 to n). Mean RT and ER data were submitted to repeated-measures ANOVAs with these four variables as factors. All significant (p < .05) and marginally significant effects from the ANOVAs are reported below. Note that the problems in each block were randomized such that each of the 16 conditions in the design occurred equally often.

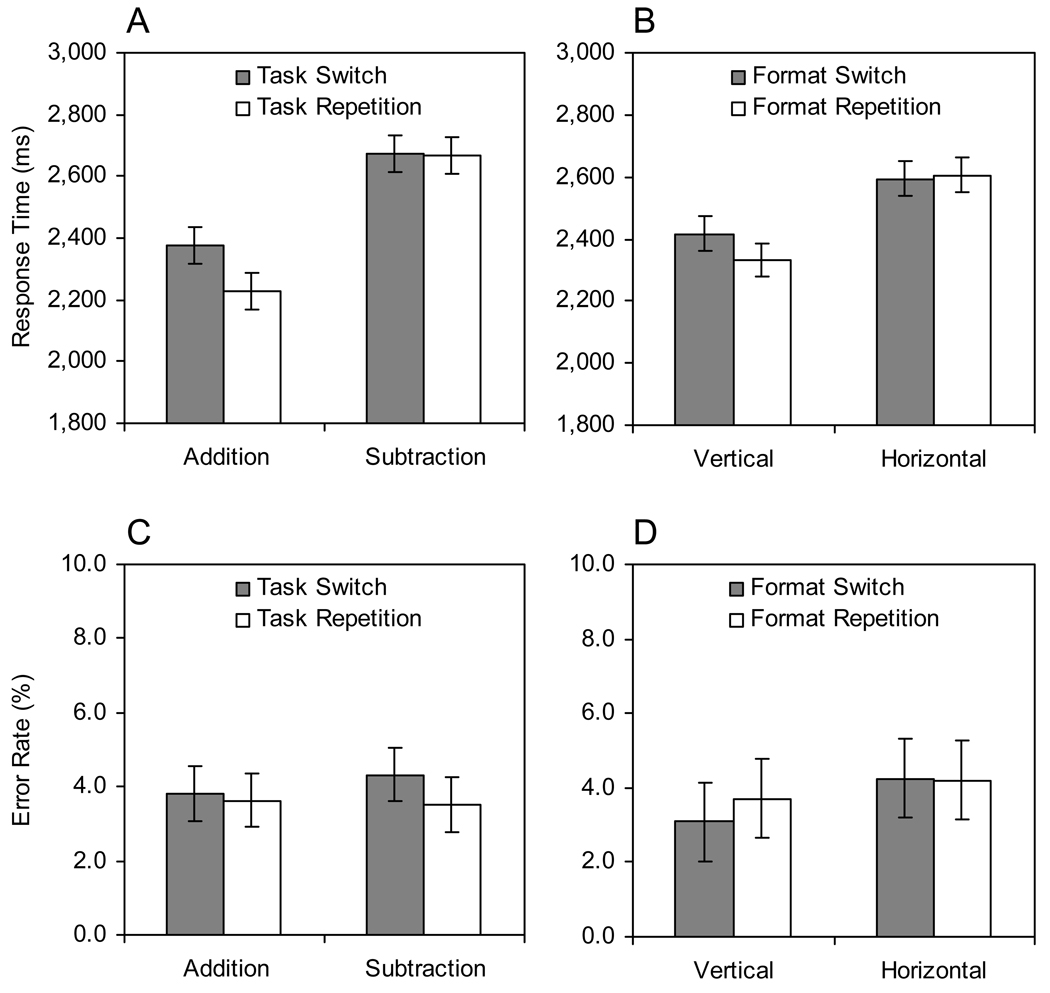
The data are summarized in Figure 4 (see Appendix B for all condition means). The RT analysis revealed that subtraction (2,671 ms) was slower than addition (2,304 ms), F(1,37) = 198.86, MSE = 102,921.16, p < .001, η_p² = .84, and task switches (2,527 ms) were slower than task repetitions (2,448 ms), F(1,37) = 18.35, MSE = 51,296.30, p < .001, η_p² = .33. As shown in Figure 4A, task and task transition interacted to produce asymmetric switch costs, F(1,37) = 11.58, MSE = 64,022.39, p < .01, η_p² = .24. There was a sizable switch cost for addition (149 ms) but not for subtraction (9 ms). These results replicate the asymmetry observed in Experiment 1 (compare Figure 3A and Figure 4A).

Figure 4.

Mean response times (panels A and B) and error rates (panels C and D) from Experiment 2. Error bars represent 95% confidence intervals.

The asymmetry was not limited to task switching. Horizontal problems (2,599 ms) were verified more slowly than vertical problems (2,375 ms), F(1,37) = 42.19, MSE = 181,179.35, p < .001, η_p² = .53, and format switches (2,505 ms) tended to be slower than format repetitions (2,469 ms), F(1,37) = 3.41, MSE = 58,432.05, p = .073, η_p² = .08. As shown in Figure 4B, format and format transition interacted to produce asymmetric format switch costs, F(1,37) = 6.31, MSE = 56,278.30, p < .05, η_p² = .15. There was a format switch cost for vertical problems (85 ms) but not for horizontal problems (−12 ms). This asymmetry was present even for arithmetic task repetitions (the three-way interaction involving format, format transition, and task transition was not significant, F(1,37) = 1.96, MSE = 26,032.28, p = .17), with format switch costs of 134 ms and 1 ms for vertical and horizontal problems, respectively, consistent with a significant interaction between format and format transition obtained in a separate ANOVA that excluded arithmetic task switches, F(1,37) = 8.79, MSE = 38,441.65, p < .01, η_p² = .19. These results indicate that asymmetric switch costs can be found with another secondary difficulty manipulation, even in the context of task repetitions.

There were no other significant effects in the RT analysis, although there were some marginally significant interactions subsumed by a marginally significant four-way interaction, F(1,37) = 3.03, MSE = 52,480.81, p = .090, η_p² = .08, which appears to reflect the lack of a format switch cost (−20 ms) for vertical subtraction problems that were task switches.

The mean ER was 3.8%. As shown in Figure 4C, subtraction (3.9%) was as error-prone as addition (3.7%), F(1,37) = 1.02, MSE = 5.89, p = .32, and task switches (4.1%) tended to be more error-prone than task repetitions (3.6%), F(1,37) = 3.58, MSE = 10.27, p = .066, η_p² = .09. Despite what might appear to be a reversed asymmetry of switch costs in Figure 4C, task and task transition did not interact, F(1,37) = 1.53, MSE = 9.81, p = .22. As shown in Figure 4D, horizontal problems (4.2%) were more error-prone than vertical problems (3.4%), F(1,37) = 10.18, MSE = 10.43, p < .01, η_p² = .22, but there was no effect of format transition, F(1,37) = 1.02, MSE = 12.15, p = .32, and, despite the numerical differences in Figure 4D, there was no interaction between format and format transition, F < 1. The only remaining significant effect in the ER analysis was a three-way interaction between task transition, format, and format transition, F(1,37) = 9.78, MSE = 6.91, p < .01, η_p² = .21, which reflects format switch costs for horizontal task switches and vertical task repetitions only.

The post-experiment difficulty ratings support the inference from the RT and ER data that horizontal problems were more difficult than vertical problems. The mean difficulty ratings were 3.9 and 2.3 for horizontal and vertical problems, respectively, t(37) = 7.30, SEM = 0.21, p < .001. Of the 38 subjects in the experiment, 33 gave higher difficulty ratings to horizontal problems than to vertical problems.

In summary, asymmetric switch costs were found not only when switching between addition and subtraction (see Figure 4A), but also when switching between vertical and horizontal problem formats (see Figure 4B), even when the arithmetic task repeated. The first result replicates Experiment 1 and the second result indicates that the asymmetry generalizes to another secondary difficulty manipulation. These results are consistent with the proposal that the asymmetries reflect sequential difficulty effects.

True or False: Another Difficulty Manipulation

The difficulty manipulations that we examined in the preceding experimental analyses were task (addition or subtraction), problem category (simple or complex), and problem format (vertical or horizontal). However, there is another difficulty manipulation associated with our experiments: the type of answer (true or false) presented with each problem. Past research involving arithmetic verification tasks has revealed that people are faster at verifying true answers than false answers (e.g., Ashcraft & Battaglia, 1978; Geary, Widaman, & Little, 1986; Parkman & Groen, 1971; Zbrodoff & Logan, 1990). If false answers were more difficult to verify than true answers in our experiments, then there may be sequential difficulty effects reflected by impaired performance following false answers.

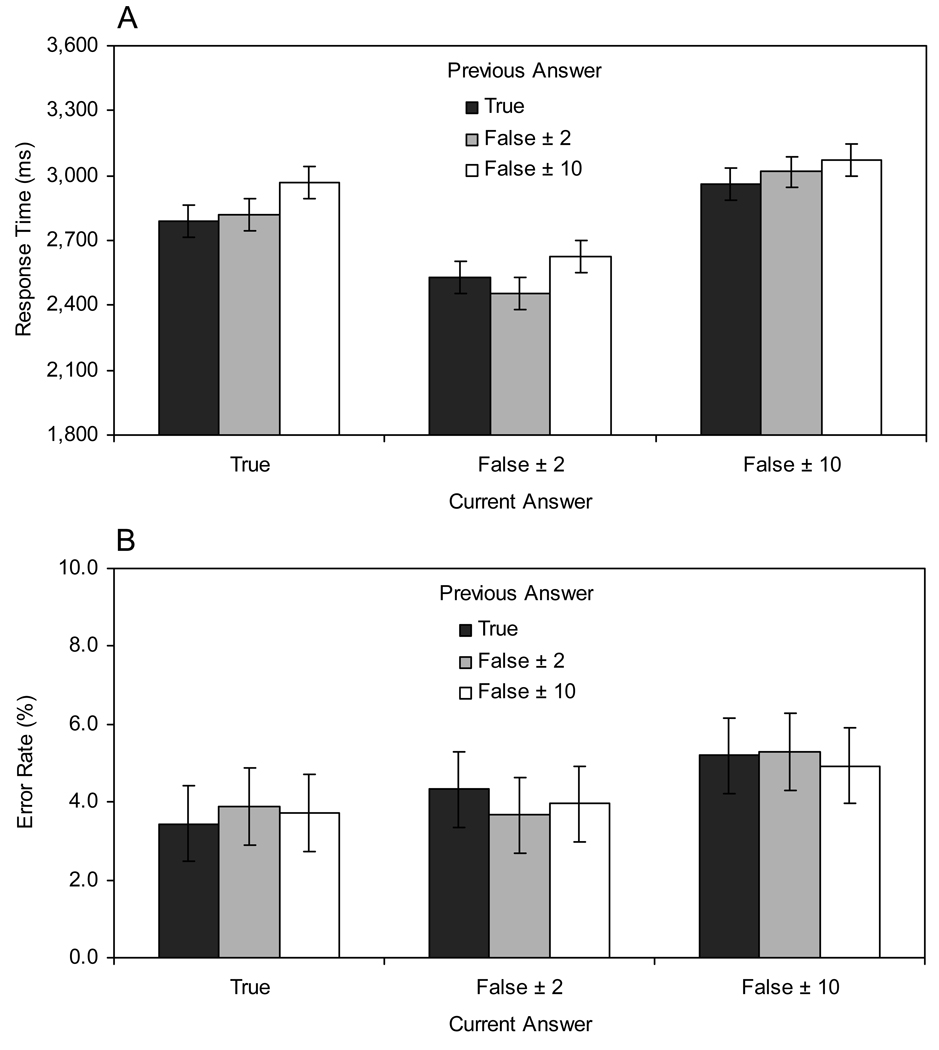
To explore this possibility, we analyzed the data from each experiment as a function of whether the current and previous answers were true or false, and, in the case of a false answer, whether it was ± 2 or ± 10 from the true answer. Mean RTs and ERs were submitted to repeated-measures ANOVAs with current answer (true, false ± 2, or false ± 10) and previous answer (true, false ± 2, or false ± 10) as factors. Data limitations precluded the inclusion of the answer variables as factors in the ANOVAs reported earlier. All significant (p < .05) and marginally significant effects from the ANOVAs are reported below.

The RT data (collapsed across experiments) are summarized in Figure 5A (see Appendix C for all condition means by experiment). The RT analysis revealed that true answers were verified more slowly than false ± 2 answers but faster than false ± 10 answers (see Figure 5A); the main effect of current answer was significant in Experiment 1, F(2,58) = 43.80, MSE = 273,416.61, p < .001, η_p² = .60; and in Experiment 2, F(2,74) = 27.79, MSE = 94,415.93, p < .001, η_p² = .43. All pairwise comparisons among marginal means were significant (p < .05).

Figure 5.

Mean response times (panel A) and error rates (panel B) as a function of current and previous answers. Error bars represent 95% confidence intervals.

The RT analysis also revealed that performance was slower after false ± 10 answers than after true answers and false ± 2 answers (see Figure 5A); the main effect of previous answer was significant in Experiment 1, F(2,58) = 8.04, MSE = 74,283.05, p < .001, η_p² = .22; and in Experiment 2, F(2,74) = 10.82, MSE = 52,793.88, p < .001, η_p² = .23. Pairwise comparisons among marginal means indicated that performance after false ± 10 answers was significantly slower (p < .05) than after true answers and false ± 2 answers in both experiments, whereas none of the differences between the latter two answer types were significant.

These effects are qualified to some extent by an interaction between current answer and previous answer, which was significant in Experiment 2, F(4,148) = 4.32, MSE = 30,558.94, p < .01, η_p² = .10; but not in Experiment 1, F < 1. In Experiment 2, the interaction predominantly reflects the lack of a previous answer effect for current false ± 10 answers; a follow-up ANOVA revealed that the previous answer effect was not significant for current false ± 10 answers in Experiment 2, F < 1.

The ER data (collapsed across experiments) are summarized in Figure 5B (see Appendix C for all condition means by experiment). The ER analysis revealed that false ± 10 answers were verified incorrectly more often than true answers and false ± 2 answers (see Figure 5B); the main effect of current answer was significant in Experiment 1, F(2,58) = 4.80, MSE = 14.82, p < .05, η_p² = .14; and in Experiment 2, F(2,74) = 4.09, MSE = 16.42, p < .05, η_p² = .10. Pairwise comparisons among marginal means indicated that false ± 10 answers were verified incorrectly significantly more often (p < .05) than true answers in both experiments and significantly more often than false ± 2 answers in Experiment 1 only. None of the differences between true answers and false ± 2 answers were significant. The analysis also revealed that ER was generally not affected by the nature of the previous answer; the main effect of previous answer and the interaction between current answer and previous answer were not significant in either experiment.

In summary, we found that false ± 10 answers were verified more slowly and less accurately than true answers and false ± 2 answers; of the latter two answer types, true answers were verified more slowly than false ± 2 answers (see Figure 5A). This data pattern suggests that the double-digit answers were verified using a serial, self-terminating strategy whereby the ones digit was verified before the tens digit (Geary et al., 1986). If the ones digit did not match the true value, then a “false” response was given without verifying the tens digit, resulting in short RTs for false ± 2 answers. If the ones digit of the answer did match the true value, then the tens digit was verified, prolonging RTs for true answers and false ± 10 answers. The shorter RTs and lower ERs for true answers than for false ± 10 answers are consistent with past research indicating that people are better at verifying true answers than false answers (e.g., Ashcraft & Battaglia, 1978; Geary et al., 1986; Parkman & Groen, 1971; Zbrodoff & Logan, 1990). Given that false ± 10 answers were the most difficult to verify, our sequential difficulty account predicts impaired performance after such answers. The data provide some evidence in support of this prediction: RT was longer following a false ± 10 answer except when the current answer was also false ± 10, in which case the effect was in the predicted direction but not always significant.

General Discussion

The aim of the present study was to propose and evaluate a new account of asymmetric switch costs in task switching performance. According to our sequential difficulty account, asymmetric switch costs are not pure task switching effects. Instead, they are sequential difficulty effects combined with what could be symmetric switch costs. We obtained evidence for our account in two experiments involving arithmetic task switching with secondary difficulty manipulations. We found asymmetric switch costs when switching between addition and subtraction, but we also observed asymmetric switch costs when switching between simple and complex problem categories (Experiment 1) and vertical and horizontal problem formats (Experiment 2), even in the context of arithmetic task repetitions. These asymmetries and the results of an analysis of answer type (true or false) are consistent with an explanation based on sequential difficulty effects. We conclude this article by discussing explanations of asymmetries in task switching and proposing a theoretical account of sequential difficulty effects in terms of resource depletion involving executive control or working memory.

Asymmetries

The present findings are challenging for existing models of asymmetric switch costs (Gilbert & Shallice, 2002; Yeung & Monsell, 2003) because the asymmetry is linked to the act of task switching in each model. Observing the asymmetry with task repetitions, as we did with our secondary difficulty manipulations, indicates that the asymmetry is not contingent on task switching. Bryck and Mayr (2008) reached a similar conclusion in the context of restart costs. In their study, subjects performed runs of easy (E) and difficult (D) tasks with either short (-) or long (---) intertrial intervals (ITIs):

E-E---E-E---D-D---D-D---E-E---E-E---D-D---D-D…

Besides finding asymmetric switch costs, Bryck and Mayr found asymmetric restart costs: RT was longer for task repetitions associated with long ITIs (E---E and D---D) than for task repetitions associated with short ITIs (E-E and D-D), and this restart cost was larger for the easier task. Bryck and Mayr argued that this asymmetry with task repetitions cannot be explained by models that depend on task switching to produce asymmetries (Gilbert & Shallice, 2002; Yeung & Monsell, 2003).

Motivated by their findings, Bryck and Mayr (2008) proposed an alternative account of asymmetric switch costs that is based on interference in long-term memory retrieval (for a related account, see Leboe et al., 2005; Wong & Leboe, 2009). They suggested that a task switch or a delayed task repetition requires retrieving information about the relevant task from long-term memory (see also Mayr & Kliegl, 2000). This task information is represented by instances of prior task performance that have been encoded into long-term memory (Logan, 1988; Mayr & Bryck, 2005; Waszak, Hommel, & Allport, 2003). A critical assumption made by Bryck and Mayr is that the probability of encoding an instance depends on the amount of attentional control exerted during task performance, with more control leading to the encoding of more instances. If more control is required to perform a difficult task than an easy task (Gilbert & Shallice, 2002; Yeung & Monsell, 2003), then more instances of the difficult task would be encoded into long-term memory. On a subsequent retrieval attempt, if the retrieval of irrelevant task traces interferes with selection of the relevant task (and the amount of interference is proportional to the number of irrelevant task traces in long-term memory), then interference would be greater for the easy task than for the difficult task, yielding a larger switch or restart cost for the former than the latter.

Bryck and Mayr’s (2008) account is interesting, but there may be a conceptual problem with it. While it is possible that more instances of the difficult task than the easy task may be encoded during the experiment (although this idea requires empirical validation), there are likely to be many more pre-experimental instances of the easy task than the difficult task in long-term memory because of differential task practice. The easy task tends to be easy because it is a well-practiced task. For example, word reading is argued to be easier than color naming with Stroop stimuli because people have had extensive practice with word reading (e.g., MacLeod, 1991; Stroop, 1935). As a result of practice, instances of the easy task should dominate in long-term memory from the start of the experiment. If the retrieval of instances from long-term memory interferes with task selection, as Bryck and Mayr suggested, then instances of the easy task should interfere more strongly with selection of the difficult task than vice versa, yielding a larger switch or restart cost for the difficult task. Thus, one could argue that Bryck and Mayr’s account actually predicts the reverse asymmetry (which is inconsistent with our results and theirs), although it may be possible to develop a variant of their account that addresses this issue (cf. Wong & Leboe, 2009).

While our sequential difficulty account is not based on interference in long-term memory retrieval, it is not incompatible with the idea that instances of prior task performance can be retrieved and produce interference that inflates switch costs, as suggested by previous research (e.g., Allport et al., 1994; Koch & Allport, 2006; Waszak et al., 2003). More generally, our account is neutral with respect to what produces switch costs. All we argue is that asymmetric switch costs for tasks of unequal difficulty may be asymmetric because of sequential difficulty effects. Our account is also neutral with respect to what produces restart costs, although one might wonder how it would explain asymmetric restart costs (Allport & Wylie, 2000; Bryck & Mayr, 2008). Here we consider one possibility in the context of Bryck and Mayr’s experimental design (see above).

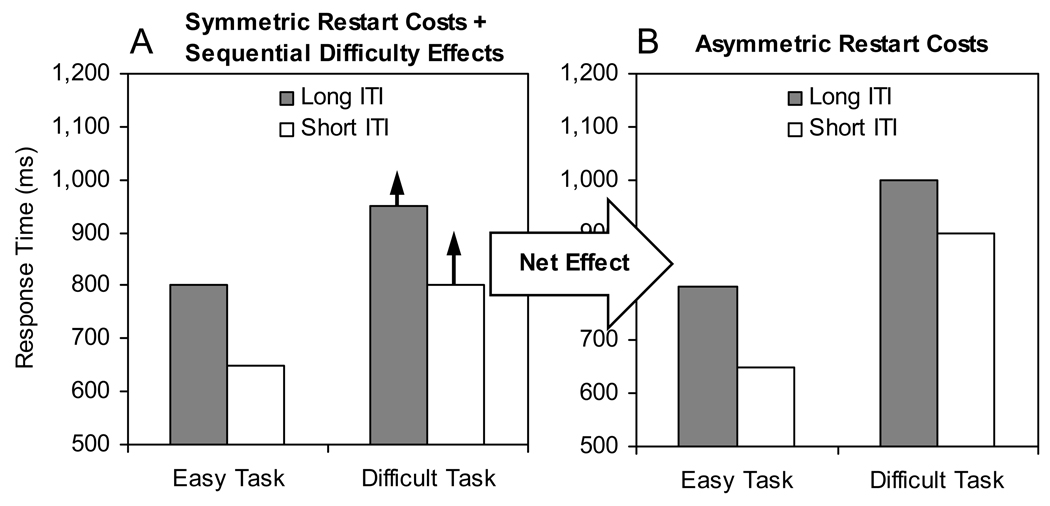
Assume that long ITIs induce restart costs because information for the repeated task decays in short-term memory over time (Altmann & Gray, 2002, 2008), perhaps necessitating retrieval of task information from long-term memory (Bryck & Mayr, 2008). For the sake of argument, assume that the true restart costs (uncontaminated by any other effects) are symmetric across tasks, as depicted in Figure 6A. Now imagine that sequential difficulty effects are present, except that they can be partially absorbed during the ITI. A longer ITI would allow for more absorption, resulting in a weaker sequential difficulty effect on the next trial (for related logic, see Pashler, 1994). If this happens, then RT would be prolonged less for difficult task repetitions associated with long ITIs (D---D) than for difficult task repetitions associated with short ITIs (D-D), as indicated by the short and long solid arrows, respectively, in Figure 6A. The symmetric restart costs and differential sequential difficulty effects, when combined, would yield the asymmetric restart costs depicted in Figure 6B, consistent with Bryck and Mayr’s data.

Figure 6.

Illustration of how sequential difficulty effects (i.e., slowing down after a difficult trial, as indicated by solid arrows) can combine with symmetric restart costs (panel A) to produce asymmetric restart costs (panel B), assuming that sequential difficulty effects are attenuated at longer intertrial intervals (ITIs).

This sequential difficulty account of asymmetric restart costs is speculative and warrants further investigation. A critical aspect of the account is the assumption that the magnitude of the sequential difficulty effect is attenuated with the passage of time. This assumption yields the testable prediction of a stronger asymmetry if the long ITI is made even longer. Fortunately, data exist that can be used to evaluate this prediction. Bryck and Mayr (2008) varied the long ITI in their experiments (500 ms versus 5,000 ms; the short ITI within each run was always 50 ms) and found that the difference in restart costs between the easy and difficult tasks was numerically larger with the 5,000-ms ITI than with the 500-ms ITI (although the relevant interaction was statistically significant in only one of their experiments). This result is consistent with the prediction of our sequential difficulty account, suggesting that it may be a viable explanation of asymmetric restart costs in addition to asymmetric switch costs.

Sequential Difficulty Effects

An outstanding issue concerns the theoretical basis of the sequential difficulty effects that may underlie asymmetric switch and restart costs. The data from the present experiments and past studies implicate a general processing impairment following difficult trials. We suggest that this impairment may be caused by a form of resource depletion. If the rate of task processing depends on the amount of a cognitive resource that can be allocated to the task, then depleting that resource could lower the processing rate. Assuming that a difficult task requires more of the resource than an easy task and it takes time to restore the resource, it follows that resource depletion would be greater following a difficult task than an easy task, producing a sequential difficulty effect.

The idea of resource depletion suggests a transition from a performance-based definition of difficulty to a construct-based definition: Difficult tasks are difficult because they require more of a limited resource than easy tasks. By this definition, sequential difficulty effects would be expected only with manipulations that vary the demand on a cognitive resource, which means that the explanatory value of our sequential difficulty account rests on specifying the resource that is depleted by task performance (see also Navon, 1984). We will consider two resources that might be depleted: executive control and working memory.

Executive control

One possible form of resource depletion is a temporary reduction in the capacity to exert executive control over task processing, an idea that has some currency in the literature (e.g., Lorist, Klein, Nieuwenhuis, De Jong, Mulder, & Meijman, 2000; Persson, Welsh, Jonides, & Reuter-Lorenz, 2007; Schmeichel, 2007; van der Linden, Frese, & Meijman, 2003). Executive control is generally considered to be involved in task switching situations, whether it be in the act of switching tasks or in task performance proper (e.g., see the contributions in Monsell & Driver, 2000). With tasks of unequal difficulty, Bryck and Mayr (2008) suggested that more executive control is needed to perform the difficult task than the easy task, which is consistent with how control is implemented in the models of Gilbert and Shallice (2002) and Yeung and Monsell (2003).

If there is a limited capacity for executive control, then it could be more depleted after a difficult task than an easy task, resulting in a sequential difficulty effect. This form of resource depletion would support sequential difficulty accounts of asymmetric switch costs observed in Stroop task switching (because more control is hypothesized for color naming than for word reading; e.g., Cohen, Dunbar, & McClelland, 1990; Gilbert & Shallice, 2002) and in language switching (because more control is hypothesized for responding in the nondominant language than in the dominant language; e.g., Meuter & Allport, 1999). It may be possible to incorporate this form of resource depletion into existing models of task switching (e.g., Gilbert & Shallice, 2002; Yeung & Monsell, 2003) by constraining the total control input supplied to both tasks and adjusting the amount of available control in response to previous task demands. This is an intriguing possibility because it would articulate how executive control is depleted and allow one to evaluate different accounts of asymmetric switch costs within the same model.

Working memory

Another possible form of resource depletion that may be more likely in the context of the present experiments is a temporary reduction in working memory capacity. It is well known that mental arithmetic depends strongly on working memory for the maintenance and manipulation of information needed to solve problems (for a review, see DeStefano & LeFevre, 2004). Difficult problems may require more working memory capacity than easy problems because of the need to maintain intermediate results (from carrying or borrowing) or manipulate problem information (as might be required to verify horizontal problems, in which the tens and ones digits of all terms are not spatially aligned; see Imbo & LeFevre, in press). Although this use of working memory affects immediate performance, it may also affect subsequent performance if the contents of working memory are not purged following the verification of a problem, effectively reducing the working memory capacity available for the next problem.

A reduction in working memory capacity could impair arithmetic verification if the rate of the verification process depends on how quickly arithmetic information can be retrieved from memory. The effect of working memory capacity on the speed of retrieval can be illustrated in the context of the Adaptive Control of Thought–Rational (ACT-R) cognitive architecture, which has been used to model performance in a wide variety of tasks, including mental arithmetic (Anderson, 2007; Anderson, Bothell, Byrne, Douglass, Lebiere, & Qin, 2004). In ACT-R, the time it takes to retrieve a piece of information from declarative memory (e.g., an arithmetic fact) depends on two things: its base-level activation (reflecting the frequency and recency with which it has been retrieved in the past) and its associative activation (reflecting the activation it receives from items in working memory). Associative activation depends on the strength of association between an item in working memory (e.g., the number 4) and the information to be retrieved (e.g., the arithmetic fact 4 + 2 = 6), as well as the attentional weight given to each item in working memory. Working memory capacity is represented in ACT-R as the total attentional weight spread among items in working memory (Anderson, Reder, & Lebiere, 1996; Daily, Lovett, & Reder, 2001; Lovett, Reder, & Lebiere, 1999). If working memory has a fixed capacity, then as the number of items in working memory increases, the attentional weight given to each item decreases. This leads to lower associative activation for retrieving information from declarative memory and gives rise to longer retrieval times.

Within this framework, consider what would happen if not all information was purged from working memory after verifying a problem. Any previous items remaining in working memory would receive some attentional weight, which would have two consequences. First, the old items could interfere with the process of retrieving information associated with new items relevant to verifying the current problem. Second, there would be a functional reduction in working memory capacity such that new items would be given lower attentional weights (because the fixed capacity would be spread among more items). The effect on verification would be slower and more error-prone retrieval of information from declarative memory, prolonging RT and possibly increasing ER. If this effect is more pronounced following a difficult problem than an easy problem—because the former makes stronger demands on working memory than the latter—then the net result would be a sequential difficulty effect.

Although this account of working memory limitations on retrieval is supported by empirical and modeling work (Anderson et al., 1996; Daily et al., 2001; Lovett et al., 1999), it has not been applied to sequential effects or explored in the domain of arithmetic task switching. A modeling endeavor of this sort is beyond the scope of the present article, but it is not outside the realm of possibility, for there are models of task switching based on the ACT-R architecture (Altmann & Gray, 2008; Sohn & Anderson, 2001) that might be adaptable to the account given here. Whether this approach to modeling sequential difficulty effects can capture the asymmetries observed in the present study is a matter for future investigation. More generally, whether some form of resource depletion (involving working memory, executive control, or another construct) can account for sequential difficulty effects underlying the myriad asymmetries that have been observed in other task switching studies remains to be seen.