Correcting Motion Artifacts in Retinal Spectral Domain Optical Coherence Tomography via Image Registration

Abstract

Spectral domain optical coherence tomography (SD-OCT) is an important tool for the diagnosis of various retinal diseases. The measurements available from SD-OCT volumes can be used to detect structural changes in glaucoma patients before the resulting vision loss becomes noticeable. Eye movement during the imaging process corrupts the data, making measurements unreliable. We propose a method to correct for transverse motion artifacts in SD-OCT volumes after scan acquisition by registering the volume to an instantaneous, and therefore artifact-free, reference image. Our procedure corrects for smooth deformations resulting from ocular tremor and drift as well as the abrupt discontinuities in vessels resulting from microsaccades. We test our performance on 48 scans of healthy eyes and 116 scans of glaucomatous eyes, improving scan quality in 96% of healthy and 73% of glaucomatous eyes.

1 Introduction

Many ophthalmologists use optical coherence tomography (OCT) to improve diagnosis of retinal diseases. OCT generates cross-sectional and 3D images of retinal structure by detecting the magnitude and echo time delay of light. The newest version of OCT, spectral domain OCT (SD-OCT) [1], detects all the light echoes in a single axial scan (A-scan) in parallel. Cross-sectional images (B-scans) are created by acquiring a series of A-scans as the OCT beam is scanned in the transverse direction. SD-OCT can image the three-dimensional retinal structure with an axial resolution of up to ≈2µm and an imaging speed of up to 50,000 A-scans per second.

An important application of retinal SD-OCT is the early diagnosis of glaucoma, a progressive blinding disease. Early intervention has been shown to slow progression [2], but early detection of the disease is challenging. The precise structural measurements available from SD-OCT volumes (such as retinal nerve fiber layer thickness maps [3]) can be used to detect structural changes before they result in noticeable vision loss.

A typical SD-OCT scan pattern contains 40,000 A-scans and takes between 1 and 1.5 seconds to complete. Any eye movement during imaging will corrupt the data, making structural measurements and glaucoma diagnosis unreliable. Eye movement during imaging is reduced by asking the subject to fixate on a target; however, our eyes remain in motion even during conscious fixation, undergoing fixational eye movements [4]. Fixational eye movements encompass three different types of motion: ocular tremor, ocular drift, and microsaccades. Microsaccades, which introduce the most severe motion artifacts, move the fixated point around 30 arcminutes almost instantaneously and occur roughly once per second in normal individuals.

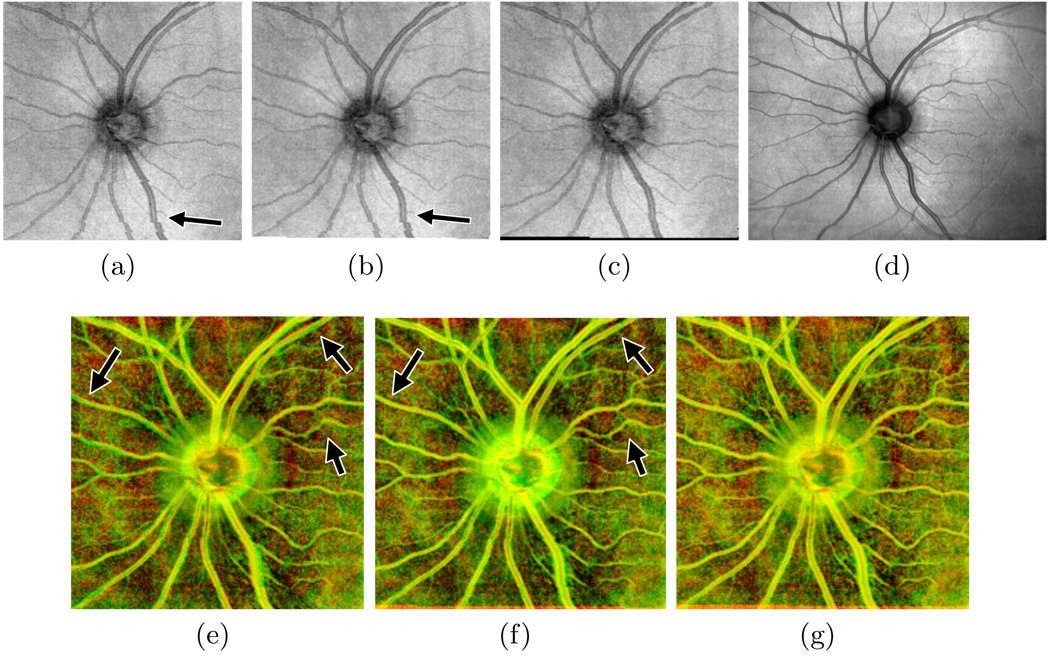
Figure 1(a) shows a two-dimensional projection of an SD-OCT volume containing motion artifacts. Here, the axial dimension has been collapsed by summing voxel intensities, resulting in a view of the eye (the en face image) analogous to a traditional fundus image or other 2D imaging techniques. Note the discontinuity in the vessels pointed out in the bottom half of the image. These discontinuities indicate that microsaccades occurred during scan acquisition.

Fig. 1.

Results of motion artifact correction on an example scan. The en face image from the uncorrected scan (a) shows vessel discontinuities (arrow) resulting from microsaccades. Correcting for tremor and drift (b) fails to correct these discontinuities, but microsaccade correction does (c), matching the SLO reference image (d). Images (e)–(g) show the en face image in the red channel and the SLO image in the green channel before correction, after correcting tremor and drift, and after full correction, respectively. Correctly aligned regions appear yellow; arrows point to improved alignment after drift correction.

Coupling the imager to a tracker [5] results in an improvement in the OCT data, but with high production costs and increased scanning time.

We take a complementary approach to eliminating transverse motion artifacts: we correct motion artifacts after imaging is complete via image registration. Immediately after capturing the SD-OCT volume, the OCT system captures an scanning laser ophthalmoscopy (SLO) image of the retina (Fig. 1(d)). Because capture of the SLO image is virtually instantaneous relative to time required for OCT capture, we can treat the SLO image as an artifact-free reference image. The OCT en face image should match the SLO image if the scan is also artifact-free. Any structural misalignment indicates that the OCT volume contains motion artifacts and does not accurately reflect the subject’s anatomy. We remove these artifacts by warping the volume to make the corresponding en face image match the SLO image as closely as possible.

Prior work on correcting motion artifacts in OCT volumes without requiring active tracking registers consecutive B-scans by finding the shifts in the Z– and X–dimensions that maximize cross-correlation between adjacent B-scans [6], correcting transverse and axial artifacts resulting from ocular drift. While our method does not correct axial artifacts, we surpass this method in correcting transverse artifacts by allowing for more complex motions, including fast motion during a single B-scan and motion in the Y –dimension.

2 Methods

We remove motion artifacts by registering the en face image constructed from an SD-OCT volume to the SLO reference image and applying the resulting warp to the volume at each depth. Registration proceeds in two steps. The first step corrects for artifacts from tremor and drift; the last step, the main contribution of our technique, corrects vessel discontinuities caused by microsaccades. Results from each correction step on an example scan are shown in Fig. 1.

2.1 Detecting Vessels

At each registration step, we focus on matching the location of vessels, the main features in retinal images. Our vessel detection algorithm is a simplified implementation of the technique proposed by Lam and Yan [7], which uses hysteresis thresholding to find ridges in the divergence of the image gradient. After scaling the computed divergence to lie between 0 and 1, we use upper and lower thresholds of 0.2 and 0.075, respectively, and discard regions containing fewer than five pixels above the upper threshold.

2.2 Correcting Tremor and Drift

We correct for tremor and drift using the elastic registration technique of Periaswamy and Farid [8]. Motion between the two images is described by an affine transformation that may vary across the image but is assumed to be constant within a local window, Ω. Specifically, we solve for the parameter vector m that solves

$$m_7{I}^{\text{SLO}}(x,y)+m_8=I^{\text{OCT}}(m_{1}x+m_{2}y+m_5,m_{3}x+m_{4}y+m_6)$$ (1)

for all locations (x, y) ∈ Ω in the least squares sense. We define our window to capture temporally distinct phenomena, including pixels corresponding to A-scans taken within a time interval τ. We use the same window for every A-scan in a given B-scan, drastically reducing the amount of computation required.

It is customary in motion estimation applications to estimate motion on a scale pyramid. Because tremor and drift are both small amplitude motions resulting in relatively small errors, we omit this coarse-to-fine scheme, eliminating the need to smooth the images and recompute gradients at each level of the pyramid. Instead, we vary the size of our window. This allows us to first compute a global deformation that brings the two images mostly into alignment before focusing on more localized motion artifacts.

After correcting for drift and tremor, we are left with en face images that are well aligned with the SLO reference image except in places where a microsaccade occurred. The result of tremor and drift correction is shown in Fig. 1(b). Note that the drift correction has improved the alignment of most vessels (correctly overlapping areas appear yellow in Fig. 1(f)), particularly in the top half of the image, but the vessel discontinuities remain.

2.3 Correcting Microsaccades

The main contribution of our algorithm is the ability to correct vessel discontinuities that result from primarily horizontal microsaccades. At a microsaccade, the location of the eye between subsequent B-scans (and between different A-scans within a single B-scan) changes significantly, causing the location of vessels in the image to shift abruptly between two adjacent rows. The necessary correction before and after the time of the microsaccade is drastically different, violating the local smoothness assumption made by many motion estimation techniques.

We correct microsaccades by finding the horizontal shift at each pixel in the scan that best aligns the result of tremor and drift correction with the SLO image. We consider the results of the earlier correction and the SLO image as signals in the time domain. We then find the least cost set of feasible correspondences between the two signals. This procedure is commonly referred to as dynamic time warping [9] in the signal processing community, and is also used on corresponding scanlines to find dense disparity maps in stereo vision [10]. This procedure corrects horizontal microsaccades but ignores vertical motion.

Our cost function penalizes matches based on the squared difference in pixel intensities. To force vessels to align properly, the intensity of pixels inside vessels should be as different as possible from pixels outside the vessels. We also want the non-vessel tissue to be as uniform as possible to avoid detecting spurious saccadic events. As vessel detection is rarely perfect, we do not rely solely on a binary mask. Instead, we apply a scheme that darkens pixels within vessels and normalizes the intensity of non-vessel tissue while tolerating errors in vessel detection. We replace the intensity at pixels detected as vessels with the result of adaptive histogram equalization. This darkens vessels but does not drastically alter the intensity of pixels incorrectly detected as vessels. We also apply a linear transformation to the intensities of the remaining pixels so that a line fit to the intensities on each row is horizontal, with corresponding rows in the SLO and en face images sharing the same mean and standard deviation in intensities.

After adjusting pixel intensities, we convert the images to one-dimensional signals and find the lowest cost set of correspondences using dynamic programming. The total cost is equal to the sum of the squared differences in intensity for each pair of matched pixels plus a constant P (we use twice the standard deviation in pixel intensity) for each unmatched pixel. The returned correspondences are converted to horizontal shifts and used to warp the partially corrected en face image. Finally, an additional iteration of tremor and drift correction removes residual vertical motion artifacts, which could not be corrected on the first pass due to the presence of significant saccades. The fully corrected en face image for the example from Fig. 1(a) is shown in Fig. 1(c).

2.4 Preserving Optic Disc Contour

Microsaccade correction is sensitive to vessels that appear darker than the surrounding tissue in the en face image but brighter than the surrounding tissue in the SLO image. This is particularly common inside the optic disc and can cause the optic disc contour to become distorted after motion correction. Because the optic disc contour is an important feature in glaucoma diagnosis, our correction must never introduce errors in this region. We therefore disallow horizontal shifts in the region surrounding the optic disc, which is automatically detected by thresholding the distance to the top surface of the retina in the volume.

3 Experimental Results

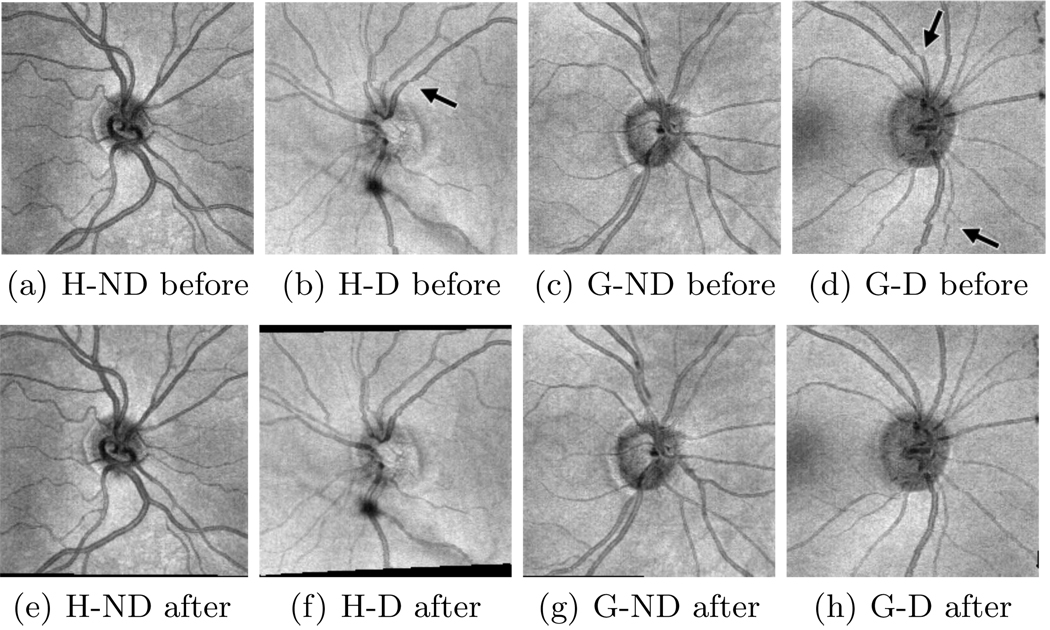
We implemented our algorithm in Matlab and tested it on 164 SD-OCT scans: 48 from healthy eyes and 116 from glaucomatous eyes. There are 24 healthy (the H-D set) and 58 glaucomatous examples (the G-D set) containing noticeable vessel discontinuities from microsaccades. The remaining examples (abbreviated as the H-ND and G-ND sets) contain drift and tremor artifacts but no noticeable microsaccades. Figure 2 shows en face images from each of the four sets before and after correction. Each volume is 200×200×1024 voxels and takes at most 50 seconds to correct on a desktop PC (Intel Pentium 3.2GHz, 2GB RAM).

Fig. 2.

Results of motion artifact correction on example scans from our four datasets (abbreviations from Sect. 3). En face images for each example are shown both before and after correction. Arrows point to vessel discontinuities before correction.

3.1 Qualitative Assessment

Two OCT experts independently compared the quality of each scan before and after correction. They evaluated both the overall fit to the SLO reference image (reflecting correction of tremor and drift artifacts) and the number of noticeable vessel discontinuities (reflecting correction of microsaccades), classifying the correction as either improved, unchanged, or degraded in both areas. The two experts’ evaluations were combined into a consensus evaluation for each scan. For the corrected scan to be considered an improvement, at least one expert must have rated the output as improved and neither can have rated it as degraded.

The results of the experts’ assessment are summarized in Table 1. Overall fit improved in 45 of the 48 of the healthy examples, remaining unchanged in the other three. In the glaucomatous examples, the overall fit improved in 96 of the 116 examples, remaining unchanged in 17 and deteriorating in 3. Of the 24 H-D examples, we improve vessel continuity in 19, leaving the remaining five unchanged. We also improve vessel continuity in 45 of the 58 G-D examples, leaving 3 unchanged and causing deterioration in the remaining 10. Ultimately, we consider the total quality of a scan to be improved if either overall fit or vessel continuity improved without either deteriorating. Our correction improved the total quality of 46 of 48 healthy (96%) and 85 of 116 glaucomatous (73%) scans.

Table 1.

A summary of the qualitative evaluation of our performance. Experts assessed improvement after correction in overall alignment (O) and vessel continuity (V). Below, + indicates improvement, − indicates degradation, and = indicates no change detected. The three bold columns are the evaluations considered to be improved total scan quality.

Dataset	O+ V+	O+ V=	O= V+	O= V=	O+ V−	O− V+	O= V−	O− V=	O− V−
H-ND	0	22	0	1	1	0	0	0	0
H-D	17	5	2	0	0	0	0	0	0
G-ND	11	27	0	6	7	0	5	1	1
G-D	43	2	2	1	6	0	3	0	1

3.2 Quantitative Assessment

We evaluate the performance quantitatively by computing the improvement in overlap between vessels in the SLO image and vessels in the motion corrected en face image. This single measurement combines the contributions of both tremor and drift correction and the correction of any microsaccades. We define overlap as the fraction of pixels belonging to each major vessel in the en face image that also belong to the corresponding vessel in the SLO image (based on manually labeled vessels). We use this variant of the Jaccard index to give a value of 1 for vessels which are correctly aligned but appear thinner in the en face image than in the SLO image due to the different imaging protocols.

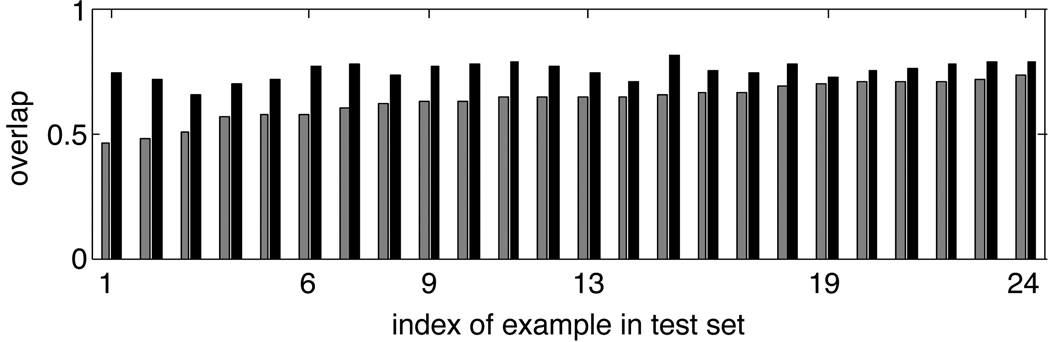
Figure 3 shows the overlap improvement on the scans from the H-D set. In every case, the overlap is greater after correction. The mean overlap before correction over these 24 examples is 0.6348, which increases to a mean of 0.7522 after artifact removal. For the other three sets of scans the mean overlap increases from 0.6083 to 0.7403 (G-D), from 0.6396 to 0.7168 (G-ND), and from 0.6486 to 0.7469 (H-ND). Overlap decreases in only five examples, all in the G-ND set.

Fig. 3.

Percent overlap between corresponding vessels in en face image and SLO reference image before and after correction for the H-D set. Gray bars show overlap before correction; black bars show overlap after motion artifact correction. Examples are sorted in order of increasing overlap before correction. Examples 9 and 19 are those judged by the experts to have no improvement in overall alignment after correction. Example 6 is shown in Fig. 2(b) and (f). Example 13 is shown in Fig. 1.

4 Discussion

In this paper, we described a system that automatically corrects transverse motion artifacts in retinal SD-OCT after scan acquisition. Both qualitative and quantitative evaluations show that our system improves the quality of the majority of scans, even in subjects with retinal diseases.

The main contribution of our technique is the ability to correct for artifacts resulting from microsaccades. We use a more flexible motion model than previous methods, allowing a different correction for individual A-scans within a single B-scan. Ophthalmologists use vessel continuity as a key measure of scan quality and often discard scans containing discontinuities larger than the vessel diameter. With our system, the majority of these previously discarded scans are now useful.

Limitations that remain to be addressed include our handling of the optic disc and artifacts from vertical saccades. Because we disallow horizontal shifts within the optic disc, we cannot correct saccades occurring at that point in the scan. Applying more sophisticated shape analysis to the optic disc may allow for saccade correction without distorting the optic disc contour. Although we do correct smooth vertical motions, we do not specifically address vertical saccades. It may be possible to consider the horizontal and vertical components of saccades independently and correct each with our current saccade correction technique.