Monte Carlo investigations of the effect of beam divergence on thick, segmented crystalline scintillators for radiotherapy imaging

Abstract

The use of thick segmented scintillators in electronic portal imagers offers the potential for significant improvement in x-ray detection efficiency compared to conventional phosphor screens. Such improvement substantially increases the detective quantum efficiency (DQE), leading to the possibility of achieving soft-tissue visualization at clinically-practical (i.e. low) doses using megavoltage (MV) cone-beam computed tomography. While these DQE increases are greatest at zero spatial frequency, they are diminished at higher frequencies as a result of degradation of spatial resolution due to lateral spreading of secondary radiation within the scintillator – an effect that is more pronounced for thicker scintillators. The extent of this spreading is even more accentuated for radiation impinging the scintillator at oblique angles of incidence due to beam divergence. In this paper, Monte Carlo simulations of radiation transport, performed to investigate and quantify the effects of beam divergence on the imaging performance of MV imagers based on two promising scintillators (BGO and CsI:T1), are reported. In these studies, 10 – 40 mm thick scintillators, incorporating low-density polymer, or high-density tungsten septal walls were examined for incident angles corresponding to that encountered at locations up to ~15 cm from the central beam axis (for an imager located 130 cm from a radiotherapy x-ray source). The simulations demonstrate progressively more severe spatial resolution degradation (quantified in terms of the effect on modulation transfer function) as a function of increasing angle of incidence (as well as of scintillator thickness). Since the noise power behavior was found to be largely independent of incident angle, the dependence of the DQE on incident angle is therefore primarily determined by the spatial resolution. The observed DQE degradation suggests that 10 mm thick scintillators are not strongly affected by beam divergence for detector areas up to ~30 × 30 cm². For thicker scintillators, the area that is relatively unaffected is significantly reduced, requiring a focused scintillator geometry in order to preserve spatial resolution, and thus DQE.

I. INTRODUCTION

The last decade has witnessed the rapid development of technology and techniques to support image-guided radiation therapy (IGRT) (Saw et al., 2006). These efforts are motivated by the desire to provide precise patient position information in the treatment room so as to assure accurate execution of advanced treatment plans for 3D conformal radiation therapy (CRT) (Purdy, 1996), intensity-modulated radiation therapy (IMRT) (Bortfeld, 2006) and volumetric modulated arc therapy (VMAT) (Otto, 2008). For this purpose, a variety of in-room volumetric imaging techniques have been extensively investigated (Fung et al., 2006; Heron et al., 2006; Huh et al., 2008; Kupelian et al., 2007; Lagendijk et al., 2005; Ma and Paskalev, 2006), including kilovoltage (kV) and megavoltage (MV) cone-beam computed tomography (CBCT) (Jaffray and Siewerdsen, 2000; Jaffray et al., 2002; Morin et al., 2006; Pouliot et al., 2005). While kV CBCT images are obtained using an additional imaging system mounted orthogonally to the treatment gantry, MV CBCT is carried out using the treatment beam and the electronic portal imaging device (EPID) that is typically already installed for routine portal imaging. Presently, most EPIDs consist of an indirect detection, active matrix flat-panel array coupled to an x-ray detector comprising a phosphor screen plus a copper plate. The EPID is mounted on the treatment gantry so that the central beam axis passes through the center of the detection area.

While image quality with a MV CBCT system is inferior compared to a kV CBCT system due to inherently lower contrast (Groh et al., 2002), the use of MV CBCT presents distinct advantages. Compared to its kV counterpart, MV CBCT information is obtained from the beam’s eye view, providing direct patient positioning verification with less apparatus. In addition, MV CBCT images are less affected by radiation scattering and streak artifacts. Finally, CT numbers obtained from MV CBCT images can, in principle, be used for high accuracy dose calculations and inhomogeneity corrections (Langen et al., 2005; Morin et al., 2005; Guan et al., 2002). However, the clinical implementation of MV CBCT is constrained by the impractically high dose required for soft-tissue visualization (Groh et al., 2002). This high dose requirement is due to the relatively low (only ~1% at 6 MV) detective quantum efficiency (DQE) of current EPIDs, resulting from the modest (~2%) quantum efficiency (QE) of their x-ray detectors (El-Mohri et al., 2001) – DQE is a widely accepted measure of imaging performance and can be regarded as the efficiency for transferring signal and noise information from the input to the output of an imaging system. In order to overcome this limitation, EPIDs based on high-efficiency x-ray detectors have been examined by various research groups (Mei et al., 2006; Monajemi et al., 2006a; Monajemi et al., 2006b; Mosleh-Shirazi et al., 1998a; Mosleh-Shirazi et al., 1998b; Pang and Rowlands, 2004; Rathee et al., 2006; Samant and Gopal, 2006; Sawant et al., 2005a; Sawant et al., 2006; Seppi et al., 2003; Sillanpaa et al., 2006; Wang et al., 2009b).

One of the most promising high-efficiency detector approaches involves the use of large-area, thick, segmented crystalline scintillators which consist of 2D matrices of scintillator crystals (e.g., CsI:T1, Bi₄Ge₃O₁₂ (BGO), CdWO₄ and ZnWO₄) separated by optically reflective septal walls (Monajemi et al., 2004; Mosleh-Shirazi et al., 1998a; Sawant et al., 2006; Seppi et al., 2003; Wang et al., 2009b). Presently, it is possible to fabricate such scintillators up to 40 mm thick, resulting in significantly improved QE (Sawant et al., 2006; Wang et al., 2009b). The replacement of the granular phosphor screen with crystalline scintillator material can reduce Swank noise – a noise originating from the variation in X ray-to-light conversion gain which degrades DQE at all spatial frequencies (Wang et al., 2009a). In addition, the use of optically reflective septal walls limits the lateral spread of the secondary optical photons, thus helping to preserve spatial resolution.

Previous Monte Carlo simulations of radiation and optical transport suggest that EPIDs employing segmented CsI:T1 and BGO scintillators up to 40 mm thick can provide DQE values of ~29% and 42%, respectively, at zero spatial frequency (Wang et al., 2009a), and studies of initial prototypes have shown considerable promise (Sawant et al., 2006; Wang et al., 2009b). However, at higher frequencies, DQE performance will be degraded by spatial resolution degradation caused by the spreading of secondary electron radiation. Moreover, the extent of such degradation will be accentuated at locations progressively further away from the central axis due to beam divergence resulting in oblique angles of the primary radiation incident on the detector. In this article, an examination of the effect of beam divergence on the performance of EPIDs employing thick, segmented crystalline scintillators is reported. The methodology is based on Monte Carlo simulation of radiation transport, and simulation results are compared to those measured from a prototype detector representative of conventional EPIDs.

II. METHODS

A. Overview

Spatial resolution degradation was quantified using the modulation transfer function (MTF), defined as the Fourier amplitude of the system response to a delta-function (Dobbins III, 2000), while detector noise was quantified using noise power spectra (NPS), which may be regarded as the variance of image intensity (i.e., image noise) divided among the various spatial frequency components of the image (Dobbins III, 2000). The MTF and NPS simulations were performed using radiation transport codes EGSnrc and DOSXYZnrc (Kawrakow and Rogers, 2000; Treurniet et al., 2001). Normalized noise power spectra (NNPS) and DQE were calculated using the simulation results for NPS and MTF. Given that the effect of beam divergence is primarily determined by radiation transport, optical transport of photons generated in the scintillator (which would significantly increase the complexity and computation demands of the simulations) was not accounted for in the study.

The simulations were carried out using a 6 MV photon beam with a spectral output corresponding to that of a Varian LINAC (Sheikh-Bagheri, 1999). For both MTF and NPS simulations and for each angle of incident X rays, the beam is modeled as a parallel rectangular beam, utilizing source model 1 of the DOSXYZnrc code. This model allows the central axis of the parallel beam to rotate with respect to the x-, y- and z-axes of the simulation coordinate system.

In the simulations, the parameters PCUT and ECUT (which correspond to cutoff energies for photons and electrons) were chosen to be 0.01 and 0.521 MeV (both corresponding to a kinetic energy of 0.01 MeV), respectively. The EXACT boundary-crossing algorithm, PRESTA-II electron-step algorithm, and NIST bremsstrahlung cross sections were used. The simulations were performed using a total of 200 CPUs on a 64-bit Linux cluster with 2.2 GHz AMD Opteron processors. The simulation calculations for this study consumed a total of ~150,000 CPU hours.

B. Segmented scintillating detectors

Each simulated detector employed a segmented scintillator covered by a 1 mm thick copper plate located on the incident x-ray side of the scintillator. Each scintillator consists of a 2D matrix of elements comprising scintillator crystals separated by septal walls. The present study examined segmented BGO and CsI:T1 detectors with thicknesses ranging from 10 to 40 mm, and a scintillator element pitch (defined as the distance between the center of two adjacent elements) of 1.016 mm – corresponding to the specifications of a series of prototypes recently developed and investigated by our group (Sawant et al., 2006; Wang et al., 2009b). The septal walls were 0.1 mm thick and consisted of either low-density material (polystyrene) or high-density material (tungsten). While examination of low-density polystyrene septal walls is motivated by the fact that they are easier to manufacture, it is of interest to investigate the potential of high-density walls to limit performance degradation due to beam divergence. The radiation energy deposited in each scintillator crystal represents the imaging signal of the corresponding scintillator element. A total of 16 detector configurations (corresponding to the two types of scintillator and septal wall material and four scintillator thicknesses) were examined.

C. Modulation transfer function

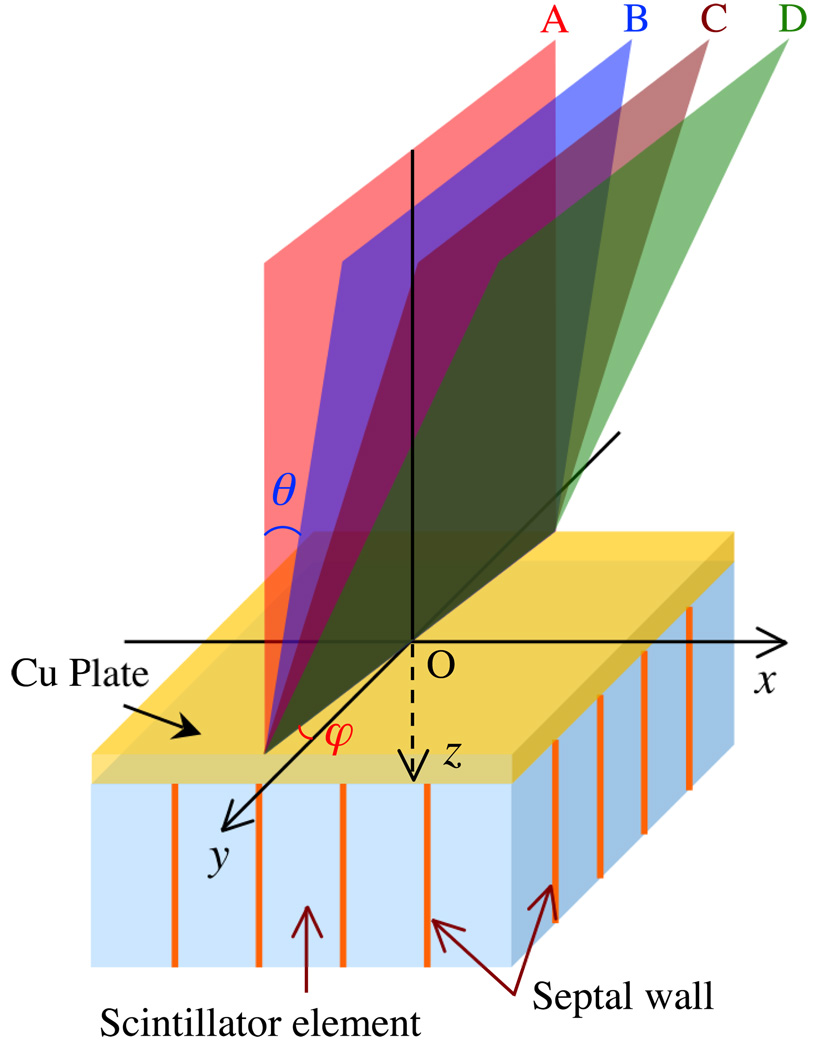
The angled slit method was used for determining the MTF (Fujita et al., 1992; Sawant et al., 2005b). In these simulations, each segmented scintillator consists of 301 × 301 elements, resulting in an area of 30.58 × 30.58 cm². Figure 1 shows a 3D schematic view of the simulation geometry. For each detector configuration, the MTF simulations were performed using parallel beams (illustrated in Fig. 1) – with each beam corresponding to the simulation of a certain incident beam angle. The beams were incident on a rectangular area (referred to as a slit) of 0.0004 × 30 cm² at the detector entrance surface. The slit, centered at point O, is oriented at a small fixed angle of 0.6° (as indicated by φ) with respect to the y-axis. In order to study MTF at a normal angle of beam incidence, one beam is set perpendicular to the detector surface, corresponding to plane A (which is at an angle, θ, equal to 0° with respect to the z-axis). To examine the effect of radiation incident at oblique angles, the beam is tilted at angles θ of 2.24°, 4.47° and 6.69° with respect to the z-axis as illustrated by planes B, C and D, respectively. The results of the simulations performed with planes A, B, C and D correspond to the performance of a detector at distances of 0, 5.08, 10.16 and 15.24 cm, respectively, from the center of that detector when irradiated by a divergent point source positioned 130 cm directly above the detector center. (This geometry corresponds to a typical orientation of an EPID with respect to a radiation therapy x-ray source, with the center of the detector located along the central beam axis.) For each MTF simulation, the energy deposited in the detector elements was used to generate a line-spread function (LSF). The LSF was determined by plotting the response of the detector elements as a function of their location with respect to the slit, and the magnitude of the 1D Fourier transform of the LSF yielded the 1D MTF along the x-direction. This method, referred to as the angled slit technique, is widely used to determine the pre-sampled MTF for digital imaging systems (Fujita et al., 1992).

FIG. 1.

Schematic view of the geometry of the detector (consisting of a segmented scintillator and an overlying copper plate), the radiation beams, and the associated coordinate system employed in the MTF simulations. The origin of the coordinate system, indicated by point O in the figure, is located at the center of the copper surface, on the x-ray side. The z-axis is perpendicular to the top surface of the detector and parallel to the detector thickness. The x- and y-axes are oriented so as to coincide with the directions of the grid formed by the septal walls. Planes A, B, C and D represent the direction of beams of parallel X rays incident on the detector at various angles θ with respect to the z-axis and at an angle φ with respect to the y-axis. Note that the dimensions of the drawing are not to scale.

D. Normalized noise power spectra and detective quantum efficiency

The NPS is particularly important because it quantifies the spatial frequency content, as well as the magnitude, of the output noise of a system. The synthesized slit method was used to calculate NPS (Giger et al., 1984; Maidment and Yaffe, 1994; Sawant et al., 2005b). In the NPS simulations, each scintillator consists of 600 × 600 elements, resulting in an area of 60.96 × 60.96 cm². These simulations were carried out using parallel beams incident at the same angles, θ, as in the MTF simulations (i.e. 0°, 2.24°, 4.47° and 6.69°), with X rays incident on an area of 60 × 60 cm² centered within the detector area. The boundaries of the square irradiated area are parallel to the x- and y-axes.

For each detector configuration and angle of incidence, a total of 40 such simulations resulting in 40 frames of data were carried out, with 360 million x-ray histories used for each frame. Data from ten non-overlapping blocks, each consisting of 250 × 100 elements, were obtained from the central 500 × 500 elements of each frame. (The use of a region of interest smaller than the actual size of the simulated detector area avoided edge effects.) Data in each block were averaged along the shorter dimension (the direction with 100 elements), resulting in a 250-point realization. Given there are 40 frames of data, a total of 400 realizations were obtained. A 1D Fourier transform was applied to each of these 400 realizations. The magnitudes of the resulting 400 power spectra were appropriately normalized and averaged to yield the 1D NPS along the x-direction. NNPS are obtained from:

$$\mathit{\text{NNPS}}(f)=\frac{{\overline{\mathit{q}}}_0\times \mathit{\text{NPS}}(f)}{{\overline{A}}^2},$$ (1)

where f is the spatial frequency, Ā is the average element signal obtained from the NPS results, and q̄₀ is the x-ray fluence used in the NPS simulations. Given the number of simulated X rays (360 million) and the beam size (600 × 600 mm²), q̄₀ is equal to 1000 X rays/mm² for all cases.

The simulated DQE was calculated, using the results for MTF and NNPS, from (Cunningham, 2000):

$$\mathit{\text{DQE}}(f)=\frac{{\mathit{\text{MTF}}}^2(f)}{\mathit{\text{NNPS}}(f)}.$$ (2)

E. Comparison of Simulation Results with Results from a Conventional EPID

Simulation results for the MTF and DQE for the segmented scintillating detectors are compared to empirical values obtained from a previously investigated prototype whose performance is representative of that of conventional EPIDs (El-Mohri et al., 2001). The prototype employs a Lanex Fast-B phosphor screen (133 mg/cm² Gd₂O₂S:Tb, Eastman Kodak, Rochester, NY) plus a 1 mm thick copper plate detector coupled to an indirect detection, active matrix flat-panel array with a pixel pitch of 0.508 mm. Data from that investigation were binned in a 2 × 2 format to match the element pitch of the simulated detectors.

III. RESULTS

A. Modulation transfer function

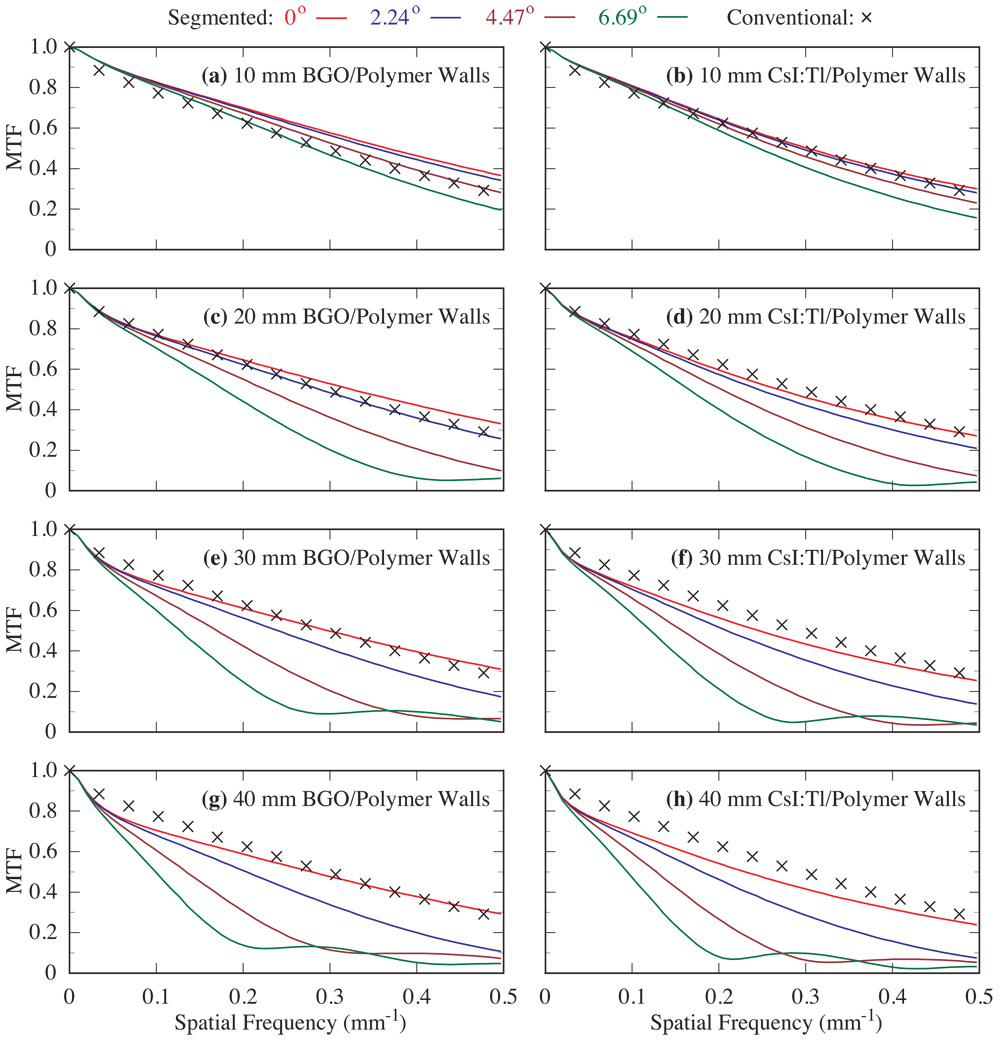
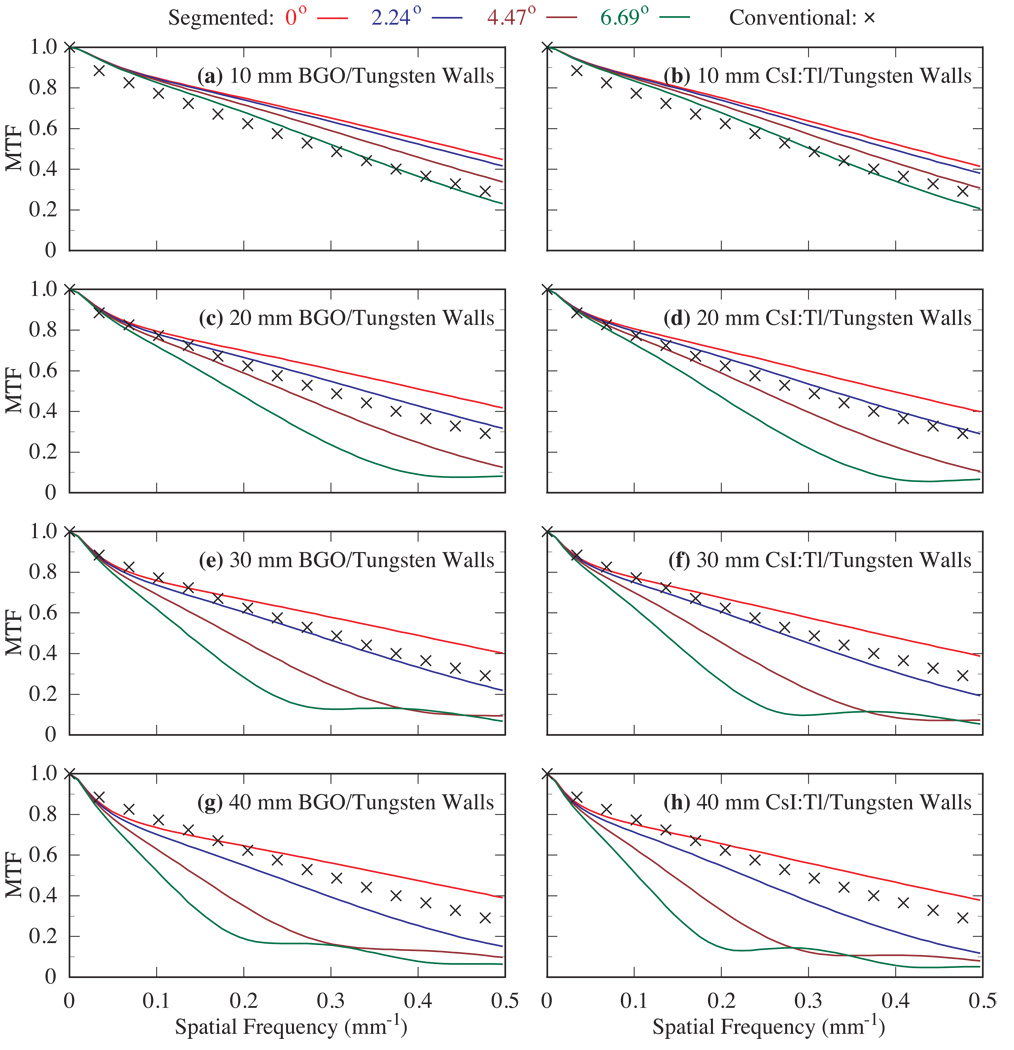
Figure 2 shows results of the simulated MTF as a function of incident beam angle for segmented BGO and CsI:T1 detectors with thicknesses ranging from 10 to 40 mm and employing polymer septal walls. Figure 3 shows similar results for segmented detectors employing tungsten walls. For each detector configuration, the simulation results are compared to the measured MTF from the conventional EPID. The results in both figures indicate that, for a given scintillator thickness and angle of incidence θ, configurations employing the higher-density scintillator (i.e. BGO versus CsI:T1) or the higher-density septal wall (i.e. tungsten versus polymer) exhibit better MTF due to higher radiation attenuation provided by these materials. For a given detector thickness, the segmented BGO detector with tungsten walls offers the highest MTF, followed by the CsI:T1 detector with tungsten walls, the BGO detector with polymer walls, and the CsI:T1 detector with polymer walls.

FIG. 2.

Pre-sampled MTF for four incident beam angles (0°, 2.24°, 4.47° and 6.69°) using segmented scintillators with polymer septal walls. The results are shown for 10 – 40 mm thick BGO scintillators in (a), (c), (e) and (g) and CsI:T1 scintillators in (b), (d), (f) and (h). In this figure and in figure 3, for each detector configuration, the progressive degradation in MTF shown by the various lines corresponds to increasing incident beam angle. Note that the simulation results are compared to the measured MTF from the conventional EPID.

FIG. 3.

Pre-sampled MTF for four incident beam angles (0°, 2.24°, 4.47° and 6.69°) using segmented scintilllators with tungsten septal walls. The results are shown for 10 – 40 mm thick BGO scintillators in (a), (c), (e) and (g) and CsI:T1 scintillators in (b), (d), (f) and (h). The simulation results are compared to the measured MTF from the conventional EPID.

The MTF performance for the segmented detectors is found to degrade with increasing incident beam angle, and such degradation is more significant for thicker detectors. For the 10 mm thick BGO and CsI:T1 detectors (Figs. 2(a), 2(b), 3(a) and 3(b)), for angles of 0°, 2.24° and 4.47°, the MTF is generally higher than that measured for conventional EPIDs. Even at 6.69°, these detectors provide reasonable performance, with MTF values of at least ~0.2 and 0.16, respectively, at the Nyquist frequency (~0.49 mm⁻¹, given by half the inverse of the element pitch of the scintillators). For the 20 mm thick detectors (Figs. 2(c), 2(d), 3(c) and 3(d)), for angles of 0° and 2.24°, spatial resolution is maintained, resulting in MTF values of at least ~0.2 at the Nyquist frequency. For larger angles (4.47° and 6.69°), the MTF results are significantly degraded, demonstrating the sine behavior of the geometric effect of obliquely incident X rays on spatial resolution, similar to that reported for simulations at diagnostic energies (Que and Rowlands, 1995; Hajdok and Cunningham, 2004). For the results corresponding to an angle of 6.69°, the first minimum appears at ~0.42 mm⁻¹. This value is consistent with the first minimum of a sine function corresponding to the Fourier transform of a rectangular function having an aperture size of 2.35 mm.

For the 30 and 40 mm thick detectors, while the MTF performance at 0° is comparable to, or better than that of the conventional EPID, it is significantly degraded at oblique angles. For 2.24°, the MTF performance of these detectors exhibits a gradual decrease with increasing scintillator thickness and decreasing septal wall density. For 4.47°, the 30 and 40 mm thick detectors exhibit a more significant MTF degradation – with the first minimum of the sine behavior occurring at ~0.42 and 0.32 mm⁻¹, corresponding to an aperture size of 2.35 and 3.12 mm, respectively. For 6.69°, an even more pronounced decrease is observed – with the first minimum of the sine behavior occurring at lower frequencies (~0.28 and 0.21 mm⁻¹ corresponding to an aperture size of 3.52 and 4.70 mm for the 30 and 40 mm thick detectors, respectively). All of the aforementioned aperture sizes correspond closely to the lateral displacement created by the projection of the possible points of interaction across the thickness of the detector. Given this simple geometrical nature of the spatial resolution degradation due to oblique angles of incidence, it is expected that such degradation would be similar in any orientation along the x-y detector plane.

B. Normalized noise power spectra

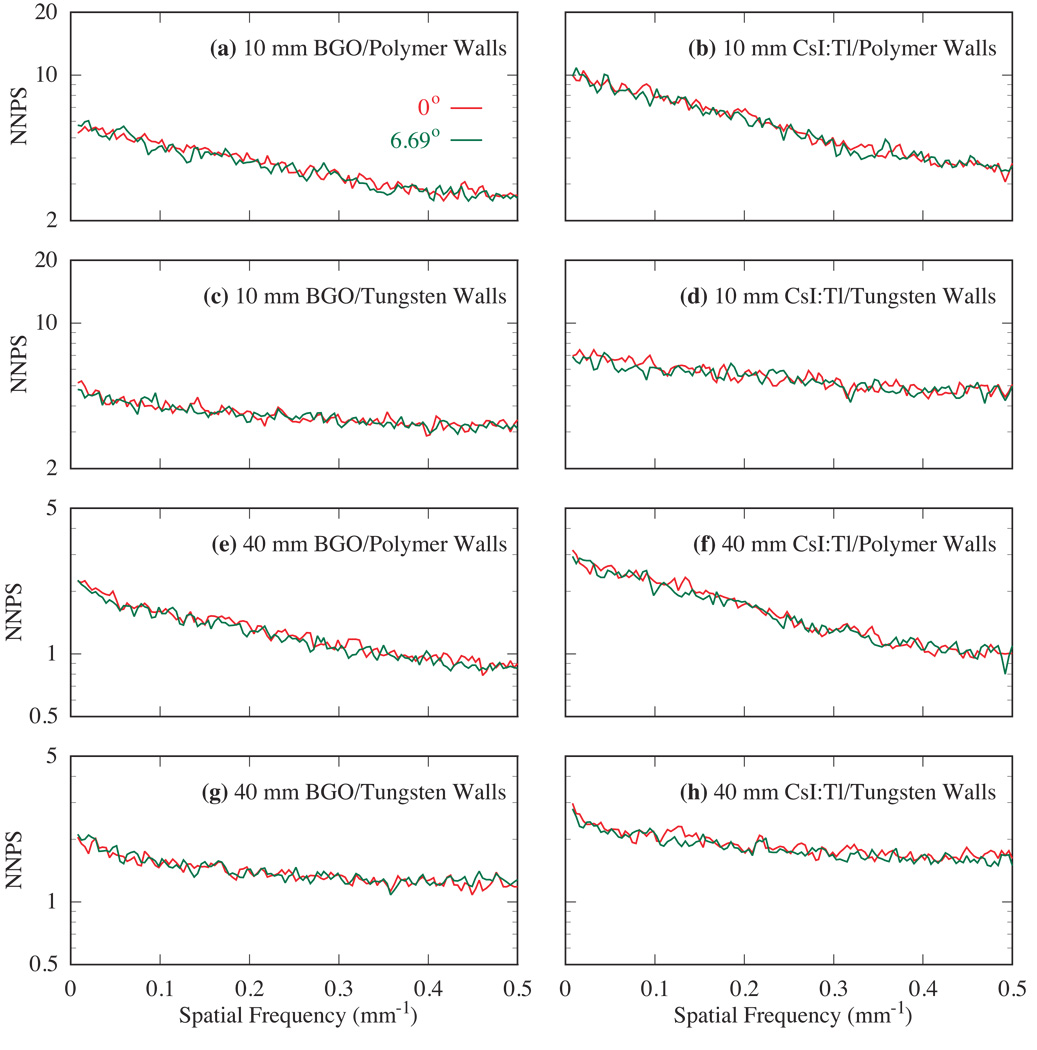
Figure 4 shows NNPS results for a normal angle of incidence (0°) and the largest simulated oblique angle (6.69°). The results are shown for 10 and 40 mm thick, segmented BGO and CsI:T1 detectors with polymer and tungsten walls. It is interesting to observe that, for each detector configuration, the NNPS results for the two angles almost overlap. Note that the results at 2.24° and 4.47°, which are not shown for reasons of clarity, also overlap with these results. For the conditions examined, the independence of NNPS on the angle of incidence is a result of the energy deposition of Compton interactions, which dominate at MV energies. The shape and size of the energy deposition of secondary Compton electrons remain largely unchanged over the range of small angles studied, resulting in negligible, additional spatial correlation to the NPS with increasing angle of incidence. All BGO configurations exhibit lower levels of NNPS, as well as reduced falloff as a function of spatial frequency, compared to their CsI:T1 counterparts. Similarly, the configurations with tungsten walls are found to show lower NNPS and reduced falloff with frequency compared to the configurations with polymer walls. These effects are a result of the higher mass density of the BGO (compared to CsI:T1) and tungsten (compared to the polymer), which leads to greater radiation attenuation that reduces the overall level of noise through reduction of Swank noise (Wang et al., 2009a). Greater radiation attenuation also leads to reduced spreading of secondary electrons, resulting in less pronounced signal correlation between neighboring scintillator elements – explaining the tendency for a flatter NPS. Finally, for a given scintillator type and septal wall material, although increasing scintillator thickness leads to lower levels of NNPS due to increased radiation attenuation, it does not significantly affect the shape of the NNPS results – an effect that is largely the result of the nature of the energy deposition of Compton interactions, discussed above.

FIG. 4.

Simulated NNPS for two incident beam angles (0° and 6.69°). Results are shown for 10 and 40 mm thick, segmented BGO and CsI:T1 detectors with polymer and tungsten septal walls.

C. Detective quantum efficiency

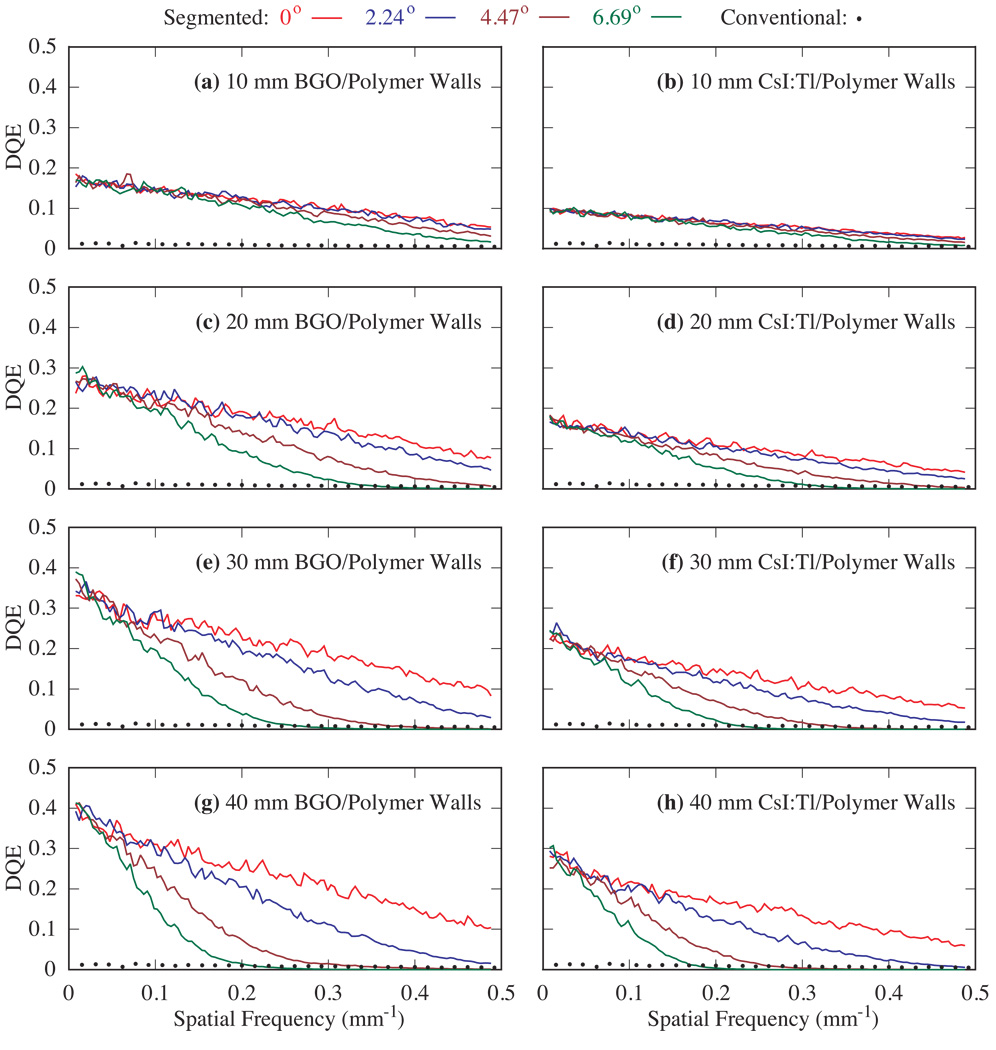
Figure 5 shows simulated DQE results as a function of incident beam angle for 10 – 40 mm thick, segmented BGO and CsI:T1 detectors with polymer septal walls. All BGO configurations exhibit higher DQE compared to their CsI:T1 counterparts, due to the higher radiation attenuation provided by the BGO material. For each detector configuration, while the low-frequency DQE results merge for all incident angles, the higher-frequency results exhibit increased degradation at progressively more oblique angles of incidence, and such degradation is more pronounced for thicker detectors. Moreover, although increasing scintillator thickness leads to increased DQE for all frequencies (up to the Nyquist frequency) at 0°, as well as for low spatial frequencies at all simulated angles, it does not necessarily result in improved DQE at high frequencies for the case of oblique angles. For example, for 2.24° and for both scintillators, the 20 mm thick detector exhibits higher DQE than the 10 mm thick detector at all frequencies. However, further increasing scintillator thickness to 30 and 40 mm results in DQE improvements only for frequencies below ~0.40 and 0.31 mm⁻¹, respectively. For 4.47° and for both scintillators, the 20, 30 and 40 mm thick detectors offer higher DQE than the 10 mm detector only for frequencies below ~0.27, 0.20 and 0.16 mm⁻¹, respectively. For larger angles, improvement in DQE is restricted to even lower frequencies. Compared to the conventional EPID, all segmented scintillator configurations exhibit substantially higher DQE at zero spatial frequency mainly due to improved radiation attenuation (up to ~75% compared to ~2% at 6 MV) (Wang et al., 2009a). At higher frequencies, however, DQE values exhibit a falloff that is more pronounced for larger angles of incidence. For some configurations, the falloff is so large that it results in DQE values below that of the conventional EPID.

FIG. 5.

DQE for four incident beam angles (0°, 2.24°, 4.47°, and 6.69°) using 10 – 40 mm thick, segmented BGO and CsI:T1 detectors with polymer septal walls. In this figure and in figure 6, for each detector configuration, the progressive degradation in DQE shown by the various lines corresponds to increasing incident beam angle. Note that the results are compared to DQE measured from the conventional EPID.

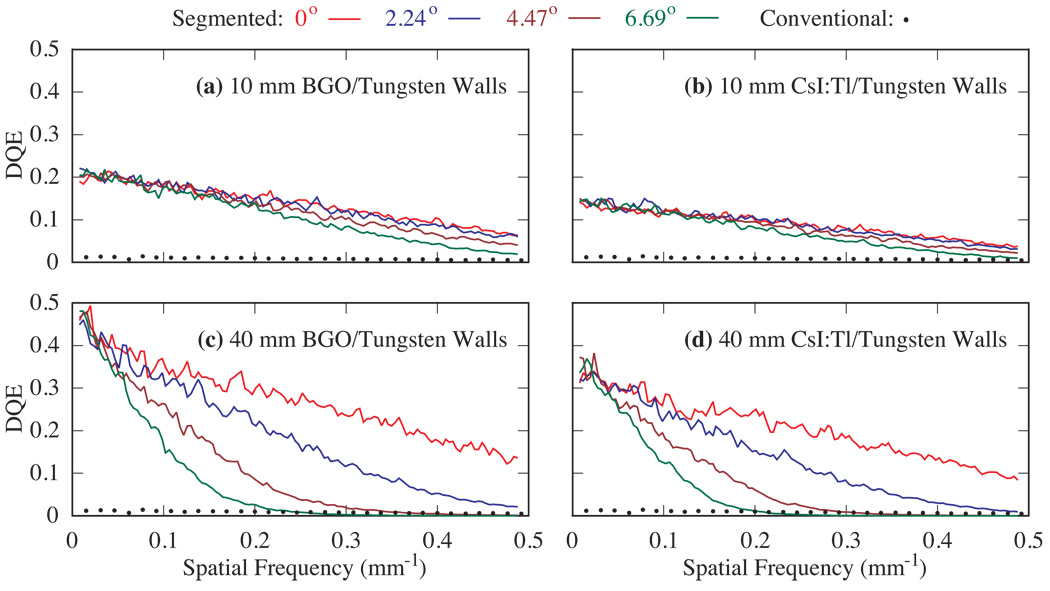
Figure 6 shows simulated DQE results as a function of incident beam angle for 10 and 40 mm thick, segmented BGO and CsI:T1 scintillators with tungsten septal walls. The use of tungsten walls as opposed to polymer walls does not change the general trends, noted above, of DQE degradation at oblique angles. However, DQE is improved at all spatial frequencies for the examined incident angles. Compared to the conventional EPID, all segmented scintillator configurations exhibit substantially higher DQE at zero spatial frequency – but degrade significantly at higher frequencies, especially for larger oblique angles.

FIG. 6.

DQE for four incident beam angles (0°, 2.24°, 4.47° and 6.69°) using 10 – 40 mm thick, segmented BGO and CsI:T1 detectors with tungsten septal walls. The results are compared to DQE measured from the conventional EPID.

IV. SUMMARY AND DISCUSSION

Thick, segmented crystalline scintillators hold considerable potential for significantly improving DQE for EPIDs. Such improvements would benefit portal imaging by allowing better image quality at current patient setup doses (i.e. few cGy), or equivalent image quality at substantially lower doses (Wang et al., 2009b). These improvements would also facilitate MV CBCT procedures (with the same imager) that could provide soft tissue visualization at clinically practical (i.e. low) doses (Wang et al., 2008; El-Mohri et al., 2010) for cases requiring greater precision in radiation delivery. To assist in the development of such scintillators, Monte Carlo simulations of radiation transport have been carried out to examine the effects of beam divergence on the MTF, NNPS and DQE performance of EPIDs. These simulations examined 10 – 40 mm thick, segmented BGO and CsI:T1 scintillators incorporating low-density polymer, and high-density tungsten walls. The simulations were carried out for incident angles up to 6.69°, corresponding to those encountered at locations up to ~15 cm from the central beam axis, for a detector located 130 cm from a radiation therapy x-ray source.

The simulation results quantify the degradation of the MTF for BGO and CsI:T1 segmented scintillating detectors as a function of increasing angle of incidence, demonstrating that such degradation is more severe for thicker scintillators. The use of the higher-density scintillator (i.e. BGO) and/or septal wall material (i.e. tungsten) helps to preserve MTF performance at all angles. For each detector configuration, the NNPS behavior is almost independent of incident angle for the examined range of angles. Given these relatively similar levels of NNPS, the dependence of DQE on incident angle is therefore primarily determined by the MTF. While segmented scintillating detectors can provide significantly increased DQE at normal incidence (0°), their DQE performance is degraded at oblique angles, and such degradation is more significant for thicker detectors. The simulation results indicate that the DQE performance of 10 mm thick detectors is not strongly affected by beam divergence for detectors areas up to ~30 × 30 cm², and remains higher than that of conventional EPIDs at all spatial frequencies. For thicker detectors, the area over which the DQE is relatively unaffected is significantly reduced.

The results of this study indicate that, with a divergent beam, the MTF and DQE performance of EPIDs based on thick, segmented scintillators will progressively degrade at locations toward the periphery of the detector (whose center is positioned along the central beam axis). This may lead to imaging artifacts when such detectors are used for MV CBCT acquisition. Given that spatial resolution in a computed tomographic image set inherently degrades with increasing distance from the iso-center (Hsieh, 2003) (which generally corresponds to data acquired progressively further from the center of the EPID detection area in the case of MV CBCT), the effects of obliquely incident radiation on CBCT may significantly exacerbate the inherent spatial resolution degradation. Therefore, in order for CBCT to benefit from the significantly increased quantum efficiency offered by segmented detectors with thicknesses greater than ~10 mm, it may be necessary to introduce some form of focused geometry to minimize (or perhaps avoid) the undesirable effects of beam divergence.

Several approaches for achieving focused geometries that could significantly limit the sharing of primary radiation between adjacent elements, and lead to a uniform MTF and DQE performance across the detector area, are conceivable. In one approach that retains the use of a conventional active matrix, flat-panel array, all scintillator crystals and septal walls are designed so as to be focused towards the radiation source – as illustrated in Fig. 1 of (Sawant et al., 2005b). Two alternative approaches that would require somewhat less complex (and perhaps more readily manufacturable) shapes for the scintillator elements would involve geometries in which the scintillator elements are arranged along a cylindrical or hemispherical surface – with the individual elements focused toward the radiation source. While either approach could employ individual photodiodes or relatively small arrays of photodiodes coupled to scintillator elements (as has been demonstrated for cylindrical geometries) (Lewis et al., 1992; Kirvan et al., 2010), the use of indirect detection, active matrix arrays fabricated on flexible plastic substrates (rather than on the rigid glass substrates used for conventional flat-panel arrays) is also conceivable. Prototypes of active matrix arrays on flexible substrates (based on low-temperature a-Si or organic semiconductor material) have been demonstrated (Street et al., 2005). Such devices can be configured in a cylindrical geometry or, through suitable layout of the array pixels along with cutting and bending of the substrate, can also be configured in an approximately hemispherical shape (Street et al., 2009).

In conclusion, the results reported in this study of the effects of beam divergence on thick, segmented scintillators designed for MV imaging are instructive – demonstrating relatively small performance degradation for scintillators up to ~10 mm thick but more substantial degradation for thicker scintillators. It is anticipated that the simulation techniques employed in this article will be of assistance in guiding the design and optimization of future prototypes involving non-focused as well as focused geometries – thereby facilitating realization of the performance-enhancing benefits of thick, segmented scintillators.