Fragile regions and not functional constraints predominate in shaping gene organization in the genus Drosophila

Abstract

During evolution, gene repatterning across eukaryotic genomes is not uniform. Some genomic regions exhibit a gene organization conserved phylogenetically, while others are recurrently involved in chromosomal rearrangement, resulting in breakpoint reuse. Both gene order conservation and breakpoint reuse can result from the existence of functional constraints on where chromosomal breakpoints occur or from the existence of regions that are susceptible to breakage. The balance between these two mechanisms is still poorly understood. Drosophila species have very dynamic genomes and, therefore, can be very informative. We compared the gene organization of the main five chromosomal elements (Muller's elements A–E) of nine Drosophila species. Under a parsimonious evolutionary scenario, we estimate that 6116 breakpoints differentiate the gene orders of the species and that breakpoint reuse is associated with ∼80% of the orthologous landmarks. The comparison of the observed patterns of change in gene organization with those predicted under different simulated modes of evolution shows that fragile regions alone can explain the observed key patterns of Muller's element A (X chromosome) more often than for any other Muller's element. High levels of fragility plus constraints operating on ∼15% of the genome are sufficient to explain the observed patterns of change and conservation across species. The orthologous landmarks more likely to be under constraint exhibit both a remarkable internal functional heterogeneity and a lack of common functional themes with the exception of the presence of highly conserved noncoding elements. Fragile regions rather than functional constraints have been the main determinant of the evolution of the Drosophila chromosomes.

The structural and functional characterization of multiple genomes enables us to uncover patterns in the evolution of the organization and the function of eukaryotic genomes. Both gene order (Hurst et al. 2004) and the distribution of the breakpoints of chromosomal rearrangements (Pevzner and Tesler 2003) are thought to be nonrandom in eukaryotes. Both phenomena, although usually treated independently, are, in fact, closely related since both imply that the rate of rearrangement is nonuniform across the genome.

Nonrandom gene order in eukaryotes is thought to result from functional interactions and dependencies between neighboring genes. Gene clustering could reflect a local enrichment for genes with shared biological properties. Examples of this would be clusters of co-expressed genes (Boutanaev et al. 2002; Lercher et al. 2002; Roy et al. 2002), clusters of genes that are progressively expressed temporally and/or spatially (Kmita et al. 2002; Mahajan and Weissman 2006), and clusters of genes that fall into similar functional classes according to the Gene Ontology or other criteria (Williams and Bowles 2004; Petkov et al. 2005). The formation of clusters would occur through tandem duplication events (Zhang and Nei 1996; Aguileta et al. 2006) and via chromosomal rearrangements juxtaposing interacting genes (Wong and Wolfe 2005; Poyatos and Hurst 2006). Natural selection would prevent these optimized gene organizations from changing, since change would have a consequential detrimental fitness effect.

Other chromosomal regions are recurrently found at the edges of chromosomal rearrangements. The reuse of breakpoints was inferred from an excess of very short synteny blocks between humans and mice (Pevzner and Tesler 2003). Comparative sequence analysis in mammals and Drosophila species has subsequently provided evidence of breakpoint reuse (Murphy et al. 2005; Ranz et al. 2007). The cause of breakpoint reuse remains unclear, although it is frequently associated with sequences prone to participate in rearrangements, for example, segmental duplications (Bailey and Eichler 2006; Ruiz-Herrera et al. 2006), or that confer fragility, for example, AT-rich regions (Strissel et al. 1998; Zhang and Freudenreich 2007).

Many aspects concerning gene clusters and fragile regions remain poorly understood. The mere detection of clusters with shared biological properties in one species, if not conserved in others, does not allow us to distinguish between chance and a lineage-specific optimized organization. Furthermore, gene clustering across species with genomes that exhibit low rates of chromosome rearrangement could merely reflect common ancestry, rather than functional constraint (Ohno 1973; Nadeau and Taylor 1984). In addition, if functional constraints are widespread, disruptions will occur wherever these functional constraints are relaxed, regardless of any particular structural feature (Mackenzie et al. 2004; Becker and Lenhard 2007; Kikuta et al. 2007). Conversely, if fragile regions are common, one can predict that there will also be clusters of adjacent genes, functionally related or not, which will rarely be separated by breakpoints (Becker and Lenhard 2007).

The study of vertebrate genomes has clarified some of these questions. Some genomic regions encompass genes that share regulatory sequences or genes separated from their regulatory regions by functionally and phylogenetically unrelated genes (Gould et al. 1997; Trowsdale 2002; Spitz et al. 2003; Li et al. 2006). The complex architecture of these regulatory landscapes could contribute significantly to the conservation of their integrity (Spitz et al. 2003, 2005; Mackenzie et al. 2004), as has been shown among vertebrate species (Goode et al. 2005; Kikuta et al. 2007). These regulatory blocks are enriched for highly conserved noncoding elements, which have been shown to affect the expression of neighboring genes (Glazov et al. 2005; Vavouri et al. 2007). The conservation of regulatory landscapes has also been documented in Diptera (Engstrom et al. 2007).

The biological relevance of different forms of biologically coherent clustering on a genomic scale, other than these regulatory landscapes, is less clear. For example, between human and mouse only 3%–5% of the genome was found to be organized as co-expressed clusters of two to three genes (Semon and Duret 2006). Mixed results were obtained when the integrity of clusters of co-expressed genes in humans was examined in mouse (Singer et al. 2005; Liao and Zhang 2008). Large-scale remodeling of chromatin structure due to actively transcribed genes, or the participation of these genes in transcription factories, could expose neighboring genes to the transcriptional machinery, and this alone could lead to a degree of basal transcription in the absence of specific repressive or tethering elements (Spitz and Duboule 2008). The promiscuous interaction of long-range enhancers with promoters of neighboring genes could also play a role (Spitz and Duboule 2008). Nevertheless, examples of coordinated co-expression have been reported (Kalmykova et al. 2005; Poyatos and Hurst 2006).

The comparison of gene organization in species with high rates of chromosome rearrangement, such as Drosophila or nematodes (Ranz et al. 2001; Coghlan and Wolfe 2002; Richards et al. 2005), and for which detailed functional information exists, can show how genome architecture has been shaped by constraints and fragile regions over time. If functional constraints do exist, they are likely to be associated with the largest homologous collinear blocks (HCBs), since regions under no functional constraint would presumably have been disrupted. Likewise, highly rearranged genomes can show precisely how widespread breakpoint reuse is and to which genomic regions it is associated.

The Drosophila genome is organized into six chromosomal elements, the so-called Muller's elements A–F, whose gene content has been virtually preserved within the genus (Muller 1940; Sturtevant and Novitski 1941). This pattern is consistent with paracentric inversions being the dominant mode of change (for why this is so, see Sturtevant and Beadle 1936; Carson 1946). A recent effort to characterize their patterns and mode of evolution has been done with a combination of approaches often applied to species pairs (Bhutkar et al. 2007, 2008). Here, we used an approach that enables multiple genome analysis and that minimizes the number of rearrangements needed to account for the observed gene orders (Bourque and Pevzner 2002). Specifically, we aimed to determine the relative weight of fragile regions and constraints in shaping gene organization in Drosophila species. We first identified the collection of orthologous landmarks—singletons and HCBs—that underlie the molecular organization of the Drosophila genome. Next, we assessed the magnitude of gene order reshuffling and reconstructed the ancestral genomes to those of the species compared. With that information we quantified the magnitude of breakpoint reuse and performed a set of simulation studies for each of the Muller's elements to gauge how the two determinants of the genome organization account for the observed patterns of both change and conservation in gene order and thus to determine how they have affected the genome architecture. Finally, we examined the correspondence between the HCBs that are most plausibly under constraints and regulatory domains, co-expression territories, and other functional signatures. Our work reveals that the observed patterns are consistent with fragile regions being more important than functional constraints during the evolution of the genus Drosophila. The notion that regulatory domains might have played a primary role in preserving the integrity of some genomic regions is reinforced.

Results and Discussion

Gene order reconstruction

We identified orthologous protein-coding genes in 11 species of Drosophila using those in Drosophila melanogaster as a reference (Ashburner et al. 2005; Richards et al. 2005; Clark et al. 2007). This was done by combining sequence similarity methods (BLASTN, TBLASTN, and PSI-TBLASTN) and synteny inference (Methods; Supplemental Text S1). The minimum number of annotated genes was 11,019 for Drosophila grimshawi. In species with a fragmented genome sequence assembly (i.e., in contigs or supercontigs), we reconstructed gene orders within a maximum parsimony framework (Supplemental Text S1). First, we used an algorithm based on the local alignment of the scaffolds of the species with fragmented assembly against the genome sequence of the most closely related species. Then, we used physical mapping information to refine our previous reconstruction and to orient the scaffolds. Finally, we explored the set of all possible assemblies with all remaining scaffolds, and selected the ones that are more similar to those of the closest species. Our reconstructed gene orders are in remarkably good agreement with others recently reported (Schaeffer et al. 2008; Supplemental Text S1).

Comparative architecture of the Drosophila genome

For the quantification of the gene order disruption, we discarded data from Drosophila sechellia, Drosophila simulans, and Drosophila persimilis, since their gene orders are similar to their sibling species D. melanogaster and Drosophila pseudoobscura, respectively. The remaining nine species represent an accumulated evolutionary time of ∼381 million years (Myr) (Powell and DeSalle 1995; Tamura et al. 2004). We compared the gene order of the five large Muller's elements (A–E) across the nine species and identified orthologous landmarks. We considered physically related genes (nested, interleaved, or overlapping) as single one-dimensional anchors (independent gene anchors or IGAs hereafter). There are many reasons why this type of anchor, rather than the number of genes or nucleotides, is convenient (Methods). Of the 11,553 IGAs as defined in the D. melanogaster genome, 9193 IGAs were mapped in at least one of the species of the subgenus Drosophila (Fig. 1A; Supplemental Text S1). Three progressively less restrictive requirements were used to identify disruptions that affect the molecular organization of IGAs along the Muller's elements. With the most stringent synteny definition, identical order and orientation (GOO) are required for all the IGAs within HCBs. In the second definition, only gene order (GO) is required, and in the third, only overall local contiguity (OLC), but not precise gene order, is necessary. All the breakpoints associated with intra-Muller's element transpositions are considered to represent alterations of gene order only under the GOO definition of synteny (Supplemental Text S1). The use of different synteny definitions translates into slightly different numbers of IGAs inferred to be part of orthologous landmarks (Supplemental Fig. S6); ∼2.3% of IGAs between the most extreme definitions, GOO and OLC (Table 1). The constructed comparative maps include ∼78% (GOO)–∼80% (OLC) of the 11,553 IGAs.

Figure 1.

Gene order evolution in the genus Drosophila. (A) Magnitude of independent gene anchor (IGA) order evolution and its phylogenetic distribution across the genus Drosophila. The magnitude of change is expressed as the number of inversions, as estimated under maximum parsimony using multiple genome rearrangement (MGR) (Bourque and Pevzner 2002), for three different synteny definitions: (red) conserved gene order and orientation (GOO); (blue) conserved gene order (GO); and (black) only overall local contiguity (OLC). (B) Box plot of the average breakpoint index (BI) across Muller's elements as inferred from MGR. (Box) Interquartile range (from the 25th to the 75th percentile, i.e., 50% of the values); (line across the box) median; (rhombus) mean; (whiskers) maximum and minimum values with the exception of the outliers (solid circles). The BI equals the number of times each of the edges of a HCB or singleton has been involved in a chromosomal rearrangement since the ancestral genome to the genomes of the species studied here divided by 2. Mann-Whitney U tests were performed between pairs of Muller's elements, and the resulting P-values were adjusted with the Bonferroni correction. All the comparisons involving Muller's element A were statistically significant (P < 1.0 × 10⁻⁴); the only additional pairwise comparison that entails statistically significant differences involves Muller's elements B and E (P = 4.5 × 10⁻³). The results shown correspond to the GO synteny definition.

Table 1.

Salient features of the comparative architecture of the Drosophila genome after comparing nine species

GOO, gene order and orientation; GO, gene order; OLC, overall local contiguity. The number of IGAs mapped was not evenly distributed across the five Muller's elements. Specifically, Muller's elements A and B have fewer IGAs identified than expected, and Muller's elements D and E have more (G_adj = 33.07, df = 4, P = 1.2 × 10⁻⁶); the number of IGAs expected to be identified per Muller's element was calculated based on the number of IGAs in D. melanogaster. For the results from multiple genome rearrangement (MGR), the number of inversions has been multiplied by 2 (Fig. 1A). For the results from neighboring gene pairs (NGP), the analysis was done with each of the nine species as outgroup; only the maximum number (using D. melanogaster and D. yakuba as the outgroup species) and the minimum number (using D. willistoni as the outgroup species) of disruptions are shown (Supplemental Fig. S15). See Supplemental Text S1 for a detailed explanation of the estimate based on number of IGA pairs. Unique inversions are those whose breakpoints disrupt two pairs of orthologous landmarks that have not been involved in any other rearrangement based on our data.

Magnitude of IGA rearrangement, breakpoint phylogenetic occurrence, and ancestral genomes

We used three approaches to estimate the number of breakpoint events that have been fixed between species (Table 1; Supplemental Text S1). Of them, the one that best accounts for the phenomenon of breakpoint reuse is that provided by a maximum parsimony reconstruction methodology implemented in the software Multiple Genome Rearrangement (MGR) (Bourque and Pevzner 2002). MGR minimizes the number of rearrangements across all the branches in the tree, and, from this most parsimonious rearrangement scenario, it enables the inference of the ancestral order of orthologous landmarks for both the internal nodes and the terminal branches in the species tree (Supplemental Data set S1). Figure 1A shows how the species tree is precisely recapitulated by the differentiation at the chromosomal level of the nine species, as well as the estimated number of inversions for each of the branches. The same trend in the phylogenetic occurrence of inversions is observed regardless of the synteny definition used. According to the GO synteny definition, at least 3058 inversions are necessary to account for the rearrangement of the order of IGAs. Assuming that all disruptions are due to inversions, the rate of change is ∼8 rearrangements/Myr or 0.021–0.040 disruptions/Mb/Myr depending on whether the smallest (D. melanogaster, 175 Mb) or the largest (Drosophila virilis, 333 Mb) genome among the species is used (Ashburner et al. 2005). The comparison of this rate with those of other organisms confirms that the Drosophila genome shows the fastest rate of gene order repatterning after nematodes (Supplemental Text S1).

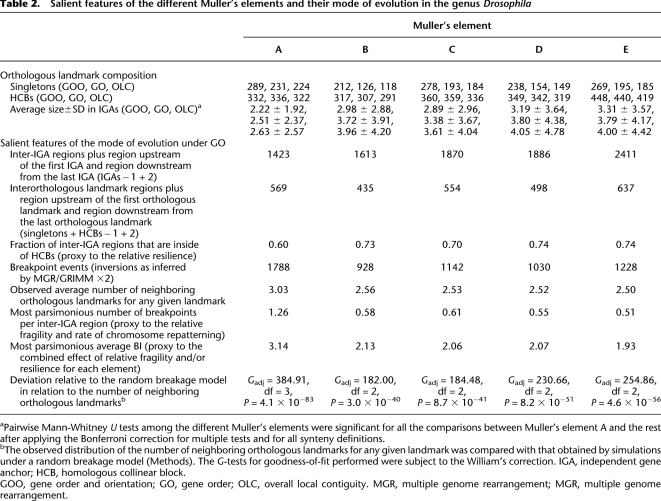
Among all the species, Drosophila willistoni stands out as having the most rearranged genome (Supplemental Table S15); this does not seem to be an artifact of its assembly (Supplemental Text S1). We find a significant heterogeneity in the rates of rearrangement across the lineages (G_adj = 1668.79, degrees of freedom [df] = 14, P < 1 × 10⁻³⁰). This is the result of a lower than expected rate of evolution in the terminal branches that lead to D. melanogaster, Drosophila erecta, and D. virilis, a higher than expected rate of rearrangement associated with the terminal branch that leads to D. willistoni and, especially, with the internal branches prior to the radiation within the Drosophila subgenus and that leading to the obscura and melanogaster species groups. Muller's element A has been more deeply rearranged, as indicated by its higher than expected proportion of HCBs and singletons, which denotes more fragmentation (G_adj = 65.45, df = 4, P = 2.1 × 10⁻¹³), and the significantly lower average size of its anchors (Table 2). The other Muller's elements do not significantly differ from each other in the extent of their rearrangement; the same result is found under the GOO and OLC synteny definitions.

Table 2.

Salient features of the different Muller's elements and their mode of evolution in the genus Drosophila

^aPairwise Mann-Whitney U tests among the different Muller's elements were significant for all the comparisons between Muller's element A and the rest after applying the Bonferroni correction for multiple tests and for all synteny definitions.

^bThe observed distribution of the number of neighboring orthologous landmarks for any given landmark was compared with that obtained by simulations under a random breakage model (Methods). The G-tests for goodness-of-fit performed were subject to the William's correction. IGA, independent gene anchor; HCB, homologous collinear block.

GOO, gene order and orientation; GO, gene order; OLC, overall local contiguity. MGR, multiple genome rearrangement; MGR, multiple genome rearrangement.

Our MGR estimates of the reshuffling of IGA order, as well as the phylogenetic distribution of chromosomal breaks, are remarkably different from those in a previous report (Bhutkar et al. 2007, 2008). This disagreement might result from differences in how breaks are inferred, the raw scaffold information used, the methodology used to reconstruct the gene order of the species, or from any combination of these factors. We analyzed the impact of using a different parsimonious framework, the neighboring gene pair method (NGP), which only requires information on the identity of pairs of adjacent landmarks (Bhutkar et al. 2007). Using our data set, the number of rearrangements inferred with NGP was substantially lower than that inferred with MGR, but the overall phylogenetic distribution of the breaks was virtually the same between both methods (Fig. 1A; Supplemental Fig. S14; Table 1). The number of chromosomal breaks inferred with NGP to have occurred between the ancestor to the species in the subgenus Drosophila and the ancestor to the species from melanogaster/obscura groups (Supplemental Fig. S14) is substantially higher than those (34 and 40, respectively) inferred previously (Fig. 8 in Bhutkar et al. 2008). In contrast, if we focus only on the breaks that occurred since the common ancestor of the species in the subgenus Drosophila and since the common ancestor of the species of the melanogaster/obscura groups, we estimate 1825 breakpoints, as compared to the 2892 previously estimated (Bhutkar et al. 2008). We did not consider the breaks associated with the lineages of D. sechellia, D. persimilis, and D. willistoni since the first two were discarded by us and the latter was not included in Bhutkar et al. (2008). The discrepancies exist even between the very well-studied species D. melanogaster and Drosophila yakuba (Lemeunier and Ashburner 1976; Ranz et al. 2007), which were used to diagnose the nature of the differences (Supplemental Text S1). We concluded that artifactual disruptions at a finer scale have inflated previous estimates.

Magnitude of breakpoint reuse

We sought to identify cases of HCBs and singletons that have repeatedly flanked chromosomal breaks. We used the reconstruction of IGA order obtained with MGR to calculate a breakpoint index (BI) associated with each orthologous landmark. The BI equals the number of breaks associated with the two edges of any given landmark divided by 2. We find that 584 (21.8%) of the orthologous landmarks are not associated with the breakpoint reuse (BI = 1), whereas 2099 (78.2%) are (BI > 1). A Drosophila orthologous landmark is associated with a BI of 2.27 on average (SD = 1.34; median = 2). This is higher than that estimated previously (Bhutkar et al. 2008), probably because our breakpoint reuse estimate is not pairwise limited. A potential overestimate of breakpoint reuse due to the use of maximum parsimony, when a large fraction of the genome is omitted from the analysis (Sankoff and Trinh 2005), does not apply in our case since our comparative maps make use of ∼78%–80% of all possible orthologous landmarks (Supplemental Text S1). Simulations in which breakpoints associate at random with the 2683 orthologous landmarks indicate that there are more orthologous landmarks than expected with either very low or very high BIs, a pattern that applies to all the Muller's elements (Supplemental Table S29). Muller's element A displays a significantly higher average BI than the other elements (Fig. 1B). Furthermore, we did not find evidence that the proportion of orthologous landmarks associated with BI > 1 varied significantly across the main clades in the tree of the species (G_adj = 3.51, df = 2, P = 0.17). These results highlight how pervasive the phenomenon of breakpoint reuse is in the genus Drosophila, and, although they do not challenge the notion of the uniqueness of inversions (Krimbas and Powell 1992; Wasserman 1992), they do indicate that the probability that a particular pair of adjacent orthologous landmarks might be broken more than once in the genus Drosophila is not negligible. In agreement with this degree of breakpoint reuse, the number of unique inversions, those whose limits disrupt two pairs of adjacent orthologous landmarks that are not associated with any other additional rearrangement, was found to be remarkably small (Table 1).

Mode of chromosome evolution

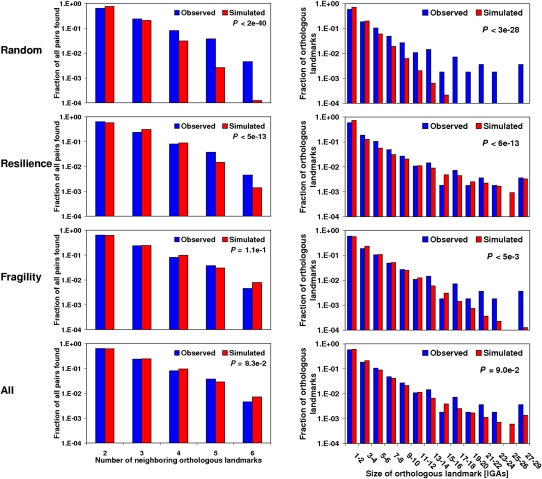
In order to determine the extent to which fragility and constraints have contributed to the patterns of change and conservation of the gene organization in the genus Drosophila, we simulated different modes of chromosome evolution (Methods). A similar analysis has been done for human–mouse (Peng et al. 2006) and for pairs of Drosophila species (Bhutkar et al. 2008). These simulations recreated a single mode of chromosome evolution in which particular genomic regions were refractory to chromosomal breaks and focused on the possibility of obtaining breakpoint reuse values similar to those observed. In our view, there will always be a degree of functional constraint (resilience) and a degree of fragility that will yield a level of breakpoint reuse identical to that observed and higher than that expected under the random breakage model (Becker and Lenhard 2007). Therefore, the breakpoint reuse value cannot properly inform us about the role played by functional constraints and fragile regions. For highly dynamic genomes, and when information from multiple species is available, other proxies for assessing the role of functional constraints versus fragile regions can be more informative. These proxies are the cumulative distribution of the size of the resulting orthologous landmarks and the distribution of the number of different neighboring orthologous landmarks to any given landmark in the nine terminal genomes (Supplemental Fig. S20), respectively. In the case of the distribution of the number of different neighboring orthologous landmarks, we distinguish between unique and multiple breakpoints. Unique breakpoints, unlike multiple breakpoints, are generally associated with scenarios in which a particular edge of an orthologous landmark shows only two different neighbors among the nine terminal species (Supplemental Fig. S20), that is, it has participated in one rearrangement only. The goodness-of-fit of the distributions resulting from mimicking different modes of chromosome evolution and the observed ones for both proxies can be evaluated with a G-test. We first tested a random breakage model and found a poor fit with the observed data for all Muller's elements: (1) the number of orthologous landmarks of small size is smaller than expected by chance, whereas the number of large orthologous landmarks is higher than expected; and (2) the number of unique breakpoints is lower than expected, whereas cases of multiple observed breakpoint events are in excess. Figure 2 illustrates the results for Muller's element C.

Figure 2.

Test to the mode of evolution for Muller's element C. Comparisons were made between the observed and simulated distributions, under four different modes of evolution, for the number of neighboring orthologous landmarks (left) and the size of orthologous landmarks (right). The distribution of the simulated data is obtained from 1000 simulations in which a chromosomal element has the same organizational features as those of Muller's element C, which is subjected to 571 chromosomal inversions, i.e., the estimate obtained from MGR. First, we show the random breakage model, which is characterized for breakages occurring at random along the chromosomes. None of the distributions are recapitulated, in part because of an excess of multiple breakpoints and large orthologous landmarks in the observed data. Second, we show a mode of evolution in which constraints prevent some genomic regions from being broken. The results for the optimum degree of resilience (r = 0.77), that for which the best fit is found for observed and simulated distributions, are shown. Notice especially the excess of multiple breakpoints observed in relation to those expected (left). Third, we show a mode of evolution in which some genomic regions tend to flank inversion breakpoints. The results for the optimum degree of fragility (f = 0.94) are shown. Notice especially the excess of large HCBs observed in relation to those expected (right). Fourth, we show a mode of chromosome evolution in which resilience and fragility coexist. The results for the optimum combination of degree of resilience and fragility (r = 0.14; f = 0.92) are shown. In this case, no statistically significant difference is found between the observed and simulated distributions. The particular ways in which constraints and fragile regions were simulated correspond to R₂ and F₁ (Supplemental Table S30). Units on the y-axes are expressed on a logarithmic scale. Supplemental Figure S21 shows equivalent comparisons for the remaining Muller's elements and combinations of them.

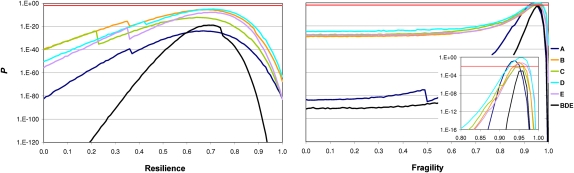
We next recreated the existence of constraints. For that, randomly selected inter-IGA regions are prevented from being broken. These constraints were assumed to be invariant during the divergence of the species. Then, we tested whether, if under different degrees of simulated resilience, the distribution of the number of different neighboring orthologous landmarks for any given landmark can be recapitulated. If not, we can conclude that resilience alone cannot explain the observed data. Our simulations showed that, regardless of the degree of resilience of the Muller's element in question, the distribution of the number of different neighboring orthologous landmarks obtained was always significantly different from that observed. The degree of resilience that generates the best fit between the simulated and the observed data is when ∼68% of the inter-IGA regions within HCBs are protected (Fig. 3). Figure 2 shows that not even under the degree of resilience that gives the most balanced fit for both proxies can the respective distributions be recapitulated. A second parameter that can vary in these simulations is the identity of the inter-IGA regions that are selected for protection. We explored five different ways the inter-IGA regions are selected (R₁–R₅) (Methods; Supplemental Table S30), and obtained virtually identical results.

Figure 3.

Assessment of the feasibility of two extreme modes of chromosome evolution to explain the observed patterns of change for different Muller's elements (A–E). The particular ways in which resilience and fragility were simulated correspond to R₂ and F₁ (Supplemental Table S30). (Left) P-values from the G-tests goodness-of-fit performed to evaluate the deviation of the observed distribution of the number of different neighboring orthologous landmarks and that resulting from simulations under different degrees of resilience (r ∈ [0, 1]). The observed and the simulated distributions show a poor fit even for that degree of resilience (r = 0.68 ± 0.03) for which the best fit between them (i.e., the largest P-value) is obtained. (Right) P-values from the G-test goodness-of-fit performed to evaluate the deviation of the observed distribution for the size of orthologous landmarks and that resulting from simulations under different degrees of fragility (f ∈ [0, 1]). If f = 0, the simulated evolutionary scenario is equivalent to the random breakage model. If f = 1, only the IGA edges flanking the 2683 + 5 inter-IGA regions chosen at random are flagged as fragile and can appear at the limit of chromosomal rearrangements. The observed and the simulated distributions do not show statistically significant differences for Muller's elements A, B, D, and E when f = 0.95 ± 0.01. For Muller's element C, there is a marginally significant difference, and for the combined Muller's element (B + D + E), P < 9 × 10⁻⁴. The statistical significance level is set to 0.01 (red horizontal line) because of the necessary correction for multiple testing. For each Muller's element and resilience/fragility value, 1000 simulations were done in which IGA order was reshuffled by a number of inversions equal to that estimated with MGR. Both the parameters of resilience and fragility were sampled with steps of 0.01. The William's correction was applied to all the G-tests performed.

Subsequently, we examined whether or not the existence of fragile regions alone could account for the observed data. For that, we simulated Muller's elements in which some of the IGAs are characterized by having ends (upstream and/or downstream regions) that are more prone to flank a breakpoint than are those of other IGAs. Increasing degrees of fragility are mimicked: from its complete absence (f = 0; all the ends of all IGAs are equally probable to participate at the edge of an inversion) to an extreme scenario in which only a number identical to that of observed orthologous landmarks plus five is allowed to participate in breakage (f = 1). For intermediate values of f, all the IGAs can be at the edge of an inversion, but the likelihood of that will vary between the edges flagged as fragile and the rest, and also among the edges flagged as fragile. Specifically, this likelihood is a function of the number of different neighboring orthologous landmarks assigned, which is done by sampling the observed distribution. Five different ways of tuning this likelihood were also explored (F₁–F₅) (Methods; Supplemental Table S30). The results for all the Muller's elements indicate that there is a degree of fragility, and a way of tuning the likelihood of flanking a breakage, for which the distribution for the size of orthologous landmarks does not differ significantly from that observed. For example, under one of the ways in which this likelihood is tuned, F₁, the degree of fragility for which the best fit is found, is ∼0.95 (Fig. 3). Nevertheless, visual inspection of the distribution of the sizes of orthologous landmarks indicates that the tail corresponding to the largest ones is never fully recapitulated, being always much less frequent than observed (Fig. 2). Therefore, the lack of statistically significant differences between the observed and the simulated data could just be the consequence of limited statistical power. To verify this, we repeated the test again upon grouping the Muller's elements that do not differ from each other for the observed data for the two proxies under analysis (Muller's elements B, D, and E) (Supplemental Tables S31, S32). Regardless of the degree of fragility, the resulting simulations for the combined element indicate that a model of chromosome evolution based on fragile regions alone can be rejected. For the Muller's elements A and C, however, we cannot reject a mode of chromosome evolution based on fragile regions alone due to our limited statistical power.

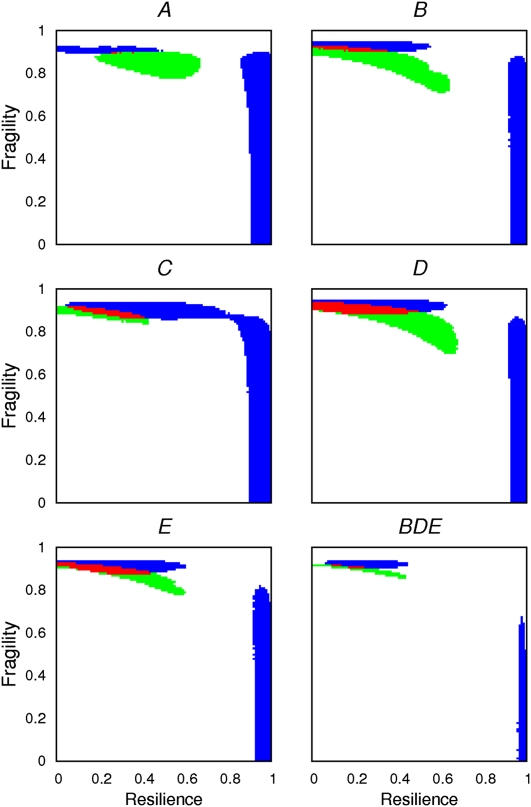
We also tested a mode of chromosome evolution in which constraints and fragile regions coexist. For different combinations of the values of resilience and fragility and different ways in which they are simulated (Supplemental Table S30), it was possible to obtain distributions for both diagnostic proxies that did not differ from those observed (Fig. 2). Figure 4 shows that the combination of high fragility and low resilience (red area on the upper-left corner in all heat maps) gives rise to the recapitulation of both distributions. In the case of the combined element, resilience must be always >0 for both distributions to be recapitulated, which is not the case for the Muller's elements B, D, and E when analyzed separately. Equivalent results for the different ways in which regions under constraint are selected and the tuning of the likelihood of breakage of an IGA edge is performed are provided in Supplemental Figure S23. The accuracy of our procedure to predict the correct mode of evolution was tested by additional simulations in which a set of simulated genomes was evolved under known parameters. Our predictions were correct in 97.5% of the cases (Supplemental Text S1).

Figure 4.

Heat map showing under which simulated conditions two key diagnostic features of chromosome evolution can be recapitulated by computer simulations. High levels of fragility and low levels of resilience yield the best recapitulation of the observed data. The existence of different degrees of resilience and fragility are simulated in steps of 0.01 according to their modes R₂ and F₁, respectively (Methods). For each Muller's element (A–E), a combination of elements B, D, and E (BDE), and resilience/fragility value, 1000 simulations were done in which IGA order was reshuffled by a number of inversions equal to that estimated with MGR. The resulting distributions for the number of neighboring orthologous landmarks and for the size of orthologous landmarks are compared with those observed using a G-test. (White) Statistically significant differences for both the distribution of the number of neighboring orthologous landmarks and for that of the size of orthologous landmarks; (blue) statistically significant differences for the number of neighboring orthologous landmarks only; (green) statistically significant differences for the size of the orthologous landmarks only; and (red) statistically significant differences neither for the size of the orthologous landmarks nor for the number of neighboring orthologous landmarks, that is, the observed distributions are recapitulated. In this particular case, constraints and fragile regions were assumed to be invariant during the simulations performed. The William's correction was applied to all the G-tests performed.

A representative simulated genome from Figure 4 would include ∼13.5 orthologous landmarks with a size ≥21 IGAs; 11.5% of the orthologous landmarks would include at least one inter-IGA region under constraint. For these orthologous landmarks, the fraction of inter-IGAs refractory to breakpoints correlates with the size and varies among Muller's elements. For example, for orthologous landmarks with size ≥21 IGAs, this fraction would be of 54% for Muller's element D and of 83% for Muller's element A, whereas for orthologous landmarks with size of 10–20 IGAs, these fractions decreased to 21% and 65%, respectively. This pattern also indicates that within orthologous landmarks associated with constraints, there are inter-IGA regions, either interspersed or at the ends of these HCBs, that are not under constraint. From a genomic perspective, the fraction of inter-IGAs that must be refractory to breakage to best recapitulate the observed data ranges from 8.1% to 20.6%, depending on the Muller's element (14.7% when considering all Muller's elements jointly), which emphasizes that most gene order conservation in the Drosophila genome is not under any kind of constraint.

Equivalent simulations were performed mimicking constraints that could vary over time in their distribution across the genome and also among lineages. Likewise, we incorporated into our simulations the possibility that the edges of particular inter-IGA regions could increase their degree of fragility, whereas others could decrease it. These dynamic resilience and fragility were simulated separately, jointly, and in mixed models (e.g., invariant resilience with dynamic fragility). None of the findings when invariant resilience and fragility were simulated changed. Nevertheless, in order to best recapitulate both distributions, a larger fraction of the inter-IGA regions must be under constraint and the edges of inter-IGA regions flagged as fragile must have a higher probability of flanking a breakage. In addition, the fraction of inter-IGA regions that is under constrain in all terminal species is substantially lower than under invariant resilience and fragility.

Supplemental Figure S22 shows the BI values for the performed simulations in Figure 4. For all Muller's elements, we find degrees of resilience and fragility alone that give rise to essentially the same BI, in good agreement with our starting prediction. Therefore, the BI, although sufficient to reject the random breakage model (resilience and fragility 0 in Figs. 3, 4) cannot be used to distinguish between modes of chromosome evolution driven by constraints or fragile regions.

Evidence and nature of constraints

Among the collection of HCBs, we find some that include genes that are known to be under the control of common regulatory sequences such as the Iroquois complex (HCB 1828) (Gomez-Skarmeta et al. 1996), the achaete–scute complex (HCB 7) (Modolell and Campuzano 1998), and the genes kni and knrl (HCB 1995) (Lunde et al. 1998). Nevertheless, this information is still scarce so that it is difficult to identify HCBs that might reflect functional constraints. The largest HCBs are the most likely genomic regions to be associated with functional constraints, in good agreement with our simulations. We focused on the GO synteny definition, and we arbitrarily set a threshold value of 21 IGAs as the minimum size for an HCB to be considered (“ultraconserved genomic regions” hereafter). We scrutinized 21 ultraconserved regions from Muller's elements B–E (∼1% of the total number of orthologous landmarks), plus the largest one on Muller's element A, for enrichment in biologically coherent patterns. Altogether, these 22 HCBs encompass 615 IGAs (∼7.2% of the total; 668 genes included) (for details about their organization, see the electronic table in the Supplemental material) and are scattered across the genome in all the species (Supplemental Fig. S8).

Clusters of co-expressed genes across species are, if the result of natural selection, firm candidates to be included within a particular HCB. Species-specific microarray experiments have uncovered clusters of co-expressed genes that evolve in a coordinated manner in males of seven species of the D. melanogaster species subgroup (Mezey et al. 2008). Thirteen clusters of five genes, the cluster size most likely to be conserved given the magnitude of fragmentation of the Drosophila genome documented here, were found within 11 ultraconserved regions. These clusters involve 73 co-expressed genes. Taking into account the proportion of genes included in the ultraconserved regions in relation to the whole genome, this is not a departure from the random expectation (two-tail Fisher's exact test, P = 0.17). In fact, 67.5% (170/252) of the clusters having associated significant co-expression were found to be broken in at least one of the lineages included in our study. We extended our analysis beyond the D. melanogaster species subgroup within the context of sex bias in gene expression of adult individuals of seven Drosophila species representing the two main subgenera (Zhang et al. 2007). Three ultraconserved regions, although not across all the species, were found to be significantly enriched for male-biased genes (false discovery rate [FDR] = 0.05) (Supplemental Table S33). Taken together, male-biased gene co-expression exhibits a weak association with ultraconserved regions. It suggests that this biased gene expression has either recently evolved or it is phylogenetically labile.

Although limited to D. melanogaster, we further asked if the ultraconserved regions are enriched for genes highly expressed across 11 adult and two larval tissues according to the data in FlyAtlas (Chintapalli et al. 2007). High tissue expression is defined by having an expression level ≥5-fold that in the whole body. Four ultraconserved regions, and again not in all the species, were found to be enriched for genes highly expressed in particular tissues (FDR = 0.05) (Supplemental Table S33).

Since functional relationship and co-expression do not always correlate significantly (Alexeyenko et al. 2006; Yanai et al. 2006), we sought for enrichment in Gene Ontology categories (Ashburner et al. 2000) and for participation in KEGG pathways (Kanehisa and Goto 2000). We did find statistically significant overrepresentation for functional classes in 11 ultraconserved regions, although the number of genes responsible for these patterns was always rather modest in relation to the total number of genes in these regions (Supplemental Table S34). The contribution of the overrepresentation of members of the same gene family and/or of genes sharing particular protein domains, as compared to the whole genome, to the patterns of enrichment detected was found in four ultraconserved regions (Supplemental Table S34).

Finally, we re-examined the association found between highly conserved noncoding elements (HCNEs) and HCBs. In a comparison between five Drosophila species, 164 high-density regions or peaks of HCNEs were identified within HCBs (Engstrom et al. 2007). These HCBs include multiple development genes, which suggests that these genomic regions might be genomic regulatory domains. We found 145 of these HCNE peaks in 123 HCBs, 21 of them in 13 of the 22 ultraconserved regions (Supplemental Table S33). Eighteen HCBs encompass ≥2 HCNE peaks, five of them being ultraconserved regions. Among the latter, those represented by HCBs 1669 and 1384 stand out, with three and four peaks, respectively; only one other HCB, and that not an ultraconserved region, also includes three HCNEs. Jackknife analyses indicated that more ultraconserved regions than expected harbor HCNEs [P(≥13) = 9.8 × 10⁻³] and that more HCNEs than expected are found in the ultraconserved regions [P(≥21) = 2.0 × 10⁻⁴] as compared to the whole genome.

Overall, one-third of the ultraconserved regions (8/22) include HCNEs and have associated at least an additional biological coherent pattern. The correspondence between regulatory domains and co-expression territories seems very limited.

Final remarks

Unlike previous reports (Peng et al. 2006; Bhutkar et al. 2008), we simulated different modes of chromosome evolution both separately and jointly. We showed that the use of breakpoint reuse values cannot unambiguously give information about the role of constraints and fragile regions in shaping gene organization. Instead, we used two separate proxies for constraint and fragility that must be jointly satisfied for a particular mode of chromosome evolution. We find that the observed data are best explained by a mode of evolution influenced primarily by fragile regions, although a role for constraints could not be discarded for any of the Muller's elements. Muller's element A shows the highest overall level of fragility, which largely results from being the element that has undergone more fixed inversions. Muller's element A is the main component of the chromosome X in all Drosophila species. Population theory predicts that chromosomal rearrangements will become fixed by drift or by selection at a higher rate on the X-chromosome as compared with the autosomes (Charlesworth et al. 1987). Mutational biases related to the nature of the sequences present at the edge of the orthologous landmarks might also be a factor. A previous analysis did not find a tight association between the reuse of breakpoint and transposable elements in regions presumably involved in multiple rearrangements (Bhutkar et al. 2008). More detailed comparative sequence analyses including a wider range of sequences will help elucidate if the differential presence of those type of sequences can contribute to the variation between the Muller's elements (Bystritskiy and Razin 2004; Durkin and Glover 2007). Likewise, the spatial organization of the chromosomes within the nucleus should also be taken into consideration (Tanabe et al. 2002).

Our results contradict, at least in Drosophila, the notion that common functional constraints are the main determinant for shaping gene order evolution (Becker and Lenhard 2007). We estimate that constraints might operate on ∼15% of the inter-IGA regions of the Drosophila genome. No single functional feature appears to be associated with all the ∼1% largest HCBs. Comparatively, HCNEs are more tightly associated with ultraconserved regions than gene co-expression or other biological patterns. This substantiates the notion that some of the largest HCBs harbor genomic regulatory domains, as reported previously using a more limited number of Drosophila species (Engstrom et al. 2007). In the absence of empirical tests, it is not possible to discard the hypothesis that some of the ultraconserved regions are the serendipitous by-products of the chromosomal repatterning. If this was the case, additional fragmentation by other chromosomal rearrangements may occur in the future or has already occurred in other Drosophila species. One example of this is provided by the polymorphic inversion 2j of Drosophila buzzatii (Puig et al. 2004), which separates six genes from the rest of the ultraconserved region represented by HCB 2533. None of the groups of genes with common functional themes found in this region (Supplemental Table S33) are disrupted by this inversion. From our simulation studies, we estimate that from 17% to 46% of the inter-IGAs regions in HCBs of size similar to that of the ultraconserved regions documented here can in theory be disrupted by chromosomal breakages. In fact, five incoming transposition events were documented to affect the 22 ultraconserved regions under the GO synteny definition. Should some constraints be dynamic, the fraction of inter-IGAs within ultraconserved regions that can be disrupted in any of the species would be even larger.

The lack of common functional themes among the largest HCBs can also result from the limited functional information available. For example, nonprotein-coding expression, which might play an important regulatory role (Kapranov et al. 2007), could contribute to prevent breakages from occurring in some genomic regions. The ultraconserved region represented by HCB 1384 encompasses eight miRNAs genes, more than any other orthologous landmark (data not shown). Engineered chromosomal rearrangements (Spitz et al. 2005) disrupting phylogenetically conserved arrays of genes should help clarify the scope of bona fide functional constraints responsible for maintaining the integrity of some regions of the Drosophila genome.

Methods

Synteny maps and reconstruction of ancestral gene order

For the construction of the synteny maps for Drosophila ananassae, D. erecta, D. grimshawi, Drosophila mojavensis, D. persimilis, D. pseudoobscura, D. sechellia, D. simulans, D. virilis, D. willistoni, and D. yakuba, we used D. melanogaster as a reference taking into account the physical overlap of some protein-coding genes in the latter species to define anchor points. We collapsed protein-coding genes with overlapping limits into single IGAs. Specifically, 13,733 protein-coding genes from release 4.1 of D. melanogaster are represented by 11,636 IGAs, 1603 of which include more than one gene (3700 genes in total). The reasons for adopting IGAs to construct synteny maps are several. First, physically related genes can generate artifactual local gene order disruptions if they are annotated in other species with a different number of exons (Supplemental Fig. S18). Second, gene sizes within and between species vary (Adams et al. 2000; Ashburner et al. 2005), making it difficult to derive a standard unit for calculating the size of orthologous landmarks, which is used as a proxy for inferring the presence of constraints. Thirdly, the constraint preserving gene organization is primarily the absence of disruption in intergenic regions; disruptions affecting genes themselves are likely to be detrimental and to be selected against. Fourthly, physically related genes appear as adjacent across species with a significantly higher probability than nonphysically related genes (Supplemental Text S1) probably because they may be under a particular class of evolutionary constraint, as has previously been shown in vertebrates (Dahary et al. 2005).

Details of the methods and algorithms used for annotation, gene order reconstruction, and detection of synteny are provided in Supplemental Text S1. Annotated protein-coding genes in the different species are provided in Supplemental Data Set S2. Table 1 shows the number of IGAs and genes that were used in our comparative analyses under different definitions of synteny (Results and Discussion). Genes excluded from our analyses fall into the following categories, which are not mutually exclusive: (1) 83 located on Muller's element F of D. melanogaster; (2) those that could not be annotated in any of the three species of the Drosophila subgenus (see Supplemental Text S1 for why this is so); (3) those involved in complex evolutionary scenarios, including interchromosomal gene transpositions and some intrachromosomal transpositions; and (4) those outside of HCBs and not annotated or not assembled in at least one species other than D. melanogaster (Supplemental Table S13). In total, 2595 (22.3%), 2443 (21%), and 2389 (20.53%) IGAs, under the GOO, GO, and OLC synteny definitions, respectively, were excluded from our downstream analysis. IGAs and genes not used in our analysis of gene order evolution are provided in Supplemental Data Set S3; their potential impact on the detection of ultraconserved regions was found to be negligible (Supplemental Text S1). Reconstructed gene orders are provided in Supplemental Data Set S4; the reconstruction is complete for all the species except D. persimilis and D. sechellia. Reconstructed gene orders for each of the nodes of the species tree, as well as estimates of the number of rearrangements for each of the branches, were obtained with MGR (Bourque and Pevzner 2002) and are provided in Supplemental Data Set S1. Nevertheless, MGR does not provide a detailed pathway of rearrangements. We used GRIMM to infer the most parsimonious scenario of rearrangements between any two nodes, and therefore to map breakpoint events between particular IGA pairs (Tesler 2002). We assumed that IGA rearrangement has occurred via inversion rather than via conservative intrachromosomal transposition, since the latter is less common than the former in Drosophila (Ranz et al. 2003). For comparison with other reconstructions of ancestral gene orders and estimates of chromosomal evolution, we used NGP (Supplemental Text S1; Bhutkar et al. 2008).

Testing the mode of chromosome evolution

Sets of simulations in which each Muller's element underwent a number of inversions were performed to test different modes of chromosome evolution. The number of inversions was identical to that estimated by MGR under the GO synteny definition (Table 1). This number is an estimate that has been demonstrated to be close to the real one (Supplemental Text S1). The size of each ancestral Muller's element is equivalent to the number of IGAs detected in our study. All the IGAs were assumed to have identical size. Breakpoints of inversions could occur only between IGAs or immediately upstream or downstream of the most distal and most proximal IGA, respectively. Inversions of the IGA order were performed starting from the ancestral genome and finishing in the nine terminal species recapitulating the number and phylogenetic distribution obtained by MGR across all the branches of the species tree. The size of the inversions was taken from the size distribution of inversions generated with GRIMM, which we did not find implausible. For example, a survey across a sample of cosmopolitan and endemic inversions from 10 Drosophila species found only 3.9% (7/180) having a size longer than 66% of the whole chromosome (Caceres et al. 1999). In the case of the inversions predicted by GRIMM, that percentage is 1.24% (38/3058). Each time an inversion was generated, its size was sampled from those previously predicted by MGR. In total, we performed 1000 simulations per Muller's element under a particular combination of parameters (see below). The fit between the simulated and the observed data were evaluated for each type of evolutionary scenario tested (see Results and Discussion). These scenarios include random breakage model; resilience alone; fragility alone; and both resilience and fragility.

Random breakage model

For each Muller's element, the number of inter-IGA regions equals the number of orthologous landmarks plus one since we allow breakpoints to occur immediately upstream and downstream of the most distal and most proximal IGA, respectively. The number of interanchor regions is 9198 (9193 + 5, Muller's elements A–E), each with the same probability of being broken.

Resilience alone

A fraction, r, of the total number of inter-IGA regions was made refractory to breakage. This parameter indicates the degree of constraint or resilience operating on the genome. The other inter-IGA regions, 1 − r, are free to be broken. Some of these inter-IGA regions will be within an HCB, and others will correspond to those in between orthologous landmarks. The degree of resilience ranges from 0, that is, no inter-IGA region is protected (as in the case of the random breakage model), to 1, when the number of inter-IGA regions protected from being broken corresponds to those within HCBs. For example, in the case of Muller's element A, which includes 1421 IGAs, the number of inter-IGA regions that can be broken is 568, that is, the number of orthologous landmarks plus 1. Between both extreme scenarios, there are others in which only a fraction of the documented HCBs are protected while the others are not. For each Muller's element, the degree of resilience was increased in steps of 0.01. We also varied how inter-IGA regions were chosen to be protected. Thus, the set of HCBs that provided a sufficient number of interanchor regions to equal r was chosen in five different ways: (1) starting with the largest HCBs (46 IGAs); (2) starting with the smallest HCBs (2 IGAs); (3) the probability of being selected being positively correlated with size (P = 0.5–1 for HCBs with >7 IGAs; P < 0.5 otherwise); (4) the probability of being selected being negatively correlated with size (P = 0.5–1 for HCBs with <7 IGAs; P < 0.5 otherwise); and (5) the probability of being selected being size independent (i.e., random). Before starting each simulation, HCBs were placed at random across the Muller's elements in order not to favor any particular starting distribution; we repeated all the simulations using the order in D. melanogaster as the base; this made very little difference to the output.

Fragility alone

Breakpoints can occur in all inter-IGA regions, but with a variable probability, the degree of fragility or f, which ranges from 0 to 1 at steps of 0.01. At the beginning of each simulation, 2683 + 5 inter-IGA regions among the total 9193 + 5 were chosen at random and the edges of the flanking IGAs flagged as fragile. The higher is f, the more likely it is that a flagged IGA will flank the breakpoint of an inversion. How more likely the flagged IGAs edges are going to be at the limits of simulated inversions, as compared to the nonflagged IGAs edges, depends on an assigned number of different neighboring orthologous landmarks, which is performed by sampling the observed distribution at random. Differences in the number of neighboring orthologous landmarks assigned among those IGAs ends flagged as fragile also translate into different likelihoods of flanking the breakpoint of an inversion. There are different ways in which this likelihood can be tuned (F₁–F₅), which are determined by different scales of values (Supplemental Table S30). How the number of neighboring orthologous landmarks is assigned to the edges of different IGAs depends also on the scale. In three of the scales (“partially random assignment”; Supplemental Table S30), the edge of an IGA with a high number of neighbors (e.g., 7) will be always adjacent to the edge of an IGA with the minimum number of neighbors implying breakage (i.e., 2). In the other two scales, the tuning values are assigned at random so that, for example, two IGAs with very fragile edges (i.e., with high number of neighbors) can be adjacent (“fully random assignment”; Supplemental Table S30). The result of this differential tuning is that the edge of an IGA with a particular associated number of neighbors has five different likelihoods of participating in a rearrangement depending on the scale.

Both resilience and fragility

A fraction r of the inter-IGA regions is protected from being broken and subsequently 2683 + 5 inter-IGA regions, with the exception of those frozen, are selected at random and flagged as fragile, as described above. Next, 3058 inversions are generated under all combinations of resilience and fragility in 0.01 steps, ways in which inter-IGA regions are chosen to be protected (R₁–R₅), and ways in how the likelihood of the edge of and IGA of participating in an inversion is tuned (F₁–F₅). The only exceptions were the parameters previously explored (random breakage model, r = 0 and f = 0; constraints alone, r ∈ [0, 1] and f = 0 under all the ways in which those constraints are simulated, R₁–R₅; and fragility alone, r = 0 and f ∈ [0, 1] under all the ways in which the likelihood of breakage—F₁–F₅—is tuned).

Both constraints and fragile regions were simulated in two different ways. In the first, or invariant way, the inter-IGA regions chosen to be under constraint and the degree of fragility at the edge of each IGA remain the same during the whole simulation process. In the second, or dynamic way, 1% of the inter-IGA regions refractory to breakage were no longer under constraint and 1% of inter-IGA regions under no constraint were allowed to become refractory to breakage for each inversion simulated. The emergence and loss of constraints in particular inter-IGA regions also translate into the expansion or contraction of genomic regions previously under constraint in a lineage-specific manner. Furthermore, dynamic fragility was mimicked by allowing pairs of inter-IGA regions to exchange the degree of fragility associated with their edges; only inter-IGA regions with different degrees of fragility were allowed to participate. Five pairs inter-IGA regions per inversion generated had their degree of fragility increased or decreased. Invariant and dynamic resilience and fragility were simulated in all possible combinations and under all the modes of resilience and fragility described above. In total, ∼1.02 × 10⁹ simulations were performed for each Muller's element. Source code in C and Perl are provided in the Supplemental material (Simulation_programme).

Expression data

For co-expressed genes in sexually mature males of D. melanogaster, D. simulans, Drosophila mauritiana, D. sechellia, D. yakuba, Drosophila santomea, and Drosophila teissieri (Mezey et al. 2008), we took the gene cluster composition indicated by the authors and compared these with the gene composition of the HCBs under the GO synteny definition. This was done at the different window sizes (n = 20, 15, 10, and 5 genes) used to assess the statistical significance of co-expression of neighboring genes. Not all the co-expression clusters were found in our syntenic blocks since some did not include enough genes mapped by us, preventing us from determining whether or not the cluster is fully encompassed within a particular HCB. The percentage of clusters of genes with inconclusive results was low: n = 20, 5.6% (6 of 107); n = 15, 7.7% (11 of 142); n = 10, 7.1% (17 of 238); and n = 5, 13.7% (40 of 292). For the clusters for which it is possible to resolve whether or not they have been disrupted in at least one of the lineages, the proportion of nondisrupted was n = 20, 3 of 101; n = 157, 7 of 131; n = 10, 26 of 221; and n = 5, 82 of 252. Clusters where n = 5 were subject to further analysis. Specifically, we examined if at least three of the genes that are part of a cluster appear as significantly co-expressed under, at least, a second cluster size. Seventy-three co-expressed genes of a total of 88 found in the ultraconserved regions met these criteria. For clusters where n = 5, 1828 co-expressed genes are part of 292 clusters (Mezey et al. 2008); 1386 of them were mapped to the orthologous landmarks documented here.

Expression data (Chintapalli et al. 2007) across 13 samples (brain, carcass, crop, head, hindgut, larval fat body, larval Malphigian tubule, male accessory gland, midgut, ovary, salivary gland, testis, and thoracic abdominal ganglion) of D. melanogaster were parsed to identify genes highly expressed in particular samples. Estimates of the expression level were calculated for probes on the array already classified as being over- or underexpressed in relation to the level of expression in the whole fly (Chintapalli et al. 2007) and for which there were at least three valid measures of its expression level. In Chintapalli et al. (2007), the number of hybridizations was four, all of them biological replicates, and the arrays contained 18,769 probes including 14,445 corresponding to 13,615 D. melanogaster protein-coding genes (the remaining probes correspond to controls, putative expressed sequences and nonprotein coding genes). According to our filtering criteria, 13,042 probes were deemed as expressed in at least one tissue. We consider a gene to be highly expressed in a particular tissue if it exhibits a level of expression ≥5-fold that seen in the whole body. The number of probes found to be highly expressed across samples was brain, 1400; carcass, 236; crop, 566; head, 719; hindgut, 455; larval fat body, 539; larval Malphigian tubule, 598; male accessory gland, 601; midgut, 648; ovary, 5; salivary gland, 535; testis, 1907; and thoracic abdominal ganglion, 1149. For sex-biased gene expression across seven Drosophila species (Zhang et al. 2007), we followed the classification of male- and female-biased genes already established by Zhang and colleagues using a nonparametric test to detect statistically significant differences between the sexes. The number of genes stated as being male-biased in gene expression was 1826/13,667 in D. melanogaster; 1503/13,561 in D. simulans; 1947/12,754 in D. yakuba; 1140/12,377 in D. ananassae; 1961/12,395 in D. pseudoobscura; 1354/11,316 in D. virilis; and 1506/9,818 in D. mojavensis. Fisher's exact tests were performed to detect statistical overrepresentation of genes with particular expression patterns in the ultraconserved regions as compared to the whole genome. Adjusted P-values after multiple test correction were obtained with the software QVALUE (Storey and Tibshirani 2003). For the expression data of Zhang et al. (2007), nine out of 154 tests performed (22 regions × 7 species) were statistically significant. For the expression data from FlyAtlas, four out of 286 tests performed (22 regions × 13 samples) were statistically significant.

Functional enrichment analysis

Statistical overrepresentation of genes belonging to particular Gene Ontology (GO) term categories (molecular function, biological process, cellular component), KEGG pathways, and InterPro protein domains (Ashburner et al. 2000; Kanehisa and Goto 2000; Hunter et al. 2009) was assessed with DAVID (Huang et al. 2009), which calculates the probability of enrichment for a particular biologically coherent pattern using a modified Fisher's exact test. The Benjamini-Hochberg correction was applied to account for multiple tests.

Highly conserved noncoding elements

Coordinates in the D. melanogaster genome (release 4) for 164 high-density regions or peaks of HCNEs (nucleotide sequences 98% identical over at least 50 bp in all pairwise species comparisons among D. melanogaster, D. ananassae, D. pseudoobscura, D. virilis, and D. mojavensis) were taken from Engstrom et al. (2007).