Abstract
Using radiation hybrid genotyping data, 99% of all possible gene pairs across the mammalian genome were tested for interactions based on co-retention frequencies higher (attraction) or lower (repulsion) than chance. Gene interaction networks constructed from six independent data sets overlapped strongly. Combining the data sets resulted in a network of more than seven million interactions, almost all attractive. This network overlapped with protein–protein interaction networks on multiple measures and also confirmed the relationship between essentiality and centrality. In contrast to other biological networks, the radiation hybrid network did not show a scale-free distribution of connectivity but was Gaussian-like, suggesting a closer approach to saturation. The radiation hybrid (RH) network constitutes a platform for understanding the systems biology of the mammalian cell.
Deciphering the genetic circuitry of the mammalian cell remains a significant challenge. One major obstacle to annotating genetic interactions is their number. In a genome of 20,000 genes, there are about 2 × 108 possible pairwise interactions.
A number of approaches have been used to map gene interactions in eukaryotes. Large-scale genetic interaction screens based on synergy and antagonism have been performed using synthetic genetic array analysis in yeast (Tong et al. 2001, 2004; Costanzo et al. 2010) and RNA interference in Caenorhabditis elegans (Lehner et al. 2006), covering about 30% and about 0.03% of all potential interactions, respectively. Protein–protein interactions have been assessed using yeast two-hybrid mapping or co-affinity immunoprecipitation (Cusick et al. 2005; Rual et al. 2005) in yeast, C. elegans, and Drosophila melanogaster (Giot et al. 2003; Li et al. 2004; Gavin et al. 2006; Yu et al. 2008; Simonis et al. 2009). The proportion of potential protein–protein interactions evaluated is more than 77% in yeast (Gavin et al. 2006; Yu et al. 2008), about 50% in Drosophila (Giot et al. 2003), and about 25% in C. elegans (Simonis et al. 2009).
Protein interaction techniques do not provide information on mechanistic consequences of protein–protein binding and suffer from high false-positive and false-negative rates, approaching 50% (Deane et al. 2002; Ito et al. 2002). Probabilistic integration of genomic data of diverse functional relationships into single networks has successfully incorporated the majority of genes but has been less successful in providing comprehensive coverage of genetic interactions as only a modest fraction of such interactions have been evaluated (Lee et al. 2004, 2008).
Our understanding of mammalian genetic interactions is even less impressive. Although large-scale efforts to map the protein interactome in humans have begun (Gandhi et al. 2006), only about 10% of potential interactions have been assayed (Rual et al. 2005; Venkatesan et al. 2009). Furthermore, genetic interactions in humans and mammals remain nearly completely unexplored.
In principle, evolutionary conservation of interactions would allow inference of mammalian interactions from yeast and C. elegans. While a significant proportion of genetic interactions (17% of synergistic or negative and 50% of antagonistic or positive) are conserved between the budding yeast Saccharomyces cerevisiae and the fission yeast Schizosaccharomyces pombe (Roguev et al. 2008), only 5% of synergistic interactions are conserved between S. cerevisiae and C. elegans (Tischler et al. 2008). Furthermore, overlap between human and yeast, C. elegans, or fly protein–protein interaction networks is limited (Gandhi et al. 2006).
Therefore it is necessary to explore mammalian genetic interactions in the mammalian setting. An additional problem for mammalian cells is the apparent lack of a simple and cheap method for combining alleles of distinct genes in the same cell.
Radiation hybrid (RH) panels have been an invaluable resource for mapping vertebrate genomes (Goss and Harris 1975; Gyapay et al. 1996; McCarthy et al. 1997; Stewart et al. 1997; Watanabe et al. 1999; Olivier et al. 2001; Hitte et al. 2005). Generation of an RH panel begins with lethal irradiation of a donor cell line, inducing random breaks in its genome. The donor cell harbors a selectable marker, typically thymidine kinase. The fragmented DNA is then rescued by fusing the donor cell to a non-irradiated host cell line lacking the selectable marker. Growing the fused cells in selective medium, for example, HAT, ensures that only host cells incorporating the selectable marker plus a random sample of donor DNA will propagate.
Surviving hybrid clones are expanded, and those with sufficient retention of donor DNA constitute the panel, usually around 100 cell lines. Across a panel, DNA markers are retained on average in 16%–35% of hybrids. The selectable marker is by definition retained at 100%.
Because of the large number of chromosome breaks induced by irradiation, genotyping the RH panel offers greatly superior resolution (often less than 150 kb) compared with meiotic mapping (Park et al. 2008). Similar to meiotic recombination, neighboring markers tend to be retained together while distant markers segregate independently. Retained autosomal genes have a copy number of three, compared with two for nonretained (Park et al. 2008). The corresponding copy numbers for sex chromosome genes are two and one.
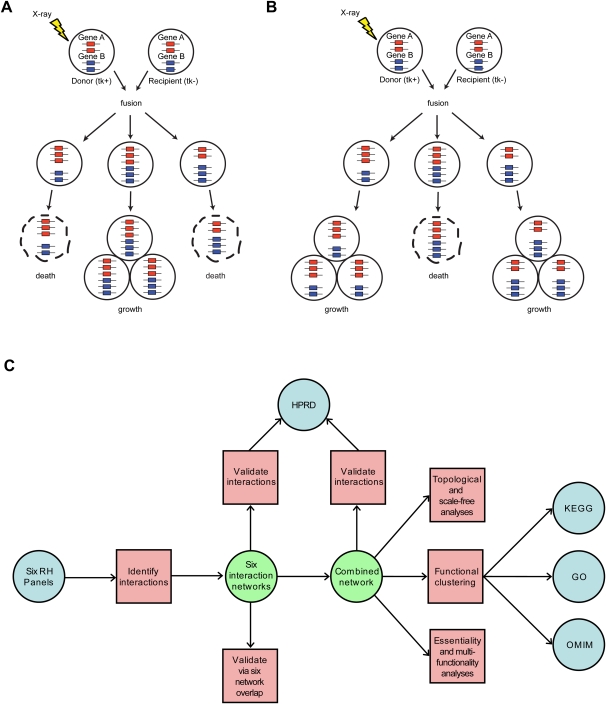
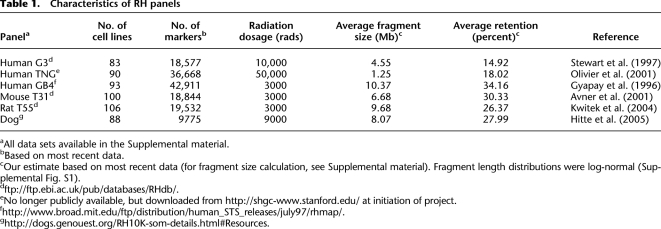
Here, we examine marker co-retention for a purpose distinct from genetic mapping, namely, identification of genetic interactions. We hypothesize that RH clone survival may depend on such interactions. If extra copies of a pair of distinct genes enhance survival, an attractive relationship results (Fig. 1A). Alternatively, if the extra pair of gene copies adversely affects survival, a repulsive relationship results (Fig. 1B).
Figure 1.
Interaction type and workflow. (A) Attractive interaction. Extra copies of gene A and gene B in the same clone promote survival. (B) Repulsive interaction. Extra copies of A and B in the same clone hinder survival effects. (C) Workflow. Tasks, red squares; externally generated data sets, blue circles; and internally generated data sets, green circles.
We demonstrate that a great number of interactions can be identified quickly and inexpensively in publicly available RH genotyping data sets (Fig. 1C). We then show that many more interactions can be identified when the different data sets are combined to improve power. The resulting, functionally organized interaction network provides the most comprehensive coverage of mammalian genetic interactions yet.
Results
RH panels
PCR genotyping data from six publicly available RH panels were used to find coretained markers as evidence of genetic interactions (Table 1). Three human panels, G3, TNG, and GB4, and three nonhuman panels, mouse T31, rat T55, and dog, were used. Across the panels, the number of markers, average fragment size, and the retention rate varied considerably. For each marker, the PCR data consisted of vectors of absent, present, and ambiguous calls, or 0, 1, and 2, respectively, where the length of each vector was the number of cell lines in the panel.
Table 1.
Characteristics of RH panels
aAll data sets available in the Supplemental material.
bBased on most recent data.
cOur estimate based on most recent data (for fragment size calculation, see Supplemental material). Fragment length distributions were log-normal (Supplemental Fig. S1).
eNo longer publicly available, but downloaded from http://shgc-www.stanford.edu/ at initiation of project.
Thymidine kinase (TK1) was used as the selectable marker for all panels, and nearby markers (<150 kb) consequently have a higher retention frequency than average. This exception aside, it was possible to seek interactions for more than 99% of the genome.
Mapping clusters of interacting pairs
To quantify the degree of co-retention between marker pairs, we constructed a 2 × 2 contingency table of joint presence and absence across all cell lines in a panel. A two-sided Fisher's exact test was then used to calculate the probability of co-retention. Multiple hypothesis correction was achieved using false discovery rates (FDRs) (Benjamini and Hochberg 1995). Since neighboring markers tend to be retained together, we did not perform this analysis on marker pairs separated by less than 10 Mb, less than 1% of all possible pairs. The 10-Mb threshold was chosen because, on average, conservatively only ∼0.6% of fragments contained two markers separated by greater than this distance in the fully combined RH data set used in this study (Supplemental material; Supplemental Fig. S1). In addition, data in which one or both of a marker pair were ambiguous were excluded from analysis.
Identifying interactions
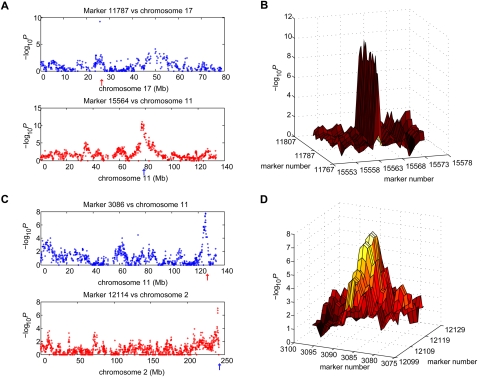
For a given FDR threshold in each data set, all significant marker pairs were placed in genomic order on an n × n matrix, where n is the number of markers for that data set. To be conservative, we eliminated all candidate interactions only one marker wide using an automated computer program and imposed the criterion that clusters made up of five or more adjacent, significant marker pairs were sufficient evidence for interaction (Methods, Supplemental material, and Supplemental Fig. S2). Examples of an excluded interaction peak with only one marker are shown in Figure 2, A and B, and an included peak in Figure 2, C and D. Marker pairs were assigned to interactions using a recursive, cluster-labeling algorithm starting at FDR <0.1% and progressing to increasingly liberal FDR thresholds.
Figure 2.
Exclusion and inclusion in G3 data set of candidate interactions. (A) Excluded candidate interaction one marker wide. (Upper panel) Marker 11787 located on chromosome 11 is coretained with a single marker on chromosome 17, marker 15564 (red arrow). (Lower panel) Marker 15564 is coretained with markers on chromosome 11 between 74 Mb and 80 Mb, including marker 11787 (blue arrow). (B) Plot of −log10P for excluded candidate shown in A. Ten markers on each side of markers 11787 and 15564 are displayed. (C) Included interaction. (Upper panel) Marker 3086 on chromosome 2 is co-retained with markers on chromosome 11 between 124 Mb and 128 Mb, including peak marker 12114 (red arrow). (Lower panel) Marker 12114 on chromosome 11 is co-retained with markers on chromosome 2 between 238 Mb and 243 Mb, including peak marker 3086 (blue arrow). (D) Plot of −log10P for interaction shown in (C). Ten markers on each side of markers 3086 and 12114 are displayed.
For each identified interaction, the genes closest to the marker pair comprising the interaction peak (largest −log10P) were selected as the most probable candidates for genetic interaction. The number of gene–gene interactions in each panel is shown in Supplemental Figure S3. The rat data set produced the largest number of interactions, with 219,307 identified at FDR <40%.
Converting markers to human
To compare interactions in the individual RH data sets and eventually combine them, we placed the markers on a common genome. Because three of our panels covered the human genome, we chose this genome as the scaffold. Using the UCSC Genome Browser liftOver utility (http://genome.ucsc.edu/cgi-bin/hgLiftOver) together with imputation exploiting synteny conservations, 89.07% of mouse, 95.87% of rat, and 99.59% of dog markers were placed on the human genome.
Overlap between RH networks
To assess the reproducibility of interaction identification, we examined the amount of overlap between interactions in each panel. Due to increased power, overlap increased as the FDR threshold was relaxed (Supplemental Table S1). At FDR <40%, the mean −log10P of the 15 pairwise comparisons between all six networks was 10.73 (overlap comparisons throughout were one-sided Fisher's exact test; Table 2).
Table 2.
Overlap between RH networks
aMean of −log10 P overlap with other data sets.
As well as having fewer interactions, the TNG and dog data sets had more limited overlap with the other panels (Supplemental Fig. S3, Table 2). Genotyping noise may be more of a problem in high-resolution panels such as TNG, where the average correlation between nearby markers is diminished. An analogous problem may occur in panels with smaller marker sets such as dog.
Combining RH data sets
Given the overlap among the interactions in the RH panels, we combined the data sets to improve power. To maintain comparability of marker and breakpoint densities in the combined data sets, we used markers from all panels. We interpolated the retention vector for each marker across other panels using data from the nearest marker in each panel (Peirce et al. 2007).
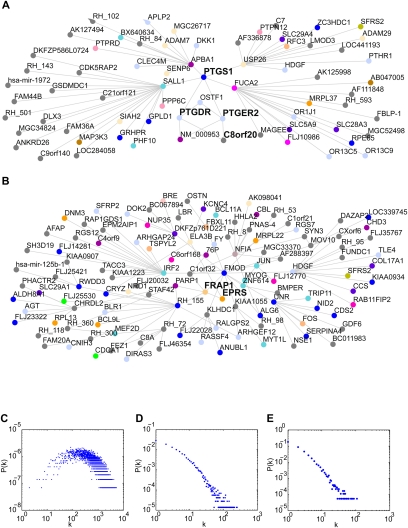
We accreted the data sets in the following arbitrary order: G3-mouse-rat, G3-mouse-rat-dog, G3-TNG-mouse-rat-dog, and the fully combined data set, G3-TNG-G4-mouse-rat-dog. To test whether data set combination would perform better when restricted to one species, we also created a human only data set, G3-TNG-GB4. The characteristics of the combined data sets are summarized in Table 3.
Table 3.
Combined RH data sets
aFor calculation, see Supplemental material.
Power
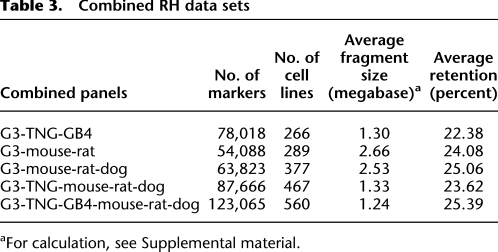
Combining data sets greatly improved sensitivity to detect interactions (Supplemental Fig. S4). An example of an interaction in the fully combined data set between a marker on chromosome 6 and two loci on chromosome 2 is shown in Figure 3A. A plot of all interactions significant at FDR <10−8 is shown in Figure 3B, and a plot indicating loci with significantly large numbers of interactions (hotspots) is shown in Figure 3C.
Figure 3.
Fully combined RH network. (A) Co-retention between marker at 130,440,601 bp (blue arrow) on chromosome 2 and markers on chromosome 6 (left). Co-retention between marker at 57,433,004 bp (red arrow) on chromosome 6 and markers on chromosome 2 (right). (B) Gene–gene interactions at FDR <10−8. (C) Number of edges per gene (degree) for fully combined network at FDR <5%. Horizontal lines show hotspots (red, FDR <40%; green, FDR <1%) assuming a Poisson distribution (Brem and Kruglyak 2005; Park et al. 2008).
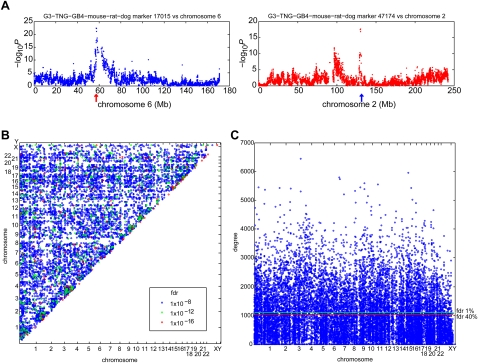
In the fully combined G3-TNG-GB4-mouse-rat-dog data set at FDR <5%, we identified about 10 times as many interactions as the sum of the six individual data sets at FDR <40% (Fig. 4A; cf. Supplemental Fig. S3). The number of interactions in the fully combined data set thus greatly overshadowed the number expected from simple summation, suggesting widespread improvements in power. We identified almost 6.7 × 106 interactions in the fully combined data set among known genes, corresponding to about 3.4% of all possible pairwise interactions.
Figure 4.
RH network interactions and overlap with Human Protein Reference Database (HPRD). (A) Number of interactions for combined panels. (B) Combined panel overlap with HPRD. (C) Adjusted −log10P for combined panel overlap with HPRD. (D) Uncertainty and combined panel overlap with HPRD at FDR <5%. (E) Uncertainty and adjusted −log10P for combined panel overlap with HPRD at FDR <5%. Data set abbreviations: M, mouse; R, rat; and D, dog.
Overlap between RH and protein–protein interaction networks
We used a protein–protein interaction network of 27,333 edges covering 7534 genes constructed from the Human Protein Reference Database (HPRD) (Peri et al. 2003; Gandhi et al. 2006) as a benchmark against which to compare the RH gene–gene interactions. For all comparisons, we limited the search space for overlapping edges to only those genes in the HPRD network.
Overall, individual RH networks did not significantly overlap with the HPRD network (Supplemental Fig. S5A). However, there were hints of improved overlap as the FDR was made less stringent. An adjusted −log10P penalized proportionally by the number of added edges remained relatively steady with relaxation of the FDR (Supplemental Fig. S5B), suggesting that overlap improvements were primarily attributable to increased power.
The combined RH networks demonstrated much stronger overlap with HPRD than did the single panel networks (Fig. 4B). The overlap improved with the addition of each RH data set and also as the FDR was relaxed. At FDR <5%, the fully combined data set overlapped with HPRD at −log10P = 25.85. Similar to the individual RH networks, the adjusted −log10P-values of the combined data sets also remained relatively steady with relaxation of the FDR (Supplemental Fig. 4C).
At FDR <5%, the data set consisting of three human RH panels, G3-TNG-GB4, showed superior interaction numbers (Fig. 4A) and overlap with HPRD (Fig. 4B) compared with the G3-M-R data set derived from three different species. Nevertheless, the fully combined data set showed the best overall performance. Species-specific interactions may be obscured when combining data sets from different species. Thus, the fully combined data set may emphasize interactions common to all mammalian cells. However, the fact that three out of the six RH panels were human means that strong human-specific interactions might still be found in the fully combined data set.
Mapping resolution
Using only the genes under each RH interaction peak could be too restrictive, since adjacent genes will be linked. Also genotyping errors can result in mapping imprecision. To evaluate mapping resolution when comparing interactions to HPRD, we permitted uncertainty regarding the location of the responsible genes in the RH data. We added an edge not only between the gene pair closest to the interaction peak but also to all pairwise combinations of n genes flanking each member of the gene pair, for uncertainty n.
Adding uncertainty to the RH networks had inconsistent effects on overlap with HPRD for individual panels as judged using nonadjusted and adjusted −log10P (Supplemental Figs. S6, S7). Some panels showed improved overlap with increased uncertainty, probably due to elevated edge number and enhanced power. A more consistent picture emerged with the combined panels, which generally showed decreased overlap as uncertainty increased (Supplemental Figs. S8, S9). The fully combined data set showed a monotonic decrease in overlap at FDR <5% as uncertainty increased (Fig. 4D,E). Thus, increasing the edge number by including flanking genes did not improve overlap for this data set, suggesting it has the best resolution. The odds ratios for the uncertainty of zero compared with the uncertainty of one for the fully combined data set was >102 and >1021, for nonadjusted and adjusted overlap, respectively.
As another measure of mapping resolution, we evaluated the −2log10P resolution for all markers within 10 Mb of each other (Supplemental material). The fully combined network had the highest resolution, with a −2log10P distance of 19.5 kb (Supplemental Fig. S10; Supplemental Table S2). These observations suggest that the resolution to identify interactions in the fully combined data set was approximately one gene-wide or less.
Many transcriptional control elements affecting DNA secondary structure, such as enhancers or silencers, can reside considerable distances from their target genes, sometimes many megabases (Visel et al. 2009). However, in the RH system such elements will not have an effect unless physically linked to the gene they control. Therefore, it is unlikely that this phenomenon affects the resolution or identity of the RH interaction peaks.
Novel genes
In the previous analyses, we ignored interactions if there was no known human gene or microRNA within 500 kb of a marker's position. At FDR <5% in the fully combined data set, this left about 525,000 interactions unannotated, or ∼7% of the total interaction number, corresponding to 617 novel genes (Supplemental material).
A single, representative RH network
For all remaining analyses, we used only the fully combined network at FDR <5%. To create the network, a set of 20,113 human genes, consisting of 18,781 known genes, 715 microRNAs, and the 617 novel genes, were used. Of the 20,113 genes, 1789 genes possessed no edges since they were located on the genome such that no marker could claim that gene as its nearest. Between the remaining 18,324 genes were 7,248,479 edges. The number of edges (degree) per node ranged from zero to 5210, with a mean of 791.15 and a median of 605, suggesting positive skewing (Supplemental Fig. S11).
The gene with the highest number of edges was a novel gene detected by the RH data, RH_167. The known gene with the highest number of edges was AUTS2, which has been linked to autism spectrum disorders (Auranen et al. 2002) and mental retardation (Kalscheuer et al. 2007). Only two genes had zero edges, VAMP7 (also known as SYBL1) and the microRNA MIR1977.
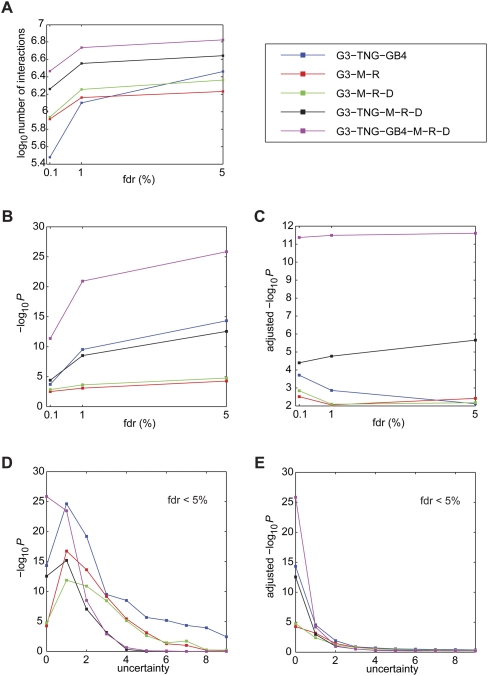
A subnetwork consisting of cyclooxygenase-1 (COX1 or PTGS1) and all nodes within two edges at FDR <10−6 is displayed in Figure 5A. Consistent with its role in prostaglandin synthesis, COX1 showed attractive connections with the prostaglandin D2 receptor (PTGDR) and the prostaglandin E receptor 1 (PTGER1) (Smith and Dewitt 1996). Interestingly, these two receptors were connected to each other by receptor expression enhancing protein 4 (C8orf20 or REEP4), itself a transmembrane protein. Family members REEP1 and REEP3 enhance surface expression of taste and odorant receptors (Saito et al. 2004; Behrens et al. 2006), and our data suggest a similar function for REEP4 in the context of prostaglandin receptors. A three-edge subnetwork centered on MTOR (FRAP1) at FDR <10−8 is shown in Figure 5B. An attractive connection between MTOR and glutamyl-prolyl-tRNA-synthetase (EPRS) reflects the role of MTOR in translational regulation.
Figure 5.
Network topology. (A) Subnetwork of gene COX1 (PTGS1) and all genes up to two edges away at FDR <10−6. (B) Subnetwork of gene MTOR (FRAP1) and all genes up to three edges away at FDR <10−8. (C) Degree distribution of fully combined RH network at FDR <5%. Number of degrees, k, and point probability of node with k degrees, P(k), plotted on log scales. (D) Degree distribution of HPRD network. (E) Degree distribution of fully combined RH network at FDR <10−8.
Most interactions are attractive
Of all edges in the RH network, the vast majority reflected attractive interactions, in which the two genes were coretained at a rate higher than chance. The proportion of interactions that were repulsive was only 4 × 10−4. The disparity was not due to lack of power, since simulations revealed equivalent power to detect repulsion and attraction for ∼96% pairs of markers (Supplemental material; Supplemental Fig. S12). It is difficult to draw a direct analogy between yeast gene networks, where interactions are identified using pairs of null or hypomorphic alleles, and the RH network, where interactions are identified using pairs of genes with extra copies. Nevertheless, in the yeast system there was a more nearly equal proportion of positive and negative interactions, with about two-thirds being negative or synergistic (Costanzo et al. 2010).
A non-scale-free genetic network
The distribution of the number of edges (connectivity or degrees) per node for many complex networks has been proposed to obey a power law, such that the point probability of finding a node with k degrees, P(k) ∼ k-λ, where λ is a constant, usually between 2 and 3 (Barabasi and Albert 1999; Jeong et al. 2000). The majority of nodes in such “scale-free” networks possess only a few links, while a small number of nodes have many links. New edges in these networks are preferentially attached to already highly connected nodes. The apparent ubiquity of the scale-free property across a diverse spectrum of networks has led to the perhaps premature suggestion that it represents a universal architecture (Keller 2005).
The degree distribution of the RH genetic interaction network was not scale-free but rather Gaussian-like (Fig. 5C), in contrast to the apparent scale-free nature of the HPRD network (Fig. 5D). This discrepancy can be explained by network coverage. Unlike the World Wide Web and social interaction networks, whole-genome interaction networks are finite and do not allow for the unlimited growth required for a scale-free network. A Gaussian-like distribution similar to the RH network is thus expected as the network approaches saturation (Albert and Barabasi 2002).
An alternative explanation for the Gaussian-like distribution is that the RH network is random. We therefore reduced the saturation of the RH network by using a more stringent FDR <10−8. At this threshold, the RH network is composed of 11,956 edges, approximately half the size of the HPRD network, and the degree distribution appears to be scale-free (Fig. 5E). The Gaussian-like distribution of the RH network is therefore due to its approach to saturation, and the apparent scale-free nature of other biological interaction networks may be due to lack of completeness.
RH network topology
To assess more thoroughly the congruence of the RH and HPRD networks, we compared their topological properties. Hub nodes are important because of the large number of interactions in which they participate. The connectivity of the RH and HPRD networks was significantly correlated (Spearman's ρ = 0.09, P = 2.31 × 10−15).
Just as hubs are central points in networks, so are bottlenecks. Betweenness centrality represents the degree to which a node is a bottleneck, by measuring how often the node comprises part of the shortest path between other pairs of nodes (Freeman 1977; Yu et al. 2007). The betweenness centralities of genes in the RH and HPRD networks were also significantly correlated (Spearman's ρ = 0.07, P = 2.53 × 10−9).
In addition, we compared clustering coefficients, a measure of the cliquishness of a node's neighbors (Watts and Strogatz 1998). The clustering coefficients of the RH and HPRD networks were not correlated (Spearman's ρ = −0.02, P > 0.05), perhaps because of selection biases in HPRD. Overall, these results suggest that our network shares hub nodes and betweenness centralities but not cliquishness with the HPRD network. This same pattern of topological overlap was found in a directed gene-regulatory network based on transcript profiling of the mouse T31 RH panel (Park et al. 2008; Ahn et al. 2009).
Essentiality and multifunctionality
In some protein–protein interaction networks, gene essentiality is positively correlated with network centrality, whether connectivity (Jeong et al. 2001; Yu et al. 2004; Hahn and Kern 2005; Deplancke et al. 2006; Lee et al. 2008; Ahn et al. 2009) or betweenness centrality (Hahn and Kern 2005; Joy et al. 2005). However, the association between essentiality and connectivity has been disputed by several studies (Gandhi et al. 2006; Yu et al. 2008) and has been attributed to bias in favor of studying essential genes (Coulomb et al. 2005). The RH network suffers from no such bias, since we examine all possible interactions outside of 10 Mb for each gene.
We found that essential genes had larger mean connectivities (Wilcoxon rank-sum test, P = 1.29 × 10−12) and betweenness centralities (Wilcoxon rank-sum test, P = 2.47 × 10−12) than nonessential. We also found significant correlations between mean connectivity and betweenness centrality with an increasing fraction of essential genes in bins of 200 genes (Spearman's ρ = 0.89, P = 3.76 × 10−7, and Spearman's ρ = 0.90, P = 1.12 × 10−7, respectively). Our unbiased approach thus confirms the association between centrality and essentiality.
Essential genes have been found to interact preferentially with other essential genes in protein–protein interaction networks (Yu et al. 2008), although a bias toward studying such genes could also underlie this finding. We were unable to replicate the association and found that essential and nonessential genes did not differ in the proportion of edges to essential genes (t(3449) = 0.1432, P = 0.89).
Recent work in yeast genetic interactions has found a correlation between gene connectivity and multifunctionality, the number of annotated functions for that gene (Costanzo et al. 2010). We have replicated this correlation, although more modestly (Spearman's ρ = 0.0525, P = 1.188 × 10−12).
Additional functional clustering in the RH network
In yeast and C. elegans, nodes with similar functions are more likely to share edges in protein–protein interaction networks (Giot et al. 2003; Rual et al. 2005; Yu et al. 2008) and gene–gene interaction networks (Lee et al. 2004, 2008; Tong et al. 2004; Kelley and Ideker 2005). To test this property for RH interactions, we determined overlap between the RH network and a Gene Ontology (GO) network (Ashburner et al. 2000) consisting of all interactions in 202 categories containing between 70 and 1000 genes. There was highly significant overlap (P < 10−300). In addition to global functional clustering, a network of all possible pairwise edges between genes associated with cell division (Kittler et al. 2007) showed significant overlap with the RH network (P < 10−300).
To test overlap of the RH network with the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa and Goto 2000; Kanehisa et al. 2006, 2008), we performed two analyses. In the first, only those genes coding for proteins directly interacting in a KEGG pathway were connected by edges. A network of all KEGG pathways combined showed significant overlap with the RH network (P = 1.32 × 10−9). In the second analysis, we connected any two genes whose proteins appeared in the same KEGG pathway, to reflect the indirect nature of genetic interactions. Here, we found that a network of all KEGG pathways combined showed highly significant overlap with the RH network (P = 7.93 × 10−313).
Disease-causing genes are more likely to interact with other disease-causing genes in HPRD, suggesting that candidate genes for genetically heterogeneous disorders can be identified using molecular networks (Gandhi et al. 2006). Using the Online Mendelian Inheritance in Man (OMIM) genetic disorders database (Hamosh et al. 2002), we found a similar property in our network (P < 10−300).
Because the RH network demonstrated clustering by disease-causing genes, we were able to predict novel interactions involving these genes. For example, the interaction between the ephrin receptor B2 gene (EPHB2) and fumarate hydratase (FH) in our network is undocumented. Mutations in EPHB2 have been linked to prostate cancer (Kittles et al. 2006), and mutations in FH have been linked to renal cell cancer (Toro et al. 2003). Together, these results suggest that genes in the RH network are functionally clustered in ways reminiscent of protein interaction networks and that RH interactions can be used to predict functions of uncharacterized genes.
Discussion
Using publicly available RH data, we have mapped millions of gene interactions in the mammalian genome. There was substantial overlap between the genetic networks from six RH panels across four species. Combining data sets improved power and yielded unexpectedly large numbers of interactions. The fully combined data set had nearly single gene resolution and consisted of more than seven million interactions, showing significant overlap with HPRD. The overlap between the fully combined RH and HPRD networks was ∼6%. A similar overlap was found with KEGG (∼5% direct; ∼4% indirect). Although modest, these overlaps were somewhat higher than the ∼1% overlap between yeast genetic interaction networks and protein–protein interaction networks (Tong et al. 2004). Limited overlap between genetic and protein–protein interaction networks is expected due to the functional, indirect nature of genetic interactions and the direct, physical nature of protein–protein interactions. The fully combined RH network also overlapped with networks derived from GO and OMIM. In addition, the network shared topological properties with HPRD, including connectivity and betweenness centrality.
Unlike HPRD, the RH network showed a Gaussian-like degree distribution rather than a scale-free degree distribution, suggesting the RH network is closer to saturation than HPRD. Consistent with this notion, the edges of the fully combined RH network comprised ∼3.4% of all possible pairwise interactions, compared to only ∼0.01% in both HPRD and a recent human yeast two-hybrid data set (Venkatesan et al. 2009). In addition to better coverage, the RH approach offers the advantage of measuring interaction strength with a −log10P score, while protein–protein interactions are binary (Li et al. 2004; Rual et al. 2005; Yu et al. 2008; Simonis et al. 2009; Venkatesan et al. 2009). Interactions involving genes that code for extracellular and membrane-bound proteins are also difficult for most yeast two-hybrid systems to detect (Bruckner et al. 2009) but were identified by RH networks (cf. prostaglandin receptors; Fig. 5A). Furthermore, the RH approach identifies interactions involving essential genes, problematic for synthetic genetic array analysis (Tong et al. 2001, 2004; Costanzo et al. 2010).
Our unbiased approach to interaction identification provides solid evidence that essential genes are central to networks, as both highly connected hubs and as highly trafficked bottlenecks. Previous reports of the relationship between connectivity and essentiality (Jeong et al. 2001; Yu et al. 2004) have been criticized for bias toward essential genes and challenged by the finding that removing this bias eliminates the essentiality–centrality relationship (Coulomb et al. 2005). Perhaps with the greater coverage of genetic interactions from the RH network, the essentiality–centrality relationship becomes apparent again.
A total of 617 novel genes participated in 525,000 interactions. Regulatory loci lacking known genes were also found through transcript profiling of the mouse T31 RH panel (Park et al. 2008). Integrating the interaction and transcript profiling data using multiregression techniques should help identify the functions of these novel genes, as well as known genes.
Although we suggest that co-retention of interacting gene pairs may confer growth or survival advantages, we cannot be certain of the mechanism of interaction without experimentation. Given the size of the RH network, comprehensive experimental validation is difficult. However, the significant overlap of the RH network with HPRD and other protein–protein interaction networks provides a reasonably extensive and objective validation, since there is no reason to believe there is bias toward overlap. Using orthogonal data sets has the additional advantage of independence. Homologous comparisons could be made between RH mapping data for yeast or C. elegans and synthetic genetic array and RNAi network analyses, respectively. Unfortunately, RH panels do not exist for these organisms.
Our work did not address whether an interaction involves more than two genes. Indeed, multigene interactions have been all but ignored in genome-wide studies. The RH data could in principle be mined for three-way or higher-order interactions, although this would be computationally intensive.
Genome-wide interaction methods such as yeast two-hybrid suffer from high false-positive and false-negative rates and, as a consequence, low reproducibility (Deane et al. 2002; Ito et al. 2002). An important consideration, then, is determining an optimum balance of false-positives and false-negatives. In this study, we found that a 5% FDR threshold yielded the best overlap with HPRD. Further relaxing the FDR would have increased the interaction number, but the Fisher's exact test P-value threshold at FDR <5% was already approaching 0.05, so new interactions would have had nominal P > 0.05 and be dubious.
Adding published RH data from other species, for example, cow (Itoh et al. 2005), pig (Hamasima et al. 2008), horse (Raudsepp et al. 2008), and monkey (Murphy et al. 2001), to the present RH data sets should provide further improvements in power and mapping resolution. High-throughput technologies such as array comparative genomic hybridization (aCGH) have decreased the genotyping costs of an RH panel by about 100-fold compared with PCR, while increasing marker density about 100-fold (Park et al. 2008). This makes it feasible to create even larger RH panels from single species to construct genetic interaction networks.
The International Cancer Genome Consortium (2010) (ICGC) is providing detailed information on genotype and copy number variation in 25,000 cancer genomes covering 50 different types. Interaction networks based on nonrandom co-retention of extra gene copies and mutations can be constructed using the same methods detailed here, although the resultant networks will be biased toward cancer cell survival and proliferation. Co-retention of naturally occurring polymorphisms can also be used to construct interaction networks (Petkov et al. 2005).
We have demonstrated that a large number of potential gene interactions can be identified quickly and inexpensively using RH retention data. Combining data sets from different species gave substantial improvements in power. The resulting networks will provide a high-confidence map of mammalian genetic interactions to help guide future studies.
Methods
Genotype vector files
Genotype data vector files were downloaded from various databases (Table 1). These vectors are currently publicly available or were previously available and downloaded when this study began. All data sets are available in the Supplemental material. Each file consisted of a matrix of m rows of n columns, where m is the number of markers in the data set and n is the number of cell lines. For an entry at row i, column j, a 0, 1, or 2 signified an absent, present, or ambiguous call, respectively, resulting from PCR screening of marker i in cell line j.
Since their initial creation, all panels but dog have been more densely genotyped by several thousand additional markers each. Using the latest marker data, we calculated new estimates of the average retention frequency, none of which deviated from the originally reported rates by more than 5% (Table 1).
Fisher's exact test for co-retention
All possible pairs of markers not within 10 Mb of each other in any data set were assessed for statistically significant co-retention, either attraction or repulsion. For each marker pair, a 2 × 2 contingency table was constructed where the first category was presence or absence of the first marker and the second category was presence or absence of the second marker within the same cell line. The joint presence and absence of a pair of markers was tallied across all cell lines and entered into the table. If the presence of either marker was ambiguous, then the data for the marker pair in that cell line were excluded. Thus, the total for each table describing a pair of markers was less than or equal to the total number of cell lines. A two-sided Fisher's exact test was performed on the contingency tables.
Interaction identification
All code for interaction identification was written in C for computational speed and control over memory allocation. All marker pairs for the single and combined data sets with P-values less than the P-value cutoff at a given FDR were placed on an m × m matrix of logicals, where m is the number of markers in the data set and where each cell can take a 1, representing a significant P-value at that FDR, or 0, nonsignificant.
Single marker interactions are probably due to marker and/or breakpoint inhomogeneities (Supplemental material). However, to be conservative, we sought to exclude such peaks. A 5 × 5 grid was centered on each marker pair. If the pair was a single 1 on the grid, the pair was changed to a 0 to eliminate singletons, candidate interactions encompassing only one marker at both interacting loci (Supplemental Fig. S2). If all other 1s on the grid were positioned in only the third row or third column or both, then all 1s in the grid were changed to 0s to eliminate horizontal and vertical streaks, candidate interactions one marker wide for either the vertical or horizontal axes, respectively (Supplemental Fig. S2). This step also eliminated crosses, coincident horizontal and vertical streaks. If a 1 appeared in any position besides the third row or third column, all 1s in the grid were retained. This process retained two-dimensional patches, which were potential interactions.
Only if a two-dimensional patch consisted of at least five significant marker pairs was it declared a potential interaction. Because genotyping errors could cause gaps in interactions, we applied a smoothing procedure to avoid overestimating the number of interactions. To smooth, a 5 × 5 grid was centered on each marker pair in the matrix surviving removal of single marker interactions. All cells in the grid were then filled with 1s. Patches of significant pairs up to three markers away from each another were thus binned to form one interaction. Marker pairs assigned a 1 from smoothing but not significant based on the FDR at that P-value were not included as a true part of the interaction and were dropped after this step.
Interaction cluster labeling and peak identification
After smoothing, a recursive cluster-labeling algorithm written in C was used to assign a unique label (number) to marker pairs constituting an interaction, starting at FDR <0.1% and progressing to increasingly liberal FDR thresholds. All marker pairs remaining at this step were placed on an m × m matrix of integers and given a −1 tag, signifying an unlabeled state, where m was the number of markers in the data set. If the marker pair was not significant or eliminated in the previous step, a zero was assigned. If the marker pair had been labeled previously at a more stringent FDR, we assigned that label to the marker pair before proceeding with the recursive algorithm. The algorithm was as follows:
Examine marker pair at top of stack data structure.
If marker pair has not been assigned an interaction label, assign that marker pair the current incremental interaction label. Remove (pop) the marker pair from the stack.
-
Check marker pairs adjacent to current pair in all four directions.
a. If adjacent pair is unlabeled, push it on top of the stack for later examination.
-
b. If adjacent pair is labeled
i. If the label is the same as the current label, do nothing and proceed to step 4.
ii. If label is less than current label, this means current marker pair is adjacent to a previously labeled interaction and will be absorbed into that interaction. Make a note that pairs newly labeled in this new interaction actually belong to a previously labeled interaction.
If the stack is not empty, proceed to step 1. If the stack is empty, the entire interaction is labeled.
The result of the algorithm was a matrix of 0s and clustered integers, ranging from 1 to k, where k was the number of interactions labeled. For each labeled interaction, a peak was identified as the marker pair with the largest −log10P in the interaction. If more than one marker pair shared the peak −log10P, all were designated as peak.
Combining data sets
We employed the UCSC Genome Browser liftOver utility (http://genome.ucsc.edu/cgi-bin/hgLiftOver) to convert mouse, rat, and dog marker genome coordinates to human. Using default settings except a minimum base-pair matching threshold of 10%, we were able to place 53.75% of mouse, 76.78% of rat, and 97.2% of dog markers on the human genome. To improve on this, we assumed conservation of synteny to impute the positions of unconverted markers using the positions of converted markers. If an unconverted marker was positioned in the original species between two markers successfully placed on the same chromosome in human, the unconverted marker was placed between the converted markers. Markers in these gaps were evenly spaced between the successfully converted anchor markers.
Converted and human markers were used in the combined data sets. The number of markers in a combined data set was approximately the sum of the number of markers in the component data sets, but because of marker overlap in the human data sets, it was at times less than the sum. For example, in the G3-mouse-rat-dog combined data set, we used the locations of the 18,577 G3 markers, the 16,785 converted mouse markers, the 18,726 converted rat markers, and the 9735 converted dog markers to generate a total of 63,823 marker positions on the human genome.
Within a panel, retention was calculated for all converted and human markers by interpolation from the nearest marker assayed in that panel (Peirce et al. 2007). Given that the correlation between neighboring markers in the original panels was around 0.8 (except for TNG, which had a lower correlation of 0.23 because of its shorter fragment lengths), this interpolation scheme was reasonable. The retention at each marker was then obtained by summing the marker retention in the various panels.
Interactions identified in each of the five combined data sets were FDR controlled up to a maximum of 5%. The large number of significant interactions meant that FDR corrections were already minimal at this threshold, reflected by the P-value ranging from 0.029–0.033 for all five data sets at FDR <5%. The gene interactions networks obtained from the fully combined RH data set are available in the Supplemental material.
Additional methods can be found in the Supplemental material.
Acknowledgments
This work was supported by the Stein Oppenheimer Endowment Award, UCLA.
Author contributions: A.L. and R.T.W. developed the methods. A.L., R.T.W., S.A., and C.C.P. performed the statistical and computational analyses. A.L. and D.J.S. wrote the paper. D.J.S. conceived the study.
Footnotes
[Supplemental material is available online at http://www.genome.org.]
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.104216.109.
References
- Ahn S, Wang RT, Park CC, Lin A, Leahy RM, Lange K, Smith DJ 2009. Directed mammalian gene regulatory networks using expression and comparative genomic hybridization microarray data from radiation hybrids. PLoS Comput Biol 5: e1000407 doi: 10.1371/journal.pcbi.1000407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert R, Barabasi AL 2002. Statistical mechanics of complex networks. Rev Mod Phys 74: 47–97 [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. 2000. Gene Ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat Genet 25: 25–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auranen M, Vanhala R, Varilo T, Ayers K, Kempas E, Ylisaukko-Oja T, Sinsheimer JS, Peltonen L, Jarvela I 2002. A genomewide screen for autism-spectrum disorders: Evidence for a major susceptibility locus on chromosome 3q25-27. Am J Hum Genet 71: 777–790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avner P, Bruls T, Poras I, Eley L, Gas S, Ruiz P, Wiles MV, Sousa-Nunes R, Kettleborough R, Rana A, et al. 2001. A radiation hybrid transcript map of the mouse genome. Nat Genet 29: 194–200 [DOI] [PubMed] [Google Scholar]
- Barabasi AL, Albert R 1999. Emergence of scaling in random networks. Science 286: 509–512 [DOI] [PubMed] [Google Scholar]
- Behrens M, Bartelt J, Reichling C, Winnig M, Kuhn C, Meyerhof W 2006. Members of RTP and REEP gene families influence functional bitter taste receptor expression. J Biol Chem 281: 20650–20659 [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y 1995. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc Ser B Methodol 57: 289–300 [Google Scholar]
- Brem RB, Kruglyak L 2005. The landscape of genetic complexity across 5700 gene expression traits in yeast. Proc Natl Acad Sci 102: 1572–1577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruckner A, Polge C, Lentze N, Auerbach D, Schlattner U 2009. Yeast two-hybrid, a powerful tool for systems biology. Int J Mol Sci 10: 2763–2788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costanzo M, Baryshnikova A, Bellay J, Kim Y, Spear ED, Sevier CS, Ding H, Koh JL, Toufighi K, Mostafavi S, et al. 2010. The genetic landscape of a cell. Science 327: 425–431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coulomb S, Bauer M, Bernard D, Marsolier-Kergoat MC 2005. Gene essentiality and the topology of protein interaction networks. Proc Biol Sci 272: 1721–1725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cusick ME, Klitgord N, Vidal M, Hill DE 2005. Interactome: Gateway into systems biology. Hum Mol Genet 14(Spec no. 2): R171–R181 [DOI] [PubMed] [Google Scholar]
- Deane CM, Salwinski L, Xenarios I, Eisenberg D 2002. Protein interactions: Two methods for assessment of the reliability of high throughput observations. Mol Cell Proteomics 1: 349–356 [DOI] [PubMed] [Google Scholar]
- Deplancke B, Mukhopadhyay A, Ao W, Elewa AM, Grove CA, Martinez NJ, Sequerra R, Doucette-Stamm L, Reece-Hoyes JS, Hope IA, et al. 2006. A gene-centered C. elegans protein–DNA interaction network. Cell 125: 1193–1205 [DOI] [PubMed] [Google Scholar]
- Freeman LC 1977. A set of measures of centrality based on betweenness. Sociometry 40: 35–41 [Google Scholar]
- Gandhi TK, Zhong J, Mathivanan S, Karthick L, Chandrika KN, Mohan SS, Sharma S, Pinkert S, Nagaraju S, Periaswamy B, et al. 2006. Analysis of the human protein interactome and comparison with yeast, worm and fly interaction data sets. Nat Genet 38: 285–293 [DOI] [PubMed] [Google Scholar]
- Gavin AC, Aloy P, Grandi P, Krause R, Boesche M, Marzioch M, Rau C, Jensen LJ, Bastuck S, Dumpelfeld B, et al. 2006. Proteome survey reveals modularity of the yeast cell machinery. Nature 440: 631–636 [DOI] [PubMed] [Google Scholar]
- Giot L, Bader JS, Brouwer C, Chaudhuri A, Kuang B, Li Y, Hao YL, Ooi CE, Godwin B, Vitols E, et al. 2003. A protein interaction map of Drosophila melanogaster. Science 302: 1727–1736 [DOI] [PubMed] [Google Scholar]
- Goss SJ, Harris H 1975. New method for mapping genes in human chromosomes. Nature 255: 680–684 [DOI] [PubMed] [Google Scholar]
- Gyapay G, Schmitt K, Fizames C, Jones H, Vega-Czarny N, Spillett D, Muselet D, Prud'homme JF, Dib C, Auffray C, et al. 1996. A radiation hybrid map of the human genome. Hum Mol Genet 5: 339–346 [DOI] [PubMed] [Google Scholar]
- Hahn MW, Kern AD 2005. Comparative genomics of centrality and essentiality in three eukaryotic protein-interaction networks. Mol Biol Evol 22: 803–806 [DOI] [PubMed] [Google Scholar]
- Hamasima N, Mikawa A, Suzuki H, Suzuki K, Uenishi H, Awata T 2008. A new 4016-marker radiation hybrid map for porcine–human genome analysis. Mamm Genome 19: 51–60 [DOI] [PubMed] [Google Scholar]
- Hamosh A, Scott AF, Amberger J, Bocchini C, Valle D, McKusick VA 2002. Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res 30: 52–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hitte C, Madeoy J, Kirkness EF, Priat C, Lorentzen TD, Senger F, Thomas D, Derrien T, Ramirez C, Scott C, et al. 2005. Facilitating genome navigation: Survey sequencing and dense radiation-hybrid gene mapping. Nat Rev Genet 6: 643–648 [DOI] [PubMed] [Google Scholar]
- The International Cancer Genome Consortium 2010. International network of cancer genome projects. Nature 464: 993–998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito T, Ota K, Kubota H, Yamaguchi Y, Chiba T, Sakuraba K, Yoshida M 2002. Roles for the two-hybrid system in exploration of the yeast protein interactome. Mol Cell Proteomics 1: 561–566 [DOI] [PubMed] [Google Scholar]
- Itoh T, Watanabe T, Ihara N, Mariani P, Beattie CW, Sugimoto Y, Takasuga A 2005. A comprehensive radiation hybrid map of the bovine genome comprising 5593 loci. Genomics 85: 413–424 [DOI] [PubMed] [Google Scholar]
- Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL 2000. The large-scale organization of metabolic networks. Nature 407: 651–654 [DOI] [PubMed] [Google Scholar]
- Jeong H, Mason SP, Barabasi AL, Oltvai ZN 2001. Lethality and centrality in protein networks. Nature 411: 41–42 [DOI] [PubMed] [Google Scholar]
- Joy MP, Brock A, Ingber DE, Huang S 2005. High-betweenness proteins in the yeast protein interaction network. J Biomed Biotechnol 2005: 96–103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalscheuer VM, FitzPatrick D, Tommerup N, Bugge M, Niebuhr E, Neumann LM, Tzschach A, Shoichet SA, Menzel C, Erdogan F, et al. 2007. Mutations in autism susceptibility candidate 2 (AUTS2) in patients with mental retardation. Hum Genet 121: 501–509 [DOI] [PubMed] [Google Scholar]
- Kanehisa M, Goto S 2000. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res 28: 27–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, Goto S, Hattori M, Aoki-Kinoshita KF, Itoh M, Kawashima S, Katayama T, Araki M, Hirakawa M 2006. From genomics to chemical genomics: New developments in KEGG. Nucleic Acids Res 34: D354–D357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, Araki M, Goto S, Hattori M, Hirakawa M, Itoh M, Katayama T, Kawashima S, Okuda S, Tokimatsu T, et al. 2008. KEGG for linking genomes to life and the environment. Nucleic Acids Res 36: D480–D484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller EF 2005. Revisiting “scale-free” networks. Bioessays 27: 1060–1068 [DOI] [PubMed] [Google Scholar]
- Kelley R, Ideker T 2005. Systematic interpretation of genetic interactions using protein networks. Nat Biotechnol 23: 561–566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kittler R, Pelletier L, Heninger AK, Slabicki M, Theis M, Miroslaw L, Poser I, Lawo S, Grabner H, Kozak K, et al. 2007. Genome-scale RNAi profiling of cell division in human tissue culture cells. Nat Cell Biol 9: 1401–1412 [DOI] [PubMed] [Google Scholar]
- Kittles RA, Baffoe-Bonnie AB, Moses TY, Robbins CM, Ahaghotu C, Huusko P, Pettaway C, Vijayakumar S, Bennett J, Hoke G, et al. 2006. A common nonsense mutation in EphB2 is associated with prostate cancer risk in African American men with a positive family history. J Med Genet 43: 507–511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwitek AE, Gullings-Handley J, Yu J, Carlos DC, Orlebeke K, Nie J, Eckert J, Lemke A, Andrae JW, Bromberg S, et al. 2004. High-density rat radiation hybrid maps containing over 24,000 SSLPs, genes, and ESTs provide a direct link to the rat genome sequence. Genome Res 14: 750–757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee I, Date SV, Adai AT, Marcotte EM 2004. A probabilistic functional network of yeast genes. Science 306: 1555–1558 [DOI] [PubMed] [Google Scholar]
- Lee I, Lehner B, Crombie C, Wong W, Fraser AG, Marcotte EM 2008. A single gene network accurately predicts phenotypic effects of gene perturbation in Caenorhabditis elegans. Nat Genet 40: 181–188 [DOI] [PubMed] [Google Scholar]
- Lehner B, Crombie C, Tischler J, Fortunato A, Fraser AG 2006. Systematic mapping of genetic interactions in Caenorhabditis elegans identifies common modifiers of diverse signaling pathways. Nat Genet 38: 896–903 [DOI] [PubMed] [Google Scholar]
- Li S, Armstrong CM, Bertin N, Ge H, Milstein S, Boxem M, Vidalain PO, Han JD, Chesneau A, Hao T, et al. 2004. A map of the interactome network of the metazoan C. elegans. Science 303: 540–543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy LC, Terrett J, Davis ME, Knights CJ, Smith AL, Critcher R, Schmitt K, Hudson J, Spurr NK, Goodfellow PN 1997. A first-generation whole genome-radiation hybrid map spanning the mouse genome. Genome Res 7: 1153–1161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy WJ, Page JE, Smith C Jr, Desrosiers RC, O'Brien SJ 2001. A radiation hybrid mapping panel for the rhesus macaque. J Hered 92: 516–519 [DOI] [PubMed] [Google Scholar]
- Olivier M, Aggarwal A, Allen J, Almendras AA, Bajorek ES, Beasley EM, Brady SD, Bushard JM, Bustos VI, Chu A, et al. 2001. A high-resolution radiation hybrid map of the human genome draft sequence. Science 291: 1298–1302 [DOI] [PubMed] [Google Scholar]
- Park CC, Ahn S, Bloom JS, Lin A, Wang RT, Wu T, Sekar A, Khan AH, Farr CJ, Lusis AJ, et al. 2008. Fine mapping of regulatory loci for mammalian gene expression using radiation hybrids. Nat Genet 40: 421–429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce JL, Broman KW, Lu L, Williams RW 2007. A simple method for combining genetic mapping data from multiple crosses and experimental designs. PLoS One 2: e1036 doi: 10.1371/journal.pone.0001036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peri S, Navarro JD, Amanchy R, Kristiansen TZ, Jonnalagadda CK, Surendranath V, Niranjan V, Muthusamy B, Gandhi TK, Gronborg M, et al. 2003. Development of human protein reference database as an initial platform for approaching systems biology in humans. Genome Res 13: 2363–2371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkov PM, Graber JH, Churchill GA, DiPetrillo K, King BL, Paigen K 2005. Evidence of a large-scale functional organization of mammalian chromosomes. PLoS Genet 1: e33 doi: 10.1371/journal.pgen.0010033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raudsepp T, Gustafson-Seabury A, Durkin K, Wagner ML, Goh G, Seabury CM, Brinkmeyer-Langford C, Lee EJ, Agarwala R, Stallknecht-Rice E, et al. 2008. A 4103 marker integrated physical and comparative map of the horse genome. Cytogenet Genome Res 122: 28–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roguev A, Bandyopadhyay S, Zofall M, Zhang K, Fischer T, Collins SR, Qu H, Shales M, Park HO, Hayles J, et al. 2008. Conservation and rewiring of functional modules revealed by an epistasis map in fission yeast. Science 322: 405–410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rual JF, Venkatesan K, Hao T, Hirozane-Kishikawa T, Dricot A, Li N, Berriz GF, Gibbons FD, Dreze M, Ayivi-Guedehoussou N, et al. 2005. Towards a proteome-scale map of the human protein–protein interaction network. Nature 437: 1173–1178 [DOI] [PubMed] [Google Scholar]
- Saito H, Kubota M, Roberts RW, Chi Q, Matsunami H 2004. RTP family members induce functional expression of mammalian odorant receptors. Cell 119: 679–691 [DOI] [PubMed] [Google Scholar]
- Simonis N, Rual JF, Carvunis AR, Tasan M, Lemmens I, Hirozane-Kishikawa T, Hao T, Sahalie JM, Venkatesan K, Gebreab F, et al. 2009. Empirically controlled mapping of the Caenorhabditis elegans protein–protein interactome network. Nat Methods 6: 47–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith WL, Dewitt DL 1996. Prostaglandin endoperoxide H synthases-1 and -2. Adv Immunol 62: 167–215 [DOI] [PubMed] [Google Scholar]
- Stewart EA, McKusick KB, Aggarwal A, Bajorek E, Brady S, Chu A, Fang N, Hadley D, Harris M, Hussain S, et al. 1997. An STS-based radiation hybrid map of the human genome. Genome Res 7: 422–433 [DOI] [PubMed] [Google Scholar]
- Tischler J, Lehner B, Fraser AG 2008. Evolutionary plasticity of genetic interaction networks. Nat Genet 40: 390–391 [DOI] [PubMed] [Google Scholar]
- Tong AH, Evangelista M, Parsons AB, Xu H, Bader GD, Page N, Robinson M, Raghibizadeh S, Hogue CW, Bussey H, et al. 2001. Systematic genetic analysis with ordered arrays of yeast deletion mutants. Science 294: 2364–2368 [DOI] [PubMed] [Google Scholar]
- Tong AH, Lesage G, Bader GD, Ding H, Xu H, Xin X, Young J, Berriz GF, Brost RL, Chang M, et al. 2004. Global mapping of the yeast genetic interaction network. Science 303: 808–813 [DOI] [PubMed] [Google Scholar]
- Toro JR, Nickerson ML, Wei MH, Warren MB, Glenn GM, Turner ML, Stewart L, Duray P, Tourre O, Sharma N, et al. 2003. Mutations in the fumarate hydratase gene cause hereditary leiomyomatosis and renal cell cancer in families in North America. Am J Hum Genet 73: 95–106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkatesan K, Rual JF, Vazquez A, Stelzl U, Lemmens I, Hirozane-Kishikawa T, Hao T, Zenkner M, Xin X, Goh KI, et al. 2009. An empirical framework for binary interactome mapping. Nat Methods 6: 83–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visel A, Rubin EM, Pennacchio LA 2009. Genomic views of distant-acting enhancers. Nature 461: 199–205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe TK, Bihoreau MT, McCarthy LC, Kiguwa SL, Hishigaki H, Tsuji A, Browne J, Yamasaki Y, Mizoguchi-Miyakita A, Oga K, et al. 1999. A radiation hybrid map of the rat genome containing 5255 markers. Nat Genet 22: 27–36 [DOI] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH 1998. Collective dynamics of “small-world” networks. Nature 393: 440–442 [DOI] [PubMed] [Google Scholar]
- Yu H, Greenbaum D, Xin Lu H, Zhu X, Gerstein M 2004. Genomic analysis of essentiality within protein networks. Trends Genet 20: 227–231 [DOI] [PubMed] [Google Scholar]
- Yu H, Kim PM, Sprecher E, Trifonov V, Gerstein M 2007. The importance of bottlenecks in protein networks: Correlation with gene essentiality and expression dynamics. PLoS Comput Biol 3: e59 doi: 10.1371/journal.pcbi.0030059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Braun P, Yildirim MA, Lemmens I, Venkatesan K, Sahalie J, Hirozane-Kishikawa T, Gebreab F, Li N, Simonis N, et al. 2008. High-quality binary protein interaction map of the yeast interactome network. Science 322: 104–110 [DOI] [PMC free article] [PubMed] [Google Scholar]