Evaluating Convergence of Within-Person Change and Between-Person Age Differences in Age-Heterogeneous Longitudinal Studies

Abstract

The distinction of between-person age differences from within-person age changes is necessary for understanding aging-related change processes. Although longitudinal studies are required to address issues relating to within person change, most studies begin using age-heterogeneous samples and conclude using survival-heterogeneous samples. Given the numerous potential confounds associated with age-heterogeneous samples, careful treatment of between-person age differences is essential to obtain the correct inferences regarding within-person age change. We demonstrate how failure to differentiate between-person age effects (and by extension, of survival age or other effects producing sample heterogeneity) will lead to uninterpretable inferences regarding within-person change. We recommend that convergence of age differences and age changes be formally evaluated whenever possible.

A major objective of developmental and aging research on cognitive functioning is to describe patterns of change across the lifespan, including differentiation of function in early developmental trajectories, age of peak performance in different cognitive abilities, and magnitude of aging and health-related declines in mid-life and later life. Many types of cross-sectional and longitudinal research designs have been used to understand such developmental trajectories across the lifespan. Age-heterogeneous cross-sectional studies that describe age differences have been used as a basis for inferring aging-related change. However, comparisons of findings from cross-sectional and longitudinal studies have often yielded different conclusions about the patterns and rates of age-related change across the lifespan. As noted by Schaie and Hofer (2000), “comparison of longitudinal to cross-sectional findings provides evidence of both concordance and disagreements (either full or in part).”

Schaie (1996, 2008) has emphasized the importance of evaluating historical factors associated with birth cohort when evaluating longitudinal patterns of cognitive change. To that end, longitudinal studies (see Schaie & Hofer, 2000) have used Schaie’s most efficient sampling design —based on a combination of cross-sectional and longitudinal sequences. This sampling approach permits investigation of how level of functioning or rate of change differs across birth cohorts or how period of testing effects influence outcomes. A more common sampling approach is that of accelerated longitudinal designs (Bell, 1953; 1954; McArdle & Bell, 2000), in which individuals from sequential cohorts (e.g., birth cohort, grade in school) are followed longitudinally for a limited period of time. Measuring different cohorts that overlap with respect to age permits estimation of a single trajectory across the entire range of observed age, a much larger range than what is observed directly through longitudinal follow-up. Although the combination of age information across cohorts and over time allows for the optimal estimation of parameters in models of change, it does so only under the assumption of age convergence, or that cross-sectional age differences and longitudinal age changes converge onto a common trajectory. That is, for such age convergence models to produce valid results predicted values should depend only on one’s age at a particular observation, and not on when the person was that particular age. Age convergence is a hypothesis that can be evaluated statistically, and there are a number of published examples of how do so when combining longitudinal data across multiple discrete cohorts (e.g., Mehta & West, 2000; Miyazaki & Raudenbush, 2000).

Age convergence models have also been used to analyze data from longitudinal studies without discrete cohorts at the first occasion, but rather that consist of individuals with continuously varying ages at baseline. For example, some studies of adult aging have applied age convergence models to samples with age ranges at baseline spanning 30 to 40 years (e.g., Ferrer et al., 2005) or even 90+ years (McArdle, Ferrer, Hamagami, & Woodcock, 2002). Such wide age ranges encompass a large number of discrete birth cohorts, and so multiple group approaches for testing convergence become impractical (Mehta & West, 2000). Accordingly, the purpose of this article is to describe an alternative approach for testing age convergence in studies with continuous age heterogeneity at baseline.

The Importance of Convergence

Consider the following model of within-person change, as shown in Equation (1):

$$y_{\mathit{ti}}={\beta }_0+{\beta }_1({\mathit{Age}}_{\mathit{ti}})+b_{0i}+r_{\mathit{ti}}.$$ (1)

This model predicts the value of outcome y at time t for individual i based on the population average intercept (β₀), the population average age slope (β₁), an individual-specific intercept deviation (b_0i), and a residual term (r_ti). Terms with a subscript i vary between individuals whereas terms with a subscript ti vary both between individuals (i) and within individuals over time (t). Accordingly, the within-person variability (across t) reflects the longitudinal component of the data (i.e., age changes) and the between-person variability (across i) reflects the cross-sectional component (i.e., age differences). The composite nature of the variability in the age predictor (i.e., age varies across both i and t) implies that the the average age slope (β₁) is a mixture of both cross-sectional and longitudinal effects. If the age convergence assumption is met, then the resulting composite age slope β₁ will be more efficient than an age slope estimated using either purely longitudinal or purely cross-sectional information.

One method of distinguishing temporal (within-person) effects from cohort (between-person) effects of age involves scaling the age variable. In between-person age scaling, the origin of the time variable is set to a common age. For example, one could set the reference age as 80 by including (Age_ti − 80) as a predictor rather than as age at birth as implied by using Age_ti. In contrast, within-person age scaling involves representing change as a function of time passed, which is specific to a given individual rather than to a given age. Within-person age scaling is usually implemented by using the person’s age at the initial assessment as the reference (i.e., by including Age_ti − Age_1i as a predictor rather than Age_ti), but other reference points have also been used (Sliwinski et al., 2003; Wilson et al., 2003). The same longitudinal information is provided from individual-level data whether age is scaled between-persons (Age_ti − 80) or within-persons (Age_ti − Age_1i). The choice of age scaling will, however, influence how between-person age variance is represented in the model for change.

Testing Age Convergence

Testing for age convergence (e.g., Hoffman & Stawski, in press) involves a simple extension of a technique described in texts on longitudinal data analysis (Diggle, Liang & Zeger, 1994) and multilevel modeling (Raudenbush & Bryk, 2002). Because Equation (1) estimates a single age slope (β_l), it constrains the longitudinal and cross-sectional age effects equal. Adding each individual’s mean age ${\overline{\mathit{Age}}}_{.i}$ to the model relaxes this constraint. Equation (2) includes ${\overline{\mathit{Age}}}_{.i}$ and groups all terms that are constant for a given individual in brackets:

$${\mathrm{y}}_{\mathit{ti}}=\left[{\beta }_0+{\beta }_2\left({\overline{\mathit{Age}}}_{.i}\right)+b_{0i}\right]+{\beta }_1\left({\mathit{Age}}_{\mathit{ti}}\right)+r_{\mathit{ti}}$$ (2)

The variable ${\overline{\mathit{Age}}}_{.i}$ conveys information only about cross-sectional age differences, and its addition to the model changes the interpretation of the β₁ slope for Age_ti. In Equation (1), the β₁ slope for Age_ti reflected the effect of both cross-sectional differences in age and longitudinal age changes. In Equation (2) the effect of the β₁ slope for Age_ti is now its unique effect after controlling for the cross-sectional age variation in ${\overline{\mathit{Age}}}_{.i}$ via β₂. The unique effect of Age_ti is its longitudinal or within-person effect. The precise interpretation of the β₂ slope for ${\overline{\mathit{Age}}}_{.i}$ is clarified by taking the person-level average on both sides of the equal sign, thus aggregating over all sources of longitudinal information in Equation (3):

$${\overline{\mathrm{y}}}_{.\mathrm{i}}=\left[{\beta }_0+{\beta }_2({\overline{\mathit{Age}}}_{.i})+b_{0i}\right]+{\beta }_1({\overline{\mathit{Age}}}_{.i})+{\overline{r}}_{.i}.$$ (3)

The terms in this equation can be rearranged as shown in Equation (4):

$${\overline{\mathrm{y}}}_{.\mathrm{i}}={\beta }_0+\left({\beta }_1+{\beta }_2\right){\overline{\mathit{Age}}}_{.i}+b_{0i}+{\overline{r}}_{.i}.$$ (4)

The result is a model that reflects information derived exclusively from between-person age differences and shows that the between-person or cross-sectional age slope is given by the quantity(β₁ + β₂). This implies that the slope β₂ reflects the difference between the longitudinal and cross-sectional age effects. If age convergence holds (i.e., if β₂ = 0), then the predicted values from Equation (2) will be equivalent to those from Equation (1). Within-person age scaling could be used as well, in which each individual’s average age is set as the reference point by including ${\mathit{Age}}_{\mathit{ti}}-{\overline{\mathit{Age}}}_{.i}$ rather than Age_ti in Equation (2). This within-person age scaling would leave the interpretation of the β_l age slope unchanged, but the β₂ slope for ${\overline{\mathit{Age}}}_{.i}$ would now directly reflect the between-person age effect rather than the difference of the within-person and between-person age effects. It is more common in longitudinal studies to set the reference to each individual’s age at baseline (e.g., Mehta & West, 2000; Sliwinski & Buschke, 2004). Using baseline age as a reference produces comparable results to the steps outlined in Equations (1-4), except that the between-person age effect would reflect how an individual’s age at the first occasion related to his or her score on the first occasion, rather than how his or her average age related to his or her average score. Age at baseline is likely to provide a better index of cohort and selection effects than would scaling relative to mean age, which is likely to be biased due to study attrition and population mortality.

Equation (4) illustrates that age convergence will fail so long as the between-person age slope and within-person age slope differ, even in the absence of cohort differences on the age slope. Figures 1a and 1b illustrate this point with hypothetical data. Figure 1a shows four-year trajectories for three overlapping birth cohorts. Individuals at any point in time differ from individuals who are four years older by an amount that is exactly equal to the amount of change that they experience over the same interval. In this case, information about longitudinal, within-person age changes and cross-sectional, between-person age differences converges on the same answer, such that the β₂ slope for ${\overline{\mathit{Age}}}_{.i}$ in Equation (2) expressing the difference in these effects would be equal to zero. Figure 1b shows the same longitudinal trajectories as Figure 1a, but with a positive effect of birth cohort (β₂ > 0), such that subsequent birth cohorts (i.e., those beginning the study at a younger age) have higher predicted outcomes than earlier birth cohorts (who began the study at an older age). The thick solid line represents the between-person age slope (β_B), as obtained from β₁ + β₂ in Equation (2), which is steeper than the within-person age slope (β_W), as obtained from β₁ in Equation (2). Thus, even if the rate of age change is identical across cohorts (as in this example), combining information about cross-sectional age differences and longitudinal age changes in the presence of intercept differences across age cohorts would yield a biased estimate of the true developmental aging effect.

Figure 1.

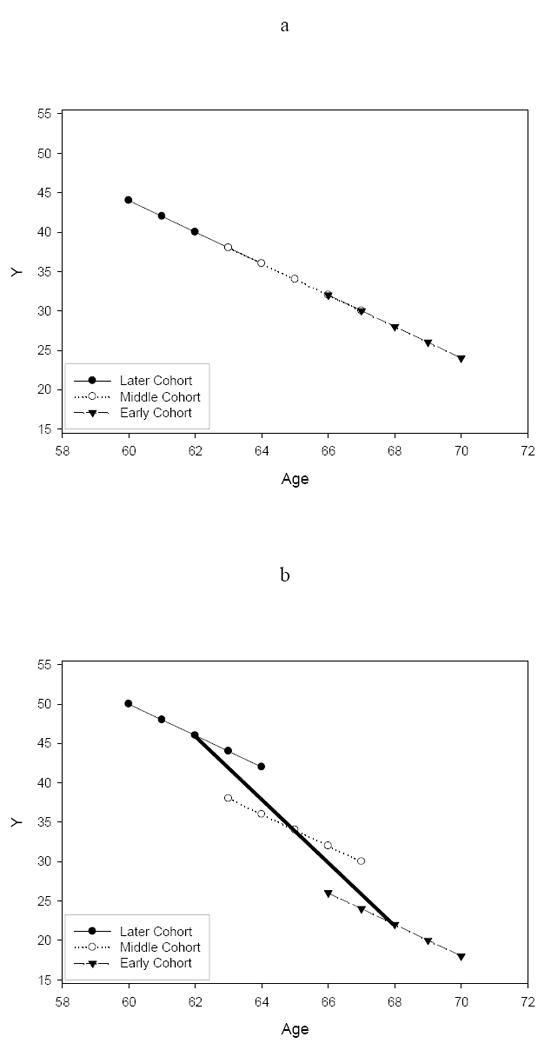
Examples of age convergence (1a) and age non-convergence (1b).

Quantifying the Longitudinal and Cross-Sectional Influences

The estimate of the age convergence slope β₁ in Equation (1) reflects information about how individuals change as they age as well as how people of different ages vary from each other. Even if age convergence obtains such that the cross-sectional and longitudinal age effects are equal, it would be useful to know the relative contribution of both types of information to the estimation of the age convergence slope, or β_C. The formal relationship among the between-person (β_B), within-person (β_W), and convergence (β_C) age slopes is expressed in Equation (5) as

$${\beta }_C=\omega {\beta }_B+(1-\omega ){\beta }_W.$$ (5)

The quantity ω is the mixing weight that controls the relative contribution of the cross-sectional (β_B) and longitudinal age slope (β_W) to the estimation of the convergence age slope (β_C). The higher the value of ω, the more β_C would reflect the cross-sectional information about between-person age differences, and the lower the value of ω̣ the more β_C would reflect the longitudinal information about age changes. A single occasion cross-sectional study would have ω̣ = 1, whereas a longitudinal study of individuals identical in age at baseline would have ω̣ = 0. Longitudinal studies with age heterogeneous samples will have values of ω that range between 0 and 1.

Calculating the value of ω for a given study informs the extent to which the results are driven by between-person age variance in the data. Although the value of ω would equal the ratio of the between-person sum of squares for age to the total sum of squares for age given ordinary least squares estimation and balanced data, the relative weighting of β_B and β_W is quite complex in the general case (Raudenbush & Bryk, 2002). Fortunately, it is possible to determine the relative contribution of cross-sectional and longitudinal information to the estimate of the age convergence slope. This can be done by using parameter estimates and rearranging the terms in Equation (5) to solve for ω̂ as shown in Equation (6):

$$\widehat{\omega }=\frac{{\widehat{\beta }}_C-{\widehat{\beta }}_W}{{\widehat{\beta }}_B-{\widehat{\beta }}_W}.$$ (6)

The weighting parameter ω̂ can be calculated by estimating the three different age effects (β̂_C, β̂_W and β̂_B for a given data set and then solving for ω̂. For example, if β̂_C = -1.0, β̂_B = -1.5, and β̂_W = -0.5, then ω̂ would be .5, indicating exactly equal weighting of the cross-sectional and longitudinal age variance in the estimation of the convergence age slope.

The relative amount of longitudinal and cross-sectional age variance available to estimate β_C is an important determinant of the magnitude of ω̂ for a given data set. In practical terms, this implies that increasing the range of age at baseline and reducing the amount of follow-up drives ω̂ upward (i.e., towards the between-person, cross-sectional age effect), whereas restricting the initial age range and increasing the amount of follow-up reduces ω̂ (i.e., towards the within-person, longitudinal age effect). The second implication is that the amount of residual within-person variance will influence estimation ofω̂. As the amount of residual variance decreases, the relative weight of the longitudinal age variance increases, and vice-versa. A formal test of age convergence coupled with an assessment of the relative weighting of cross-sectional and longitudinal age information can help to understand why age convergence does or does not obtain in a given application. However, in extreme cases, such as when 95% of the age variance is between-persons, it may be harder to detect non-convergence because there would be so little information on which to base the test of age convergence.

Application to Simulated Data

The purpose of this simulation study is twofold. First, we will illustrate that cohort differences in level of an outcome (intercept) but not rate of change are sufficient to bias age convergence slopes. Second, we examine how different study design features (e.g., follow-up frequency, interval, and duration) and sample characteristics (e.g., age range) systematically influence estimates of age convergence effects. This is important because results from a longitudinal study do not necessarily reflect exclusively or even mostly intraindividual change. Depending on the study design, sample characteristics, and the analytic model, estimates of aging effects from longitudinal data could reflect primarily cross-sectional age differences, telling us very little about developmentally relevant intraindividual change.

Each simulated data set consisted of an age-heterogeneous sample measured longitudinally. Three design factors were varied across simulations. The first factor was age range at baseline, which was set to either 20 or 40 years. Age was uniformly distributed across its range. The second factor was the number of assessments, which was set to 2, 3, 4, or 5. The third factor was the interval between assessments, which was set to either 1 or 2 years. Sample size was fixed to 500 for each simulated sample. Data for the simulations were generated using the model in Equation (7):

$$y_{\mathit{ti}}={\beta }_0+{\beta }_1\left({\mathit{Age}}_{\mathit{ti}}\right)+{\beta }_2\left({\mathit{BirthYear}}_i\right)+b_{0i}+b_{1i}\left({\mathit{Age}}_{\mathit{ti}}\right)+r_{\mathit{ti}},$$ (7)

in which β₀ is the population average intercept, β₁ is the population average age slope, and β₂ is the linear effect of cohort (i.e., birth year). The parameters b_0i and b_1i represent each person’s deviation from the population average intercept and age slope, respectively. Each simulation specified values for the fixed effects (β₀, β₁, and β₂). The population values for β₀ and β₁ were set to be 50 and -.25 for all simulations. The value for β₂ was set to either 0 or -.20. When β₂ = 0, the cross-sectional age effect (β₁ + β₂) corresponded exactly to the longitudinal effect. When β₂ = -.20, the cross-sectional age effect was equal to -.45. Note that there is no interaction between age and cohort; the difference between cohorts, if present, was constant across all ages. The random intercept and age slope were assumed to follow a bivariate normal distribution with variances of ζ₀ and ζ₁, respectively. For simplicity, the covariance between the two random effects was assumed to be 0 and the values for ζ₀ and ζ₁ were set to 100 and .5, respectively, for all simulations. In addition, the variance of the level-1 residual (r_ti) was assumed to be independently distributed from a univariate normal distribution, with a mean of 0 and variance σ², set to either 30 or 10 for all simulations. The values for the intercept variance (ζ₀) and residual variance (σ²) implies a dependent measure with a SD = 10 and an intraclass correlation (an index of reliability) of either .77 or .91 when σ² is set to 30 and 10, respectively. Crossing all elements of the simulation design resulted in 64 different simulations, and each simulation consisted of 1000 samples, producing a total of 64,000 simulations. Simulations were conducted in SAS (v 9.1) and analyses of the simulated data sets were performed using PROC MIXED.

Analysis and Results of Simulation Study

Two models were fit to each simulated data set, using SAS PROC MIXED and full information maximum likelihood estimation, as shown in Equations (8) and (9):

$$y_{\mathit{ti}}={\beta }_0+{\beta }_1({\mathit{Age}}_{\mathit{ti}})+b_{0i}+b_{1i}+r_{\mathit{ti}}$$ (8)

$$y_{\mathit{ti}}={\beta }_0+{\beta }_1({\mathit{Age}}_{\mathit{ti}})+{\beta }_2({\overline{\mathit{Age}}}_{\mathit{ti}})+b_{0i}+b_{1i}+r_{\mathit{ti}}$$ (9)

Model (10), the age convergence model, assumes no effect of birth cohort and hence that longitudinal and cross-sectional age effects are equivalent. Model (9), the age change + age differences model, is identical to the model (7) used to generate the data because birth year and average age are perfectly correlated. In practice, birth year and average age would be perfectly correlated if the baseline assessment occurred on the same date for all individuals and there were no missing data (i.e., no attrition). Although this circumstance would likely never occur, the correlations between birth year and average age should tend to be extremely high in most circumstances.

The top portion of Table 1 shows that both the models in (8) and (9) recovered the true value for the age slope (β̣_l = -0.25) when there was no effect of birth year (β₂ = 0). Model (9) also accurately recovered the null birth year effect (average β₂ = 0.001 across all simulations) and the age slope and birth year effects when fit to simulated data with a birth year effect of β₂ = -0.20. Variance components closely approximated their populations values in all simulations. However, the age convergence slope estimate from model (8) was consistently biased in the presence of cohort effects, with an average β= -0.35 across all simulations. Bias tended to be larger for simulations with the shorter compared to longer follow-up interval (-0.38 vs -0.33) and when reliability was lower (-0.37 vs -0.34).

Table 1.

Simulation Results

β1 = −0.25, β2 = 0.00
	Model 8					Model 9
σ2	Interval	$\widehat{{\beta }_1}$	$\widehat{{\zeta }_0}$	$\widehat{{\zeta }_1}$	$\widehat{{\sigma }^2}$	$\widehat{{\beta }_1}$	$\widehat{{\beta }_2}$	$\widehat{{\zeta }_0}$	$\widehat{{\zeta }_1}$	$\widehat{{\sigma }^2}$
10	1	-0.250	99.712	0.498	9.984	-0.251	0.000	99.541	0.498	9.978
10	2	-0.250	99.802	0.498	9.981	-0.250	0.001	99.582	0.498	9.978
30	1	-0.251	99.653	0.500	29.957	-0.251	0.000	99.528	0.500	29.937
30	2	-0.250	99.638	0.499	29.948	-0.250	0.002	99.433	0.499	29.934
	Average=	-0.250	99.701	0.499		-0.250	0.001	99.521	0.499

β1= −0.25, β2 = −0.20
	Model 8					Model 9
σ2	Interval	$\widehat{{\beta }_1}$	$\widehat{{\zeta }_0}$	$\widehat{{\zeta }_1}$	$\widehat{{\sigma }^2}$	$\widehat{{\beta }_1}$	$\widehat{{\beta }_2}$	$\widehat{{\zeta }_0}$	$\widehat{{\zeta }_1}$	$\widehat{{\sigma }^2}$
10	1	-0.360	100.186	0.499	10.000	-0.251	-0.450	99.538	0.499	9.978
10	2	-0.311	101.211	0.499	10.001	-0.250	-0.449	99.570	0.499	9.977
30	1	-0.395	99.622	0.499	29.986	-0.250	-0.449	99.315	0.499	29.935
30	2	-0.346	100.455	0.499	30.001	-0.250	-0.451	99.454	0.499	29.938
	Average=	-0.353	100.368	0.499		-0.250	-0.450	99.469	0.499

This bias reflects a mixture of both longitudinal (-0.25) and cross-sectional (-0.40) effects. Importantly, these results show that an effect of cohort on the intercept can bias estimates of convergence age slopes, even when there is no cohort by age change interaction. Next, a value of ω was computed for each simulated data set and these were averaged across data sets for each of the 128 simulation conditions. Preliminary inspection of the results indicated that presence or absence of cohort effects did not influence values of ω, and therefore were collapsed across this condition, yielding a total of 64 values.

Figures 2a and 2b and plot values of ω as a function of years of follow-up years for residual variances equal to 30 (ICC = .77) and 10 (ICC = .91), respectively. Figure 2a shows results from simulations with a reliability of .77 (σ² = 30). Age convergence slopes reflected primarily cross-sectional information (i.e., ω̣ > .80) when follow-up was less than 2 and 3 years for samples with a 30 and 40 year age ranges, respectively. Four years of follow-up was required for convergence age slopes to mostly reflect longitudinal information for samples with a 20 year age range, and 6 years of follow-up was required for samples with a 40 year age range. Eight years of follow-up was required for samples with 20 year age ranges and > 8 years would be required for samples with a 40 year age range to primarily reflect longitudinal information (ω̣ < .20). Comparing Figures 2a and 2b indicates that smaller values of ω are associated with the smaller residual variance (i.e., higher reliability) for a given follow-up duration, interval, and age range. When reliability is high (.91), age convergence slopes from samples with a 20 year age range primarily reflected longitudinal information after 4 years of follow-up, and convergence estimates from samples with a 40 year age range primarily reflected longitudinal information after about 7 years of follow-up. Thus, increasing reliability (i.e., reducing residual variance) increases the relative weighting of longitudinal information.

Figure 2.

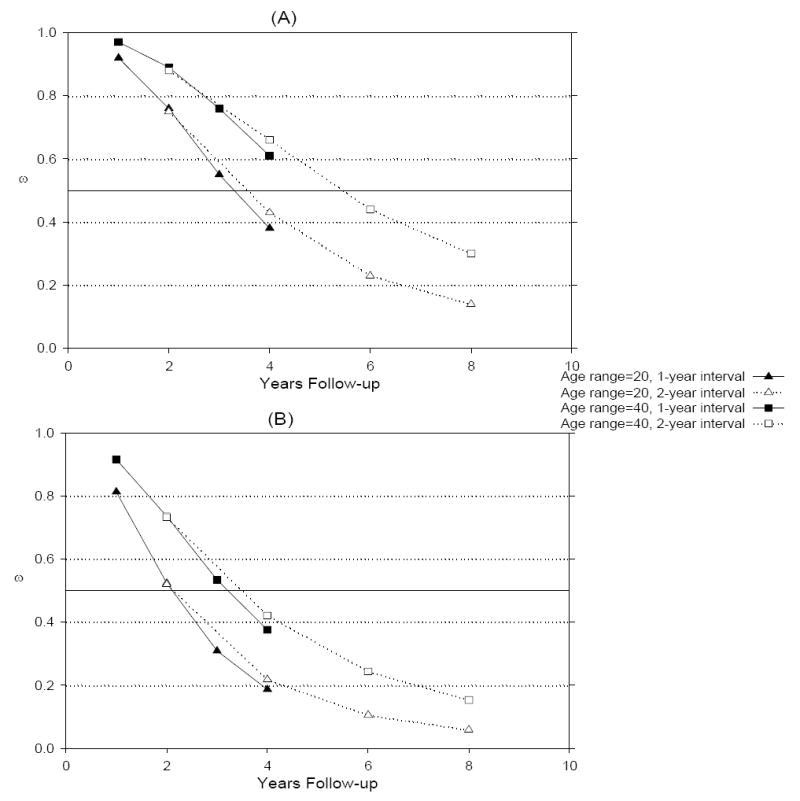
Simulation results for proportion of cross-sectional to longitudinal information in convergence age slope for reliabilities of .77 (a) and .91 (b)

The solid lines in Figures 2a and 2b represent results from simulations with 1 year intervals between assessments, and dotted lines represent results from simulations with 2 years separating each assessment. For a given amount of follow-up, results indicated by the solid lines are based on twice the number of assessments than are results indicated by the dashed lines for a given age range. The graphs show that ω decreases slightly with increased assessments, but that this effect is not nearly as large as the decrease that results from additional follow-up time. Overall, these results indicate that under moderate reliability (.77), at least 6 years of follow-up is required for age convergence slopes to primarily reflect information about intraindividual developmental change. When follow-up is short (i.e., < 2 years), age convergence slopes mostly reflect cross-sectional information about age differences, even if reliability is very high.

Discussion

Longitudinal studies are necessary to directly measure within person change. However, most longitudinal studies begin as age-heterogeneous samples and, particularly in studies of change in later life, will conclude as survival-heterogeneous studies. Careful treatment of the between-person age differences observed in such studies is essential to obtain correct inferences about within-person age change. This article demonstrated how to empirically assess the differential effects of cross-sectional age differences and longitudinal age changes rather than simply assuming that they converge onto the same trajectory. We have shown how omission of between-person age effects (by extension, survival age or other effects producing sample heterogeneity) will lead to estimated within-person age effects that in reality reflect an uninterpretable blend of both kinds of effects, the weighting of which depends on the particular parameters of the sampling design (e.g., age range at baseline, length of follow-up).

There are a number of potential causes for a lack of convergence of the between- and within-person effects of age. The importance of context in individual development has long been recognized (e.g., Kuhlen, 1940; Schaie, 1965; 2008;) and perhaps most frequently made manifest in terms of birth cohort differences. The importance of influences related to birth cohort was underscored in Schaie’s (1965) most efficient design that involved repeated assessments of individuals sampled from different birth cohorts initially, with additional samples added at subsequent occasions. This design permits evaluation of cohort-sequential, time-sequential, and cross-sequential studies within a single sampling design. The inherent confounds of age, period, and cohort mean that these effects cannot be independently evaluated—one factor must be assumed to be zero or some other fixed value so that the other two random factors may be analyzed instead.

Mortality selection is also likely to have an important role in the lack of age convergence. In longitudinal studies of aging, at each new wave of testing the sample becomes less representative of the population from which it originated and generalizations from the sample of continuing participants to the initial population become more difficult to justify (e.g., Baltes, Schaie, & Nardi, 1971; Hofer & Hoffman, 2007). Whereas some forms of non-participation can logically permit inference to a single population, in the case of mortality, such an inference is impossible because individuals have left the population. In this case, inferences must be defined as conditional on the probability of surviving and/or remaining in the study (e.g., DuFouil, Brayne, & Clayton, 2004). Initial sample selection and attrition relate to population inference differently for designs based on either age-heterogeneous or age-homogeneous sampling. In age-heterogeneous samples, whether cross-sectional or longitudinal, inference to individual aging processes is not possible in the aggregate sample because initial sample selection of individuals varying in age is confounded with population mortality (Schaie, Labouvie, & Barrett, 1973).

Retest effects may also cause a lack of age convergence (e.g., Salthouse, 2009) by biasing estimates of longitudinal aging effects. Age convergence models that also include parameters for retest rely on the effects of between-person age differences to correct for the within-person retest effects (e.g., Ferrer et al., 2005), but seldom explicitly evaluate the age convergence assumption. Simply because longitudinal estimates may be biased (e.g., due to retest effects) does not imply that cross-sectional age differences do not reflect cohort, selection, mortality or other contaminating influences. In general, studies that correct for retest effects in longitudinal data produce estimates of aging effects that primarily reflect cross-sectional information (i.e., high values of ω̣ because statistically partially for retest will remove much of the longitudinal information from the age variable. This approach is a defensible approach only if one can be confident that cross-sectional age differences represent an unbiased estimate of maturational effects. Unfortunately most analyses that correct for retest effects in longitudinal data do not attempt to formally assess the convergence assumption, check for cohort or mortality effects, or in any way evaluate whether cross-sectional age differences can serve as a valid anchor for estimation of true aging effects.

The question then arises of whether estimates that primarily reflect cross-sectional information should be framed as a “longitudinal result” that reflects “change”, even if based on a sample with lengthy follow-up. There is no single value of ω that should be deemed acceptable or unacceptable for all circumstances. However, we can identify values less than .50 as a natural threshold at which the convergence age slopes mostly reflect longitudinal and opposed to cross-sectional information. In general, values of ω̣ < .20 indicate that the convergence age slope primarily reflects longitudinal information, and values > .80 indicate that the convergence age slope primarily reflects cross-sectional information. As a rule of thumb, we would caution against fitting age convergence models without testing the convergence assumption, especially when ω̣ >.80. Failure to test for convergence under this circumstance undermines the rationale for having conducted a longitudinal study.

Finally, we wish to recognize that the extent to which tests of age convergence have sufficient power to be practically useful depends to a great extent on the longitudinal sampling design used. Although tests of age convergence on the intercept are likely to have sufficient power, tests of convergence on the age slopes (or on higher-order age terms) may be problematic except in studies that have large amounts of longitudinal follow-up. In such cases, the most useful alternative approach would likely depend on the context of the study. For instance, in studies of children in successive grade cohorts, it may be reasonable to utilize a between-person age scaling that assumes convergence of the higher-order coefficients of age change (e.g., quadratic terms), given that the children were sampled largely from the same specific context, that the total amount of time covered across grade cohorts is rather limited, and that differential selection and attrition may not be an issue. In contrast, in longitudinal studies of adult development and aging that feature a wide range of age at baseline, it may not be reasonable to assume convergence of higher-order rates of change, given that the study recruitment itself is likely the only commonality of the individuals sampled, and given the likely effects of non-random selection processes over time. In this case, it may be more reasonable to use within-person age scaling instead, which requires no assumptions of age convergence.

In summary, although longitudinal studies provide direct estimates of within-person change, they usually also provide information about between-person age differences. Failure to explicitly account for the differential effects of these two sources of age information can lead to incorrect estimates of age change. When relying on between-person age scaling in models of change, it is critical that one tests explicitly for convergence of the effects of between-person age differences and within-person age changes. Although between-person age scaling may result in more efficient estimates when age convergence obtains, this rarely seems to occur in samples of older adults in practice. In such cases, a within-person age scaling that provides a clear demarcation of the cross-sectional and longitudinal age effects may be more useful instead. Regardless, however, results that are based on models that falsely assume convergence of the effects of between-person age differences and within-person age changes cannot be interpreted, as they represent an unknown mix of two different kinds of effects.