Relaxed Molecular Clocks, the Bias–Variance Trade-off, and the Quality of Phylogenetic Inference

Abstract

Because a constant rate of DNA sequence evolution cannot be assumed to be ubiquitous, relaxed molecular clock inference models have proven useful when estimating rates and divergence dates. Furthermore, it has been recently suggested that using relaxed molecular clocks may provide superior accuracy and precision in phylogenetic inference compared with traditional time-free methods that do not incorporate a molecular clock. We perform a simulation study to determine if assuming a relaxed molecular clock does indeed improve the quality of phylogenetic inference. We analyze sequence data simulated under various rate distributions using relaxed-clocks, strict-clocks, and time-free Bayesian phylogenetic inference models. Our results indicate that no difference exists in the quality of phylogenetic inference between assuming a relaxed molecular clock and making no assumption about the clock-likeness of sequence evolution. This pattern is likely due to the bias–variance trade-off inherent in this type of phylogenetic inference. We also compared the quality of inference between Bayesian and maximum likelihood time-free inference models and found them to be qualitatively similar.

The concept of a molecular clock has played a central role in evolutionary biology since its introduction nearly half a century ago by Zuckerkandl and Pauling (1962). Despite its auspicious beginnings, however, the concept of a universal, strict molecular clock has fallen out of favor (Li 1993; Ayala 1997; Bromham and Penny 2003; Kumar 2005). It is now widely recognized that nucleotide and amino acid substitutions do not generally accumulate at a constant and universal rate even across closely related lineages. Instead, the molecular clock fluctuates. So-called relaxed molecular clock inference models lie on a continuum between strict-clock inference models, which assume a constant evolutionary rate across lineages, and time-free inference models, which do not incorporate evolutionary rates across lineages at all.

Relaxed molecular clocks were introduced by Sanderson (1997, 2002) and Thorne et al. (1998) to estimate the time to most recent common ancestor (tMRCA) in the absence of rate constancy. Their models assumed that the sequences evolve with an inherent temporal component, even though this clock does not tick uniformly across the entire phylogeny or through time. Sanderson's method relied upon semiparametric penalized likelihood estimation, whereas Thorne et al. embedded the problem of rate estimation in a Bayesian Markov chain Monte Carlo (BMCMC) framework; an expectation of autocorrelation of rates along closely related branches is a feature of both methods. More recently, developments in BMCMC relaxed-clock phylogenetic inference models have allowed uncorrelated rates to be sampled from a variety of distributions, including exponential and lognormal (Drummond et al. 2006). These rate distributions differ in their assumptions of where on the phylogeny changes in the evolutionary rates occur: at internal nodes (exponential) or along branches (lognormal). Drummond et al. (2006) modeled uncorrelated rates because their phylogenetic analysis suggested that autocorrelation of rates is not predominant. While testing these new relaxed-clock inference models, Drummond et al. (2006) put forth the intriguing proposition that incorporation of relaxed molecular clocks might improve the topological accuracy and precision of phylogenetic inference. If true, relaxed molecular clock inference models should supersede traditional time-free phylogenetic analyses, whether or not estimations of substitution rates or tMRCA are desired.

Correctly modeling nucleotide substitution parameters generally increases the probability of inferring the correct phylogenetic tree. This pattern has been demonstrated for the classic 4-taxon tree using simulated sequence data (Gaut and Lewis 1995) as well as for real sequence data (Sullivan and Swofford 1997). These observations have led to the development and implementation of more realistic models of molecular sequence data, including unequal base frequencies (Felsenstein 1981), rate heterogeneity (Yang 1993), and codon position partitioning (Shapiro et al. 2006), along with computational tools designed to determine the appropriate model for a given data set (Posada and Crandall 1998). Furthermore, seminal work by Huelsenbeck and Hillis (1993) explicitly examined the ability of inference models that assumed a strict molecular clock to reconstruct a tree from sequence data that clearly violated this assumption. They found that, although this model correctly inferred phylogenies for clock-like data, it fared extremely poorly on non–clock-like data. Therefore, it seems reasonable to expect that if one can correctly model the rate of evolution along the branches of a tree, one should better be able to correctly infer the topology of that tree.

Statistical theory, however, does not necessarily support this supposition because of the bias–variance trade-off (Burnham et al. 2002). Bias reflects the ability of a model to accurately predict the data, whereas variance refers to the sensitivity of the model to the sampled data. As variance increases, the precision of the estimate decreases. A model that underfits the data, because it has fewer parameters, is generally highly biased but has low variance. A low-parameter model may not be realistic, but it might be useful when encountering new data. Increasing the number of parameters may well increase the fit of the model to the data, but this comes at the expense of a decrease in both explanatory power and the precision of estimates. Theoretically, the best model is one with an intermediate number of parameters that simultaneously minimizes bias and variance. The question remains whether, in practice, modeling rate variation among branches can improve phylogenetic inference.

Drummond et al. (2006) set out to answer this question by testing the quality of relaxed-clock, strict-clock, and time-free inference models in a variety of taxa, including bacteria, yeast, and mammals. They inferred a “true tree” from large sequence data sets, broke these data sets into subregions, and compared the inferred phylogenies for each of the subregions to the true tree. Their results suggested that relaxed-clocks provide more accurate and precise phylogenetic inference; however, their analyses had several limitations. First, their data sets contained relatively few (8 or 9) taxa and their true trees were highly asymmetrical. Second, given the nature of coalescent processes and horizontal gene transfer, their true tree was likely the incorrect tree for many subregions (Ochman et al. 2000; Edwards et al. 2007). Finally, their conclusion regarding the superiority of relaxed molecular clocks was not accompanied by statistical analyses. In many cases, the differences in accuracy and precision among the clock models were slight or nonexistent.

Here, we study whether or not the assumption of a relaxed molecular clock significantly improves the quality of phylogenetic inference. We simulated sequence data under relaxed-clock and strict-clock scenarios and inferred phylogenies under the assumptions of various clock models. Our findings shed light on the bias–variance trade-off in phylogenetic inference, find little evidence in support of the conclusions of Drummond et al. (2006), and suggest that additional metrics beyond accuracy and precision are needed to determine whether relaxed-clocks improve the quality of phylogenetic topological reconstructions.

METHODS

Sequence Simulation

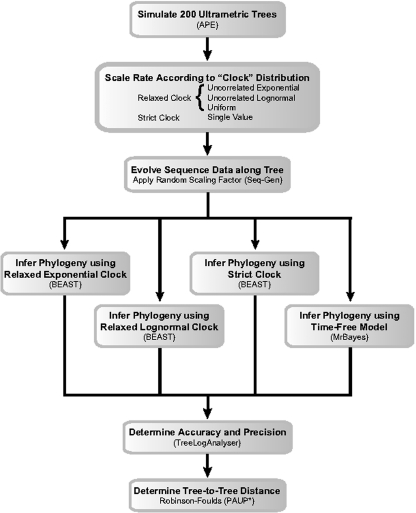
We constructed 800 sequence alignments that conformed to several models of sequence evolution (Fig. 1). First, we used APE (Paradis et al. 2004) to simulate 200 ultrametric trees ranging in size from 5 to 50 taxa, in 5-taxon intervals (i.e., 20 trees per interval). Individual branch lengths are the product of the time elapsed between nodes and the rate of evolution along a branch. The study by Drummond et al. (2006) explicitly recognized that all sequences evolve with an inherent temporal component. Therefore, we manipulated only the rate component along each branch by sampling from distributions comprised of 10,000 “rates.” Specifically, 4 rate distributions (exponential, lognormal, strict, and uniform) were separately applied to each of the 200 tree topologies, and each branch was assigned its own randomly selected number (Fig. 2). These trees are available as supplemental online data files (available from http://www.sysbio.oxfordjournals.org). The exponential (mean and standard deviation equal to 0.01) and lognormal (mean equal to 0.01 and variance equal to 0.5) distributions represent relaxed-clock models of sequence evolution. The shapes of these rate distributions were based on previous simulations by Drummond et al. (2006). The strict distribution, representing a strict molecular clock, was defined by a single value (1). The uniform distribution (range from 0.0001 to 1.0) is also a relaxed-clock model, which essentially minimized the model's information about rates among all possible probability distributions but retained the biologically relevant assumption that all sequences evolve over time. We emphasize that this uniform distribution is not intended to reflect the assumptions made by the time-free phylogenetic inference model.

FIGURE 1.

Flowchart of Bayesian inference simulation study. Software packages used at each step are noted in parentheses.

FIGURE 2.

Distributions sampled to model evolutionary rates among branches according to a) exponential, b) lognormal, c) strict, and d) uniform distributions.

After the heights (i.e., time from root to tip) of these 800 phylogenies were standardized in TreeEdit (Rambaut and Charleston 2002), we proceeded to generate sequence data for each tree using Seq-Gen v1.5.3 (Rambaut and Grassly 1997). Each sequence generated was 1000 bases in length and was evolved according to an HKY+Γ₄ (κ = 2;α = 1) substitution matrix. To incorporate variable root height into the data, each tree's root height was scaled by a random integer (1–30) in Seq-Gen. This scaling created alignments with uncorrected pairwise distances consistent with biologically relevant sequence data used in studies of molecular evolution (approximately 2–40% maximum pairwise distance).

Phylogenetic Analysis

Each of these 800 alignments was analyzed using 4 different molecular clock models utilizing BMCMC phylogenetic inference (2 relaxed-clock models, 1 strict-clock model, and 1 time-free model where no estimation of rates is performed). The 2 relaxed-clock inference analyses and strict-clock inference analysis were performed using BEAST v1.4.6 (Drummond and Rambaut 2007) under an HKY+Γ₄ substitution model. Uninformative priors were assigned for both kappa and alpha. Each analysis was performed for 30,000,000 generations, and the first 10% were removed as a burn-in. For each run, 9000 post–burn-in trees were sampled. Convergence of the BMCMC was confirmed using Tracer v1.4 (Rambaut and Drummond 2007). If the effective sample size (ESS) for a given parameter was < 100, the analysis was rerun for up to 100,000,000 generations until the ESS values for all parameters were > 100. Root height ESS values of  < 100 were not addressed as the subsequent analyses were performed on unrooted trees (see below). BEAST infers the position of the root as a by-product of its rate estimation analysis. Twenty-nine percent of the BEAST analyses needed to be rerun. BEAUti templates, the input files for BEAST, for each inference model are available as online Appendices 1–3 (available from http://www.sysbio.oxfordjournals.org).

Time-free phylogenetic analysis (i.e., what Drummond et al., 2006, referred to as the unrooted Felsenstein model) was performed using MrBayes v3.1 (Ronquist and Huelsenbeck 2003) under an HKY+Γ₄ substitution model. Time-free analysis is not an available feature of BEAST. Each MrBayes analysis was performed for 1,000,000 generations, and the first 10% were removed as burn-in. If ESS values for a given parameter were  < 100, the analysis was rerun for up to 3,000,000 generations until sufficient ESS values were achieved. Generations compute severalfold faster in BEAST, making a direct comparison of run times difficult. Thirty-eight percent of the MrBayes analyses needed to be rerun. For each run, 9000 post–burn-in trees were sampled. The MrBayes block template is available as online Appendix 4 (available fromhttp://www.sysbio.oxfordjournals.org).

We also compared the overall quality of maximum likelihood (ML) time-free inference methods with the aforementioned Bayesian inference methods. The 800 ML trees were inferred in PAUP* v4.1 (Swofford 2002) under an HKY+Γ₄ substitution model with a heuristic search utilizing the subtree pruning regrafting branch swapping algorithm. We also performed nonparametric bootstrapping (100 replicates) on all 800 sequence alignments.

Metrics of Phylogenetic Inference Quality

To compare the BEAST and MrBayes analyses, we unrooted all post–burn-in trees using PAUP*. Measurements of accuracy and precision of the phylogenetic analyses were performed using TreeLogAnalyser (part of the BEAST package). First, the 95% credible set of trees from each analysis was identified. If the true tree, the topology generated in APE, was found in that credible set, then the analysis was categorized as accurate. The number of trees in the 95% credible set was used to quantify precision. We also used a third metric, the Robinson–Foulds tree-to-tree distance (Robinson and Foulds 1981), which calculates the number of nodes separating 2 trees. We determined the distance between the true tree topologies and each of the post–burn-in topologies sampled (for the Bayesian analyses) and the ML tree or the bootstrap replicates (for the ML analyses). These values were scaled by the theoretical maximum Robinson–Foulds tree-to-tree distance to standardize across topologies with varying taxon number. The mean of these values was used as an indicator of the overall distance of the sampled trees from the true tree.

We used these 3 metrics (accuracy, precision, and Robinson–Foulds tree-to-tree distance) to compare the performance of each of the molecular clock models of phylogenetic inference on sequences generated under all 4 rate distributions. Accuracy, a binary outcome, was assessed using logistic regression. Precision, given its non-normalizable distribution, was partitioned into quintiles and analyzed using ordinal logistic regression. Robinson–Foulds tree-to-tree distance data were analyzed using multiple linear regression. We chose to analyze the data using regression analyses so that we could adjust for taxon number, Seq-Gen scaling factor, and Colless's imbalance as fixed effects. Colless's imbalance (Colless 1995) is a measurement of topological asymmetry and was calculated using Mesquite (Maddison WP and Maddison DR 2007). We also treated the 200 tree topologies as a random effect in the regression analyses. All statistical analyses were performed in Stata v9.2 (StataCorp 2005). For each statistical analysis, significance was assessed with α = 0.05. Because we performed a simulation study, and our power to detect significant differences was dependent on the length of the simulation, we also employed an additional relevance cutoff. We discounted differences in mean Robinson–Foulds tree-to-tree distances whose β-coefficients were < 1%. Any difference smaller than this would not actually result in a different final tree topology and would therefore not be biologically meaningful. This second cutoff was employed only for the strict-clock inference model in which the variance was so low that small differences, β-coefficient  < 1%, were significantly different.

RESULTS

To determine if incorporating a relaxed molecular clock improved the quality of phylogenetic inference, we analyzed sequences simulated under a variety of rate distributions and constructed phylogenies assuming relaxed molecular clocks, a strict molecular clock, and time-free inference.

Accuracy of Inference Methods

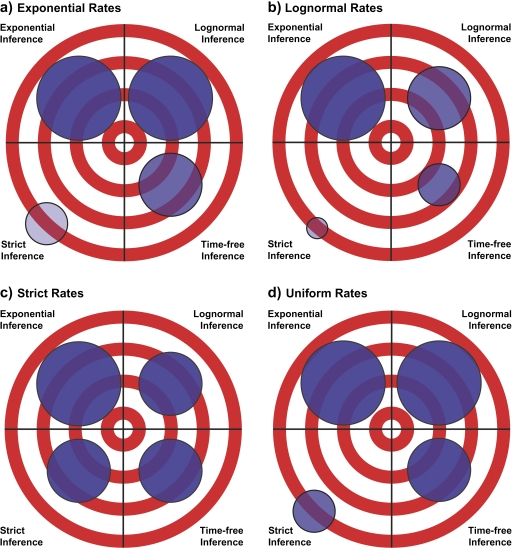
The first metric we used to assess the quality of phylogenetic inference was accuracy (i.e., whether or not the true tree was recovered in the 95% credible set). Analyses using relaxed molecular clock inference models consistently were the most accurate (Table 1), though the differences in accuracy were significant only if the sequences had been simulated under an exponential or lognormal relaxed molecular clock (i.e., darker colored circles on the targets; Fig. 3).

TABLE 1.

Performance of inference models on sequence simulated under various rate distributions

Metric	Inference model	Rate distribution
		Exponential	Lognormal	Strict	Uniform
Accuracya (%)	Exponential	57.0	81.5	85.0	68.5
	Lognormal	55.0	76.5	84.5	66.5
	Strict	19.0	56.5	84.0	41.0
	Time-free	49.0	74.0	83.5	64.5
Precisionb	Exponential	3944	2148	1396	2858
	Lognormal	4035	1881	1097	2718
	Strict	2866	1721	1076	2065
	Time-free	3782	1738	1032	2469
RF distancec (%)	Exponential	21.5	12.8	10.0	15.1
	Lognormal	21.6	12.3	9.2	15.1
	Strict	28.8	14.1	9.1	17.4
	Time-free	22.3	12.6	9.6	15.4
	ML time-freed	15.5	9.0	7.0	11.3
	ML time-free bootstrap	20.3	13.2	10.4	15.4

^aPercentage of the runs in which the true tree was recovered in the 95% credible set.

^bMean number of trees in the 95% credible set.

^cMean Robinson–Foulds (RF) tree-to-tree distance between the true tree and sampled trees expressed as a percentage of the maximum possible distance.

^dML time-free RF tree-to-tree distance is always significantly closer (P < 0.001) to the true tree than the Bayesian inference methods (see text for details).

FIGURE 3.

Summary of Bayesian phylogenetic inference quality. Accuracy, precision, and Robinson–Foulds tree-to-tree distance of exponential, lognormal, strict, and time-free inference models on sequence data evolved under a) exponential, b) lognormal, c) strict, and d) uniform rate distributions. For a given rate distribution (i.e., target), the darker the circle, the more accurate the inference model on sequences evolved under that rate distribution. Smaller circles indicate better precision. The distance from the center of each circle to the middle of its target represents the Robinson–Foulds distance of the sampled trees from the true tree. Within each target, differences in darkness, size, and distance from the center represent significance at α = 0.05.

Analysis using a strict-clock inference model resulted in significantly poorer accuracy if the sequences were evolved under an exponential, lognormal, or uniform relaxed molecular clock distributions of rates (i.e., the circles for strict inference models are lighter in Fig. 3a, b,d); however, when sequences were evolved under a strict clock, there were no significant differences in accuracy among the 4 inference models (Fig. 3c). There was not a pattern of increased accuracy of inference models when analyzing sequence data that fit the assumptions of that inference model. In general, relaxed-clock inference models were the most accurate, followed by the time-free model, whereas the strict-clock inference model was consistently the least accurate.

Precision of Inference Methods

The precision estimates of the inference models (i.e., the number of distinct topologies sampled in the 95% credible set) appear to show the opposite trend of accuracy (Table 1 and Fig. 3). Relaxed-clock inference models were the least precise in every case, with the exponential relaxed clock faring the worst under every rate distribution except exponential. The strict-clock inference model was almost always the most precise (Table 1). When analyzing sequences generated under exponential, lognormal, and uniform rate distributions, the strict-clock inference model sampled significantly fewer trees than the other 3 inference models (i.e., the strict inference model has the smallest circles on the targets in Fig. 3a,b,d). There were no significant differences in precision among the 4 inference models, when sequences were evolved under a strict clock (Fig. 3c). The time-free inference model generally resulted in intermediate precision, sampling significantly fewer trees than the relaxed-clock inference models when the rates were generated under nonstrict distributions. Similar to accuracy, there was not a pattern of greater precision of inference models when analyzing sequence data that fit the assumptions of that inference model.

Robinson–Foulds Tree-to-Tree Distance

Relaxed-clock models are the most accurate, but the least precise, of the inference models tested here. But these results still do not answer the question, which inference model provides the highest quality of phylogenetic inference? We found that a third metric, the Robinson–Foulds tree-to-tree distance (i.e., the number of nodes that separate the sampled trees from the true tree), best encapsulates the relative quality of phylogenetic inference (Table 1). For exponential, lognormal, and uniform rate distributions, strict-clock inference found topologies that were significantly more distant from the true tree than those of the other inference models (i.e., strict-clock circles are the farthest from the center of the target in Fig. 3a,b,d). When sequences were simulated under a strict molecular clock, all 4 inference models sampled trees with indistinguishable Robinson–Foulds distances (i.e., all 4 circles are equidistant from the center of the target in Fig. 3c). Among exponential, lognormal, and time-free inference models, there were no significant differences in the observed Robinson–Foulds tree-to-tree distance measurements (i.e., circles are equidistant from the center of the target; Fig. 3). Relaxed molecular clocks fared no better or worse than the time-free inference model. Although informative, neither accuracy nor precision completely summarized the quality of phylogenetic inference. Robinson–Foulds tree-to-tree distance, however, was the most revealing metric of phylogenetic inference quality because it was informed by both accuracy and precision.

In addition, we tested for interaction between the inference models and 3 fixed effects (i.e., number of taxa, maximum pairwise distance, and Colless's imbalance) using Robinson–Foulds distance as an outcome. As taxon number increased, strict-clock inference performed increasingly worse than lognormal and exponential relaxed-clock inference methods (P < 0.05) and marginally worse than time-free inference (P = 0.08). Strict-clock inference also performed worse than the other 3 inference methods as the maximum pairwise distance among the taxa increased (P < 0.001). There were no significant interactions between Colless's imbalance and the inference model. In general, the more complex the sequence data, the worse strict-clock inference performed.

ML Inference Quality

Our data set provided us the opportunity to explore how the quality of ML inference compares to Bayesian approaches. We measured the Robinson–Foulds tree-to-tree distance from the true tree to the tree inferred under time-free ML phylogenetic inference. This mean distance (for sequences simulated under each of the 4 rate distributions) was always smaller than the mean Robinson–Foulds distance from the true tree to the 9000 post–burn-in Bayesian topologies (P < 0.001) (Table 1). We note, however, that nonparametric bootstrapping is commonly used to assess confidence in the ML topology. Therefore, we also calculated the mean Robinson–Foulds distance between the true tree and the bootstrap replicates (Table 1). For sequences simulated under an exponential rate distribution, the ML bootstrap trees were significantly closer to the true tree than the posterior trees from all 4 Bayesian inference methods (P < 0.05). For sequences simulated under a lognormal rate distribution, there were no significant differences among the ML bootstrap trees and the Bayesian trees according to our β-coefficient criterion (see Methods section). Surprisingly, for sequences evolved under a strict rate distribution, ML bootstrap trees were significantly farther from the true tree than trees inferred under all 4 Bayesian inference methods (P < 0.001). Finally, for sequences evolved under a uniform rate distribution, ML bootstrap trees were better than strict-clock inference (P < 0.001) but similar to the other Bayesian inference methods.

DISCUSSION

When comparing relaxed molecular clock and time-free methods of Bayesian phylogenetic inference, a trade-off exists between accuracy and precision in our simulation study. Both these methods sample trees with indistinguishable Robinson–Foulds tree-to-tree distances from the true tree, but their levels of accuracy and precision are model-dependent (Fig. 3). The Robinson–Foulds tree-to-tree distance measurements do not change among these 3 clock models; as accuracy increases, precision must decrease, and vice versa. Therefore, the quality of the trees sampled when a relaxed molecular clock is assumed is no different than when no assumption is made about a molecular clock. However, if a strict molecular clock is assumed for non–strict-clock sequence data, this trade-off is not discernible. Inference under a strict clock on non–strict-clock sequence data has extremely high precision, but its accuracy is so poor that the Robinson–Foulds tree-to-tree distance measurements are significantly worse than if the clock was relaxed or was not assumed at all.

These results support the existence of a bias–variance trade-off in topological inference when incorporating a relaxed molecular clock. Relaxing the clock, by adding rate parameters, increases the probability of finding the true tree (accuracy/bias), but it comes at the expense of sampling many more trees (precision/variance). Not making an assumption about a molecular clock (i.e., the time-free inference model) decreases variance (better precision) but biases the analyses (less accurate). Time-free inference appears to underfit the data, but relaxed molecular clock inference may tend to overfit (i.e., overparameterize) the data. In contrast, when a strict molecular clock is violated, the analysis is so highly biased that the true answer is rarely recovered when using a strict-clock inference model. Collectively, these patterns indicate that assuming a relaxed molecular clock does not improve the quality of phylogenetic inference over a time-free inference model because of a trade-off between bias and variance. We note that overparameterization does not necessarily mean increasing the total number of parameters in the inference model. Relaxed-clock inference models technically have fewer parameters than time-free models; however, relaxed-clock inference models parameterize rates. Our analysis suggests that including information about rates does not improve topological inference and is therefore an overparameterization. Nonetheless, unreasonable assumptions, such as a strict molecular clock when multiple evolutionary rates exist, can severely decrease the quality of phylogenetic inference and should be avoided unless there is strong evidence that the sequences in question evolved under a single evolutionary rate.

Our findings contradict those reported by Drummond et al. (2006). Whereas they found an increase in both accuracy and precision of relaxed molecular clock phylogenetic inference compared with the time-free model, we found a trade-off between these metrics suggesting no difference in inference quality. This discrepancy might be due to the decision by Drummond et al. (2006) to remove the least precise 10% of runs from their comparisons. This might have led to artifactually improved precision estimates by relaxed-clock methods, which we found to be the least precise.

This study casts doubt on the claim that relaxed molecular clock inference results in improved topological reconstruction. However, one important difference between the study of Drummond et al. (2006) and ours is that they used real sequence data, whereas we looked at simulated sequenced data. There are 2 possible explanations for our differing results. First, they may have failed to detect the bias–variance trade-off in their analysis. An alternative explanation may be that there are important differences between real and simulated sequence data, and relaxed-clock inference models may actually be superior when analyzing real sequence data (e.g., Liu et al. 2008). Future work will be required to distinguish between these 2 possibilities.

There does appear to be a relationship between the underlying distribution of rates and the ability of an inference model to reconstruct high-quality trees as measured by Robinson–Foulds tree-to-tree distance. Specifically, all inference models (Bayesian and ML) performed best on sequences simulated under a strict rate distribution, followed by lognormal and uniform; inference methods always performed the worst on sequences simulated under an exponential rate distribution (Table 1).

The single ML time-free topology was strikingly closer to the true tree than the posterior distribution of Bayesian trees; however, comparisons between the bootstrapped ML trees and the Bayesian posterior distribution of trees appeared to be qualitatively similar. This finding is in concordance with previous studies that have compared ML and Bayesian phylogenetic inference methods on empirical and simulated data (Alfaro et al. 2003; Cummings et al. 2003; Douady et al. 2003; Erixon et al. 2003; Mar et al. 2005). Nevertheless, there certainly appear to be instances where ML analysis is preferable to Bayesian inference (and vice versa). Our findings suggest that a systematic exploration of the conditions (beyond rate distribution) that favor ML or Bayesian topological inference should be undertaken. Our findings also support the notion that the Robinson–Foulds tree-to-tree distance is a highly useful metric for gauging the overall quality of phylogenetic inference.

SUPPLEMENTARY MATERIAL

Supplementary material can be found at http://www.sysbio.oxfordjournals.org/.

FUNDING

Funding was provided by the Department of Ecology and Evolutionary Biology and BIO5 at the University of Arizona, the David and Lucile Packard Foundation, and a National Institutes of Health Institutional Research and Academic Career Development Award Fellowship.