Population pharmacokinetics of tamsulosin hydrochloride in paediatric patients with neuropathic and non-neuropathic bladder

Abstract

AIMS

The main objective of this study was to characterize the population pharmacokinetics of tamsulosin hydrochloride (HCl) in paediatric patients with neuropathic and non-neuropathic bladder. A secondary objective was to compare the pharmacokinetics in paediatric patients and adults.

METHODS

Tamsulosin HCl plasma concentrations in 1082 plasma samples from 189 paediatric patients (age range 2–16 years) were analyzed with NONMEM, applying a one compartment model with first-order absorption. Based on the principles of allometry, body weight was incorporated in the base model, along with fixed allometric exponents. Covariate analysis was performed by means of a stepwise forward inclusion and backward elimination procedure. Simulations based on the final model were used to compare the pharmacokinetics with those in adults.

RESULTS

Beside the priori-implemented body weight, only α₁-acid glycoprotein had an effect on both apparent clearance and apparent volume of distribution. No other investigated covariates, including gender, age, race, patient population and concomitant therapy with anti-cholinergics, significantly affected the pharmacokinetics of tamsulosin HCl (P < 0.001). The results of simulations indicated that the exposure in 12.5 kg paediatric patients was 3.5–4.3 fold higher than that in 70.0 kg adults. After a weight-based dose administration, the exposure in paediatric patients was comparable with that in healthy adults.

CONCLUSIONS

A population pharmacokinetic model of tamsulosin HCl in paediatric patients was established and it described the data well. There was no major difference in the pharmacokinetics of tamsulosin HCl between paediatric patients (age range 2–16 years) and adults when the effect of body weight was taken into consideration.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

Tamsulosin is available on prescription as a modified release capsule in the US (Flomax®), and in most European countries for the treatment of the signs and symptoms of benign prostatic hyperplasia (BPH). The pharmacokinetics of tamsulosin hydrochloride (HCl) have been extensively studied in adults, but no pharmacokinetic data for paediatrics have been published to date.

WHAT THIS STUDY ADDS

A population pharmacokinetic model of tamsulosin HCl was developed in paediatric patients. Covariate analysis revealed that body weight and α₁-acid glycoprotein influenced both the apparent clearance and the apparent volume of distribution. This study confirms that there is no major difference in the pharmacokinetics of tamsulosin HCl between paediatrics (age range 2–16 years) and adults when the effect of body weight is taken into consideration.

Introduction

Tamsulosin hydrochloride is an α₁-adrenoceptor blocking agent that exhibits selectivity for α_1a-receptors [1]. The α_1a-receptor subtype mediates smooth muscle contraction in human prostate, urethra, and bladder neck and this subtype is the target of tamsulosin HCl [2]. Classically, α_1a-receptor blockers have been the mainstay of therapy for lower urinary tract symptoms due to benign prostatic hyperplasia (BPH) in adult men. Tamsulosin decreases bladder outlet resistance at the bladder neck and improves urine flow rates leading to decreased residual urine volumes and improvement of irritative bladder symptoms [3]. Tamsulosin 0.4 and 0.8 mg is available on prescription as a modified release capsule in the US (Flomax®), and in most European countries for the treatment of the signs and symptoms of BPH. In addition to its benefits in BPH, tamsulosin has been evaluated in adults with urinary dysfunction. One study showed that long-term tamsulosin treatment (0.4 or 0.8 mg daily) was effective and well tolerated and led to improved bladder storage and emptying as well as decreased symptoms of autonomic dysreflexia [4]. These results were confirmed in another study, in which tamsulosin reduced functional urethral resistance during voiding and improved flow rate in patients with neuropathic bladder [5]. Therefore the efficacy of tamsulosin in paediatric patients with voiding disorder due to neuropathic bladder is anticipated.

The pharmacokinetics of tamsulosin HCl has been evaluated in adult healthy volunteers and patients with BPH after oral administration at doses ranging from 0.1 mg to 1.0 mg [6]. In brief, absorption of tamsulosin HCl is essentially complete (>90%) following oral administration under fasting conditions [7]. Tamsulosin should be used in a fed condition and taking Flomax® capsules in a fed condition results in an approximately 20% decrease in bioavailability (AUC) and 30% to 40% decrease in peak concentration (C_max) compared with a fasted condition [6]. The maximum concentration is reached in 6 to 7 h in a fed condition and 4 to 5 h in a fasted condition. Tamsulosin HCl exhibits linear kinetics following single and multiple dosing, achieving steady state concentrations by the fifth day of once daily dosing. Tamsulosin exhibits high plasma protein binding, largely to α₁-acid glycoprotein (AAG) [8]. The clearance of tamsulosin was 48 ml min⁻¹, which was considerably lower than the hepatic plasma flow of 800 ml min⁻¹ [7]. It is metabolized mainly by CYP3A4 and CYP2D6 to compounds with low abundance and/or low affinity for α₁-adrenoceptors [9, 10]. Nine to fifteen percent of an oral dose is excreted renally as the parent compound. The pharmacokinetics of tamsulosin HCl in paediatric patients has not been reported so far. Therefore, plasma concentration data from paediatric patients with neuropathic and non-neuropathic bladder were collected from three paediatric trials and used for a population pharmacokinetic analysis. The objective of this study was to develop a population pharmacokinetic model and to identify factors that influence the pharmacokinetics of tamsulosin HCl in paediatric patients. In addition the pharmacokinetics in paediatrics and adults were compared by means of simulation.

Methods

Patients and trial design

A total of 1082 plasma concentrations obtained from 189 patients who participated in three paediatric clinical trials were used in this analysis (Table 1A). All trials were performed in accordance with the Declaration of Helsinki with ethics approval in each institution (Appendix), and with written informed consent of each patient. A precise mg kg⁻¹-based scheme was not possible due to the modified release formulation characteristics of tamsulosin HCl capsules.

Table 1A.

Sources of plasma tamsulosin HCl concentration data collected in paediatric clinical trials

Trial number	Phase	Number of patients	Number of measurements	Sampling points
1	I	45	393	Pre-dose, 1, 3, 4, 5, 6, 8, 10, 24, 26 h
2	II	29	272	First dose (optional): Pre-dose, 2, 4, 6, 8 h after the first dose
				Multiple dose: Pre-dose, 2, 4, 6, 8, 10, 24, 33 h after the last dose
3	IIb/III	115	417	Week 6: first sample taken pre-dose, second sample
				taken at least 2 h after the first sample
				Week 10: first sample taken at least 6 h after
				drug intake, second sample taken at least
				2 h after the first sample
Total		189	1082

Trial 1 was an open-label single dose phase I study which investigated the pharmacokinetics, safety, and tolerability of single oral doses (0.1, 0.2, 0.4 and 0.8 mg) of tamsulosin HCl capsule in paediatric patients with non-neuropathic bladder in a fed condition. Patients were randomized to one of four tamsulosin HCl dose levels based upon their weight [low weight (15–45 kg) or high weight (46–75 kg)] (Table 1B). For each dose group, males and females were planned to be randomized equally. Plasma concentrations from 45 patients were included in the model building.

Table 1B.

Dosing scheme for trial 1

	Tamsulosin HCl dose group
Body weight	Low dose	High dose
Low weight (15–45 kg)	0.1 mg	0.4 mg
High weight (46–75 kg)	0.2 mg	0.8 mg

Trial 2 was an uncontrolled, open-label, titration, long-term safety (up to 12 months) and efficacy study of tamsulosin HCl in paediatric patients with elevated detrusor leak point pressure with a known neurologic defect (neuropathic bladder). A sub-study for pharmacokinetic evaluation was performed in the lead-in phase of this long-term safety trial. Patients were stratified by age and randomized to one of three tamsulosin weight-based dose levels (Table 1C). All patients started at the lowest dose, regardless of randomization. The dose was uptitrated to the next dose after 1 week of treatment and was further increased weekly thereafter up to the randomized dose level. Once the patients had reached their respective randomized dose level, they remained at this level for 2 weeks. Blood sampling was performed on the first day at the low dose level (11 out of 29 patients) and after 2 weeks of treatment at the randomized dose level for 29 patients who contributed to the blood sampling. For the weight-based dose in trials 2 and 3, all patients received their medication once daily via opened capsules with the contents sprinkled over a single teaspoonful (5 ml) of applesauce or yogurt in a fed condition. Biowaiver was granted for this clinical product based on the comparative in vitro dissolution profiles with commercial product.

Table 1C.

Weight-based dosing scheme for trials 2 and 3

	Tamsulosin HCl once daily
	Low dose	Medium dose	High dose
Body weight	0.001–0.002 mg kg−1	0.002–0.004 mg kg−1	0.004–0.008 mg kg−1
12.5a–25 kg	0.025 mg	0.05 mg	0.1 mg
25.1–50 kg	0.05 mg	0.1 mg	0.2 mg
50.1–100 kg	0.1 mg	0.2 mg	0.4 mg

^a12.1 kg for trial 2.

Trial 3 was a 14-week, double-blind, randomized, dose-ranging, placebo-controlled trial in paediatric patients with neuropathic bladder. All patients were randomly assigned to one of four treatment groups, placebo, or low-, medium- or high-dose tamsulosin HCl (Table 1C). All patients started at the lowest dose, regardless of randomization. The dose was uptitrated to the next dose after 1 week of treatment and was further increased weekly thereafter up to the randomized dose level. Once the patients had reached their respective randomized dose level, they remained at this level. Blood sampling was performed after at least 4 weeks of treatment at the randomized dose level. Plasma concentrations from 115 patients in this trial were included in the analysis.

Due to the availability of the data, a population pharmacokinetic base model was developed first with the frequent blood sampling data from trials 1 and 2 (step 1). Then covariate analysis was performed together with the sparse data from trial 3 (step 2). Demographic and clinical characteristics of the patients in step 1 and step 2 are summarized in Table 2.

Table 2.

Main characteristics of patients in analysis 1 and analysis 2

	Step 1	Step 2
Covariate	Trials 1 and 2	Trials 1,2 and 3
Age (years)	8.5 (2–16)	8 (2–16)
Body weight (kg)	31.5 (12.1–92.2)	25.0 (12.1–92.2)
Height (cm)	135 (83–173)	125 (63–175)
Body mass index (kg m−2)a	18.74 (10.65–36.02)	17.41 (10.65–36.32)
Body surface area (m2)b	1.04 (0.51–2.03)	0.94 (0.43–2.03)
Serum creatinine (mg dl−1)	1.00 (0.60–7.00)	0.96 (0.60–7.00)
Creatinine clearance (ml min−1)c	55.03 (5.76–197.5)	46.85 (5.76–197.5)
Gamma glutamyl transferase (U l−1)	28.36 (12.24–81.25)	29.25 (10.71–130.0)
Haemoglobin (g dl−1)	14.42 (9.81–17.23)	14.29 (7.18–23.76)
α1-acid glycoprotein (µm)	18.25 (9.76–43.33)	19.95 (9.76–74.53)
Anti-cholinergic treatment	11.7d	16.5d
Sex	74	189
Male	38	105
Female	36	84
Race	74	189
White	52	87
Asian	20	83
Black or African American	2	6
American Indian or Alaska native	0	13
Native Hawaian or other Pacific islander	0	0
Population	74	189
Paediatric non-neurogenic patients	45	45
Paediatric neurogenic patients	29	144

Median (range) for continuous covariate and N for categorical covariate.

^aBody mass index was calculated as weight in kilograms/(height in metres)².

^bBody surface area was calculated by the method of DuBois & DuBois [31].

^cCreatinine clearance was calculated according to the Cockroft–Gault equation [32].

^dPercent of observation records.

Blood sampling and bioanalytical method

Blood samples (1 ml) were collected into standard blood sampling tubes containing lithium heparin as an anticoagulant. Immediately after collection, blood samples were kept on ice until centrifugation. After centrifugation (10 min, 1500–2000 g), plasma samples were collected and stored at −20°C or below until analysis. Quantitative measurement of tamsulosin HCl was performed with a validated high performance liquid chromatography with tandem mass spectrometry (HPLC-MS/MS) method [11]. The method consisted of liquid/liquid extraction under alkaline conditions, reversed-phase chromatography and atmosphere pressure chemical ionization (APCI) detection. Tamsulosin HCl was calibrated and quantified using (±)-(R)-5-[3-[[2-(o-ethoxy-phenoxy)ethyl]amino]butyl]-2-methoxy-benzenesulfonamide hydrochloride (AB-289) as internal standard. Briefly, the internal standard was added to 0.2 ml of plasma and then extracted under alkaline conditions. The extract was centrifuged and the supernatant was evaporated. The residue was dissolved in acetonitrile : ammonium acetate 20 mm (75/25; v/v) and an aliquot of dissolved residues were injected into the HPLC-MS/MS system. The analytical procedure in human plasma was linear over the concentration range from 0.100 to 50.0 ng ml⁻¹ with a plasma volume of 0.2 ml. The in-study imprecision for quality control samples was less than 9.2%. The average inaccuracy was within ±6.7%.

Population pharmacokinetic modelling

Population non-linear mixed effects modelling was performed with NONMEM, version V level 1.1, NM-TRAN version III level 1.1, and PREDPP version IV level 1.1 (ICON Development Solutions, Ellicott City, MD, USA) [12]. One compartment and two compartment linear models with first-order absorption were initially evaluated for fitting the tamsulosin HCl plasma concentration data. In addition to the first order absorption model, zero-order and sequential zero and first-order absorption models were fitted to the data based on inspection of diagnostic plots and parameter estimates.

First-order conditional estimation (FOCE) with η-ε interaction [13] was used throughout the model-building procedure. All inter-individual variability (IIV) was modelled with an exponential random effect model, i.e. individual parameters were assumed to have log-normal distribution around the typical parameter estimates (θ) with variance (ω²). The initial model for the residual variability incorporated both an additive and a proportional component: Y = Ŷ x (1 + ε₁) + ε₂, where Y represents the observation (i.e. tamsulosin HCl concentration), Ŷ represents the individual predicted concentration and ε₁ and ε₂ are symmetrically distributed, zero-mean random variables with variance (σ²).

In this analysis, the population pharmacokinetic model was developed in two steps. The population pharmacokinetic base model were developed first (step 1) based on the frequent blood sampling data from trials 1 and 2, and followed by a comprehensive covariate model development including the sparse data from trial 3 (step 2).

Step 1: Basic population model development (data from trials 1 and 2)

Base model development was performed with the frequent blood sampling data from trials 1 and 2. Initially, a structural model without any covariates was formed and the base model was constructed as follows. Based on the allometric principles, body weight was introduced to the structural model as a base covariate of apparent clearance (CL/F) and apparent volume of distribution (V/F) as advocated by others [14, 15]. It has been shown that flow dependent parameters follow an allometric exponent of 0.75 and volume-like parameters follow an allometric exponent of 1 and surprisingly, this relationship apparently holds true for nearly all organisms [16, 17]. Application of the allometric clearance model for 91 different xenobiotics showed that the mean allometric coefficient was not different from 0.75 except for drugs primarily excreted by the kidneys [18]. Therefore, fixed allometric exponents of 0.75 and 1 were initially used for CL/F and V/F of tamsulosin HCl, respectively. Later, allometric exponents were estimated for the final model at step 2 and if the 95% confidence interval of the estimates included the fixed parameters, the fixed parameters were used.

Step 2: Covariate model development (data from trials 1, 2 and 3)

In step 2, a comprehensive covariate analysis was performed with the dataset from all three clinical trials. Since it is known that tamsulosin binds to the AAG and that increase of AAG concentration decrease the unbound fraction of tamsulosin HCl in plasma resulting in a decrease of CL/F and V/F in adult data [19, 20], AAG on CL/F and V/F was tested and implemented a priori before the forward inclusion of other covariates. The relationship between covariates and individual parameter estimates was explored graphically. The covariates (age, body weight, height, body mass index, body surface area, serum creatinine, creatinine clearance, alanine transaminase, asparate transaminase, AAG, gamma glutamyl transferase, glucose, lactate dehydrogenase, creatine kinase, haemoglobin, bilirubin, total protein, triglycerides, cholesterol, gender, ethnic origin, concomitant therapy with anti-cholinergics and patient population) were tested using generalized additive modelling (GAM) analysis for η_CL/F, η_V/F and η_Ka as implemented in Xpose 4 [21]. Subsequently, covariate analysis was performed using the stepwise forward inclusion and backward elimination procedure. As a first step in the forward inclusion, all covariates selected by GAM and additional covariates which were of specific interest even if not suggested by GAM (patient population, race and concomitant therapy with anti-cholinergics on CL/F and V/F and dose on CL/F, V/F and Ka) were evaluated in NONMEM one by one (i.e. univariately). The covariates which resulted in a decrease of at least 3.84 in objective function (OBJF) value were ranked beginning with the largest drop in OBJF. Covariates were added sequentially to the base model as suggested by the ranking. If the addition of a further covariate resulted in a drop of the OBJF value by at least 3.84, it was retained, otherwise it was removed. This was repeated until the full model was obtained. Backward elimination was then performed. Each covariate was removed separately from the full model. Covariates that caused an increase in the OBJF smaller than 10.8 (P < 0.001, χ², 1 d.f.) were again ranked starting with the covariate that generated the slightest increase in the OBJF value. Following this ranking the covariate with the smallest increase was removed separately and the remaining covariates were ranked again as described above. If there were still some covariates that increased by less than 10.8, the one with the smallest increase was removed and the above cycle was repeated. If the removal of covariates resulted in an increase in the OBJF value of at least 10.8, they were retained. To finalise the model building process in step 2, the necessity to include a complete or part of variance covariance matrix was tested. Furthermore the residual error model was tested again (initial covariate model). Allometric exponents of body weight for CL/F and V/F were estimated for the final model and if the 95% confidence interval of the estimates included the fixed parameters, the fixed parameters were used.

Model evaluation

Basic goodness-of-fit plots including observed concentrations vs. population and individual predictions as well as conditional weighted residuals vs. population predicted concentrations and time were used for diagnostic purpose with Xpose 4. η- and ε- shrinkage was calculated for the final model [22].

A visual predictive check (VPC) was used to evaluate the adequacy of the developed model for describing the data [23, 24]. One thousand new datasets with the same patients, dosing history, number of observations, sampling scheme, and covariate values as trials 1, 2 and 3 were simulated with the estimated final model parameters. The concentration–time profiles of median and the 90% prediction interval of dose-normalized simulated concentrations in the total datasets and observed data at steady state were compared by box and whisker plots for the appropriate time intervals. In addition, VPC was also performed with stratification by body weight (low weight: 12.1–25.0 kg, medium weight: 25.1–50.0 kg and high weight: 50.1–100 kg).

Further, individual-derived model-based C_max,ss and AUC_ss(0,τ) from empirical Bayes estimates of the final model were calculated and compared with the available results from non-compartmental analysis in trials 1 and 2.

Simulation

The first objective of the simulation was to visualize the effects of important covariates on the exposure in typical patients. The second objective was to inspect whether the weight-based dosing scheme adopted in trial 3 can adequately achieve similar exposure in each weight category compared with the exposure in adults. For visual inspection of the covariate effect, the concentration–time profiles of tamsulosin HCl were simulated 1000 times using the final model. In the evaluation of the effect of body weight, simulation was performed for four different body weights (12.5, 25.0, 50.0 and 70.0 kg). Dose and AAG were fixed to 0.1 mg and the median value of AAG (20.0 µm), respectively. In the evaluation of the effect of AAG, simulation was performed for four different AAG concentrations (10, 20, 30 and 40 µm). Dose and body weight were fixed to 0.1 mg and the median value of body weight (25.0 kg), respectively. In each simulated dataset, individual C_max and AUC values were calculated from the estimated parameters and the median of those parameters was calculated. In the evaluation of the weight-based dosing scheme, simulation was performed for eight different body weights (12.1, 18.6, 25.0, 25.1, 37.5, 50.0, 50.1 and 70.0 kg). The body weights of 12.1, 18.6 and 25.0 kg were used as representatives for low weight patients, 25.1, 37.5 and 50.0 kg for medium weight patients, and 50.1 and 70.0 kg for high weight patients. AAG was fixed at the median value (20.0 µm). Dose was the high weight-based dose in Table 1C (0.1–0.4 mg). Again, individual C_max and AUC values were calculated from the estimated parameters and are shown in box and whisker plots using SAS™ System, Version 8.2 (SAS institute, Cary, USA). These simulated pharmacokinetic parameters were compared with the pharmacokinetic parameters obtained by non-compartmental analysis (NCA) in the two adult studies after multiple oral administrations of 0.4 mg tamsulosin HCl in a fed condition.

Non-compartmental analysis

Individual pharmacokinetic parameters (C_max and AUC) in non-compartmental analysis were calculated with WinNonlin professional software (Pharsight Corporation, Mountain View, CA, USA).

Results

The main demographics and baseline characteristics of all evaluable patients are provided in Table 2.

All paediatric patients were between 2 and 16 years old. In this study, the population pharmacokinetic model was developed in three steps as described in the methods section.

Model building

Step 1: Basic population model development (data from trials 1 and 2)

One compartment and two compartment disposition models combined with first-order absorption manner were tested. A one compartment model was selected because the AIC value of the two compartment model (1352.744) was not superior to the one compartment model (1052.928) Then, the one compartment model was tested with other absorption models (zero-order absorption and sequential zero- and first-order absorption). The sequential zero- and first-order absorption model was not stable and the zero-order absorption model did not improve the OBJF (OBJF = 1164.917) compared with the first-order absorption model (OBFJ = 1032.928). The first-order absorption model with a lag-time and IIV on CL/F, V/F and absorption rate constant (Ka) described the data adequately. Therefore the first-order absorption model was adopted in this study. As described in the methods section, body weight was included a priori as a fixed covariate with an allometric exponent of 0.75 for CL/F and 1 for apparent V/F in the base model. Inclusion of body weight as a covariate for CL/F and V/F resulted in a substantial decrease in the value of OBJF (−37.5). Furthermore, significant decreases were observed in the estimates of IIV on CL/F and V/F. Implementation of WT on CL/F and V/F reduced the IIV on CL/F and V/F by 5.8% and 11.0%, respectively. The combined error model was best for modelling of residual variability compared with additional error and proportional error models. The omega matrix between IIV on CL/F and V/F was tested and incorporated with a reduction of OBJF of 33.6.

Step 2: Covariate model development (data from trials 1, 2 and 3)

In step 2, comprehensive covariate analysis was performed against the initial covariate model with the combined dataset of all three clinical trials. As the effect of AAG on CL/F and V/F was physiologically reasonable [8, 19, 20], the effect of AAG on CL/F and V/F was added to the final model in step 2 before further evaluation of other covariates. As a result, AAG on CL/F was incorporated into the model with a reduction in the OBJF of 35.4 (P < 0.001). Then AAG on V/F was incorporated into the model with a reduction in the OBJF of 17.1. The implementation of AAG as a covariate of CL/F and V/F reduced the IIV of CL/F and V/F by 8.6% and 6.1%, respectively. All covariates selected by GAM and additional covariates which were of specific interest (patient population, race and concomitant therapy with anti-cholinergics on CL/F and V/F and dose on CL/F, V/F and Ka) were tested univariately and added one-by-one during forward inclusion as described in the methods section. In the stepwise forward inclusion procedure, firstly, inclusion of GGT as a covariate for CL/F to the base model resulted in the maximum decrease (−6.617) in the OBJF. Secondly, inclusion of BMI as a covariate for V/F resulted in the maximum decrease (−5.583) in the OBJF. No further covariates were found to be significant in the forward inclusion. In the full model, the effect of AAG and GGT on CL/F and the effects of AAG and BMI on V/F remained significant (P < 0.05). During backward elimination the impact of GGT on CL/F and BMI on V/F were no longer significant and they were removed from the full model. Finally, the effect of AAG on CL/F and V/F in addition to the effect of body weight on CL/F and V/F remained in the final model (Table 3). Allometric exponents of body weight were estimated for the final covariate model. The estimates (95% confidence interval) were 0.768 (0.598, 0.938) for CL/F and 0.807 (0.603, 1.01) for V/F. As the 95% confidence interval included the fixed parameters, they were used in the final model. The fixed effect of population PK parameters were estimated with reasonable precision (SE <30%). The inter-subject variabilities for CL/F, V/F and Ka were 54.4, 61.2 and 117%. The estimated residual proportional error was 28.4% (%CV) and the additive error was 0.178 ng ml⁻¹ (± SD).

Table 3.

Parameter estimates from the population pharmacokinetic final model for trials 1, 2 and 3

Structural model:
CL/F = θCL × (WT/70)0.75 × (AAG/20.0)θAAG_CL × eηCL
V/F = θV × (WT/70) × (AAG/20.0)θAAG_V × eηV
Ka = θKa × eηKa, ALAG1 = θALAG1
Residual random effect model:
Y = Ŷ + Ŷ × ε1 + ε2
Parameter	Estimate	%RSE	Description
CL/F (l h−1)	2.28	4.21	Apparent clearance
θAAG_CL	−0.844	−15.1	Effect of AAG on the apparent clearance
V/F (l)	37.5	6.35	Apparent volume of distribution
θAAG_V	−0.663	−24.3	Effect of AAG on the apparent volume of distribution
Ka (h−1)	0.368	12.0	First order absorption rate constant
ALAG1 (h)	0.957	1.14	Absorption lag time
IIV in CL/F (CV%)	54.4	11.4a	Inter-individual variability in the apparent clearance
IIV in V/F (CV%)	61.2	17.7a	Inter-individual variability in the apparent volume of distribution
IIV in Ka (CV%)	117	19.7a	Inter-individual variability in the first order absorption rate constant
Cov_V/CL	0.238	16.7a	Covariance between inter-individual variability in the apparent clearance and inter-individual variability in the apparent volume of distribution. The estimate translates to a coefficient of correlation of 0.715
Proportional residual variability (CV%)	28.4	6.13b
Additive residual variability (SD ng ml−1)	0.178	27.0b

^aSE is given on the variance scale.

^bSE was derived by coding the residual error using THETAs.

Model evaluation

Figure 1 shows the goodness-of-fit plots for tamsulosin HCl plasma concentrations for the final model and various residual plots. No bias or tendency could be observed between the observed and the population or the individual predicted plasma tamsulosin HCl concentrations. Also no systematic relationship could be seen in the conditional weighted residual plots, confirming that the model provided an adequate description of the data. Shrinkage values for η_CL/F, η_V/F, η_Ka, and ε were 5.15%, 18.5%, 21.0% and 17.1%, respectively, indicating that enough information was available to estimate the individual parameters reliably and that individual predictions could be used for model evaluation [25].

Figure 1.

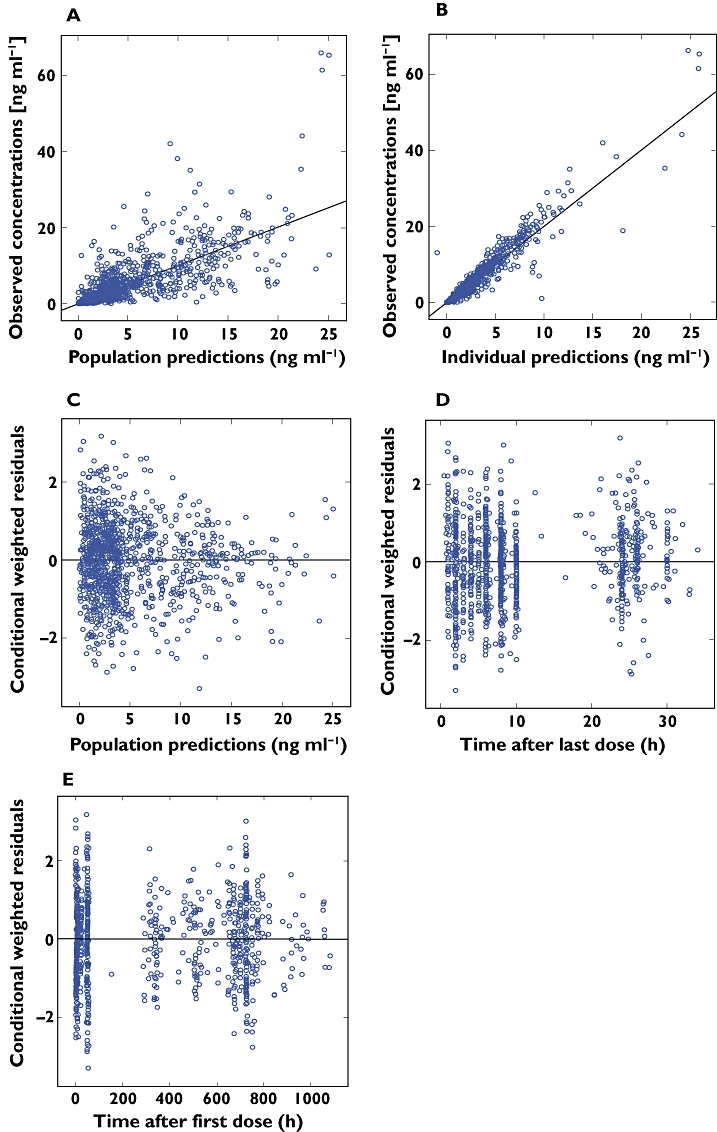
Goodness-of-fit plots for the final population model. (A) observed vs. population predicted concentrations; (B) observed vs. individual predicted concentrations. The solid line represents the line of identity. (C) conditional weighted residuals vs. population predicted concentration; (D) conditional weighted residuals vs. time after last dose; (E) conditional weighted residuals vs. time after first dose

Model qualification using VPC confirmed acceptable agreement between the observed data and model-simulated data at steady state (Figure 2A). In additon, VPC was performed for each weight category of low (12.1–25.0 kg), medium (25.1–50.0 kg) and high weight (50.1–100.0 kg). Although under prediction of the median value especially for the time interval of 4–8 and 8–12 h was observed in the high weight group (Figure 2D), acceptable agreement between the observed data and model-simulated data was observed for the low and medium weight patients (Figure 2B,C). Considering the small number of high weight patients (n = 16), more patients will be required to evaluate the predictability of this model for high weight patients.

Figure 2.

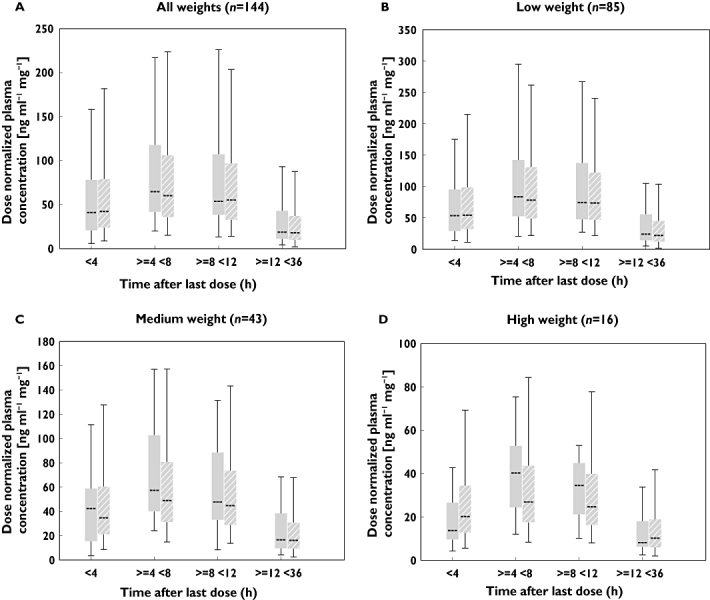
Model qualification using visual predictive check. Plots contain the box and whisker plots of time intervals of observed concentrations and predicted concentrations from the final model at steady-state. Evaluation was performed for (A) all patients, (B) low weight patients (12.1–25.0 kg), (C) medium weight patients (25.1–50.0 kg) and (D) high weight patients (50.1–100.0 kg). Box = 25 and 75th percentile, whisker = 95th and 5th percentile. Observed (); Final model ()

C_max and AUC were calculated from the empirical Bayes estimates based on the final model and compared with the results from the NCA performed in trials 1 and 2 (Figure 3). There was a slight under-prediction of C_max, but in general, the model predicted the actual data well.

Figure 3.

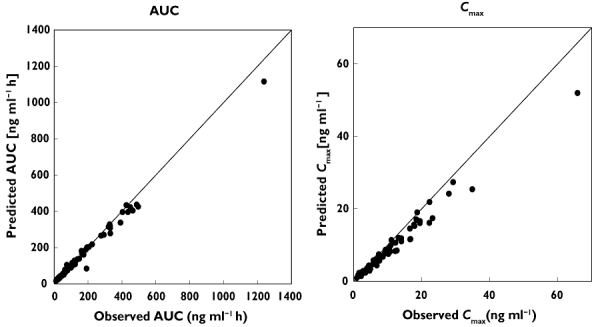
Model qualification by comparison of AUC (left panel) and C_max (right panel) calculated based on the NCA and empirical Bayes estimate of the final model. Data from trials 1 and 2 were utilized

Simulation

Significant covariate effects were quantitatively evaluated by simulating the exposure in typical patients with various body weights and AAG values 1000 times based on the final model estimates, as described in the methods section. Simulation was performed up to 70 kg because the number of patients who weighed more than 70 kg was too small (only five patients). The AUC_ss(0,τ) and C_max,ss values both increased with the decrease of body weight and the median AUC_ss(0,τ) and C_max,ss values in 12.5 kg patients were 3.5- and 4.3-fold higher, respectively, than those in 70.0 kg patients (Figure 4). For AAG, the AUC_ss(0,τ) and C_max,_ss values both increased with increase in AAG concentration and the median AUC_ss(0,τ) and C_max,ss values in patients with AAG concentrations of 40 µm were 3.2- and 3.0-fold, respectively, higher than those in patients with an AAG concentration of 10 µm.

Figure 4.

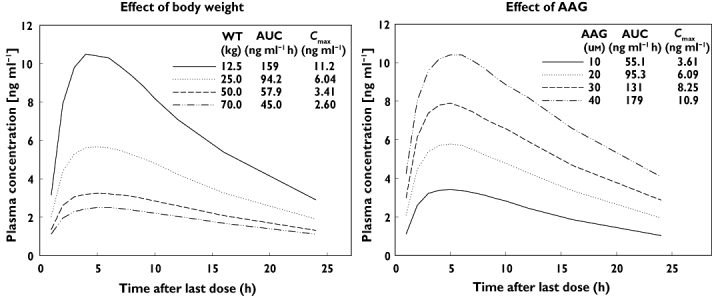
Simulation to visualize the effect of covariates in the final model. Simulation was performed 1000 times. The dose was fixed at 0.1 mg. The left panel shows the median plasma concentrations and pharmacokinetic parameters for patients with different body weights. AAG was fixed at the median value of 20.0 µm. The right panel shows those for the patients with different AAG concentrations. Body weight was fixed at the median value of 25.0 kg

To inspect the appropriateness of the weight-based dosing scheme adopted in trial 3, the exposure after administration of the high weight-based dose (0.004–0.008 mg kg⁻¹; 0.4 mg for patients with more than 50 kg, 0.2 mg for patients with 25.1–50.0 kg and 0.1 mg for patients with 12.1–25.0 kg) was simulated for the patients with median AAG and various body weights. The results are shown in Figure 5.

Figure 5.

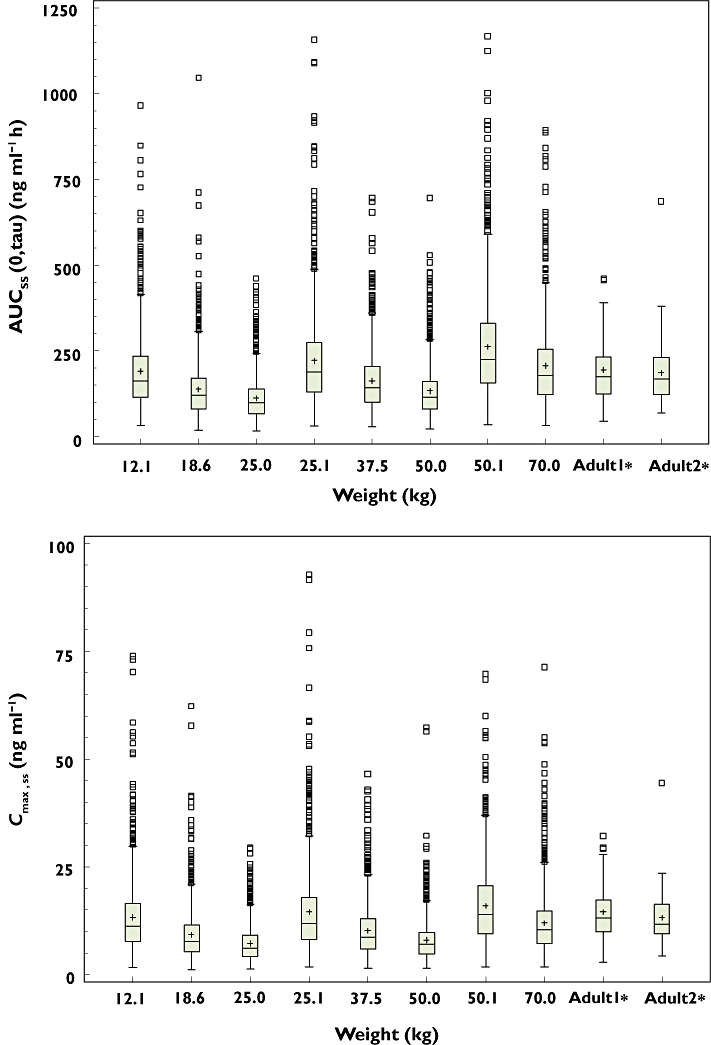
Comparison of AUC_τ,ss (upper panel) and C_max,ss (lower panel) in paediatric patients after administration of a high weight-based dose as described in Table 1C with those in adults after multiple administrations of 0.4 mg tamsulosin HCl. Simulation was performed 1000 times for paediatric patients with median AAG (20.0 µm) and various body weights after administration of the high weight-based dose adopted in trial 3. Box = 25 and 75th percentile, lower whisker = minimum observation, upper whisker = maximum observation below 1.5 times the interquartile range above the 75th percentile, open squares = value outside upper whisker. Simulated results in paediatric patients were compared with NCA results from two adult studies ‘adult 1’ and ‘adult 2’. Median body weights for ‘adult 1’ and ‘adult 2’ were 73.0 and 74.0 kg, respectively

Although the effect of body weight was pronounced (Figure 4), the C_max and AUC overlapped among paediatric patients with different weights after application of this weight-based dose. Considering the different weights for which patients received the same dose with this applied dosing scheme (e.g. 12.5 kg and 25.0 kg patient received the same dose), the exposure to tamsulosin HCl was well controlled among the different weight categories.

When the simulated results were compared with the NCA results of two studies in healthy volunteers (median body weights were 73 and 74 kg), the simulated exposure (C_max and AUC) in paediatric patients was comparable with that in adult healthy volunteers (Figure 5). The median AUC_ss(0,τ) in paediatric patients with different weights was in the range of 56.5–133% of that in adults and the median C_max,ss was 46.3–119% of that in adults.

Discussion

A population pharmacokinetic model of tamsulosin HCl in paediatric patients with non-neuropathic and neuropathic bladder aged 2–16 years was built based on a one compartment model with first-order absorption, lag-time, and first-order elimination. Although there are some reports on the pharmacokinetics of tamsulosin HCl in adults, no information about its pharmacokinetics in paediatrics has been reported so far. Therefore this population pharmacokinetic model is expected to be useful to characterize the pharmacokinetics of tamsulosin HCl in paediatric patients. In this study, the population pharmacokinetic model was developed in two steps. A population pharmacokinetic base model (step 1) was developed based on the frequent blood sampling data from trials 1 and 2 followed by comprehensive covariate model development including the sparse data from trial 3 (step 2).

During base model development, the effect of body weight as a covariate for CL/F and V/F was included a priori because i) previous NCA analysis suggest a pronounced effect of body weight on tamsulosin pharmacokinetics and ii) the trend of over-prediction in the base model without any covariate (data not shown) disappeared after inclusion of body weight as a covariate on CL/F and V/F. In addition, allometric scaling for CL/F and V/F (exponent value of 0.75 and 1, respectively) was used because there is much evidence that supports the fixed allometric exponent model theoretically [16, 17] and empirically [14, 18]. The results of model validation by VPC indicated that final PPK model slightly under-predicted the concentrations (up to 33%) at the time intervals of 4–8 and 8–12 h in patients with a body weight of more than 50 kg (high weight patients) (Figure 2D). Possible reasons for this are that (i) the number of patients in the high weight group was too small (n = 16 for steady state data) to allow evaluation of this sub-population with sufficient confidence, and (ii) fixed theoretical allometric power of WT on V/F might over-predict V/F of the high weight patients. Median BMI values for high weight patients (24.22 kg m⁻²) were much higher than those for the low and medium weight patients (16.01 and 18.40 kg m⁻², respectively). The volume of distribution of tamsulosin HCl after intravenous administration in adults was 16 l [7], suggesting no extensive distribution to the tissue including fat. Therefore the effect of obesity on V/F needs to be further evaluated and maybe another covariate such as lean body mass and fat free mass has to be collected and investigated to best describe the dependence of V/F on body weight. This potential underprediction in the high weight patients might not be clinically relevant since the safety of tamsulosin HCl was confirmed up to 0.8 mg in adults, which is twice as high a dose as the dose used in the adult studies shown in Figure 5. The overall predictive ability of this model was well confirmed for all patients in the paediatric population (Figure 2A). The goodness-of-fit plots and the comparison of the pharmacokinetic parameters predicted by the population pharmacokinetic model with those calculated by NCA showed that overall, the pharmacokinetic model well described the plasma concentrations of tamsulosin HCl (Figures 1, 4).

In the final model, the effect of AAG was incorporated on CL/F and V/F in a power function in addition to the effect of body weight on CL/F and V/F. Tamsulosin is well known to bind to AAG in vitro and high positive correlation was found between AAG and exposure (AUC) to total (unbound + bound) tamsulosin in renal impairment studies [8, 19, 20]. In this population pharmacokinetic model, the results of simulation supported a positive correlation between AAG and exposure (C_max and AUC) (Figure 4). These results are therefore in line with previous observations and the physiological situation, indicating that the effect of AAG is described appropriately by this model.

This 3/4 power law for metabolic rate (CL) adopted in our model was derived from a general model that described how essential materials are transported through space-filled fractal networks of branching tubes. The most obvious application of assuming the allometric theoretical model is in separating effects of growth (weight) and maturation (age) on the pharmacokinetic parameters [14, 26]. In our study, no age effect was identified with the allometric theoretical model. Therefore, it can be concluded that maturation in addition to body size did not impact on the pharmacokinetics of tamsulosin HCl in patients over the age of 2 years. Tamsulosin is metabolized mainly by CYP3A4 and CYP2D6. CYP3A4 activity increases to adult levels by 1 year [27] and no significant difference was observed between the half-life of CYP3A4 substrates in children (2–12 years old) and adults [28]. For CYP2D6, it was suggested that development is complete by 1 year of age although only limited data are available for CYP2D6 developmental expression after 1 month of age [27]. These results support our conclusion that there are no apparent maturation effects on the pharmacokinetics of tamsulosin HCl. However, it should be noted that this model cannot be applied to patients under the age of 2 years because no patients under the age of 2 years were included in the trials. No other tested covariates including gender, patient population (neuropathic or non-neuropathic), race (Caucasian and Asian) and co-medication with anti-cholinergics had a significant effect (P < 0.001) on the pharmacokinetics of tamsulosin HCl.

The effect of body weight and AAG concentrations on exposure to tamsulosin HCl are simulated in Figure 4. Generally, changes in plasma protein binding (e.g. associated with AAG concentrations) have little clinical relevance because it does not have impact on the unbound AUC [29]. In fact, it was reported in a renal impairment study in adults that an increase in AAG concentration reduced the unbound fraction resulting in similar exposure to unbound tamsulosin HCl [8, 19, 20]. Although the exposure to total tamsulosin HCl increases with increasing AAG concentration (Figure 4), AAG has only a minor impact on the unbound concentration of tamsulosin HCl, which is responsible for the efficacy of tamsulosin HCl. In addition, the AAG concentration matures to the adult concentration before the age of 1 year [30]. Therefore, only body weight would be a clinically relevant factor in paediatric patients to achieve comparable exposure to tamsulosin HCl with that seen in adults. The exposure in paediatric patients after application of the high weight-based dosing scheme (Table 1C) is simulated in Figure 5. Although the effect of body weight was pronounced (Figure 4), the exposure in paediatric patients with various body weights was widely overlapping. When compared with the NCA results in two studies in adult healthy volunteers (median body weight was 73 and 74 kg), the simulated exposures (C_max and AUC) in paediatric patients were comparable with those in the adult volunteers (Figure 5). In addition, simulated median plasma concentrations for paediatric patients with a body weight of 70 kg reached a peak at around 6 h (Figure 4), which is in line with the results in adult healthy volunteers (6 or 7 h). The typical half-life for the paediatric patients with a body weight of 73 kg calculated based on the final model was 12 h, which is not far from the median half-life in healthy adults (13 or 16 h). These results suggest that there are no major pharmacokinetic differences for tamsulosin HCl between paediatrics and adults when the effect of body weight is taken into consideration.

In conclusion, a populaton pharmacokinetic model for tamsulosin HCl in paediatric patients was developed in this study and it well describes the observed plasma concentrations of tamsulosin HCl. Body weight and AAG were identified as significant covariates, but no significant effect of age, race (Caucasian or Asian), patient population (neuropathic or non-neuropathic), gender or co-treatment with anti-cholinergics was found in paediatric patients older than 2 years. Only body weight would be clinically relevant in paediatric patients to achieve comparable exposure to that in adults, as the AAG concentration has only a minor impact on the unbound concentration, which is responsible for the pharmacodynamic effect in adults. The dosing scheme in Table 1C for paediatric patients would be appropriate to achieve a comparable exposure to adults. This study has confirmed that there is no major difference in the pharmacokinetics of tamsulosin HCl between paediatrics (age range 2–16 years) and adults when the effect of body weight is taken into consideration.

Appendix

The following investigators participated in these studies.

Trial 1

Canada: A. Khoury (Hospital for Sick Children), USA: L. Palmer (Pediatric Urology Associates, P.C.), M. Cain (Riley Hospital for Children), J. Pope (Vanderbilt Childrens Hospital), P. Austin (St Louis Children's Hospital), Y. Homsy (Children's Urology Group), J. Campbell (University of Oklahoma Health Sciences Center), P. McKenna (SIU School of Medicine).

Trial 2

Canada: R. Jednak (Montreal Children's Hospital), Germany: H. Knispel (Institut für KFE Berlin), R. Stein (Johannes-Gutenberg-Universität), Philippines: M. Lapitan (Philippine General Hospital), D. Bolong (Philippine Children's Medical Center), USA: M. Cain (Riley Hospital for Children), P. Austin (St. Louis Children's Hospital), J. Van Savage (Regional Urology), M. Erhard (Nemours Children's Clinic), C. deVries (Primary Children's Hospital), A. Herndon (Children's Hospital of Alabama), Y. Homsy (Children's Urology Group).

Trial 3

Brazil: C. Bezzera (Faculdade de Medicina do ABC), H. Bruschini (Hospital Das Clínicas Da FMUSP), Germany: H. Knispel (Gesellschaften der Alexianderbrueder), R. Stein (Urologische Klinik und Poliklinik der Johannes Gutenberg Universitaet Mainz), India: M. Desai (Muljibhai Patel Urological Hospital/Kidney Hospital), A. Goel (King George Medical College/Chhatrapati Shahuji Maharaj Medical University), P. Hegde (Kasturba Hospital), R. Kapoor (Sanjay Gandhi Postgraduate Institute of Medical Sciences (SGPGI)), K. Mammen (Christian Medical College & Hospital), G. Mathew (Amrita Institute of Medical Sciences and Research Centre), N.K. Mohanty (V.M. Medical College and Safdurjang Hospital), R.B. Nerli (KLES Prabhakar Kore Hospital), M. Reddy (Hyderabad Institute of Urology, C/o. Hyderabad Nursing Home Pvt. Ltd), S. Shah (Kidneyline healthcare Pvt. Ltd), S. Swain (B Y L Nair Hospital & TN Medical College), S.S. Vasan (Ankur, Medical Centre of Excellence), S. Yande (Grant Medical Foundation), Italy: M.D. Gennaro (Ospedale Bambino Gesu'), G.D. Popolo (A.O. Universitaria Careggi), G. Masnata (A.O. G. Brotzu), Korea: H. Choi (Seoul National University Hospital), S. W.Han (Yonsei Severance Hospital), K.S. Kim (Asan Medical Center), T. Lee (Inha University Hospital), S-D. Lee (Pusan National University Hospital), Mexico: F.C. Lopez (Hospita Para El Niño Poblano), J.Q. Guerrero (Hospital Regional de alta Especialidad del Bajio), Philippine: D. Bolong (Philippine Children's Medical Center), D. Bonzon (Manila Doctors Hospital), Russia: A. Galustyan (St Petersburg Pediatric Medical Academy), S.N. Zorkin (State Institute. Scientific Centre of Children Health), South Africa: R. Barnes (Red Cross Children's Hospital), M. Fockema (Mayo 9), I.J.V. Heerden (Pretoria Urology Hospital), Spain: C.M. Lago (Hospital Materno Infantil – H.Carlos Haya), Ukraine: A. Irinchyn (Bukovinian State Medical University), USA: A. Chang (Children's Hospital Los Angeles), I. Franco (Pediatric Urology Association), Y. Homsy (Comprehensive Research Institute), D. McMahon (Pediatric & Adolescent Urology).

Competing interests

This work was sponsored by Boehringer Ingelheim Pharmaceuticals, Inc. YT, ST, NY, TA, NS, KL, AS and HS are employees of Boehringer Ingelheim.