Quantitative design and experimental validation for a single-molecule DNA nanodevice transformable among three structural states

Abstract

In this work, we report the development and experimental validation of a coupled statistical thermodynamic model allowing prediction of the structural transitions executed by a novel DNA nanodevice, for quantitative operational design. The efficiency of target structure formation by this nanodevice, implemented with a bistable DNA molecule designed to transform between three distinct structures, is modeled by coupling the isolated equilibrium models for the individual structures. A peculiar behavior is predicted for this nanodevice, which forms the target structure within a limited temperature range by sensing thermal variations. The predicted thermal response is then validated via fluorescence measurements to quantitatively assess whether the nanodevice performs as designed. Agreement between predictions and experiment was substantial, with a 0.95 correlation for overall curve shape over a wide temperature range, from 30C to 90C. The obtained accuracy, which is comparable to that of conventional melting behavior prediction for DNA duplexes in isolation, ensures the applicability of the coupled model for illustrating general DNA reaction systems involving competitive duplex formation. Finally, tuning of the nanodevice using the current model towards design of a thermal band pass filter to control chemical circuits, as a novel function of DNA nanodevices is proposed.

INTRODUCTION

DNA is a useful material for the construction of nanostructures (1,2) and functional nanodevices (3,4), due to its natural compliance with a simple Watson–Crick base pairing rule, by which complementary sequences in one or more DNA strands hybridize with specificity. The function of DNA nanodevices is realized by structural transitions, generated in response to external stimuli according to the physical properties of DNA. In addition to stepwise hybridization directed by the addition of short DNA strands (5–7), various characteristic DNA reactions, including the B–Z transition of a helix triggered by an ionic strength change (8), a structural transition triggered by a pH change (9,10) and the melting of a DNA hairpin triggered by heating (11) have been introduced as engines to drive nanodevices.

A physical model that enables a designer to predict the efficiency behavior of the structural transitions executed in a reaction system is essential to the rational design of DNA nanodevices. In general, both the intramolecular folding of a DNA strand into its optimal fold and intermolecular hybridization between complementary DNA strand pairs are intrinsically incomplete reactions, due to competition between the formation of optimal and suboptimal structures. Beyond predicting the optimal structure, a quantitative assessment of the impact of such competition requires a coupled model of system behavior. To date, an experimental study to characterize a DNA nanodevice in vitro at equilibrium was implemented under an isolated condition, which was virtually optimized so that a small number of DNA species were assumed to perform hybridization only to form the targeted optimal structure as expected. It is required to bridge a gap between experimental analysis of elementary nanodevices and the construction of nanodevice systems for achieving advanced functionality. The number of target structures and/or DNA species will increase to comprise practical nanodevice systems, accompanied by an increase in the probability of forming undesired non-target structures via accidental hybridization between partially complementary regions. Moreover, it might be expected that useful behaviors will emerge from complex nanodevice systems, due to competition between multiple competing structures. However, such behaviors can be difficult to predict and design via isolated models of structure formation.

For achieving practical tasks using DNA nanodevices, the development of novel methodologies allowing identification of systems characteristics such as efficiency and error rate is, therefore, inevitable. In this regard, we have previously developed a coupled statistical thermodynamic model for assessing error upon DNA hybridization (12,13), yielding an ensemble average error measure referred to as the computational incoherence. Although such a coupled model of efficiency that allows the quantitative prediction of the behavior of nanodevices on a molecular scale is theoretically regarded as promising, its experimental validation still remains to be performed.

In this study, we report the development and experimental validation of a coupled statistical thermodynamic model for predicting the efficiency of the structural transition of a novel DNA nanodevice. The present DNA nanodevice is implemented with a so-called bistable DNA molecule that transforms between three distinct structures. First, the sophisticated thermal response of this nanodevice, in which formation of a target structure is controlled in a competitive manner, is quantitatively predicted as the operational design of the nanodevice. The efficiency of structural transition is represented in terms of the distribution of DNA molecules across the accessible structures of the reaction system, under equilibrium conditions. The efficiency behavior of formation of the targeted hairpin by the bistable DNA, which potentially forms two hairpin structures and a fully melted coil, is modeled by coupling the isolated equilibrium models for the individual hairpins. The peculiar behavior of this bistable DNA as a DNA nanodevice, which forms the targeted hairpin structure within a limited temperature range by sensing thermal variations was predicted.

Then, the predicted thermal response is validated via an experimental analysis based on fluorescence measurements with a dual fluorophore-labeled DNA. It is usually difficult to confirm suboptimal structure formation, as the corresponding fractional population (FP) is too small to be measured, due to competition with formation of the optimal structure. In this study, a relatively high FP of 0.2 was set as a consequence of careful sequence design. Beyond the conventional use of fluorescence quenching between the two fluorescent dyes in close proximity for qualitatively assessing formation of an optimal structure by a DNA nanodevice, the rare formation of the targeted suboptimal structure was quantitatively validated. Comparison between the predictions and experiment demonstrated good agreement over a wide temperature range from 30C to 90C, yielding a correlation of 0.95. The current results indicated that a model based on the statistical thermodynamics of DNA duplex formation is reliably applicable to quantitative design of the efficiency behavior of DNA nanodevices. It should be noted that the assignment of ‘target’ versus ‘error’ labels to individual structures is arbitrary. Therefore, both the transforming efficiency of DNA nanodevices similar to that in the present study and error hybridization (12,13) upon intermolecular duplex formation are predicted by following the same modeling framework. The current results are taken to provide general experimental validation of the application of a coupled statistical thermodynamic model to provide quantitative predictions of both efficiency and error behaviors of DNA nanodevices.

Finally, we propose a novel design principle for a DNA nanodevice according to coupled statistical thermodynamic considerations, for achieving advanced functionality that is novel to DNA nanodevices, based on the intentional use of the suboptimal structure adopted in this study. The transforming efficiency behavior of the present DNA nanodevice could be modified by tuning the lengths of the elementary structures, which comprise the DNA hairpin structures. We found the stringently limited formation of the targeted hairpin structure to be applicable as a thermal band pass filter to control chemical circuits.

MATERIALS AND METHODS

Bistable DNA system

The structural formation of DNA at equilibrium is governed by statistical thermodynamics (12,14). In general, complementary sequences that are longer and more GC-rich preferentially bind with each other, resulting in formation of the optimal structure due to their greater energetic stabilization. However, it is inevitable that a small fraction of DNA molecules competitively performs duplex formation between shorter or less GC-rich complementary sequences, to form less favorable structures. Thus, an isolated physical model, which considers only formation of the optimal structure, cannot provide a comprehensive illustration of a DNA reaction system, even if the system is composed of a single DNA species. In particular, evaluation of unintended duplex formation as erroneous operation by DNA nanodevices or of crosstalk between them is beyond the scope of such a model. Moreover, to support the design of DNA reaction systems that intentionally utilize the formation of suboptimal structures as a key process rather than as an error, it is necessary to establish a model that discusses both the formation of optimal and sub-optimal structures. The distribution of DNA molecules across the various accessible structures, which occurs under equilibrium conditions, may be discussed via a statistical thermodynamic apparatus.

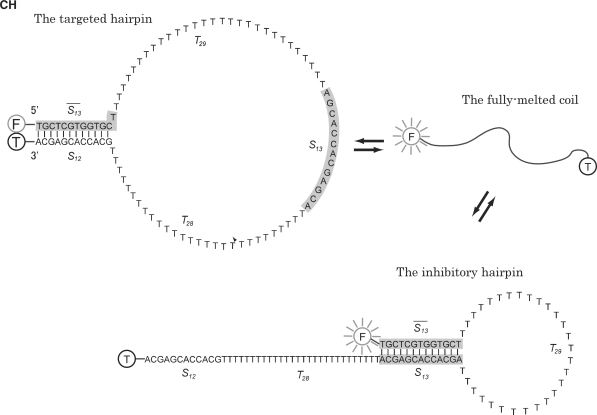
To validate application of a statistical thermodynamic model to reliably predict the rare formation of substable structures, transformation by a DNA nanodevice between three distinct structures was modeled. The 95-nt bistable DNA, CH employed in this study was designed to comprise a reversible reaction system consisting of the two competing hairpin structures and a melted coil (Figure 1). A coupled equilibrium model was developed to support the quantitative prediction of the efficiency behavior of competitive hairpin formation, by coupling the isolated equilibrium models governing the formation of each of the independent hairpins. The equilibrium constant of folding for each system hairpin was modeled via the structure's statistical weight, estimated by the corresponding Gibbs factor. An equation was derived for predicting the FP of DNA strands which fold into the targeted hairpin formed by a 12-bp mode of duplex formation between the complementary 5′ and 3′ terminal sequences as an energetically suboptimal structure, in competition with the inhibitory hairpin formed by a 13-bp mode of duplex formation between the 5′ end and an internal sequence as the optimal structure.

Figure 1.

Fluorescence bistable DNA system. A bistable DNA, CH employed for competitive hairpin formation was encoded to have a sequence of the form: - - - - (5′–3′). The subsequence of length 13 nucleotides and its fully complementary subsequence are indicated by shading. and are poly-T subsequences of length 29 and 28 nt, respectively. Vertical lines represent base pairings. The fully melted coil form is depicted simply as a curved line. FAM and TAMRA fluorophores, attached for discrimination of the targeted hairpin structure, are indicated by F and T in gray and black circles, respectively. Upon formation of the targeted hairpin structure, the emission from FAM attached to the 5′ end of CH is preferentially quenched by the proximal TAMRA attached to the 3′ end.

Thermodynamic simulation of FP

The equilibrium behavior for CH was simulated using a statistical thermodynamic approach, in which the occupancies of the various accessible structures of the system are modeled according to the Boltzmann distribution. Statistical weights of folding for each hairpin, which are independent of folding context, were then estimated via the corresponding Gibbs factors. In addition, a duplex-wise all-or-none model was also adopted, which neglects contributions due to partially melted intermediates for each of the full-length duplex structures in the present system. A sequence-dependent Gibbs free energy, of duplex stacking was estimated via the Watson–Crick nearest-neighbor model, using the parameters in Ref. (14). For each hairpin stem, was estimated as a sum of the temperature and ionic strength-dependent free energy contributions of each doublet, with contributions from dangling ends included as an energetic perturbation. The statistical weight of stacking for each hairpin stem was then estimated by the Gibbs factor, , where is the molar gas constant, with any dangling end modeled as an energetic perturbation, as in Ref. (14). The statistical weight of loop formation was modeled via a composition of the statistical weights expected due to helix cooperativity and loop closure, as follows. First, the statistical penalty of unraveling at both duplex ends was modeled via the cooperativity parameter, , where was estimated as the sum of two helix initiation parameters (i.e. one for each end) listed in Ref. (14). Next, the statistical weight of hairpin loop closure was estimated via the Jacobson–Stockmeyer inverse-1.5 power law, (15), where is the number of loop nucleotides. It is assumed that the impact of volume exclusion and chain stiffness on loop closure can be neglected due to the use of large hairpin loops. The net equilibrium constant for formation of each hairpin structure is then given by the product of these weights, , which corresponds to the overall statistical weight of the structure. Finally, the estimated equilibrium constants for the targeted and inhibitory hairpin species, and were employed to model the efficiency of formation of the targeted hairpin structure, . This quantity, which predicts FP, was estimated for the competitive hairpin system, CH via the coupled equilibrium expression,

(1)

Here, the total strand concentration for the coupled equilibrium is given by , where , and denote the equilibrium concentrations of melted coils, fully formed targeted hairpins and fully formed inhibitory hairpins, respectively. Mass action expressions for the component equilibria, and were also employed to obtain the final expression.

For comparison, a melting curve was also separately simulated for the isolated hairpin structure, which is formed by CH as the targeted suboptimal hairpin in the coupled system above, assuming the absence of competition (). Under an all-or-none model for formation of the structure's single full-length duplex, the fraction of folded DNA strands for this hairpin is then given by

(2)

Experimental implementation of CH

To investigate whether the actual behavior of FP for the targeted hairpin is the same as designed, the competitive hairpin formation of the bistable DNA was characterized experimentally via a set of fluorescence measurements. Fluorescence spectroscopy is a suitable probe for analyzing nucleic acid conformations and estimating thermodynamic properties (16). In addition, fluorescence measurements can be readily performed under a variety of solution conditions and over a wide temperature range. We took advantage of the Förster resonance energy transfer (FRET) and the contact quenching technique (17,18), by which the change in the distance between the donor and acceptor fluorescent dyes accompanying a structural transition can be monitored via the corresponding change in fluorescence intensity (FI). We adopted two fluorescent dyes, carboxyfluorescein (FAM) and carboxytetramethylrhodamine (TAMRA), which are commercially available and the most commonly used donor and acceptor pair in fluorescence measurements for nucleic acids. FAM and TAMRA were attached to the 5′ and 3′ ends of CH, respectively (Figure 1), so that emission from FAM is efficiently quenched upon formation of the targeted hairpin structure by placing them in proximity.

In conventional studies of DNA nanodevices, fluorescence spectroscopy has been applied only to qualitatively confirm the formation of the expected optimal structure. However, it is expected that the FP of DNA nanodevices that forms a certain structure is quantitatively assessed by making appropriate calibrations, according to the measurement conditions. The FI emitted from fluorescent dyes varies according to the surroundings, including the temperature condition and attached DNA sequence (18,19). Thus, it was necessary to calibrate and normalize the raw thermal profile of FI obtained for the dual-labeled bistable DNA, CH via direct monitoring of the emission from FAM versus temperature. For this purpose, an oligonucleotide, F-CH having a DNA sequence identical to that of CH, but modified only by 5′ attachment with FAM, was used as the control for calibrating both the sequence dependence and thermal variation of FAM emission. All oligonucleotides were commercially synthesized and purified by Nippon EGT (Toyama, Japan).

Poly-T sequence insertion

The sequence of the bistable DNA, CH (Figure 1) was designed to optimally implement the current fluorescence spectroscopy experiment. A 28-nt poly-T sequence, was inserted to reduce undesired FRET upon formation of the inhibitory hairpin structure, by effecting a spacing between the FAM and TAMRA fluorophores. The fluorophore separation due to the introduced 40-nt spacing was expected to become sufficiently larger than the Förster radius of the pair ( Å), defined as the distance at which the FRET efficiency is 50%.

Experimental values for the persistence length of single-stranded DNA (ssDNA) have been obtained using a variety of conditions and techniques, including electronic birefringence (20) and Cy3/Cy5 FRET (21), yielding values in the range from 14 to 30 Å. A minute value for the current experimental system and conditions was determined as a best-fit value of Å, by maximizing the correlation between the predicted and measured fluorescence footprint, described below, over values within the reported range. Combining this value for the persistence length with the measured value for the ssDNA inter-chain phosphate spacing of Å adopted in Ref. (21), and the well-known limiting expression for the mean square end-to-end distance for a freely rotating chain in the infinite-chain limit derived in Ref. (22),

(3)

yielded an approximate FAM/TAMRA root mean square spacing of Å for our design ( nt), upon formation of the inhibitory hairpin. At this spacing, the FRET efficiency of the FAM/TAMRA pair, estimated via the expression,

(4)

where the separation distance, , approximated by , is roughly . Thus, a 14% FRET efficiency was predicted upon formation of the inhibitory hairpin.

Fluorescence measurements

Fluorescence Measurement was performed using a real-time PCR machine, Mx3005P (Stratagene Japan Networks) in a 20 l solution of 1× SSC buffer (150 mM NaCl, 15 mM sodium citrate, pH 7.0 (23C); Life Technologies Japan Ltd), containing 0.5 M CH or F-CH. After heating, FI was monitored by cooling gradually to avoid kinetic trapping and to ensure formation of the hairpin structure under equilibrium conditions. The temperature was incrementally changed after every 1-min incubation by 0.3C from 30°C to 96C for heating, and by −0.3C from 96°C to 30C for cooling. FI data was obtained at the endpoint of every 1-min incubation.

Calibration and normalization of the measured FI profile

The thermal profile of FI obtained for the dual-labeled bistable DNA, CH was calibrated with that obtained for the FAM-labeled control oligonucleotide, F-CH by monitoring the emission from FAM versus temperature under identical experimental conditions. The calibrated FI values approached a maximum value, and saturated around 80C and above (details of calibration described in Supplementary Figure S3). The calibrated FI values were then normalized to allow comparison between three independent measurements by clarifying the relative FI values. The maximum calibrated FI value of each independent measurement was set to unity for normalization. By subtracting each value from 1, the fluorescence footprint [i.e. thermal profile for ] was obtained.

Tuning of transforming efficiency behavior

The melting temperatures for short DNAs are conventionally tuned to assure expected hybridization as a PCR primer, etc., with the absence of consideration on the efficiency of suboptimal structure formation. It is an interesting challenge to tune the equilibrium behavior of FP for the suboptimal structure by variation of the DNA sequence. Beyond the simple tuning of melting behavior, the development of the sophisticated tuning of coupled behavior based on the present model is expected to achieve advanced functions of DNA nanodevices. For validating the tunability of FP as the transforming efficiency of a DNA nanodevice at equilibrium, the thermal profile of FP for the targeted suboptimal hairpin was tuned by varying the lengths of the elementary structures comprising the DNA hairpins.

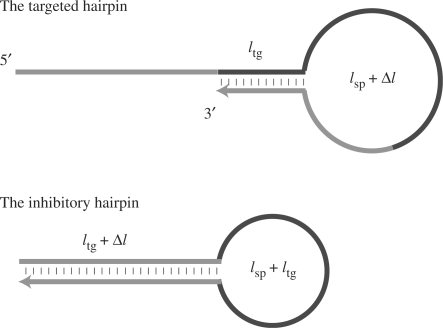
To investigate the general dependency of FP on DNA length via simulation, mean-case free energies were estimated by adopting mean values for the energetic parameters for the elementary structures (i.e. average values for the nearest-neighbor parameters in Ref. (14) for base-pair doublets, duplex initiation and 5′ dangling ends). The difference in the lengths of the stem regions between the targeted suboptimal hairpin and the inhibitory optimal hairpin, , was then varied (Figure 2). The value of the full-width half-maximum (FWHM) was adopted as an index for the tuning of FP behavior. For purposes of comparison, the lengths of the total strand and the stem region of the targeted suboptimal hairpin structure, were fixed at 95 nt and 12 bp, respectively (the same values as CH). Note that the targeted suboptimal hairpin was set to form a duplex between the complementary 5′ and 3′ terminal sequences, in a manner opposite to that of CH, with the intent of enabling the targeted hairpin to implement subsequent hybridization by its single-stranded overhang as a functionally active form.

Figure 2.

Tuning by variation of the lengths of elementary structures. The difference in the lengths of stem regions between the targeted suboptimal hairpin and the inhibitory optimal hairpin, was varied for simulation. The total length and length of the stem region of the targeted suboptimal hairpin structure, were fixed to 95 nt and 12 bp, respectively (the same values as CH).

RESULTS

Predicted thermal profile of transforming efficiency

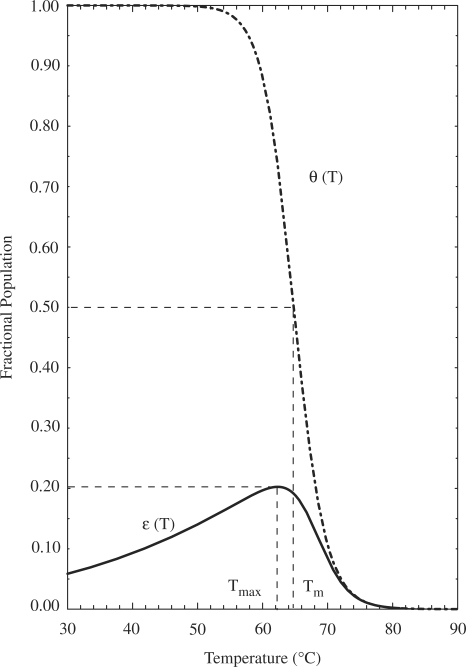
The predicted efficiency behavior of CH, in terms of FP versus temperature, , exhibited a characteristic non-symmetric hill-shaped curve, as shown in Figure 3. The resulting curve indicates that the present DNA nanodevice promotively forms the targeted hairpin only in the vicinity of a specific temperature. The temperature at which FP reached its peak and the maximum FP value were 62.3C and 0.20, respectively. In contrast, the predicted efficiency behavior, under an isolated condition assuming formation of only the single target hairpin (i.e. in the absence of competition), exhibited a simple melting curve with a sigmoidal shape.

Figure 3.

Efficiency behavior of the targeted hairpin formation. Solid curve depicts the predicted efficiency behavior of CH, in terms of the fractional occupancy of the target structure, which shows a non-symmetric and singly peaked curve. The efficiency, reaches a maximum value of 0.20 at = 62.3C. For comparison, the dash-dotted curve indicates , the predicted occupancy of the target hairpin structure when predictions are made via an isolated equilibrium model, along with the corresponding melting temperature, . The characteristic temperatures of the two models are each indicated, with dashed lines added for clarity. The above prediction for , for a model system restricted to form the single target hairpin only, was experimentally validated in (28).

Simulated and measured fluorescence footprints

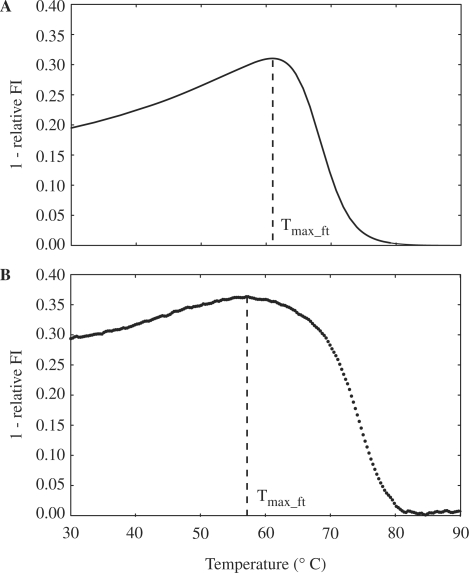
To enable a direct comparison of simulated behavior with experiment, was further converted into the predicted fluorescence footprint, by including the unintended quenching effect by FRET that occurs upon formation of the inhibitory hairpin. This minor quenching is unavoidable due to the rather large FRET radius. Based on the estimated distance between the FAM and TAMRA fluorophores (74 Å), the FRET efficiency of the FAM/TAMRA pair in the inhibitory hairpin was determined via Equation (4) as . The resulting fluorescence footprint (Figure 4A) demonstrated good agreement with the measured fluorescence footprint (Figure 4B), with a correlation of 0.95. The temperatures, at which the reached its peak, and the corresponding maximum values of for the simulated versus measured fluorescence footprint were 61.0C versus 57.0C, and versus , respectively.

Figure 4.

Simulated and measured fluorescence footprints. (A) The predicted FP shown in Figure 3 was converted to the simulated fluorescence footprint (thermal profile of ), by taking into account the unintended 14%-FRET quenching upon formation of the inhibitory hairpin. (B) The measured fluorescence footprint exhibited good agreement with the simulated fluorescence footprint, with a correlation of 0.95.

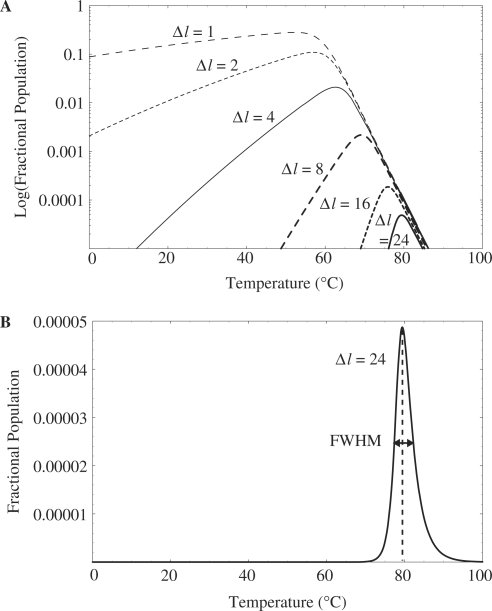
Stringently limited formation of the targeted hairpin structure

The simulated FP curves for various values of are shown as semi-log plots in Figure 5A. The results indicated that the width of the FP curve, in terms of the FWHM, was narrowed by increasing the difference in stem length between the optimal and suboptimal hairpin structures. Concurrently, the maximum value of FP decreased. We found the stringently limited formation of the targeted hairpin structure, with a FWHM of <5C (Figure 5B). The predicted maximum value of FP and peak temperature were 0.0050% and 79.4C, respectively, for 24 bp.

Figure 5.

Simulated FP curves. (A) Simulated FP curves for various values of are shown as semi-log plots. The width (FWHM) and maximum value obtained for FP decreased with increasing . (B) Stringently limited formation of the targeted suboptimal hairpin was found after tuning. The predicted maximum value for FP and peak temperature were 0.0050% and 79.4°C, respectively, for 24 bp.

DISCUSSION

Comparison between simulation and experiment

The application of statistical thermodynamics, along with nearest-neighbor parameters is commonly adopted for the prediction of melting behaviors for simple DNA systems (14,15,23,24). However, its applicability to quantitatively discuss the formation of alternative structures in a composite system composed of competing structures remains to be investigated. For achieving practical tasks using DNA systems, the development of methodologies allowing the estimation of systems characteristics such as operational efficiency is essential. The quantitative confirmation of competitive structural formation, provided by comparing simulation and experiment over a wide temperature range in this study is a benchmark validation of its applicability. The present results, shown in Figure 4, indicated that the method of using a coupled equilibrium model for the quantitative control and design of DNA reaction systems is promising for DNA nanodevice construction. In particular, model predictions of the transforming efficiency behavior for CH, accompanied by a revision according to experimental conditions, exhibited substantial quantitative similarity to the measurements. The maximum values of the fluorescence footprint, 0.31 (simulation) versus 0.36 (experiment) differed by 15%, providing substantial quantitative agreement. The corresponding peak temperatures, = 61.0C (simulation) versus 57.0C (experiment) differed by 4.0C, indicating that the expected accuracy is comparable to the conventional prediction of the melting behaviors of DNA duplexes [e.g. agreement within 3.9C, for hairpin s (14)].

The simulated overall curve shape in Figure 4A, indicating a non-symmetric singly-peaked hill, also provided good agreement with that obtained by the measurement in Figure 4B, with a correlation 0.95. On the other hand, a substantial sharpening of the simulated, relative to the measured curve, was also present. This discrepancy indicates that adoption of an all-or-none model for each system duplex may not be fully adequate, even for coupled systems involving rather short DNA duplexes. In particular, the observed sharpening might be attributed to the negligence of the contribution of partially melted intermediates to duplex melting behavior inherent in an all-or-none model. Detailed identification of the limitations and accuracy of the present model, and its improvement is, therefore, expected to be achieved by adopting a more complete model, such as a statistical zipper model.

It should be noted that the singly peaked hill-shaped FP curve predicted for the substable structure formation is beyond the scope of illustrations based on considerations of the uncoupled component equilibria. As shown in Figure 3, uncoupled model predictions similar to that for , which assume the absence of competition, commonly provide sigmoidal FP curves. Accordingly, the design of DNA nanodevices based on an uncoupled model or with the use of only the optimal structure may limit the function of such devices to that of simple low or high pass filters. For the construction of devices with advanced functions, the quantitative illustration of complex behaviors, beyond the simple melting behaviors expected for individual duplexes in isolation, is required.

Bistable DNA nanodevice

The transformation of the present nanodevice implemented with a bistable DNA is controlled by temperature. In contrast to DNA nanodevices controlled by intermolecular DNA hybridization (5–7), our device can operate at a rate independent of DNA concentration. In addition, among environmental triggers, including an ionic strength change (8) and a pH change (9,10), a temperature change appears promising, as it could be provided locally and quickly by laser irradiation. Identification of the kinetic properties of the present nanodevice, along with kinetic modeling is another interesting challenge.

The design principle for the present DNA nanodevice, which utilizes a substable structure as the target, is a novel one. As a consequence, a peculiar transforming efficiency behavior, namely, exhibiting formation of the targeted structure limited within a certain temperature range, was established beyond the common simple melting behavior.

Tuning of the transforming efficiency behavior of the bistable DNA nanodevice in this study was motivated by riboswitches (25,26) and RNA thermometers (27), found in many biological events to control chemical circuits in vivo by mediating translation. Certain messenger RNAs are not simply substrates for translation, but also contain control elements that modulate their own expression via structural transition. In contrast to riboswitches that transform between alternative structures triggered by ligand binding, to our current knowledge, RNA thermometers consisting of several hairpins basically rely on simple dynamics of structure formation and melting. Therefore, they can function only as thermal low or high pass filters for subsequent chemical circuits. Here, we propose the tuning of the behavior of the current bistable DNA nanodevice, in order to endow it with an advanced function as a thermal band pass filter. The current simulation results indicate that DNA nanodevices can exhibit the stringently limited formation of the targeted structure. This behavior after tuning could not be observed via the fluorescence measurements performed in the present study, since the maximal FP for the targeted structures formed by the nanodevice is fairly small. However, it is expected to be applicable as a regulator of chemical reactions that possess amplification procedures triggered by DNA structure formation. A single DNA molecule would be programmed via sequence design according to a coupled thermodynamic model, to act as a thermal band pass filter for chemical circuits.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Grant-in-Aid for Scientific Research (B 18300100 to J.R.). Grants-in-Aid for Young Scientists (B 18700298, 21700331 to K.K.). Grant-in-Aid for Scientific Research on Innovative Areas (20200005 to K.K.) from the Japan Society for the Promotion of Science (JSPS). Funding for open access charge: Grant-in-Aid for Scientific Research on Innovative Areas (20200005 to K.K.) from JSPS.

Conflict of interest statement. None declared.