Abstract
Temporal lobe epilepsy (TLE) characterized by an epileptogenic focus in the medial temporal lobe is the most common form of focal epilepsy. However, the seizures are not confined to the temporal lobe but can spread to other, anatomically connected brain regions where they can cause similar structural abnormalities as observed in the focus. The aim of this study was to derive whole brain networks from volumetric data and obtain network-centric measures which can capture cortical thinning characteristic for TLE and can be used for classifying a given MRI into TLE or normal, and to obtain additional summary statistics which relate to the extent and spread of the disease. T1 weighted whole brain images were acquired on a 4T magnet in 13 patients with TLE with mesial temporal lobe sclerosis (TLE-MTS), 14 patients with TLE with normal MRI (TLE-no) and 30 controls. Mean cortical thickness and curvature measurements were obtained using the Freesurfer software. These values were used to derive a graph, or network, for each subject. The nodes of the graph are brain regions, and edges represent disease progression paths. We show how to obtain summary statistics like mean, median and variance defined for these networks and to perform exploratory analyses like correlation and classification. Our results indicate that the proposed network approach can improve accuracy of classifying subjects into 2 groups (control and TLE), from 78% for non-network classifiers to 93% using the proposed approach. We also obtain network “peakiness” values using statistical measures like entropy and complexity - this appears to be a good characterizer of the disease, and may have utility in surgical planning.
Introduction
Temporal lobe epilepsy (TLE) is characterized by an epileptogenic focus in the mesial temporal lobe structures and is the most common form of partial epilepsy with a prevalence of 0.1% in the general population. Based on imaging and histopathology two types of non-lesional TLE can be distinguished: 1. TLE with mesial-temporal lobe sclerosis (TLE-MTS, about 60–70%), characterized by an atrophied hippocampus with clear MRI abnormalities and severe neuronal loss. Depth EEG shows a relatively circumscribed epileptogenic zone in mesial temporal structures. 2. TLE with normal appearing hippocampus on MRI (TLE-no, about 30–40%) and mild or no neuronal loss on histological examination. In TLE-no depth EEG shows a more widespread, less well defined epileptogenic area in the mesial temporal lobe extending into the inferior and lateral temporal lobe (Vossler et al. 2004). In both TLE types however, seizures are not restricted to the temporal lobe but can spread to other anatomically connected extratemporal brain regions, and can cause similar if less severe abnormalities. The pathophysiology of these extratemporal changes is not entirely clear and possible mechanisms include secondary neuronal loss due to deafferentiation and neuronal loss/dysfunction due to local excitotoxic effects of seizure spread with propagation of epileptogenic activity to secondary regions (Zumsteg et al., 2006; Huppertz et al., 2001).
The anatomically defined projections of the epileptogenic focus to other temporal and extratemporal regions will determine the distribution and severity of extrafocal abnormalities. Therefore, a description of the distribution of extratemporal abnormalities might provide additional information regarding the exact location of the epileptogenic focus. Recently regionally unbiased whole brain cortical thickness measurements based on T1 weighted images were reported (Fischl and Dale, 2000; Thompson et al., 2005), and their use in TLE have shown them to be very sensitive for the detection of distributed atrophic effects in TLE-MTS and TLE no (Lin et al., 2007; MacDonald et al., 2008; Bernhardt et al., 2008; Mueller et al. 2009a).
However, these studies have not considered the network-level architecture (i.e. topology) of the observed pattern of extrafocal cortical thinning. The overall goal of this study was therefore to test if it is possible to derive, for each patient, a TLE-related network within the brain by looking at extrafocal abnormalities in cortical thinning. The nodes of this network are the regions significantly affected by the disease, and the link between any two nodes represents the probability of the two regions having a disease progression path between them. Prior studies have already demonstrated that it is possible to derive connectivity between cortical regions in terms of statistical associations between brain regions across subjects in terms of cortical thickness (Lerch et al., 2006; He et al., 2007 and 2008; Chen et al., 2008) or volume (Bassett, et al., 2008).
In this work we propose a generalized Gibbs probability model for network connectivity, attempt to derive individual brain networks from this model (rather than group networks proposed by previous authors), and propose a graph-theoretic method for performing conventional statistical analysis like correlation and classification using network-level information. Finally we explore traditional network features such as degree distribution and clustering, and novel features such as network entropy and complexity. Our chosen disease model is TLE, for which the following questions were addressed. 1. Do networks derived by this approach differ between TLE-MTS and TLE-no? 2. How do these networks contribute to the focus localization in TLE-MTS and TLE-no? 3. Can the information contained in the structure of these networks be used to correctly classify a subject into disease group?
Theory
A Generalized Gibbs Probability Distribution Model For Cortical Thickness
Our input consists of the 68 cortical ROIs provided by Freesurfer (Fischl et al., 2004) and 4 sub-cortical ROIs from hippocampal volumetry – details are in the Methods section. Each of these ROIs is mapped to a node in our hypothesized network. Suppose we are given N subjects each of whom belongs to one of the three groups {control, TLE-MTS, TLE-no}. Let a subject k ∈ {1, …, N}, have a (n × n) table Tk of cortical thickness values, where Tk (i) denotes the cortical thickness of the i-th ROI of the k-th subject, and i ∈{1,.., n}. Let the mean and standard deviations of each ROI thickness over all known healthy subjects be μT (i) and σT (i). Define the normalized z-scores of these subjects as follows
| (1a) |
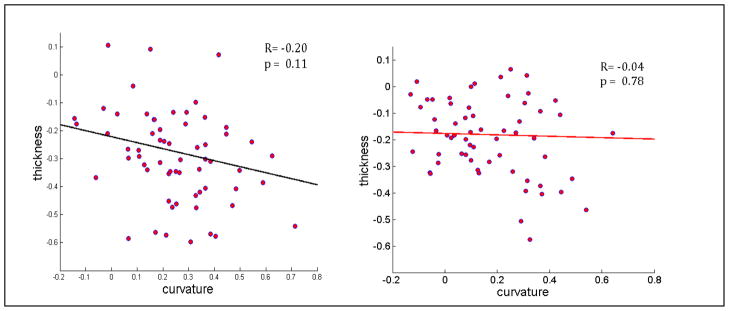
Observations of TLE subjects indicated significant cortical thinning, and also higher surface irregularity reflected by higher average curvature. In Figure 1 a scatter plot of cortical thickness versus curvature (normalized z-scores) indicates a moderate negative correlation between the two for TLE patients and almost no correlation for healthy subjects. Therefore we define the z-scores corresponding to cortical curvature, given curvature tables Ck:
| (1b) |
Figure 1.
Normalized cortical thickness versus curvature of various ROIs from TLE (a) and Healthy (b) subjects. The data was condensed by averaging over their respective groups before plotting. Correlation coefficient R and significance value (p) are shown inside the plots.
For subcortical structures, thickness is difficult and/or inappropriate to measure. Instead we obtain their volume tables Volk using Freesurfer and from hippocampal subfield volumetry (see Methods), and normalize them in the same way as thickness and curvature:
| (1c) |
Since the data have been normalized by noise variance of each ROI, it is now possible to use these values irrespective of whether they came from thickness, curvature or volume.
Given the preponderance of evidence that statistical association of cortical thickness or volume denotes cortical connectivity (Lerch et al., 2006; He et al., 2007 and 2008; Chen et al., 2008) or volume (Bassett, et al., 2008), we now attempt to fit a probabilistic model to this data and ask whether individual networks can be created from this model that captures the network properties of the disease. We hypothesize that there exists a function χ: R × R → R such that the probability of a disease progression path between any two nodes i and j of the k-th subject is given by
| (2) |
The distribution over the entire brain network is given by
| (3) |
Where  is the normalizing constant and is called Partition Function. This is a generalized version of Gibbs distributions defined over a Markov Random Field (Geman and Geman, 1984; Li, 1995). Gibbs distributions were originally used in statistical mechanics, and have since appeared in diverse fields to capture the statistics of images (Geman and Geman 1984; Besag, 1986), chaotic systems (Beck and Schlogl, 1993), and as natural spatial priors in MRI image reconstruction (Raj et al., 2007).
is the normalizing constant and is called Partition Function. This is a generalized version of Gibbs distributions defined over a Markov Random Field (Geman and Geman, 1984; Li, 1995). Gibbs distributions were originally used in statistical mechanics, and have since appeared in diverse fields to capture the statistics of images (Geman and Geman 1984; Besag, 1986), chaotic systems (Beck and Schlogl, 1993), and as natural spatial priors in MRI image reconstruction (Raj et al., 2007).
Clearly from equations (2) and (3), the set of pairwise potentials χ(Zi, Zj) form a sufficient statistic for the entire distribution, and have a special connotation as Potential Functions in statistical mechanics. This paper treats them simply as a matrix of connection strength between nodes, but their meaning should always be understood in terms of the probability distribution shown in equations (2,3).
A New Proposal To Create Networks Characteristic of TLE
The correct form of χ, which depends on the disease process, may be chosen from a set of candidate formulas by optimizing over some reasonable objective function, for instance using a Gibbs learning algorithm (Li, 1995). In Appendix A we show that a particular choice of the model, with χ(Zi, Zj) = Zi · Zj amounts to the Pearson correlation which has appeared in previous reports. Here we do not rigorously go into the problem of model selection. We created a short list (Appendix B) of so-called robust L1-norm models (e.g. Raj et al., 2007) and selected the following formula for χ that gave the highest classifying power, as shown in Figure 6. Define a (n × n) connectivity matrix ℂk of subject k, for each pair of nodes i and j in the network as
Figure 6.
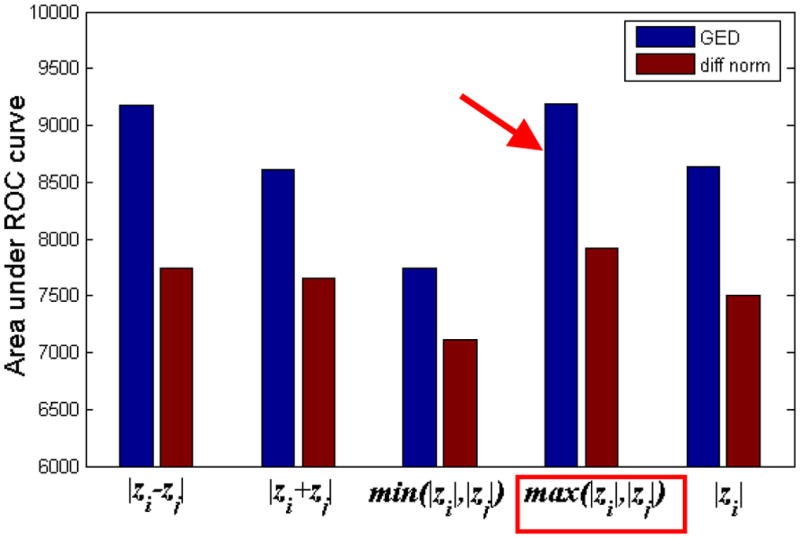
Area under ROC curves, for 5 different edge weight formulas. The formula producing best classification power is indicated by red arrows and boxes. Note the, max() function appears to be most informative edge weight for Epilepsy.
| (4a) |
For subcortical regions we have volume but not thickness or curvature, and a comparable connectivity score is defined as
| (4b) |
Network Pruning
Noise reduction is accomplished by imposing the condition that affected regions exhibit both thinning and curvature increase:
| (5a) |
For subcortical regions:
| (5b) |
Finally, nodes which have zero or very small connections (using a user-defined threshold) to other nodes are eliminated.
Graph Theoretical Features of an Individual Network
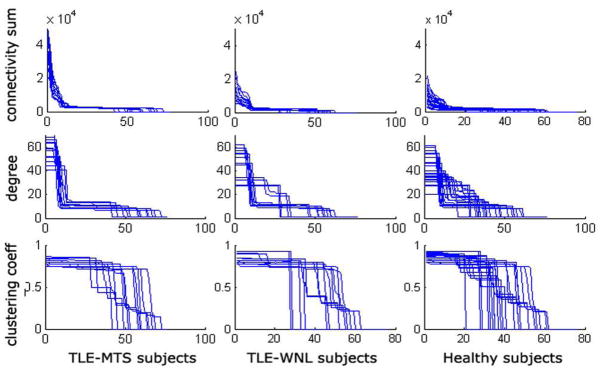
Several network-level summary measures are known (Watts et al., 1998). The degree of a node is the average number of connections to that node. The clustering coefficient of a node is the average number of connections between the node’s neighbors divided by all their possible connections. Chen et al. (2008), Bassett et al. (2008) and He et al. (2007, 2008) found these measures to indicate so-called small world properties in the brain. In this study degree is computed as the sum of connectivity weights. In contrast to prior work our individual subjects’ networks obtained from cortical thickness data simply do not show enough group-wise differences in terms of the above popular network metrics to make them useful for classification (see Figure 7). We therefore propose three additional summary features that do capture relevant group differences and measure the “peakiness” of the network: Network Entropy, Statistical Complexity (Crutchfield and Young, 1989), and Mono-exponential decay of degree curve.
Figure 7.
Plots of 3 network metrics for 3 disease classes: TLE-MTS (left column), TLE-no (middle column) and Healthy (right column). Sum of outgoing connectivities for each node (top row), degree of each node (middle row) and clustering coefficient of each node (bottom row). No summary statistic was significantly different between groups except the scale difference of connectivity sum.
First we transform a given network into a Markovian transition matrix, where the sum of the connectivity exiting any node adds up to 1, and therefore each edge weight can be thought of as the probability of moving from that node to its neighbor. Define a new connectivity matrix ℂ̃k from ℂk whose rows have been normalized to sum to 1. The transition probabilities between any two nodes are given directly by the edge weights of this normalized matrix: pij = ℂ̃k (i, j). It is well-known (Zhang et al., 2008) that the left-most eigenvector v1 of ℂ̃k represents the stationary distribution of the network, and gives node probabilities according to pi = v1 (i). Then the new summary features are:
Network Entropy: . Low entropy denotes a “peaky” connectivity curve.
Network Statistical Complexity: . Complexity is an information measure representing uniformity in connection weights, thus low complexity denotes higher “peakiness”.
Mono-exponential decay constant τ of sorted degree curve: s(i) ∝ smax e−i/τ, where s(i) is the sorted connectivity sum for node i, and smax is its largest value. Small τ denotes peakiness.
A Proposal For Classifying Networks
Let the TLE network of subject k be given by the graph Gk = {Vk, Ek}, where Vk is the set of nodes or vertices of the graph, and Ek is the set of edges. Denote the set of all such graphs by Ω. Since the epileptogenic network of different subjects may vary in terms of affected nodes, severity and spatial distribution, we allow graphs to have varying number of nodes, edges and topologies, in particular, |Gk|≠|Gk′|, Vk≠Vk′. This is to be contrasted with traditional similarity measures defined on scalars or vectors, which require equal size of all constituents.
We propose a new method for specifying the “distance” between individual networks, as follows. Suppose we start with the network Gk, and insert or delete nodes as well as edges one by one, until we match the network Gk′ - such that there exists a graph isomorphism between Gk and Gk′. Each of these modifications comes at a pre-defined cost, in our case, a unit cost for inserting or deleting a node, and a cost of |eij| for inserting or deleting an edge of weight |eij|, and a cost of |eij − e′ij| for modifying the cost of edge eij to e′ij. Let us define the edit cost of this edit path from Gk to Gk′ as the sum of all these pre-defined costs added over all the insert/delete/modify steps. Then the Graph Edit Distance (GED) between Gk and Gk′ is the edit cost of the edit path from Gk to Gk′ which gives the minimum cost:
| (6) |
Details are in Appendix C. The GED allows us to treat individual networks like random variables, by a mapping from graphs to non-negative scalar variables, as described in Appendix C. Pairwise GED distances are then embedded into a Cartesian feature space using a popular algorithm called MultiDimensional Scaling (MDS) (Seber, 1984). MDS has been successful in several biomedical data analysis problems, particularly genomic data analysis (Tzeng et al., 2008).
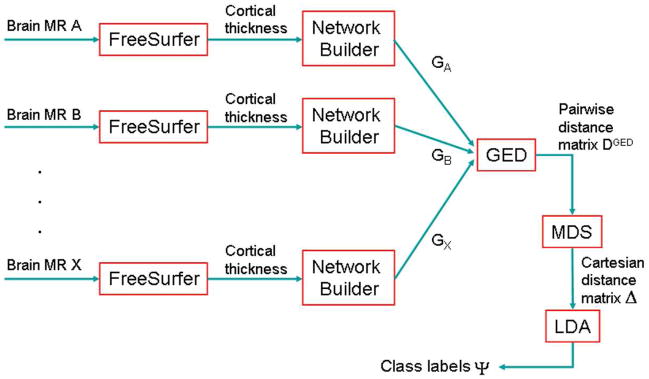
The entire process beginning with FreeSurfer analysis on MR images, to network formation, to GED distance to the MDS mapping is depicted in a flowchart in Figure 2. Finally, the Cartesian feature vectors are fed to a classification routine to obtain class labels for each subject. We chose a classical clustering method for this purpose, called linear discriminant analysis (LDA) (Krzanowski, 1988; Appendix C).
Figure 2.
Summary flowchart of GED-based network classification. Various MR brain volumes from different subjects are processed by FreeSurfer to get cortical thickness and curvature of parcellated cortical structures. A network is built for each subject. These networks are fed into the GED algorithm to compute pairwise distances between them. The MDS (multi-dimensional scaling) algorithm is applied to convert these pairwise distances into Cartesian coordinates in the embedded Euclidean space. Finally, LDA (linear discriminant analysis) is performed to get disease class for each subject.
New TLE-Specific Measures: Dispersion, Severity and Temporal Lobe Specificity
Dispersion
We define a new network measure of “peakiness” called Dispersion. For maximum descriptive power we propose the first Principal Component (PC1) of the 3 previously defined peakiness measures (entropy, complexity, exponential decay), each normalized to have unit variance. PC1 is determined simply as follows (Jolliffe, 2002).
| (7) |
In order to convert PC1 in the range (0,1), we perform the logit transform (Ashton, 1972)
| (8) |
Severity
Overall brain atrophy or severity can be defined as the sum of connectivity over all nodes
| (9) |
Temporal Lobe Specificity
The clinician is also interested in assessing how specific the disease is to the temporal lobe, and how much it has dispersed outside the temporal lobe. A simple measure of TL specificity, as a ratio of connectivity within ipsilateral temporal lobe, over the entire brain is:
| (10) |
TL specificity could be an important measure for patients slated for temporal lobe resection surgery.
Methods
Study Population
This study was approved by our institution’s IRB and written informed consent was obtained from each subject according to the Declaration of Helsinki. Twenty-seven patients suffering from drug resistant TLE were recruited between mid 2005 and end of 2007 from the Pacific Epilepsy Program, California Pacific Medical Center and the Northern California Comprehensive Epilepsy Center, UCSF, where they underwent evaluation for epilepsy surgery. Thirteen patients had evidence for MTS on 1.5T MRI (TLE-MTS) and 14 patients had normal appearing hippocampi and normal reads on 1.5T MRI (TLE-no). The presence of MTS in TLE-MTS was confirmed by hippocampal subfield volumetry using high resolution T2 weighted images aimed at the hippocampus. The absence of MTS was confirmed in all but one TLE-no who had a significant volume loss in the ipsilateral subiculum. TLE groups were matched for lateralization: 9 left/8right (female), and 5 left/5 right (male). Subjects were grouped into ipsilateral and contralateral, by side-flipping one group, so that all patients had the focus on the left side. Identification of epileptogenic focus was based on seizure semiology and prolonged ictal and interictal Video/EEG/Telemetry (VET) in all patients. The control population consisted of 30 healthy volunteers. Table 1 displays subject characteristics.
Table 1.
Study subject characteristics. Number of subjects (age range, mean ± stdev)
| Gender | Control | TLE-MTS | TLE-no |
|---|---|---|---|
| Female | 20 (38.8 ± 9.7) | 8 (39.6 ± 9.9) | 9 (35.0 ± 7.5) |
| Male | 10 (37.9 ± 9.7) | 5 (44.4 ± 6.4) | 5 (37.0 ± 5.8) |
MRI acquisition
All imaging was performed on a Bruker MedSpec 4T system controlled by a Siemens Trio™ console and equipped with an eight channel array coil (USA Instruments). The following sequences were acquired: 1. For cortical thickness and thalamus measurements a volumetric T1-weighted gradient echo MRI (MPRAGE) TR/TE/TI = 2300/3/950 ms, 1.0 × 1.0 × 1.0 mm3 resolution, acquisition time 5.17 min. 2. For the measurement of hippocampal subfields, a high resolution T2 weighted fast spin echo sequence (TR/TE: 3500/19 ms, 0.4 × 0.4 mm in plane resolution, 2 mm slice thickness, 24 slices acquisition time 5:30 min., and 3. For the determination of intracranial volume (ICV), a T2 weighted turbospin echo sequence (TR/TE 8390/70 ms, 0.9 × 0.9 × 3 mm nominal resolution, 54 slices, acquisition time 3.06 min).
Cortical Thickness Measurement
All T1 images were segmented using EMS (van Leemput et al., 1999a,b). The bias field maps and tissue maps obtained during this process were used for bias correction and skull stripping of the T1 image. FreeSurfer (version 3.05, https://surfer.nmr.mgh.harvard.edu) was used for cortical surface reconstruction and cortical thickness estimation. The procedure has been extensively described elsewhere (Fischl et al., 1999a,b; Fischl and Dale, 2000; Fischl et al., 2001; Fischl et al., 2002; Fischl et al., 2004a,b; Dale et al., 1999; Segonne et al., 2005). Visual inspection by raters unaware of the clinical diagnosis was used to manually correct errors due to segmentation miss-classification, if necessary. An automatic parcellation technique was used to subdivide each hemisphere into 34 gyral labels (Desikan et al., 2006).
Hippocampal subfield volumetry
The method used for subfield marking has been described previously (Mueller et al. 2009b). The marking scheme depends on anatomical landmarks, particularly on a hypointense line representing myelinated fibers in the stratum moleculare/lacunosum (Eriksson et al. 2008) which can be reliably visualized on high resolution images. Therefore external and internal hippocampal landmarks are used to further subdivide the hippocampus into subiculum, CA1, CA1-2 transition zone and CA3 dentate gyrus.
Network-level Processing
Means of healthy male and female controls were subtracted from all gender-grouped datasets in order to remove systematic gender-related bias. Since gender-specific healthy mean values are available, it was not necessary to perform the usual correction involving intra-cranial volume as a covariate. Our subjects are approximately age-matched, and therefore no age effect adjustment was needed. A connectivity matrix was then obtained each subject’s tables using Eqs. (4–5).
Group networks
A summary network for the entire group (c.f. He et al., (2007)) was obtained as follows. Across the entire group, a count was maintained of all non-zero edge weights and the strongest 15-percentile of edges were retained. The summary network has the same nodes as an individual network, and its edge weight are given by the number of times that edge appeared in individual networks.
Classification
Euclidean embedding of proposed Graph Edit distance between subjects was performed using the MDS algorithm. Classification using linear discriminant analysis yielded TLE-MTS, TLE-no and Control groups. In order to avoid using the same data for both training and classification, we adopted the jack-knife or leave-one-out approach. Each subject, whether control or TLE, was classified by using the remaining subjects as training set. Results of this leave-one-out validation were summarized by the Receiver Operator Characteristics (ROC) curve (Kraemer et al., 1992).
Lateralization
The sum of outgoing connectivities (“severity”) of each node was computed and sorted. Then a lateralization label (“left” or “right”) was assigned to each subject, depending on which hemisphere had the larger number of such highly-connected nodes. A concordance score (from 0–100%) was computed by comparing with the lateralization obtained by VET.
Network-level metrics
Traditional network measures (degree, clustering), new ones (network entropy, statistical complexity and monoexponential decay parameter fit), and TLE-specific ones (Dispersion, Severity, TL-specificty) were computed. Histograms of these features were compiled, a 2-sample one-sided student’s T-test was performed between each group pair, and their p-values were obtained.
Results
Cortical Thickness and Curvature
Normalized thickness maps are consistent with earlier reports (Mueller et al., 2009a) and are not shown here. Briefly, TLE-MTS was associated with prominent cortical thinning in ipsilateral medial posterior temporal and lateral prestriatal structures, additional regions with less severe cortical thinning were found in superior frontal, pre/postcentral and superior temporal regions bilaterally. TLE-no was associated with prominent cortical thinning in ipsilateral anterior inferior, lateral and superior temporal, opercular and insular regions. Less prominent cortical thinning was also found in superior frontal regions and pre/postcentral regions bilaterally. As reported before, there was more widespread contralateral involvement in TLE-no than in TLE-MTS. We did not find significant (p<0.05) curvature changes as a stand-alone measure, however Figure 1 shows that moderate correlation exists between thickness and curvature in TLE but none in healthy subjects.
Summary Group Network
Figure 3 shows summary networks for TLE-MTS and TLE-no groups, displayed using a novel illustration method whereby cortical nodes are mapped to an ellipse except for the cingulate which are mapped as arcs within the ellipse for ease of visualization. High threshold (85-percentile) and low threshold (70-percentile) cases are shown separately in order to give a sense of how frequently the edges appear in their group. Localized nature of TLE-MTS is easily distinguished from more diffuse TLE-no. While TLE-no has a larger number of edges at low threshold than TLE-MTS, the opposite is true at high threshold. This implies that TLE-MTS has a few very strong edges, while TLE-no has more, well-distributed, but weaker edges. Table 2 shows that node connectivity strength is distributed in the brain as expected from prior studies, with dominant ipsilateral temporal involvement in TLE-MTS and bilateral involvement in TLE-no.
Figure 3.
Epilepsy-derived brain network connectivity of TLE subjects. For visual convenience cortical networks are depicted as 2D circular rings, with cortical ROIs residing on the circumference, except for cingulate structures which are shown as brown arcs within the circle.
Following a dorsal view, frontal lobe is represented in light blue arc, temporal lobe (dark blue), parietal lobe (green) and occipital lobe (orange). A histogram of the 5 most popular connections across all subjects was compiled and this histogram was then thresholded to obtain the connectivities above. The straight lines between ROIs denote the presence of the most frequently occurring connections among all subjects in the specified group. Plots on the left ((a) and (b)) show the first few most frequent connections by setting a high threshold, and on the right (c) and (d) show a few more of these frequent connections by relaxing the threshold a little.
Table 2.
Total node strength in each lobe, as percentage of total. Connections weights lower than the low threshold in Fig. 2 were not counted.
| Lobe | TLE-MTS | TLE-no | ||
|---|---|---|---|---|
| Ipsi | Contra | Ipsi | Contra | |
| Occipital | 0 | 3 | 0 | 5 |
| Parietal | 3 | 3 | 3 | 5 |
| Temporal | 47 | 3 | 25 | 20 |
| Cingulate | 8 | 8 | 10 | 6 |
| Frontal | 14 | 11 | 14 | 12 |
| Total | 72 | 28 | 52 | 48 |
Classification Using Individual Networks
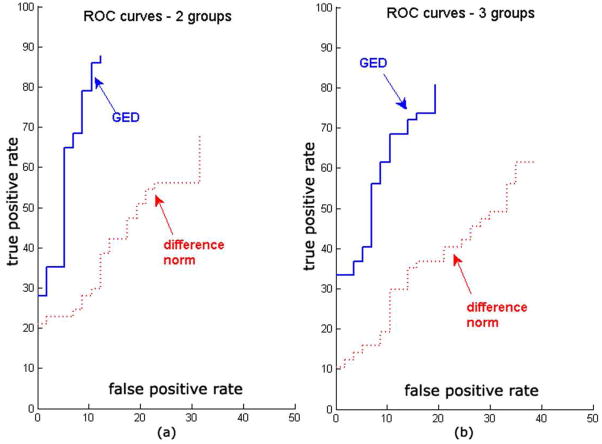
Figure 4 shows 2-way (Control vs. TLE) and 3-way (Control vs. TLE-MTS vs. TLE-no) ROC classification curves from the leave-one-out analysis. Best accuracy is obtained by graph edit distance measure (93% area under ROC Curve, compared to 78% for vector distance classifier). The classification performance is higher for the 2-group case compared to the 3-group case, as expected. Figure 6 shows that the max() function (Eq. 4) produces the best classifier AUC of all alternatives listed in Appendix B. Supplementary Figure S1 shows that classification accuracy increases substantially when one uses both thickness and curvature rather than thickness alone.
Figure 4.
Receiver Operator Characteristic (ROC) curves for the GED-distance based classification, as well as the standard difference norm-based classification. (a) corresponds to 2-group classification (TLE vs Healthy), and (b) corresponds to 3-group classification (TLE-MTS vs TLE-no vs Healthy). Note that there is some loss of performance from the 2-group case to the 3-group case, but the GED-based method consistently outperforms the standard non-graph approach.
Lateralization
Concordance between lateralization from VET with the network approach is plotted in Figure 5 against the number of highest-connected nodes used in the calculation of laterality. Only 40% concordance is achieved by looking at the first 3 most well-connected nodes in the networks, rising to 100% with increasing number of nodes.
Figure 5.
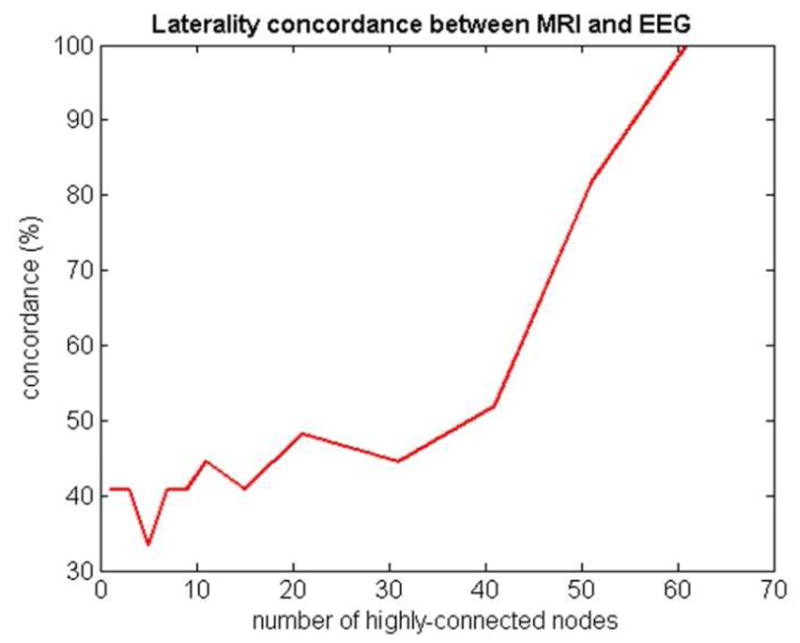
Concordance between VET-based lateralization of epileptic focus and MRI-based lateralization. The x-axis depicts the number of highly-connected nodes used to estimate lateralization.
Summary Network Measures
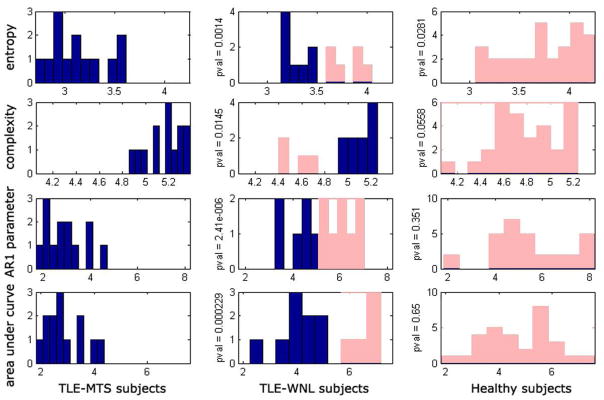
Degree distribution, clustering coefficient, and sum of outgoing connection weights are presented in Figure 7 after sorting from highest to lowest. Only the last measure showed significant group differences. The 3 new summary measures (network entropy, network statistical complexity and mono-exponential decay of sorted degree curve are shown in Figure 8. The p-values corresponding to a 2-tailed t-test between the 3 groups are significant, as shown between each group pair. Note how these measures impose a specific order on the 3 groups: the TLE-MTS patients are distinguished by “peaky” summary curves, which indicate a well-localized epileptic focus. The TLE-no patients show greatly reduced peakiness in their curves, as expected. Healthy subjects show the least amount of peakiness, indicating no specific focus, as expected.
Figure 8.
Histograms of network metrics. TLE-MTS (left column), TLE-no (middle column) and Healthy (right column). Network entropy for each subject (top row), statistical complexity (2nd row), monoexponential decay parameter fit (3rd row), and area under the connectivity sum curves shown in top row of figure 6 (bottom row). The p-values corresponding to a 2-way T-test between the 3 groups, for each of these 4 summary metrics, are shown between corresponding group pairs. TLE-no group shows network characteristics somewhat between the TLE-MTS and Healthy groups. We conjecture that the TLE-no group can be separated into TLE-MTS-like and Healthy-like subgroups, as shown by the two colors in the middle column: blue for TLE-MTS-like subgroup, and pink for Healthy-like subgroup. The “Healthy-like” subgroup show high dispersion of epileptic focus in terms of their network properties more akin to the Healthy group.
TLE-Specific measures
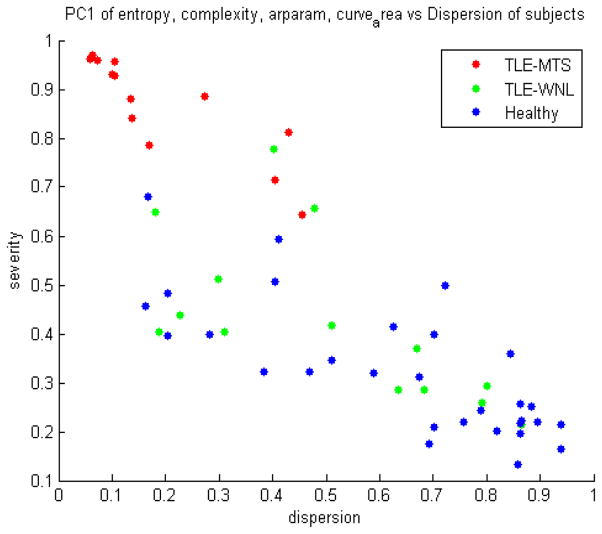
A scatter plot of severity versus dispersion is shown in Figure 9, which demonstrates that while all TLE-MTS fall comfortably within the expected quadrant of high-severity-low-dispersion, the TLE-no is more dispersed as well as less severe. Figure 10 shows a scatter plot of dispersion versus TL specificity, and again indicates that TLE-MTS subjects fall in the expected quadrant of low-dispersion-high TL specificity.
Figure 9.
Network-derived measures of epilepsy severity and dispersion. These measures can prove useful to a clinician interested in surgical planning.
Figure 10.
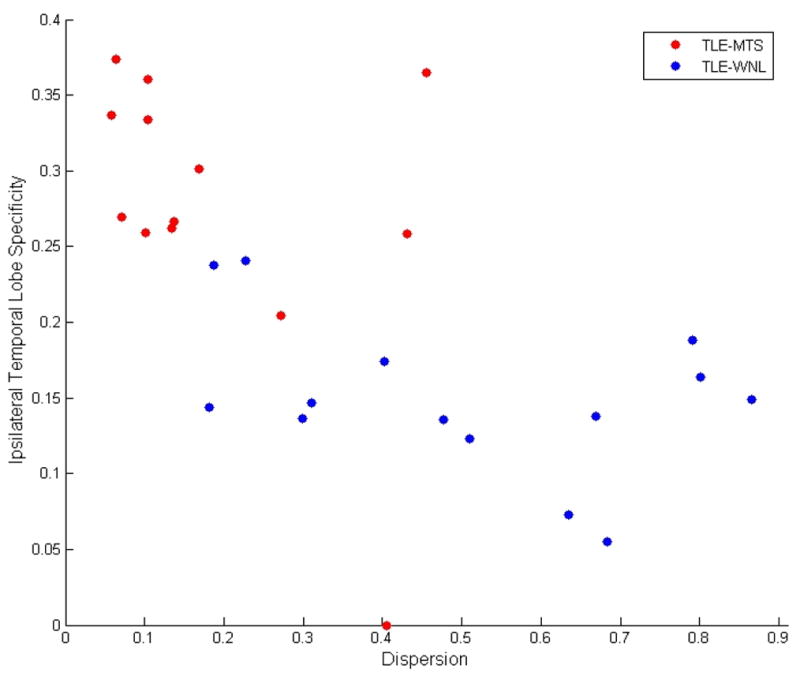
Scatter plot of Dispersion versus Temporal Lobe Specificity of cortical atrophy. The inverse relationship between dispersion and TL specificity of most TLE subjects indicates that the dispersion is a result of out-migration of epileptogenic regions from TL to other regions of the brain. Among TLE-MTS patients this out-migration is limited. However, some TLE-no subjects, as indicated in the figure, exhibit high dispersion as well as low TL specificity.
Discussion
Summary of findings
Network-centric results of Figure 3 and Table 2 are consistent with prior findings of Mueller et al., (2007,2009a, McDonald et al. 2008, Lin et al. 2008) and that TLE-MTS shows significant focal cortical thinning in the ipsilateral temporal lobe, and TLE-no shows weaker but more widespread bilateral involvement. However, the network approach brings added value by improving classification and providing new metrics like degree distribution, clustering coefficient, entropy and complexity. New metrics like severity and dispersion may also improve characterization of epilepsy. Network analysis seems to provide especially better characterization of TLE-no, which was traditionally problematic due to lack of measureable sclerosis on MRI exams. Voxel-based morphometry on the 1.5T (Mueller et al., 2006) found no significant hippocampal or cortical atrophy in TLE-no compared to healthy subjects. Mueller et al., 2009b confirmed the absence of hippocampal atrophy in TLE-no using high resolution T2 subfield mapping at 4T but reported about 17% of TLE-no to have non-specific abnormalities which were inadequate for focus localization. Network-based classification results in Figure 4 are significantly improved compared to the presented volumetric assessment based conventional classifier using the same volumetric data. However, we have not investigated other contrast mechanisms like T2 relaxation (Mueller et al., 2007) and MRSI (Mueller et al. 2004) which might provide additional information not possible by volumetrics alone. The laterality result in Figure 5 showing 100% concordance with VET, if replicated in future studies, might be significant for clinical practice.
Comparison with previous network studies
Network methods have been utilized in different biomedical fields, e.g. to study biochemical and metabolic interactions, epidemiological relationships or protein interaction and gene expression interactions (Guimera et al., 2007; Price et al., 2007; Steuer et al., 2007; Beneito et al., 2008; Charbonier et al., 2008; Liang et al., 2008). Similar network methods have also been applied to MR diffusion tractography (Hagmann et al., 2008), functional MRI (fMRI) (Achard et al., 2006) and magnetoencephalography (MEG) (Kujala et al., 2008). In prior thickness- or volume-based studies (Lerch et al., 2006; He et al., 2007; Chen et al., 2008; He et al., 2008; Bassett et al., 2008) anatomical connection was defined as statistical association between brain regions, as measured by the Pearson correlation coefficient across subjects.
Properties of an unweighted version of their network were characterized in terms of degree, clustering coefficient, and path length, and confirmed so-called “small-world” attributes in the brain as well as modular architecture in healthy development (Chen et al., 2008). There are several important differences between our approach and these papers, which provide insight into disease groups but little practical diagnostic information or exploratory analysis of individual subjects.
GED methods have recently appeared in the graph processing and machine learning (Robles et al., 2005) where they were mainly used for hand-writing detection, face recognition, line drawing matching and feature matching. GED does not previously appear to have been reported in biomedical imaging. Its use in performing statistical analysis in any context also appears to be novel.
The Individual TLE-Specific Network Approach
Unlike previous group networks where ensemble correlation signifies connectivity, links in our networks come from potential functions (Eq 4) between a pair of ROIs, and must be interpreted as the probability of disease path (Eq 2–3) rather than anatomic connectivity. Since they come from a single pair of thickness values, not ensemble average, these probabilities can be very noisy due to substantial noise embedded at various points in the data pipeline - in the MRI signal, in the segmentation step, inhomogeneity correction step, or the registration step, and finally in the cortical measurement step. Further uncertainty is introduced by natural anatomic variations present in human brains. Yet we are able to infer individual networks reliably enough to perform accurate classification and to obtain lateralization information. Why? First, only significantly atrophied ROIs show up as network nodes due to normalization to z-scores, and are further pruned by joint thickness and curvature constraints. Second, even if individual links in the network are noisy, the network as a whole should still be informative. Since all subsequent computations, whether edit distance classification or aggregate network measures like degree, clustering, entropy and complexity, are performed on whole networks and depend on overall network topology, they are quite reliable.
What explains the suitability of max() function over other potential functions for epilepsy classification? Progression of atrophy in epilepsy is likely caused by excitotoxicity accompanied by grey-matter loss and damage of the white matter tracts which channel the disease from one cortical or subcortical region to another (Shin et al., 1994; Zumsteg et al., 2006; Huppertz et al., 2001). We speculate that since the more affected node in the node pair will dominate atrophic progression in this model, the likelihood of a pathway to become a disease propagation path depends only on the more affected region irrespective of whether the other terminal is healthy or atrophic. However, we stress that the proposed network-centric approach does not rely on a particular connectivity formula – we simply chose the one that was demonstrably the most informative.
Interpreting TLE-Specific measures
Histograms of network peakiness measures (Entropy, statistical complexity, exponential decay) shown in Figure 8 strongly suggest that the TLE-no group shows network characteristics somewhat between the TLE-MTS and Healthy groups. Due to this mixture effect, neither conventional summary network statistics (Figure 7) nor conventional vector distance metrics appear to give good 3-way classification. Figure 8 further suggests that the TLE-no group might in fact be a mixture of MTS-like and Healthy-like subgroups, as indicated in the figure by blue and pink. The “Healthy-like” subgroup show high dispersion of epileptic focus in terms of their network properties more akin to the Healthy group. This conclusion is also supported by Figure 9, where TLE-MTS subjects uniformly appear to have high-severity and low-dispersion, but TLE-no subjects are more dispersed and less severe. Figure 10 indicates that TLE-MTS subjects fall in the expected quadrant of low-dispersion-high TL specificity. Within the temporal lobe, these patients have high severity, but the disease has not dispersed outside of the TL. However, a look at the TLE-no shows that while some of these subjects display TLE-MTS-like properties, others possess high dispersion.
Significance, Limitations and Future Work
Classification results in Figure 4 show added clinical value of TLE networks compared to volumetric data, but cannot serve as replacement for ictal EEG recordings which is the gold standard for focus localization. Instead, our intent was to show how to quantify and analyze the information contained in networks derived from volumetry, whether for epilepsy or (in the future) for diseases with more challenging clinical diagnoses, like Alzheimer’s disease, Parkinson’s disease, schizophrenia and multiple sclerosis. Networks analysis could be used to obtain an initial indication of TLE-MTS, or TLE-no or of a different from of epilepsy, and a strong indication of lateralization. This information may prevent unnecessary invasive EEG recordings in inappropriate subjects. It will be interesting to see if there is a difference in success rate of resection surgery between the TLE-no in the high dispersion versus low dispersion regions of Figure 9. If network measures are indeed shown to be predictive of surgical outcome, then they could provide another tool for surgical planning. These ideas are speculative and need to be carefully validated through a larger study with sufficient statistical power and long-term post-surgical follow-up. Future cortical parcellation techniques with more ROIs might produce more localized node information. Functional (fMRI and MEG) data as well as DTI data elucidating fiber architecture perhaps in combination with cortical thickness might yield larger, more reliable brain networks. Proposed graph edit distance-based network analysis technique will continue to be useful in these applications. We also note that applying proposed technique to TLE is just a first step. The ultimate goal is to use such techniques for focus localization in types of partial epilepsy where the standard methods fail, e.g. non lesional neocortical epilepsy.
Limitations
Many attendant limitations of preprocessing steps that may adversely affect our results were described by Mueller et al., (2009a). Other limitations include:
Cortical atrophy is the macro-structural irreversible endpoint of a pathophysiological cascade induced by epilepsy. Therefore proposed approach is not promising for early detection or characterization of more subtle alterations in the brain. Other MRI contrasts (T2, DTI, ASL, MRSI) might be more sensitive in this respect. T2 relaxation (Mueller et al., 2007) and MRSI (Mueller et al. 2004) were shown to provide sensitive characterization of epilepsy but it is unclear how to apply proposed network approach on these datasets. However, DTI may be ideal for this purpose and will be undertaken in future studies.
Cortical networks inherit the errors and inconsistencies of Freesurfer. Preliminary analysis of back-to-back scans (unpublished) indicate up to 10% variation in thickness of smaller cortical structures even in healthy subjects. Accuracy of cortical parcellation depends on MR image quality – Freesurfer did not succeed on a 1.5T data set from Cornell due to lower SNR and diffuse grey-white boundary.
Initial classification into 3 groups (healthy, TLE-MTS, TLE-no) was based on MRI exams at 1.5T, which has limited SNR and resolution. This classification was subsequently supported by 1) histopathological exam on a subset of 10 patients that has undergone surgery, and 2) All subjects also had subfield volumetry as described in Mueller et al. 2009. The presence of MTS was confirmed in all TLE-MTS. Except for one TLE-no who had a significant volume loss in the ipsilateral subiculum, absence of MTS was confirmed in all TLE-no. However, the gold standard to determine if pathology and VET focus lateralization were correct are the histopathological examination of the resected tissue and seizure-freedom after surgery. Since not all patients have undergone surgery yet, we cannot eliminate the possibility that the 3 groups are less distinct than initially assessed based on 1.5T scans.
Supplementary Material
APPENDIX A: CONNECTION BETWEEN GIBBS POTENTIAL AND CORRELATION
Let us write the thickness correlation between two cortical regions as , where is the ensemble expectation over all subjects, and by definition. Now consider a candidate Gibbs potential formula χ(Zi, Zj) = ZiZj, and assume that data from different subjects are independently distributed. Then the joint probability over all subjects is given by
In other words, the Pearson correlation computed in previous anatomical connectivity work reduces to a special case of our proposed Gibbs potential, when χ(Zi, Zj) = Zi · Zj.
APPENDIX B: IDENTIFYING THE BEST CONNECTIVITY FORMULA
The results described in this paper were obtained using a specific potential formula: Eq. (4) because it was found to give the best classification results. In fact, a number of other formulas were evaluated, as summarized below.
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
Each of these is a heuristic, and the “correct” formula is at this point only justifiable by its classification performance in terms of area under the ROC curve (Figure 6) though some arguments for its suitability were given in Discussion. Area under ROC is a good measure of fitness because it measures how informative any network is regarding the disease mechanism it is supposed to capture.
APPENDIX C: CLASSIFYING NETWORKS USING GRAPH EDIT DISTANCE
Specifying a Distance Between Two Networks
Starting with network Gk, and inserting or deleting nodes as well as edges one by one, until we arrive at an isomorphism of Gk′, we define the minimum cost of this edit path as the Graph Edit Distance (GED) between Gk and Gk′:
| (C1) |
Where each insert/delete modification comes at a pre-defined cost, in our case, a unit cost for inserting or deleting a node, and a cost of |eij| for inserting or deleting an edge of weight |eij|, and a cost of |eij − e′ij| for modifying the cost of edge eij to e′ij. Note that as defined, this distance is not commutative: dGED (Gk, Gk′) ≠ dGED (Gk′, Gk).
The GED allows us to treat individual networks like random variables, by the following mapping from graphs to non-negative scalar variables:
| (C2) |
where Ḡ is a centroid graph defined below, and σGED is the variance of dGED (Gk, Ḡ) for all k. The mapping Z: Ω → ℜ converts a given network into a distance from some centroid graph. The centroid graph is a graph such that the sum of its GED distances from all subjects’ graphs is smallest:
| (C3) |
Converting pairwise distances to points in Euclidean space
In order to completely convert individual networks into random vectors for the purpose of statistical analysis, a geometric embedding of the pairwise GED distances into Euclidean space is performed via a popular algorithm called Multi-Dimensional Scaling (MDS) (Seber84). MDS has been successful in several biomedical data analysis problems, particularly genomic data analysis (Tzeng et al., 2008). MDS converts a matrix of pairwise GED distances, DGED = {dGED (Gk, Gk′)|} into a matrix Δ of size ndims × N, ndims < N, such that its columns represent Cartesian coordinates of the geometric embedding of i-th subject’s network. The coordinate vectors given by the columns of Δ, i.e. δi = Δ(:, i), faithfully satisfy the GED distance criteria between every subject, such that
| (C4) |
Further statistical analysis can be performed on Cartesian vectors δi. This procedure is useful for classification algorithms that can only take feature vectors as input, rather than pairwise distances between points in feature space. Given a database of graphs, the procedure for Gaussian statistical analysis will proceed as follows.
Obtain pairwise distance matrix DGED for all graphs in database.
Perform MDS to obtain Δ = MDS(DGED)
Determine covariance matrix C =
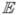 (ΔΔH)
(ΔΔH)
A number of routine statistical tasks can now be performed, for example any supervised or unsupervised (clustering) algorithm that utilizes distance measurements. For instance, suppose it is determined that the graphs belong to 2 distinct groups, such that in Cartesian space
A given graph Gk can be assigned to either group A or B according to which of
is smaller. Hypothesis testing to determine whether two graphs Gk and Gk′ belong to the same Gaussian distribution can similarly be performed.
Classification Using Linear Discriminant Analysis
Multiple-group classification on δi is performed via. Linear Discriminant Analysis (LDA), which is a classical method for separating data points into groups. It works by fitting normal distributions to each group and finding the classification which maximizes the linear discriminant between groups (Krzanowski, 1988). Suppose there are ng groups, and the mean and covariance of the embedded coordinates (e.g. δk) for each group are given by μ1, …, μng, and C1, …, Cng. Let the overall mean of the data set be given by μ̄ = mean(μ1, …, μng). Then the LDA method finds the classification Ψ: ℝndims → ℤng that maximizes the so-called linear discriminant:
| (C5) |
where the between-class and within-class scatter matrices SB, SW are defined by
| (C6) |
In this work LDA was solved using standard eigen-decomposition method (Krzanowski, 88).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashton WD. The logit transformation: with special reference to its uses in bioassay. Griffin; London: 1972. [Google Scholar]
- Bassett DS, Bullmore E, Verchinski BA, Mattay VS, Weinberger DR, Meyer-Lindenberg A. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28(37):9239–48. doi: 10.1523/JNEUROSCI.1929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck C, Schlogl F. Therodynamics of Chaotic Systems. Cambridge University Press; 1993. [Google Scholar]
- Besag J. On the statistical analysis of dirty pictures (with discussion) J Royal Statistical Society. 1986;B48:259–302. [Google Scholar]
- Charbonnier S, Gallego O, Gavin AC. The social network of a cell: Recent advances in interactome mapping. Biotechnol Annu Rev. 2008;14:1–28. doi: 10.1016/S1387-2656(08)00001-X. [DOI] [PubMed] [Google Scholar]
- Chen ZJ, He Y, Rosa-Neto P, Germann J, Evans AC. Revealing Modular Architecture of Human Brain Structural Networks by Using Cortical Thickness from MRI. Cerebral Cortex. 2008;18:2374–81. doi: 10.1093/cercor/bhn003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clauset A, Moore C, Newman ME. Hierarchical structure and the prediction of missing links in networks. Nature. 2008;453(7191):98–101. doi: 10.1038/nature06830. [DOI] [PubMed] [Google Scholar]
- Collins DL, Neelin P, et al. Data in Standardized Talairach Space. J Comput Assist Tomogr. 1994;18(2):292–205. [PubMed] [Google Scholar]
- Eriksson SH, Thom M, Bartlett PA, Symms MR, McEvoy AW, Sisodiya SM, Duncan JS. PROPELLER MRI visualizes detailed pathology of hippocampal sclerosis. Epilepsia. 2008;49:33–39. doi: 10.1111/j.1528-1167.2007.01277.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the Thickness of the Human Cerebral Cortex from Magnetic Resonance Images. Proceedings of the National Academy of Sciences. 2000;97:11044–49. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical Surface-Based Analysis I: Segmentation and Surface Reconstruction. NeuroImage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat D, Busa E, Seidman L, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale A. Automatically Parcellating the Human Cerebral Cortex. Cerebral Cortex. 2004;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Patt Anal Machine Intel. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Guimerà R, Sales-Pardo M, Amaral LA. Classes of complex networks defined by role-to-role connectivity profiles. Nat Phys. 2007;3(1):63–69. doi: 10.1038/nphys489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. Mapping the Structural Core of Human Cerebral Cortex. PLoS Biol. 2008;6(7):59. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC. Small-World Anatomical Networks in the Human Brain Revealed by Cortical Thickness from MRI. Cerebral Cortex. 2007;17:2407–2419. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC. Structural Insights into Aberrant Topological Patterns of large scale cortical networks in Alzheimer’s Disease. J Neuroscience. 2008;28:4756–4766. doi: 10.1523/JNEUROSCI.0141-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu Y, Schuff N, Du AT, Mark K, Zhu X, Hardin D, Weiner MW. Comparison of automated and manual MRI volumetry of hippocampus in normal aging and dementia. J Magnetic Resonance Imaging. 2002;16:305–310. doi: 10.1002/jmri.10163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huppertz HJ, Hoegg S, Sick C, Lucking CH, Zentner J, Schulze-Bonhage A, et al. Cortical current density reconstruction of interictal epileptiform activity in temporal lobe epilepsy. Clin Neurophysiol. 2001;112:1761–72. doi: 10.1016/s1388-2457(01)00588-0. [DOI] [PubMed] [Google Scholar]
- Jolliffe IT. Principal Component Analysis. 2. Springer; 2002. [Google Scholar]
- Kale R. Bringing epilepsy out of the shadows. BMJ. 1997;315:2–3. doi: 10.1136/bmj.315.7099.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer HC. Evaluating medical tests: objective and quantitative guidelines. Newbury Park, CA: Sage Publications; 1992. [Google Scholar]
- Krzanowski WJ. Principles of Multivariate Analysis. Oxford University Press; 1988. [Google Scholar]
- Kujala J, Gross J, Salmelin R. Localization of correlated network activity at the cortical level with MEG. Neuroimage. 2008;39(4):1706–20. doi: 10.1016/j.neuroimage.2007.10.042. [DOI] [PubMed] [Google Scholar]
- Large-Scale Cortical Networks in Alzheimer’s Disease. The Journal of Neuroscience. 28(18):4756–66. doi: 10.1523/JNEUROSCI.0141-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerch JP, Worsley K, Shaw WP, Greenstein DK, Lenroot RK, Giedd J, Evans AC. Mapping anatomical correlations across cerebral cortex (MACACC) using cortical thickness from MRI. NeuroImage. 2006;31:993–1003. doi: 10.1016/j.neuroimage.2006.01.042. [DOI] [PubMed] [Google Scholar]
- Li S. Markov random field modeling in computer vision. Springer-Verlag; Berlin: 1995. [Google Scholar]
- Liang KC, Wang X. Gene regulatory network reconstruction using conditional mutual information. EURASIP J Bioinform Syst Biol. 2008:253894. doi: 10.1155/2008/253894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez-Beneito MA, Conresa D, López-Quílez A, López-Maside A. Bayesian Markov switching models for the early detection of influenza epidemics. Stat Med. 2008;27(22):4455–68. doi: 10.1002/sim.3320. [DOI] [PubMed] [Google Scholar]
- Mueller SG, Laxer KD, Barakos J, Cashdollar N, Flenniken DL, Vermathen P, Matson GB, Weiner MW. Identification of the epileptogenic lobe in neocortical epilepsy with proton MR spectroscopic imaging. Epilepsia. 2004;45:1580–1589. doi: 10.1111/j.0013-9580.2004.53003.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller SG, Laxer KD, Cashdollar N, Buckley S, Paul C, Weiner MW. Voxel-based optimized Morphometry (VBM) of Gray and White Matter in Temporal Lobe Epilepsy (TLE) with and without Mesial Temporal Sclerosis. Epilepsia. 2006;47:900–907. doi: 10.1111/j.1528-1167.2006.00512.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller SG, Laxer KD, Schuff N, Weiner MW. Voxel-based T2 relaxation rate measurements in temporal lobe epilepsy (TLE) with and without mesial temporal sclerosis. Epilepsia. 2007;48(2):220–8. doi: 10.1111/j.1528-1167.2006.00916.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller SG, Laxer KD, Barakos J, Cheong I, Garcia P, Weiner MW. Widespread neocortical abnormalities in temporal lobe epilepsy with and without mesial sclerosis. Neuroimage. 2009;46(2):353–9. doi: 10.1016/j.neuroimage.2009.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller SG, Laxer KD, Barakos J, Cheong I, Garcia P, Weiner MW. Subfield atrophy pattern in temporal lobe epilepsy with and without mesial sclerosis detected by high-resolution MRI at 4 Tesla: preliminary results. Epilepsia. 2009;50(6):1474–83. doi: 10.1111/j.1528-1167.2009.02010.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price ND, Shmulevich I. Biochemical and statistical network models for systems biology. Curr Opin Biotechnol. 2007;18(4):365–70. doi: 10.1016/j.copbio.2007.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rademacher J, Galaburda AM, Kennedy DN, Filipek PA, Caviness VS. Human cerebral cortex: localization, parcellation and morphometry with magnetic resonance imaging. J Cogn Neurosci. 1992;4:352–374. doi: 10.1162/jocn.1992.4.4.352. [DOI] [PubMed] [Google Scholar]
- Raj A, Singh G, Zabih R, Kressler B, Wang Y, Schuff N, Weiner M. Bayesian Parallel Imaging With Edge-Preserving Priors. Magn Reson Med. 2007;57(1):8–21. doi: 10.1002/mrm.21012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robles-Kelly A, Hancock ER. Graph edit distance from spectral seriation. IEEE Trans Pattern Anal Mach Intell. 2005;27(3):365–78. doi: 10.1109/TPAMI.2005.56. [DOI] [PubMed] [Google Scholar]
- Seber GA. Multivariate Observations. John Wiley; 1984. [Google Scholar]
- Shin C, McNamara JO. Mechanisms of Epilepsy. Annual Review of Medicine. 1994;45:379. doi: 10.1146/annurev.med.45.1.379. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Steuer R. Computational approaches to the topology, stability and dynamics of metabolic networks. Phytochemistry. 2007;68(16–18):2139–51. doi: 10.1016/j.phytochem.2007.04.041. [DOI] [PubMed] [Google Scholar]
- Thompson PM, Lee AD, et al. Abnormal Cortical Complexity and Thickness Profiles Mapped in Williams Syndrome. Journal of Neuroscience. 2005;25(16):4146–58. doi: 10.1523/JNEUROSCI.0165-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng J, Lu HH, Li WH. Multidimensional scaling for large genomic data sets. BMC Bioinformatics. 2008;9:179. doi: 10.1186/1471-2105-9-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossler DG, Kraemer DL, Haltiner AM, Rostad SW, Kjos BO, Davis BJ, Morgan JD, Caylor LM. Intracranial EEG in temporal lobe epilepsy: location of seizure onset relates to degree of hippocampal pathology. Epilepsia. 2004;45(5):497–503. doi: 10.1111/j.0013-9580.2004.47103.x. [DOI] [PubMed] [Google Scholar]
- Watts D, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–2. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Wiebe S, Bellhouse DR, Fallahay C, Eliasziw M. Burden of epilepsy: the Ontario Health Survey. Can J Neurol Sci. 1999;26:263–270. doi: 10.1017/s0317167100000354. [DOI] [PubMed] [Google Scholar]
- Crutchfield JP, Young K. Inferring statistical complexity. Phys Rev Lett 10. 1989;63(2):105–108. doi: 10.1103/PhysRevLett.63.105. [DOI] [PubMed] [Google Scholar]
- Zhang F, Hancock ER. Graph spectral image smoothing using the heat kernel. Pattern Recognition. 2008;41(11):3328–3342. [Google Scholar]
- Zumsteg D, Friedman A, Wieser HG, Wennberg RA. Propagation of interictal discharges in temporal lobe epilepsy: Correlation of spatiotemporal mapping with intracranial foramen ovale electrode recordings. Clinical Neurophysiology. 2006;117:2615–2626. doi: 10.1016/j.clinph.2006.07.319. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.