Atlas-Guided Tract Reconstruction for Automated and Comprehensive Examination of the White Matter Anatomy

Abstract

Tractography based on diffusion tensor imaging (DTI) is widely used to quantitatively analyze the status of the white matter anatomy in a tract-specific manner in many types of diseases. This approach, however, involves subjective judgment in the tract-editing process to extract only the tracts of interest. This process, usually performed by manual delineation of regions of interest, is also time-consuming, and certain tracts, especially the short cortico-cortical association fibers, are difficult to reconstruct. In this paper, we propose an automated approach for reconstruction of a large number of white matter tracts. In this approach, existing anatomical knowledge about tract trajectories (called the Template ROI Set or TRS) were stored in our DTI-based brain atlas with 130 three-dimensional anatomical segmentations, which were warped non-linearly to individual DTI data. We examined the degree of matching with manual results for selected fibers. We established 30 TRSs to reconstruct 30 prominent and previously well-described fibers. In addition, TRSs were developed to delineate 29 short association fibers that were found in all normal subjects examined in this paper (N=20). Probabilistic maps of the 59 tract trajectories were created from the normal subjects and were incorporated into our image analysis tool for automated tract-specific quantification.

Introduction

The white mater consists of axons that connect different areas of the brain. Axons that share similar destinations tend to form large bundles called white matter tracts. The anatomy of prominent tracts, which have a size as large as a few centimeters in the human brain, has been well-characterized in previous anatomical studies using postmortem samples (Dejerine, 1895; Krieg, 1963). Recently, it has been shown that many of these tracts can be reconstructed non-invasively and three-dimensionally based on pixel-by-pixel diffusion orientation information obtained from diffusion tensor imaging (DTI) (Basser et al., 2000; Conturo et al., 1999; Jones et al., 1999b; Lazar et al., 2003; Mori et al., 1999; Mori et al., 2005; Parker et al., 2002; Poupon et al., 2000; Wakana et al., 2004). Although it is known that the DTI-based anatomical information is oversimplified compared to the underlying neuroanatomy, this 3D reconstruction technique, often called tractography, is an important tool to delineate the macroscopic architecture of the human brain white matter and investigate its status under pathological conditions.

Tractography, however, has several known limitations. As mentioned above, the raw pixel-by-pixel DTI data is only an approximation of the axonal fiber orientations, and, therefore, the detailed connectivity information obtained from the reconstructed tracts could be inaccurate and the validation is not straightforward (this problem will be referred to as the “accuracy issue” hereafter in this paper). This method may also suffer from reproducibility problems (“precision issue”). Specifically, if the same person is scanned several times or the same data are analyzed multiple times, the results of tractography may differ each time. One of the major sources of this precision issue is the technique’s dependency on manually defined regions of interest (ROIs), or seed pixels. If tractography is performed from every pixel inside the brain, we would obtain millions of streamlines. It is, therefore, a common practice to manually define ROIs to extract only those streamlines that belong to a selected white matter tract. Previous studies have shown that the use of multiple ROIs, based on existing anatomical knowledge, could impose strong anatomical constraints and greatly enhance the precision of tractography results (Huang et al., 2004; Posner and Dehaene, 1994). However, the placement of the ROIs requires a fair amount of anatomical knowledge and extensive training. In addition, it is not always straightforward to develop ROI-placement protocols for reproducible reconstruction of tracts of interest that have convoluted trajectories.

In our previous publication, we designed and tested protocols for ROI placements for various white matter tracts and generated protocols for 11 major tracts, which passed the precision tests (intra and inter-rater reproducibility) (Wakana et al., 2007). One of the limitations of the protocols for manual ROI placement is that the ROIs are usually confined in a 2D plane in one of the three orthogonal viewing angles. Some important tracts, such as the corpus callosum and thalamic radiation, are often difficult to define by a single 2D plane. Smaller association (cortico-cortical) tracts are also difficult to define by this type of approach due to the complex shape of the cortex. Another important limitation of the manual ROI approach is that it can become prohibitively labor-intensive if a comprehensive reconstruction of a large number of tracts in multiple-subject brain data is necessary.

To overcome this limitation, we designed and tested automated placements of 3D ROIs (Zhang et al., 2008). The concept is simple. In a representative 3D brain image (atlas), 3D ROIs are predefined by an expert (called the Template ROI Set, or TRS). Then, the atlas, which carries the predefined TRS for tractography, is linearly or non-linearly warped to each subject’s data. In our previous publication, we tested this approach for the aforementioned 11 major tracts, for which tractography protocols were well-established. The tractography results, based on the automated ROI placement, were compared to the manual method and excellent agreement between the two methods was found for the 11 major tracts (Zhang et al., 2008).

This study is an extension of the previous studies, with several important improvements. First, we tried to establish a system for a systematic, comprehensive, and whole-brain tractography well beyond the initial 11 tracts. Rather than developing a specific TRS set for every tract, we used our DTI-based human brain atlas (Oishi et al., 2009), in which 130 gray and white matter areas are pre-segmented. Second, the study focused on those tracts that had been difficult to systematically reconstruct with manual ROIs, such as the thalamic radiation and short association tracts. Third, for accurate mapping of the TRS to each subject, dual-contrast Large Deformation Diffeomorphic Metric Mapping (LDDMM) (Ceritoglu et al., 2009) was employed. Fourth, we created probabilistic maps of a comprehensive set of tracts, which were built into our atlas for automated tract-specific analyses. In this paper, reconstructions of 59 tracts are reported and validated through comparison with the manual method, and the cross-subject reproducibility was measured. The newly developed tools are now incorporated into our widely available MRIstudio/RoiEditor software (www.mristudio.org).

Materials and Methods

MRI Data

DTI data from 20 healthy subjects (36.4 ± 13.3 years old of age; 10 males, 10 females; right-handed) were acquired at the University of California Los Angeles under the International Consortium of Brain Mapping (ICBM) collaboration (Mazziotta et al., 2001). DTI data were obtained on Siemens 1.5 T MR units, using single-shot echo-planar imaging sequences with sensitivity encoding (SENSE EPI) and a parallel imaging factor of 2.0 (Pruessmann et al., 1999). The imaging matrix was 96×96, with a field of view of 240 mm × 240 mm (nominal resolution: 2.5 mm). Transverse sections of 2.5 mm thickness were acquired parallel to the anterior commissure - posterior commissure line (AC-PC). A total of 60 sections covered the entire hemisphere and brainstem without gaps. Diffusion weighting was encoded along 30 independent orientations (Jones et al., 1999a), and the b-value was 1000 s/mm². Five additional images with minimal diffusion weighting (b0 images) were also acquired. The scanning time per dataset was approximately 4 min. To enhance the signal-to-noise ratio, imaging was repeated twice.

The raw diffusion-weighted images (DWIs) were first co-registered to one of the b0 images and corrected for eddy current and subject motion with affine transformation using Automated Image Registration (AIR) (Woods et al., 1998). The average of all DWIs (aDWI) was calculated and used for the DTI-based anatomic image. The six elements of the diffusion tensor were calculated for each pixel with multivariate linear fitting using DTIStudio (H. Jiang and S. Mori, Johns Hopkins University, Kennedy Krieger Institute) (Basser et al., 1994; Jiang et al., 2006). After diagonalization, three eigenvalues and eigenvectors were obtained. For the anisotropy map, fractional anisotropy (FA) was used (Pierpaoli et al., 1996). The eigenvector (v1) associated with the largest eigenvalue was used as an indicator of fiber orientation. After the tensor calculation, the B0 susceptibility distortion was reduced by warping the b0 image to the T2-weighted anatomical image using LDDMM and the resultant transformation matrix was applied to the tensor field (Huang et al., 2008; Xu et al., 2003).

The DTI-based human brain atlas

We used a single-subject white matter atlas in the ICBM-152 space, called the “Type II Eve Atlas” (Oishi et al., 2009). A detailed description of this atlas can be found in (Oishi et al., 2009). Briefly, the atlas contains T1-weighted, T2-weighted, FLAIR, and DTI images from a single, 32-year-old female brain, which was segmented into 56 deep white matter (DWM) and 52 superficial white matter (SWM) structures (combined with the associated cortical areas), based on common anatomical features defined and assigned in population-averaged DTI data (Mori et al., 2008). This segmentation map also contains 22 deep gray matter, midbrain, and brainstem structures (see Appendix I). The atlas has a matrix dimension of 181 × 217 × 181, with a 1 mm isotropic pixel size.

Image registration

A two-step image transformation was used to warp the atlas to individual data. First, affine transformation was used to globally adjust the brain position, rotation, and the size. Then a non-linear transformation using LDDMM was applied to ensure better registration between the two. For LDDMM, the dual-contrast LDDMM was used (Ceritoglu et al., 2009) in which both the b0 image and the FA map were used simultaneously. These procedures are reciprocal, meaning that the atlas can be warped to each data segment, and each data segment can be warped to the atlas space. Once the transformation matrix defining the reciprocal transformation was determined, the gray and white matter parcellation map was transferred from the atlas to the data, enabling the automated segmentation of the data into 130 brain regions.

Automated fiber reconstruction algorithm

For automated 3D tract reconstruction, the Fiber Assignment by Continuous Tractography (FACT) method (Mori et al., 1999; Xue et al., 1999) was used with an FA threshold of 0.2, and a principal eigenvector turning-angle threshold of 40° between two connected pixels. A multi-ROI approach was used to reconstruct tracts of interest (Conturo et al., 1999; Huang et al., 2004; Mori et al., 2005; Wakana et al., 2004), exploiting the existing anatomical knowledge of tract trajectories. In this study, tracking was performed from all pixels inside the brain (the so-called “brute-force” approach). Once each brain was automatically segmented, fibers that penetrated the atlas-segmented ROIs were assigned to the specific tracts associated with those ROIs. In Fig. 1A, the tract reconstruction processes by manual ROI placement (Wakana et al., 2007) and the TRS-based method are demonstrated for the cortico-spinal tract (CST). For manual tractography, the white matter beneath the motor cortex (the blue ROI in Fig. 1A) and the cerebral peduncle (the red ROI in Fig. 1A) were defined, through which the CST is known to penetrate. These two ROIs were called “AND” ROIs, respectively, meaning that the logic operation “AND” will be applied on these two ROIs for their functions in the logic operations. The result contained the known trajectory of the CST, but it also contained other pathways, some of which could be artifacts (e.g., connections to the contralateral hemisphere), and some of which were anatomically correct, such as the cortico-ponto-cerebellar connections, as shown by a white arrow. Additional regions (“NOT” ROIs, shown as green in Fig. 1A) were added to select these branches and eliminate them. The placements of these ROIs were partly based on anatomical knowledge and partly empirical. Fig. 1A also shows a TRS-based automated reconstruction of the CST, in which the superficial white matter parcel beneath the pre-central gyrus (noted as the pre-central blade in (Oishi et al., 2008)) and the cerebral peduncle served as “AND” ROIs, while surrounding structures that often contained non-CST fibers served as “NOT” ROIs.

Figure 1.

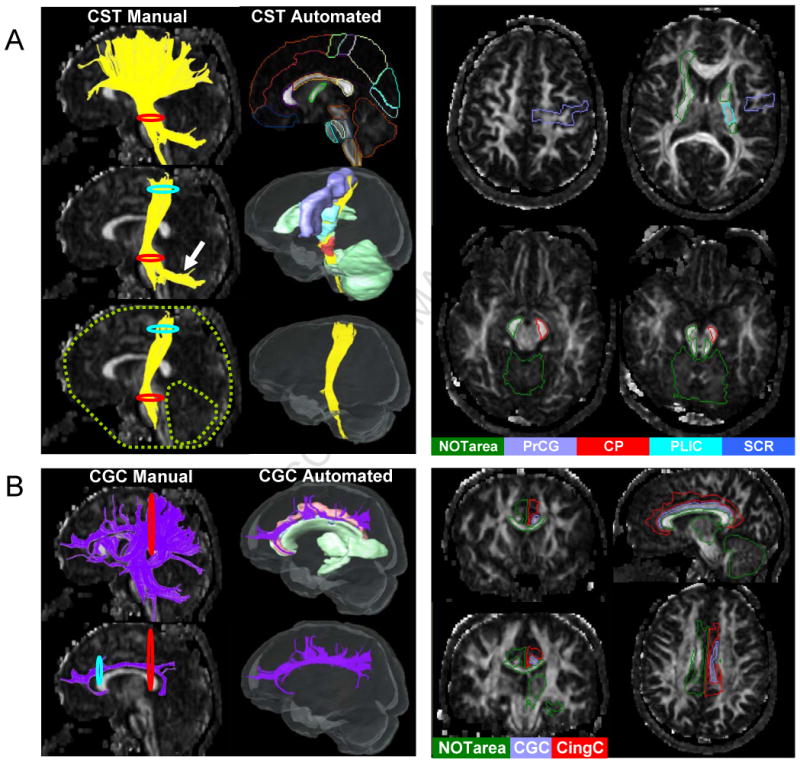
Comparison of manual and automated fiber-tracking strategies in the cortico-spinal tract (Fig. 1A), and in the cingulum of cingulate gyrus (Fig. 1B). Fig. 1A: For manual tracking, the 2D red and blue circles represent the ROI operations “AND”, while the green dashed-line circles represent the ROI operation “NOT”. The cortico-ponto-cerebellar connection is shown as contamination by the white arrow. In automated tracking, the 3D red and blue solids represent “AND”, while the green solids represent “NOT” regions. Each brain was automatically segmented by the TRS pre-defined in the type II Eve Atlas (Fig. 1A- top right and 2D slices). Fig. 1B: For the manual tracking of the cingulum of cingulate gyrus (CGC), the pathway between the two 2D ROIs were placed at the anterior and posterior ends of the CGC, which reconstructed the core part of the CG with no branching in between (Fig. 1B-bottom left and 2D slices). With the atlas-based reconstruction, two 3D ROIs define the core CGC section and the cingulate gyrus, leading to a fundamentally different view of the CGC (Fig. 1B-bottom right).

The tracts reconstructed in this study using the automated method are displayed in Table 1. These included 12 commissural tracts, 10 projection tracts, 8 long association tracts, and 29 short association tracts. The table also includes information about the ROI locations and their logic functions in fiber regulations. The detailed anatomical descriptions of segmented brain regions are described in (Oishi et al., 2009). The selections of the regions as ROIs for tract reconstructions were based on anatomical knowledge. For example, for fibers passing through the corpus callosum, ROIs were chosen at the symmetric cortical sites in addition to the corpus callosum segment at the mid-sagittal level. This type of knowledge-based approach, however, cannot be applied to short cortico-cortical association fibers, for which the locations and trajectories are not well-known. We, therefore, performed an exhaustive search examining connections among all 24 superior white matter (SWM) segments associated with different areas of the cortex. To increase the specificity of the short cortico-cortical connections, the 24 SWM ROIs were thresholded by an FA < 0.21. The relatively low FA threshold minimizes the inclusion of the white matter beneath the cortex and thus removes the involvement of the long association and projection fibers, some of which penetrate the multiple SWM segments and would contaminate the results. The 56 DWM segments were all used as “NOT” ROIs to remove long association fibers.

Table 1.

Locations of ROIs used in the TRS of each tract

	1st ROI	2nd ROI	Additional “AND”	“NOT”
CST	CP	PrCG	SCR, PLIC	Contralateral hemisphere, cerebellum, MOG, ALIC, RLIC, PCT, ICP, ML, SCP
IFO	Frontal	Occipital	[IFO, SS]	Corpus callosum, thalamus, superior parietal lobule, pre-cuneus, SCR, UNC
ILF	Occipital	Temporal	SS	Contralateral hemisphere, cerebellum, thalamus, corpus callosum, frontal lobe, IFO, SLF, cingulum, ALIC, ACR, SCR, Fx/St, AG, pre-cuneus, cuneus, SMG
UNC	Frontal	Temporal	—	Corpus callosum, cerebellum, thalamus, PTR, PHG, occipital lobe, PLIC, RLIC, SLF
CGC	CGC	Cingulate gyrus	—	Corpus callosum, right hemisphere, cerebellum, thalamus, midbrain, hippocampus, CGH, PTR
CGH	CGH	—	—	Cingulate gyrus, CGC, right hemisphere, corpus callosum, amygdala, Fx/ST
SLF-t	Frontal	Temporal	—	Occipital lobe, corpus callosum, cerebellum, IFO, ALIC, PLIC, insular, Fx/ST, EC
SLF-fp	Frontal	[AG, SMG]	—	Occipital lobe, corpus callosum, temporal lobe, IFO, EC, ALIC, PLIC, insular
SLF-pt	Temporal	AG	—	Occipital lobe, corpus callosum, frontal lobe, insular, ALIC, PLIC, EC, SLF
TRs (9 components)	Thalamus	Each cortical area J	—	Corpus callosum, cerebellum
CC1	Corpus callosum	SPG_L	SPG_R	Thalamus, caudate, putamen, globus pallidus, RLIC, EC, STG in both hemispheres
CC2	Corpus callosum	CingG_L	CingG_R	Thalamus, caudate, putamen, globus pallidus in both hemispheres
CC3	Corpus callosum	SFG_L	SFG_R	Thalamus, EC, PLIC in both hemispheres
CC4	Corpus callosum	MFG_L	MFG_R	Thalamus, EC, cerebellum, SS, PTR in both hemispheres
CC6	Corpus callosum	PrCG_L	PrCG_R	Thalamus, RLIC, cerebellum, SS, PTR in both hemispheres
CC7	Corpus callosum	PoCG_L	PoCG_R	Cerebellum in both hemispheres
CC9	Corpus callosum	PrCu_L	PrCu_R	Thalamus, RLIC, cerebellum, SS in both hemispheres
CC10	Corpus callosum	Cu_L	Cu_R	Thalamus, RLIC, cerebellum, SS, PTR in both hemispheres
CC11	Corpus callosum	LG_L	LG_R	Thalamus, RLIC, cerebellum, SS in both hemispheres
CC14	Corpus callosum	SOG_L	SOG_R	Thalamus, RLIC, cerebellum, SS in both hemispheres
CC16	Corpus callosum	MOG_L	MOG_R	Cerebellum in both hemispheres
CC24	Corpus callosum	RG_L	RG_R	Cerebellum in both hemispheres
Short association fibers	Cortical area I	Cortical area J	—	Corpus callosum, core white matter parcellations and tracts (insular, amygdala, hippocampus, cerebellum, CST, ICP, ML, SCP, CP, ALIC, PLIC, CGC, CGH, Fx/ST, PCT, MCP, Fx, RedNc, Snigra, TAP, Caud, Put, Thal, GP, Midbrain, Pons, Medulla).

^*Abbreviations are summarized in the Appendix I. Fiber types are indicated by the different text colors (red - projection fibers; blue - long association fibers; green - commissural fibers; black - short association fibers)

Comparison with manual-based tractography

In order to evaluate the accuracy of the automated tracking results, we compared the automated tract reconstruction with manually-based tractography results from the cortical spinal tract (CST), the inferior fronto-occipital tract (IFO), the inferior longitudinal fasciculus (ILF), and the uncinate fasciculus (UNC). The manual tractography protocols for these four tracts were established and shown to be reliable in (Wakana et al., 2007). The spatial matching between manual and automated results was examined using the kappa analysis (Landis and Koch, 1977). The automated and manual tracking results were first converted to binary images with the same dimension as the DTI data (181×217×181), in which pixels that were occupied by the tracts were assigned a value of 1, and other non-occupied pixels were assigned a value of 0. The two tracking results were then superimposed, and pixels were grouped into three categories: (1) pixels that did not contain the tract in either trial (nn); (2) pixels that contained the tract in only one of the two trials (pn, np); and (3) pixels that contained the tracts in both trials (pp). The ê (kappa) value of the manual and automated reconstruction of a selected tract was calculated, and an average ê was determined from the 20 normal subjects. According to the criteria set by (Landis and Koch, 1977), a ê value of 0.11–0.2 is considered “slight”, 0.21–0.4 is “fair”, 0.41–0.60 is “moderate”. 0.61–0.80 is “substantial”, and 0.81–1.0 is “almost perfect” agreement.

Generation of spatial probabilistic maps of white matter tracts in the atlas space

After the fiber tracts were constructed in the subject data space, the tract coordinates were normalized to the atlas, using the aforementioned affine and LDDMM transformation (in fact, the inverse transformation used to warp the TRS to each subject image). The normalized fiber streamlines of each tract were converted to binary images, which were averaged across 20 subjects to generate the probabilistic maps. The atlas and the fiber probability maps were incorporated into RoiEditor (www.mristudio.org).

Results

Comparison between the automated and manual methods

In this study, we classified the tracts into three categories (Type A, B, and C) depending on similarities in tract reconstruction approaches between the manual and automated methods.

Type A

This category includes the cortico-spinal tract (CST), the fronto-occipital fasciculus (IFO), the inferior-longitudinal fasciculus (ILF), and the uncinate fasciculus (UNC). These tracts share the common trait that similar ROI-placement strategies were used for both manual and automated reconstruction, as shown in Fig. 1A, and, therefore, their results can be directly compared. We tested the spatial matching agreement between automated and manual methods by kappa values (see Table 2). The kappa values for the four selected tracts were well above 0.6, which indicated almost perfect agreement (greater than 0.8), and substantial agreement (greater than 0.6, but less than 0.8) between the two methods. In Appendix II, visual comparisons between the manual and automated methods are shown for the cases with the best and worst agreement.

Table 2.

Agreement between automated and manual methods of the four Type-A tracts (average of 20 subjects)

Tract	CST_L	CST_R	IFO_L	IFO_R	ILF_L	ILF_R	UNC_L	UNC_R
Kappa value	0.83+/− 0.06	0.82+/− 0.07	0.83+/− 0.07	0.89+/− 0.04	0.80+/− 0.04	0.76+/− 0.08	0.67+/− 0.09	0.77+/− 0.10

Type B

For several white matter tracts, different reconstruction strategies were used for the automated and manual methods, and different results were produced. Fig. 1B compares the manual and automated reconstructions of the cingulum of cingulate gyrus (CGC) for demonstration. With the manual approach, in which two 2D ROIs were used, only the core part of the CGC was reconstructed, and no fibers that branched out from the CGC into the cingulate gyrus were reported because they did not pass through both 2D ROIs. In comparison, the TRS-based automated approach, which used two 3D ROIs that defined the core CGC section and the cingulate gyrus, reconstructed both the core of the CGC and the fibers that branched out from the CGC into the cingulate gyrus. Because the strategies used by the two approaches for reconstruction of the CGC were fundamentally different, kappa analysis could not be used to judge the validity of the results of the automated method. These types of tracts were called the Type B tracts.

Fig. 2 further explains the difference between the results of the automated and manual approaches for two tracts that belong to the Type B category. In Fig. 2A, three representative individual cases and the probabilistic maps of the cingulum of cingulate gyrus (CGC) are shown for automated results (upper row, red fibers) and manual tracking results (lower row, purple fibers). As explained before, the differences between the ROI strategies led to fundamental differences in reconstructed tracts, which were reproducible among subjects.

Figure 2.

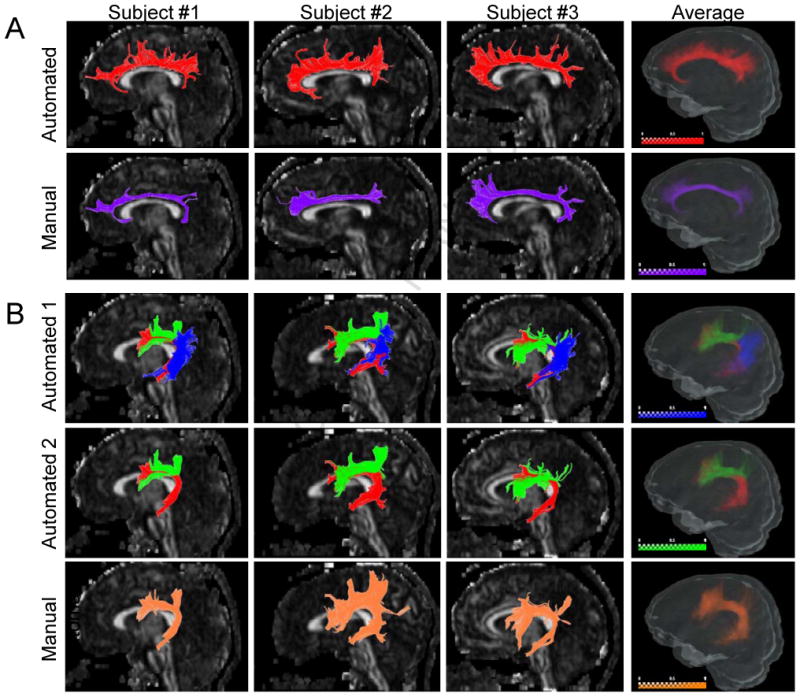
Comparison of manual and automated results from Type-B tracts. Fig. 2A: Three representative individual cases and the probabilistic maps of the cingulum of cingulate gyrus (CGC) are shown for automated results (upper row, red fibers) and manual tracking results (bottom row, purple fibers). Fig. 2B: Three representative individual cases and the probabilistic maps of the superior longitudinal fasciculus (SLF) were shown for three components (upper row), and two components based on automated results (middle row), compared to the manual results (bottom row). In the upper row, the long, anterior, and posterior segments of the SLF are shown by red, green, and blue colors, respectively. In the middle row, the anterior segment (blue) is removed to demonstrate the similarity to the manual results. The intensity scale bar represents the probability.

Fig. 2B shows reconstruction examples of the superior longitudinal fasciculus (SLF), in which the manual results (the bottom row) were based on the protocol described in a previous paper (Wakana et al., 2007). The SLF is known to project to three distinct cortical regions and, with the automated method, we could readily reconstruct them separately by using combinations of three SWM ROIs: a) the medial and inferior frontal lobe; b) the temporal lobe; and c) the angular and supermarginal gyri in the parietal lobe, which are shown as red, green, and blue colors in Fig. 2B (upper and middle rows). The manual results (Fig. 2B bottom row) were similar to the collection of two of the segments (red and green components, middle row), but lacking the posterior segment (blue component) that connects the parietal and temporal lobes.

Type C

There are also tracts that were classified as yet another type (Type C), for which the manual results are difficult to obtain. These include the thalamic radiations to different cortical areas and the cortico-cortical short association tracts. These types of tracts are difficult to reconstruct by manual ROIs because they require time-consuming cortical parcellation and delineation of 3D ROIs (Behrens et al., 2003; Thottakara et al., 2006). In Figs. 3, 4, and 5, automated reconstruction of three subsets of Type-C tracts, the thalamo-cortical projections (thalamic radiation), the commissural projections through the corpus callosum, and the cortico-cortical short association fibers, are shown.

Figure 3.

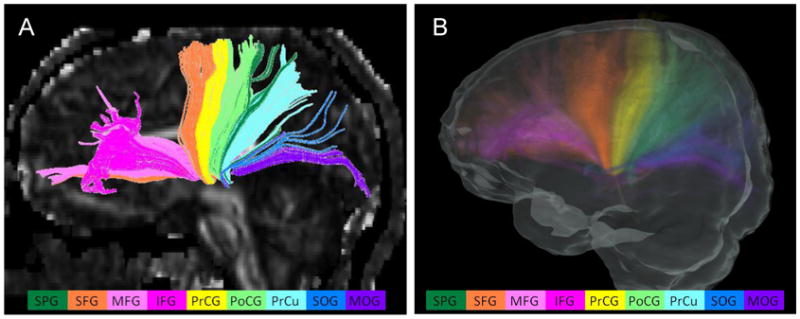
Thalamic radiations of an individual case (A) and the probabilistic map (B). The reconstructed thalamic radiations include the projection fiber bundles to the frontal, parietal, and occipital lobes. Different colors of components represent the connections to different cortical regions defined in the atlas. The projections from the thalamus to the following cortical areas were observed in all subjects and are shown in different colors: superior parietal gyrus (dark green), superior frontal gyrus (orange), middle frontal gyrus (pink), inferior frontal gyrus (rose pink), pre-central gyrus (yellow), post-central gyrus (light green), pre-cuneus (light blue), superior occipital gyrus (navy blue), and middle occipital gyrus (purple). The intensity scale of the probabilistic map is the same as in Fig. 2

Figure 4.

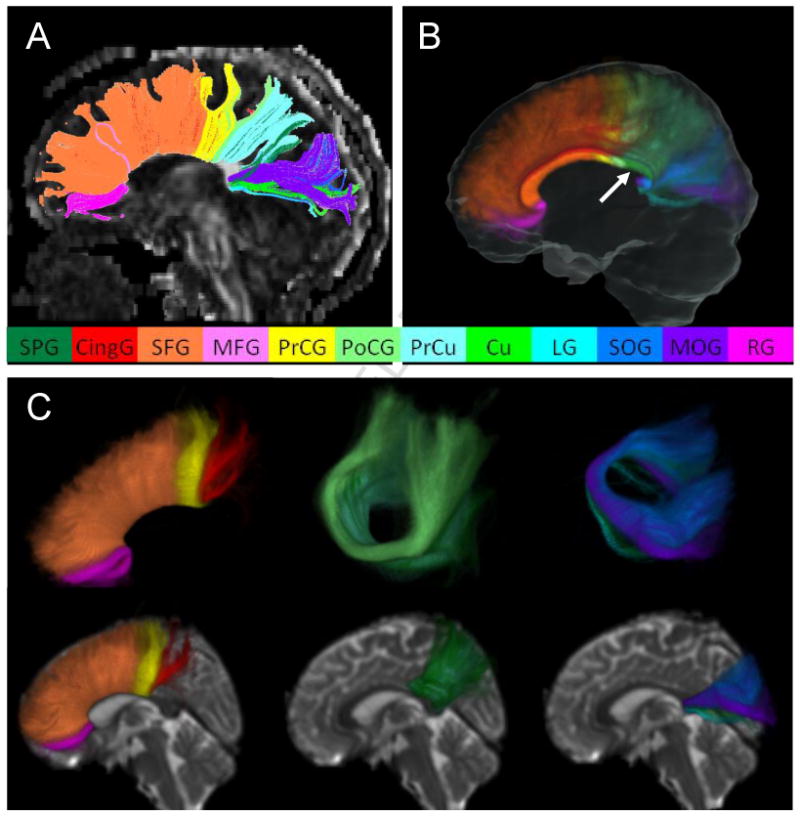
Commissural fibers from an individual case (A) and the probabilistic map (B and C). The fiber bundles penetrating the corpus callosum at the mid-sagittal section and connecting the cortices in both hemispheres are reconstructed. The fibers connecting the following cortical areas were reproducibly detectable and are shown in different colors: superior parietal gyrus (dark green), cingulate gyrus (red), superior frontal gyrus (orange), middle frontal gyrus (pink), pre-central gyrus (yellow), post-central gyrus (light green), pre-cuneus (light blue), cuneus (green), lingual gyrus (cyan), superior occipital gyrus (navy blue), middle occipital gyrus (purple), and rectus (rose pink). The mid-sagittal cross-section of the probabilistic map is shown in Fig. 4B, from which the subdivision of the corpus callosum can be seen. The unlabeled area of the corpus callosum (indicated by white arrows) corresponds to the projection to the tapetum, which is believed to connect the temporal lobes, and could not be reconstructed by the proposed automated approach. Fig. 4C shows several 3D views of the probabilistic maps of the fibers connecting the frontal lobe (left column), the parietal lobe (middle column), and the occipital lobe (right column), respectively. The intensity scale of the probabilistic map is the same as in Fig. 2

Figure 5.

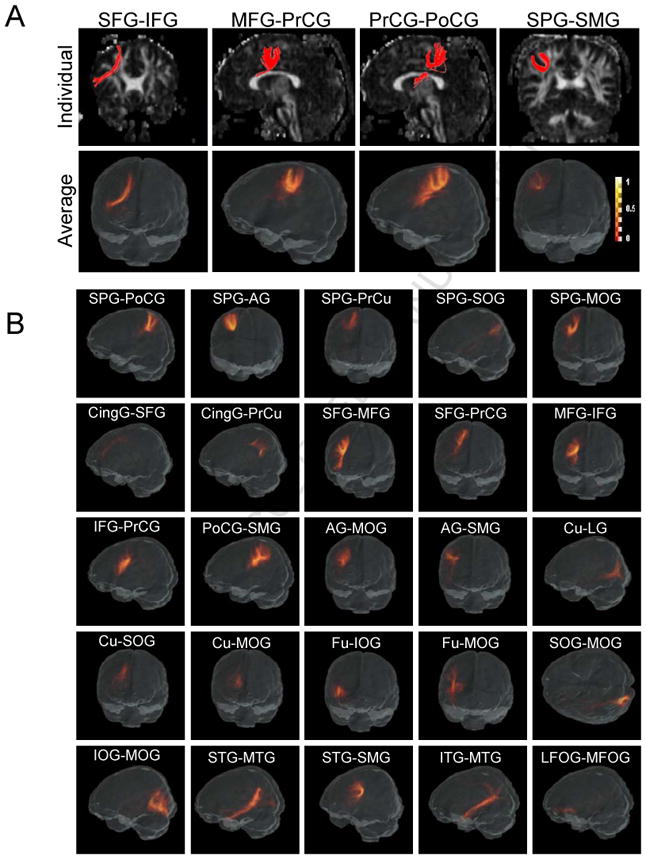
The short association fibers reconstructed by the TRS automated method. Fig. 5A: The individual cases and the probabilistic maps of four U-fibers connecting the following cortical region pairs are shown: a) the superior frontal - inferior frontal gyrus (SFG-IFG) (frontal short association fibers); b) the medial frontal - precentral gyrus (MFG-PrCG) (fronto-central short association fibers); c) the precentral - postcentral gyrus (PrCG-PoCG) (central short association fibers); and d) the superior frontal - supramarginal gyrus (SFG-SMG) (parietal short association fibers), which is consistent with our previous report. Fig. 5B: The probabilistic maps of the other 25 short association fibers that are identified in this report connect the cortical region pairs as indicated in the figure. * The color scale bar is the same for Fig. 5A and Fig. 5B.

Thalamic Radiation

Fig. 3 shows one representative case and the spatial probabilistic map of the thalamic radiations in the left hemisphere. The projections from the thalamus to the following cortical areas were found in all subjects: the superior parietal gyrus (SPG), the superior frontal gyrus (SFG), the middle frontal gyrus (MFG), the inferior frontal gyrus (IFG), the pre-central gyrus (PrCG), the post-central gyrus (PoCG), the pre-cuneus (PrCu), the superior occipital gyrus (SOG), and the middle occipital gyrus (MOG).

Corpus Callosum

The fiber bundles penetrating the corpus callosum and connecting the two hemispheres are shown in Fig. 4. The fibers connecting the following cortical areas in both hemispheres through the corpus callosum are reproducibly detectable: the superior parietal gyrus (SPG), the cingulate gyrus (CingG), the superior frontal gyrus (SFG), the medial frontal gyrus (MFG), the pre-central gyrus (PrCG), the post-central gyrus (PoCG), the pre-cuneus (PrCu), the cuneus (Cu), the lingual gyrus (LG), the superior occipital gyrus (SOG), the medial occipital gyrus (MOG), and the rectus (RG). The cross-section of the probabilistic map at the mid-sagittal level is shown in Fig. 4B, from which we can appreciate the details of the subdivision of the corpus callosum where a specific connection penetrates. For example, the fiber bundle in the rose-pink color that connects both rectus areas mostly penetrates the rostrum of the corpus callosum.

Short association fibers (SAF)

In our study, automated fiber tracking was applied to search for all possible cortico-cortical connections between adjacent cortical regions. Table 3 summarizes the “connection counts” between each pair of the 24 cortical divisions in the 20 normal subjects. Some combinations have already been used to reconstruct the long association fibers, as shown in Table 1, and they are color-filled (except the red color) in Table 3. We detected 29 subcortical connections that obtained “20/20” reproducibility (red-filled in Table 3), which are shown in Fig. 5. Fig. 5A shows an individual case and the probabilistic map of the four U-fibers that were previously reported in (Oishi et al., 2008), which connect the following cortical region pairs: the superior frontal - inferior frontal gyrus (SFG-IFG) (frontal short association fibers), the medial frontal - precentral gyrus (MFG-PrCG) (fronto-central short association fibers), the precentral - postcentral gyrus (PrCG-PoCG) (central short association fibers), and the superior frontal - supramarginal gyrus (SFG-SMG) (parietal short association fibers). The probabilistic maps reflect common and reproducible trajectories with relatively large spatial variations, compared to well-defined big bundles. Fig. 5B shows the probabilistic maps of the other 25 short association fibers with “20/20” reproducibility, which mainly connect adjacent cortical areas and form U shapes. While these tracts were found in all 20 subjects, some tracts showed highly variable trajectories among the subjects in the atlas space, leading to relatively low probability (smeared appearance) in the probability maps. These included the superior parietal - superior occipital gyrus (SPG-SOG), the cingulate - superior frontal gyrus (CingG-SFG), and the cingulate - precuneus gyrus (CingG-PrCu) connections. Other short association fibers were well-defined in the probabilistic maps.

Table 3.

The “connection” matrix between each pair of cortical regions.

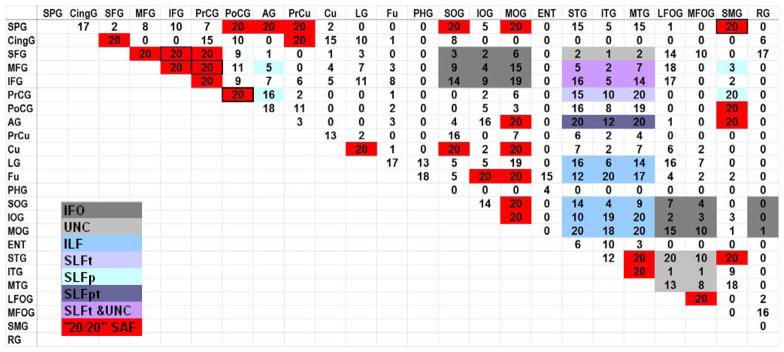The numbers represent the number of subjects in which the connection was found. The color-coded boxes (except the red boxes) represent connections by known long association fibers. The red-filled boxes indicate the 29 short association fiber connections found, with “20/20” reproducibility. The boxes outlined in black are the four short association fibers previously reported by (Oishi et al., 2008).

Discussion

Advantages of the proposed TRS-based approach and limitations

Tractography with manual ROI placement has several limitations caused by primarily three factors: operator experience, feasibility of ROI placement, and reproducibility.

1. Operator experience: The operator is required to have a certain level of anatomical knowledge, the degree of which may vary considerably.

2. ROI placement feasibility: We can reliably reconstruct only tracts that are well known (therefore, we can design the locations of multiple ROIs), can be readily identified on MR images (therefore, we can place the ROIs at the proper places), and have relatively simple trajectories (therefore, the tract can be captured by simple 2D ROIs in one of the three orthogonal planes).

3. Reproducibility: The ROI placement relies on the operator’s judgment, and, unless a robust protocol is established, there would be a concern about the intra- and inter-operator reproducibility.

These requirements limit the number of tracts we can investigate by manual tractography with high reliability.

In the proposed TRS-based approach, the anatomical knowledge is stored in the TRS and eliminates the need for extensive operator experience (Issue #1). The TRS is transferred by the automated image normalization, which eliminates the reproducibility issues (Issue #3). The comprehensive 3D brain segmentation makes it possible to investigate various tracts that would be difficult to reconstruct by manual 2D ROI placement (Issue #2).

There are two important limitations, however, in the proposed approach. First, the results rely on the accuracy of the warping of the TRS to each subject’s data. Second, the feasibility of tract reconstruction relies on the segmentation in the employed atlas; if the atlas does not contain a segmentation of a brain structure of interest, a trajectory to such an area cannot be specifically studied. The accuracy of the warping depends on the warping algorithm and the anatomy of the subject. Therefore, it is not possible to make a generalized statement about the accuracy. For example, the proposed approach may not work for a patient with severely distorted anatomy, such as brain tumor and stroke patients. For such patients, the manual method by experts should provide more accurate investigation of the anatomical status.

In this study, we used dual-contrast LDDMM for image transformation, the accuracy of which was reported previously for normal and Alzheimer’s disease (AD) populations (Oishi et al., 2009). Within the anatomical abnormalities of the AD population, a consistently high accuracy level (kappa > 0.7) of brain segmentation was observed. Therefore, within the anatomical range of these brains, the results reported in this paper can be expected.

Comparison with manual approach

In this paper, we classified the tracts into Types A–C, and compared the automated results with manual results. For the manual tracking, we used the protocols we published in a previous publication (Wakana et al., 2007) for well-defined tracts. For Type-A tracts, we could perform direct comparisons between the two approaches due to the similarity in ROI placement strategies. The comparison results suggest the automated approach can provide results comparable to the manual method. In this study, the Type-A tracts served as proof-of-principle and the merit of using the automated approach may be limited because they could also be reproducibly reconstructed by manual ROI placement. The advantages of the automated approach could be more evident for Type C tracts, which had been difficult to reconstruct manually in a reproducible manner. For Type-B tracts, the availability of a large number of 3D ROIs in TRS makes it possible to reveal comprehensive views of tracts compared to what the simple 2D ROI placement could provide. For example, the reconstruction of multiple branches of the SLF has been demonstrated previously (Catani et al., 2005). However, it would be difficult to pose consistent and reliable criteria for the manual ROI placement of these branches across different operators or different data. The reconstruction of the cingulum is another interesting example. Manual ROI approaches could reliably reconstruct this tract (Wakana et al., 2007), which serves well if the goal is to quantify the core section of the cingulum. In the presented TRS approach, two ROIs were chosen between the entire cingulate gyrus and the core cingulum white matter, which lead to the fundamentally different views of the cingulum. Currently, the cingulated gyrus is defined as one entity in the TRS. By subdividing the cingulate gyrus and combining two different sections of the cingulate gyrus as ROIs, it is possible to obtain an automated result similar to the manual approach. This type of modification of TRS by users is straightforward and could be a useful tool for developing protocols for specific tracts of interest.

This versatility of the TRS-based approach extends our capability to reconstruct Type-C tracts, which are difficult to study by manual methods. These include projections of the corpus callosum, the thalamic radiation, and the short association fibers, all of which require multiple 3D ROIs to delineate. These examples highlight the potential of the TRS-based automated method to systematically investigate white matter anatomy.

Currently, the LDDMM takes approximately 30 – 180 minutes depending on the file size and the extent of anatomical deformation. Using the automated method, tracts of all types (Type A, B, and C) are reconstructed simultaneously. For Type A and B tracts, there are only a limited number of tracts, and experienced operators could reconstruct all of them within an hour. Therefore, there would be no added time benefit in a one-to-one comparison. However, the automated computation could be performed in the background and multiple data can be submitted at once with minimum involvement of the operators. The reconstruction of Type C would be far more time-consuming, even for expert operators.

Study of short association fibers

The term “short association fiber” is not well-defined in publications. In this paper, we used this term to describe the inter-gyri and intra-lobule tracts. For major white matter tracts, we used existing anatomical knowledge for the TRS design (Table 1). For short association fibers, however, we do not have detailed knowledge about their locations and trajectories. We, therefore, used the “brute-force” method to investigate them. Our assumption is that the reproducible detection of specific ROI-ROI connections among normal subjects strongly suggests the existence of such pathways, or at least the strong and reproducible alignment of local fiber orientations along the path. We could find 29 tracts, including the four tracts we reported previously (Oishi et al., 2008). These four tracts were reconstructed in the previous paper using manually placed ROIs, by experts. Because of the convoluted structure of the cortex, the identification of specific regions across different subjects, and placing ROIs to extract the corresponding short association fibers, was a painstaking process (in addition, we must confirm the existence of each fiber in all participants to evaluate the population-consistency). Using TRS for the exhaustive search enabled us to find 25 additional tracts that were reproducibly found in all participants. Further validation of these tracts would require direct stimulation or dye injection, which are difficult to perform. However, it would be interesting to investigate the perturbation of these reproducible results in various pathological conditions, which may provide important clues about the status of local short-range connections.

Limitations of DTI fiber tracking

It is well known that DTI oversimplifies the underlying neuroanatomy by averaging all water motion within a pixel and forcing the results to be fitted to six parameters. There are many brain regions in which this leads to inaccurate estimation of the actual axonal anatomy. In our approach, fiber tracking cannot penetrate these problematic regions and connect two ROIs that should be anatomically connected. These include the projections of the lateral cortical areas through the corpus callosum and the thalamic radiation. The reported results, therefore, underestimate the trajectories, missing many existing connections. It is also possible that this method contains some bias due to subtle alteration of fiber orientations along their paths due to the inaccuracy. This issue could be especially problematic for SWM regions where axonal configuration is expected to be more complicated compared to large axonal bundles in the deep WM areas (Jones, 2003; Zhu et al., 2009), which may explain why the probabilistic maps of certain short association tracts have a large degree of dispersion compared to larger axonal bundles. To ameliorate this problem, high-angular diffusion imaging and probabilistic tract estimation have been proposed for more detailed delineation of axonal anatomy. It should be straightforward to combine our TRS method with these new approaches. However, it should be stressed that the advantage of using MRI for the study of the neuroanatomy is its capability to extract key quantitative information from the astronomically complex anatomical information available. It is, thus, inevitable that a vast amount of macroscopic anatomical information would be degenerated and could never be recovered, even with the use of sophisticated data acquisition and processing. This leads to degradation of accuracy, but, as long as the tool is precise (reproducible), it has the potential to provide useful information about the status of the neuroanatomy and to detect differences in pathological conditions. It is, therefore, important to know the limitations of the tools that are used, how the tools should be used, and how the results should be interpreted. For example, the probabilistic maps and the connectivity matrix (Table 3) should not be interpreted a priori as functional or microscopic anatomical notions such as “connectivity”. If systematic and reproducible differences are observed in one of these measures between two groups of subjects, it simply suggests that there should be a group of pixels with different water diffusion properties along the pathways, which would account for the differences.

The population-based probabilistic analysis using image normalization

Although the tracts reported in this paper were found in all 20 subjects scanned in this study, there was variability in the locations and the trajectories among subjects, which were quantitatively measured by creating probabilistic maps. The variability was larger for short association fibers, which was partly attributed to the complex axonal configuration in the SWM, but also to the limitation in precisely matching the cortical anatomy among the subjects.

In this study, the TRS in the atlas space was warped to each subject’s data in its native space for tractography. If the final purpose is to perform a group analysis, such tractography results need to be “back” normalized to the atlas space (this is how we created the population-based probabilistic maps). In this case, it would be more straightforward to warp the tensor field of each subject to TRS and perform tractography in the atlas space (Alexander et al., 2001; Jones et al., 2002; Xu et al., 2003), thereby eliminating the need to perform the image transformation twice.

There are important unresolved issues during the normalization process to create probabilistic tract maps. For example, we converted the tractography results to binary maps, which were then normalized by nonlinear transformation. During this normalization process, local contraction or expansion takes place and it is not clear whether the “1/0” intensity of the binary map should be modulated based on the local volume changes (e.g. see (Ashburner and Friston, 2000)). Another unanswered issue is how to deal with the information about the number of streamlines in each pixel. In our approach, all voxels that contain at least one streamline were assigned “1” in the binary tract map, in which the streamline density information is lost. There are several ways to approach these issues and further research is needed to carefully evaluate the impact of these issues on the final outcome.

Applications for the automated tracking

There are two ways to use the proposed tools. First, the TRS can be used for automated tracking of an individual subject’s data. In this approach, the TRS of interest is transformed to the shape of individual brains (Zhang et al., 2008). Once reconstructed, the tract volume and MR intensities (e.g., FA, eigenvalues, T2) can be determined along the tract. Second, individual MR images (e.g., FA, eigenvalues, and T2 maps) can be transformed to the Eve Atlas and can use the probabilistic tract maps to quantify the pixel intensities along the probabilistic tracts. The latter approach was tested in a previous paper for 11 major tracts, using linear transformation (Hua et al., 2008). Our paper can be considered an extension of the previous paper, providing a more comprehensive set of tracts (59 tracts) and a more accurate non-linear transformation. Our MR quantification program, RoiEditor (www.mristudio.org), has incorporated the 59 probabilistic maps into the Eve Atlas, and the tract-specific reports can be generated automatically once the images are normalized. All tools, including TRS and the probabilistic maps reported in this paper can be found at www.mristudio.org and http://lbam.med.jhmi.edu/cmrm/Data_Yajing/fiberMenu.htm, and visualized by RoiEditor.

In conclusion, we have introduced an atlas-guided method of automated fiber tract reconstruction. We investigated systematic and comprehensive whole-brain tractography using predefined TRS sets, based on our white matter atlas. Using the non-linear transformation by Large Deformation Diffeomorphic Metric Mapping (LDDMM), the atlas-based TRS approach was able to consistently reconstruct 30 major white matter tracts, as well as 29 short association fibers. The techniques developed in this study could enhance our ability to study these tracts that have been difficult to reconstruct systematically and consistently with manual approaches.

Appendix I. Table of the segmented structures

ROI #	Label	Region	ROI #	Label	Region
1	SPG_L	Superior parietal gyrus left	66	SPG_R	Superior parietal gyrus right
2	CingG_L	Cingulate gyrus left	67	CingG_R	Cingulate gyrus right
3	SFG_L	Superior frontal gyrus left	68	SFG_R	Superior frontal gyrus right
4	MFG_L	Middle frontal gyrus left	69	MFG_R	Middle frontal gyrus right
5	IFG_L	Inferior frontal gyrus left	70	IFG_R	Inferior frontal gyrus right
6	PrCG_L	Precentral gyrus left	71	PrCG_R	Precentral gyrus right
7	PoCG_L	Postcentral gyrus left	72	PoCG_R	Postcentral gyrus right
8	AG_L	Angular gyrus left	73	AG_R	Angular gyrus right
9	PrCu_L	Pre-cuneus left	74	PrCu_R	Pre-cuneus right
10	Cu_L	Cuneus left	75	Cu_R	Cuneus right
11	LG_L	Lingual gyrus left	76	LG_R	Lingual gyrus right
12	Fu_L	Fusiform gyrus left	77	FuG_R	Fusiform gyrus right
13	PHG_L	Parahippocampal gyrus left	78	PHG_R	Parahippocampal gyrus right
14	SOG_L	Superior occipital gyrus left	79	SOG_R	Superior occipital gyrus right
15	IOG_L	Inferior occipital gyrus left	80	IOG_R	Inferior occipital gyrus right
16	MOG_L	Middle occipital gyrus left	81	MOG_R	Middle occipital gyrus right
17	ENT_L	Entorhinal area left	82	ENT_R	Entorhinal area right
18	STG_L	Superior temporal gyrus left	83	STG_R	Superior temporal gyrus right
19	ITG_L	Inferior temporal gyrus left	84	ITG_R	Inferior temporal gyrus right
20	MTG_L	Middle temporal gyrus left	85	MTG_R	Middle temporal gyrus right
21	LFOG_L	Lateral fronto-orbital gyrus left	86	LFOG_R	Lateral fronto-orbital gyrus right
22	MFOG_L	Middle fronto-orbital gyrus left	87	MFOG_R	Middle fronto-orbital gyrus right
23	SMG_L	Supramarginal gyrus left	88	SMG_R	Supramarginal gyrus right
24	RG_L	Gyrus rectus left,	89	RG_R	Gyrus rectus right
25	Ins_L	Insular left	90	Ins_R	Insular right
26	Amyg_L	Amygdala left	91	Amyg_R	Amygdala right
27	Hippo_L	Hippocampus left	92	Hippo_R	Hippocampus right
28	cerebrellu m_L	Cerebellum left	93	cerebellu m_R	Cerebellum right
29	CST_L	Corticospinal tract left	94	CST_R	Corticospinal tract right
30	ICP_L	Inferior cerebellar peduncle left	95	ICP_R	Inferior cerebellar peduncle right
31	ML_L	Medial lemniscus left	96	ML_R	Medial lemniscus right
32	SCP_L	Superior cerebellar peduncle left	97	SCP_R	Superior cerebellar peduncle right
33	CP_L	Cerebral peduncle left	98	CP_R	Cerebral peduncle right
34	ALIC_L	Anterior limb of internal capsule left	99	ALIC_R	Anterior limb of internal capsule right
35	PLIC_L	Posterior limb of internal capsule left	100	PLIC_R	Posterior limb of internal capsule right
36	PTR_L	Posterior thalamic radiation (include optic radiation) left	101	PTR_R	Posterior thalamic radiation (include optic radiation) right
37	ACR_L	Anterior corona radiata left	102	ACR_R	Anterior corona radiata right
38	SCR_L	Superior corona radiata left	103	SCR_R	Superior corona radiata right
39	PCR_L	Posterior corona radiata left	104	PCR_R	Posterior corona radiata right
40	CGC_L	Cingulum (cingulate gyrus) left	105	CGC_R	Cingulum (cingulate gyrus) right
41	CGH_L	Cingulum (hippocampus) left	106	CGH_R	Cingulum (hippocampus) right
42	Fx/ST_L	Fornix (cres)/stria terminalis (can not be resolved with current resolution) left	107	Fx/ST_R	Fornix (cres)/stria terminalis (can not be resolved with current resolution) right
43	SLF_L	Superior longitudinal fasciculus left	108	SLF_R	Superior longitudinal fasciculus right
44	SFO_L	Superior fronto-occipital fasciculus (could be a part of anterior internal capsule) left	109	SFO_R	Superior fronto-occipital fasciculus (could be a part of anterior internal capsule) right
45	IFO_L	Inferior fronto-occipital fasciculus left	110	IFO_R	Inferior fronto-occipital fasciculus right
46	SS_L	Sagittal stratum (include inferior longitidinal fasciculus and inferior fronto-occipital fasciculus) left	111	SS_R	Sagittal stratum (include inferior longitidinal fasciculus and inferior fronto-occipital fasciculus) right
47	EC_L	External capsule left	112	EC_R	External capsule right
48	UNC_L	Uncinate fasciculus left	113	UNC_R	Uncinate fasciculus right
49	PCT_L	Pontine crossing tract (a part of mcp) left	114	PCT_R	Pontine crossing tract (a part of mcp) right
50	MCP_L	Middle cerebellar peduncle left	115	MCP_R	Middle cerebellar peduncle right
51	Fx_L	Fornix (column and body of fornix) left	116	Fx_R	Fornix (column and body of fornix) right
52	GCC_L	Genu of corpus callosum left	117	GCC_R	Genu of corpus callosum right
53	BCC_L	Body of corpus callosum left	118	BCC_R	Body of corpus callosum right
54	SCC_L	Splenium of corpus callosum left	119	SCC_R	Splenium of corpus callosum right
55	RLIC_L	Retrolenticular part of internal capsule left	120	RLIC_R	Retrolenticular part of internal capsule right
56	RedNc_L	Red nucleus left	121	RedNc_R	Red nucleus right
57	Snigra_R	Substancia nigra left	122	Snigra_R	Substancia nigra right
58	TAP_L	Tapetum left	123	TAP_R	Tapetum right
59	Caud_L	Caudate nucleus left	124	Caud_R	Caudate nucleus right
60	Put_L	Putamen left	125	Put_R	Putamen right
61	Thal_L	Thalamus left	126	Thal_R	Thalamus right
62	GP_L	Globus pallidus left	127	GP_R	Globus pallidus right
63	Midbrain_L	Midbrain left	128	Midbrain_R	Midbrain right
64	Pons_L	Pons left	129	Pons_R	Pons right
65	Medulla_L	Medulla left	130	Medulla_R	Medulla right

^*Color represents deep white matter structures (black), superficial white matter with associated cortices (blue), and other structures (green).

Appendix II

Figure.

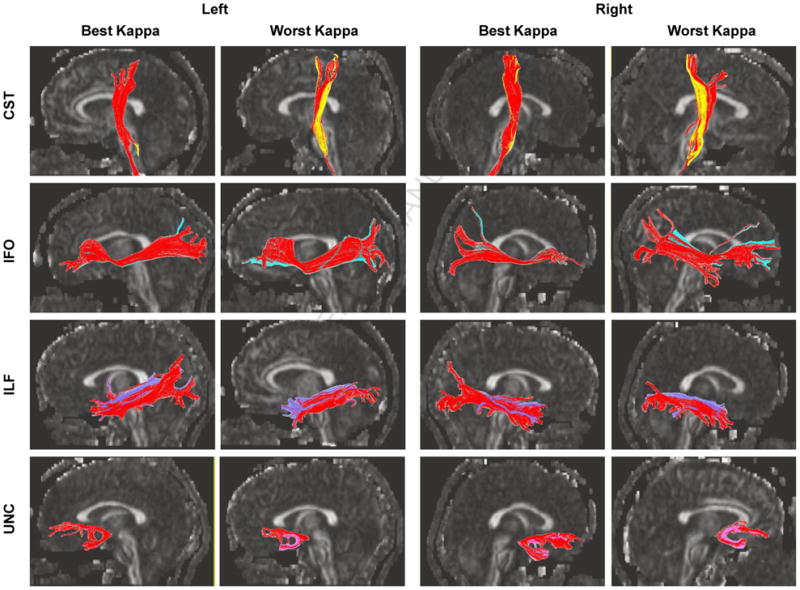
Comparison between the manual and automated (red) reconstruction results for four white matter tracts. The results for the best and worst matching among 20 subjects are demonstrated.