Quantum Molecular Interaction Field Models of Substrate Enantioselection in Asymmetric Processes

Abstract

Computational models correlating substrate structure to enantioselection with asymmetric catalysts using the QMQSAR program are described. In addition to rapidly providing predictions that could be used to facilitate the screening of catalysts for novel substrates, the QMQSAR program identifies the portions of the substrate that most directly influence the enantioselectivity. The lack underlying relationship between all the substrates in one case, requires two quantitative structure selectivity relationships (QSSR) models to describe all of the experimental results.

1. Introduction

The ultimate goals of asymmetric catalysis are the discovery of reactions that provide desired products with high enantioselectivities and yields. Given the immense effort applied in this endeavor, computational tools are a logical resource to facilitate the design and optimization of asymmetric reactions.^i,ii However, even with massive increases in computer speed, the number of variables in any asymmetric transformation makes modeling of discrete transition states often challenging. The use of other computational tools encompassing linear free energy relationships, such as quantitative structure activity relationships (QSAR),^iii,iv has been shown to provide useful information. In prior reports^{v,vi,vii,viii} we introduced the development of grid-based quantitative structure selectivity relationship (QSSR) models using quantum mechanical molecular interaction fields for correlating enantiomeric excess with catalyst structure. Other workers have embraced this approach with success.^{ix,x,xi,xii, xiii} In addition, intriguing reports utilizing QSSR models to predict substrate enantioselection with chiral catalysts have appeared.^xiv,xv Here, we report our independent efforts toward generating models to predict enantioselection for substrates which has also led to a tool to identify potential mechanistic differences between substrate classes.

2. Methods and experimental data

2.1 Quantum Molecular Interaction Fields

The enantiomeric excesses arising from the aldehyde substrates were analyzed with 3D-QSSR (quantitative structural selectivity relationship) methods employing quantum molecular interaction fields as implemented in the program QMQSAR.^xvi Although, detailed descriptions on how this program computes and utilizes molecular fields are described elsewhere,^v–viii,xvi a short introduction is provided here.

For the aldehydes, generation of a model to explain the enantioselection commences with calculation of the lowest energy substrate conformers. Initially, conformers of the compounds were constructed and computed using the semi-empirical method PM3 in Spartan.^xvii The lowest energy conformers of the substrates were aligned and were then used with the QMQSAR program. The important feature here is that all the substrates are treated and aligned in the same way so that their relationships can be interrogated; similar relationships (i.e. t-Bu is larger than Me, methoxy is more electron rich than trifluoromethyl, etc.) would likely hold even in a higher energy ground state accounts for the predominant reaction pathway. The requisite quantum mechanical interaction fields were computed using single-point PM3 semi-empirical calculations with Divcon^xviii and were in the form of electrostatic potential field (EPF) values at ordered grid points encompassing the substrates.

2.3 Model Generation

Grid spacing in the EPF was initially 0.35 Å and was adjusted during the course of the model building to a finer grid around correlated EPF points according to a MAXMIN diversity algorithm.^xix The EPF values represent the pool of independent variables from which the multi-linear regression (MLR) models were built. The MLR models between the EPF points and the ΔG_ee values of the substrates were optimized by a simulated Monte Carlo approach.^xvi Initial models were constructed using all substrates and from 1–4 EPF points generating expressions according to the following equation: ΔG_calc = a + b*EPF₁ + c*EPF₂+ d*EPF₃+ e*EPF₄ where a-e are constants/coefficients calculated by the program and where EPF_1–4 are the values of the EPF at gridpoints 1–4 selected by the program. Models were evaluated by their goodness-of-fit (r²) and the standard deviation (SD) with respect to the experimental data. Models were further refined using a leave-one-out^xx analysis, where n models containing all the combinations of n−1 substrates were constructed; for each model the substrate absent in the parameterization set was then calculated giving rise to a predicted enantioselection. The goodness-of-fit of these leave-one-out (LOO) cross-validated predictions is summarized in the term r²_LOO.

2.3 Experimental Data

All experimental data was obtained from references xxi and xxii. Substrates were compared only for reactions conducted in the same solvent, at the same temperature, and with the same catalyst and catalyst loading. For all the analyses, the enantioselectivities are converted to ΔG_ee using the relationship: ΔG_ee = −RTln[(S)/(R)] so that the variables used in the correlation possess an underlying linear relationship.

3. Results and Discussion

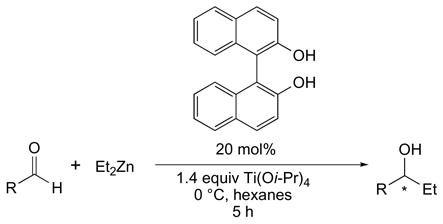
In this study, instead of correlating catalyst structure to selectivity, we correlate the substrate structure to selectivity for reactions with the same catalyst. A prerequisite for this process is data for ≥ 10 substrates that encompass a wide enantioselectivity range. One candidate is outlined in Eq 1.^xxi These calculations are even simpler than those described for the chiral catalysts,^v–viii since only the structures of the substrates (no metals etc.) need to be calculated. In this case, after the rapid calculation of the ground state structures, the substrates were aligned about the aryl ring of the aldehyde and the EFP fields were calculated quickly (seconds to minutes). Models with 1–4 EPF points per substrate were then constructed and evaluated. Two EPF points were sufficient to generated models with high r² and SD values. Furthermore, a leave-one-out analysis^xx indicated that the models were highly predictive for the 11 substrates listed in Table 1 with a SD_LOO of 0.35 kcal/mol.

Table 1.

Experimental and Calculated Substrate Enantioselection for the Reaction in Eq 1.

entry	RCHO	calculated		experimental
		ΔGeea,b (kcal/mol)	ee (%)	ΔGeea,c (kcal/mol)	ee (%)d
1		1.49	88	1.72	92
2		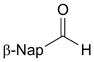1.39	86	1.22	81
3		2.09	96	1.88	94
4		1.45	87	1.49	88
5		1.24	82	0.94	70
6		1.37	85	1.49	88
7		1.64	91	1.49	88
8		1.56	89	1.16	79
9		0.71	57	0.92	69
10		0.96	71	0.73	59
11		1.67	91	1.40	86

^aΔG_ee refers to the energy difference between the transition structures of the pathways leading to the S and R enantiomeric products.

^bCalculated values from a leave-one-out model constructed from the 10 remaining substrates.

^cValues obtained from ee results by using ΔG = −RTln[(S)/(R)].

^dFrom reference ^xxi.

(1)

The plot of experimental and calculated ΔG_ee values in Figure 1 confirms the ability of the leave-one-out models to predict the selectivity of substrates that were not used in construction of the actual model. Notably, a good cross validation correlation was observed with r²_LOO = 0.67 and a correlation coefficient (CC) of 0.82 (CC offers a rough gauge of the ability of the program to correctly rank the selectivities of different substrates). This tool would be invaluable in the many instances when asymmetric transformations of novel substrates through a well-known process (i.e. asymmetric hydrogenation) are required. With the wealth of data available for a broad range of substrates and catalysts, it would be straightforward to construct models for each catalyst and then screen the novel substrates in silico in a matter of minutes. Such a process would allow the chemist to rapidly refine selection of catalysts for initial screening.

Figure 1.

Cross validation results of substrates from entries 1–11 (Table 1): Plot of predictions from leave-one-out models constructed from the 10 remaining substrates (y = 0.85x + 0.30, r²_LOO = 0.67, CC = 0.82)

In addition, the EPF points identified in the models (Figure 2) indicate that two regions of the substrates account for most of the variance in enantiomeric excess; groups of different sizes or electronic aspects at these positions modify the enantioselection. In line with our general understanding of this transformation, the ESP points are primarily near the aldehyde group, probably reflecting electronic differences in the aldehyde carbonyl which coordinates the catalyst, or the point of variation on the aromatic ring, most likely reflecting steric biases between these sites and the catalyst.

Figure 2.

Superposition of the EPF points from the 11 leave-one-out models around the 11 aldehyde substrates listed in Table 1 (blue = positive EFP value correlates to higher ee, red = positive EFP value correlates to lower ee).

With this success in hand, a second more challenging case with a broader range of substrates (Eq 2, Table 2, R = alkyl and aryl) was analyzed.^xxii After aligning the substrates using the CHO atoms of the aldehyde, these structures were analyzed with the QMQSAR program as described above.

Table 2.

Experimental and Calculated Substrate Enantioselection for the Reaction in Eq 1.

entry	RCHO	calculated		experimental		entry	RCHO	calculated		experimental
		ΔGeea,b (kcal/mol)	ee (%)	ΔGeea,c (kcal/mol)	ee (%)d			ΔGeea,e (kcal/mol)	ee (%)	ΔGeea,c (kcal/mol)	ee (%)d
1		1.98	96	2.62	99	11		1.63	93	1.81	95
2		1.98	96	2.07	97	12		1.69	94	1.72	94
3		1.82	95	1.64	93	13		2.72	99	2.07	97
4		0.04	4	0.96	75	14		1.80	95	1.93	96
5		1.44	90	1.81	95	15		0.03	3	0.02	2
6		0.23	23	1.18	83	16		1.00	76	0.64	57
7		2.16	97	2.27	98	17		0.10	10	0.22	22
9		1.76	94	1.81	95	19		0.69	60	0.56	51
10		0.97	75	1.46	90	20		2.19	97	0.56	51

^aΔG_ee refers to the energy difference between the transition structures of the pathways leading to the S and R enantiomeric products.

^bCalculated values from a leave-one-out model constructed from the 9 remaining substrates in entries 1–10.

^cValues obtained from ee results by using ΔG = −RTln[(S)/(R)].

^dFrom reference ^xxii.

^eCalculated values from a leave-one-out model constructed from the 9 remaining substrates in entries 11–20.

(2)

Interestingly, one model does not account for all of the results. In undertaking the model construction, models with 1–4 EPF points per substrate were evaluated again. Fitted models employing two points initially appeared promising and took on the form: ΔG_calc = 2.35 + 0.55* EPF₁ − 0.15* EPF₂ (SD = 0.43, r² = 0.68). However, the high standard deviation was troublesome. Furthermore, despite a thorough evaluation of the parameters, one model could not be identified that yielded highly cross-validated results in a leave-one-out analysis.^xx

To locate the source of this problem, partial substrate sets were employed. When two sets of models were generated, two-point models with much lower standard deviations could be identified. For example, with entries 11–20 of Table 2 the model displayed a standard deviation of 0.09 kcal/mol and an r² value of 0.98. In addition, satisfactorily cross-validated models were obtained. For entries 1–10, one model was obtained with r²_LOO = 0.61 and CC_LOO = 0.77 (Figure 3). For entries 11–20, a second model was obtained with r²_LOO = 0.61 and CC_LOO = 0.78 (Figure 4). The fact that no single model could accommodate all the results in spite of the large number of potential EFP variables explored and the success of this method with highly different substrates and catalysts in the past^v–xv suggests that there is no underlying relationship between all the substrates in this instance. One of the assumptions in constructing these type of QSSR models is that each substrate (or catalyst) interacts with its corresponding catalyst (or substrate) in the same way. The presence of two distinct models here may indicate different mechanistic regimes. For example, interaction of the substrate and catalyst may not be constant. The aryls of the catalyst may undergo a π-stacking interaction with the aryl groups in the first group of substrates in Table 2 resulting in a different set of low energy transition states compared to those from the in the second group of substrates. Similar breaks observed with other linear free energy relationships.^xxiii As a consequence, this MLR QSSR method probe potential mechanism changes in silico and indicate when further experimental study is warranted.

Figure 3.

Cross validation results of substrates from entries 1–10 (Table 2): Plot of predictions from leave-one-out models constructed from the 9 remaining substrates (y = 0.82x + 0.01, r²_LOO = 0.61, CC_LOO = 0.77)

Figure 4.

Cross validation results of substrates from entries 11–20 (Table 2): Plot of predictions from leave-one-out models constructed from the 9 remaining substrates (y = 0.89x + 0.38, r²_LOO = 0.61, CC_LOO = 0.78)

4. Conclusion

The ability to predict the enantioselectivity of novel substrates in asymmetric transformations as demonstrated above with QMQSAR, would be invaluable in the many instances when a well-known process (i.e. asymmetric hydrogenation) needs to be applied. Such a process would allow the chemist to rapidly refine selection of catalysts to optimize productivity in reaction screening. Furthermore, the output of the QMQSAR program provides direct information to the user as to which portions of the substrates are most relevant to enantioselection. In addition to predicting the selectivity of new substrates, the QSSR method described herein may be a simple, rapid means of assessing mechanism shifts in many experimental systems. Further mechanism experiments to investigate this proposed mechanism shift will be reported in due course.