A tract-specific framework for white matter morphometry combining macroscopic and microscopic tract features

Abstract

Diffusion tensor imaging plays a key role in our understanding of white matter both in normal populations and in populations with brain disorders. Existing techniques focus primarily on using diffusivity-based quantities derived from diffusion tensor as surrogate measures of microstructural tissue properties of white matter. In this paper, we describe a novel tract-specific framework that enables the examination of white matter morphometry at both the macroscopic and microscopic scales. The framework leverages the skeleton-based modeling of sheet-like white matter fasciculi using the continuous medial representation, which gives a natural definition of thickness and supports its comparison across subjects. The thickness measure provides a macroscopic characterization of white matter fasciculi that complements existing analysis of microstructural features. The utility of the framework is demonstrated in quantifying white matter atrophy in Amyotrophic Lateral Sclerosis, a severe neurodegenerative disease of motor neurons. We show that, compared to using microscopic features alone, combining the macroscopic and microscopic features gives a more complete characterization of the disease.

1. Introduction

Diffusion tensor imaging (DTI) (Basser et al., 1994a,b) has become an indispensable tool for studying white matter both in normal populations and in populations with brain disorders. Aided by water diffusion’s unique sensitivity to microstructure, DTI has demonstrated great success in depicting in vivo the intricate architecture of white matter (Pajevic and Pierpaoli, 1999) as well as in providing quantitative imaging measures indicative of white matter integrity (Basser and Pierpaoli, 1996; Pierpaoli et al., 1996). Using such measures, most commonly fractional anisotropy (FA) and mean diffusivity (MD), whole-brain voxel-based analysis has traditionally been used to identify differences in white matter microstructure across populations of interest (e.g. Eriksson et al., 2001; Ciccarelli et al., 2003; Simon et al., 2005; Buchsbaum et al., 2006).

Recently, a number of alternative techniques have been proposed to improve white matter morphometry by taking into account white matter’s unique geometry and functional organization. Leveraging the fact that white matter structures are geometrically thin tube- or sheet-like objects, the tract-based spatial statistics (TBSS) (Smith et al., 2006) pioneered the idea of projecting volumetric data onto the white matter skeleton to harness increased statistical power gained from this dimensionality reduction. The TBSS approach significantly advanced the state-of-the-art of voxel-based analysis of white matter, evidenced by its increasingly ubiquitous adoption in recent clinical studies (e.g. Anjari et al., 2007; Giorgio et al., 2008; Ciccarelli et al., 2009). However, white matter is organized as individual functional units, known as tracts, that form pathways interconnecting distinct brain regions. By deriving white matter skeletons from segmentations computed by thresholding FA maps, the TBSS approach lacks the ability to distinguish certain adjacent white matter tracts and thus has limited capacity for anatomical specificity.

Recognizing that, functionally, white matter are organized into distinct tracts, other recent techniques have been developed to enable the analysis of individual white matter tracts, a capability essential for testing specific a priori hypothesis as well as for reducing confounding effects of neighboring tracts. The majority of these methods are tailored for tracts with tubular geometry, such as the cingulum and fornix, or portions of tracts that are tube-like, such as the genu and splenium of the corpus callosum (Corouge et al., 2006; Goodlett et al., 2009; Niethammer et al., 2009; O’Donnell et al., 2009). The common feature of these algorithms is the construction of tract center-line to capture the essence of tubular geometry and the projection of data onto the center-line for statistical analysis. To support the analysis of tracts with sheet-like geometry, such as corpus callosum and cortico-spinal tract, we have recently developed a new technique called tract-specific analysis (TSA) (Yushkevich et al., 2008). Similar to TBSS, the TSA approach derives skeletons for dimensionality reduction of data; but unlike TBSS, it constructs skeletons for individual tracts and represents skeletons as parametric surface patches to enforce sheet-like geometry of the modeled tracts.

These recent innovations in analysis of white matter tracts are supported by the broad availability of techniques to segment individual tracts robustly using diffusion data. The most widely used tract segmentation approach is deterministic streamline tractography, which produces tracking results of major white matter tracts with excellent agreement with definitions based on classical postmortem dissection (See Mori and van Zijl, 2002, for a review). The advance in virtual white matter dissection culminates in the creation of the first fiber tract-based atlas of human brain white matter by Wakana et al. (2004), using a combination of the fiber assignment by continuous tracking (FACT) algorithm (Mori et al., 1999) and the multiple regions-of-interest (ROI) selection strategy (Conturo et al., 1999).

In addition to being a prerequisite for tract-specific assessment of microscopic features, e.g. FA or MD, the availability of tract segmentations presents a unique opportunity for quantifying changes in macroscopic properties of tracts, e.g. changes in tract size and shape. Such capability to quantify macroscopic atrophy has already played a critical role in monitoring disease effects on grey matter structures (See Thompson et al., 2007, for a review). However, in the case of white matter tracts, similar capability exists only for tracts with tubular geometry (O’Donnell et al., 2009; Azadbakht et al., 2009), but not yet for sheetlike tracts.

In this paper, we propose a tract-specific framework for quantifying macroscopic properties of sheet-like tracts. A preliminary version of this work can be found in (Zhang et al., 2009). The proposed framework is underpinned by the continuous medial representation (cm-rep) (Yushkevich et al., 2006; Yushkevich, 2009), a deformable modeling and shape analysis technique uniquely suited for our purpose. The cm-rep can not only accurately model major white matter tracts with sheet-like geometry (Yushkevich et al., 2008), but also establish shape-based correspondence over entire tract interior and across subjects for simultaneous group analysis of shape and appearance features (Sun et al., 2007; Yushkevich et al., 2007). Here, we use the cm-rep to derive a tract thickness map, defined over its skeleton, and show how the resulting thickness information can be combined with the FA map projected onto the same skeleton to improve the detection of white matter changes. To the best of our knowledge, the proposed framework enables for the first time the joint analysis of white matter morphometry at both macroscopic and microscopic scales. We illustrate its potential in an application to examine white matter damages in Amyotrophic Lateral Sclerosis (ALS), a progressive and fatal neurodegenerative disease of motor neuron resulting in known gross atrophy in the motor pathway (Wang et al., 2006).

The rest of the paper is organized as follows: Sec. 2 gives the detail of the proposed framework. The application to ALS study is described in Sec. 3. Finally, in Sec. 4, we discuss potential limitations of the proposed framework and how it may be improved with future works.

2. Methods

2.1. Overview of the framework

The proposed tract-specific morphometry framework takes as input a set of DTI volumes, in the native space of their corresponding subjects, and outputs statistics on tract shape and microstructure in three processing steps: subject-space segmentation, shape-based normalization, and statistical analysis. First, subject-space segmentation parcellates the whole of white matter into individual tracts or identifies just the tract(s) of interest. This step is repeated for each subject and is done in each subject’s native space to faithfully capture the specific shape char-acterisitcs of the tracts in individual subjects. Second, shape-based normalization makes use of the cm-rep based shape matching to establish spatial correspondence of the tracts across the study cohort. This step draws on the success of modeling sheet-like tracts with the cm-rep (Yushkevich et al., 2008) and enables thickness measurement on the tracts that, crucially, can be compared, along with microstructural features, across subjects. Finally, statistical analysis involves the analyses of shape and microstructure both individually and jointly. The latter employs a novel multivariate inference technique based on the analysis of the joint probability density function (pdf) of the feature set whose efficacy has been demonstrated in a cortical folding study of neonatal brains using the joint analysis of folding complexity and shape indices (Awate et al., 2009b,a). In the following, we discuss each component in detail.

2.2. Subject-space tract segmentation

For tract segmentation in individual subjects, we adopt the strategy of atlas-based segmentation, which has been successfully applied for white matter parcellation (Goodlett et al., 2009). Atlas-based segmentation is a strategy rooted in the theory of deformable template (Grenander, 1994). In this paradigm, an atlas, which serves as the deformable template, is annotated with detailed anatomical or functional labels. To segment the image of an individual, an image registration algorithm is first used to establish the spatial correspondence between the image and the atlas. The resulting spatial correspondence is expressed in terms of a spatial transformation. The segmentation of the image is then achieved by deforming the labels in the atlas space onto the native space of the image with the spatial transformation. Traditionally, this strategy has been widely used in the analysis of structural images, such as, T1-weighted volumes (e.g. Joshi et al., 2004). The atlas is preferably a population-averaged T1 image, rather than that of a single subject, to accommodate the natural inter-subject variability, and is manually annotated with the labeling of different cortical and subcortical structures. In the current context, the desirable atlas is a population-averaged DTI template, i.e., a DTI volume capturing the average shape and diffusion features of an entire population. Such an atlas is segmented into individual white matter tracts robustly using deterministic streamline tractography (Lawes et al., 2008; Yushkevich et al., 2008).

We choose atlas-based segmentation over the alternative of directly applying streamline tractography to individual subjects because the latter is less robust for processing DTI data acquired in typical clinical studies, such as our ALS study described in Sec. 3.1. Streamline tractography with an algorithm such as FACT combined with the multiple-ROI selection strategy has been shown to be highly reproducible (Wakana et al., 2007) and effective in excluding outliers (Huang et al., 2004). However, for the signal-to-noise ratio (SNR) typically seen in clinical DTI data, the approach has also been found to systematically underestimate the extent or size of tracts (Huang et al., 2004), making it less desirable for quantifying tract size and shape. For higher quality diffusion data, such as those acquired with high angular resolution diffusion imaging (HARDI), potentially superior alternative approaches exist and they are discussed in Sec. 4.

The detail of our atlas-based segmentation implementation is given below, which includes three steps: simultaneous construction of the population-averaged DTI template and spatial normalization of individual subjects to the template; tract parcellation in the template; tract parcellation in the subjects.

2.2.1. Template construction and spatial normalization

We use DTI-TK (Zhang et al., 2007b) (http://www.nitrc.org/projects/dtitk), an atlas construction and spatial normalization toolkit optimized for DTI data, to construct the population-averaged DTI template and establish spatial correspondence between the template and individual subjects in a study population simultaneously. DTI-TK follows the general principle of constructing unbiased population-averaged template from a cohort of images (Guimond et al., 2000; Joshi et al., 2004; Avants and Gee, 2004). The resulting template captures the average shape and appearance features of the entire cohort and minimizes the deformations required to align individual images to the template.

Furthermore, to improve the alignment between white matter tracts, DTI-TK leverages a novel deformable DTI registration algorithm (Zhang et al., 2006), in which image similarity is computed on the basis of full tensor images, rather than scalar features. When measuring similarity between tensor images, it is essential to take into account the fact that when a transformation is applied to a tensor field, the orientation of the tensors is changed (Alexander et al., 2001). A unique property of this registration algorithm is the ability to model the effect of deformation on tensor orientation as an analytic function of the Jacobian matrix of the deformation field. By using full tensor information in the similarity metric, the method aligns white matter tracts better than scalar-based registration methods, as demonstrated by Zhang et al. (2007a) in a task-driven evaluation study.

The detailed implementation of DTI-TK is given in Zhang et al. (2007b). Here we summarize the process. When building the atlas, the initial average image is computed as a Log-Euclidean mean (Arsigny et al., 2006) of the input DTI data. The average is then iteratively refined by repeating the following procedure: register the subject images to the current average with the DTI registration algorithm in Zhang et al. (2006), then compute a refined average for the next iteration as the Log-Euclidean mean of the normalized images. This procedure is repeated until the average image converges.

2.2.2. Tract parcellation in the template

We follow the approach described by Yushkevich et al. (2008) and parcellate the template into individual white matter tracts using an established streamline tracking protocol (Wakana et al., 2004). The validity of this approach has recently been demonstrated by Lawes et al. (2008) in a comparison to classic postmortem dissection. Furthermore, a population-averaged DTI template has significantly higher SNR than any individual DTI volume, making streamline tractography with the chosen protocol in a template substantially less prone to underestimate tract size than an individual volume (Huang et al., 2004).

Our framework focuses on the tracts that have a major portion that is sheet-like. As identified in (Yushkevich et al., 2008), six major tracts fit into this category: corpus callosum (CC), corticospinal tracts (CST)¹, inferior fronto-occipital tracts (IFO), inferior longitudinal tracts (ILF), superior longitudinal tracts (SLF), and uncinates (UNC). White matter tracts that are more appropriately represented by tubular models have been extensively studied in the literature (Corouge et al., 2006; Goodlett et al., 2009; Niethammer et al., 2009; O’Donnell et al., 2009) and are not considered here.

Specific detail of the parcellation is given in (Yushkevich et al., 2008). Here we outline the procedure. First, apply the FACT algorithm to the DTI template, which outputs all candidate fibers. Then, for each tract of interest, extract the subset of the candidate fibers belonging to the tract using the multiple ROI selection strategy. Next, generate the binary 3D segmentation of each tract by labeling voxels in the template through which at least one member fiber of the tract passes. Finally, edit the binary segmentations to remove portions of tracts that are not sheet-like, such as the tapetum of the corpus callosum.

2.2.3. Tract parcellation in the subjects

The tracts of interest in each subject are parcellated by mapping the binary segmentations delineated in the template to the subject space using the spatial correspondence between the template and the subject determined using DTI-TK as described in Sec. 2.2.1. In practice, this involves, for each subject, first inverting the spatial transformation that aligns the subject to the template and then applying the resulting inverse transformation to deform the template space segmenation into the subject space. The procedure requires the inverse of each spatial transformation to be well-defined. The DTI-TK implementation satisfies this condition by constraining the resulting spatial transformations to be diffeomorphic, i.e., with strictly positive Jacobian determinant everywhere in the image domain.

2.3. Shape-based tract normalization

After segmenting each tract of interest in individual subjects, this processing step employs shape-based normalization, i.e., fitting the cm-rep model of a tract to each of its subject-space segmentations, to establish tract-wise spatial correspondence across the subjects over the interiors of segmented white matter tracts. The cm-rep is particularly suited for this task for a number of reasons. First, it has been successfully applied to accurately model the major sheet-like white matter tracts described in Sec. 2.2.2 (Yushkevich et al., 2008). Second, it establishes a continuous shape-based coordinate system, supporting the parametrization of its entire interior with a one-to-one mapping and spatial correspondence across subjects over its interior. Lastly, because the interior of individual white matter tracts is largely homogeneous, spatial correspondences computed from image registration are primarily determined by a local smoothness prior and thus may not be reliable. Shape-based normalization with the cm-rep offers a suitable alternative to registration for normalizing object interiors, relying on global shape as the principal basis for correspondence. For objects with non-informative interior, its benefit in reducing spurious variations in deformation often associated with registration has been demonstrated by Sun et al. (2007) in the matching of 2-D midsagittal cross section of the corpus callosum. The details of the cm-rep, its shape-based coordinate system, and the tract fitting procedure are given below.

2.3.1. Formulation of the cm-rep

The cm-rep describes the geometrical relationship between the skeleton and the boundary by defining a synthetic skeleton consisting of a parametric medial surface represented as a dense triangular surface mesh and a radial field defined over the surface. The radial field specifies, for each vertex on the mesh, the radius of a sphere centered at the vertex. The boundary of the object represented by the cm-rep is uniquely determined and can be computed from the synthetic skeleton via inverse skeletonization (Damon, 2004, 2005; Yushkevich et al., 2006).

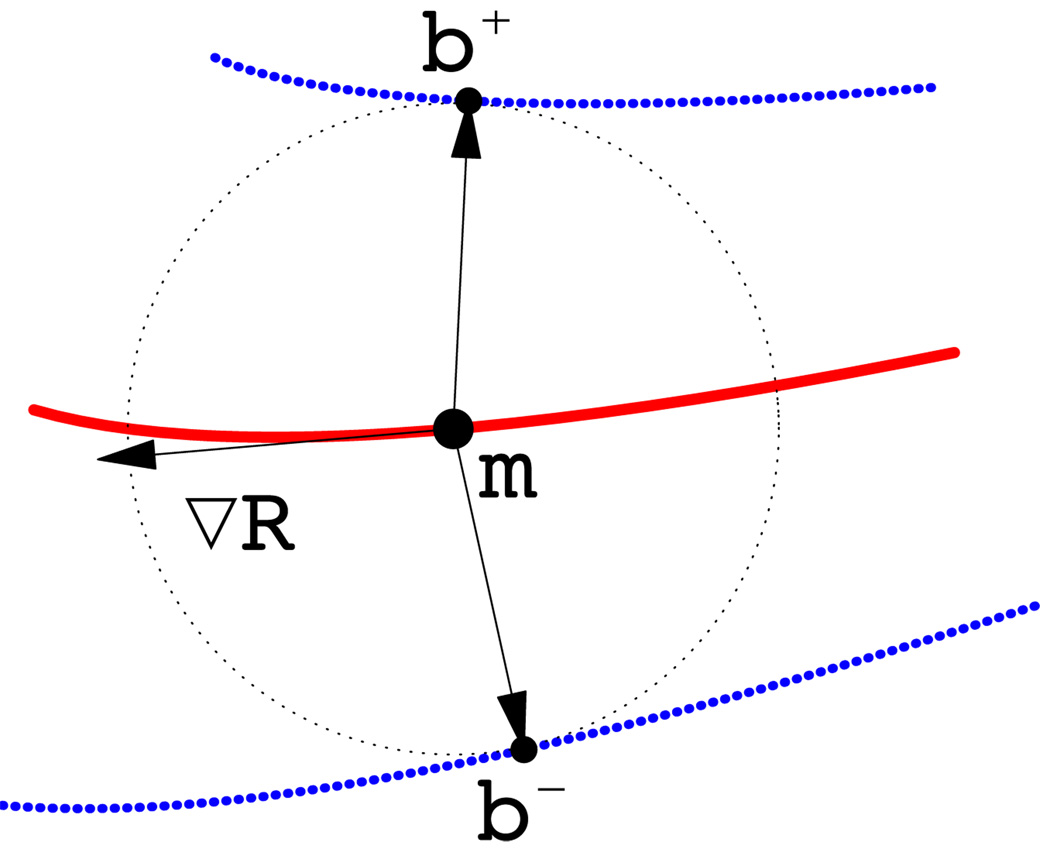
More concretely, a cm-rep model is a triangular mesh S, each of its vertices is a tuple {m_i, R_i}, where m_i ∈ ℝ³ is the coordinate of the vertex i and R_i ∈ ℝ⁺ is the radius value, describing the local thickness of the model. For the current application, the mesh is a single surface patch defined over some domain Ω with boundary ∂Ω. The corresponding boundary surface mesh b consists of two halves, b+ and b ⁻, lying on the opposite sides of the skeleton S but sharing a common edge (See Figure 1 for an illustration). The boundary halves are uniquely determined by the skeleton S via inverse skeletonization:

$${\mathbf{b}}^{\pm }=\mathbf{m}+R{\mathbf{U}}^{\pm },$$ (1)

$${\mathbf{U}}^{\pm }=-{\nabla }_{\mathbf{m}}R\pm \sqrt{1-{\Vert {\nabla }_{\mathbf{m}}R\Vert }^2}{\mathbf{N}}_{\mathbf{m}},$$ (2)

where N _m denotes the unit normal to the skeleton, ∇_m R the Riemannian gradient of R on the manifold m, and U^± the unit normals to the boundary halves b ^± (Yushkevich et al., 2006). The boundary surface b will have a desired topology of a sphere when a number of constraints on m and R are met, including the condition that ∥∇_m R∥ < 1 on Ω except for ∂Ω where ∥∇_m R∥ = 1 (Damon, 2004, 2005; Yushkevich et al., 2006). These constraints are enforced as penalty terms during fitting.

Figure 1.

Two-dimensional diagram of medial geometry. The red curve represents the medial surface (skeleton) m. The circle has radius R, given by the radial field on m. The boundary, shown in blue, consists of two parts, b⁺ and b⁻, derived from the skeleton and radial field by inverse skeletonization (Yushkevich et al., 2006). The vector ∇_mR lies in the tangent plane of m and points in the direction of greatest change in R. The arrows pointing from m to b⁺ and b⁻ are called spokes.

2.3.2. Shape-based coordinate system

The cm-rep model defined above endows the following shape-based coordinate system. Let us refer to the vector RU^± with tail on the medial surface m as spokes. Because the spokes span the interior of the model, i.e., the region enclosed by the boundary b, and because each point within the region belongs to one spoke only, each interior point can be uniquely parametrized by the tail of the spoke it belongs to and its position along the spoke. Let (u, v) ∈ Ω denote the coordinates of the tail of the spoke, a point on the medial surface m, and ξ ∈ [−1, 1] the position along the spoke (when ξ > 0, it references the spoke RU⁺, and when ξ < 0, the spoke RU⁻). Every interior point x can then be assigned the coordinates (u, v, ξ), such that:

$$\mathbf{x}(u,\upsilon ,\xi )=\{\begin{array}{l}\mathbf{m}(u,\upsilon )+\xi R(u,\upsilon ){\mathbf{U}}^{+}(u,\upsilon )\text{\hspace{1em}if}\xi >0;\hfill \\ \mathbf{m}(u,\upsilon )-\xi R(u,\upsilon ){\mathbf{U}}^{-}(u,\upsilon )\mathrm{o}/\mathrm{w}.\hfill \end{array}$$ (3)

The assignment is unique and one-to-one, except when (u, υ) ∈ ∂Ω, in which case the spokes R U ⁺ and R U ⁻ coincide. This property of the mapping ensures that the projection of volumetric diffusion data onto skeleton surfaces, described in Sec. 2.4, is well defined.

2.3.3. Fitting the cm-rep to tract segmentations

To fit a set of subject-space binary segmentations of a particular tract, a template cm-rep model of the tract is first generated, which is then fitted to each subject-space binary segmentation to achieve shape-based normalization. The detailed description of the cm-rep fitting algorithm is given in Yushkevich et al. (2006). Briefly, fitting a cm-rep model to a binary segmentation is formulated as an optimization problem. The parameters in the search space consists of the location and the radius of every vertex in the medial surface mesh. The optimization seeks the combination of the parameters that maximize the overlap between the binary segmentation and the object represented by the deforming cm-rep model while minimizing a number of penalty terms constructed to enforce the various constraints for the cm-rep model to represent valid objects. An additional penalty term regularizes the parametrization of the skeleton to provide correspondence along the medial surface.

To create the template cm-rep model, we follow the procedure described in Yushkevich et al. (2008), which is summarized below. An initial cm-rep model is built from the template-space binary segmentation of the tract with a four-stage pipeline: (1) computing the initial skeleton via direct skeletonization; (2) pruning the initial skeleton by finding its two-dimensional embedding, which assigns a pair of coordinates (u, v) ∈ ℝ² to each vertex in the skeleton; (3) determining the domain Ω as the smallest region in ℝ² enclosing the (u, v) coordinates of all vertices; (4) producing a quality triangulation of Ω with comforming constrained Delaunay triangulations. The template cm-rep model is then generated by fitting the initial model to the template-space binary segmentation using the cm-rep fitting algorithm described above.

2.4. Statistical analysis of thickness and diffusion features

For any given tract, shape-based normalization determines, for each subject-space binary segmentation of the tract, its fitted cm-rep model. This processing step makes use of these fitted cm-rep models to compute statistics on tract thickness and features of diffusion. Tract thickness, as discussed in Sec. 2.3.1, is naturally captured with the cm-rep model: Given a point with the coordinates (u, v) on the skeleton surface of subject i, the tract thickness at the point is defined as the diameter of the sphere centered around the point, i.e., 2R_i(u, v).

Diffusion features of the same tract can be projected onto the same skeleton surface using the dimensionality reduction approach described in Smith et al. (2006) and Yushkevich et al. (2008). For illustration, we describe the strategy originally proposed in Smith et al. (2006) to minimize the effect of image misregistration and recently adapted for the cm-rep formulation in Yushkevich et al. (2008). In the cm-rep adapted version, the diffusion tensor projected onto a point (u, v) on the skeleton of subject i is chosen as the one with the largest FA of all the tensors sampled along the two spokes at the point in the native-space DTI volume of the subject, i.e.,

$$\begin{array}{l}{\tilde{D}}_i(u,\upsilon )=D_i(\mathbf{x}(u,\upsilon ,{\xi }^{*}(u,\upsilon ))),\text{where}\hfill \\ {\xi }^{*}(u,\upsilon )=\text{arg}\underset{\xi \in [-1,1]}{\text{max}}\text{FA}(D_i(\mathbf{x}(u,\upsilon ,\xi ))).\hfill \end{array}$$ (4)

These maps of thickness and diffusion properties computed for each subject in the same shape-based coordinate frame enable a combined analysis of both macroscopic and microscopic features. In our framework, we apply univariate statistical mapping on thickness and diffusion features separately to gain complementary tract information at different scales. A nonparametric statistical mapping of group differences is implemented as described in Yushkevich et al. (2008). Briefly, we compute a two-sample t-test at each point on the skeleton surface of a tract and correct for multiple comparison with the standard permutation-based non-parametric cluster analysis that controls for the family-wise error rate (FWER) (Nichols and Holmes, 2001).

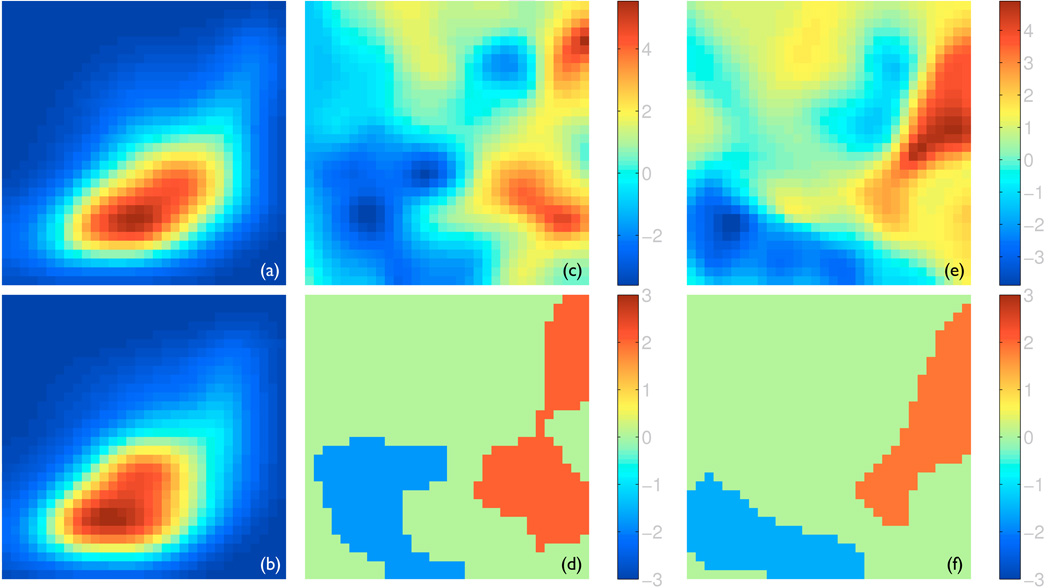
In addition, we utilize a novel multivariate analysis (Awate et al., 2009b,a) to directly exploit the relationship between thickness and diffusion properties. Specifically, for each subject, we build a joint probability density function (pdf) of thickness and diffusion properties which captures the interdependencies of thickness and diffusion features as provided solely by the data. The pdf of a subject is estimated by determining the fraction of points on its skeleton surface with a particular value of thickness and diffusion properties (See Fig. 3 for an example). We use this pdf as the multivariate high-dimensional descriptor of the associated white matter tract to summarize its macroscopic and microscopic properties jointly. Statistical testing for group differences with these high-dimensional descriptors is then done via the same nonparametric test as the univariate statistical mappings above, except here the test is done in the functional domain of the pdf rather than the spatial domain of the skeleton surface. The implementation requires the discretion of the joint pdfs on an appropriate Cartesian grid. The choice of the grid resolution is constrained by the amount of data available, i.e., the sample size underlying the density estimation. For example, a larger sample size will support a higher-resolution probing of the data to search for finer-scale changes. Within this constraint, the choice of the grid resolution adjusts the trade-offs similar to those involved in voxel-based morphometry studies in standard fMRI literature regarding smoothing of the data and the scale at which statistically significant effects are searched for in the data, e.g., coarser grids result in a higher degree of smoothing, implicitly.

Figure 3.

The joint analysis of thickness and FA. In all panels, FA is plotted along the horizontal axis and varies from 0.1 to 0.7, while thickness is plotted along the vertical axis and varies from 0 to 8 mm. Both values are plotted in linear scale. Panels (a) and (b) show the joint probability density functions (pdf) of the left CST averaged for all the healthy controls and all the ALS patients, respectively, with the hot color corresponding to higher density. Panels (c) and (e) show the t-statistics maps of comparing the joint pdfs of the healthy controls to those of the ALS patients for the left and right CSTs, respectively. Panels (d) and (f) show the significant clusters with z-scores determined via permutation-based non-parametric testing for the left and right CSTs, respectively. The red clusters corresponds to larger density in the healthy controls and the blue clusters higher density in the ALS patients.

3. Experimental Evaluation

We demonstrate the proposed analysis in an application to identify white matter changes in ALS. Because of the existing hypothesis that ALS strongly affects the motor pathway, only the left and right CSTs were included in the analysis. Two univariate statistical mappings on thickness and FA were first performed, followed by the multivariate analysis using the joint pdfs of thickness and FA. The clusters with FWE-corrected p-value < 0.05 were deemed significant in all analyses.

3.1. Subjects and imaging protocol

The subjects used in this evaluation were recruited from the community served by the University of Pennsylvania Health System (UPHS) as part of an ongoing clinical investigation into white matter changes in ALS using magnetic resonance imaging (MRI). Out of a total of 29 subjects scanned, only 16 were acquired with the same diffusion imaging protocol and they were chosen for the present study. Among them were 8 ALS patients (age 42–77, mean age and standard deviation 60±11; 6 male, 2 female) and 8 healthy controls (age 40–56, mean age and standard deviation 46±6; 6 male, 2 female). All subjects provided informed consent, following procedures approved by the local Institutional Review Board of the UPHS. Diffusion tensor imaging was performed using a single-shot, spin-echo, diffusion-weighted echo-planar imaging sequence on a 3.0-T Siemens Trio scanner (Siemens Medical Solutions, Erlangen, Germany). The diffusion sampling scheme consisted of one image with minimal diffusion weighting (b = 0 s/mm²), followed by 12 images measured with 12 non-collinear and non-coplanar diffusion encoding directions isotropically distributed in space (b = 1000 s/mm²). Additional imaging parameters for the diffusion-weighted sequence were: TR = 6500 ms, TE = 99 ms, 90° flip angle, number of averages = 6, matrix size = 128 × 128, slice thickness = 3.0 mm, spacing between slices = 3.0 mm, 40 axial slices with in-plane resolution of 1.72×1.72 mm, resulting in voxel dimensions equal to 1.72 × 1.72 × 3.0 mm³.

The diffusion-weighted images were corrected for motion and eddy-current artifacts using the method described in (Mangin et al., 2002), prior to extracting brain parenchyma with the Brain Extraction Tool (Smith, 2002). The diffusion tensor images were then reconstructed from the diffusion-weighted images using the standard linear regression approach Basser et al. (1994a). Finally, the resulting tensor volumes were resampled to a voxel space of 128 × 128 × 64 with voxel dimensions equal to 1.72 × 1.72 × 2.5 mm³. The resampled volume, with axial dimension equal to a power of 2, is better suited for registration algorithms that require the construction of standard multi-resolution image pyramids.

3.2. Results

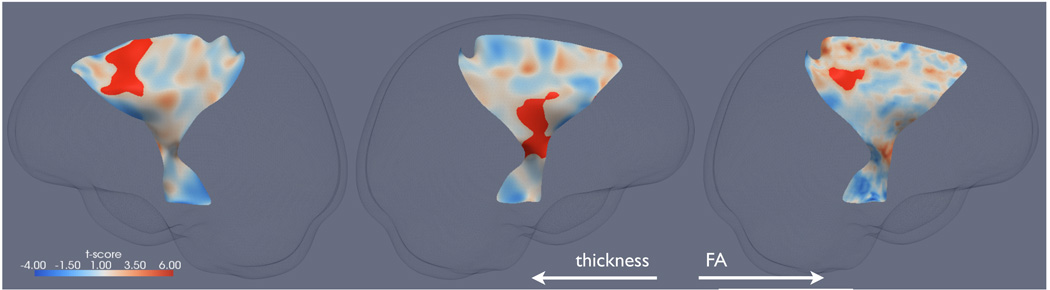
The results of the two univariate statistical mappings are shown in Fig. 2. Two significant clusters of reduced thickness in ALS compared to healthy controls were found with one on each CST. The cluster on the left CST corresponds to the internal capsule and the one on the right CST maps to Broadmann area (BA) 6, the premotor cortex and supplementary motor cortex. One significant cluster of reduced FA in ALS was found on the left CST, which maps to BA 1, 2 & 3, the primary somatosensory cortex, BA 4, the primary motor cortex. Evidently, the macroscopic changes highlighted by the thickness analysis provides a more complete picture of white matter atrophy caused by ALS than the microscopic changes identified by the FA analysis alone.

Figure 2.

The significant clusters of reduced thickness and FA in ALS compared to healthy controls (in red) overlaid on the corresponding t-statistics maps on the skeleton surfaces of the CSTs. From left to right: the thickness cluster and t-statistics map for the right CST, the thickness cluster and t-statistics map for the left CST, the FA cluster and t-statistics map for the left CST.

The results of the multivariate analysis using the joint pdfs of thickness and FA are shown in Fig. 3. We show the results for the joint pdfs discretized on a Cartesian grid of size 32-by-32, although the findings are consistent for a range of grid resolutions. The appearance of the joint pdfs is illustrated in Panels (a) and (b) using the joint pdfs of the left CSTs averaged for the healthy controls and the ALS patients, respectively. The two visibly different pdfs indicate that the healthy controls have more regions of large FA and thickness while the ALS have more areas of low FA and thickness. A similar pattern is observed for the right CST (not shown). These observations are supported by subsequent non-parametric statistical testing. Panels (c) and (e) show the t-statistics maps of comparing the joint pdfs of the healthy controls to those of the ALS patients. The significant clusters, determined by permutation-based multiple comparison correction, were shown in Panel (d) for the left CST and (f) for the right CST. The red clusters represent the areas of higher density in the healthy controls − high FA, while the blue clusters pinpoint the regions of higher density in the ALS patients − low FA and low thickness.

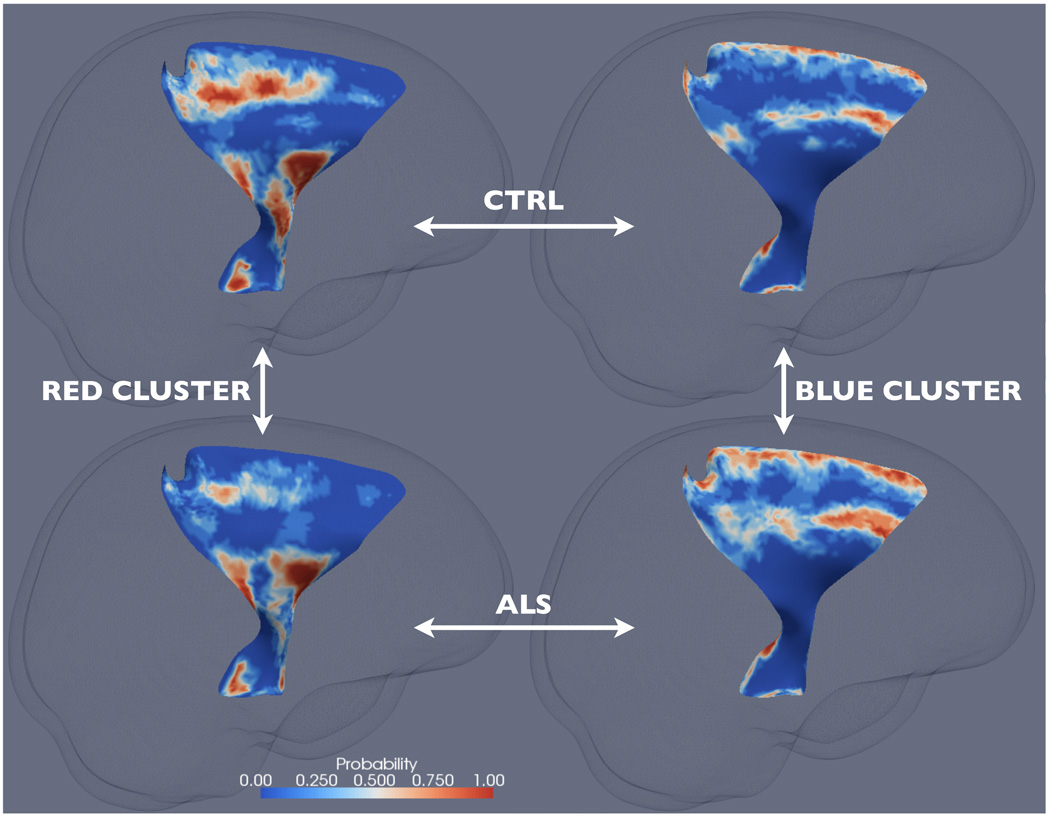
The significant clusters from the joint analysis can be better understood by mapping them back into the spatial domain, i.e., onto the skeleton surfaces of the CSTs of the individual subjects. Specifically, for each of the four clusters and for each subject group, we determined a cluster-membership probability map of the corresponding CST skeleton surface. Each of these maps were computed by finding, at each point on the corresponding skeleton surface, the probability of the location with their FA and thickness values falling within the corresponding cluster for the corresponding subject group. For instance, for some point V on the left CST, if 4 out of 8 healthy controls have their FA and thickness values at V fall within the red cluster on the left CST, then the probability map of the healthy controls for the red cluster on the left CST will have a value of 0.5 at V.

The four probability maps corresponding to the two clusters on the left CST are shown in Fig. 4. One striking observation is that, for both the healthy controls and the ALS patients, the red cluster is mapped to almost identical anatomical areas, including, from interior to superior, the cerebral peduncle, the internal capsule, and the primary motor and somatosensory areas (BA 1–4). For these areas, the cluster-membership probability is significantly less in ALS compared to the healthy controls. Because the red cluster corresponds to high FA, this finding indicates that some of the high FA normally found in these areas in the healthy controls are compromised and replaced by lower FA in ALS. Similarly, the blue cluster is mapped to near identical anatomical areas, including the premotor area (BA 6) and the peripheral of the structures. For these areas, the cluster-membership probability is significantly higher in ALS compared to the healthy controls. Since the blue cluster corresponds to low FA and thickness, this finding suggests that some of the normal FA and thickness found in these areas in the healthy controls are compromised and replaced by lower FA and thickness. Similar observations can be made with the probability maps on the right CST (not shown). Compared to the results of the univariate results, these results appear to give a more complete depiction of the extent of white matter atrophy in this severe neurodegenerative disease.

Figure 4.

The cluster-membership probability maps on the left CST for the red cluster and the healthy controls (top left), the red cluster and the ALS patients (bottom left), the blue cluster and the healthy controls (top right), and the blue cluster and the ALS patients (bottom right). See Sec. 3.2 for details.

4. Discussion

In this paper, we described a complete pipeline for extracting macroscopic features of white matter tracts using clinical DTI data and analyzing such features in conjunction with information about tract microstructure derived from DTI. The feasibility and utility of the pipeline were demonstrated with a clinical study. This work builds on the geometric modeling of sheet-like white matter tracts using the cm-rep developed to support our TSA framework (Yushkevich et al., 2008). There, the focus was on fitting a cm-rep model to the atlas-space segmentation of a tract and leveraging the shape-based coordinate system induced by the cm-rep model to support dimensionality reduction of diffusion data onto the medial skeleton. In doing so, the gain in statistical sensitivity through dimensionality reduction of data, a powerful idea pioneered by TBSS (Smith et al., 2006), and the reduction in confounding effect of neighboring structures through structure-specific analysis can be enjoyed in one single framework. Here, we focused on taking advantage of another opportunity enabled by structure-specific analysis, i.e., the access to the shape and size of tracts, information about tract macrostructure, By fitting the cm-rep model to the tract segmentations in the native-space of individual subjects, we were able to establish spatial correspondence across subjects through shape-based normalization, derive macroscopic tract features in the same space as microscopic tract features, and analyze these features jointly.

We evaluated the pipeline with a study of ALS, a disease of severe upper motor neuron degeneration. In patients with ALS, the corticospinal tracts have both reduced FA and volume compared to healthy subjects (Wang et al., 2006), making the disease ideal for evaluating the proposed pipeline. Although the cm-rep model captures a rich set of tract features, such as local tract thickness, area, and curvature, the present evaluation focuses on the application of local tract thickness in particular due to its direct relation to tract size, most relevant to understanding the pathology of ALS. We found that ALS patients have reduced FA in the portion of the right CST projecting to the primary motor cortex and the primary somatosensory cortex, and reduced thickness in the internal capsule of the right CST, which are consistent with previous findings of the disease, such as (Wang et al., 2006). Despite the significant age differences between our study populations (p-value = 0.0057), this finding can be attributed primarily to disease effect rather than aging, because normal aging has been shown to spare the degeneration of motor pathway (Salat et al., 2005). On the other hand, our finding of reduced FA in the portion of the left CST prjecting to the premotor cortex and supplementary motor cortex is consistent with aging-induced FA reduction in frontal white matter (Salat et al., 2005) and may not be manifestation of ALS pathology.

The proposed framework has been designed to work with clinical-quality DTI data. In particular, we chose atlas-based segmentation strategy for parcellating white matter tracts in subject-space because it is the most robust and feasible option given the quality of such data. However, because the segmentation depends on the spatial correspondence established through image registration, the accuracy of tract thickness will depend on the accuracy of image registration. Because image registration relies on spatial smoothness prior when boundary features are absent, it may not reliably separate the boundary between adjacent white matter tracts that traverse in parallel direction but connect to different brain regions. Furthermore, under pathological conditions, boundary features derived from properties of tensors may not correspond to the true boundary between white matter tracts. Hence, it is prudent to intepret the thickness results carefully and consider alternative factors that may contribute to the apparent thickness changes.

Despite our current focus on DTI data, the proposed framework can be adapted to support the analysis of HARDI data in principle. The significantly higher angular resolution of HARDI data supports both better estimation of single fiber orientation and resolution of multiple crossing fibers. Subject-space tract segmentation may be carried out in the native-space of individual subjects directly without the potential confounding effects of image registration. Furthermore, in addition to deterministic tractography, sophisticated probabilistic tractography may be applied as done in Azadbakht et al. (2009). The combination of high-quality HARDI data and ever more sophisticated tractography alogrithms afford us the ability to reconstruct white matter tracts in their full complexity. Shape modeling of tracts for which the sheet representation proves inadequate will be a key future challenge.

There are many alternative approaches to the statistical methods demonstrated in this paper. For instance, for univariate analysis, point-wise hypothesis testing with false discovery rate correction (Benjamini and Yekutieli, 2001) could be used instead of the permutation-based cluster-level inference. For multivariate analysis, Hotelling’s T² test could be used for point-wise or cluster-level inference as an alternative to the joint analysis based on the joint pdf of thickness and FA. The novel multivariate statistical framework proposed by Goodlett et al. (2009) may be another powerful alternative. The authors model the diffusion data collected along the centerline of a tubular tract as a continuous function of arc length to explicitly capture the spatial dependency of these samples. Although extending this analysis concept to sheet-like tracts will require substantial research and development effort, the powerful parametrization provided by the cm-rep lays the foundation for such endeavor.