Development and validation of GFR-estimating equations using diabetes, transplant and weight

Abstract

Background. We have reported a new equation (CKD-EPI equation) that reduces bias and improves accuracy for GFR estimation compared to the MDRD study equation while using the same four basic predictor variables: creatinine, age, sex and race. Here, we describe the development and validation of this equation as well as other equations that incorporate diabetes, transplant and weight as additional predictor variables.

Methods. Linear regression was used to relate log-measured GFR (mGFR) to sex, race, diabetes, transplant, weight, various transformations of creatinine and age with and without interactions. Equations were developed in a pooled database of 10 studies [2/3 (N = 5504) for development and 1/3 (N = 2750) for internal validation], and final model selection occurred in 16 additional studies [external validation (N = 3896)].

Results. The mean mGFR was 68, 67 and 68 ml/min/ 1.73 m² in the development, internal validation and external validation datasets, respectively. In external validation, an equation that included a linear age term and spline terms in creatinine to account for a reduction in the magnitude of the slope at low serum creatinine values exhibited the best performance (bias = 2.5, RMSE = 0.250) among models using the four basic predictor variables. Addition of terms for diabetes and transplant did not improve performance. Equations with weight showed a small improvement in the subgroup with BMI <20 kg/m².

Conclusions. The CKD-EPI equation, based on creatinine, age, sex and race, has been validated and is more accurate than the MDRD study equation. The addition of weight, diabetes and transplant does not significantly improve equation performance.

Introduction

Glomerular filtration rate (GFR) is an important indicator of kidney function, critical for detection, evaluation and management of chronic kidney disease (CKD). GFR cannot be practically measured for routine clinical or research purposes, and therefore, serum creatinine is often used to estimate GFR. Several factors affect the level of serum creatinine other than GFR, including the generation of creatinine from muscle metabolism. GFR-estimating equations, such as the Modification of Diet in Renal Disease (MDRD) study equation, including age, sex and race, account for the average differences in muscle mass among these subgroups and have been shown to be a more accurate assessment of the level of kidney function than serum creatinine alone. National and international organizations recommend that clinical laboratories report estimated GFR (eGFR) and that clinicians use eGFR to evaluate kidney function for all patients [1–4].

This is now a considerable body of the literature demonstrating limitations in the performance of the MDRD study equation in people with higher levels of GFR, such as younger patients with diabetes [5–7]. A potential explanation for this limitation is that the MDRD study equation was developed in people with CKD who did not have type 1 diabetes and who were not transplant recipients, who may have differences in creatinine generation that are compared to the people who were included in the MDRD study population that were not captured by the average values for the regression coefficients for age, sex and race. We hypothesized that the performance of the MDRD study equation could be improved by a new equation developed in a diverse study population including individuals with and without diagnosed kidney disease, diabetes and transplants that utilizes novel transformations of creatinine and age, new predictor variables and pairwise interactions among its predictor variables. Our goal was to develop an equation that had improved performance at higher levels of GFR and had consistent performance among subgroups based on clinical and demographic characteristics. We recently reported a new equation, the CKD-EPI equation, based on creatinine, age, sex and race, which is more accurate than the MDRD study equation [8]. However, the precision of this equation remains limited, in part due to non-GFR determinants of serum creatinine that are not captured by creatinine level, age, sex and race. Here, we report on the development and validation of this equation as well as other equations that were developed that also included diabetes, transplant and weight as additional predictor variables.

Methods

Sources of data and measurements

CKD-EPI is a research group funded by the National Institute of Diabetes, Digestive and Kidney Disease (NIDDK) to address challenges in the study and care of CKD, including development and validation of improved GFR-estimating equations by pooling data from research studies and clinical populations (hereafter referred to as ‘studies’) [5,9–27].

The methods and studies have been previously described [8] and are briefly reviewed here. We developed and internally validated new equations in a database of 10 studies (6 research studies and 4 clinical populations) with a total of 8254 participants, divided randomly into separate datasets for development (n = 5504) and internal validation (n = 2750). The equations were then externally validated in a separate dataset of 16 other studies with a total of 3896 participants. GFR was measured using urinary clearance of iothalamate in the first set of studies and using iothalamate or other filtration markers in the second set of studies. For all studies, we recalibrated serum creatinine values to the standardized creatinine measurements using the Roche enzymatic method (Roche-Hitachi P-Module instrument with Roche Creatininase Plus assay) at the Cleveland Clinic Research Laboratory (Cleveland, OH, USA) as previously described [28,29].

Development

We used least-squares linear regression to relate measured GFR to serum creatinine and clinical characteristics available in the development dataset. Predictor variables included serum creatinine, age, sex and race (black versus white and other) in all equations, as in the MDRD study equation, and additional variables [diabetes (yes/no), prior organ transplant (yes/no), and weight, as assigned by the individual studies] in some equations. Transplant recipients who were known to be on trimethroprim were excluded from the dataset. Type of diabetes was not known for all study participants and therefore categorization by type was not performed. Type of transplant was not specified. The optimal transformation of weight was quadratic and this was the transformation used in all equations.

GFR was adjusted for body surface area (BSA) as ml/min/1.73 m² [30]. GFR and serum creatinine were transformed to natural logarithms to reflect their inverse relationship and to stabilize variance across the range of GFR. Logarithmic transformation of age was used in the MDRD study equation, and therefore, it was first compared to the linear form of age. The linear form was demonstrated to have improved performance and therefore was used for all further analyses. The optimal transformations of log serum creatinine and linear age were determined by first fitting nonparametric smoothing splines to characterize the shape of the relationship of these factors with mean log mGFR and then creating piecewise linear splines to correspond to observed non-linearity. This led to consideration of spline terms in log serum creatinine to allow the accommodation of a potentially reduced magnitude in the slope relating log GFR to log serum creatinine at lower values for serum creatinine, and a spline term in age to accommodate a potentially smaller age effect below 40 years.

A step-wise process for developing equations using new transformations of continuous variables and inclusion of new variables and pairwise interaction terms to develop a large number of candidate equations was delineated a priori [8]. The two-way combinations of the two transformations of creatinine (spline of log serum creatinine and log serum creatinine), age (spline age and linear age), together with race and sex yielded four base equations. Within each base equation, more complicated equations were developed by the addition of diabetes, transplant and weight and pairwise interactions. Each of the additional variables was first individually added to a given base equation, and retained in further equation development steps if that variable was itself statistically significant or if the pairwise interaction of that variable with the creatinine term(s) was statistically significant (P < 0.01), and the addition of the variable and/or its interaction with serum creatinine improved equation performance as defined by a relative reduction in the equation's root mean square error (RMSE) of at least 2%. Significance was tested overall and within subgroups defined by the variable.

Within each base equation, multivariable equations were then developed using a backward selection process to select among the new variables. Additional multivariable equations were developed by sequentially adding to the above equations pairwise interactions terms among the previously selected variables. Pairwise interaction terms which were statistically significant at the P < 0.001 level were retained. Three-way interaction terms were also tested but none were significant. This process led to the development of four different equations (with and without inclusion of additional predictor variables, and with and without pairwise interaction terms) for each of the four base equations, for a total of 16 equations. Within each base equation, performance of the more complicated equations was compared to the simpler equation in the overall development dataset and in subgroups defined by ranges of eGFR and clinical characteristics. Only equations that exhibited improved performance compared to simpler equations were brought forward into internal validation.

Internal validation

The goal of this phase was to determine how models developed in a random sample of pooled studies performed in the remaining sample of pooled studies. The statistical significance of individual regression coefficients and equation performance were reassessed using the coefficient estimates from the development set using the same criteria as in the development phase. The development and internal validation datasets were subsequently combined and validated equations were refit to yield more precise final coefficients to be used in subsequent analyses.

External validation

The goal in this phase was to select a final generalizable equation as determined by testing it in separate datasets other than in which it was developed. The selection process consisted of a pre-specified series of steps. We first compared the performance of the four base equations in the external validation dataset to their performance in the development and internal validation datasets and to the MDRD study equation. Then we selected the optimal transformation of age and creatinine in the external validation dataset by examining performance of the four base equations within relevant subgroups specific for each transformation: eGFR 60–89 and 90–119 ml/min/1.73 m² for creatinine transformations and age <40 years for the age transformations. Finally, we ranked all remaining equations on the basis of the combination of the ranking in the overall external validation dataset, in subgroups and ease of application.

Statistical analyses

Performance of the equations was evaluated using similar metrics in all three datasets. Bias was measured as the difference (mGFR − eGFR) and percentage difference (100^*[mGFR-eGFR]/mGFR) between measured and estimated GFR, with positive values indicating lower eGFR than mGFR (under-estimation). Bias is not shown for the overall development dataset, where it is expected to be approximately zero. Precision was measured as an inter-quartile range (IQR) for the differences. Accuracy was measured as the percentage of estimates within 30% of the measured GFR (P₃₀) that takes into account higher errors at higher values and RMSE. RMSE was used as the primary metric in the development dataset, as it is calculated on the scale of the regression (log scale). In external validation, equations were considered to be potentially clinically meaningful if their RMSE's differed by >2% and their biases differed by >5 ml/min/1.73 m² of each other.

For analyses within subgroups, subgroups were defined by clinical characteristics as follows: age (less than 40, 40–65, greater than 65 years); sex; race (Black, White or other); diabetes (yes, no), prior organ transplant (yes, no); body mass index (BMI, <20, 20–25, 26–30 and >30 kg/m²). The level of estimated GFR (eGFR) was categorized as >120, 90–119, 60–89, 30–59, 15–29 or <15 ml/min/1.73 m², as used for staging the severity of CKD [2].

Confidence intervals were calculated by bootstrap methods (2000 bootstraps) for difference, percentage difference and for P_30. Significance testing between metrics for each equation was computed using the sign test on the bootstrapped estimates.

Analyses were computed using the R (Version 2, Free Software Foundation, Inc., Boston, MA, USA) and SAS software (version, 9.1, Cary, NC, USA). Smooth estimates of the mean in the figures were created using the lowest function in R.

The institutional review boards of all participating institutions approved the study.

Results

The distribution of age, sex and diabetes was similar across the development, internal validation and external validation datasets (Table 1). The mean GFR (5th–95th) was 68 (14–136), 67 (14–136) and 68 (17–130) ml/min/1.73 m² in the development, internal validation and external validation datasets, respectively. The external validation data had a lower proportion of blacks and a higher proportion of organ transplant recipients.

Table 1.

Demographic and clinical characteristics

			Combined
		Internal	development and	External
	Development	validation	internal validation	validation
	dataset	dataset	datasets	dataset
	Mean% (SD)	Mean% (SD)	Mean% (SD)	Mean% (SD)
Total	5504	2750	8254	3896
Age	47 (15)	47 (15)	47(15)	50 (15)
Sex (female %)	43	44	44	45
Race
Black (%)	32	31	32	10
White and others (%)	68	69	68	90
Kidney donor (%)	13	12	12.5	16
Transplant recipient (%)	4	4	4	29
Diabetes (%)	29	30	29	28
Height (cm)	170 (10)	170 (10)	170(10)	170 (10)
Weight (kg)	82 (20)	82 (20)	82(20)	79 (18)
BMI (kg/m2)	28 (6)	28 (6)	28(6)	27 (6)
BSA (m2)	1.93 (0.22)	1.93 (0.24)	1.93 (0.24)	1.90 (0.23)
GFR, adjusted (ml/min/1.73 m2)	68 (40)	67 (40)	68(40)	68 (36)
Serum creatinine (mg/dl)	1.65 (1.15)	1.67 (1.17)	1.66 (1.16)	1.52 (0.99)

In the development dataset, equations with all four combinations of transformations of creatinine and age (base equations) demonstrated improved performance compared to the MDRD study equation. Table 2 shows improvements in fit due to refitting coefficients using the same forms as in the MDRD study equation, as well as using different transformations of age and creatinine. The spline form of log serum creatinine had the largest impact on performance with a RMSE (95% CI) of 0.231 (0.223, 0.238).

Table 2.

Performance of MDRD study equation and CKD-EPI base equations in development dataset compared to measured GFR

		Overall			eGFR 60–89
Creatinine	Age	IQR	P30	RMSE	Bias	IQR
MDRD study equationa
Log	Log	16.4 (15.9, 17.1)	83 (82, 84)	0.247 (0.240, 0.254)	9.4 (8.0, 10.5)	25.4 (24.0, 27.1)
Refit MDRD study equation
Log	Log	15.2 (14.6, 15.8)	83 (82, 84)	0.240 (0.233, 0.248)	4.8 (3.6, 5.8)	23.0 (21.7, 24.3)
CKD-EPI base equations
Log	Linear	15.0 (14.4, 15.7)	84 (83, 85)	0.238 (0.231, 0.246)	4.2 (2.8, 5.5)	23.2 (21.5, 22.3)
Log	Spline	14.9 (14.3, 15.6)	84 (83, 85)	0.237 (0.230, 0.244)	3.3 (2.1, 4.6)	22.9 (21.3, 24.2)
Splineb	Linear	14.7 (14.2, 15.3)	86 (85, 86)	0.231 (0.224, 0.238)	1.4 (0.3, 3.0)	21.4 (20.1, 22.9)
Spline	Spline	14.6 (14.2, 15.2)	85 (84, 86)	0.231 (0.223, 0.238)	1.2 (0.1, 2.2)	21 (19.6, 22.7)

95% confidence intervals are in the parentheses.

^aMDRD study equation re-expressed for use with the serum creatinine values standardized to isotope dilution mass spectroscopy (IDMS) [GFR = 175 × standardized S_cr^−1.154 × age^−0.203 × 1.212 (if black) × 0.742 (if female)] [36].

^bThis is the CKD-EPI equation. If male: 141 × min(Scr/0.9),1)^0.4111 × max(Scr/0.9),1)^1.298 × 0.993^Age × 1.159 (if black).

If female: 144 × min(Scr/0.7),1)^0.329 × max(Scr/0.7),1)^1.298 × 0.993^Age × 1.159 (if black).

The addition of diabetes, transplant and weight was significant when each was added alone to the base models. When the three variables were added together, the models demonstrated improved performance compared to the four base models in the overall development dataset or in relevant subgroups. Table 3 shows the magnitude of the effect for each of the new variables in models that included all three variables. Transplant has the largest effect size with a decrease in 9% of estimated GFR for transplant compared to non-transplant recipients, while diabetes and weight had smaller effects. The effect of greater weight initially leads to a higher eGFR for the same age, sex, race and serum creatinine, but after 100 kg, the greater weight leads to a lower estimated GFR.

Table 3.

Change in estimated GFR with the addition of diabetes, transplant and weight in main effect models

Base equation		Difference in estimated GFR (%)b according to clinical characteristics
		Diabetes versus	Transplant versus
Creatinine	Age	non-diabetic status	non-transplant statusa	Weight 60 versus 40 kg	Weight 160 versus 140 kg
Log	Linear	0 (0%)	−8 (−9%)	16 (28%)	−18 (−38%)
Log	Spline	1 (1%)	−8 (−10%)	15 (25%)	−18 (−34%)
Splinea	Lineara	3 (3%)	−8 (−10%)	15 (25%)	−18 (−34%)
Spline	Spline	4 (4%)	−8 (−10%)	14 (21%)	−18 (−31%)

^aThis is the CKD-EPI equation. If male: 141 × min(Scr/0.9),1)^0.4111 × max(Scr/0.9),1)^1.298 × 0.993^Age × 1.159 (if black).

^bUnit of GFR ml/min/1.73 m².

If female: 144 × min(Scr/0.7),1)^0.329 × max(Scr/0.7),1)^1.298 × 0.993^Age × 1.159 (if black).

In the internal validation dataset, performance of all equations was similar to their performance in the development dataset. In addition, all equations showed similar improvement in performance compared to the MDRD study equation as was seen in the development dataset (Appendix Table A1).

In the external validation dataset, all equations performed better than the MDRD study equation (Table 4). The best base equation was the one that included spline of log serum creatinine and linear age (herein called ‘equation 1’ and reported elsewhere as the ‘CKD-EPI creatinine equation’); and therefore, further equation selection was restricted to the more complicated equations that used this base equation. Equation 2 not only contains the same variables but also includes pairwise interactions among them. Equations 3 and 4 contain additional predictor variables, without and with pairwise interactions, respectively. In external validation, the inclusion of new variables and interactions to this base equation did not have a substantial effect on performance in the overall dataset.

Table 4.

Performance of MDRD and CKD-EPI equations in external validation dataset compared to measured GFR

	Equation descriptionb				Equation performance
	Base equation				Difference
			New
Equation namea	Creatinine	Age	variables	Interactions	Median	IQR	P30	RMSE	R2
MDRD study equation	Log	Log	N	N	5.5 (5.0, 5.9)	18.3 (17.4, 19.3)	80.6 (79.5, 82.0)	0.274 (0.264, 0.282)	0.839 (0.827, 0.851)
Equation 1c (CKD-EPI equation)	Spline	Linear	N	N	2.5 (2.1, 2.8)	16.6 (15.9,17.2)	84.1 (83.0, 85.3)	0.250 (0.241, 0.259)	0.852 (0.840, 0.863)
Equation 2	Spline	Linear	N	Y	2.5 (2.1, 2.9)	16.6 (15.9,17.3)	84.1 (83.0, 85.3)	0.250 (0.241, 0.259)	0.852 (0.840, 0.863)
Equation 3	Spline	Linear	Y	N	3.6 (3.2, 3.9)	15.7 (16.4, 17.0)	83.2 (82.0, 84.3)	0.256 (0.247, 0.266)	0.851 (0.839, 0.862)
Equation 4	Spline	Linear	Y	Y	3.7 (3.2, 4.1)	16.2 (15.5, 16.8)	83.1 (81.9, 84.2)	0.256 (0.247, 0.269)	0.852 (0.840, 0.863)

^aMDRD study equation re-expressed for use with the serum creatinine values standardized to isotope dilution mass spectroscopy (IDMS) [GFR = 175 × standardized S_cr^−1.154 × age^−0.203 × 1.212 (if black) × 0.742 (if female) [36].

^bAll equations included race and sex. The first row is the MDRD study equation. Equation 1 is the CKD-EPI equation. Equations 2–4 have the same forms of creatinine and age as the CKD-EPI equation but differ by the presence or absence of new variables (diabetes, transplant and weight) or interactions. Weight is expressed as a quadratic.

^cThis is the CKD-EPI equation: If male: 141 × min(Scr/0.9),1)^0.4111 × max(Scr/0.9),1)^1.298 × 0.993^Age × 1.159 (if black).

If female: 144 × min (Scr/0.7),1)^0.329 × max(Scr/0.7),1)^1.298 × 0.993^Age × 1.159 (if black).

Table 5 shows the relative ranking of these equations by categories of eGFR. Addition of interactions among creatinine, age, sex and race (equation 2) yielded a small decrease in bias at eGFR >90 ml/min/1.73 m². The addition of the new variables (equations 3 and 4) improved bias and precision at eGFR >90 ml/min/1.73 m², but worsened performance at lower-level eGFRs and overall.

Table 5.

Comparison of equations by level of eGFR in the external validation dataset

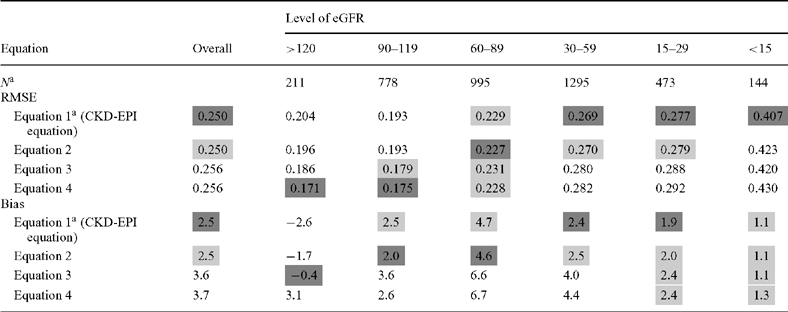^aSample size of each eGFR category determined from the CKD-EPI-1 equation.

The dark grey shaded cells in these tables indicate the equation with the best performance for that subgroup according to the point estimate for the metric, with the lighter grey shaded cells indicated those equations whose performance was similar to the best performing equation.

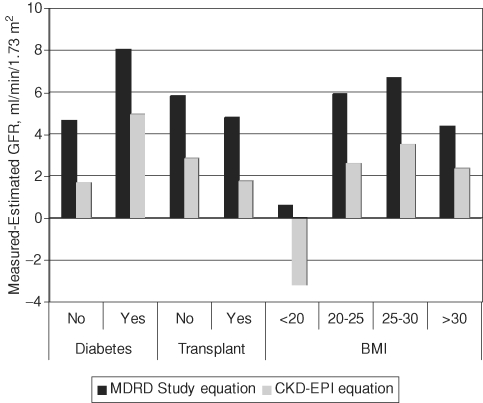
Table 6 shows the relative ranking of the equations by subgroup. Equation 1 or 2 resulted in greater bias and lower accuracy in people with diabetes than in people without diabetes. However, the addition of diabetes (equation 3 or 4) did not improve the performance for people with diabetes and worsened the performance in people without diabetes. Equations 1 and 2 resulted in similar bias across the top three BMI categories, but showed an overestimate in people with lowest levels of BMI (<20 kg/m², respectively). The addition of weight improved both bias and accuracy for people with BMI <20 kg/m², but not for people in the other BMI groups, including those with BMI >30 kg/m². Using equation 1 or 2, there was no difference in bias, but accuracy was worse among people with a history of organ transplantation compared to those with no history of organ transplantation. The addition of the transplant term worsened bias and accuracy for transplant recipients (equations 3 and 4 compared to equations 1 and 2). The CKD-EPI equation has less bias than the MDRD study equation across all subgroups other than low BMI [CKD-EPI: −3.5 (−4.7, −1.6) versus MDRD study equation 0.6 (−1.5, 2.1)] (Figure 1).

Table 6.

Comparison of equations by subgroups in the external validation dataset

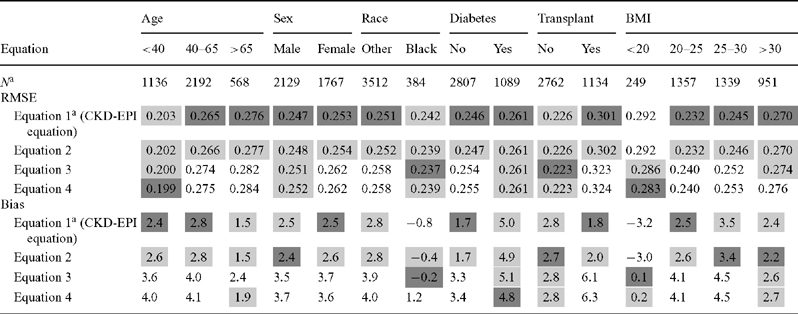^aSample size of each eGFR category determined from the CKD-EPI-1 equation.

Age is measured in years; BMI is measured in kg/m².

The dark grey shaded cells in these tables indicate the equation with the best performance for that subgroup according to the point estimate for the metric, with the lighter grey shaded cells indicated those equations whose performance was similar to the best performing equation.

Fig. 1.

Comparison of performance for the MDRD study and CKD-EPI equations by subgroups. The comparison between the bias, defined as the difference between measured and estimated and between the MDRD study and CKD-EPI equations are shown across three subgroups: diabetes, solid organ transplant recipient and body mass index (<20, 20–25, 25–30 and >30 kg/m²).

Discussion

In our previous report, we described the CKD-EPI equation and showed that the CKD-EPI equation performed substantially better than the MDRD study equation, especially among people with eGFR >60 ml/min/1.73 m²; however, precision remained limited. We had hypothesized that the addition of new predictor variables or interactions would lead to further improvement in performance, as these terms would capture variation in the non-GFR determinants of serum creatinine, not accounted for by age, sex and race. Diabetes, history of organ transplantation and weight were selected a priori as predictor variables because these conditions and the medications used to treat them may affect muscle mass and because they were available in all datasets. Although we did observe small improvements in the development dataset with the addition of these terms, they did not substantially improve equation performance in a separate validation dataset. There are implications of these findings for interpretation of eGFR in clinical practice and for future efforts to develop GFR estimating equations.

The diabetes term was small in the development dataset and did not improve performance in the external validation dataset. These findings are consistent with some prior studies that showed no difference in the accuracy of GFR estimates in patients with CKD with and without diabetes [14,31]. Other studies, however, had showed inaccuracy of GFR estimates in populations with diabetes with a higher level of GFR [5–7]. We suspect that these findings are more likely due to the higher range of GFR rather than to diabetes status. The findings suggest that the new CKD-EPI equation can be applied to patients with diabetes.

The transplant term was large in the development dataset, but resulted in worse performance among transplant recipients in the external validation dataset. These results were not expected and suggest that there may be heterogeneity in factors affecting creatinine generation among transplant populations. In the development dataset, the transplant recipients were from two clinical populations in the United States. In the external validation dataset, the transplant recipients were from three other US clinical practices and from two Northern European clinical practices. Only two of the five studies included in the validation dataset demonstrated worse performance: one was a population of liver transplant recipients from the United States and one was a population of kidney transplant recipients from Europe, both of the studies had used iothalamate as the exogenous filtration marker to measure GFR. Elimination of the liver transplant recipients did not substantially change performance, suggesting that the variation in performance of the transplant term, from development to validation datasets is not related to transplant type. Rather, the variation is likely to be related to greater heterogeneity in creatinine generation among all transplant recipients due to steroid use, unrecorded trimethoprim use and medical history. This may also explain why the variation in single-centre reports of the presence or absence of a difference in the relationship of creatinine with GFR in people between people with native kidney disease and transplant recipients, as well as the variation among equations developed for use in transplant recipients [32,33]. One should apply with caution equations for transplant recipients developed in one centre to other centres to other transplant recipients given the observed inter-study variation noted here.

The relationship between weight and GFR changed at different levels of weight. This may reflect malnutrition (and decreased muscle mass) in the underweight as well as in the obese [34,35]. In the external validation dataset, the CKD-EPI equation overestimates GFR in individuals with low BMI (<20 kg/m²), and equations that included weight and the other new variables demonstrated improved accuracy in people with the low BMI, but not at higher levels. It is possible that it is not the addition of weight per se that is leading to an improved performance at low BMI, but rather it reflects the studies that included people with low BMI. Given these results, we do not suggest that the equation with the additional variables should be used in people of low body mass.

The strengths of the study include the large diverse study population of people with and without kidney diseases; calibration of the creatinine assays in each study to standardize values; and rigorous statistical techniques for equation development including testing of all transformations, addition of new variables and interactions among variables, and evaluation of the developed equations in a separate dataset of multiple studies, which maximized external generalizability. Comparison of equations in a separate validation dataset overcomes some of the limitations of differences among studies in patient characteristics and methods for measurement of GFR and serum creatinine.

There are limitations to the study. First, we have pooled studies of different populations to develop and validate the CKD-EPI equation. We performed extensive analyses to examine possible study effects and cannot rule out that some of the observed relationships of variables with measured GFR may reflect differences across studies. Secondly, participants were included or excluded from each study because they were thought to have or not to have kidney disease and this selection bias may lead to errors in the equation performance. Because the populations with higher levels of GFR were selected for not having kidney disease, the pooled dataset may not be the representative of the general population, and we are therefore less certain of the accuracy of eGFR at higher levels. Nevertheless, the comparison to the MDRD study equation is still valid since the populations are the same in evaluating all equations, and the improved performance is likely to be seen in the general populations. We are not aware of studies of measured GFR in the general population. This is a particular problem for the elderly and for minority racial and ethnic groups, where the prevalence of kidney disease is high. Thirdly, GFR is measured with error and these errors may differ among GFR protocols. While in the development database all participants underwent GFR measurement using urinary clearance of iothalamate, in the validation database, other markers and methods were used in 45% of subjects, and thus the differences among subgroups in equation performance may be due, in part, to differences in errors in measured GFR. However, differences in relative performance of equations between the pooled iothalamate and non-iothalamate studies were minimal, and thus, we do not consider that differences in protocols had a major influence on the results. Finally, we had incomplete data on ethnicity, diabetes type, immunosuppressive agents for transplantation, measures of muscle mass and other clinical conditions and medications that might affect serum creatinine independently from GFR. However, the variables that we evaluated were the most readily available and easy to ascertain for widespread clinical application.

In summary, we present here the rigorous development and validation of a new CKD-EPI equation to estimate GFR that is more accurate than the MDRD study equation. Persistent bias in low BMI groups and imprecision in all groups reflect non-GFR determinants of serum creatinine and is not improved substantially by the addition of diabetes, transplant, weight and their interactions as predictor variables. We suggest the use of the CKD-EPI equation rather than MDRD study equation for general clinical use. Future studies should consider new filtration markers and representative populations.

Appendix 1:

Table A1.

Performance of MDRD study equation and CKD-EPI-based equations in internal validation

		Overall			eGFR 60–89
Creatinine	Age	IQR	P30	RMSE	Bias	IQR
MDRD study equationa
Log	Log	16.0 (15.1,17.1)	82 (81,84)	0.258 (0.247,0.271)	7.9 (6.2,10.0)	25.4 (22.9,28.0)
Refit MDRD study equation
Log	Log	14.5 (13.6,15.7)	82 (81,83)	0.252 (0.240,0.265)	2.5 (1.3,4.7)	21.9 (20.2,23.9)
CKD-EPI-based equationsb
Log	Linear	14.6 (13.8,15.6)	82 (81,84)	0.250 (0.238,0.263)	2.1 (1.0,4.0)	22.0 (20.0,23.4)
Log	Spline	14.7 (13.8,15.7)	83 (81,84)	0.250 (0.238,0.263)	2.2 (0.9,3.6)	21.5 (19.2,23.2)
Splinec	Linear	14.2 (13.4,15.0)	83 (82,85)	0.245 (0.233,0.258)	0.0 (−1.1,1.8)	20.5 (18.1,22.8)
Spline	Spline	14.4 (13.5,15.2)	83 (82,85)	0.245 (0.233,0.258)	0.2 (−1.3,1.3)	21.0 (18.3,22.7)

All equations included race and sex. Difference is equal to measured GFR − estimated GFR where units are in ml/min/1.73 m².

IQR, interquartile range; RMSE, root mean square error.

^aMDRD study equation re-expressed for use with the serum creatinine values standardized to isotope dilution mass spectroscopy (IDMS) (GFR = 175 × standardized S_cr^−1.154 × age^−0.203 × 1.212 [if black] × 0.742 [if female]) [36].

^bThis is the CKD-EPI equation:

If male: 141 × min(Scr/0.9),1)^0.4111 × max(Scr/0.9),1)^1.298 × 0.993^Age × 1.159 (if black).

If female: 144 × min(Scr/0.7),1)^0.329 × max(Scr/0.7),1)^1.298 × 0.993^Age × 1.159 (if black).

^cSpline is the same as described in the CKD-EPI equation.