GFR-estimating models in kidney transplant recipients on a steroid-free regimen

Abstract

Background. How to best estimate glomerular filtration rate (GFR) in kidney transplant recipients on steroid-free immunosuppression has not been established.

Methods. Within 3 months of transplantation, iothalamate GFR (iGFR) was measured in 107 recipients on steroid-free and 27 on steroid-maintenance immunosuppression. A year later, a second GFR was performed. Serum creatinine was calibrated against a reference laboratory, and GFR was estimated (eGFR) using the re-expressed Cockcroft–Gault equation, eGFRCG; the Mayo Clinic equation, eGFRMC; the Modification of Diet in Renal Disease (MDRD) study equation, eGFRMDRD; and the newly introduced Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation.

Results. All models overestimated GFR regardless of steroid use or timing of GFR. In those not receiving steroids, eGFRCG was least biased: 1.85 ± 15.2 ml/min at the first GFR and 0.23 ± 15.2 ml/min at the second. eGFRMC and eGFRCKD-EPI were most biased and were within 30% of iGFR less than 60% of the time in contrast to eGFRCG which was within 30% of iGFR 80.2% of the time. eGFRMDRD was intermediate in its performance at the first GFR but was comparable to eGFRCG at the second measurement. Importantly, the four models had comparable but poor precision. Exposure to steroids for a whole year did not appreciably alter the models’ bias or relative accuracy but resulted in a dramatic fall in their precision, R2 = 0.05–0.12.

Conclusions. GFR prediction equations overestimate measured GFR in recipients on and off steroid regimens. Long-term exposure to steroids results in a marked reduction in the precision of all models. In all, eGFRCG and eGFRMDRD are the two best available models.

Introduction

Accurate assessment of kidney function in kidney transplant recipients is important and is recommended by the international Kidney Disease: Improving Global Outcomes initiative [1]. Realizing that using serum creatinine alone has significant limitations in adequately reflecting glomerular filtration rate (GFR) and the fact that direct measurement of GFR through administration of exogenous markers is generally impractical for most transplant centers, serum creatinine-based GFR estimating equations are widely used by the transplant community [2–4]. The utility and performance of these models have been extensively studied in kidney transplant recipients but have yet to be specifically validated in recipients who are on steroid-free immunosuppression. Maintenance steroid is associated with muscle wasting with an attendant decrease in creatinine production and thus has the potential to lead to gross overestimation of GFR in models that depend on serum creatinine. How to best estimate GFR in kidney transplant recipients who are not on long-term steroid maintenance is very relevant since steroid-free regimens are currently used in over 30% of kidney transplant recipients in the USA [5].

Herein, we study the performance of three commonly used GFR estimating equations in kidney transplant recipients maintained on a steroid-free regimen, compare it to that in recipients who are maintained on long-term steroids and provide appraisal of the newly introduced Chronic Kidney Disease Epidemiology Collaboration equation estimated GFR. We hypothesized that GFR-estimating models would perform better in kidney transplant recipients who are steroid free since muscle mass loss is minimized by steroid avoidance.

Materials and methods

This analysis was performed using data from the ongoing National Institutes of Health sponsored Angiotensin II Blockade for Chronic Allograft Nephropathy Trial (clinicaltrials.gov NCT 00067990). In this 5-year long trial, 153 kidney transplant recipients were randomized to placebo or losartan at 58 ± 34 days after receiving a living- or a deceased-donor transplant. Recipients were transplanted at either the University of Minnesota (UMN) or Hennepin County Medical Center (HCMC), Minneapolis, MN. The primary endpoint of this trial was the change in cortical interstitial volume from postperfusion allograft biopsies to those performed at 5 years after transplantation. Exclusion criteria included: age < 18 years, serum creatinine ≥ 2.5 mg/dL, potassium > 5.4 mEq/L, known hypersensitivity to losartan or iodine allergy, documented renal artery stenosis, recipients of grafts from an HLA-identical sibling, recipients whose primary renal disease is primary hyperoxaluria, dense-deposit disease, focal segmental glomerulosclerosis or hemolytic uremic syndrome, women of childbearing age who wished to become pregnant and/or were unwilling to use contraceptive measures or who were pregnant and had a cardiovascular indication for ACE inhibitors or AII blockers. Those transplanted at the UMN received induction with five doses of Thymoglobulin® (Genzyme) and a 5-day course of steroids in tapering doses (methylprednisolone 500 mg, given in the operating room, followed by prednisone, 1 mg/kg on postoperative day 1; 0.5 mg/kg on days 2 and 3; and 0.25 mg/kg on days 4 and 5). Recipients who were on prednisone prior the transplantation (mainly for lupus or having a prior functioning allograft) remained on previous maintenance dose. For maintenance therapy, patients received a combination of a calcineurin inhibitor (cyclosporine or tacrolimus) with mycophenolate mofetil or sirolimus. Rejection episodes were treated with a rapid steroid taper (methylprednisolone 500 mg × 3 days followed by prednisone taper over 10–14 days down to 5 mg daily indefinitely) or Thymoglobulin® for 7–10 days for steroid-resistant or histologically moderate-severe rejection episodes and remained on maintenance steroids as well. Recipients transplanted at HCMC, in contrast, received induction therapy with two doses of an interleukin 2 antagonist: Basiliximab® (Novartis) or Daclizumab® (Roche), and Solumedrol 500 mg IV × 3 doses followed by prednisone taper down to maintenance dose 12 mg by 6 months. For maintenance therapy, they received a calcineurin inhibitor, mycophenolate mofetil and prednisone. Rejection episodes were treated with high dose of steroids or Thymoglobulin based on severity.

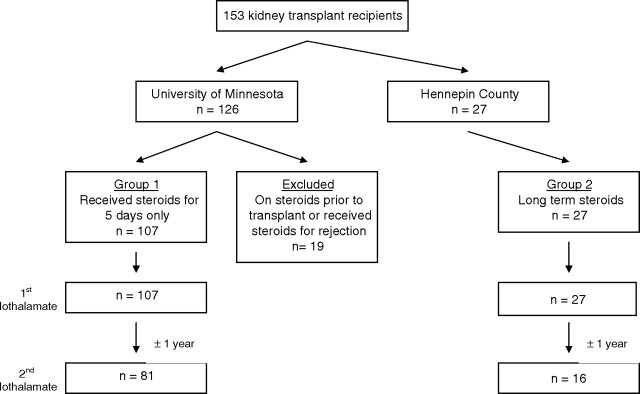
The steroid group (Group 1) consists of UMN recipients who received steroids for 5 days only in perioperative period, and therefore those who received additional steroids beyond that time either for treatment of rejection or were on maintenance prednisone therapy for other reasons were excluded from this analysis (Figure 1). In contrast, recipients from the HCMC program, who remained on maintenance steroids per their protocol, constitute our steroid maintenance group (Group 2). The steroid-free group (n = 107) were the main interest of this analysis but were also compared to 27 contemporaneous renal transplant recipients from Hennepin County Medical Center who were maintained on steroids. To guard against the possibility that these recipients may not have reached a steady state and the exposure to steroids may have been too brief at the time of the first iGFR to cause a significant muscle wasting, we studied 81 of the University of Minnesota recipients who remained steroid free at 1 year (26 recipients either missed their 1-year GFR or dropped out of the study) after the first measurement and 16 HCMC recipients (11 recipients missed their 1-year GFR) who remained on steroids between the two measurements (Figure 1). All recipients were on single-strength trimethoprim-sulfamethoxazole, and none were on cimetidine.

Fig. 1.

Study participants.

All trial participants underwent direct measurement of GFR by iothalamate clearance (iGFR) 58 ± 34 days posttransplantation at which time they were also randomized to losartan or placebo. A second iGFR was performed 11–13 months after the one performed at randomization. Iothalamate GFR was done after giving an intravenous loading dose of iothalamate followed by maintenance infusion. All recipients received a water load of 10 ml/kg to maintain urine flow rates at >3 ml/kg/h. If this flow rate was not achieved, an additional water load of 5 ml/kg was given. Five timed urine and plasma collections were performed, and the average of these was calculated. The CV of iGFR was <10%, and GFR was corrected to body surface area (BSA) of 1.73 m².

Serum creatinine was obtained on the morning of the iGFR, after an 8–12-h fast, and was calibrated against the Cleveland Clinic Biochemistry Laboratory (Cleveland, OH) where serum creatinine was assayed for the Modification of Diet in Renal Disease (MDRD) study as previously described [6–8]. In May 2008, the creatinine assay at our institution changed from the Jaffe’/CXR Synchron method to the isotope-dilution mass spectroscopy (IDMS)-traceable creatinine [9,10]. The laboratory provided us with a formula to convert the Jaffe’ assay-based creatinine to the IDMS-traceable creatinine. We used this formula to convert all creatinine values to IDMS-traceable values. To verify the accuracy of the conversion formula in these recipients, we randomly selected 30 serum samples from the pool of 153 recipients and measured serum creatinine using the new IDMS-traceable method, and they were identical. Since values provided by the regression formula provided serum creatinine values that were identical to the directly measured ones, we used the values obtained from it in the 153 recipients.

GFR was estimated using the re-expressed Cockcroft–Gault equation for estimation of GFR for use with standardized creatinine (eGFRCG), the Mayo Clinic equation (eGFRMC) and the MDRD study equation (eGFRMDRD). eGFRCG was calculated using the formula (140 − age) × weight/(72 × SCr) × (0.85 if female) ( $\frac{1.73}{\text{BSA}}$) [11] multiplied by 0.8 to correct for the bias in the MDRD study sample [9]. It is of note that only standardized creatinine can be used for this model. eGFRMC was calculated using the quadratic equation that estimates logarithmic GFR from serum creatinine, age and gender and after indirectly calibrating serum creatinine by applying the following regression relation: IDMS-traceable creatinine = 0.906[−0.213 + (1.098 × Mayo Clinic creatinine)] [12,13]. eGFRMDRD was calculated using the formula: GFR = 175 × standardized SCr−1.154 × age−0.203 × 1.212 (if black) × 0.742 (if female) [14]. eGFRCKD-EPI was calculated using the formula: 141 × min(SCr/κ, 1)α × max(Scr/κ, 1)−1.209 × 0.993age × 1.018 [if female] × 1.159 [if black], where Scr is serum creatinine, κ is 0.7 for females, 0.9 for males, α is −0.329 for females and −0.411 for males, min indicates the minimum of Scr/κ or 1 and max indicates the maximum of Scr/κ or 1 [15].

We assessed the performance of the four models against iGFR early after transplant and a year later by formally testing the differences in bias, precision and relative accuracy calculated as follows: bias, the average prediction error = Σ (eGFR − iGFR)/n, where n is the number of GFR studies performed and iGFR is iothalamate GFR; relative bias, percent deviation from the iGFR; precision, the value of R2 from the linear regression of iGFR on eGFR; relative accuracy, the percent of estimates falling within 10%, 30% and 50% of iGFR. We also assessed the ability of these four GFR prediction equations to correctly identify recipients with iGFR < 45 and 60 ml/min/1.73 m². This was achieved by comparing the proportion of eGFR < 45 and 60 ml/min/1.73 m² to the proportion of iGFR< 45 and 60, by calculating kappa statistic for agreement and by calculating the sensitivity and specificity of each equation to accurately classify recipients. The equations were compared using a paired t-test for bias, a paired test of proportions for relative accuracy and the Hotelling–Williams test for precision [16–18]. Statistical significance was assessed with a Bonferroni-adjusted threshold (P < 0.008) since multiple comparisons were performed. The four equations were ranked from 1 to 4 based on the results of the paired tests, with ‘ties’ assigned the same ranking. Though not formally tested, the interquartile range and the root mean squared error of the bias were computed.

Analyses and graphs were completed using statistical software SAS, version 9.1 (SAS, Cary NC), and R version 2.8.0 (R, Boston, MA).

Results

A total of 153 renal transplant recipients were enrolled in the trial (126 at the University of Minnesota and 27 at HCMC) and underwent a baseline iGFR measurement. A total of 19 subjects from the UMN were excluded as they had received steroids before the transplant or required additional steroids beyond Day 5 (Figure 1); 107 had iGFR early after transplantation, and 81 of them underwent a second iGFR. A total of 27 HCMC recipients maintained on steroids underwent a first iGFR, and 16 of them underwent a second one (Figure 1). The overall characteristics of 107 recipients not on steroids (Group 1) and the 27 who were on steroids (Group 2) at the time of the first iothalamate GFR were highly comparable (Table 1). Recipients in the steroid-free group were older (50.1 ± 11.8 vs 43.6 ± 12.9), 59.3% were men and 89.4% were white. Moreover, serum creatinine was similar between the two groups; 1.22 ± 0.4 mg/dL in Group 1 and 1.25 ± 0.4 mg/dL in Group 2. The average prednisone dose at 1, 3 and 12 months in Group 2 was 29.2 ± 9.6, 13.8 ± 4.8 and 12.7 ± 11.2 mg/day, respectively. In total, 10 recipients had delayed graft function requiring dialysis, and one HCMC recipient had an episode of acute rejection that was treated with bolus steroids.

Table 1.

Recipient characteristic, eGFR and iothalamate GFR in study participants

	All	Steroid free	Steroid
n	134	107	27
Age (years)*	48.5 ± 12.4	50.1 ± 11.8	43.6 ± 12.9
Male (%)	60.5	59.3	64.1
White (%)	86.2	89.4	76.9
BMI (kg/m2)	26.4 ± 5.0	26.0 ± 4.7	27.3 ± 5.9
BSA (m2)	1.87 ± 0.3	1.87 ± 0.2	1.90 ± 0.3
Baseline GFR measurement
n	134	107	27
Serum creatinine (mg/dL)	1.23 ± 0.4	1.22 ± 0.4	1.25 ± 0.4
iGFR	56.2 ± 17.0	55.5 ± 17.0	58.3 ± 17.1
eGFRCG	57.6 ± 15.4	56.8 ± 15.5	60.2 ± 15.0
eGFRMC	67.6 ± 20.5	67.2 ± 20.1	69.0 ± 21.9
eGFRMDRD	63.6 ± 19.9	63.1 ± 20.1	65.2 ± 19.5
eGFR CKD-EPI	68.8 ± 20.7	68.0 ± 20.5	71.3 ± 21.5
1 year GFR measurement
n	97	81	16
Serum creatinine (mg/dL)	1.25 ± 0.4	1.24 ± 0.4	0.26 ± 0.4
iGFR	56.4 ± 16.9	56.8 ± 17.7	56.3 ± 12.1
eGFRCG	57.5 ± 14.1	56.9 ± 14.5	60.5 ± 11.3
eGFRMC	64.2 ± 20.6	63.9 ± 20.8	65.0 ± 16.1
eGFRMDRD	59.0 ± 17.9	58.7 ± 18.1	59.4 ± 11.5
eGFR CKD-EPI	63.9 ± 18.2	63.2 ± 18.6	65.2 ± 13.5

BMI, body mass index; BSA, body surface area; mean ± SD; iGFR, iothalamate GFR; GFR is in milliliters per minute per 1.73 m².

^*P < 0.05.

All subjects collected a 24-h urine the day before the GFR measurement. For recipients in Group 1, daily creatinine excretion was 16.1 ± 4.4 mg/kg for men and 13.0 ± 5.1 mg/kg/day for women at the first GFR and 17.0 ± 4.2 and 13.8 ± 3.3 mg/kg at the second. For those on steroids, it was 16.0 ± 7.3 mg/kg/day in men and 15.5 ± 3.20 mg/kg/day for women at baseline and 19.2 ± 4.9 and 14.4 ± 2.0 at the time of the second measurement. Of note, one recipient in the steroid-free group had bilateral above-knee amputations, and his daily creatinine excretion was 16.7 mg/kg/day at baseline and 15.2 mg/kg/day at follow-up. Measured and estimated GFR for both groups are shown in Table 1.

eGFRCG

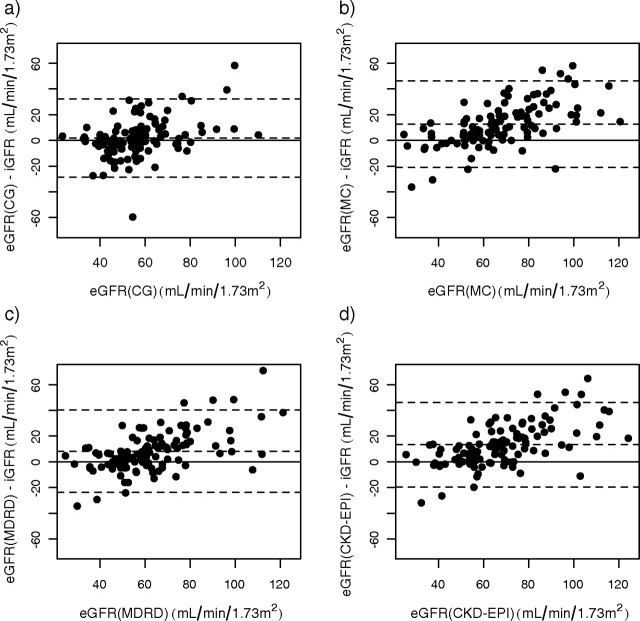
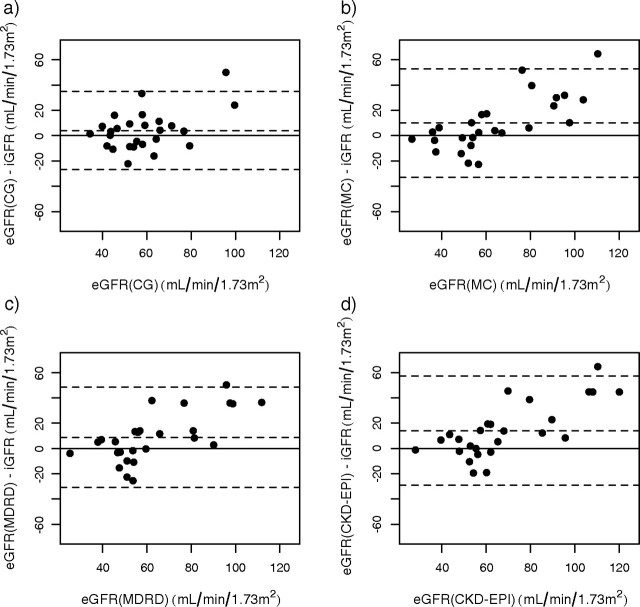
The relationship between eGFRCG and baseline iGFR in recipients on steroid-free immunosuppression is shown in Figure 2. eGFRCG overestimated iGFR by 1.85 ± 15.2 ml/min/1.73 m² and had a relative bias of 8.93 ± 33.6%. Inspection of the residual plot revealed that bias of eGFRCG is different below and above 60 ml/min/1.73 m². Therefore, we determined the bias for those with iGFR < 60 ml/min, and it was 7.82 ± 13.5 ml/min and −7.09 ± 13.2 ml/min for those with iGFR > 60 ml/min; P < 0.0001. eGFRCG fell within 10%, 30% and 50% of iGFR in 44.3%, 80.2% and 87.7% of cases, respectively (Table 2). Performance of eGFRCG for those on steroids was similar; eGFRCG overestimated iGFR by only 4.05 ± 15.5 ml/min/1.73 m², had a relative bias of 13.76 ± 37.9% and fell within 10%, 30% and 50% of iGFR in 30.8%, 76.9% and 88.5%, respectively (Table 2, Figure 3). Its precision in Group 2 was identical to that observed in Group 1: 0.30 vs 0.30. A similar pattern emerged in the 81 recipients who remained steroid free at 1 year after transplantation (Table 3). In contrast, for the 16 recipients who were still on steroids at the second iGFR measurement there was a marked drop in precision from 0.30 to 0.05 but no appreciable change in bias or relative accuracy (Table 3).

Fig. 2.

Residual plots of GFR-estimating models against iothalamate GFR in steroid-free recipients early after transplantation; (a) eGFRCG, (b) eGFRMC, (c) eGFRMDRD, (d) eGFRCKD-EPI. The solid line indicates zero difference between iGFR and eGFR and the dashed lines indicate ±2 SD of the difference.

Table 2.

Overall performance of eGFRCG, eGFRMC, eGFRMDRD and eGFRCKD-EPI in the early posttransplant period

	Bias(mL/min)	IQRa	Relative bias(%)	R2	RMSEb	Within 10%of iGFR	Within 30%of iGFR	Within 50%of iGFR
Steroid free (n = 107)
eGFRCG	1.85 ± 15.2	14.3	8.93 ± 33.6%	0.30	15.2	44.3%	80.2%	87.7%
(Rank)	(1)		(1)	(1)		(1)	(1)	(1)
eGFRMC	12.57 ± 16.8	18.6	27.92 ± 38.8%	0.35	20.9	25.5%	59.4%	80.2%
(Rank)	(3)		(3)	(1)		(2)	(2)	(1)
eGFRMDRD	8.23 ± 16.0	18.3	19.60 ± 36.0%	0.38	17.9	30.2%	71.7%	84.9%
(Rank)	(2)		(2)	(1)		(2)	(1)	(1)
eGFRCKD-EPI	13.30 ± 16.3	20.5	29.25 ± 37.9%	0.38	21.1	27.4%	58.5%	76.4%
(Rank)	(3)		(3)	(1)		(2)	(2)	(2)
Steroid maintenance (n = 27)
eGFRCG	4.05 ± 15.5	16.8	13.76 ± 37.9%	0.30	15.7	30.8%	76.9%	88.5%
(Rank)	(1)		(1)	(1)		(1)	(1)	(1)
eGFRMC	9.96 ± 21.4	24.5	24.74 ± 54.1%	0.21	23.2	34.6%	65.4%	84.6%
(Rank)	(1)		(1)	(1)		(1)	(1)	(1)
eGFRMDRD	8.78 ± 19.8	17.2	21.67 ± 43.9%	0.24	21.3	19.2%	61.6%	80.8%
(Rank)	(1)		(1)	(1)		(1)	(1)	(1)
eGFRCKD-EPI	14.0 ± 21.6	22.8	31.85 ± 49.6%	0.23	25.3	30.8%	57.7%	76.9%
(Rank)	(2)		(2)	(1)		(1)	(1)	(1)

Rank of Performance based on paired tests: 1 = Best. Ties are assigned the same rank. CG, Cockcroft–Gault; MC, Mayo Clinic. ^aIQR, interquartile range of differences, ^bRMSE, root mean squared error of differences.

Fig. 3.

Residual plots of GFR estimating models against iothalamate GFR in steroid-maintenance recipients early after transplantation; (a) eGFRCG, (b) eGFRMC, (c) eGFRMDRD, (d) eGFRCKD-EPI. The solid line indicates zero difference between iGFR and eGFR, and the dashed lines indicate ±2 SD of the difference.

Table 3.

Overall performance of eGFRCG, eGFRMC, eGFRMDRD and eGFRCKD-EPI at 1 year

	Bias(mL/min)	IQRa	Relative Bias(%)	R2	RMSEb	Within 10%of iGFR	Within 30%of iGFR	Within 50%of iGFR
Steroid free (n = 81)
eGFRCG	0.23 ± 15.2	16.0	8.52 ± 45.1%	0.32	15.1	41.7%	75.0%	88.1%
	(1)		(1)	(1)		(1)	(1)	(1)
eGFRMC	7.80 ± 17.7	20.8	21.46 ± 49.2%	0.33	19.3	32.1%	61.9%	83.3%
(Rank)	(3)		(3)	(1)		(1)	(2)	(1)
eGFRMDRD	2.40 ± 15.7	17.2	11.24 ± 40.9%	0.37	15.8	39.3%	75.0%	86.9%
(Rank)	(1)		(1)	(1)		(1)	(1)	(1)
eGFRCKD-EPI	6.91 ± 15.9	18.1	19.99 ± 44.8%	0.37	17.3	33.3%	66.7%	83.3%
(Rank)	(2)		(2)	(1)		(1)	(2)	(2)
Steroid maintenance (n = 16)
eGFRCG	4.79 ± 17.0	18.4	13.32 ± 32.8%	0.05	17.2	25.0%	81.3%	81.3%
eGFRMC	9.35 ± 17.3	19.2	20.45 ± 35.4%	0.08	19.2	18.8%	68.8%	75.0%
eGFRMDRD	3.71 ± 13.6	16.0	9.99 ± 26.9%	0.11	13.8	43.8%	81.3%	87.5%
eGFRCKD-EPI	9.47 ± 14.8	15.4	20.52 ± 30.5%	0.12	17.2	18.8%	68.8%	87.5%

Rank of performance based on paired tests: 1 = Best. Ties are assigned the same rank. CG, Cockcroft–Gault; MC, Mayo Clinic. ^aIQR, interquartile range of differences, ^bRMSE, root mean squared error of differences. Ranking was not performed for the 16 subjects on no steroids due to the small n.

eGFRMC

In the 107 recipients maintained on a steroid-free protocol, eGFRMC overestimated baseline iGFR by 12.57 ± 16.8 ml/min/1.73 m² and had a relative bias of 27.92 ± 38.8%. The performance of eGFRMC against iGFR in these subjects is shown graphically in Figure 2. The bias of eGFRMC was more pronounced for those with iGFR < 60 ml/min; 15.9 ± 17.0 vs 5.5 ± 17.1 ml/min for those with iGFR > 60 ml/min; P = 0.0009. eGFRMC was within 10%, 30% and 50% of iGFR in only 25.5%, 59.4% and 80.2% of cases. Its precision, however, was similar to eGFRCG (Table 2). eGFRMC in the 27 recipients on steroids at baseline also overestimated GFR by 9.96 ± 21.4 ml/min/1.73 m² and had a lower precision of 0.21 (Figure 3). In regard to its relative accuracy, eGFRMC fell within 10%, 30% and 50% of iGFR in 34.6%, 65.4% and 84.6%, respectively (Table 2). At 1 year after transplantation, eGFRMC became less biased (7.80 ± 17.7 ml/min) but continued to have the lowest relative accuracy (Table 3). While bias and relative accuracy remained almost identical from baseline to 1 year in the 16 recipients who were on steroids, the precision dropped sharply, from 0.21 to 0.08.

eGFRMDRD

eGFRMDRD overestimated iGFR by 8.23 ± 16.0 ml/min/1.73 m², had a relative bias of 19.6 ± 36.0% and precision at 0.38 in Group1 at the baseline GFR (Table 2). Similar to what we observed with eGFRMC, the bias was greater in those with iGFR < 60 ml/min: 12.3 ± 15.1 vs 1.59 ± 17.4 ml/min; P = 0.0003. eGFRMDRD fell within 10%, 30% and 50% of iGFR in 30.2%, 71.7% and 84.9% of cases, respectively (Table 2). In the steroid group, its bias was identical; it overestimated iGFR by 8.78 ± 19.8 ml/min/1.73 m² and had a relative bias of 21.67 ± 43.9% but with lower precision of 0.24, and eGFRMDRD fell within 30% of iGFR in only 61.6% of cases (Table 2, Figure 3). At the 1-year measurement, eGFRMDRD performed better in all domains in all recipients regardless of steroid use (Table 3).

eGFRCKD-EPI

eGFRCKD-EPI overestimated iGFR the most, by 13.30 ± 16.3 ml/min/1.73 m², had a relative bias of 29.25 ± 37.9% and precision at 0.38 (Figure 2). The bias of eGFRCKD-EPI in those with iGFR < 60 ml/min was 17.1 ± 16.0 ml/min vs 7.2 ± 18.2 for those with iGFR > 60 ml/min; P = 0.0015. Early after transplantation, eGFRCKD-EPI fell within 10%, 30% and 50% of iGFR in 27.4%, 58.5% and 76.4% of cases, respectively (Table 2). In the steroid group, it overestimated iGFR by 14.0 ± 21.6 ml/min/1.73 m² and had a relative bias of 31.85 ± 49.6%, and precision of 0.23. eGFRCKD-EPI fell within 30% of iGFR in 57.7% of cases (Table 2, Figure 3). At 1 year, the bias of eGFRCKD-EPI decreased significantly to 6.91 ± 15.9 ml/min in the steroid-free recipients and to 9.47 ± 14.8 ml/min in those who remained on steroids (Table 3). Interestingly, its precision fell by 50% in the 16 recipients who were still receiving steroids at 1 year (Table 3).

We next compared the ability of these models to accurately classify recipients by the following GFR categories: <45 and <60 ml/min/1.73 m². There were only six recipients with GFR < 30 ml/min/1.73 m^2, and therefore this category was not studied. The percentage of estimates falling within these two categories for those on and off steroids is shown in Table 4. In those not maintained on steroids, all models except eGFRCG predicted a lower percentage in these categories than actual GFR, i.e., they were less likely to classify recipients as having GFR < 45 and < 60 ml/min/1.73 m². A similar pattern existed in the steroid-maintenance group at the time of first GFR for the GFR cut point of 45 ml/min but almost a reverse pattern at the time of the second GFR; i.e., long-term exposure to steroids overclassified the proportion of those < 45 ml/min/1.73 m². For the GFR cut point of < 60 ml/min/1.73 m², long-term steroid use resulted in underclassifying individuals (Table 4). In all, eGFRCG was superior in its ability to accurately classify recipients, and the eGFRCKD-EPI was least accurate, particularly for the GFR < 60 ml/min/1.73 m² threshold. In general, the Kappa statistic was comparable for those on and off steroids (Table 5). It is clear that the eGFRCG is the most sensitive model in detecting eGFR < 60 ml/min/1.73 m² in the steroid-free group but with a marginal specificity, and eGFRMC and eGFRCKD-EPI were most specific in this category. For GFR < 45 ml/min/1.73 m², the four models had highly comparable sensitivity and specificity in those on steroid-free regimen. A similar pattern was seen in the steroid-maintenance group, i.e., eGFRCG was most sensitive and marginally specific for <60 ml/min/1.73 m² but had very comparable sensitivity and specificity to the other models for those <45 ml/min/1.73 m².

Table 4.

Accuracy in classifying recipients to two GFR cut points; 45 ml/min and 60 ml/min/1.73 m²

	Steroid free		Steroid maintenance
	At baseline (n = 107)	At 1 year (n = 81)	At baseline (n = 27)	At 1 year (n = 16)
< 45 ml/min/1.73 m2
iGFR (%)	24.5	20.7	33.3	5.9
eGFRCG (%)	19.8	25.0	23.1	6.3
eGFRMC (%)	12.3	19.1	19.2	12.5
eGFRMDRD (%)	14.2	21.4	11.5	12.5
eGFRCKD-EPI (%)	11.3	15.5	11.5	6.3
< 60 ml/min/1.73 m2
iGFR (%)	65.1	59.8	51.9	70.6
eGFRCG (%)	67.9	58.3	65.4	62.5
eGFRMC (%)	34.9	41.7	53.9	50.0
eGFRMDRD (%)	46.2	54.8	61.5	62.5
eGFRCKD-EPI (%)	35.9	44.1	42.3	31.3

Table 5.

Agreement between models by Kappa statistic in detecting GFR < 45 and < 60 ml/min/1.73 m²

		Steroid free		Steroid maintenance		Steroid free				Steroid maintenance
		GFR < 60	GFR < 45	GFR < 60	GFR < 45	GFR < 60		GFR < 45		GFR < 60		GFR < 45
Estimation method						SN	SP	SN	SP	SN	SP	SN	SP
eGFRCG	Baseline	0.30 (0.11, 0.49)	0.43 (0.22, 0.63)	0.45 (0.11, 0.78)	0.35 (−0.02, 0.73)	78	51	50	90	86	58	44	88
	1 year	0.44 (0.25, 0.64)	0.23 (−0.01, 0.48)	NS	NS	75	69	43	81	NS	NS	NS	NS
eGFRMC	Baseline	0.24 (0.09, 0.39)	0.42 (0.21, 0.62)	0.38 (0.21, 0.62)	0.43 (0.07, 0.79)	45	84	38	96	71	67	44	94
	1 year	0.45 (0.27, 0.62)	0.35 (0.09, 0.60)	NS	NS	60	87	43	89	NS	NS	NS	NS
eGFRMDRD	Baseline	0.34 (0.17, 0.50)	0.49 (0.30, 0.70)	0.22 (−0.16, 0.59)	0.40 (0.06, 0.73)	59	78	46	96	71	50	33	100
	1 year	0.55 (0.37, 0.73)	0.38 (0.13, 0.63)	NS	NS	77	78	50	87	NS	NS	NS	NS
eGFRCKD-EPI	Baseline	0.22 (0.07, 0.37)	0.44 (0.23, 0.64)	0.31 (−0.03, 0.67)	0.40 (0.06, 0.73)	45	81	38	98	57	75	33	100
	1 year	0.44 (0.26, 0.63)	0.43 (0.17, 0.68)	NS	NS	62	84	43	93	NS	NS	NS	NS

SN, sensitivity, SP, specificity. Both sensitivity and specificity are displayed as percentages. NS, not studied as the number of recipients in this category (i.e., 16) is too small.

We then addressed the performance of the four models by gender and body mass index (BMI). To avoid creating too many categories (steroid vs no steroids, early GFR vs late), we used the pooled information from the 134 recipients with baseline iGFR. The four models were significantly more biased in women, but the models were comparable in correctly classifying recipients with GFR < 60 ml/min (Table 6). In regard to the effect of BMI, the models behaved differently; the bias of eGFRCG increased at BMI > 30 kg/m², while the bias of the other three actually decreased (Table 6).

Table 6.

Performance of estimating equations by gender and BMI category

		Gender			BMI
		Male (n = 81)	Female (n = 53)	P value*	< 30 (n = 99)	> 30 (n = 34)	P value*
eGFRCG	Bias (ml/min)	0.96 ± 14.6	7.78 ± 14.8	0.001	0.97 ± 14.7	6.21 ± 16.2	0.08
	Relative bias (%)	2.93 ± 29.3	21.67 ± 39.2	0.002	7.18 ± 33.5	18.02 ± 36.2	0.11
	% agreement for GFR < 60 ml/min	65.5%	75.5%	0.226	68.7%	70.6%	0.83
eGFRMC	Bias (ml/min)	7.37 ± 16.3	20.00 ± 17.4	< 0.0001	14.08 ± 16.6	5.98 ± 19.8	0.02
	Relative bias (%)	16.26 ± 33.3	46.01 ± 48.5	< 0.0001	31.27 ± 41.1	15.39 ± 42.9	0.05
	% agreement for GFR < 60 ml/min	59.5%	61.2%	0.84	58.6%	64.7%	0.52
eGFRMDRD	Bias (ml/min)	6.02 ± 15.5	12.27 ± 18.1	0.03	9.88 ± 16.2	3.71 ± 17.8	0.06
	Relative bias (%)	14.12 ± 31.2	29.99 ± 45.1	0.01	23.02 ± 38.0	11.00 ± 35.3	0.11
	% agreement for GFR < 60 ml/min	63.1%	67.4%	0.62	63.6%	67.7%	0.67
eGFRCKD-EPI	Bias (ml/min)	10.50 ± 16.6	18.42 ± 17.9	0.01	15.2 ± 16.8	8.29 ± 18.7	0.05
	Relative bias (%)	22.48 ± 34.1	42.1 ± 46.7	0.006	33.08 ± 40.2	19.80 ± 39.2	0.10
	% agreement for GFR < 60 ml/min	57.1%	61.2%	0.64	57.6%	61.8%	0.66

^*Two-sample t-test, chi-square test.

Discussion

These data demonstrate that the eGFRCG is the best available model in kidney transplant recipients not receiving steroid maintenance, with eGFRMDRD being very comparable to eGFRCG particularly at 1 year after transplantation. In contrast, both eGFRMC and the newly introduced CKD-EPI equations were the most biased. Importantly, exposure to steroids for a full year resulted in a significant drop in the precision of these models. Therefore, it seems that steroid exposure does indeed alter the performance of these models, at least from these small numbers of participants we have studied. In light of the preliminary and small number of participants, the hypothesis that GFR-estimating models work better in recipients on steroid-free immunosuppression is plausible but needs to be confirmed.

Published validations of commonly used GFR estimates in renal transplant recipients yielded variable results [4,19–21]. Perhaps the most comprehensive effort to assess the utility of these formulas in kidney transplant recipients comes from the recent systematic review by White et al. [19]. In their assessment of 23 studies that measured GFR in 3487 transplant recipients at least 6 months after transplantation, a wide range of bias and accuracy was demonstrated even in the three studies that calibrated serum creatinine level to the Cleveland Clinic laboratory. The Cockcroft–Gault model (not the Cockcroft–Gault estimated GFR we used here) fell within 30% of measured GFR in 73% of the cases in comparison to 76% for the four-variable MDRD study equation. It is important to note that there was no reference made to the type of immunosuppression in these recipients, and the majority of these studies used non-IDMS-traceable creatinine values. Additionally, the almost universal use of trimethoprim-sulfamethoxazole, which blocks tubular secretion of creatinine, at different dosages between centers may also explain some of the variability observed regarding the performance of these models in transplant recipients [22].

At least two other studies have shown the Cockcroft–Gault model to be superior to the MDRD study equation [23, 24], but to our knowledge the analyses presented here are the first to use the IDMS-traceable serum creatinine and correct for the bias in the MDRD study sample. A novel aspect of this analysis is the assessment of the utility of the CKD-EPI equation [15]. This equation was developed in 8254 participants in 10 clinical trials and validated in 3896 subjects with a variety of kidney diseases. There were 241 transplant recipients in the development set and 1253 in the internal and external validation sets. Information was not available on whether these transplant recipients were receiving steroids. Considering the time frame of the studies used to develop the CKD-EPI equation, we suspect most, if not all, were receiving steroids. We do not believe this entirely explains the poor performance of the CKD-EPI equation. In reality, this new equation only has a 3-ml/min improvement in bias and 3.3% improvement in relative accuracy over eGFRMDRD. Of course, studying this equation in a larger sample would be highly desirable.

All formulas incorporate age and gender as factors which influence muscle mass and therefore creatinine generation. However, kidney transplant recipients may have rapid changes in body composition with disproportional increase in body fat and loss of muscle mass due to long-term steroid exposure [25]. Steroid use is also correlated with a significant reduction in the predicted to actual urinary creatinine excretion [26]. This may potentially explain the significant drop in precision of GFR estimates in the steroid group after 1 year, although we were not able to show the differences in 24-h urinary creatinine excretion between those on and off steroids regardless of time post transplant.

Similarly, performance of those formulas is affected by obesity. eGFRCG increasingly overestimates true GFR in patients with high BMI. The formulas behaved differently and showed decreased bias in those with BMI > 30. While this improvement of performance cannot be readily explained, our data indicate that advantage of eGFRCG and eGFRMDRD is alleviated in obese recipients. All four models had similar performance in identifying GFR < 45 ml/min/1.73 m², regardless of whether on and off steroids. Ideally, performance of those formulas in more advanced kidney disease should be done but was not possible because of the small number of recipients with lower GFR.

This study has limitations. The majority of our recipients are white, and only recipients with well-functioning grafts were studied (i.e., creatinine <2.5 mg/dL). The number of subjects in the steroid-maintenance group was very small and therefore limits the conclusions drawn regarding the comparison to the non-steroid group. Despite the small size, the careful calibration of the serum creatinine, the use of IDMS values and the low coefficient of variation of the iothalamate GFR strengthen the findings, but a larger group is clearly needed to confirm these findings.

In conclusion, we have demonstrated that GFR estimation models are inferior to measured GFR in both recipients on steroid-free and steroid-maintenance immunosuppression protocols. eGFRCG was the least biased and most accurate model regardless of steroids use. While limited by the small numbers, these preliminary data suggest that long-term exposure to steroids is associated with a reduction of precision in all models. More studies are needed to test the applicability of current GFR prediction models in a larger number of recipients of diverse ethnic backgrounds on steroid-free immunosuppression.

Conflicts of interest statement. None declared.