Evaluating the Impact of Prior Assumptions in Bayesian Biostatistics

Abstract

A common concern in Bayesian data analysis is that an inappropriately informative prior may unduly influence posterior inferences. In the context of Bayesian clinical trial design, well chosen priors are important to ensure that posterior-based decision rules have good frequentist properties. However, it is difficult to quantify prior information in all but the most stylized models. This issue may be addressed by quantifying the prior information in terms of a number of hypothetical patients, i.e., a prior effective sample size (ESS). Prior ESS provides a useful tool for understanding the impact of prior assumptions. For example, the prior ESS may be used to guide calibration of prior variances and other hyperprior parameters. In this paper, we discuss such prior sensitivity analyses by using a recently proposed method to compute a prior ESS. We apply this in several typical Bayesian biomedical data analysis and clinical trial design settings. The data analyses include cross-tabulated counts, multiple correlated diagnostic tests, and ordinal outcomes using a proportional-odds model. The study designs include a phase I trial with late-onset toxicities, a phase II trial that monitors event times, and a phase I/II trial with dose-finding based on efficacy and toxicity.

1 Introduction

Understanding the strength of prior assumptions relative to the likelihood is a fundamental issue when applying Bayesian methods. The processes of formulating a putatively non-informative prior or eliciting a prior from an area expert typically require one to make many arbitrary choices, including the choice of particular distributional forms and numerical hyperparameter values. In practice, these choices are often dictated by technical convenience. A common criticism of Bayesian analysis is that an inappropriately informative prior may unduly influence posterior inferences and decisions. However, it is difficult to quantify and critique prior information in all but the most stylized models. These concerns may be addressed by quantifying the prior information in terms of an equivalent number of hypothetical patients, i.e., a prior effective sample size (ESS). Such a summary allows one to judge the relative contributions of the prior and the data to the final conclusions. A useful property of prior ESS is that it is readily interpretable by any scientifically literate reviewer without requiring expert mathematical training. This is important, for example, for consumers of clinical trial results.

The purpose of this paper is to discuss prior sensitivity analyses in Bayesian biostatistics by computing the prior ESS for six case studies chosen from the recent literature. We apply an ESS method proposed by Morita, Thall and Müller (MTM) [7]. Some of our case studies require prior ESS values for a subvector θ₁ of the parameter vector θ = (θ₁, θ₂). The general definition allows the ESS to be specified for a subvector θ₁ of θ = (θ₁, θ₂). However, ESS(θ₁) + ESS(θ₂) typically does not equal ESS(θ₁, θ₂), because θ₁ in its marginal distribution often has a very different meaning than θ₁ in the joint distribution of (θ₁, θ₂).

The case studies consist of three Bayesian data analyses and three study designs. The data analysis examples include small-sample cross-tabulated counts from an animal experiment to evaluate mechanical ventilator devices, bivariate normal modeling of paired data from multiple correlated diagnostic serologic tests, and proportional odds modeling of ordinal outcomes arising from a study of viral effects in chick embryos. The study design examples include a phase I trial with dose-finding using the time-to-event continual reassessment method (TITE-CRM) [2], a phase II trial with a stopping rule for monitoring event times, and a phase I/II clinical trial in which doses were assigned based on both efficacy and toxicity.

Section 2 provides a motivating example. In section 3, we briefly summarize MTM. We discuss prior sensitivity in the real examples of Bayesian data analyses and study designs in Section 4. We close with a brief discussion in Section 5.

2 A Motivating Example

The following example illustrates how the prior ESS may be used as an index of prior informativeness in a Bayesian sensitivity analysis and as a tool for critiquing a Bayesian data analysis when interpreting or formally reviewing the analysis.

Carlin [1] analyzed small-sample contingency table data from an experiment carried out to examine the effects of mechanical ventilator devices on lung damage in rabbits. In the experiment, the lungs of newborn rabbits were altered to simulate lung defects seen in human infants with underdeveloped lungs due to premature birth. The aim was to learn about the joint effects of different frequency and amplitude settings of the ventilators on lung damage. Six groups of six to eight animals each were compared using a factorial design with three frequency values crossed with two amplitudes. For amplitude g (= 1, 2 for 20 and 60, respectively) and frequency h (= 1, 2, 3 for 5, 10, and 15 Hz, respectively), let Y_g,h denote the number of animals with lung damage out of n_g,h studied and let π_g,h denote the probability of lung damage in cell (g, h). The data are shown in Table 1. Each cell reports the empirical frequency Y_g,h/n_g,h. Carlin [1] assumed the following logistic regression model

Table 1.

Lung damage data from Carlin [1]. Each cell contains the number of animals with lung damage over the number studied at the (amplitude, frequency) combination.

	Frequency (Hz)
Amplitude	5	10	15
20	1/6	0/6	0/6
60	4/6	0/6	4/8

$${\pi }_{g,h}(\mathit{\theta })={\mathit{logit}}^{-1}\left(\mu +{\alpha }_g+{\beta }_h+{\gamma }_h{I}_{(g=2)}\right),$$

where I_(g=2) indicates g = 2. Note that α_g and β_h are main effects for amplitude and frequency while γ_h is the interaction effect at frequency h and amplitude g = 2. Hence, the model parameter is θ = (μ, α₁, α₂, β₁, β₂, β₃, γ₁, γ₂, γ₃), with dimension d = 9. Carlin [1] assumed independent normal priors for μ, {α_g}, {β_h}, and {γ_h},

$$\mu \sim N(0,{1000}^2),{\alpha }_g\sim N(0,{\stackrel{\sim }{\sigma }}_{\alpha }^2),{\beta }_h\sim N(0,{\stackrel{\sim }{\sigma }}_{\beta }^2),{\gamma }_h\sim N(0,{\stackrel{\sim }{\sigma }}_{\gamma }^2).$$ (1)

Since the numbers of animals studied were very small, Carlin [1] explored the effect of a range of non-informative prior distributions in the analysis.

We use prior ESS to investigate sensitivity of the inferences to hyperparameter values by considering ten alternative choices that cover a range of reasonably non-informative settings. The ten hyperparameter choices, labeled N1 to N10, are shown in Table 2. We add the four priors N1 to N4 which would have smaller ESS values than those considered by Carlin [1] for priors N5 to N10. We apply MTM’s method to compute an overall ESS for p(θ|θ̃), and also ESS_μ, ESS_α, ESS_β, and ESS_γ, for the marginal priors on the subvectors μ, α = (α₁, α₂), β = (β₁, β₂, β₃), and γ = (γ₁, γ₂, γ₃) of θ.

Table 2.

Summary of priors (standard error parameters) and computed ESSs of the example for cross-tabulated counts in Carlin [1].

	σ̃α	σ̃β	σ̃γ	ESS	ESSμ	ESSα	ESSβ	ESSγ
N1	2.0	2.0	2.0	2.3	< 0.001	2.0	3.0	6.0
N2	1.5	2.0	2.0	3.7	< 0.001	3.6	3.0	6.0
N3	2.0	1.5	2.0	3.0	< 0.001	2.0	5.3	6.0
N4	2.0	2.0	1.5	3.0	< 0.001	2.0	3.0	10.6
N5	1.5	1.5	1.5	4.1	< 0.001	3.6	5.3	10.6
N6	1.5	1.5	1.0	6.0	< 0.001	3.6	5.3	23.9
N7	1.5	1.5	0.5	16.3	< 0.001	3.6	5.3	96.1
N8	0.5	0.5	1.5	24.4	< 0.001	32.0	48.0	10.6
N9	0.5	0.5	1.0	26.3	< 0.001	32.0	48.0	24.0
N10	0.5	0.5	0.5	36.6	< 0.001	32.0	48.0	96.1

The prior N10 with σ̃_α = σ̃_β = σ̃_γ = 0.5 has ESS = 36.6, so that its impact is roughly equal to that of the data (sample size n = 38) on the posterior inference. Thus, based on its ESS, the prior N10 may be criticized as being overly informative. Moreover, this prior has ESS_γ = 96.1, thus it assumes very high prior information for the interaction effects. Because the prior means of the interactions are 0, this prior has the effect of shrinking the posterior estimates of the interaction parameters excessively toward 0. This illustrates two important points. First, a seemingly reasonable choice of (σ̃_α, σ̃_β, σ̃_γ) may give an excessively informative prior. Second, it is important to evaluate not only the overall ESS, but also the ESS values of subvectors of θ of particular interest. Such ESS computations help readers to interpret the reported posterior results, such as the estimates between the frequency groups displayed in Carlin (Figure 5.1) [1]. We will revisit this example below in Section 4.

3 Prior Effective Sample Size

We briefly summarize the definition of ESS proposed by MTM [7]. While the discussion following this section does not require these details, we include this brief review for completeness.

Let f(Y | θ) be the sampling model for a random vector Y indexed by parameter vector θ = (θ₁, …, θ_d). We use f(Y | θ) generically to denote either a probability density function (pdf) or a probability mass function (pmf). The ESS is defined for a given prior p(θ | θ̃) on θ, having hyperparameters θ̃, with respect to the sampling model f(Y | θ). The approach of MTM is constructive. First, an ε-information prior q₀(θ | θ̃₀) is defined that is similar to p(θ | θ̃) but is very vague in a suitable sense. The ESS is then defined to be the sample size m of outcomes Y_m = (Y₁, ···, Y_m) that, starting with q₀(θ | θ̃₀), yields a posterior q_m (θ | Y_m) very close to p(θ | θ̃). While the ESS can be obtained analytically in some cases, in most applications numerical methods must be used.

This constructive definition may be understood in terms of the simple example where p(θ | θ̃) is a beta distribution, Be(α̃, β̃), for which the ESS is commonly considered to be α̃ + β̃. In this case, the ε-information prior q₀(θ | θ̃₀) is specified as Be(α̃/c, β̃/c) using an arbitrarily large value c > 0, so that the ESS (α̃ + β̃)/c = ε of q₀ is very small while the mean α̃/(α̃ + β̃) is the same as that of p(θ | θ̃). If m = α̃ + β̃ observations are obtained with α̃ successes and β̃ failures then, starting with the ε-information prior q₀(θ | θ̃₀), the posterior would be Be(α̃ + α̃/c, β̃ + β̃/c), which has ESS = m + ε ≐ m.

For the general construction, denote Y_m = (Y₁, …, Y_m), with Y_i ~ f(Y_i | θ) an i.i.d. sample, so the likelihood is $f_m({\mathbf{Y}}_m\mid \mathit{\theta })={\prod }_{i=1}^{m}f(Y_i\mid \mathit{\theta })$. An ε-information prior, q₀(θ | θ̃₀), is defined by requiring matching means, E_q0(θ) = E_p (θ), and correlations, Corr_q0(θ_j, θ_j′) = Corr_p(θ_j, θ_j′), j ≠ j′, while inflating the variances of the elements of θ on the domain where the variance under q₀, Var_q0(θ_j), must exist for each j = 1, …, d. The subscripts p and q₀ indicate that the moments are obtained under p(θ | θ̃) and q₀(θ | θ̃₀), repectively. Given a sample Y_m, possibly a predictor X_m = (X₁, ···, X_m), and an ε-information prior q₀(θ | θ̃₀), the posterior is

$$q_m(\mathit{\theta }\mid {\stackrel{\sim }{\mathit{\theta }}}_0,{\mathbf{Y}}_m,{\mathbf{X}}_m)\propto q_0(\mathit{\theta }\mid {\stackrel{\sim }{\mathit{\theta }}}_0)f_m({\mathbf{Y}}_m\mid {\mathbf{X}}_m,\mathit{\theta }).$$

The ESS is the interpolated value of m minimizing the prior-to-posterior distance δ between q_m (θ | θ̃₀, Y_m) and p(θ | θ̃).

MTM define the prior-to-posterior distance as the difference between the traces of the information matrix of p(θ | θ̃) and the expected information matrix of q_m (θ | θ̃₀, Y_m, X_m), where the expectation is with respect to the prior predictive distribution f_m (Y_m | θ̃, ξ̃). Here, θ̄ = E_p (θ) denotes the prior mean. To compute the distance between p(θ | θ̃) and q_m (θ | Y_m), MTM define

$$\delta (m,\overline{\mathit{\theta }},p,q_0)=\left|\sum _{j=1}^d{D}_{p,j}(\overline{\mathit{\theta }})-\sum _{j=1}^d\int D_{q,j}(m,\overline{\mathit{\theta }},{\mathbf{Y}}_m)\text{d}{f}_m({\mathbf{Y}}_m\mid \stackrel{\sim }{\mathit{\theta }})\right|$$ (2)

where D_p,j and D_q,j are the curvatures of the original prior and the posterior under the ε-information prior, $D_{p,j}(\mathit{\theta })=-{\partial }^2/\partial {\theta }_j^{2}logp(\mathit{\theta }\mid \stackrel{\sim }{\mathit{\theta }})$ and $D_{q,j}(m,\mathit{\theta },{\mathbf{Y}}_m)=-{\partial }^2/\partial {\theta }_j^{2}log{q}_m(\mathit{\theta }\mid {\stackrel{\sim }{\mathit{\theta }}}_0,{\mathbf{Y}}_m)$

If interest is focused on a subvector θ_r of θ, the ESS can be determined similarly in terms of the marginal prior p(θ_r | θ̃). When the expectation cannot be obtained analytically, a simulation-based numerical approximation is used. For regression models of Y_m as a function of a predictor X_m, the likelihood is $f_m({\mathbf{Y}}_m\mid \mathit{\theta },{\mathbf{X}}_m)={\prod }_{i=1}^{m}f(Y_i\mid \mathit{\theta },X_i)$. In such settings, MTM augment the model by assuming a sampling model g_m(X_m | ξ) and prior r(ξ | ξ̃), and define

$$f_m({\mathbf{Y}}_m\mid \stackrel{\sim }{\mathit{\theta }},\stackrel{\sim }{\mathit{\xi }})=\int f_m({\mathbf{Y}}_m\mid {\mathbf{X}}_m,\mathit{\theta })g_m({\mathbf{X}}_m\mid \mathit{\xi })p(\mathit{\theta }\mid \stackrel{\sim }{\mathit{\theta }})r(\mathit{\xi }\mid \stackrel{\sim }{\mathit{\xi }})d\mathit{\theta }d\mathit{\xi }.$$

4 Case Studies of Data analysis and Study Design

The following examples show how prior sensitivity may be evaluated using ESS in data analysis and clinical trial design settings. The first three, Examples 1 to 3, are data analyses and the latter three, Example 4 to 6, are clinical trial designs. In each example, we explain how the prior ESS can be used as a tool to calibrate prior hyperparameters. Following Gelman et al. [6], we write Unif(α, β), Be(α, β), Bin(n, θ), Ga(α, β), IG(α, β), Exp(θ), N(μ, σ²), and MVN(μ, Σ), for the uniform, beta, binomial, gamma, exponential, normal, and multivariate normal distributions.

4.1 Cross-tabulated counts from small-samples – Example 1

This example was described earlier, in Section 2. The goal of Carlin’s analysis was to examine the effects of mechanical ventilator devices on lung damage in rabbits. Because of the very small numbers of studied animals, as shown in Table 1, the effect of a range of non-informative priors was explored. Recall that π_g,h was the probability of lung damage in cell (g, h) for amplitude g (= 1, 2) and frequency h (= 1, 2, 3), and π_g,h(θ) =logit⁻¹ (μ + α_g + β_h + γ_hI_(g=2), where the model parameter θ = (μ, α₁, α₂, β₁, β₂, β₃, γ₁, γ₂, γ₃).

Assuming a binomial model, Y_g,h | θ ~ Bin(n_g,h, π_g,h(θ)), the likelihood is

$$f({\mathbf{Y}}_m\mid \mathit{\theta })\propto \prod _{g=1}^2\prod _{h=1}^3{\pi }_{g,h}{(\mathit{\theta })}^{Y_{g,h}}{\{1-{\pi }_{g,h}(\mathit{\theta })\}}^{n_{g,h}-Y_{g,h}}.$$

Using MTM’s method, we compute an overall ESS, and also ESS_μ, ESS_α, ESS_β, and ESS_γ of the subvectors which characterize the overall mean, the main effects for amplitude and frequency, and their interaction effects, respectively. The ESS values obtained for the ten alternative choices for the independent normal priors are summarized in Table 2. As discussed in Section 2, since the sample size is 38, the prior N10 having the ESS = 36.6 may be criticized as being excessively informative. The priors N7 and N10 both assume very high prior information for the interaction effects. Both priors have ESS_γ = 96.1. In this example, the ESS_γ computation shows that the value σ̃_γ = 0.5 is far too small.

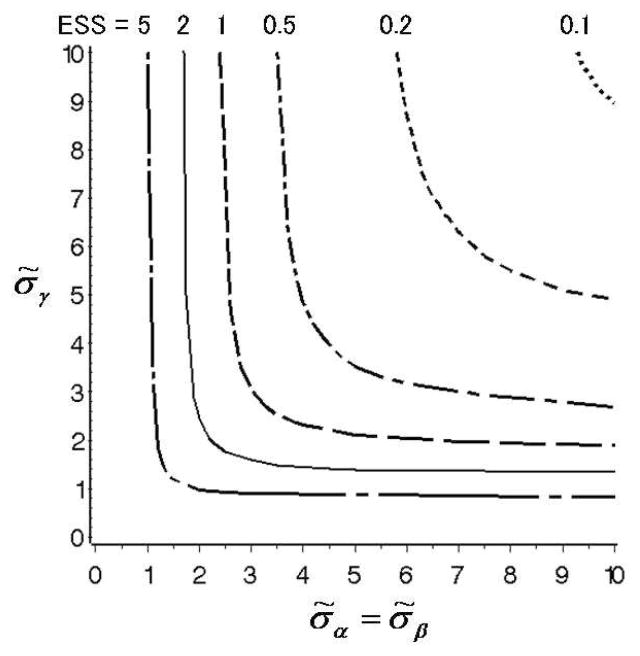
While each of the hyperparameters σ̃_α, σ̃_β, σ̃_γ can have an important impact on posterior inferences, they may be difficult to elicit or calibrate. We demonstrate here how one can use prior ESS graphically to assist in choosing these parameters. The idea is to compute the ESS for different combinations of the hyperparameters θ̃, similar to Table 2. The ESS values are then plotted as a function of θ̃. A practical problem is that one must first reduce the dimension of θ̃ to d = 2 to allow one to construct a contour plot of ESS as a function of two hyperparameter values. As a general strategy, we suggest the use of simple restrictions on elements of θ̃. In this example, we will use σ̃_α = σ̃_β ≡ σ̃, allowing us to plot ESS contours as a function of the two remaining hyperparameters (σ̃, σ̃_γ). Figure 1 shows the contours for ESS = 0.1, 0.2, 0.5, 1.0, 2.0 and 5.0. From Figure 1 one might, for example, decide to set σ̃_α = σ̃_β = 2.6 and σ̃_γ = 4.7 to obtain ESS = 1.0.

Fig. 1.

Contour plots of ESS values for σ̃_α = σ̃_β (x-axis) and σ̃_γ (y-axis), obtained in Example 1 ([1]). Dotted, dashed, dashed-dotted, longer dashed, solid, longer dashed-dotted lines show the plots of ESS = 0.1, 0.2, 0.5, 1.0, 2.0, and 5.0, respectively.

4.2 Bivariate normal model for multiple correlated diagnostic tests – Example 2

Choi et al. [3] used a bivariate normal model to analyze multiple correlated diagnostic tests. They considered the problem of comparing two serologic tests, both enzyme-linked immunosorbent assays (ELISA) for detection of antibodies to Johne’s disease in dairy cattle. Data from n₁ = 88 diseased animals and n₀ = 393 disease-free animals were reported. The two tests have continuous outcomes, which we denote by Y_1iD and Y_2iD for the i^th diseased animal, and by Y_1i′D̄ and Y_2i′D̄ for the i₀^th disease-free animal. Provided that the same prior and likelihood pair are used for the two independent data sets, they will have the same ESS value. Therefore, hereafter we will consider the sampling model and prior distributions for one of the two groups, and we drop the subscripts for disease status.

A bivariate normal distribution is assumed for the test scores, (Y_1i, Y_2i), from the i^th animal. Let μ = (μ₁, μ₂) denote the means and let Σ = Σ(τ₁, τ₂, ρ) denote a 2 × 2 covariance matrix with marginal variances ( ${\tau }_1^{-1},{\tau }_2^{-1}$) and correlation ρ. Choi et al. [3] assume

$$(Y_{i1},Y_{i2})\sim N(\mathit{\mu },\mathrm{\sum }),$$ (3)

so that θ = (μ₁, μ₂, τ₁, τ₂, ρ) and d = 5. To complete the model Choi et al. [3] assume independent prior distributions

$${\mu }_j\sim N({\stackrel{\sim }{\mu }}_j,{\stackrel{\sim }{\tau }}_j^{-1})\text{and}{\tau }_j\sim \text{Ga}({\stackrel{\sim }{a}}_j,{\stackrel{\sim }{b}}_j),j=1,2$$ (4)

with μ̃_j = 0, τ̃_j = 0.001, ã_j = b̃_j = 0.001, j = 1, 2, and ρ ~ Unif(−1, 1). The intention is to formalize vague prior information. In anticipation of the upcoming discussion we use instead a more general scaled Beta prior, ρ ~ rBe(α̃, β̃). The scaled Beta model x ~ rBe(a, b) for L < x < U is defined as (x − L)/(U − L) ~ Be(a, b), i.e., ρ~ Unif(−1, 1) for α̃ = β̃ = 1. We apply MTM’s method to compute an overall ESS for θ = (μ₁, μ₂, τ₁, τ₂, ρ), and the two additional values, ESS_μ and ESS_Σ, for the subvectors θ_μ = (μ₁, μ₂) and θ_Σ = (τ₁, τ₂, ρ). The computation yields ESS < 0.001, ESS_μ = 0.001, and ESS_Σ < 0.001. We interpret these ESSs as evidence of very vague priors, as intended.

To show how ESS may be applied as a tool for prior elicitation in this setting, we consider the four alternative priors shown in Table 3. This serves as an informal sensitivity analysis. Also, similar to the discussion in Section 4.1 we plot ESS as a function of the hyperparameters. We compute the ESS for τ̃₁ = τ̃₂ and ã₁ = ã₂ = b̃₁ = b̃₂ each ranging from 0.001 to 10, keeping α̃ = β̃ = 1 fixed. Figure 2 gives plots of the resulting ESS values. For example, the prior ESS for τ̃₁ = τ̃₂ = 10, ã₁ = ã₂ = b̃₁ = b̃₂ = 10, α̃ = β̃ = 1 is 9.5. This may be criticized as unacceptably high, considering the sample size of n = 88 diseased animals. In contrast, priors with all hyperparameters less than 1 correspond to reasonably small prior ESS.

Table 3.

Computed ESSs for the correlated diagnostic tests in Choi et al. [3].

τ̃1 = τ̃2	ã1 = b̃1 = ã2 = b̃2	α̃, β̃	ESS	ESSμ	ESSΣ
0.001	0.001	1, 1	< 0.001	0.001	< 0.001
1	1	1, 1	0.25	1.0	0.14
10	10	1, 1	9.5	10.0	9.1
1	1	5, 5	0.54	1.0	0.53
10	10	5, 5	11.3	10.0	12.4

Fig. 2.

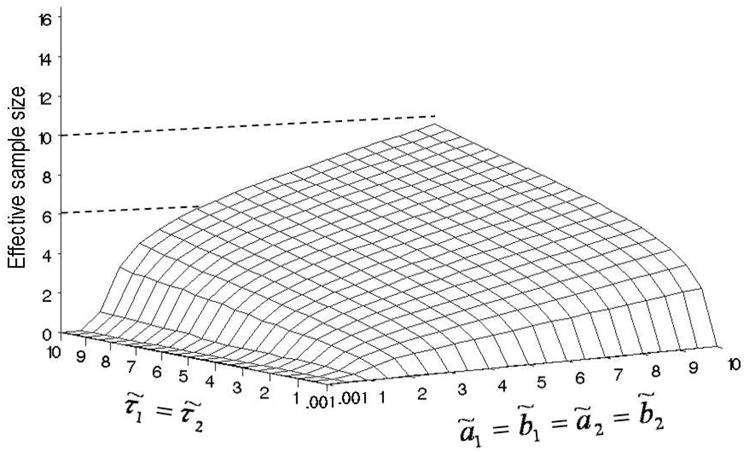
ESS surface computed for τ̃₁ = τ̃₂ and ã₁ = ã₂ = b̃₁ = b̃₂ ranging from 0.001 to 10, keeping α̃= β̃ = 1, in Example 2 (Choi et al. [3]).

4.3 Proportional odds model for ordinal outcomes – Example 3

Congdon [4] (Section 10.3.2) reports a data analysis based on a proportional odds model for ordinal response data, as shown in Table 4. The data report deformity or mortality in chick embryos as a result of arbovirus injection. Two virus groups, Facey’s Paddock (g = 1) and Tinaroo (g = 2), and a control group (g = 0) were investigated. The control group received no virus. The two virus groups and the control group contained n₁ = 75, n₂ = 72, and n₀ = 18 embryos, respectively. Each embryo in the Facey’s Paddock group received one of the four doses, {3, 18, 30, 90}, denoted by {d_1,1, d_1,2, d_1,3, d_1,4}. For the Tinaroo group, the doses were {3, 20, 2400, 88000}, denoted by {d_2,1, d_2,2, d_2,3, d_2,4}. The response Y_g,i for embryo i in group g was ordinal with three possible values: survival without deformity (Y = 0), survival with deformity (Y = 1), and death (Y = 2).

Table 4.

Arbovirus injection data (three outcomes: survival without deformity, survival with deformity, and death) reported in Congdon [4].

Virus group	Dose level	Survival without deformity	Survival with deformity	Death	Total
Control	0	17	0	1	18
Facey’s Paddock	3	13	1	3	17
	18	14	1	4	19
	30	9	2	8	19
	90	2	1	17	20
Tinaroo	3	18	0	1	19
	20	17	0	2	19
	2400	2	9	4	15
	88000	0	10	9	19

In this example, a nonzero probability of death was assumed for zero dose. This accounts for a possible background mortality effect. In fact, one death was observed among the controls. The response in the control group Y_0,i is assumed to be binary (0 or 2) rather than trinary, with Pr(Y_0,i = 2 | α) = α, and Pr(Y_g,i = h) is assumed to be a mixture

$${\pi }_{g,i,h}=Pr(Y_{g,i}=h)=\alpha +(1-\alpha )P_{g,i,h}.$$ (5)

with P_g,i,2 = γ_g,i,2, P_g,i,1 = γ_g,i,1 − γ_g,i,2, P_g,i,0 = 1 − γ_g,i,1, and

$${\gamma }_{g,i,h}={\mathit{logit}}^{-1}({\kappa }_{g,i}+{\beta }_g{X}_{g,i})$$ (6)

for h = 1, 2 with γ_g,i,0 ≡ 1.0. The covariates are log dose, X_g,(z) = log₁₀{d_g,(z)}, for z = 1, 2, 3, 4. In this example, θ = (α, β₁, β₂, κ_1,1, κ_1,2, κ_2,1, κ_2,2) and d = 7. We consider the two subvectors θ₁ = (α) and θ₂ = (β₁, β₂, κ_1,1, κ_1,2, κ_2,1, κ_2,2), which characterize the background mortality effect and the dose-response model, respectively. Using dummy indicators Z_g,i,h = 1 if Y_gi = h and 0 otherwise, the likelihood for m₀, m₁ and m₂ embryos in the control group, group 1 and group 2 is

$$f({\mathbf{Z}}_m\mid \mathit{\theta })\propto \prod _{i_0=1}^{m_0}{(1-\alpha )}^{Z_{0,i_0,0}}{\alpha }^{Z_{0,i_0,2}}\prod _{i_1=1}^{m_1}{\pi }_{1,i_1,0}^{Z_{1,i_1,0}}{\pi }_{1,i_1,1}^{Z_{1,i_1,1}}{\pi }_{1,i_1,2}^{Z_{1,i_1,2}}\prod _{i_2=1}^{m_2}{\pi }_{2,i_2,0}^{Z_{2,i_2,0}}{\pi }_{2,i_2,1}^{Z_{2,i_2,1}}{\pi }_{2,i_2,2}^{Z_{2,i_2,2}}.$$

Congdon [4] assumes independent prior distributions:

$$\alpha \sim Be(\stackrel{\sim }{\phi },\stackrel{\sim }{\phi }),{\beta }_j\sim N({\stackrel{\sim }{\mu }}_{\beta },{\stackrel{\sim }{\sigma }}_{\beta }^2),\text{and}{\kappa }_{j,h}\sim N({\stackrel{\sim }{\mu }}_{\kappa },{\stackrel{\sim }{\sigma }}_{\kappa }^2),j=1,2,h=1,2$$

with φ̃ = 1, μ̃_β = 0 and ${\stackrel{\sim }{\sigma }}_{\beta }^2=10$, μ̃_k = 0 and ${\stackrel{\sim }{\sigma }}_{\kappa }^2=100$.

We evaluate the overall ESS for θ, and subvector-specific ESS values ESS_BG for θ₁, and ESS_DR for θ₂. The computations yield ESS = 3.3, ESS_BG = 3.6, and ESS_DR = 0.85. Compared to the sample size of n = 165, the prior distributions used in this example appear appropriately non-informative. Figure 3 shows an ESS_DR surface computed for ${\stackrel{\sim }{\sigma }}_{\beta }^2$ and ${\stackrel{\sim }{\sigma }}_{\kappa }^2$ ranging from 5 to 100, fixing φ̃ = 1. The ESS surface suggests that ${\stackrel{\sim }{\sigma }}_{\beta }^2$ and ${\stackrel{\sim }{\sigma }}_{\kappa }^2$ both over 50 provide a dose-response model with sufficiently vague priors.

Fig. 3.

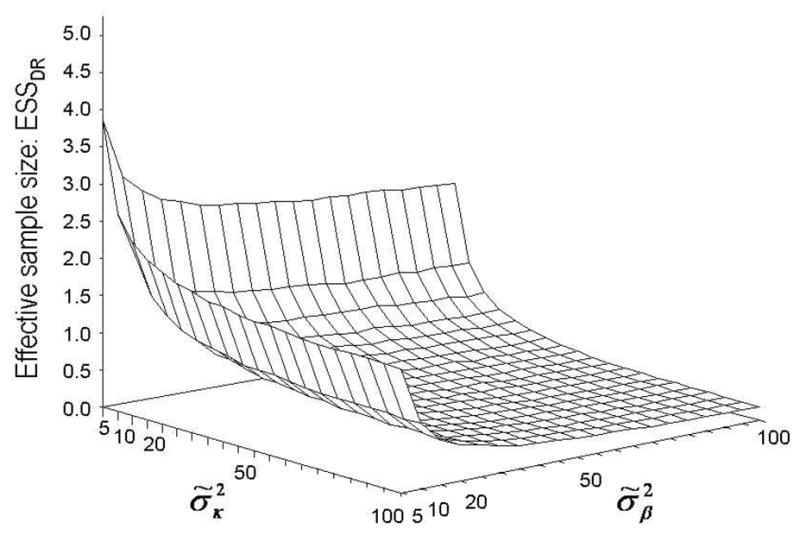
ESS surface obtained for the priors of the parameters modeling the dose-response relationships, for ${\stackrel{\sim }{\sigma }}_{\beta }^2={\stackrel{\sim }{\sigma }}_{\kappa }^2$ ranging from 5 to 100, keeping φ̃ = 1, in Example 3 (Congdon [4]).

4.4 Time-to-event continual reassessment method – Example 4

The continual reassessment method (CRM) [9] is used for dose-finding in phase I clinical trials based on a binary indicator of toxicity. The CRM requires complete follow-up of the current patient (or cohort) before enrolling a new patient or cohort. Depending on how long it takes to evaluate toxicity, this may lead to an unduly long study duration that make the method impractical. Cheung and Chappell [2] proposed an extension, the time-to-event (TITE) CRM, that uses time to toxicity or right censoring as the outcome.

Elkind et al. [5] applied the TITE-CRM to determine the maximum tolerated dose (MTD) of short-term high-dose lovastatin in stroke patients treated within 24 hours of symptom onset. Each patient received one of five initial doses 1, 3, 6, 8, 10 mg/kg, on days 1–3 post onset and received 20 mg/day for the next 27 days. Toxicity was assessed up to day 30, that is, the observation window was T_up = 30 days. Denote the time-to-toxicity in patient i by u_i, and the toxicity indicator Y_i = 1 if u_i ≤ T_up, 0 if not, so that u_i is right-censored at T_up. The dose-toxicity model

$$Pr(Y_i=1\mid d_{[i]},\beta )=F(d_{[i]},\beta )=d_{[i]}^{\mathit{exp}(\beta )}$$

was assumed, where d_[i] is the standardized dose level assigned to patient i. A N(0, 1.34) distribution was assumed for the prior of β. The five standardized doses d = (d₁, d₂, d₃, d₄, d₅) in the model were assumed to be (0.02, 0.06, 0.10, 0.18, 0.30). In general, the TITE-CRM is implemented using the weighted working likelihood for m patients given by

$$f_m({\mathbf{Y}}_m,{\mathbf{u}}_m\mid {\mathbf{d}}_m,\beta )=\prod _{i=1}^{m}F{(d_{[i]},\beta )}^{Y_i}{\left\{1-w_{i}F(d_{[i]},\beta )\right\}}^{1-Y_i},$$ (7)

where w_i is a suitable weight function. For the lovastatin trial, w_i = u_i/T_up was used, and patients were assumed to arrive according to a Poisson process. This is equivalent to assuming that the inter-arrival times are i.i.d. Exp(λ). In the trial, λ= 2 patients per month was assumed.

In Table 5, we assume five dose-toxicity scenarios in order to assess effects of the prior ESS. Scenario (1) corresponds to toxicity probabilities equal to the standardized doses. Scenarios (2)–(5) were constructed by starting with Scenario (1) and increasing the toxicity probabilities. In Scenarios (2) and (3), the toxicity probabilities increase linearly with dose, with all doses too toxic in Scenario (3). In Scenario (4), only d₁ is safe, with toxicity increasing rapidly from d₂ onward. In Scenario (5), all doses are very toxic.

Table 5.

Toxicity scenarios for a dose-toxicity relationship (TITE-CRM example).

Scenario	1 mg/kg	3 mg/kg	6 mg/kg	8 mg/kg	10 mg/kg
(1)	0.02	0.06	0.10	0.18	0.30
(2)	0.10	0.20	0.35	0.55	0.70
(3)	0.30	0.35	0.50	0.70	0.80
(4)	0.10	0.50	0.80	0.90	0.90
(5)	0.40	0.70	0.85	0.90	0.90

As Cheung and Chappell [2] do, we assume three models for the patients’ times to toxicity, including a conditionally uniform model, a Weibull model (with a fixed shape parameter 4), and a log-logistic model (with a fixed shape parameter 1). The cumulative distribution function (CDF) of the Weibull model with a scale parameter α is F(u, α) = 1 − exp{−(u/α)⁴} and the CDF of the log-logistic model with a scale parameter α is F(u, α) = (1 + exp[−{log(u) − log(α)}])⁻¹.

We compute the ESS values under each model. Figure 4 gives plots of the ESS values as a function of σ̃² under the five toxicity scenarios, assuming the conditionally uniform model for time-to-toxicity and with the prior mean of β fixed at μ̃ = 0. Since the ESS computed at σ̃² = 1.34 is less than 2 under Scenario (1), the information from the likelihood will dominate the prior after enrolling 3 patients, hence the prior specified in the lovastatin trial seems quite reasonable. The prior also makes sense under Scenarios (2) and (3). The plot of ESS under Scenarios (4) and (5) indicates that the prior may be problematic, however. Under Scenario (5), it appears that σ̃² > 2.5 may be needed to ensure an ESS < 2. The findings are similar under the Weibull and log-logistic models. This example illustrates that prior ESS computations can be a useful device to help calibrate the prior to improve the behavior of the TITE-CRM.

Fig. 4.

Plots of ESS values against σ̃² under the five toxicity scenarios given in Table 5, in Example 4 (Cheung and Chappell [2]). The vertical line at σ̃² = 1.34 indicates the hyperpa-rameter value that was actually used in the lovastatin trial.

4.5 Trial monitoring for time-to-event outcomes – Example 5

Thall et al. [11] present a series of study designs for monitoring time-to-event outcomes in early phase clinical trials. We focus on one of the study designs, which was applied to a single-arm phase II trial for advanced kidney cancer. In the trial, the plan was to enroll up to 84 patients, with each patient’s disease status evaluated up to 12 months. In this example, we focus on the mean time-to-event, μ. For patient i, let T_i denote the time to disease progression (failure), let $T_i^o$ be the observed value of T_i or the administrative right-censoring time, and let $Y_i=I(T_i^o=T_i)$. We assume the t_i’s are i.i.d. Exp(μ), exponential with mean μ, which has pdf f(t | μ) = μ⁻¹exp(−t/μ) and survivor function F (t | μ) = Pr(T > t | μ) = exp(−t/μ). The likelihood for m patients is

$$f_m({\mathbf{Y}}_m,{\mathbf{T}}_m^o\mid \mu )={\mu }^{-{\sum }_{i=1}^m{Y}_i}exp(-\sum _{i=1}^m{T}_i^o/\mu ).$$ (8)

Using the relationship μ = mean(T) = median(T)/log(2), Thall et al. [11] established the prior of μ_S corresponding to the historical standard treatment from elicited mean values and a 95% credible interval of median(T). This gave an inverse gamma IG(α̃, β̃) with (α̃, β̃)=(53.477,301.61) as the prior p(μ_S | μ̃_S). Here, IG(α̃, β̃) denotes an inverse gamma distribution with mean β̃/(α̃−1) and variance β̃²/{(α̃−1)²(α̃−2)}, which requires α̃ > 2. The prior of μ_E in the experimental treatment p(μ_E | μ̃_E) was calibrated to have the same mean but inflated variance to reflect much greater prior uncertainty about the experimental treatment. This yielded μ_E ~ IG(5.348, 30.161). The time scale of the event time and its corresponding parameter μ is in months.

The prior ESS in a simple inverse gamma-exponential model with an inverse gamma prior, μ ~ IG(α̃, β̃), and the exponential sampling model, T ~ Exp(μ), is analytically determined to be α̃ − 2. Thus, the ESS of the IG(5.348, 30.161) prior is 3.348 under this model. This prior ESS is obtained under the assumption that T is observed for all accrued patients, that is, no censoring occurs. Since in general the ESS is defined as a property of a prior and likelihood pair, a given prior might have different ESS values for different likelihoods. As mentioned in Section 3, our approach defines the ESS to be the sample size that yields a posterior containing the same amount of information as the prior. It is well known that the amount of information for time-to-event data depends on the number of observed events, not the sample size. Therefore, when T_i is right censored for some patients, the prior ESS should be larger than α̃ − 2. We apply MTM’s method to compute an ESS under the inverse gamma prior μ_E ~ IG(5.348,30.161) with respect to the likelihood (8). The computation yields ESS = 4.8.

In clinical trials with Bayesian adaptive decision making, it is important to evaluate the impact of the prior on the stopping rule. In the study design of Thall et al. [11], the trial should be stopped early if, based on the current data,

$$Pr({\mu }_S+4.3<{\mu }_E\mid \mathit{data})<\mathrm{0.015.}$$ (9)

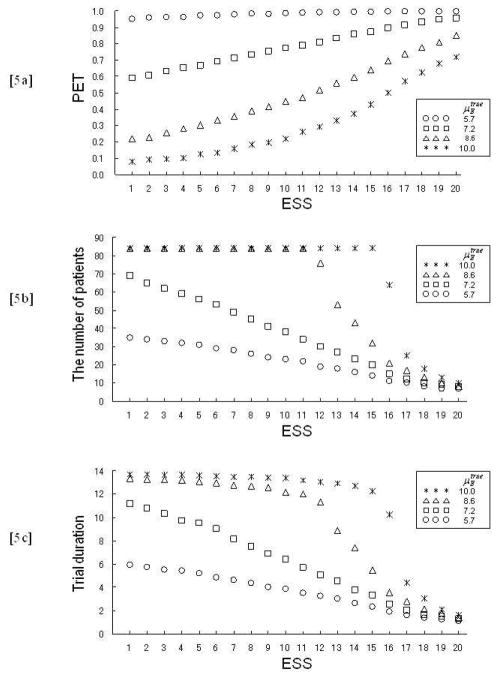
This rule stops the trial if it is unlikely that the mean failure time with the experimental treatment is at least a 4.3 month improvement over the historical mean with the standard treatment. The 4.3 month improvement in mean failure time corresponds to a 3.0 month improvement in median failure time, since 4.3 = 3.0/log(2). In order to evaluate the impact of the prior of p(μ_E | μ̃_E) on the stopping rule, we simulated the trial under each of a set of priors having different variances, corresponding to prior ESS values ranging from 1 to 20. We generated exponential patient event times using fixed (true) parameters ${\mu }_E^{\mathit{true}}=5.7$, 7.2, 8.6, 10.0, which correspond to median failure times 4, 5, 6, 7 months. Each case was simulated 2,000 times.

Figures 5a, 5b, and 5c illustrate the simulation results in terms of the probability of early termination (PET), the number of patients and trial duration, respectively. Figure 5a shows plots of PET as a function of ESS for four values of ${\mu }_E^{\mathit{true}}$. Since the prior mean of μ_S under IG(53.477, 301.61) is 5.7, the PET values obtained under the four ${\mu }_E^{\mathit{true}}$ values are reasonable for ESS values up to about 10. In contrast, for ESS > 15, the prior, rather than the data, dominates early stopping decisions. With respect to the number of patients and trial duration, plots of the 50^th percentiles of their distributions are shown in Figures 5b and 5c, respectively. The same findings as with PET are observed, that is, a prior ESS > 15 may be excessively informative.

Fig. 5.

Plots of (a) PET and the 50^th percentile points of the distributions of (b) the number of patients and (c) trial duration, under ${\mu }_E^{\mathit{true}}=5.7$ (circle), 7.2 (square), 8.6 (triangle), and 10.0 (star) against prior ESS (Example 5: Thall et al. [11]).

4.6 A dose-response model for bivariate binary outcomes – Example 6

Thall and Cook [10] use a bivariate binary regression model in a dose-finding trial where each patient is treated at one of four doses {0.25, 0.50, 0.75, 1.00} mg/m². Denoting these by d₁, d₂, d₃, d₄, the standardized doses $X_{(z)}=log(d_z)-(1/4){\sum }_{e=1}^{4}log(d_e)$ are used in the model. Let Y = (Y_E, Y_T) be indicators of efficacy and toxicity, and let π_a,b(X, θ) = Pr(Y_E = a, Y_T = b | X, θ) for a, b ∈ {0, 1}. The marginal probabilities are modeled as π_k(X, θ_k) = logit⁻¹ {η_k(X, θ_k)}for k = E, T with linear predictors η_E(X, θ_E) = μ_E + X β_E,1 + X²β_E,2 and η_T(X, θ) = μ_T + Xβ_T. The joint probabilities π_a,b are modeled in terms of these marginal probabilities and one real-valued association parameter ψ:

$${\pi }_{a,b}={\pi }_E^a{(1-{\pi }_E)}^{1-a}{\pi }_T^b{(1-{\pi }_T)}^{1-b}+{(-1)}^{a+b}{\pi }_E(1-{\pi }_E){\pi }_T(1-{\pi }_T)\left(\frac{e^{\psi }-1}{e^{\psi }+1}\right),$$ (10)

for a, b ∈ {0, 1}. Thus, θ = (μ_E, β_E,1, β_E,2, μ_T, β_T, ψ) and d = 6. The likelihood for m patients is

$$f({\mathbf{Y}}_m\mid {\mathbf{X}}_m,\mathit{\theta })=\prod _{i=1}^m\prod _{a=0}^1\prod _{b=0}^1{\pi }_{a,b}{(X_i,\mathit{\theta })}^{\text{I}\{Y_i=(a,b)\}}.$$

The prior p(θ| θ̃) was established from elicited mean values of π_E(X, θ) and π_T(X, θ), which yielded normal distributions with hyperparameters (μ̃_μE, ${\stackrel{\sim }{\sigma }}_{{\mu }_E}^2$) = (−1.496, 1.113²), (μ̃_βE,1, ${\stackrel{\sim }{\sigma }}_{{\beta }_{E,1}}^2$) = (1.180, 0.869²), (μ̃_βE,2, ${\stackrel{\sim }{\sigma }}_{{\beta }_{E,2}}^2$) = (0.149, 1.192²), (μ̃_μT, ${\stackrel{\sim }{\sigma }}_{{\mu }_T}^2$) = (−0.619, 0.941²), (μ̃_βT, ${\stackrel{\sim }{\sigma }}_{{\beta }_T}^2$) = (0.587, 1.659²), and (μ̃_ψ, ${\stackrel{\sim }{\sigma }}_{\psi }^2$) = (0, 10) where ${\stackrel{\sim }{\sigma }}_{\psi }^2$ is modified for this illustration. We apply MTM’s method to compute the ESS of p(θ | θ̃), and ESS_E, ESS_T, and ESS_ψ for the subvectors of the efficacy parameters θ_E = (μ_E, β_E,1, β_E,2), toxicity parameters θ_T = (μ_T, β_T), and the association parameter ψ. The computations yield ESS = 8.9, ESS_E = 13.7, ESS_T = 5.3, and ESS_ψ = 9.0.

ESS values computed for the subvectors of the parameters, as well as the full parameter vector, are useful feedback in the prior elicitation process. We assume fixed hyperparameters μ̃_μE, μ̃_βE,1, μ̃_βE,2, μ̃_μT, μ̃_βT, and μ̃_ψ, and discuss the choice of the variance parameters σ̃_μE, σ̃_βE1,σ̃_βE2, σ̃_μT, σ̃_βT, and σ̃_ψ. We demonstrate how to calibrate the priors in this example. In the design described by Thall and Cook [10], up to N = 36 patients are treated in cohorts of size = 3. Therefore, it may be desirable that the overall ESS and the subvector ESSs are at most 2 so that the accumulating data dominates the posterior inferences after enrolling 3 patients.

Figure 6 shows the contours of ESS_E, ESS_T, and ESS_ψ. In order to plot a contour of ESS_E for σ̃_μE, σ̃_βE1, σ̃_βE2, we constrain σ̃_βE1, σ̃_βE2 ≡ σ̃_βE and fix {σ̃_μT, σ̃_βT, σ̃_ψ} = {0.941, 1.659, 3.162}. This allows us to plot ESS as a function of the two (σ̃_μE, σ̃_βE). Figure 6a shows the contour for ESS_E = 2.0. Inspection of the ESS contours provides a basis for an informed choice of the hyperparameters (σ̃_μE, σ̃_βE). For example, σ̃_μE = σ̃_βE,1 = σ̃_βE,2 = 2.68 may be chosen, to ensure that ESS_E = 2.0. Similarly, we plot the contour for ESS_T = 2.0, fixing (σ̃_μE, σ̃_βE, σ̃_ψ) = (2.68, 2.68, 3.16), shown in Figure 6b. Inspecting this curve, one may choose values of σ̃_μT, σ̃_βT, for example, σ̃_μT, σ̃_βT= 1.89. We next focus on the interaction parameter and compute ESS_ψ values for a range of σ̃_ψ. The plot is shown in Figure 6c. One may choose, for example, σ̃_ψ = 5.70, which provides ESS_ψ = 2.0. The overall ESS value for the hyperparameter values chosen above is 2.0. If desired, one may repeat the procedure, starting with the choice of (σ̃_μE, σ̃_βE), until a satisfactory overall ESS is obtained. In a last step one may drop the constraint on σ̃_βE1 = σ̃_βE2 and allow different values for these two parameters.

Fig. 6.

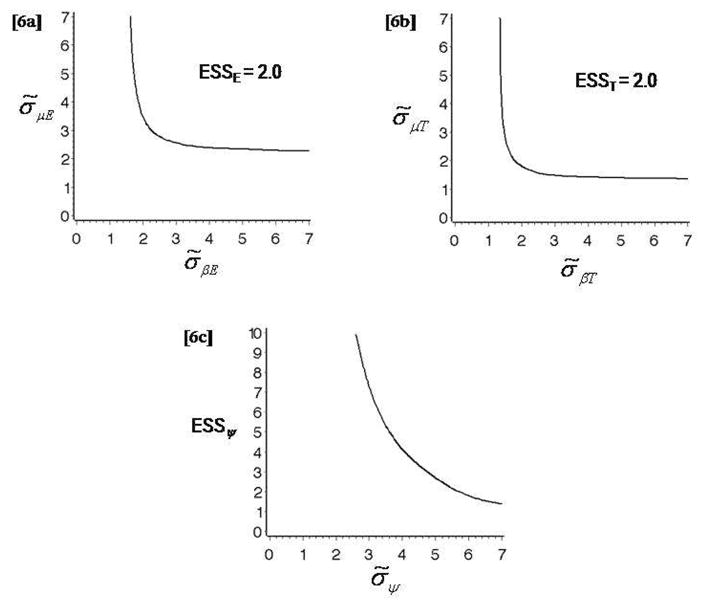
(a) Contour plot of ESS_E = 2.0, fixing (σ̃_μT, σ̃_βT, σ̃_ψ) = (0.941, 1.659, 1). (b) Contour plot of ESS_T = 2.0, fixing (σ̃_μE, σ̃_βE, σ̃_ψ) = (2.68, 2.68, 3.16). (c) Plot of ESS_ψ values against σ̃_ψ, fixing σ̃_μE, σ̃_βE, σ̃_μT, σ̃_βT = (2.68, 2.68, 1.89, 1.89). The three plots are obtained in Example 6 (Thall and Cook [10]).

5 Discussion

We have discussed prior sensitivity analyses in Bayesian biostatistics by using prior ESS, illustrated by examples of data analysis and study design for biomedical studies. The main advantage of using ESS is practical feasibility. The definition is pragmatic and allows one to report a meaningful prior ESS summary for most problems. Another important feature is ease of communication. A user need not understand the mathematical underpinnings of the approach to interpret the final report, since the ESS is a hypothetical sample size, in terms of patients (or animals or experimental units), which is readily interpretable.

The ESS provides a numerical value for the effective sample size of a given prior. If one wishes to utilize this methodology to construct a prior having a given ESS, two important cases may be identified. When designing a small to moderate sized clinical trial using Bayesian methods, it is desirable that the prior ESS be small enough so that early decisions are dominated by the data (e.g. the first cohort of 3 patients in a dose-finding study) rather than the prior. In this case, an ESS in the range 0.5 to 2.0 may be appropriate. On the other hand, if one is eliciting a prior for analysis of a given data set of n observations, then a desirable ESS may be specified relative to n. In this case, an ESS of .10 ×n or smaller might be appropriate.

Morita, Thall, and Müller (MTM2) [8] develop a variation of the ESS suitable for conditionally independent hierarchical models (CIHMs). For a two-level CIHM with K subgroups, in the first level, Y_k follows distribution f(Y_k | θ_k), the subgroup-specific parameters θ=(θ₁, ···, θ_K), are i.i.d. with prior π₁(θ_k |θ̃), and the hyperparameter θ̃ has a hyperprior π₂(θ̃ | φ) with known φ. MTM2 define ESS under a CIHM in two cases, focusing on either the first level prior or second level prior, in order to address different inferential objectives. In case 1, the target is the marginalized prior, π₁₂(θ | φ) = ∫ π₁(θ| θ̃)π₂(θ̃ | φ)dθ̃, which may be of interest, for example, if θ₁, …, θ_K are the treatment effects in K different canine breeds in a dietary study. In case 2, the target prior is π₂(θ̃ | φ), which would be the focus if the parameter of primary interest is an overall effect θ̃ for canines, obtained by averaging over the K breeds.

Some important limitations remain. The methodology is based on comparing curvatures of the marginal prior and the posterior distribution under an ε-information prior. Consequently, when an analytic solution does not exist a limitation is computational complexity. While the actual computational effort is negligible, the choice of a suitable ε-information prior and the evaluation of the prior-posterior distance require some problem-specific input from the investigator. That is, it is difficult to completely automate the ESS evaluation. However, the examples given here are intended to provide a basis for interested readers to compute and utilize prior ESS in similar problems. A computer program, ESS_RegressionCalculator.R, to calculate the ESS for a normal linear or logistic regression model is available from the website http://biostatistics.mdanderson.org/SoftwareDownload.