Modeling Missing Binary Outcome Data in a Successful Web-based Smokeless Tobacco Cessation Program

Abstract

Aim

To examine various methods to impute missing binary outcome from a Web-based tobacco cessation intervention.

Design

The ChewFree randomized controlled trial used a two-arm design to compare tobacco abstinence at both the 3- and 6-month follow-up for participants randomized to either an Enhanced web-based intervention condition or a Basic information-only control condition.

Setting

Internet in US and Canada.

Participants

Secondary analyses focused on 2523 participants in the ChewFree trial.

Measurements

Point-prevalence tobacco abstinence measured at 3- and 6-months follow-up.

Findings

The results of this study confirmed the findings for the original ChewFree trial and highlighted the use of different missing-data approaches to achieve intent-to-treat analyses when confronted with substantial attrition. The use of different imputation methods yielded results that differed in both the size of the estimated treatment effect and the standard errors.

Conclusions

The choice of imputation model used to analyze missing binary outcome data can substantially affect the size and statistical significance of the treatment effect. Without additional information about the missing cases, they can overestimate the effect of treatment. Multiple imputation methods are recommended, especially those that permit a sensitivity analysis of their impact.

INTRODUCTION

Loss of participant data – especially when related to outcome – can threaten the validity (external and internal) and undermine the ability to make causal inferences in randomized controlled trials (RCTs) with longitudinal data [1-3]. Three categories of missing data can be considered [4-7]: (a) missing completely at random indicates that the missingness patterns are entirely random and that they do not depend on any observed or unobserved factors; (b) missing at random implies that the missing data mechanism can be predicted from observed results in other variables in the data set, which makes the data missing at random when controlling for the predictors of missingness; and (c) missing not at random, for those missing data where the missing pattern depends on some unobserved source. A more complete description of these terms can be found in Little and Rubin [6] and Shafer and Graham [7].

One analytic approach focuses only on complete cases. Unfortunately, complete case analyses have been shown to bias the results, which have led many to advocate for an intent to treat (ITT) analysis that includes all cases as they were randomized to condition [8,9]. Models used to approximate an ITT analysis, in the face of incomplete data, have included (a) single imputation (SI), where each missing data point is replaced with a single value; (b) multiple imputation, where each missing value is replaced with a set of values generated through a stochastic process; or (c) maximum likelihood methods that estimate the various moments directly. These general procedures each have multiple options. For example, SI approaches include (a) mean substitution; (b) setting missing data to predicted values estimated from a regression equation or the expectation-maximization (EM) algorithm; (c) setting all missing data to an affirmative response, such as “missing = tobacco use” in a tobacco cessation trial; (d) setting missing values to last observation of the same measure carried forward (LOCF) or baseline observation carried forward (BOCF); and so on [10,11]. The present paper focuses primarily on the frequent use of SI and its consequences.

Single imputation approaches tend to underestimate the variance or standard errors and overestimate covariances between variables [12], resulting in inflated Type I error rates. Bias—the difference between the expected value of an estimator and the true parameter value—can also be introduced by using methods such as LOCF, BOCF, and setting missing to an affirmative response [6,9,13-16], possibly overestimating or even underestimating treatment effects [8,15,17,18]. Nonetheless, many of these methods are quite common in tobacco cessation and similar research [cf, 19]. If missing data depend on observable versus unobservable measures (i.e., if the data are missing at random), an appropriate analysis can provide results with less bias [7]. Therefore, many ITT approaches also miss the opportunity to produce less biased results when the investigator can reasonably make the missing-at-random assumption.

The EM algorithm, frequently used to impute a single value for each missing data point, employs maximum likelihood estimation and available data to calculate values for missing observations [10,20-22]. Although the details of the procedure can vary, many papers report few specifics other than that data were imputed with the EM algorithm. An EM analysis, however, might include all available measures, including the independent and dependent variables of interest, when imputing values for missing data, or it might exclude the independent variable and measures not considered theoretically relevant. A SI procedure based on the EM algorithm, as well as other methods, is now included in SPSS [23], and the EM algorithm can be used for multiple imputation with the SAS procedure MI [7,24,25]. Because the EM algorithm can be used with a range of approaches, its results can vary depending on the choice of variables selected, the ordering of steps used, and the specific procedures employed. The specific use of the EM algorithm may introduce bias into estimates.

Hedeker, Mermelstein, and Demirtas [15] recommend the use of an underlying logistic regression model and multiple imputation when faced with missing dichotomous outcomes. They use a conditional distribution that incorporates the relationship between missing status and outcomes, as well as a random process, to impute missing values [7]. This multiple imputation approach accounts for variation in the estimates and thus provides a nominal level of precision, and it can be extended to allow for stratification of the relationship between missing status and outcomes on previous values of the outcome or other relevant variables. It provides a sound approach to the imputation of data for use in an ITT analysis.

A number of tobacco cessation trials have examined statistical approaches to missing data [15,16,26-31]. Many of these studies [e.g., 32,33,34] have used both a complete cases and an imputation model in which in the tobacco research area is typically defined as missing = tobacco use or BOCF. A thorough understanding of the approaches for analyzing missing data is fundamental to make valid inferences from such research. In this paper, we compare the multiple imputation method and sensitivity analysis recommended by Hedeker et al. [15] to an analysis of complete cases and several common SI procedures intended to maintain an ITT sample. The SI methods include LOCF, missing = use, and a sample of SI approaches based on the EM algorithm. We examine many of these approaches as often implemented, not necessarily as intended, to demonstrate the potential for bias and inflated Type I error rates. The analyses were conducted on data derived from the ChewFree Web-based smokeless tobacco (ST) cessation RCT as described by Severson and colleagues [32].

Methods

ChewFree RCT

The ChewFree RCT used a two-arm design to compare tobacco abstinence at 6 weeks, 3 months, and 6 months. After enrollment, participants were randomized to one of two conditions. The Enhanced intervention condition (N= 1260) provided tailored content using graphics, interactive activities, testimonial videos and two Web forums, one hosted by ST cessation experts and the other peer-based. The Basic web-based control condition (N= 1263) provided text-based content similar to what could be obtained in websites identified via a reasonably thorough Internet search, such as a printable self-help ST cessation booklet, printable overviews of cessation resources, and an annotated list of other helpful websites for tobacco cessation.

Participant recruitment and characteristics

ChewFree RCT participants were recruited through a multifaceted campaign that included paid and unpaid listings in print and broadcast media, coding web pages to improve placement via Internet searches, and links placed on other websites. Targeted mailings were also sent to health care and tobacco control professionals. To be considered eligible, chewers had to (a) speak English; (b) use at least one ST can/week for 1 year or more; (c) have interest in quitting all tobacco use; (d) be 18 years of age or older; (e) reside in the U.S. or Canada; (f) use personal e-mail at least weekly; (g) provide name, home address, and phone number; and (h) agree with the Informed Consent as approved by the Oregon Research Institute Institutional Review Board. A detailed description and analysis of recruitment methods are available in Gordon et al. [35].

Data from the baseline assessment indicated that participants were mostly male (98%), Caucasian (98%), married or living with a partner (73%), and had attended at least some college (81%). Their average age was 37 years (SD= 9.6), prior ST use was 18 years, current ST use was one can every 2 days, and most (54%) used ST within 30 minutes of waking. Most (57%) had made a serious attempt to quit using ST during the previous year and indicated that they were ready to quit (M= 8.12; SD= 1.83) using an adaptation of the “contemplation ladder” [36]. No between-group differences were found in these baseline participant characteristics. A detailed description of the ChewFree methodology and analysis can be found in Severson et al. [32].

Participant attrition

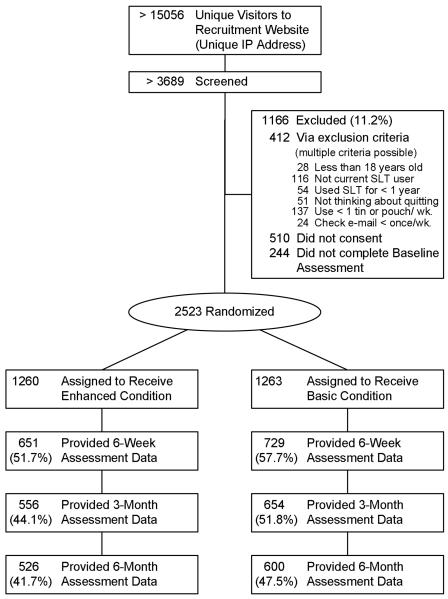
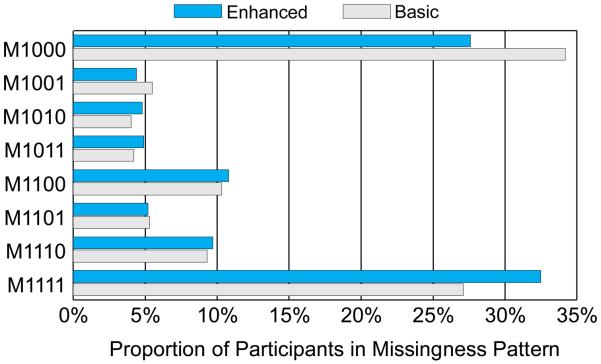
We observed substantial attrition (failure to complete a scheduled assessment) at 6 weeks (45%; 1143/2523), 3 months (52%; 1313/2523), and 6 months (55%; 1397/2523) (see Figure 1). The pattern of missingness for the present sample (see Figure 2) reveals that almost the same proportion of participants completed all assessments (30%; 752/2523) as failed to complete any assessments following baseline (31%; 780/2523) with the remainder of participants (39%; 991/2523) completing some but not all assessments beyond baseline.

Figure 1.

Research design and participant flow for the ChewFree randomized controlled trial. All participants assigned to condition completed baseline assessments.

Figure 2.

Patterns of missingness in ChewFree assessments (N= 2,523) by Condition*

* The 4-digit binary code describes participant cohorts by their assessment missingness (0= missing; 1= completed) for each of four assessments (baseline and follow-ups at 6 weeks, 3 months, and 6 months). For example, M1001 indicates completion of baseline, missing both the 6-week and 3-month assessments, and completion of the 6-month assessment.

Measures

Tobacco abstinence outcome

Self-reported 7-day point prevalence measures of tobacco use (ST, cigarette smoking, or pipe/cigar smoking) were obtained at baseline or T₀, and at each of three follow-up assessments: T₁ (6 weeks), T₂ (3 months), and T₃ (6 months).

Readiness to quit

As noted earlier, each participant indicated at baseline their readiness to quit using an adaptation of the “contemplation ladder” [36] which asked them to assign a rating using the following scale: 1= I am not ready to quit; 2= I think I need to consider quitting some day; 4= I think I should quit, but I am not quite ready, 6= I am thinking about cutting down or quitting spit tobacco; 8= I have cut down or am seriously thinking about quitting; and 10= I am ready to quit now. The mean rating for all participants was 7.77 (SD= 1.77).

Predictor Measures

Imputation with the EM algorithm requires predictor variables to impute the missing values, as described below. At T₀ (baseline), the following measures were available as predictors: gender, participants age, ethnicity, marital status, lives alone, rurality, level of education, felt depressed, could not get going, trouble focusing, thought my life had been a failure, body mass index, self-efficacy with respect to smokeless cessation, readiness to quit, ever a smoker, currently a smoker, age began ST use, years of ST use, dips per day, number of cans per week, days of use per week, ever seriously tried to quit ST, keeps chew in almost all the time, use of ST while sick or with mouth sores, swallows tobacco juices on purpose, severity of ST cravings, number of quit tries in last 12 months, uses ST upon waking, number of alcoholic drinks per week, and binge drinker. The predictor variables also included readiness to quit at T₀ and tobacco abstinence at T₁, T₂, and T₃, described above, and assessment via the Web at each time point. Participants not assessed via the web were assessed by mail or telephone. For more information about these measures, see Severson et al. [32].

Statistical Analyses

Multiple imputation approach recommended by Hedeker et al. [15]

Hedeker and colleagues [15] provide an alternative to imputation methods for dichotomous outcomes such as setting missing data to the most recent observation or the affirmative. Their approach (a) introduces an imputation strategy based on the relationship between missing status and tobacco use, (b) allows for stratification of that relationship based on another measure, (c) incorporates multiple imputation (MI), and (d) allows for a sensitivity analysis with respect the assumed relationship between missing status and tobacco use.

Hedeker et al. [15] base their imputation strategy on the specification of the odds ratio (OR) to describe the relationship between missing status and tobacco use. To illustrate, Table 1 depicts a classification table of missing status and tobacco use. The sample size for row 1 and column 1 is n₁₁, and so on, and the dot (·) used in the marginal cells indicates summation across the associated index. Due to the missing data, the numbers n₂₁ and n₂₂ and the marginal cells, n_·1 and n_·2, are unknown. If all data were present—that is, if we somehow knew the values for those cases with missing data—we could compute an odds ratio that specifies the relationship between smoking status among those subjects without data and those with: OR = (n₂₂/n₂₁)/(n₁₂/n₁₁). This represents the ratio of the odds of smoking given missing data to the odds of smoking given those with observed outcomes.

Table 1.

Matrix of comparisons used in imputation tests

	Tobacco Use
Missing	No	Yes	Total
No	n 11	n 12	n 1·
Yes	n 21	n 22	n 2·
Total	n ·1	n ·2	n

Provided with a reasonable approximation of OR, ideally estimated from theory or past results, we can compute the expected values for the missing-data cells. Hedeker et al. [15] used assumed values of the OR and the reported tobacco use outcomes to estimate the probability of tobacco use given missingness as

$$\pi =\frac{\mathit{OR}\times (n_{12}∕n_{11})}{1+(\mathit{OR}\times (n_{12}∕n_{11}))}.$$

With this probability, the number of unobserved tobacco users can then be computed as n₂₂ = n_2· × π, and the number of unobserved tobacco nonusers is defined as n₂₁ = n_2· × (1 − π). Choosing different values for OR allows for tests of different assumptions about the relationship between missing status and tobacco use.

The analysis can be further refined by stratifying on a third variable, such as baseline use, to create two tables: one for prior users and one for prior nonusers. This approach allows for better approximation of missing cases, since participants who initially used tobacco would be more likely to use tobacco at a subsequent assessment than those who did not. Stratification, then, should improve estimates of the number of cases with missing data in each of the four cells—the two missing data cells in the prior-user table and the two missing data cells in the prior-nonuser table—if the two tables differ meaningfully on the likelihood of tobacco use at follow-up.

The overall imputation process incorporates the above logic into several steps: (a) the creation of multiple datasets, each with data imputed using the assumptions just discussed as well as repeated random draws; (b) analyses of each dataset with a logistic regression; and (c) summarization of the results across the tests of each different dataset. Hedeker et al. [15] provide a more detailed description of the methods and the underlying logic.

We were unable to mirror Hedeker et al.'s [15] use of baseline tobacco use to stratify the missing data relationships because all participants in the ChewFree trial used ST at baseline and most participants who dropped out did so before their first follow-up assessment. As a result, we stratified participants according to their baseline ratings of readiness to quit and derived estimates of the number of tobacco users among participants with missing data at T₃. For purposes of the present analysis, we dichotomized these scores at the median into ready to quit (score ≥ 8) versus less ready to quit (scores ≤ 7). Among observed cases at T₃, approximately 32% (116/360) of participants who described that they were not ready to quit on the baseline assessment were subsequently tobacco abstinent compared with 41% (313/766) of those individuals who reported a higher readiness to quit. Therefore the observed odds for tobacco use, n₁₂/n₁₁, depended partially upon whether participants were ready to quit before the intervention began. Based on the approach recommended by Hedeker et al., imputed values depended upon whether participants were ready to quit before the intervention began. Participants' baseline readiness-to-quit status did not differ by condition (χ² = .72, df = 1, p = .3959).

We attempted to choose a reasonable specification for OR, but to explore the sensitivity of our assumptions about the relationship between missing status and tobacco use, we varied the values of OR. Hedeker et al. [15] showed that, as OR approaches positive infinity, the analysis converges with the missing = tobacco use approach. Because it was not plausible to assume that the OR would equal infinity, or zero, we varied OR values from 0.5 to 5.0 in order to investigate the sensitivity, or insensitivity, of the results to different assumptions about missingness. We also included one analysis with OR = 100.0 to approximate missing = use (i.e., OR → ∞).

Continuing with the Hedeker et al. [15] approach, we next used MI to address both sampling variability and uncertainty due to missing data. Specifically, we modified the SAS code provided by Hedeker (http://www.uic.edu/~hedeker/long.html) and conducted each analysis 100 times with PROC LOGISTIC. Each analysis used the complete sample of 2,523 participants, and we then used PROC MIANALYZE to combine results from the multiple analyses. This procedure allowed us to report standard errors and tests statistics adjusted for sample variability.

EM imputation procedure

We imputed missing data with the EM algorithm as implemented in the SPSS Missing Value Analysis module [23]. The EM algorithm allows for estimates of missing data from available data via an iterative maximum likelihood procedure, which is “useful in a variety of incomplete data problems” (p. 1) [22]. The EM algorithm can be used with multiple or single imputation procedures. We use it here for single imputation because we find this use most common, but even when used for single imputation the specifics of the implementation can vary substantially. To demonstrate this variability, we explored four different methods to impute data with the EM algorithm and analyzed the resulting data sets with logistic regression. The methods differed in the variables that were included as predictors and the order in which measures were imputed.

In the description of the procedures, the predictor variables refer to those used to impute values for missing data. Predicted variables represent those with missing data that receive the imputed values. For all four methods, and prior to imputation, we identified baseline measures that we hypothesized would predict the missingness. The measures section provides a list of all variables by assessment time. A few of these measures were incomplete but to a lesser extent than the tobacco abstinence variables collected at follow-up. We dummy coded nominal variables before including them in the imputation process. The first three methods also included two variations: the first included condition as a predictor and the second did not. We stress that these methods are not necessarily ideal. Rather they approximate procedures described by colleagues, conference presenters, and other sources.

In Method 1, then, we included all baseline variables and outcomes as both predictor and predicted variables, including tobacco cessation outcome measures at all three follow-up assessments. The imputed T₃ quit outcome, a real number between 0 and 1, was then transformed back into a dichotomous variable. For each imputed value, we randomly drew a zero or one with probability equal to the EM estimate of that variable. We used this process for all methods.

Method 2 employed a three-step process. First, we included all baseline and T₁ variables and imputed missing values excluding T₂ and T₃ measures. Next we added the T₂ variables and repeated the process to impute their values. Then we repeated the process with the T₃ measures.

Methods 2 and 3 use post-intervention data to impute (i.e., “backfill”) baseline values. With Method 3, we imputed baseline variables separately from T₁ variables. Specifically, we first included all baseline measures as predictors to impute missing data among them. Second, we added the T₁ variables and repeated the process to impute missing T₁ data. Third, we imputed T₂ data with all baseline, T₁, and T₂ variables. Finally, we imputed the T₃ data with all variables.

In Method 4, we predicted the T₃ outcome using only the readiness to quit baseline measure, dichotomized as discussed above for the Hedeker et al. [15] imputation method.

In summary, the four methods differed in the way predictor variables were staged during the imputation process. Method 1 used all available measures at once, without staging the predicted variables by time. Methods 2 and 3 staged the predicted variables. Method 3, however, did not impute baseline values with follow-up data, as did Methods 1 and 2. The first three methods also included condition in the model, and we tested a second variation that excluded condition. Finally, before analysis, the T₃ quit outcome was transformed into a dichotomous variable (0, 1) by randomly drawing a one with a probability equal to the EM estimate of the T₃ outcome.

RESULTS

A considerable proportion (31%) of participants in the ChewFree RCT dropped out or failed to provide completed assessments at the 6 week follow-up assessment (T_1; Figures 1 and 2). Only 30% of cases provided data at every assessment. Table 2 presents results for all imputation methods and the complete case analysis. All tests were statistically significant at p < .05; all confidence bounds excluded zero. For the MI analysis, the test statistics represent a summary of the results from 100 different complete samples of 2523 participants each with missing data imputed. The sample sizes for the complete case analysis was 1126, the number of participants that completed the T₃ assessment. All other tests were based on the complete sample.

Table 2.

Tests of condition on tobacco use at 6-months follow-up (T₃) under varying methods for the handling missing data

			95% Conf. Interval
Analysis Assumptions	Estimate	S.E.	Lower	Upper	Test Statistic a	p
Multiple Imputation
OR = 0.5	−.309	.102	−.509	−.109	−3.04	.0025
OR = 1	−.283	.107	−.493	−.074	−2.65	.0082
OR = 3	−.284	.105	−.490	−.078	−2.71	.0068
OR = 5	−.295	.109	−.509	−.081	−2.70	.0070
OR = ∞ (Missing = Use)b	−.323	.107	−.533	−.113	−3.02	.0026
Missing = Tobacco Use	−.325	.107	−.534	−.115	9.24	.0024
Last Observation Carried Forward	−.386	.097	−.575	−.197	15.95	<.0001
Complete Case	−.648	.124	−.891	−.404	27.17	<.0001
EM Imputation, Method 1	−.592	.084	−.757	−.426	49.11	<.0001
Method 1 without Condition	−.284	.084	−.449	−.120	11.47	.0007
EM Imputation, Method 2	−.629	.084	−.794	−.464	55.79	<.0001
Method 2 without Condition	−.375	.084	−.538	−.211	20.09	<.0001
EM Imputation, Method 3	−.668	.084	−.833	−.502	62.66	<.0001
Method 3 without Condition	−.477	.084	−.642	−.313	32.32	<.0001
EM Imputation with Readiness to Quit	−.261	.082	−.422	−.100	10.18	.0014

Note. OR is the odds ratio that describes the relationship between tobacco use and missingness. All analyses had 2523 cases except for Complete Case which had 1126.

^aMultiple imputation analyses provided t values (df ≥ 598). All other analyses provided Wald χ² values with a single degree of freedom.

^bAs an approximation to OR = ∞, which represents missing=use, we set OR = 100.

Treatment Effect

The MI analyses provided a reference for comparing other models because it produces unbiased estimates with nominal precision under varying assumptions that can be examined through sensitivity analysis. With these models, the treatment effect estimate ranges from −.283 to −.323, depending on the assumed odds ratio (OR). Recall that OR represents the ratio of the odds of missing data given tobacco use to the odds of missing data given abstinence from tobacco. With an OR between 0.5 and 5, the results indicate that the treatment condition contained approximately 28.3% to 30.9% fewer tobacco users. Thus, our sensitivity analysis indicated that the size of the effect did not differ much between the assumed strong and weak relationships between tobacco use and missingness. We also set the OR to 100 as a proxy for infinity and obtained a treatment effect estimate of 32.3% under the missing = use assumption.

Next we examined analyses that used missing = tobacco use and LOCF imputation and complete cases. The effects for the two imputed models favored the intervention condition more than the MI approach. The missing = tobacco use model, which for the ChewFree study was equivalent to BOCF, estimated a 32.5% decline in tobacco use in the intervention condition. This was nearly identical to the estimate obtained when using the MI approach with OR = 100. The LOCF analysis estimated a larger reduction among the treated, 38.6%, and the complete case analysis provided the largest treatment effect, a 64.8% reduction in tobacco users.

The final set of results relied on single imputation with the EM algorithm to produce complete data. The analyses yielded treatment effect estimates between a 26.1% and a 66.8% reduction in tobacco use. The size of the effect clearly depended on the specific method employed for imputation. In particular, including condition during imputation provided substantially larger treatment effect estimates than when excluding it. We found similar effects when we added condition as a predictor and when we imputed the data separately for Enhanced and Basic samples (stratified imputation), so we report only the results of the former analysis.

Finally, the use of the SPSS Missing Data Analysis procedure requires some care as it will impute values for missing data even if the EM algorithm fails to converge. This is noteworthy for two reasons: (a) the software indicates the failed convergence with only a small footnote to some output tables, which can be easy for users to miss when inspecting results; and (b) we estimated treatment effects from three datasets when the EM algorithm failed to converge and found an effect estimate as high as −1.129, much higher than other effect estimates. We thus recommend increasing the number of iterations and careful inspection of the output when using the SPSS Missing Data Analysis procedure.

Standard Errors and Sample Sizes

The standard errors of the treatment effect from the MI analyses ranged from .102 to .109, values that were similar to the standard error of .107 obtained for the missing = tobacco use model. The LOCF analysis provided a smaller standard error, (.097) and the single imputation models with the EM algorithm produced even smaller standard errors, all between .082 and .084. The complete cases analysis, with the smallest sample, gave us the largest standard error .124.

DISCUSSION

Because participant attrition cannot be eliminated from all research, especially trials of many public health and Web-based interventions there is a salient need to identify more sophisticated and potentially less biased assessment models than the widely-used LOCF, missing = tobacco use, BOCF, and similar methods. The present study compares two general approaches that merit consideration as potential alternatives: (a) multiple imputation with a sensitivity analysis based on the approach recently described by Hedeker et al. [15], and (b) single imputation relying on the EM algorithm [10]. The differences we observed between the treatment effects produced from variously imputed datasets as well as our analysis with complete cases strongly suggest the possibility of an important bias, at least with some of the methods. Unfortunately, our results do not clearly indicate which tests introduce more or less bias, only that they disagree. To identify potential biases, we rely on the literature on missing data analysis [6,7].

From these results, we have come to three broad conclusions. First, the ChewFree Enhanced condition appeared to produce stable decreases in ST use compared to the Basic condition regardless of the assumed missing-data mechanism or associated imputation method. Second, the Hedeker et al. [15] approach allowed for a useful and interesting comparison of results under varying assumptions of the relationship between missingness and smoking. Third, the specific use of the EM algorithm to impute data, as implemented with standard statistical packages, can strongly influence the results and, hence, may require additional guidance about appropriate use from statisticians and more detailed descriptions of its use in manuscripts.

ChewFree Intervention Effects

The results of this study confirmed the findings for the original ChewFree study [32]. Even with the most conservative assumptions, the differences between conditions were statistically significant (p < .05). Although the analyses of data imputed with different methods confirmed the presence of a significant advantage for the Enhanced condition over the Basic condition, the results differed in both the size of the estimated treatment effect and the standard errors, which we discuss in depth below. Improving methods for analyzing the results of innovative Web-based behavioral interventions can directly inform research on eHealth, generally [37], and promising research on Web-based tobacco cessation interventions, specifically [38].

Multiple Imputation

Given the arguments presented by Hedeker and colleagues [15], based heavily on methodological literature [5-7,39], the treatment effects estimated from this MI approach would be expected to contain the least bias of the methods tested here and provide nominal standard errors. This MI approach assumes data are missing not at random, an assumption that we cannot test in the present study. We consider the estimates of the treatment effect derived from MI analyses that assumed an OR of 1 or 3 the most reliable, where the different OR values allow for a sensitivity analysis of the treatment effects given varying assumptions of the relationship between missingness and tobacco use. This analysis also produced the smallest treatment effect, indicating a 28% reduction in tobacco use in the Enhanced condition when compared to controls.

Our analysis differed from the methods presented by Hedeker et al. [15] in that we stratified our relationship between tobacco use and missingness on self-reported readiness to quit at baseline, rather than baseline tobacco use, in order to impute missing data. The MI approach, then, essentially filled in most of the missing 1397 cases with values that were not influenced by condition and added those cases to the 1126 participants with complete data. The results from data generated from the MI approach essentially equal a weighted average of the complete case analysis results, a 65% reduction, for 45% of the participants and a zero effect for the 55% of participants missing data. The weighted average, 65% reduction times 45% of the participants plus no reduction times 55% equals 29% (29% + 0%), very similar to the MI estimates.

Ideally, one would condition on tobacco use values from an earlier assessment, as described in Hedeker et al [15]. In the present study, however, all subjects were required to be smokeless users at the outset and most participants with missing data at the T₃ assessment were also missing both earlier post-treatment assessments. Our implemented of this method, therefore, could have led to an underestimate of the treatment effect. This would not be due to the method, per se, but because of the lack of variation in tobacco use at baseline. On the other hand, all methods of imputation were handicapped by this same fact. Also, it may be inappropriate to condition on prior post-treatment tobacco outcomes (e.g., T₂) unless one could assume that the relationship between the earlier post-treatment tobacco use variable and later tobacco use (e.g., T₃) was the same for participants with and without missing data. Participants at T₃, however, may be more likely to have missing data at T₃ if they did not use tobacco at T₂ but began using again at T₃ than the opposite. Given the plausibility that early post-treatment tobacco use may influence later missingness, we believe the MI approach to provide the most appropriate data for analysis.

Single Imputation with the EM Algorithm

The specific methods for SI with the EM algorithm led to substantial differences in the estimate of the treatment effect. We cannot necessarily argue that the results from analyses that rely on SI introduce bias, but given the broad variation in estimates of treatment effects and the absence of information about the missing data mechanism, it seems reasonable to assume that some of the imputed data sets lead to inflated estimates. In particular, the addition of condition strongly increases the apparent effect of condition in the first three methods. These substantially larger treatment effects seem difficult to justify. Method 1, for example, included all variables as both predictor and predicted variables, including tobacco cessation outcome measures at all three follow-up assessments. The inclusion of condition as a predictor in the EM model increased the treatment effect estimate from 28% to 59%. We obtained similar to the results when imputing data sets stratified by condition. The research question of interest, however, concerns whether differences exist between conditions for the complete sample at T₃. The imputation process, when it includes condition, appears build in the very relationship in question. In an additional experiment (unreported), we found that imputation of T₃ tobacco use with condition as the only predictor resulted in differences between conditions among imputed cases. This can only be justified by assuming that missing values depend on condition or observed data, an example of affirming the consequent. It is therefore appears difficult to justify including condition during imputation as such a process may imputing condition effects into the sample of participants with missing data when the intent of the analysis is to test whether such effects in fact exist.

Similarly, the staged introduction of follow-up assessments at T₁, T₂, and T₃ also appeared to increase the apparent treatment effect. When excluding condition, Method 1 resulted in a 28% difference between conditions while Method 3 produced a 48% difference. All three methods included the same predictors, but introduced them at different times. The imputed data appeared again to have introduced condition effects for T₃, likely based on earlier follow-up assessments for participants missing T₃ tobacco status. Notice, for example, that Method 2, without condition, produces a similar condition effect estimate to that given with LOCF. The point of the long-term follow-up analysis, however, is to assess maintenance of the treatment effects because many participants who stop using tobacco early on frequently relapse and take up tobacco use at a later time. It therefore seems inappropriate to allow T₁ and T₂ tobacco-use status, and any differences between conditions that their values may imply, to influence the imputation of the six-month follow-up data. As with condition, such imputation methods may introduce a relationship into the imputed data that the analyses are intended to test.

The EM algorithm may be used with MI, which introduces variation into the estimates to allow for nominal precision but does not appreciably change mean values or relationships among the variables imputed [6,7]. The SI methods employed herein provide standard errors that are likely too small [6,7], overestimating the precision of the estimate (e.g., narrower confidence intervals and smaller p-values than nominal). One must therefore treat with caution the results from this and other studies that contain a large proportion of missing data yet address that problem with SI [23,25]. Furthermore, if one considers that the larger treatment effects produced by many of the tested SI methods were a product of bias or the inappropriate application of the EM algorithm, then those problematic treatment effects should appear when missing data are replaced through a MI procedure that relied on similar methods for including variables. That is, we would expect MI, employed with the EM algorithm, our Method 1, and including condition as predictor to produce nominal precision but with similarly large mean estimates (59%).

Finally, we included an estimate of the treatment effect with data imputed using only the readiness to quit variable, the same measure used to stratify the MI approach discussed above. This produces a smaller difference between conditions, 26%, than any other model, but relatively closer to the results after MI than those from SI, except for Method 1 with condition excluded, which produced a treatment effect equal to that of the MI approach with an OR of 3.

Limitations

The present analyses were intended to demonstrate how variation in missing-data methods and their specific applications, when implemented in a real-world efficacy trial, can lead to very different results. Although the conclusion for this study would not change appreciably with a smaller sample, the interpretation of the significance of the intervention effects could have differed substantially from one method to another if the study has less statistical power.

Without simulation, “true effects” cannot be determined in such an analysis. Consequently, we cannot say for certain that the MI approach of Hedeker et al. [15] provides unbiased, consistent, or nominally precise estimates of treatment effects, nor can we say that any one method outperforms the others in this respect. We can, however, speculate, given the literature on missing data [6,7] and the results presented here, that it is possible to artificially, and perhaps accidentally, inflate the size and statistical significance of treatment effects in an ITT analysis through differences in the specific methods used to impute missing data.

Summary and Future Directions

First, we were able to confirm the results of the original ChewFree trial [32]. The analysis of data produced through MI provided a statistically significant treatment effect, as did all methods. These results increase our confidence in the efficacy of the Enhanced ChewFree program to increase tobacco abstinence among ST users.

The results presented above, however, demonstrate that the choice of method used to impute missing data can have a substantial impact on the size and statistical significance of the treatment effect. In the published reports of RCTs that use the EM algorithm for imputation, many authors may provide some detail about the software used or the general value of the imputation, but seldom do they provide sufficient detail to allow readers to evaluate – and potentially to replicate – the approach. We therefore strongly recommend that manuscripts include a detailed description of precisely how data were imputed.

Further, researchers would benefit greatly from practical guidance about the appropriate ways to impute data, whether with the EM algorithm or similar approaches. The present analysis raises several questions. At what proportion of missing data does single imputation become problematic? Schafer and Graham [7] have noted that single imputation with the EM algorithm may be appropriate for studies with only 3% missing for any given variable, but what about 5% or 10% missing? In what manner or order should the analyst enter variables into the imputation model? Can the EM algorithm overfit a data set, resulting in sample-specific rather than population parameter estimates for imputation, as has been found for regression and other models [40]? Does adding condition as a predictor during imputation truly influence the estimates of treatment effects, as we have assumed herein? Additional guidance is critical for the appropriate application of missing data methods in RCTs and other research.