Exploiting Graphics Processing Units for Computational Biology and Bioinformatics

Abstract

Advances in the video gaming industry have led to the production of low-cost, high-performance graphics processing units (GPUs) that possess more memory bandwidth and computational capability than central processing units (CPUs), the standard workhorses of scientific computing. With the recent release of general-purpose GPUs and Nvidia's GPU programming language, CUDA, graphics engines are being adopted widely in scientific computing applications, particularly in the fields of computational biology and bioinformatics. The goal of this article is to concisely present an introduction to GPU hardware and programming, aimed at the computational biologist or bioinformaticist. To this end, we discuss the primary differences between GPU and CPU architecture, introduce the basics of the CUDA programming language, and discuss important CUDA programming practices, such as the proper use of coalesced reads, data types, and memory hierarchies. We highlight each of these topics in the context of computing the all-pairs distance between instances in a dataset, a common procedure in numerous disciplines of scientific computing. We conclude with a runtime analysis of the GPU and CPU implementations of the all-pairs distance calculation. We show our final GPU implementation to outperform the CPU implementation by a factor of 1700.

INTRODUCTION

Market demand for high-resolution, three-dimensional graphics have led to the production of low-cost, highly parallel, many-core graphics processing units (GPUs). These computing components have higher memory bandwidth and more computing power than central processing units (CPUs), and are now regularly included in standard laptop and desktop computers. Nvidia, a leading GPU vendor, has released a proprietary development platform known as the compute unified device architecture (CUDA) (Nvidia Corporation, 2009), which allows for the general purpose programming of their consumer graphics hardware in a C-like language. This has generated a surge of interest in exploiting GPUs for scientific computation, particularly in the fields of computational biology and bioinformatics. For example, GPU adaptations of algorithms for sequence alignment (Manavski and Valle, 2008; Schatz et al., 2007), epistasis analysis (Greene et al., 2010; Sinnott-Armstrong et al., 2009), feature detection (Hussong et al., 2009), phylogenetics (Suchard and Rambaut, 2009), and artificial vision (Pinto et al., 2009) have recently been developed and have been shown to offer dramatic speedups over their serial counterparts.

The goal of this article is to present the basics of GPU hardware and programming to the computational biologist or bioinformaticist in a concise form. Our only assumption of the reader is a basic understanding of the C programming language. After introducing the essentials of GPUs and the CUDA programming language, we address three fundamental GPU programming practices: the proper use of (1) coalesced reads, (2) data types, and (3) memory hierarchies. We highlight these principles with an example: that of computing the all-pairs distance between instances in a dataset. We conclude with an empirical runtime analysis of the GPU and CPU implementations of the all-pairs distance calculation.

GPU AND CUDA ESSENTIALS

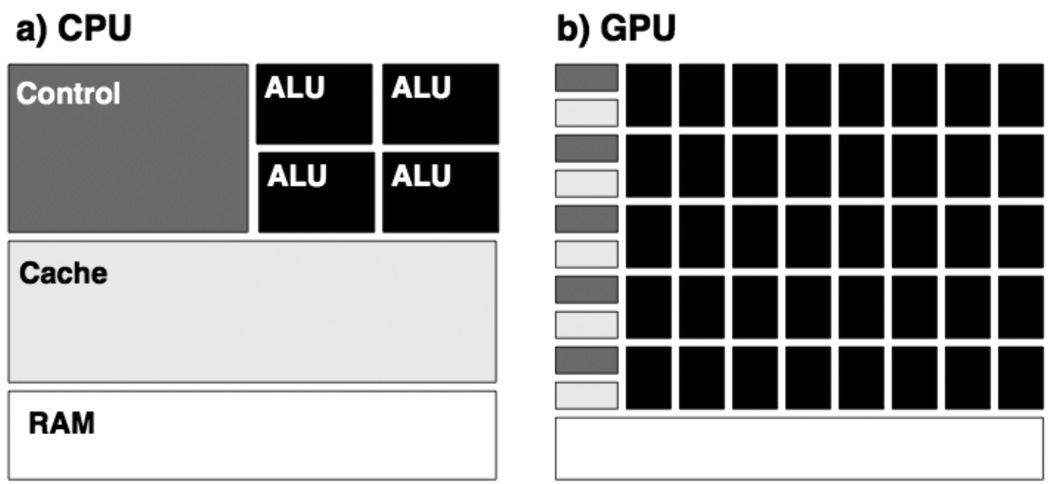
GPUs dedicate much more hardware per core to data processing than CPUs, but possess far less hardware per core for data caching and flow control (Figure 1) This makes GPUs ideal for problems in which the same (small) program is executed on many data elements in parallel, as is the case in the all-pairs distance calculation (Appendix 1), and numerous other applications.

Fig. 1.

Schematic of the architectures of the (a) central processing unit (CPU) and the (b) graphics processing unit (GPU). The color scheme used in (a) to denote the arithmetic logic units (ALU), control and cache hardware, and random access memory (RAM) is the same as in (b). Note that the GPU dedicates much more hardware to processing units and much less to control and caching

CUDA allows the developer to mix CPU and GPU code seamlessly, through an intuitive extension of the C programming language. The developer can design a program such that code portions exhibiting little parallelism are executed on the CPU (referred to as the host), and portions exhibiting high parallelism are executed on the GPU (referred to as the device). The developer should attempt to minimize the amount of code executed on the host, as the potential speedups of parallelization are inherently limited by these code portions (Amdahl, 1967). Program execution begins on the host and is executed serially until a GPU-specific section of the code is encountered, which is then executed on the device in parallel. The data that is needed by the device is copied from host memory (RAM) to device global memory. After the GPU code has finished execution, its output is transferred from global memory to RAM, and control is returned to the CPU. This swapping of control between the CPU and GPU can occur as many times as needed in an application, though writing between these memory resources is very slow and should be performed sparingly. This encourages the developer to send data to the device once and then perform many operations on it, so that the memory stays on the device and is not transferred between memory types.

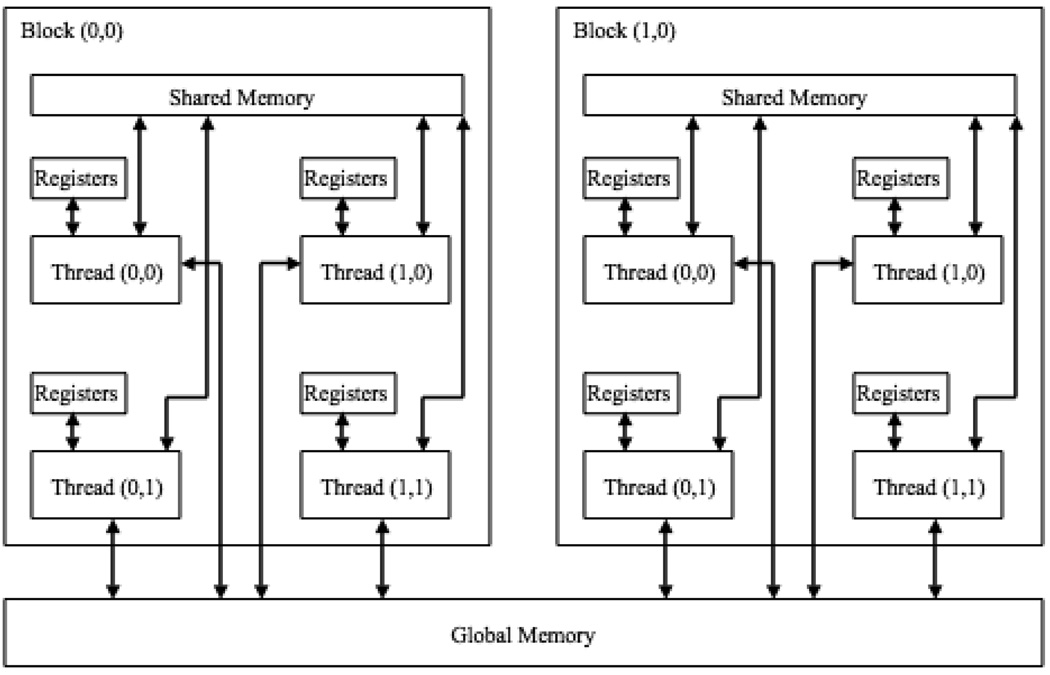
Device code is executed by many independent threads, which are hierarchically organized; groups of threads are organized into thread blocks, and thread blocks are organized into grids (Figure 2). Threads within a block are organized into groups of 32, referred to as warps. Each multiprocessor schedules and executes threads at the warp level.

Fig. 2.

Schematic of the CUDA memory hierarchy. In this example, the grid is a 1×2 array of blocks, where each block contains a 2× matrix of threads. Each thread has exclusive access to its own register file. All threads within a block have access to the same shared memory, and threads in all blocks have access to global memory

Each thread possesses its own registers (Figure 2). Memory accesses to registers are very fast, but register file size is extremely small. Each block possesses its own memory, which is referred to as shared memory (Figure 2). All threads within a block have access to shared memory, which is also very fast and can be used to efficiently transfer information between threads. Threads in all blocks have access to global memory (Figure 2), which is the largest form of memory on the GPU, but extremely slow to access (almost 100 times slower than registers or shared memory).

The task of the developer is to divide a problem into small, independent subtasks that can be executed in parallel at the block level. Within each block, these subtasks are further divided, such that individual threads cooperate to solve the subtask in parallel. This block-level, coarse-grained parallelism contributes to the scalability of a GPU program, since individual subtasks can be sent to any available multiprocessor. The more multiprocessors, the higher the parallelism. As different Nvidia GPUs have a differing number of multiprocessors, the number of blocks should be high enough that running on large devices does not lead to the under-utilization of resources – ideally, at least 250 blocks would be sufficient for current generation devices.

However, it is important to keep in mind that the degree of parallelism obtained by a program depends on the amount of resources requested by each thread, and on the specifics of the underlying GPU. In the GeForce 9600M GT employed in this study, a maximum of 8 blocks can be assigned to each multiprocessor. If a multiprocessor cannot satisfy the resource needs of those blocks, then the number of blocks is reduced until the resource demand can be met. For example, the GeForce 9600M GT has 8K registers for each multiprocessor. If each block requests 2K worth of registers, than only 4 blocks can reside on each multiprocessor. Thus, maximum parallelization requires the careful use of hardware resources. A useful tool for measuring the resource utilization of CUDA code on a specific GPU architecture is provided by the Nvidia Corporation (2009b).

CUDA BASICS

Data is shared between the CPU and GPU by writing from host RAM to global memory. CUDA provides a very simple syntax to allocate global memory and to perform the data transfer. For example, if we want to write a 100-element integer array (named outputHost) from the host to the device, we would do the following.

int *outputDevice;
cudaMalloc((void**)&outputDevice, 100*sizeof(int));
cudaMemcpy(outputDevice, outputHost, 100*sizeof(int), cudaMemcpyHostToDevice);

First, we allocate global memory using the CUDA version of malloc, which is intuitively named cudaMalloc. Then we call the CUDA function cudaMemcpy to write the host data to the global memory space allocated on the GPU, using the cudaMemcpyHostToDevice option.

Device code, referred to as a kernel, operates on data stored in global memory. Kernel prototypes in CUDA are very similar to function prototypes in C. For example, the prototype for a function named foo could be

__global__ void foo(int *input, int *output);

The __global__ qualifier indicates that the function is a kernel, implying that it is called by the host and can only be executed on the device. Kernel output must be void. The first operand is the integer array input, upon which some operation will be performed. The output of this operation will then be written to the second operand, the integer array output. Both input and output must exist in global memory and therefore must be copied from host to device using cudaMemcpy. If arguments are not passed by reference (e.g., if they are not pointers), then they are stored in a fast, cached memory space, which does not suffer the same read penalties as the very slow global memory.

Kernels are executed in parallel across many threads. The organization of threads into blocks, and blocks into a grid is specified with the following two commands:

dim3 dimBlock(2,2);
dim3 dimGrid(1,2);

These commands state that each block will contain a 2×2 matrix of threads, and the grid will contain a 1×2 array of blocks, as depicted in Figure 2. Once the block and grid dimensionality are established, the kernel can be invoked as follows:

foo<<<dimGrid,dimBlock>>> (inputDevice, outputDevice);

Note that dimGrid and dimBlock are structures with fields x,y, and z for the first, second, and third dimensions; they can be modified individually after creation. Following kernel execution, its output must be read from global memory into host RAM, using the following command:

cudaMemcpy(outputHost, outputDevice, 100*sizeof(int), cudaMemcpyDeviceToHost);

With these concepts, we can begin to write CUDA kernels for calculating the all-pairs distance between instances in a dataset.

A NAÏVE IMPLEMENTATION

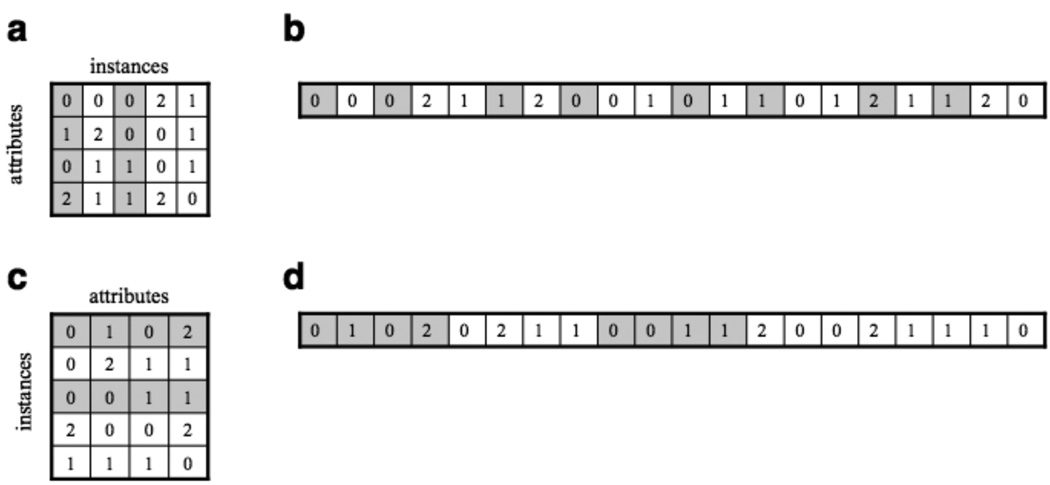
In this section, we provide a naïve implementation of the all-pairs distance kernel. The kernel is designed such that each block calculates the distance between a pair of instances, and the threads within a block calculate part of this distance by focusing on specific attributes. The grid is arranged as a square of blocks, where the grid dimensions correspond to the number of instances. Thus, each block writes a single output value, corresponding to a unique pairing of instances. For example, block (0, 2) would compare instances 0 and 2 (Figure 3a), with each thread assigned a subset of the attributes. We assume a ternary alphabet, such as encountered with single nucleotide polymorphism (SNP) data, and measure distance as the number of attributes that differ between two instances. This assumption is easily relaxed to alternative alphabets, such as Cartesian coordinates. For simplicity, we assume that the number of instances, attributes, and threads are held fixed and stored in the global variables INSTANCES, ATTRIBUTES, and THREADS, respectively.

1. __global__ void GPUnaive(int *data, int *distance) {
2. int idx = threadIdx.x;
3. int gx = blockIdx.x;
4. int gy = blockIdx.y;
5.    for (int i = idx; i < ATTRIBUTES; i+=THREADS) {
6.        if (data[INSTANCES*i + gx] != data[INSTANCES*i + gy]) {
7.             atomicAdd(distance + INSTANCES*gy + gx, 1);
8.                }
9.             }
10. }

Fig. 3.

Data organization and accessing patterns impact program efficiency. In (a), the data are written such that each row corresponds to the instances of a single attribute and (b) shows this data stretched into a one-dimensional array, by row-major order. In (c), the data are written such that each row corresponds to the attributes of a single instance, and (d) shows the corresponding one-dimensional representation of these data. The data highlighted in gray depict the memory access patterns of the threads within block (0,2)

The kernel takes two operands: the input and output data, both as integer arrays (line 1). Each thread obtains its unique identification number idx (line 2), and the x and y coordinates of its block in the grid, gx (line 3) and gy (line 4), so it knows what data elements to operate on. The kernel then loops over all of the attributes (line 5), such that the individual threads leapfrog over one another to calculate the distance between the two instances. If the attribute assigned to a thread differs between the two instances (line 6), then the thread increments the value corresponding to the respective pair of instances in the output array (line 7). This is executed atomically, meaning that if two threads attempt to update this array location simultaneously, their requests will be serialized.

GPU PROGRAMMING PRINCIPLES

We present four programming principles for developing GPU applications. We complement the presentation of these principles with extensions of the naïve all-pairs distance calculation presented above. For the sake of clarity, we only provide code for the kernels. However, we provide the full, compilable, and documented code as supplementary material (Computational Genetics Laboratory, 2010).

Coalesced reads

The time required to access global memory can be reduced if threads request a single contiguous segment of global memory. Such a request results in a single memory transaction for every 32 bytes transferred, assuming that each thread accesses a successive address and the base address is a multiple of the segment size, 32 bytes. In contrast, if threads request n non-contiguous global memory addresses, then n memory transactions occur. The following implementation of the all-pairs kernel includes coalesced reads through a transposition of the input data and a row-major access pattern. Figure 3c shows how the input data would be restructured and how block (0, 2) would access the rows corresponding to data instances 0 and 2, as opposed to the column-major order access patterns in the naïve implementation (Figure 3a).

1. __global__ void GPUcoalesce(int *data, int *distance) {
2. int idx = threadIdx.x;
3. int gx = blockIdx.x;
4. int gy = blockIdx.y;
5. for (int i = idx; i < ATTRIBUTES; i+=THREADS) {
6.     if(data[i + ATTRIBUTES*gx] != data[i + ATTRIBUTES*gy]) {
7.            atomicAdd(distance + INSTANCES*gy + gx, 1);
8.       }
9.    }
10. }

The only difference between this kernel and the naïve implementation is that the input data is transposed (compare Figure 3c with 3a) and the accesses to global memory (line 6) occur in row-major order. Together, these two changes dramatically reduce the number of global memory accesses (compare Figure 3d with 3b), since requests to contiguous blocks of memory are coalesced into a single transaction. As we will later show, this leads to appreciable speedups.

Data types

In the previous examples, we have represented our input data using integers, a data type that requires 32 bits of storage. Since our input data uses a ternary encoding (0, 1, and 2), the majority of these 32 bits are not actually needed. As an alternative, we propose to use a character representation, which allows four attributes to be packed into 32 bits. This reduces both the memory footprint of the program and the number of global memory accesses.

1. __global__ void GPUchar(char *data, int *distance) {
2.  int idx = threadIdx.x;
3.  int gx = blockIdx.x;
4.  int gy = blockIdx.y;
5.  for (int i = 4*idx; i < ATTRIBUTES; i+=THREADS*4) {
6.      char4 j = *(char4 *)(data + i + ATTRIBUTES*gx);
7.      char4 k = *(char4 *)(data + i + ATTRIBUTES*gy);
8.      if (j.x ^ k.x)
9.          atomicAdd(distance + INSTANCES*gy + gx, 1);
10.     if ((j.y ^ k.y) && (i+1 < ATTRIBUTES))
11.         atomicAdd(distance + INSTANCES*gy + gx, 1);
12.     if ((j.z ^ k.z) && (i+2 < ATTRIBUTES))
13.         atomicAdd(distance + INSTANCES*gy + gx, 1);
14.     if ((j.w ^ k.w) && (i+3 < ATTRIBUTES))
15.         atomicAdd(distance + INSTANCES*gy + gx, 1);
16.  }
17. }

This kernel expects the input data to be stored as an array of characters (line 1). As in the previous examples, the kernel loops over the attributes, with the threads leapfrogging over one another (line 5). However, the duration of this loop is shortened by a factor of four because each thread accesses four characters per memory transaction using the char4 data type (lines 6 and 7). These four attributes are stored as fields (x,y,z,w) of the two instances j and k, which are compared using an exclusive-or operation in each iteration of the loop (lines 8–15). Note that the second clause of the if statement in lines 10, 12, and 14 is required because ATTRIBUTES need not be a multiple of four. Also note that the reduction in global memory accesses comes at the expense of an increased number of atomic add instructions. We will later show this to have an undesired effect on program execution speed.

Memory hierarchy

So far, we have written all of our output directly to global memory, and these writes have been performed atomically. In this section, we will demonstrate how the memory hierarchy of the GPU (Figure 2) can be exploited to further improve performance. We start at the thread level and demonstrate the use of registers, and then move to the block level, demonstrating the use of shared memory.

Each thread has its own registers, which are small, but writing to them is significantly faster than writing to global memory. In our example, these registers can be used to store the intermediate results of the comparisons between the two data instances.

1. __global__ void GPUregister(char *data, int *distance) {
2.     int idx = threadIdx.x;
3.     int gx = blockIdx.x;
4.     int gy = blockIdx.y;
5.     for (int i = 4*idx; i < ATTRIBUTES; i+=THREADS*4) {
6.         char4 j = *(char4 *)(data + i + ATTRIBUTES*gx);
7.         char4 k = *(char4 *)(data + i + ATTRIBUTES*gy);
8.         char count = 0;
9.         if (j.x ^ k.x)
10.             count++;
11.        if ((j.y ^ k.y) && (i+1 < ATTRIBUTES))
12.             count++;
13.        if ((j.z ^ k.z) && (i+2 < ATTRIBUTES))
14.             count++;
15.        if ((j.w ^ k.w) && (i+3 < ATTRIBUTES))
16.             count++;
17.         atomicAdd(distance + INSTANCES*gx + gy, count);
18.   }
19. }

Whereas in our previous example we wrote to global memory after each comparison, we now only write to global memory once (line 17), and this occurs after all four comparisons have been made. This eliminates the tradeoff between global memory accesses and increased atomic add instructions encountered in the previous example. The intermediate results of the four comparisons are stored in the variable count (lines 8, 10, 13, 14, 16), which is local to each thread and stored in a register. Using registers in this way reduces the number of global memory writes by three quarters. Since these writes were previously performed atomically, the use of registers to store intermediate results also reduces much of the contention overhead that occurs when multiple threads request write permission to the same global memory location.

This contention can be further reduced using shared memory. In fact, it can be eliminated. Shared memory is accessible by all threads within a block, allowing for efficient communication and cooperation between threads. Like registers, writing to shared memory is significantly faster than writing to global memory. The same is true of reading shared memory.

1. __global__ void GPUshared(char *data, int *distance) {
2.   int idx = threadIdx.x;
3.   int gx = blockIdx.x;
4.   int gy = blockIdx.y;
5.   __shared__ int dist[THREADS];
6.   dist[idx] = 0;
7.   __syncthreads();
8.   for (int i = idx*4; i < ATTRIBUTES; i+=THREADS*4) {
9.      char4 j = *(char4 *)(data + i + ATTRIBUTES*gx);
10.     char4 k = *(char4 *)(data + i + ATTRIBUTES*gy);
11.     char count = 0;
12.      if (j.x ^ k.x)
13.         count++;
14.     if ((j.y ^ k.y) && (i+1 < ATTRIBUTES))
15.         count++;
16.     if ((j.z ^ k.z) && (i+2 < ATTRIBUTES))
17.         count++;
18.     if ((j.w ^ k.w) && (i+3 < ATTRIBUTES))
19.         count++;
20.     dist[idx] += count;
21.  }
22. __syncthreads();
23. if (idx == 0) {
24.     for (int i = 1; i < THREADS; i++)
25.         dist[0] += dist[i];
26.     distance[INSTANCES*gy + gx] = dist[0];
27.  }
28. }

Above, we present our final kernel, to which we have made several changes. First, is the introduction of a shared array (line 5), which is used to store the calculations of each thread. This array is initialized in parallel, with each thread writing zero to a single element of the array (line 6). To ensure the array is fully initialized before moving on, the CUDA function __syncthreads() is called (line 7), which pauses execution until all threads within the block have reached this instruction. As in the previous example, the kernel loops over the attributes with the threads leapfrogging over one another, and intermediate results are written to the local variable count. However, these intermediate results are then written to shared memory (line 20), instead of performing an atomic write to global memory. Since each thread is writing to a unique location in the shared array, there is no risk of contention. The threads are then synchronized again (line 22) and thread zero (line 23) adds the results from all the other threads in the block to its own value (lines 24–25), which are all stored in the shared memory array. This sum, which is the total distance between instances j and k, is then written to the corresponding element of the output array in global memory (line 26). Note that this write need not be atomic, since only one thread in each block is doing the writing, and each element of the output array corresponds uniquely to one block.

EMPIRICAL RUNTIME ANALYSIS

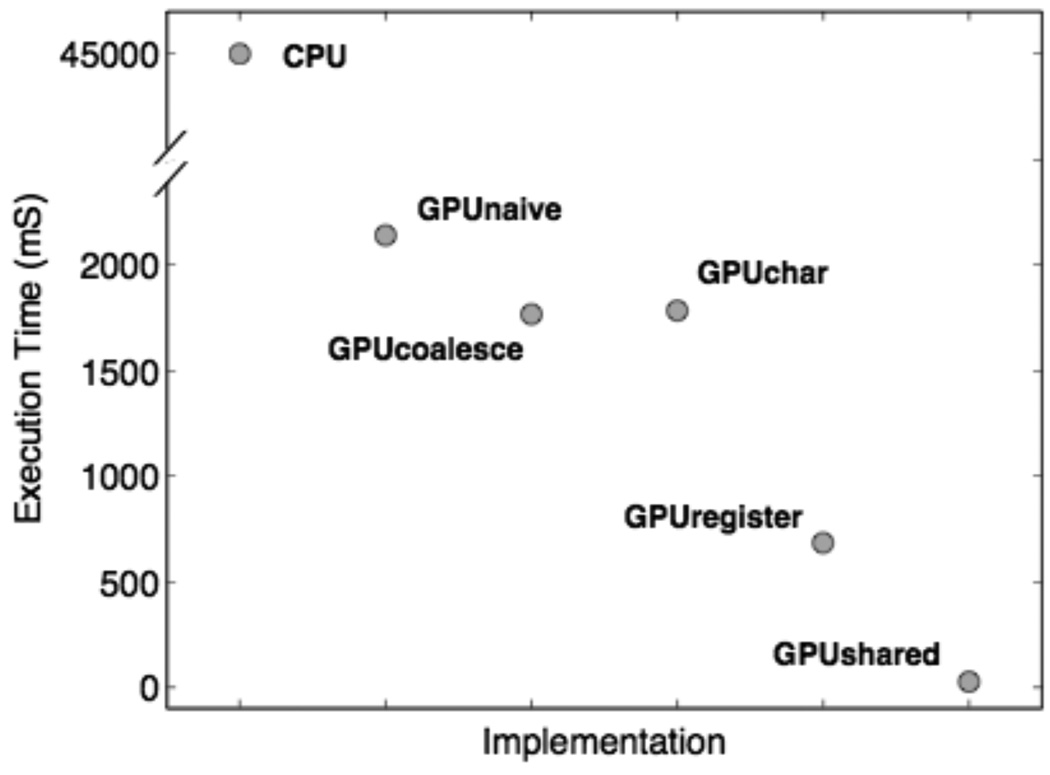
In Figure 4, we present an empirical runtime analysis of the CPU and GPU implementations of the all-pairs distance calculation. For each of the six methods, we consider twenty-five independent analyses, using randomly generated data sets with a ternary alphabet, 112 instances, and 512 attributes. All experiments used 128 threads per block. The CPU implementation was executed on a 2.66 GHz Intel Core 2 Duo with 4GB of RAM and the GPU implementations were executed on an Nvidia GeForce 9600M GT with 512MB of RAM. Both are standard issue on the current MacBook Pro (MacBookPro5,3). The code used to perform this analysis is available as supplementary material (Computational Genetics Laboratory, 2010).

Fig. 4.

Execution time in milliseconds (mS) for the CPU and GPU implementations of the all-pairs distance calculation. Data points represent the average execution time on 25 randomly generated datasets with ternary alphabets, 112 instances, and 512 attributes. Standard errors are smaller than the symbol size and are therefore not shown. Symbol labels correspond to the kernel names (see text). Note the break in scale on the y-axis

As shown in Figure 4, the CPU implementation required an average of 44,865 mS to complete the all-pairs distance calculation. The naïve GPU implementation brought this execution time down to an average of 2,140 mS, improving efficiency by a factor of 20. Execution time was further reduced to 1,766 mS by coalescing the global memory reads. This led to a speedup of 25, relative to the CPU implementation. Changing the data type to characters reduced the memory footprint of the program, but slightly increased execution time (1,784 mS) due to the increase in atomic add instruction contention. However, this tradeoff was overcome through the use of registers, resulting in an execution time of 683 mS and a speedup of 65, relative to the CPU implementation. Finally, using shared memory to eliminate global writes reduced execution time to 26 mS, which is 1700 times faster than the CPU implementation.

DISCUSSION AND CONCLUDING REMARKS

The goal of this article was to present GPU hardware and programming practices to computational biologists and bioinformaticists in a succinct form. We used the example of computing all-pairs distance between instances in a dataset. After presenting a CPU implementation of this algorithm, we discussed five GPU implementations, each one building upon its predecessor. This allowed for the incremental introduction and discussion of several important GPU programming concepts within the framework of a concrete example. In particular, we focused on the incorporation of coalesced reads from global memory, the implications of using various data types, and the proper usage of GPU memory hierarchies. Numerous other optimizations are possible with CUDA, as GPUs are designed to take advantage of a number of graphics optimizations. In particular, the use of constant memory and texture memory (Nvidia Corporation, 2009) can lead to significant speedups, as they avoid reading global memory. Another powerful technique is parallel reduction (Harris, 2009). However, as evidenced by our runtime analysis, sufficient speedups can be obtained using even these less than optimal kernels. In the example presented here, the GPU implementation outperformed its serial counterpart by a factor of 1700.

APPENDIX 1

Computing the all-pairs distance between instances in a dataset is a common task in scientific computing. Here, we provide a simple C function to accomplish this task. We assume that INSTANCES and ATTRIBUTES are globally defined variables.

1. void CPU(int * data, int * distance) {
2.  for (int i = 0; i < INSTANCES; i++) {
3.    for (int j = 0; j < INSTANCES; j++) {
4.      for (int k = 0; k < ATTRIBUTES; k++) {
5.          distance[i + INSTANCES * j] +=
6.             (data[i * ATTRIBUTES + k] != data[j * ATTRIBUTES + k]);
7.      }
8.    }
9.  }
10.}

This code is used in the runtime analyses performed in the final section of this article.