Spatial Heterogeneity in the Effects of Immigration and Diversity on Neighborhood Homicide Rates

Abstract

This paper examines the connection of immigration and diversity to homicide by advancing a recently developed approach to modeling spatial dynamics—geographically weighted regression. In contrast to traditional global averaging, we argue on substantive grounds that neighborhood characteristics vary in their effects across neighborhood space, a process of “spatial heterogeneity.” Much like treatment-effect heterogeneity and distinct from spatial spillover, our analysis finds considerable evidence that neighborhood characteristics in Chicago vary significantly in predicting homicide, in some cases showing countervailing effects depending on spatial location. In general, however, immigrant concentration is either unrelated or inversely related to homicide, whereas language diversity is consistently linked to lower homicide. The results shed new light on the immigration-homicide nexus and suggest the pitfalls of global averaging models that hide the reality of a highly diversified and spatially stratified metropolis.

In a context of record increases in the ethnic and foreign-born population in the US in recent years, heated debates over immigration policy have rekindled old fears about the threat of the “criminal alien.” Due to post-1965 changes in the composition of immigration waves, especially the decade of the 1990s, a wider range of immigrant and ethnic groups is coloring neighborhoods across the country. Yet the implications of immigration and diversity for neighborhood change and crime are not well understood. In this paper, we focus on homicide as a leading indicator of violence and seek to advance our knowledge of the role that immigration plays. We do so by making two analytical moves.

First, we argue that to properly understand the effects of immigration on violence requires a framework that distinguishes segregation, or spatial concentration, from diversity. In this paper we focus equal attention on the separate roles of immigrant concentration, on the one hand, and diversity, on the other, in predicting homicide rates across urban neighborhoods. This analytical distinction is potentially important for understanding the complex social processes leading to homicide. The immigration literature to date has insufficiently tackled this issue.

Second, we argue that the effect of immigration and diversity on neighborhood homicide rates is fruitfully conceptualized as a phenomenon that is contingent on local structural and spatial contexts. Traditional “global” methods of analysis reveal the role of neighborhood characteristics on homicide averaged across space. While we often use these methods ourselves and while they have spawned a rich literature across many decades by a large group of scholars, what remains largely unexplored is the extent of spatial heterogeneity in macrolevel processes. Baller et al. (2001) assert that “[c]oefficients obtained in macrolevel studies of homicide based on samples of units encompassing different regions are likely to yield misleading results unless regional interactions are explicitly take into account.” The same logic applies to models that assess locally specific covariations within a city (Cahill and Mulligan 2007), and may help explain why the immigration-crime research so far has produced inconsistent results. We argue that this inconsistency, on which we elaborate more in the following sections, may be due in part to the typical use of “one-size-fits-all” models, which mask potential variations in the spatial conditions that differentially shape social processes and outcomes across neighborhoods.

Immigration and Neighborhood Crime

In the first half of the 20th century, scholars inspired by Park and Burgess (1925) showed great interest in the relationship between immigrants and neighborhood crime, depicting a somewhat grim picture that was thought to result from factors such as: a) immigrants' presumed “cultural predispositions” toward certain crimes (Sutherland 1947); b) inter-group conflicts driven by wide normative differences within diverse neighborhoods (Sellin 1938); and c) neighborhood environments. The between-neighborhood component was linked to the fact that immigrants tend to settle in neighborhoods that are poor, culturally heterogeneous, and with high crime rates to begin with (Thomas and Znaniecki 1927; Shaw and McKay 1969 [1942]).

Nevertheless, research has largely found an insignificant or negative link between immigrant status and crime (Tonry 1997; Martinez 2002; Martinez and Lee 2000). Controlling for concentrated disadvantage, heterogeneity and residential stability in a community, recent immigrants are typically found to be less involved in violence than are natives. For example, an analysis of Chicago neighborhoods found that first generational immigrant status is protective against engagement in violence for most racial and ethnic groups, adjusting for individual and neighborhood level factors (Sampson, Morenoff, and Raudenbush 2005). In other cities and contexts as well, there is evidence that immigrant groups and Latinos have lower levels of lethal violence than similarly disadvantaged African Americans (Peterson and Krivo 2005; McNulty and Bellair 2003b). In a direct comparison, Martinez and Lee (2000) found that Mariel, Cuban, Haitian, and Jamaican immigrants in Miami were less involved in homicide compared to natives.

Building on Chicago-School notions of social control at the family and community level, segmented assimilation theory (Portes and Zhou 1993; Zhou 1997) suggests that when children of immigrants learn American customs and English at a faster pace than their parents' (dissonant acculturation), assimilation into a highly disadvantaged neighborhood may lead to adoption of inner-city oppositional subcultures (Portes and Rumbaut 2001) and indirectly may lead to higher odds of involvement in gangs or crime. Morenoff and Astor's (2006) analysis of self-reported offending by Chicago youth finds that linguistic acculturation predicts higher involvement in crime. Moreover, disadvantaged neighborhoods are associated with higher levels of violence by the third generation youth. These patterns suggest that neighborhoods with high concentrations of first generation immigrants may be more successful in overcoming structural conditions that boost crime than neighborhoods dominated by equally disadvantaged native-born co-ethnics.

Immigrant Communities and Segregation

Immigrant concentration has complex implications for neighborhood homicide rates. On the one hand, high immigrant concentrations may be the result of segregation and discrimination in the housing market. Segregated and highly disadvantaged ghettos may trap immigrants of low socioeconomic standing under conditions that amplify frustration, tensions, and ultimately increase crime rates. In addition, Putnam (2007) finds that, controlling many individual and contextual characteristics, a neighborhood's proportion of immigrants is strongly and negatively correlated with indicators of social capital and trust in neighbors. Ethnic enclaves may also be harmful by restricting ethnics' market opportunities, social mobility, and acculturation, which may consequently increase engagement in crime (Borjas 2000).

On the other hand, high concentrations of immigrants in a neighborhood may bring about benefits related to information sharing, network formation, symbolic representations of shared identities, or even to labor market opportunities (Chiswick and Miller 2005). Immigrant and ethnic neighborhoods may revitalize social, cultural, and economic institutions (Sampson 2008), simultaneously enhancing overall well-being and tamping down the risk of criminal involvement. Even when resources are scarce, immigrant neighborhoods may provide dense ties, ethnic solidarity, closure, and social control. Portes and Sensenbrenner (1993) describe in more detail immigrant enclaves that include tight-knit social circles characterized by what they call enforceable trust. Highly connected social networks lower the costs of monitoring members' behavior and amplify reputational costs of deviance from norms (Coleman 1988), thereby helping to regulate neighborhood crime levels.

The preservation of traditional culture is another hypothesized reason why, compared to native born Mexican Americans, Mexican immigrants have lower risks of developing mental health problems and engaging in risky behaviors such as alcohol and drug abuse over their lifetime (Escobar 1998). Without collective support, the assimilation experience of newly arrived immigrants in tough inner city neighborhoods would likely follow the same path into crime as similarly disadvantaged native-born minorities (Martinez, Lee, and Nielsen 2004).

There is evidence to support the concentrated immigration thesis. Controlling for an individual's immigrant status, residents in Chicago neighborhoods with 40% or more immigrants are 20% less likely to commit violence than residents in immigrant free neighborhoods (Sampson et al., 2005), suggesting that immigrant concentration functions as a buffer against crime by both immigrants and the native-born. In Miami and San Diego, Martinez et al. (2004) find that drug related homicides are not related to immigrant concentration in the 1970s and negatively related to the percent of the neighborhood population that immigrated in the 1960s.

By contrast, the concentration of more recent immigrant population (from the 1980s) is positively related to drug related homicide in the same city. Lee, Martinez and Rosenfeld (2001) found that in El Paso and Miami the percentage of new immigrants in a census tract associates non-significantly or negatively to Latino, Black, or White homicide. In contrast, San Diego's Black homicide is positively predicted by the concentration of new immigrants. The slightly inconsistent predictions across cities constitute an indication that processes increasing homicide rates may vary in important ways from one place to another.

Diversity of Population

Social disorganization theorists propose that the heterogeneity of a neighborhood population increases crime rates (Kornhauser 1978) by limiting the capacity of residents to communicate effectively with one another, form ties, achieve common values, and come together to solve shared problems. Heterogeneity is thus posited to reduce informal social control (Bursik 1988) leading to increased tensions and the amplified likelihood of conflict and violent crime. Putnam (2007) also found that diversity is associated with lower confidence in local leaders and government, higher protest levels, lower involvement in community projects, lower likelihood of giving to charity and volunteering, fewer friends, and lower happiness levels.

Although measures of racial heterogeneity are typical in studies of crime, language diversity may capture more nuanced variations in the cultures of reference, norms, traditions, beliefs, and values that differentially affect behavior and interaction patterns associated with violence. The cultural diversity of a population may benefit the community if it increases the variety and complementarity of goods, skills, abilities and services (Lazear 1999), spurring innovation and creativity (Florida 2002), cultural diffusion, and hybridization (Fischer 1975), in turn promoting conditions that prevent inter-group conflict and violent crime. The diversity of neighborhood residents may also, in time, increase the levels of inter-cultural tolerance and decrease the risk of crime, contributing to lower homicide rates. There is some evidence of a positive role of language diversity on natives' wages and employment (Ottaviano and Perri 2005). However, few if any studies have examined language diversity and rates of violence.

Local variations in Spatial Processes of Immigration and Diversity

Criminal events tend to cluster across space and scholars have long speculated why this is the case. Usual suspects include spatially clustered structural characteristics such as poverty and unemployment. Other suspects include spatial spillover processes and crime diffusion, whereby a criminal incident in a particular neighborhood triggers a retaliatory criminal event in a neighboring area (Tita and Cohen 2004). The question we raise here is whether the processes linking immigration and diversity to crime are stationary, that is, do they operate uniformly across space? We are also motivated by a small but revealing body of research assessing homicide across states, counties, and neighborhoods that has found distinct differences in the patterns of structural covariation across spatial regimes, even after accounting for spatial spillovers. Suggesting the need for further investigation, the few studies that have tackled spatial heterogeneity in crime have done so mainly by examining whether variables exert significantly different effects across spatial “regimes” (e.g., Baller et al. 2001; Morenoff, Sampson, and Raudenbush 2001). More recently, Cahill and Mulligan (2007) used geographical regression procedures that formally estimate spatial heterogeneity in an analysis of violent crime in Portland, Oregon at the census block group level. They found significant variations across block groups in the effects of four out of eight predictors of violent crime. Population diversity was among the predictors that revealed a spatially varying parameter.

In short, spatial heterogeneity emerges as an independent problem from spatial spillovers, indicating that coefficients of substantive interest may vary significantly across space. The goal of this paper is to explicitly model this phenomenon with respect to immigration, diversity, and homicide. We do not test a specific theoretical mechanism but are guided by the long tradition of urban ecological research and theory noted above. Our study is based on the city of Chicago, the site of many previous inquiries on the immigration-crime nexus.

A Geographically Weighted Regression Approach

We advance a relatively new approach in the quantitative analyses of crime, one that searches the data for systematic spatial regularities while attempting to preserve and model the complexity that non-randomly diverges from average global patterns. In pursuing this goal, we also employ a GIS analytical framework and spatial regression methods (Anselin 1988).

In conventional regression, one parameter is estimated for the relationship between each independent variable and the dependent variable and the relationship is assumed to be constant across the study area. The Geographically Weighted Regression (GWR) approach extends this regression framework to estimate local rather than global parameters. Instead of calibrating a single regression equation, GWR generates a separate regression equation for each observation. Each equation is calibrated using a different weighting of the observations contained in the data. At each regression point (in this paper we let it be a data point, which is represented by the centroid of a census tract) the model is reformulated this way:

$$y_i={\beta }_0(u_{i,}{v}_i)+{\sum }_k{\beta }_k(u_{i,}{v}_i)x_{\mathit{\text{ik}}}+{\epsilon }_i$$ (1)

where (u_iv_i) represents the coordinate location of the data point i (e.g. in our case, the census tract centroid), and β _k(u_iv_i) is a realization of the continuous function β _k(uv) at point i. We estimate β as in the following:

$$\stackrel{\wedge }{\beta }\left(u_i,v_i\right)={\left({\text{X}}^T\text{W}\left(u_i,v_i\right)\text{X}\right)}^{-\text{1}}{\text{X}}^T\text{W}\left(u_i,v_i\right)$$ (2)

where W(u_i,v_i) is an n by n matrix whose off-diagonal elements are zero and whose diagonal elements denote the geographical weighting of observed data for point i (Brunsdon, Fotheringham, and Charlton 1996; Fotheringham, Brunsdon, and Charlton 2002). Each observation is weighted according to its proximity to i. As we move across space the weight of an observation is no longer constant in the calibration, as in OLS or WLS, but varies with i.

Spatial regression models likewise relax the assumption of spatial independence and adjust for spatially autocorrelated processes by incorporating local relationships in the error covariance structure (Anselin 1988), in contrast to GWR, they are still global models. They produce global parameter estimates and the influence of neighbors is stipulated by a spatial weight function that is not calibrated at each observation point (Fotheringham et al. 2002).

When the spatial weighting function is fixed or applied equally at each calibration point, one assumes that the weight-distance relationship is globally applicable at all calibration points across space, which can be problematic for several reasons: a) the global statement may not be true, for instance in situations where physical (built or natural) buffers such as highways or parks between two neighborhoods radically affect their impact on one another; b) if in parts of the larger area data are sparse the local regressions may be based on too few data points. To account for these possibilities, in our GWR models we use a spatially adaptive weighting function instead. This function allows for smaller “bandwidths” where data are dense and for larger bandwidths where data are sparse. Specifically, a bandwidth represents how far out from a focal neighborhood, i, the other neighborhoods will count in the calibration of parameters at point i. The following bi-square function allows for such spatially adaptive bandwidths:

$${\text{w}}_{\text{ij}}=\left\{\begin{array}{l}{\left[\text{1}-{\left({\text{d}}_{\text{ij}}/{\text{h}}_{\text{i}}\right)}^{\text{2}}\right]}^{\text{2}}\text{if}{\text{d}}_{\text{ij}}<{\text{h}}_{\text{i}}\\ 0\text{otherwise}\end{array}\right\}$$ (3)

where h_i denotes the bandwidth, the distance of the Nth nearest neighbor from i, while d_ij represents the distance between points i and j. Instead of fixing the distance, we fix the number of nearest neighbors and allow the kernel to go as far in space as it needs to find that number of neighbors. This is a continuous, near-Gaussian weighting function up to distance h from the regression point, becoming zero at any data point beyond h (Fotheringham et al. 2002, p. 57).

The estimated parameters will in part depend on the weighting function and bandwidth selected. The selection of the weighting function does not appear to be as consequential for the results as the selection of the bandwidth. When the bandwidth tends to infinity the weights become uniformly close to one and the spatial variance of the estimated parameters tends to zero, rendering GWR equivalent to OLS. We calibrate the weight function using the Akaike Information Criterion (AIC) minimization procedure (Hurvich, Simonoff, and Tsai 1998), which provides a trade-off between goodness-of-fit and degrees of freedom. We also compare AIC indices to assess if GWR provides a better fit than a global model while adjusting for the different degrees of freedom in the two models.

Some of the local spatial variability may result from sampling variation. As a check we use the computationally intensive Monte Carlo method, which tests if the observed variation in a parameter is sufficient to reject the null hypothesis of a globally fixed parameter. When no real spatial pattern in the parameter exists, any permutation of the regression variables against their locations should be equally likely, providing a model for the null distribution of the variance. Using the Monte Carlo approach we randomly permute the geographical coordinates of the observations against the variables a certain number of times (n). This produces n values of the variance of the coefficient of interest, which we next use as an experimental distribution. Comparing the actual variance against this distribution is used to obtain an experimental significance level for the spatial variability of each individual parameter.

Data and Measures

To construct our neighborhood level variables we used Decennial Census data for census tracts from the years 1990 and 2000, a combination of public files with tabulations from the Neighborhood Change Data Base (NCDB). The NCDB data normalizes the census tract definitions so that the census tract boundaries are consistent across time. We include only Chicago city census tracts with more than 100 residents as our operational ecological unit.

Population density is defined as the population of a census tract divided by the total land area measured in square kilometers. Concentrated Disadvantage is defined as a function of a set of four indices that typically are strongly associated with each other: unemployment rate, poverty rate, female-headed households, and households with public assistance. Unemployment is the percent of all tract residents, 16 years old or older in the civilian labor force and unemployed, of all residents 16 years old or older in the civilian labor force. Poverty is the percent of all tract residents with income below the poverty level the year before the Census, of all residents with poverty status determined that year. Female-Headed Households is the percent of female-headed families with own children of all families with own children in a census tract. Public Assistance Households equals the percent of all census tract households with public assistance income (including SSI) the year before the Census of all households. Residential Stability is defined as a weighted function of two indices—the percent of 5-year old or older residents who resided in the same house five years before the survey, and owner occupied housing units, which is the percent of all owner occupied housing units over total occupied housing units in a tract.

The disadvantage index and the residential stability index are composite indices calculated as regression factor scores weighing the contribution of each item according to the generated loadings from a Varimax rotated component solution of a principal component analysis. The analysis revealed a consistent diversity and socioeconomic factor structure both in 1990 and 2000. In additional checks of consistency of the results across the two census decades, we repeated the PCA on the pooled data using a dummy to flag for the Census year. There were no significant loadings by any of the input variables on the dummy variable factor. Thus, to produce comparable indices across time we constructed the disadvantage and residential stability factor scores based on the pooled data.

Language Diversity refers to the language that neighborhood residents speak at home and is based on 25 language groups that can be classified identically in both the 1990 and 2000 census. Among the language groups included in this index are Spanish, French, Italian, Portuguese, German, Polish, Russian, Greek, Japanese, Koreans, Vietnamese, Arabic, and Hungarian. We measure language diversity using the well known Herfindahl formula:

$${\text{L}}_t=1-{(\sum {\Pi }_r^2)}_{t,}$$ (4)

where t refers to a particular census tract, r (r = 1…R) refers to a particular language group in the tract, Π _r is the proportion of the language group in the tract population. The index reflects the probability that two randomly selected individuals from a neighborhood belong to different language groups. When all subgroups are equally represented the index has a maximum statistically possible score of [1- 1/R], where R represents the total number of language groups in a tract, and a minimum of 0, when only one language is spoken at home by all neighborhood residents. The heterogeneity index reflects both the number of different subgroups in the population and the evenness in the size of the different subgroups. Thus, a tract with 10 equally sized language groups, for instance, will be assigned a higher diversity score than a tract with only 4 equally sized groups, whereas a tract with two unequal groups will be ranked as less diverse than one with two equally sized groups. In 1990, Chicago's language diversity was ranked overall below San Francisco, New York, Los Angeles, but above Washington DC, Dallas, Philadelphia, and Atlanta (Otaviano and Peri 2005).

Our dependent variable is the homicide rate per 100,000. Homicide events tallied by the Chicago Police Department were geocoded to census tracts for the individual years 1995 to 2006 using established procedures. As described below we estimate a predictive model to reduce the odds of feedback effects and pool homicide across years to stabilize rates and increase precision of estimates. To reduce skewness we also analyze the natural log of the rates per population, with our models examining homicide in five year intervals—1995-1999 (used in one model as a lag control before the 2000 census) and 2002-2006 as the outcome predicted by the 2000 census.

Results

Our basic strategy is to estimate the separate impact of foreign-born concentration and language diversity on homicide rates, controlling for neighborhood-level indices of concentrated disadvantaged, residential stability, and population density. As a conservative test we add lagged homicide rates as a control in select models. In Table 1 we present the first set of multivariate estimations. As a reference, the first two models are estimated using ordinary least squares (OLS) while the third model is estimated using maximum likelihood (ML) spatial regression. The results indicate that percent foreign-born in 2000 does not significantly predict later homicide rates (2002-2006). The language diversity index in 2000, by contrast, is significantly related to lower homicide rates in 2002-2006. The results are robust to controlling for the earlier 5-year average of homicide rates (Model 2) and for spatial dependence (Model 3).

Table 1. Estimates of Log Homicide Rate 2002-2006.

2000 PREDICTORS	Foreign Born			Language Diversity
	(1)	(2)	(3)	(1)	(2)	(3)
Intercept	2.057 *** (.099)	1.280 *** (.129)	.710 *** (.139)	2.411 *** (.116)	1.595 *** (.148)	.949 *** (.164)
Socioeconomic Disadvantage	.890 *** (.055)	.563 *** (.065)	.397 *** (.064)	.725 *** (.059)	.465 *** (.065)	.333 *** (.063)
Residential Stability	.328 *** (.053)	.275 *** (.051)	.185 *** (.048)	.291 *** (.052)	.250 *** (.050)	.173 *** (.048)
Population Density (a)	.252 * (.117)	.269 * (.112)	.216 * (.104)	.286 * (.112)	.282 ** (.108)	.235 * (.101)
Log Homicide Rate 1995-1999		.302 *** (.034)	.206 *** (.032)		.283 *** (.034)	.198 *** (.032)
Percent Foreign Born	-.001 (.003)	-.003 (.003)	-.001 (.003)
Language Diversity				-1.268 *** (.249)	-1.016 *** (.242)	-.652 ** (.232)
Spatial Dependence (Rho)			.372 *** (.039)			.354 *** (.040)
R-Square	.322	.381	.458	.343	.393	.462
Akaike Info Criterion	2859	2778	2698	2833	2761	2690

Notes: Standard errors in parantheses. N = 836. Models 1 and 2 are estimated using OLS. Models 3 are estimated using ML. (a) Coefficients and SE are multiplied by 10000.

^*p<.05;

^**p<.01;

^***p<.001.

We next employ the geographically weighted regression (GWR) procedure (see Table 2) to estimate models parallel to the ones presented in Table 1. Here the main coefficients represent the median of all local coefficients estimated across space, and in parentheses we show the interquartile range of local coefficients. The probability markers reflect results from Monte Carlo tests, not t-tests. The optimal bandwidth, calculated based on the AIC criterion, varies across models between 149 and 229 nearest neighborhoods. The results indicate that the estimated coefficients of both foreign-born percent and language diversity vary significantly across space in predicting later rates of homicide. The extent to which coefficients vary across space within Chicago departs significantly from a random distribution, with a 95% confidence level.

Table 2. GWR Estimates of Log Homicide Rate 2002-2006 across Chicago Neighborhoods.

2000 PREDICTORS	Foreign Born		Language Diversity
	Coeff. (MC)	Coeff. (MC)	Coeff. (MC)	Coeff. (MC)
Intercept	2.244 ₤₤₤ (1.89, 2.85)	1.921 ₤₤₤ (1.36,2.31)	2.718 ₤₤₤ (2.30, 3.20)	2.354 ₤₤₤ (1.81,2.62)
Socioeconomic Disadvantage	.892 ₤₤₤ (.42, 1.27)	.643 ₤₤₤ (.32,1.15)	.785 ₤₤₤ (.22, 1.26)	.569 ₤₤₤ (.16,1.02)
Residential Stability	.200 ₤₤₤ (.03, .36)	.189 ₤₤₤ (.04,.38)	.213 ₤₤ (.02, .37)	.208 ₤₤ (.05,.39)
Population Density (a)	.170 (-.17, .55)	.150 (-.11,.48)	.250 (-.08, .50)	.240 (.00,.45)
Log Homicide 1995-1999		.149 (.09,.25)		.163 (.09,.23)
Percent Foreign Born	-.003 ₤₤₤ (-.02, .01)	-.004 ₤₤₤ (-.01,.01)
Language Diversity			-1.340 ₤₤₤ (-2.21, -.52)	-1.281 ₤₤ (-1.93,-.65)
R-Square	.521	.522	.512	.507
Akaike Info Criterion	2695	2691	2699	2690
Local Sample Size	149	184	165	229

NOTE: N=836. Coeff. refers to the median of all local coefficients . Interquartile range of local coefficients in parantheses. (a) Coefficients and SE multiplied by 10,000. MC refers to Monte Carlo tests of spatial variability: ^₤ p<.05; ^₤₤ p<.01; ^₤₤₤ p<.001. These tests indicate the extent to which the variation in coefficients across space is significantly different from a random distribution.

The spatial distribution of results is presented in the maps of Figure 1. The grey shades indicate t-test values (classified in intervals with a range of one-half of a standard deviation). The estimated local parameters for language diversity tend to be non-significant or significantly negative in predicting homicide. In contrast, while for more than 50% of neighborhoods, the parameter estimates for foreign-born are also negative, for more than a quarter of the neighborhoods the parameter estimates are positive. Nevertheless, three quarters of the estimated coefficients have a t-value lower than 2, suggesting that across most neighborhoods immigrant concentration does not significantly predict homicide (at p < .05). About 16% of the neighborhoods indicate significant negative coefficients while about 7% exhibit significant positive coefficients.

Figure 1. T-Surface for Estimated Local Parameters of % Foreign Born 2000 (First Map) and for Language Diversity 2000 (Second Map) in Predicting Log Homicide 2002-2006, Net of Concentrated Disadvantage, Residential Stability, and Population Density.

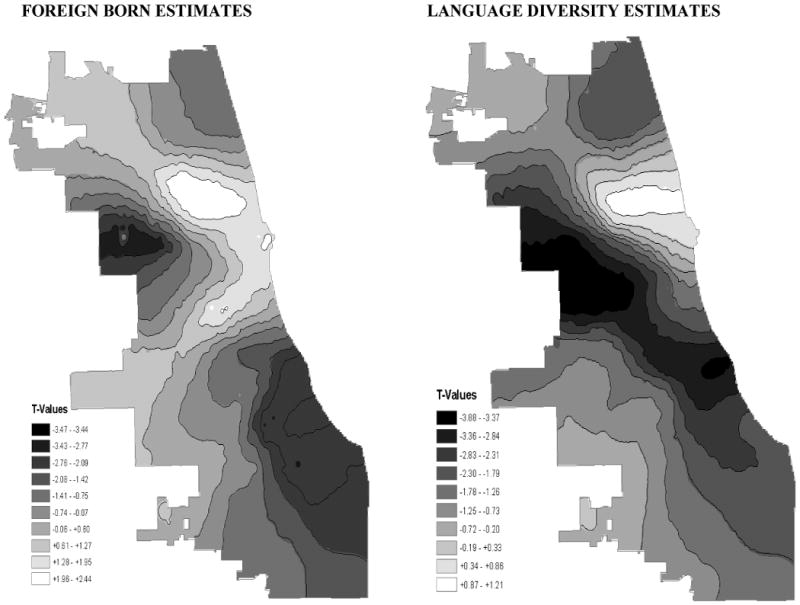
What differentiates the neighborhoods with negative effects from those with positive or nonsignificant effects? Compared to neighborhoods with nonsignificant foreign-born coefficients, the neighborhoods that exhibit a significant foreign-born “protective effect” have on average higher poverty rates, percent black, and concentrated disadvantage, indicating that immigration may function as a buffer against homicide in neighborhoods of higher disadvantage located on the south and west side of the Chicago. Although tracts with negative foreign-born coefficients have higher residential stability scores, they have about the same level of home ownership as the tracts with positive significant coefficients. It is interesting as well that both concentrated socioeconomic disadvantage and residential stability have estimated effects on later rates of homicide that vary significantly over the space of the city. Monte Carlo simulations indicate that this spatial heterogeneity diverges significantly from any variation that may occur randomly across space. All of the significant estimated parameters of disadvantage are positive, which is consistent with the theory and empirical findings so far. Nevertheless, while for about 30% of the neighborhoods the disadvantage effects seem quite strong, with t-values over 4, for more than a quarter of neighborhoods the disadvantage effect is non-significant.

The improvements in the AIC index and R-square indicate that the local model provides a better fit than the global model. Compared to a global R-square of .381 for the foreign-born model and .393 for the language diversity model, the spatial models yield larger R-squares, of .458 and .462 respectively. Greater still, the average local R-square is .522 and .507 for foreign-born and language diversity, respectively, indicating that the GWR models explain more of the variance in the data than the global OLS or spatial ML models.

In the next set of analyses (Table 3), we estimate the role that percent foreign born and language diversity in 1990 and their change scores between 1990 and 2000 play in predicting variations in logged homicide rate change between 1995 and 2006 panels. In other words, we estimate a difference-in-difference model that eliminates stable unmeasured differences between neighborhoods as a confounding factor. The global (Model 1) and the spatial global (Model 2) estimates indicate that both the 1990 levels and the change scores of percent foreign born do not significantly predict changes in log homicide, net of 1990 levels and change over time in disadvantage, stability, and population density. By contrast, language diversity and change in language diversity significantly predict decreases in homicide rates over time. Importantly, the results remain the same before and after controlling for earlier rates of homicide.

Table 3. Estimates of Changes in Log Homicide 1995-2006.

	Foreign Born			Language Diversity
	GLOBAL	SPATIAL GLOBAL	SPATIAL (MC) LOCAL	GLOBAL	SPATIAL GLOBAL	SPATIAL (MC) LOCAL
Intercept	1.332 *** (.131)	1.597 *** (.148)	1.709 ₤ (1.30,1.97)	1.641 *** (.151)	1.955 *** (.172)	2.022 (1.67,2.24)
Socioeconomic Disadvantage 1990	.641 *** (.071)	.708 *** (.080)	.667 ₤₤₤ (.52,.98)	.556 *** (.072)	.592 *** (.080)	.541 ₤₤₤ (.30,.88)
Change in Disadvantage 90-00	.549 *** (.107)	.499 *** (.108)	.453 ₤₤₤ (.30,.85)	.502 *** (.106)	.448 *** (.107)	.393₤₤₤ (.25,.78)
Residential Stability 1990	.301 *** (.056)	.251 *** (.066)	.275 ₤₤₤	.279 *** (.055)	.222 *** (.064)	.273₤ (.11,.41)
Change in Residential Stability 90-00	.331 *** (.088)	.227 ** (.086)	.379 (.18,.53)	.322 *** (.087)	.220 ** (.086)	.376 (.24,.48)
Population Density 1990 (a)	.246 * (.113)	.114 (.119)	.130 (.01,.40)	.240 * (.110)	.148 (.116)	.170 (.06,.41)
Change in Pop.Density 90-00 (a)	1.141 *** (.300)	.984 *** (.292)	.820 (.37,1.50)	1.119 *** (.290)	1.013 *** (.286)	.630 (.50,1.17)
Foreign Born % 1990	-.003 (.004)	.000 (.004)	.001₤ (-.01,.01)
Change in Foreign Born % 90-00	-.004 (.006)	.000 (.006)	.001 (-.01,.01)
Language Diversity 1990				-.947 *** (.254)	-1.049 *** (.319)	-1.067₤₤₤ (-1.72,-.33)
Change in Language Diversity 90-00				-1.502 *** (.436)	-1.467 ** (.472)
Log Homicide 95-99	-.711 *** (.035)	-.810 *** (.035)	-.791 (-.87,-.75)	-.733 *** (.034)	-.823 *** (.035)	-.808 (-.87,-.77)
Spatial Dependence (Lambda)		.366 *** (.043)			.352 *** (.044)
R-Square	.357	.415	.468	.371	.424	.469
Akaike Info Criterion	2775	2723	2710	2756	2708	2699
Local Sample Size	n/a	n/a	331	n/a	n/a	358

Notes: For Global and Spatial Global models coefficients are shown and standard errors are included in parantheses. * p<.05; ** p<.01; *** p<.001. For the Spatial Local models median local coefficients are shown and interquartile interval of local coefficients is indicated in parantheses. Monte Carlo (MC) tests of local spatial variability: ^₤ p<.05; ^₤₤ p<.01; ^₤₤₤ p<.001. These tests indicate the extent to which the variation in coefficients across space is significantly different from a random distribution. (a) Coefficients and SE multiplied by 10,000.

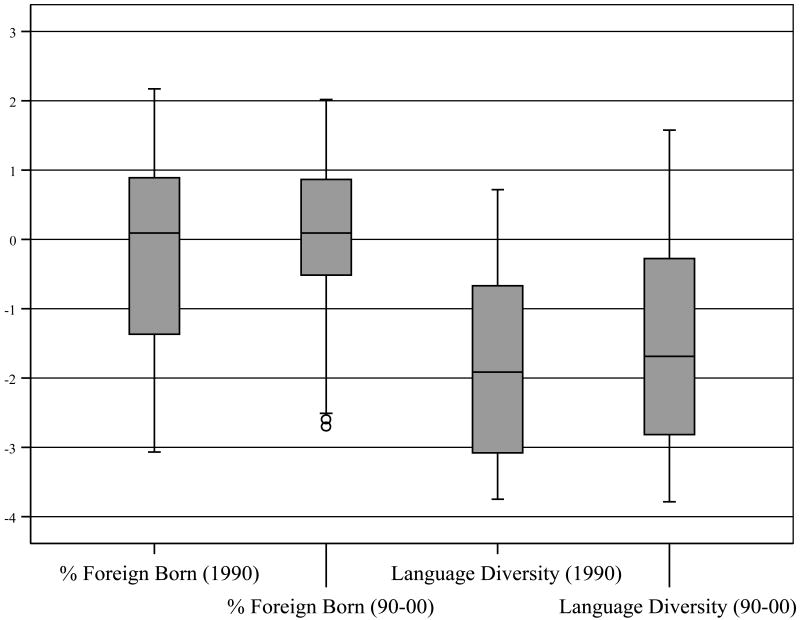
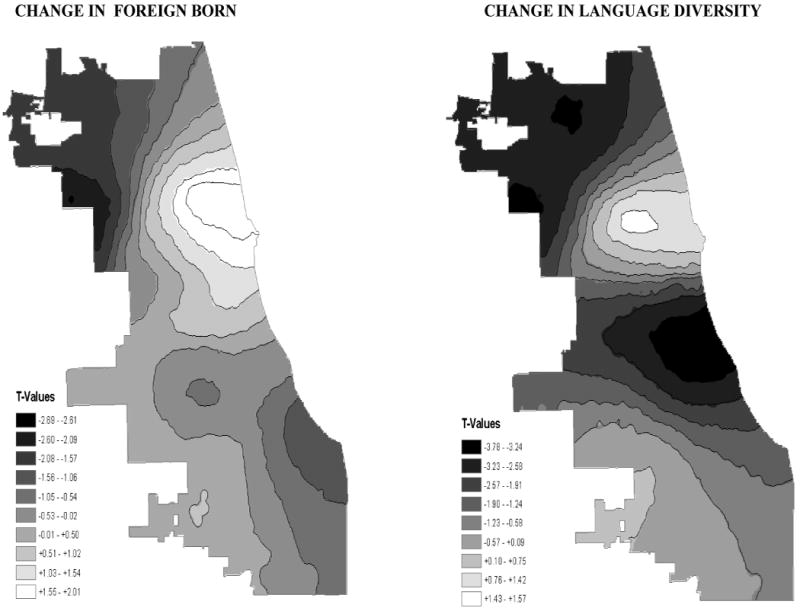
When applying the geographically weighted regression procedure (third column in Table 3) on models otherwise equivalent to the change models presented above we obtain divergent results. A little over 50% of the estimated parameters of percent foreign born and its change scores between 1990 and 2000 are positive (see Figure 2). However, compared to the negative local coefficients, few, if any, of the positive coefficients are significant. In the first GWR change model presented in Table 3 (column 3), 14.5% of all tracts have t-values for the 1990 foreign born coefficient that are lower than -1.96, and only 3.6 % have t-values larger than 1.96. Of all tracts, 2.5% have t-values for the coefficient of change in foreign born that are lower than -1.96, and 1.7 % of tracts have t-values for this coefficient larger than 1.96. Monte Carlo tests reveal significant spatial variation across the city for the 1990 index of foreign born concentration, as Table 3 and Figure 2 also indicate. The fact that these parameter estimates vary from negative to positive across space may explain in part the resulting nonsignificant coefficients in the global models.

Figure 2. Frequency Distribution of T-Values of Estimated Local Parameters for % Foreign Born 2000, Language Diversity 2000, and Corresponding Change Values in Predicting Log Homicide 2002-2006, Net of Concentrated Disadvantage, Residential Stability, and Population Density.

A slightly different story emerges when examining the local coefficients of language diversity (last column in Table 3). Both sets of estimated coefficients for the initial level and change in language diversity in predicting change in log homicide over time vary significantly across space based on formal tests against random variation. Nevertheless, while the value of the estimated local parameter predicting increases in homicide over time changes, the direction of its influence does not. As Figures 2-3 show, most of the local coefficients are negative, and the few that are not yield t-values lower than 2. The coefficients for socioeconomic disadvantage and residential stability are positive and significant in predicting change in homicide rate, as they also are in all previous models. The corresponding GWR estimations indicate the same positive direction of influence on change in homicide rate for the local coefficients, although the magnitude also varies significantly across space. The finding that residential stability is positively related to homicide rates may appear surprising but it has been found before in Chicago data (Sampson, Raudenbush, and Earls 1997). We are pursuing the spatially heterogeneous effects of disadvantage, stability and other factors in another paper.

Figure 3. T-Surface for Estimated Local Parameters of Change in % Foreign Born 1990-2000 (First Map) and for Change in Language Diversity 1990-2000 (Second Map) in Predicting Change in Log Homicide 1995-2006, Net of Disadvantage, Residential Stability, and Population Density.

Finally, it is notable that across all models, the AIC values indicate that the global spatial models offer a better fit than the global nonspatial models. Moreover, the AIC tests in the GWR estimations show that the models accounting for local spatial variability are more appropriate not only compared to the simple global models, but compared to the spatial global models as well.

Discussion

This paper aimed to advance spatially informed criminology by exploring the geographic dimensions of immigration and by modeling the heterogeneous spatial patterns underlying the risk of homicide across neighborhoods of Chicago. While caution must of course be used in interpreting the models, and while we would certainly not claim to have identified causal mechanisms underlying individual behavior, we believe our results underscore systematic spatial-structural interactions shaping homicide patterns. In particular, while our results are consistent with processes of spatial diffusion, they suggest that larger spatial structures condition the role of neighborhood characteristics in amplifying or inhibiting violence. Similar to Baller and colleagues (2001) but at a lower level of analysis, we found that the same neighborhood characteristics differentially predicted homicide rates in different parts of Chicago. Neighborhoods may thus be said to interact with the spatial geography of the city.

Rather then identify these regions a priori, our approach was to use advances in geographically weighted regression (GWR) to estimate what can be thought of as spatially moving clusters of structural covariations. Adding specifications of more proximate social processes (e.g. collective efficacy, subculture intensity) is the critical next step in understanding what mediates the significant spatial variations we identified here, one we are currently taking. In the meantime, the results point to a number of substantive implications with regard to the primary substantive focus of this paper on immigration and diversity.

First, we found an insignificant role for immigrant concentration in promoting or decreasing neighborhood homicide rates. For a minority of neighborhoods, however, the estimated parameters of immigrant concentration were significant, with the largest share reflecting negative coefficients in predicting homicide. These findings indicate some support for arguments that immigrant (or ethnic) neighborhoods may be able to successfully enforce norms and practices that support parental authority and strongly discourage family disruption, substance abuse, and other forms of deviance, which taken together protect residents against violence (Portes and Rumbaut 2001). If one ethnic group is more (or less) successful than another or than native-born residents in enforcing such norms, differences in the protective effects of immigrant concentration on crime will emerge as well, perhaps explaining the spatial variation we found in immigrant concentration effects on crime. Thus despite a few neighborhood pockets of positive association with homicide, concentrated immigration is not as detrimental for neighborhoods as many arguments in the mass-media and academia tend to assume. Immigration may in fact be beneficial (Sampson 2008). Part of the reason empirical research so far has yielded contradictory results may be attributable to the common use of global methods which average across very heterogeneous cities and areas of the country.

Second, we have argued and presented evidence that empirical assessments of the effects of immigration on neighborhoods should be taken beyond the effects of foreign-born concentration. One can think of immigrant effects as entailing two equally important components: the element of segregation, which accounts for the immigrant enclave effects of select urban neighborhoods, and the element of diversity, brought about by the influx of new cultures, skills, and worldviews into urban neighborhoods. The effects of segregation and the effects of diversity may confound each other—also perhaps explaining some of the contradictory findings in the literature so far. In this paper, we attempted to focus our attention on the diversity element of immigration, as conceptually distinct from segregation. We measured diversity so that its lowest score reflects neighborhoods that have no foreign language speaking households as well as neighborhoods where most of its households speak the same foreign language.

The results are consistent with the idea that the diversity element of immigration may lower the risk of homicide over time. Although varying in magnitude across the spatial landscape of Chicago, the language diversity estimates were consistently associated with lower homicide rates in the shorter term as well as in the longer term, net of disadvantage, residential stability, population density, and time-invariant factors. This finding therefore supports our argument that diversity constitutes a dimension of immigration with different implications for shaping neighborhood crime rates than immigrant concentration per se. It follows that there is a need for a reformulation of the traditional “negative” interpretation of heterogeneity and crime from the social disorganization tradition (Kornhauser 1978). At the very least our study suggests the need to move beyond racial aspects of heterogeneity and toward a consideration of some of the more recent arguments about the benefits of cultural heterogeneity generally defined (Florida 2002). Despite its promising theoretical features, language diversity has rarely been used in analyses of homicide victimization and thus may prove to be important in future inquiry.

On a broader and final note, we would conclude by stressing the need for future research on immigration and diversity to explore the urban geography of social inequalities and local variations in processes shaping homicide patterns, an approach that may simultaneously inspire policy interventions that are locally tailored. Global models by definition reflect averages in the processes shaping neighborhood patterns of violence, averages that hide the reality of a highly diversified and spatially stratified urban scene.