Segmentation of the Optic Disc in 3-D OCT Scans of the Optic Nerve Head

Abstract

Glaucoma is the second leading ocular disease causing blindness due to gradual damage to the optic nerve and resultant visual field loss. Segmentations of the optic disc cup and neuroretinal rim can provide important parameters for detecting and tracking this disease. The purpose of this study is to describe and evaluate a method that can automatically segment the optic disc cup and rim in spectral-domain 3-D OCT (SD-OCT) volumes. Four intraretinal surfaces were segmented using a fast multiscale 3-D graph search algorithm. After surface segmentation, the retina in each 3-D OCT scan was flattened to ensure a consistent optic nerve head shape. A set of 15 features, derived from the segmented intraretinal surfaces and voxel intensities in the SD-OCT volume, were used to train a classifier that can determine which A-scans in the OCT volume belong to the background, optic disc cup and rim. Finally, prior knowledge about the shapes of the cup and rim was incorporated into the system using a convex hull-based approach. Two glaucoma experts annotated the cup and rim area using planimetry, and the annotations of the first expert were used as the reference standard. A leave-one-subject-out experiment on 27 optic nerve head-centered OCT volumes (14 right eye scans and 13 left eye scans from 14 patients) was performed. Two different types of classification methods were compared, and experimental results showed that the best performing method had an unsigned error for the optic disc cup of 2.52±0.87 pixels (0.076±0.026 mm) and for the neuroretinal rim of 2.04 ± 0.86 pixels (0.061 ± 0.026 mm). The interobserver variability as indicated by the unsigned border positioning difference between the second expert observer and the reference standard was 2.54 ± 1.03 pixels (0.076 ± 0.031 mm for the optic disc cup and 2.14 ± 0.80 pixels (0.064 ± 0.024 mm for the neuroretinal rim. The unsigned error of the best performing method was not significantly different (p > 0.2) from the interobserver variability.

I. Introduction

Glaucoma is the second leading cause of blindness in the developed world, and is characterized by gradual cupping of the optic nerve head and visual field loss [1]. Traditionally, the optic disc is imaged two-dimensionally with stereo color fundus photography. The hallmark of glaucoma is cupping of the optic disc, which is the visible manifestation of a 3-D structure, the optic nerve head (ONH), in two dimensions. The ratio of the optic disc cup and rim surfaces, or cup-to-disc ratio in these images is an important structural indicator for assessing the presence of glaucoma and may help in quantifying the progression of glaucoma. To quantify the ratio, planimetry has commonly been performed by glaucoma specialists from stereo color photographs of the optic disc [2]. However, we and others have previously shown that manual planimetry is time-consuming with substantial interobserver variability [2]. With the introduction of spectral-domain optical coherence tomography (SD-OCT) scanners [3], [4], some of which are capable of acquiring close-to-isotropic 3-D ONH-centered volumes (Fig. 1), imaging of the 3-D structure of the ONH is now possible. The shape of the cup can potentially be measured more precisely than with stereo photographs, and the cup shape is an important feature that experts use in planimetry. Though direct quantification of optic nerve head parameters, such as axonal volume, in 3-D seems attractive, clinical management is historically based on planimetry of the optic disc as discussed above. Because glaucoma is a slowly progressive disease, with changes occurring over many years, it is currently not clear what 3-D ONH parameters, if any, are suitable for glaucoma progression measurement. Properties of the optic disc, including those indicated by color, tissue vascularization and transparency, are also lost in (narrow band) SD-OCT imaging. Therefore, in order to allow comparisons with historically accepted optic disc planimetry, a segmentation of the optic disc directly from SD-OCT is attractive. For example, Chrástek et al. proposed an automated segmentation method of the ONH in Heidelberg retinal tomography images using morphological operations, Hough transform, and an anchored active contour model [5]. However, they focused only on the segmentation of the neuroretinal rim, not the optic disc cup.

Fig. 1.

Cross-sectional images of the spectral-domain OCT volume in glaucoma. (a) X-Y image of the OCT volume. (b) X-Z image of the OCT volume corresponding to the horizontal line in (a). (c) Y-Z image of the OCT volume corresponding to the vertical line in (a).

Several groups, including ours, have studied methods to segment and quantify the optic disc from 2-D images [6]–[8]. Carmona et al. introduced an automatic system to locate and segment the ONH in eye fundus images using genetic algorithms [6]. The genetic algorithm was used to find an ellipse containing the maximum number of hypothesis points. However, this method has a potential error if the shape of the rim is not a perfect ellipse, and the method did not segment the optic cup.

Xu et al. developed an automated system for assessment of the optic disc on stereo disc photographs [7]. They used a deformable model technique, which deformed an initial contour to minimize an energy function defined from contour shape and contour location, to detect cup and disc margins.

Abràmoff et al. presented a study of an automated segmentation method of the optic disc cup and rim from stereo color photographs using pixel feature classification, including a depth from stereo disparity feature, and compared the segmentation results to glaucoma experts and glaucoma experts in training [8].

The question whether automated planimetry can be performed directly from close-to-isotropic SD-OCT scans is open and, to the best of our knowledge, has not been studied previously although a preliminary version of this research appeared in [9]. The major contribution of this paper is the presentation of a fast, fully automatic method to segment the optic disc cup and rim in 3-D SD-OCT volumes and extensive evaluation of its performance.

II. Methods

The method (Fig. 2) starts by segmenting four intraretinal surfaces in the original spectral-domain OCT volume using a multiscale 3-D graph search-based method (Section II-A). To obtain a consistent ONH shape, the retina in the original spectral-domain OCT volume was flattened by adjusting A-scans up and down in the z-direction using the segmented second intraretinal surface (Section II-B). An OCT projection image was created by averaging in the z-direction the OCT sub volume between the second and fourth intraretinal surfaces (Section II-C). The flattened OCT volume and intraretinal surface segmentations, OCT projection image and vessel probability map from the OCT projection image [10] were used as features for the classification of the optic disc cup and neuroretinal rim. The optic disc cup and neuroretinal rim were segmented by a k-NN classifier and a contextual k-NN classifier incorporating neighboring A-scans (Section II-D). Finally, prior knowledge about the shapes of the optic disc cup and neuroretinal rim regions was incorporated through the application of convex hull-based fitting (Section II-E).

Fig. 2.

Block diagram of our ONH segmentation method.

A. Intraretinal Surface Segmentation Using Multiscale 3-D Graph Search

There are several reasons for intraretinal surface segmentation in ONH-centered OCT volumes. The first reason is that at least one intraretinal surface is necessary for flattening the retina in the original SD-OCT volume to have a consistent ONH shape (Section II-B). The second reason is that two of the segmented intraretinal surfaces are required to create the projection image of the OCT volume in which the cup and rim boundary independent standard is represented after registration with fundus photographs (Section II-C). The image intensity of the OCT projection image is also utilized as one of the features for the ONH classification of the OCT volume (Section II-D).

Li et al. had developed a 3-D/4-D graph-based optimal surface detection method which is capable of detecting multiple interacting surfaces simultaneously [11]. The surface segmentation problem in 3-D can be directly converted to the minimum closed set detection problem in a 3-D graph. The minimum closed set detection problem can be solved by computing the minimum s-t cut of the graph with a low-order polynomial time complexity. This approach was further extended and used for macular layer segmentation in 2-D and 3-D OCT images [12], [13].

We developed a fast multiscale extension of 3-D graph search to detect four intraretinal surfaces in ONH-centered OCT volumes. The basic idea of the multiscale 3-D graph search is to detect the intraretinal surface in the highest resolution image using the intraretinal surface segmented in the lower resolution images. Fig. 3 shows an example of our intraretinal surface segmentation method. To reduce the speckle noise in the OCT volume, for each 3 × 3× 3 image neighborhood, the voxel values were first ordered according to their intensities. The middle 7 values in this ordering were averaged and the resulting value assigned to the central voxel of the 3 × 3 × 3 neighborhood [Fig. 3(b)]. Therefore, the speckle-noise reduction approach exhibits combined properties of median filtering and averaging-based smoothing. As a cost function, the gradient magnitude of the dark-to-bright transition from top to bottom of the smoothed OCT volume was calculated, and five gradient magnitude volumes in different resolutions (levels 0,1,2,3, and 4) were created for the multiscale approach. Level 4 represents full resolution, and the gradient magnitude volume in level i is subsampled by a factor of 2 in the z-axis from that in level i + 1 (0 ≤ i ≤ 3).

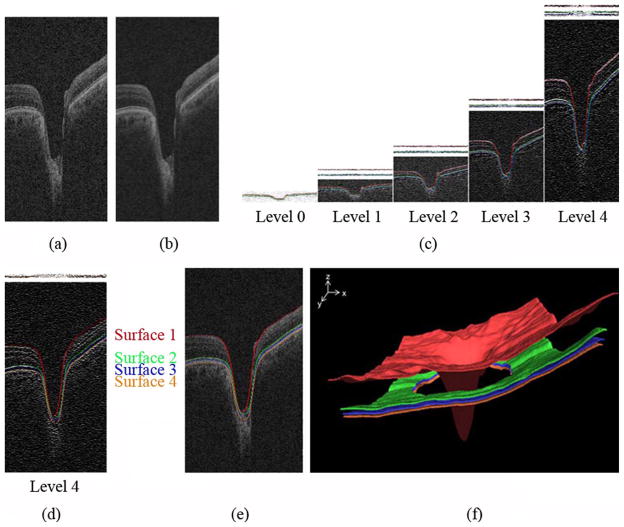
Fig. 3.

Intraretinal surface segmentation. (a) Original ONH-centered OCT volume. (b) Smoothed OCT volume. (c) Gradient images across scales with segmented surfaces 1, 2, and 3 overlaid. The 2 panels above the gradient images in multiscale levels i (1 ≤ i ≤ 4) show the inverted gradient magnitudes constrained by the surfaces already determined in the immediately-lower-scale level i − 1. The top panel part shows the constrained search space for surface 1, the second panel portion from top shows the constrained space for simultaneously detecting the pair of surfaces 2 and 3. The gradient images are gray-level stretched for visualization purposes. (d) The segmentation of surface 4 using 3-D single surface graph search, shown overlaid on the image gradient data. The search space for surface 4 is constrained by the previously segmented surface 3 in level 4 as shown in the top portion of this panel. (e) Our intraretinal surface segmentation result overlaid on the original OCT volume. (f) 3-D rendering of four segmented intraretinal surfaces. The regions of surfaces 2, 3, and 4 around the optic nerve head were ignored since intraretinal surfaces are ambiguous in these regions.

In level 0, the top intraretinal surface (surface 1) and the combined surface of the second and third intraretinal surfaces (surfaces 2 and 3) were detected by applying a 3-D double surface graph search method to the cost function consisting of the inverted gradient magnitudes. For the segmentation of surface 1 in level 1, the gradient magnitude volume to be searched in level 1 was constrained by surface 1 in level 0. In general, the z-values of the gradient magnitude volume to be searched in level i are constrained according to the following equation:

$${\mathbf{z}}_{i-1}\times 2-\alpha \le z\le {\mathbf{z}}_{i-1}\times 2+\alpha \text{for}1\le i\le 4$$ (1)

where z_i−1 = f_i−1i (x, y) is the surface segmented in level i − 1, and α is a margin in the z-axis. After finding surface 1 in the constrained, inverted gradient magnitude volume using 3-D single surface graph search, it was transformed into the original gradient magnitude volume in level 1. In the same fashion, surfaces 1 in levels 2, 3, and finally 4 were detected. The segmentation of surfaces 2 and 3 is similar to that of surface 1 except that it uses a 3-D double surface graph search approach [Fig. 3(c)]. Finally, the inferior intraretinal surface (surface 4) was detected by applying 3-D single surface graph search to the cost function composed of inverted gradient magnitudes of the bright-to-dark transitions from top to bottom of the smoothed OCT volume constrained by surface 3 in level 4 [Fig. 3(d)]. The advantage of the multiscale 3-D graph search over our prior work [12], [13] is the resulting faster processing speed by detecting intraretinal surfaces in OCT subvolumes instead of entire OCT volumes. Fig. 3(e) shows segmentation result with the four final intraretinal surfaces projected over the original spectral-domain OCT volume, and Fig. 3(f) represents the 3-D rendering of four segmented intraretinal surfaces. The question of the histological equivalent of the optical interfaces seen on OCT is still not fully settled, but surface 1 corresponds to the internal limiting membrane (ILM), surface 2 is located at the boundary between inner and outer segments of the photoreceptors, and surface 4 is the outer boundary of the retinal pigment epithelium (RPE), while surface 3 was used to constrain the OCT volume for segmentation of surface 4, and does not seem to have a histological equivalent. Additionally, surfaces 2 and 3 are not present in the ONH region.

B. Retinal Flattening

The retinal volume in the original SD-OCT volume is deformed because of the position of the scanner relative to the patient’s pupil and because of eye movement. In order to normalize the optic nerve head shape across patients, the retina in the original SD-OCT volume was flattened using the second intraretinal surface (surface 2) segmented in Section II-A because it has a consistent shape over its surface. Based on a thin-plate spline [14] fitted to the second intraretinal surface (surface 2, excluding the circular region associated with the optic nerve head), the retina in the original SD-OCT volume was flattened by adjusting A-scans up and down in the z-direction [13]. The thin-plate spline was used to flatten the retina in the ONH-centered OCT scan as well as to reduce eye movement artifacts. The four intraretinal surfaces segmented in the original spectral-domain OCT volume were similarly transformed into the flattened OCT volume. Fig. 4 shows the X-Z, Y-Z images and top intraretinal surface of the original and flattened OCT volumes. In Fig. 4(f), some blood vessels are visible in the top intraretinal surface.

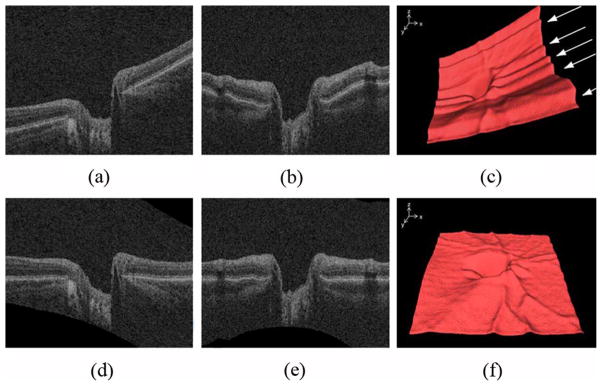
Fig. 4.

Retinal flattening of the ONH-centered OCT volume. (a) X-Z image of the original OCT volume. (b) Y-Z image of the original OCT volume. (c) 3-D rendering of the top intraretinal surface in the original OCT volume shows eye movement artifacts in the y-axis (parallel ridges across the surface, arrows). (d) X-Z image of the flattened OCT volume. (e) Y-Z image of the flattened OCT volume. (f) 3-D rendering of the top intraretinal surface in the flattened OCT volume. The eye movement artifacts are reduced so that major blood vessels are visible.

C. OCT Projection Image

An OCT projection image is necessary for creating the ONH reference standard in SD-OCT scans as described in Section III. In contrast with the unprocessed 3-D OCT scan, the retinal vasculature is visible in the projection image. A previously developed approach [10] was used to detect vessels in the OCT images. Feature points derived from the vasculature such as bifurcations can be used to register the fundus image with the OCT volume. Additionally, the projection image also serves for calculation of a local feature for the cup and rim classification of the OCT volume as described in Section II-D. The OCT projection image was created by averaging in the z-direction the OCT subvolume between the second and fourth intraretinal surfaces segmented in Section II-A (surfaces 2 and 4). These two surfaces define a layer that, due to its position in the retina and high contrast with the retinal background, contains a large number of high contrast vessel shadows [10].

D. Optic Disc Cup and Neuroretinal Rim Segmentation Using a k-NN Classifier and Contextual k-NN Classifier

To segment the optic disc cup and rim from the background, a supervised classification method was used. This method assigned one of three labels (i.e., background, cup, rim) to each A-scan (voxel column) in the SD-OCT scan. In order to make all training data as similar as possible, all left eye (OS) OCT scans were reflected in the x-direction to resemble scans of the right eye (OD). A set of 15 features, obtained from flattened OCT volumes and intraretinal surfaces, OCT projection images and vessel probability maps [10] were calculated for each voxel column in the OCT volume.

• The distance between surface 1 and the thin-plate spline fitted to surface 2. This measures the depth of the optic disc cup

• The distance between surface 1 and 2

• The gradients of surface 1 (Δz/Δx, Δz/Δy). This is motivated by the fact that the gradient of the retinal surface (i.e., surface 1) is a feature used by glaucoma specialists to determine the cup and disc areas in stereo fundus photographs

• The x and y positions with respect to the center of the optic disc cup. The center of the optic disc cup is defined as the (x, y) position of the lowest point of the top intraretinal surface in the z-axis

• The probability that the voxel column is part of a vessel, based on the vessel probability map derived from the vessel segmentation. Vessels can distort the depth measurements, and knowledge about their position helps to compensate for this

• The intensity of the pixel in the OCT projection image corresponding to the voxel column. The projection image contains information about the vasculature and the location of the neuroretinal rim edge

• The average intensity of all voxels in the voxel column

• A 6-bin average voxel column intensity histogram (i.e., 90 voxels above and 90 voxels below the thin-plate spline fitted to surface 2). Each bin represents the average voxel intensity of 30 voxels around the voxel column

Each feature was normalized to have zero mean and unit variance. A k.-NN classifier [15] was used to perform the classification. For each voxel column the classifier determined k = 31 nearest neighbors in the feature space and assigned the most common label amongst the nearest neighbors to the query voxel column [Fig. 5(b)]. To design the k-NN classifier, classifier performance considering 11 k-values (k = 1,11,…, 101) was compared (showing little sensitivity to the k-value), while k = 31 showed the best performance using a holdout strategy. In all cases, the training and testing sets were completely disjoint

Fig. 5.

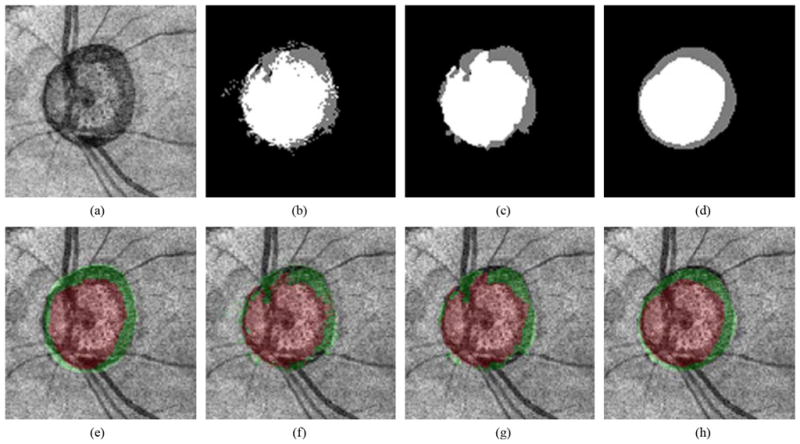
Example of our optic disc cup and neuroretinal rim segmentation. (a) OCT projection image. (b) Our segmentation result using a k-NN classifier. The optic disc cup is in white, the neuroretinal rim is in gray, and the background is in black. (c) Segmentation result using a 9-k-NN classifier. (d) Segmentation result using the 9-k-NN classifier with convex hull-based fitting. (e) OCT projection image overlapped with the reference standard. The optic disc cup is in red, and the neuroretinal rim is in green. (f) OCT projection image overlapped with (b). (g) OCT projection image overlapped with (c). (h) OCT projection image overlapped with (d)

Voxel column classification based on the regular k-NN classifier can result in noisy output due to the fact the classification is based on individual A-scans, and the classifier does not take information from neighboring voxel columns into account. It is known from prior knowledge that the method should find two 8-connected objects (i.e., the neuroretinal rim and optic cup) surrounded by the background. As such, one can assume that A-scans that are close together have a high probability of having the same label. This observation led us to incorporate information from neighboring voxel columns in the classification of the query A-scan. Instead of just determining the k nearest neighbors for the voxel column under consideration, all k = 31 nearest neighbors for each of the individual A-scans in the 3 × 3 neighborhood centered on the query voxel column were determined. The most frequent label amongst these 3 × 3 × 31 = 279 nearest neighbors was assigned to the query voxel column [Fig. 5(c)]. From this point forward, this classification method is referred to as “9-k-NN” classification

E. Convex Hull-Based Fitting

To preserve the shapes of the optic disc cup and neuroretinal rim, a local fitting method using the convex hulls of the segmentation was developed. This postprocessing step was performed to smooth the segmentation results for both the optic disc cup and neuroretinal rim. Fig. 6 visually illustrates the procedure. Fig. 6(a) shows the segmentation result obtained by the 9-k-NN classifier. The optic disc cup is used as an example here but the same procedure is applied to the neuroretinal rim segmentation. The procedure starts by determining the convex hull of the segmentation [Fig. 6(b)]. To detect the innermost boundary of the segmented object we turn it “inside-out.” Each edge point located at distance r from the center [Fig. 6(c)] is relocated to a position R − r from the center [Fig. 6(d)]. Here, R is the radius of a circle around the segmentation; the circle should be large enough so that it covers the segmentation. We define it such that R = 2 × max(r). The red line in Fig. 6(e) indicates the convex hull of the inside-out segmentation edge. The innermost boundary of the segmentation edge [the red line in Fig. 6(f)] was acquired by inversely applying the previously described transformation to the convex hull in Fig. 6(e). The line centered between the inner and outer border [the red line in Fig. 6(h)] formed the final segmentation result

Fig. 6.

Convex hull-based fitting. (a) Optic disc cup segmentation result obtained by a 9-k-NN classifier. (b) Outermost region surrounded by the convex hull of the segmentation in (a). (c) Boundary of the segmentation in (a). Here, r is the distance between the center of the optic disc cup and the boundary of (a), and R is the radius of the circle whose origin is the center of the optic disc cup. The R is the maximum r multiplied by 2. (d) Boundary after an “inside-out” transformation that replaced r with R − r based on the center of the optic disc cup. (e) B-spline (red line) connecting the convex hull of (d). (f) Innermost boundary (red line). (g) Innermost region. (h) The middle boundary (red line) forms the final segmentation result

III. Data

27 spectral-domain OCT scans (14 right eye scans and 13 left eye scans) centered at optic nerve heads from 14 glaucoma patients at the University of Iowa using Cirrus HD-OCT (Carl Zeiss Meditec, Inc., Dublin, CA) were acquired. Each SD-OCT scan consisted of 200 × 200 × 1024 voxels, the voxel size was 30 × 30 × 2 μm, and the voxel depth was 8 bits in grayscale. We also acquired 27 stereo color photograph pairs of the optic disc on the same day from the same patients, corresponding to the SD-OCT scans, using a stereo-base Nidek 3-Dx stereo retinal camera (Nidek, Newark, NJ). The size of the stereo color photographs was 4096 × 4096 pixels, and the pixel depth was 3 × 8-bit red, green and blue channels

Since experts are not yet familiar with annotating the optic disc cup and neuroretinal rim margins directly in spectral-domain OCT scans, the cup and rim annotations were acquired from the optic disc ground truth based on stereo color photographs assessed by two expert observers. Two sets of repeated cup and rim tracings by the first glaucoma expert were averaged and used as the reference standard. Cup and rim tracings by the two glaucoma experts were used to determine interobserver variability. Fig. 7 shows how the ONH reference standard of the SD-OCT volume was created from the tracings obtained from the stereo color fundus photographs. The left image of the stereo color photographs, on which the experts had annotated their (stereo-based) cup and rim segmentation [Fig. 7(a)], was registered to the corresponding OCT projection image [Fig. 7(c)] (Section II-C) by a similarity transformation using two correspondence points manually indicated in both the stereo color photograph and OCT projection image [Fig. 7(d)]. After registration, the ONH reference standard of the SD- OCT scan [Fig. 7(e)] was obtained by applying the same transformation to the stereo color photograph based reference standard [Fig. 7(b)]. The entire process of obtaining the annotations on stereo fundus photographs is described in detail in [8]

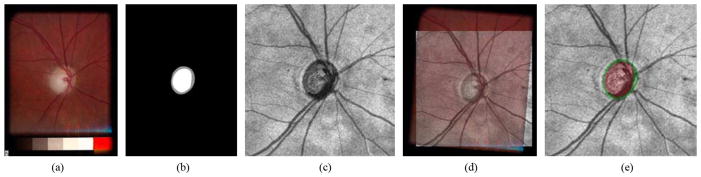
Fig. 7.

Acquisition of the ONH ground truth of the spectral-domain OCT scan. (a) One of a pair of stereo color photographs. (b) Optic disc ground truth of (a), which is manually segmented by a glaucoma expert through planimetry on one (left) of the pair of stereo fundus photographs while viewing the pair through a stereo viewer. The optic disc cup is in white, and the neuroretinal rim is in gray. (c) OCT projection image. (d) Fundus photograph (panel a) registered onto OCT projection image (panel c). (e) OCT projection image overlapped with the ONH ground truth. The optic disc cup is in red, and the neuroretinal rim is in green

IV. Experiments

To evaluate our optic disc cup and rim segmentation approach, a leave-one-subject-out experiment was performed on the 27 spectral-domain OCT scans. Our ONH segmentation results were compared with the expert-defined reference standard. The accuracy of cup and rim segmentation was estimated by Dice similarity coefficient (DSC), as well as using unsigned and signed border positioning errors. The DSC measures the spatial overlap between two regions, A and B, and is defined as DSC(A,B) = 2(A ∩ B)/(A + B). The unsigned border positioning errors of the optic disc cup and neuroretinal rim were calculated by averaging the closest distances between all boundary points from our segmentation result and those from the reference standard. Note that these border position difference measures can only be calculated after convex hull fitting has been applied. The signed error was calculated as the difference in the distance to the center of the optic disc cup. If the distance from a boundary point from our segmentation result to the center of the optic disc cup is shorter than that of a boundary point distance from the reference standard to the center of the optic disc cup, the signed error is negative, otherwise positive. To validate our ONH segmentation, the unsigned and signed errors of our segmentation results were compared with the interobserver variability represented by unsigned and signed border positioning differences between the manual segmentations from the second observer and the reference standard from the first observer. A paired t-test was used to compare the two segmentation results, and a p-value of 0.05 was considered significant

V. Results

From Table I reporting DSC values, in comparison between the k-NN and 9- k-NN classifiers, the 9- k-NN classifier showed significantly larger DSCs for both the optic disc cup (p < 0.001) and neuroretinal rim (p < 0.002). While optic disc cup segmentation results from the 9- k-NN classifier with convex hull-based fitting were not significantly different from those from the 9- k-NN classifier (p > 0.3), neuroretinal rim segmentation results from the 9- k-NN classifier with convex hull-based fitting showed significantly larger DSCs than those from the 9- k-NN classifier (p < 0.001)

TABLE I.

Dice Similarity Coefficients (Mean ± SD)

	k-NN	k-NN + Convex	9-k-NN	9-k-NN + Convex
Cup	0.841 ± 0.054	0.850 ± 0.054	0.851 ± 0.058	0.853 ± 0.057
Rim	0.603 ± 0.137	0.617 ± 0.146	0.637 ± 0.136	0.646 ± 0.139

Based on the unsigned border positioning errors reported in Table II, optic disc cup segmentation results from the two classifiers with convex hull-based fitting did not show a statistically significant difference (p > 0.2). However, in neuroretinal rim segmentation results, the 9-k-NN classifier with convex hull-based fitting showed significantly smaller unsigned errors than the k-NN classifier with convex hull-based fitting (p < 0.04). There was no statistically significant difference between the unsigned error of the 9- k-NN classifier with convex hull-based fitting and the unsigned border positioning difference of the second observer for the optic disc cup (p > 0.2) and neuroretinal rim (p > 0.2)

TABLE II.

Unsigned Border Positioning Errors (Mean ± SD)

	Cup (pixel)	Cup (mm)	Rim (pixel)	Rim (mm)
k-NN + Convex vs. Ref. standard	2.621 ± 0.912	0.079 ± 0.027	2.438 ± 1.178	0.073 ± 0.035
9-k-NN + Convex vs. Ref. standard	2.525 ± 0.869	0.076 ± 0.026	2.043 ± 0.858	0.061 ± 0.026
2nd observer vs. Ref. standard	2.536 ± 1.028	0.076 ± 0.031	2.144 ± 0.804	0.064 ± 0.024

From the signed border positioning errors reported in Table III (i.e., segmentation bias), the optic disc cup and neuroretinal rim segmentation results from the 9- k-NN classifier with convex hull-based fitting had significantly smaller bias for both the optic disc cup and neuroretinal rim than those from the k-NN classifier with convex hull-based fitting (p < 0.001). The bias of the 9- k-NN classifier with convex hull-based fitting was also significantly smaller than the (absolute) signed border positioning difference of the second observer to the reference standard (p < 0.001 for both the optic disc cup and neuroretinal rim)

TABLE III.

Signed Border Positioning Errors (Mean ± SD)

	Cup (pixel)	Cup (mm)	Rim (pixel)	Rim (mm)
k-NN + Convex vs. Ref. standard	0.481 ± 1.932	0.014 ± 0.058	0.990 ± 2.080	0.030 ± 0.062
9-k-NN + Convex vs. Ref. standard	0.008 ± 1.904	0.000 ± 0.057	−0.062 ± 1.602	−0.002 ± 0.048
2nd observer vs. Ref. standard	2.211 ± 1.280	0.066 ± 0.038	1.728 ± 1.091	0.052 ± 0.033

Figs. 8 and 9 show our ONH segmentation results of the best and worst performance obtained by the 9- k-NN classifier with convex hull-based fitting which have the minimum and maximum sums of unsigned errors of the optic disc cup and neuroretinal rim, respectively

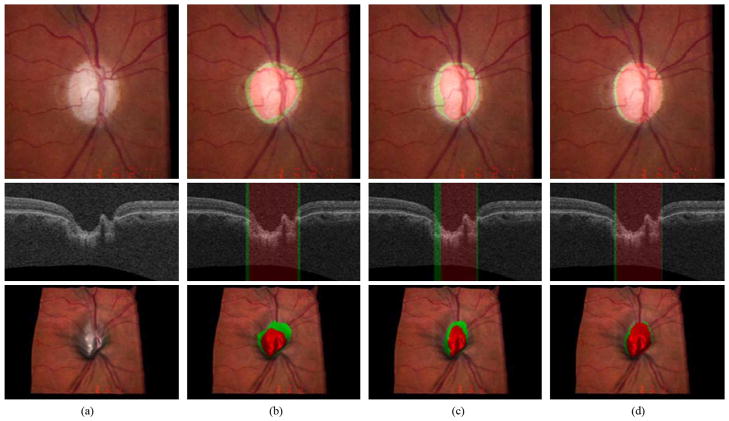
Fig. 8.

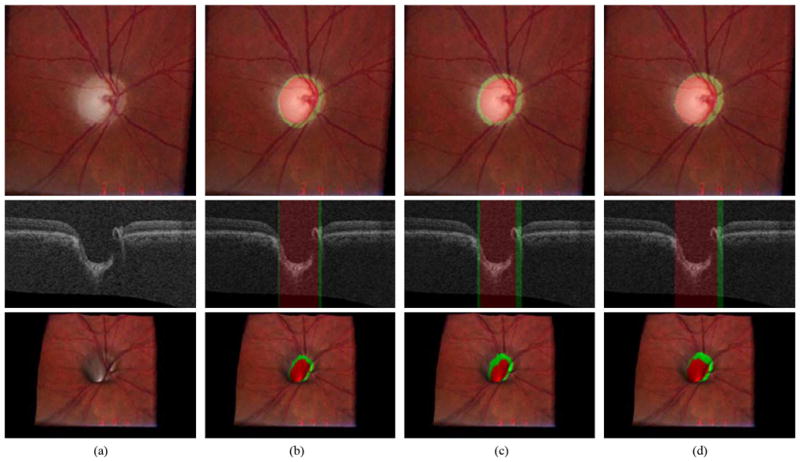
Example of the best ONH segmentation performance case [unsigned error for the optic disc cup = 1.26 pixels (0.038 mm) and unsigned error for the neuroretinal rim = 0.87 pixels (0.026 mm)]. From top to bottom, left stereo color photograph, X-Z image at the center of the OCT volume and 3-D rendering of the top intraretinal surface mapped with the left stereo color photograph. (a) Without any overlap. (b) Overlapped with the result from the 9-k-NN classifier with convex hull-based fitting. The optic disc cup is in red and the neuroretinal rim is in green. (c) Overlapped with the reference standard. (d) Overlapped with the manual segmentation from the second observer

Fig. 9.

Example of the worst segmentation performance case [unsigned error for the optic disc cup = 4.19 pixels (0.126 mm) and unsigned error for the neuroretinal rim = 3.30 pixels (0.099 mm)]. From top to bottom, left stereo color photograph, X-Z image at the center of the OCT volume and 3-D rendering of the top intraretinal surface mapped with the left stereo color photograph. (a) Without any overlap. (b) Overlapped with the result from the 9-k-NN classifier with convex hull-based fitting. The optic disc cup is in red and the neuroretinal rim is in green. (c) Overlapped with the reference standard. (d) Overlapped with the manual segmentation from the second observer

VI. Discussion and Conclusion

We have presented a method to automatically segment the optic disc cup and rim surfaces in optic nerve head-centered 3-D spectral-domain OCT volumes. The method uses a multiscale 3-D graph search method to segment the retinal layers and a k-NN classifier that employs contextual information combined with convex hull fitting to segment the optic disc cup and neuroretinal rim. The method shows excellent results when compared with our stereo-fundus photography derived independent standard and interobserver variability

The presented results confirm that the contextual 9- k-NN classifier outperforms the regular k-NN classifier when no postprocessing is applied. If postprocessing is applied, the9- k-NN classifier has a significantly better Dice similarity coefficient (p < 0.001) on the rim segmentation. Even though the difference in Dice similarity coefficients between the 9- k-NN and 9- k-NN with post processing is much smaller, it is still significant, illustrating the need for the postprocessing step in the proposed method. In addition, the use of postprocessing also improves the pixelated appearance of the segmentation result

An additional interesting result was the fact that there was no significant difference (p > 0.2 for both the optic disc cup and the neuroretinal rim) between the unsigned error of the best performing automatic method and the interobserver variability assessed as unsigned border positioning difference between the two observers. In fact, the unsigned error of the automatic method is slightly lower than the unsigned border positioning difference of the second observer. This is most likely caused by overtraining on a single observer. In this study, the reference standard was set by a single expert. We have previously shown that there is substantial interobserver variability of planimetry of the optic disc in stereo color fundus photographs [2]. By training the automatic method on the segmentations from a single expert observer, the method produces results that are biased towards the opinion of this observer. This hypothesis seems to be confirmed by the signed errors in Table III that show that the computer method has a lower bias with respect to the reference standard (based on observer 1) than with respect to the second observer. Training the system using a reference standard that is based on the opinion of multiple experts should alleviate this issue

Overall, the method shows very good performance. Some issues remain with the ability of the method to adapt to normal anatomical variations inside the optic nerve head. The shape of the optic nerve head in 3-D is similar across the patients in this study. However the width and depth of the cup can vary considerably across subjects. The optic nerve head in the worst performing case (Fig. 9) has a very wide optic disc cup, and a vessel is running along the cup disturbing the optic disc cup depth measurement. This example illustrates one of the largest issues for the current method. Vessels near the optic nerve head tend to be wide, and they can run partially along the optic disc cup disturbing the local geometry and depth measurements. This in turn can lead to misclassified A-scans on the vessels and a less accurate rim or cup border location after postprocessing. We have attempted to alleviate this problem by including the output of a vessel segmentation system applied to the projection image in the feature set. It is likely that the method would benefit from additional processing steps to compensate for the presence of vessels in and around the optic nerve head

There are a number of other possible improvements to the system. The layer segmentation results are a possible source of errors. When large variations in the surface are present, segmentation errors can occur, and this can influence the depth measurements within the optic nerve head. This is primarily an issue for the top surface. Several additions to the basic graph search algorithm used in this work can be considered. The addition of regional information to the edge-based cost function for 3-D graph search could potentially increase the segmentation accuracy [12], [13]. Feature selection is often used in pattern recognition to select the most important features in a set. However, due to the limited amount of data available and the leave-one-subject-out nature of the performed experiment, which would mean we needed to perform feature selection 14 times, we decided not to perform feature selection. In the future, the use of an independent set to select the most important features may lead to a faster system with a further improved performance. As a general comment, close-to-isotropic SD-OCT is preferable for this type of classification given its higher sample ratio; however, 3-D-OCT is not necessarily superior to 2-D-OCT in general, see for example [16]

The average processing time of the complete method is 132 s. The segmentation of the four intraretinal surfaces using the multiscale 3-D graph search approach takes approximately 80 s, and the feature extraction and classification require 52 s. The method was implemented using C + + on a PC (Microsoft Windows XP Professional x64 edition, Intel Core 2 Duo CPU at 3.00 GHz, 4 GB RAM). As the implementation was not optimized for speed, additional speed improvements can be expected

To summarize, we have presented a method for the segmentation of the optic disc cup and neuroretinal rim from 3-D spectral OCT scans of the optic nerve head. The unsigned error of the method is not significantly different from the interobserver variability