Distributed Versus Exclusive Preference in Discrete-Trial Choice

Abstract

Two experiments on discrete-trial choice examined the conditions under which pigeons would exhibit exclusive preference for the better of two alternatives as opposed to distributed preference (making some choices for each alternative). In Experiment 1, pigeons chose between red and green response keys that delivered food after delays of different durations, and in Experiment 2 they chose between red and green keys that delivered food with different probabilities. Some conditions of Experiment 1 had fixed delays to food and other conditions had variable delays. In both experiments, exclusive or nearly exclusive preference for the better alternative was found in some conditions, but distributed preference was found in other conditions, especially in Experiment 2 when key location varied randomly over trials. The results were used to evaluate several different theories about discrete-trial choice. The results suggest that exclusive preference for one alternative is a frequent outcome in discrete-trial choice. When distributed preference does occur, it is not the result of inherent tendencies to sample alternatives or to match response percentages to the values of the alternatives. Rather, distributed preference may occur when two factors (such as reinforcer delay and position bias) compete for the control of choice, or when the consequences for the two alternatives are similar and difficult to discriminate.

How animals distribute their behaviors in choice situations depends in part on the duration of the choice period. In situations with extended choice periods, such as concurrent variable-interval (VI) schedules, many responses are made between reinforcer deliveries, and animals distribute their responses between the alternatives in ways that usually can be described by the generalized matching law (e.g., Baum, ^{1974, 1979;} Davison & McCarthy, 1988). In contrast, in discrete-trial choice procedures, where subjects make just one brief response per trial, the pattern of results is less consistent. In some studies with discrete-trial choice procedures, animals showed exclusive preference for one of the two alternatives (e.g., Foster & Hackenberg, 2004^; Graf, Bullock, & Bitterman, 1964^; Woolverton & Rowlett, 1998). However, there are many other studies with discrete-trial procedures in which the animals exhibited gradations of preference, distributing their choice responses between the two alternatives rather than choosing one alternative exclusively (e.g., Green & Estle, 2003; Mazur, ^{2007, 2008;} Spetch, Belke, Barnet, Dunn, & Pierce, 1990^; Spetch, Mondloch, Belke, & Dunn, 1994^; Young, 1981).

Studies in the 1950s and 1960s by Bitterman and others examined some of the factors that determine whether animals showed either exclusive preference or probability matching, in which choice percentages approximately matched the relative probabilities of reinforcement for the two alternatives. Some evidence for species differences was found--monkeys and rats typically exhibited exclusive preference for the better alternative (Bitterman, Wodinsky, & Candland, 1958; Meyer, 1960), whereas fish and pigeons often exhibited probability matching (Bitterman et al., 1958; Bullock & Bitterman, 1962). However, Graf, Bullock, and Bitterman (1964) reported that, depending on the exact conditions of training and testing, pigeons would sometimes show exclusive preference and sometimes probability matching. For instance, their pigeons exhibited probability matching when a correction procedure was used, but they exhibited maximizing (exclusive preference for the higher-probability option) under a non-correction procedure. They also found maximizing by pigeons when the two alternatives differed in their spatial locations, but probability matching when the two alternatives were keys of different colors. These early studies therefore identified a number of factors that could affect behavior in discrete-trial choice situations, but they did not provide a theoretical account about why these factors made a difference.

The purpose of the two experiments reported here was to examine further the conditions under which pigeons would exhibit either exclusive preference or distributed preference in a discrete-trial procedure, and to use the results to evaluate several different theories of choice that have been proposed since those early studies on choice were conducted. In Experiment 1, pigeons chose between two alternatives that delivered food after delays of different durations, and in Experiment 2 they chose between two alternatives that delivered food with different probabilities. For example, in one condition of Experiment 1, pigeons chose between a green key on the left and a red key on the right. A peck on the green key led to food after a variable delay that averaged 8 s but ranged from 0.8 s to 15.2 s. A peck on the red key led to food after a variable delay that averaged 5 s but ranged from 0.5 s to 9.5 s. Considering the abundant evidence that animals prefer shorter delays to reinforcement over longer delays, one might predict that a pigeon should exhibit exclusive preference for the red key. But if the pigeon does not show exclusive preference for the red key, there are several possible explanations. One explanation is that the pigeon’s behavior had not reached its final asymptotic level of performance, and that if it received more training, exclusive preference would eventually be observed. Another explanation is based on assumptions about what constitutes an evolutionarily advantageous strategy. Some theorists have proposed that because the contingencies of reinforcement for different choices can change unpredictably over time in the natural environment, it is to the animal’s benefit to sample periodically from all alternatives (e.g., Lea, 1979). Therefore, even when one of two alternatives is clearly better, animals may be predisposed to choose the less favorable alternative occasionally.

A third possible explanation is that because of the overlap in the two delay distributions, some of the green-key delays are shorter than some of the red-key delays, and non-exclusive preference is a result of this overlap. For example, although the average delay is shorter for the red key in the example described above, a pigeon might choose the red key on one trial and receive a 9.5-s delay, and it might choose the green key on the next trial and receive a 0.8-s delay. Under these circumstances, the pigeon might distribute its responses among the two alternatives, possibly exhibiting a type of probability matching in which its percentage of red-key responses matches the probably that the red key will have a shorter delay on any given trial (c.f., Behrend & Bitterman, 1966^; Bullock & Bitterman, 1962).

A fourth explanation is based on the concepts of scalar expectancy theory (Gibbon, Church, Fairhurst, & Kacelnik, 1988). According to this theory, animals may exhibit non-exclusive preference even in conditions where there is no overlap in the delays for the two alternatives (e.g., a fixed delay of 5 s for the red key and a fixed delay of 8 s for the green key). Scalar expectancy theory assumes that on each trial, the animal forms a memorial representation of the delay, but the memories formed from many presentations of the same fixed delay will not be identical because of inaccuracies in the animal’s timing abilities. Therefore, the animal’s memory for the red key’s fixed 5-s delay will consist of a distribution of representations, some longer than 5 s and some shorter, with a mode at 5 s. A similar memorial distribution will be formed for the green key’s fixed 8-s delay. Scalar expectancy theory proposes that on each choice trial, the animal selects one sample at random from each of these two memory distributions and chooses whichever sample happens to be shorter. Therefore, as long as there is some overlap between the two memory distributions, the animal will exhibit distributed rather than exclusive preference.

A fifth explanation of distributed preference is based on the idea that an animal will match its response proportions to the relative values of the two alternatives. Numerous studies have suggested that as the delay to a reinforcer increases, the value or reinforcing strength of the reinforcer decreases according to a hyperbolic function (e.g., Mazur, ^{1987, 2001}). However, the exact form of the decay function is not important for this discussion: As long as there is some inverse relation between delay and reinforcer value, a reinforcer with a 5-s delay will have greater value than one with an 8-s delay, but both will have some positive value, and one could theorize that animals will match their response percentages to the relative values of the two reinforcers (c.f. Baum & Rachlin, 1969; Couvillon & Bitterman, 1991) instead of showing exclusive preference for the alternative with the higher value.

A sixth explanation is based on a recent theory developed by Shapiro, Siller, and Kacelnik (2008) called the sequential choice model. These authors suggested that in nature, most choices occur sequentially rather than simultaneously: An animal encounters one possible reinforcer at a time, and must decide whether or not to pursue it. The speed at which the animal decides to pursue an option depends on its value—the greater the reinforcer’s value, the more quickly the animal responds. When an animal is presented with two simultaneous options in a laboratory choice situation, Shapiro et al. proposed that “each triggers its own latency, and the one timing out earliest results in a response to that option” (2008, p. 87). This does not result in exclusive preference for the option with the higher value (and the shorter mean latency), because response latencies vary from trial to trial, leading to two overlapping distributions of response latencies that are conceptually similar to the overlapping distributions of memory representations in scalar expectancy theory. Shapiro et al. tested their theory in a discrete-trial choice situation with European starlings by using response latencies from no-choice trials (in which only one of the two alternatives was presented) to predict choice proportions for choice trials. For example, if a starling’s response latency for the better option was shorter than the latency for the lesser option 80% of the time when the two options were presented separately on consecutive trials, Shapiro et al. predicted that the starling should choose the better alternative on 80% of the choice trials. They presented evidence for this type of correspondence between response latencies on no-choice trials and response percentages on choice trials, and argued that their theory provides a viable alternative to theories of choice that derive their predictions by calculating the values of the two reinforcers (e.g., Couvillon & Bitterman, 1991^; Mazur, 2001^; Shapiro, 2000).

The present experiments were designed to evaluate these different hypotheses about discrete-trial choice (and others) by attempting to arrange some conditions where exclusive preference would be observed and others where distributed preference would be observed. Experiment 1 included choices between two fixed delays and between two variable delays with different amounts of overlap in their distributions. This allowed a test of those hypotheses that distributed preference is a result of this overlap in the contingencies for the two alternatives. Experiment 2 featured choices between two alternatives with different probabilities of reinforcement. In that experiment, the locations of the red and green response keys were constant in some conditions and varied randomly in other conditions. In both experiments, response latencies were examined to test the predictions of the sequential choice model.

EXPERIMENT 1

Method

Subjects

The subjects were four male White Carneau pigeons (Palmetto Pigeon Plant, Sumter, South Carolina) maintained at approximately 80% of their free-feeding weights. All had previously participated in a variety of other experiments on choice, so no pretraining was necessary.

Apparatus

The experimental chamber was 30 cm long, 30 cm wide, and 31 cm high. The chamber had three response keys, each 2 cm in diameter, mounted in the front wall of the chamber, 24 cm above the floor and 8 cm apart, center to center. A force of approximately 0.15 N was required to operate each key. Behind each key was a 12-stimulus projector (Med Associates, St. Albans, VT) that could project different colors or shapes onto the key. A hopper below the center key provided controlled access to grain, and when grain was available, the hopper was illuminated with a 2-W white light. A shielded 2-W white houselight was mounted at the top center of the rear wall of the chamber. The chamber was enclosed in a sound-attenuating box containing a ventilation fan. All stimuli were controlled and responses recorded by a personal computer using MED-PC software.

Procedure

Experimental sessions were usually conducted six days a week. The experiment included three phases, each consisting of seven conditions in which the mean delay for a green key (the standard alternative) was constant, and the mean delay for a red key (the comparison alternative) varied across conditions. Each condition continued until a pigeon satisfied certain stability criteria, as described below.

Phase 1: Fixed delays

Each session continued for 64 trials of 60 min, whichever came first. The 64 trials were divided into 16 blocks, with each block including two forced trials followed by two choice trials. At the start of each trial the center key was illuminated with a white light, and the houselight was off. A single key peck to the center key initiated the start of the trial. On choice trials, after a response on the center key, the key light was turned off, and the two side keys were lit, the left key green and the right key red. A choice of the green key led to the standard delay of 8 s, and a choice of the red key led the comparison delay, which varied across the seven conditions of Phase 1. If the green key was pecked during the choice period, both side key lights were turned off and the 8-s standard delay began, during which the center key was green (and responses on this key had no effect). At the end of the standard delay, the center key was turned off, the white hopper light was turned on, and grain was presented for 3 s. Then the white houselight was lit and an intertrial interval (ITI) began. After a standard trial, the duration of the ITI was 39 s, so the total time from a choice response to the start of the next trial was 50 s.

If the red key was pecked during the choice period, both keylights were turned off and the comparison delay began, during which the center key was red (and pecks on this key had no effect). In the seven conditions of this phase, the comparison delay was 4, 16, 5, 12.8, 6.4, 10, and 8 s, respectively. Thus, this phase began with comparison delays that were most different from the standard delay (i.e., 4 s and 16 s), the comparison delays became more similar to the standard delay across conditions, and the key with the shorter delay was switched in each successive condition. At the end of the comparison delay, the center key was turned off, the white hopper light was turned on, and grain was presented for 3 s. Then the white houselight was lit and the ITI began. After a comparison trial, the ITI was set so that the total time from the choice response to the start of the next trial was 50 s.

The procedure on forced trials was the same as on choice trials, except that only one side key was lit, and a peck on this key was followed by the same sequence of events as on a choice trial. A peck on the opposite key, which was dark, had no effect. Of every two forced trials, there was one for the standard key and one for the comparison key, and the temporal order of the two types of trials varied randomly. Because the delays for the green and red keys were fixed in this phase, it was possible to predict the delays on the choice trials based on the delays on the fixed trials that preceded them.

Conditions were switched individually for each pigeon according to the following rules. A condition was terminated immediately if a pigeon chose the shorter of the two delays on 95% or more of the choice trials for two consecutive sessions. If this did not happen, a condition continued for a minimum of 12 sessions, and ended when (1) the choice percentages from the last 6 sessions did not include a new high or a new low for that condition, and (2) the mean choice percentage from the last 2 sessions was not the highest or lowest 2-session mean for that condition. These criteria for changing conditions were used in all five phases of the experiment.

Phase 2: Mixed delays

The procedure was the same as in Phase 1, except that each fixed delay was replaced with a mixed delay—a pair of delays that had the same arithmetic mean as the fixed delay, either of which might occur on a given trial. The two delays were 0.5 and 1.5 times as long as the corresponding fixed delay from Phase 1. For example, in the first condition of this phase, a choice of the standard (green) key led to a delay of either 4 s or 12 s (instead of a fixed delay of 8 s) and a choice of the comparison (red) key led to a delay of either 2 s or 6 s (instead of a fixed delay of 4 s). On each trial, the shorter or longer delay of the pair was selected at random with a probability of .5. The duration of the ITI that followed each trial depended on the duration of the delay, so that the total time from a choice response to the start of the next trial was always 50 s. In the seven conditions of Phase 2, the mean delays for the comparison key and their order of presentation was the same as in Phase 1. In all other respects, the procedure was the same as in Phase 1. However, because either the shorter or longer delay of each pair could occur on any trial, it was not possible to predict which of the two delays would occur on the choice trials based on which occurred on the immediately preceding forced trials.

Phase 3: Variable delays

The procedure was the same as in Phase 1, except that in each condition, both the standard and comparison delays could assume any one of seven possible durations. The arithmetic means of these delays were equal to the corresponding fixed delays in Phase 1, and the seven component delays were 0.1, 0.4, 0.7, 1, 1.3, 1.6, and 1.9 times as long as the mean delay. For example, in the first condition of this phase, a choice of the standard key led to a randomly chosen delay that could be 0.8, 3.2, 5.6, 8, 10.4, 12.8, or 15.2 s (for a mean delay of 8 s), and a choice of the comparison key led to a delay that could be 0.4, 1.6, 2.8, 4, 5.2, 8.4, or 7.6 s (for a mean delay of 4 s). In the seven conditions of Phase 3, the mean delays for the comparison key and their order of presentation was the same as in Phase 1. In all other respects, the procedure was the same as in Phase 1. However, because any one of the seven component delays could occur on any trial, it was not possible to predict which of the seven delays for either the standard or comparison would occur on the choice trials based on which occurred on the immediately preceding forced trials.

Results and Discussion

The number of sessions per condition needed to satisfy the stability criteria ranged from 2 to 25 sessions. The data from the last two sessions of each condition were used in all analyses.

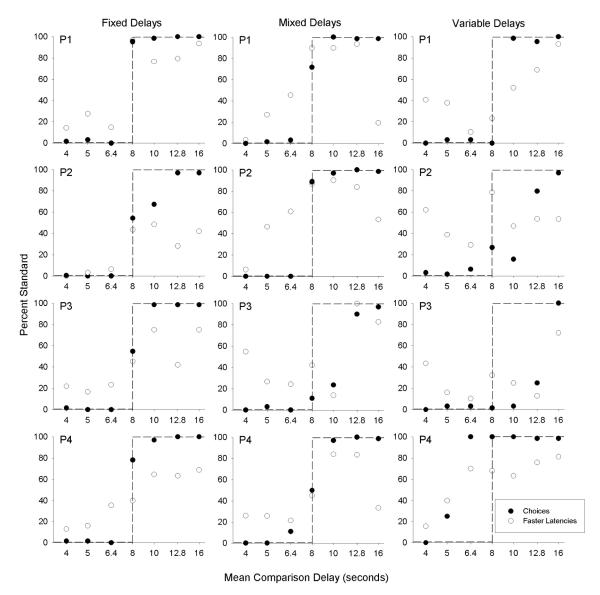
For each pigeon, the filled circles in Figure 1 show the choice percentages for the standard (red) key from the three phases of the experiment. These percentages were based on the 32 choice trials of each session. The dashed lines show the step functions that represent exclusive preference for the alternative with the shorter mean delay to reinforcement. For the purposes of this discussion, an animal’s performance will be described as “exclusive preference” if it made 95% or more of its choices for one alternative, which is consistent with the criteria used to terminate one condition and go to the next. When the two alternatives were fixed delays (left column), the pigeons exhibited exclusive preference in all conditions with unequal delays, with just one exception (Pigeon P2 with the 10-s comparison delay). When the two alternatives were mixed delays (center column), Pigeons P1 and P2 continued to show exclusive preference for the shorter alternative in each condition, as did Pigeon P4 except for the condition with a mean comparison delay of 6.4 s. The performance of Pigeon P3 was the least like a step function, with the percentage of choices increasing gradually as the comparison delays increased from 8 s to 16 s.

Figure 1.

The percentage of choice responses for the standard key (filled circles) and the percentage of forced-trial response latencies that were faster for the standard key (open circles) are shown for each pigeon in the three phases of Experiment 1. See text for details about the calculation of the latency percentages.

In Phase 3, where the two alternatives were variable delays (right column of Figure 1), there was more variability across pigeons. Pigeon P1 continued to show exclusive preference for the alternative with the shorter mean delay, but the other three pigeons did not. Pigeon P2 exhibited a gradual increase in preference for the standard alternative as the mean comparison delay increased from 6.4 s to 16 s. The results from Pigeons P3 and P4 did not follow the step functions shown by the dashed lines, but notice that these two pigeons did show exclusive preference in six of the seven conditions, though not always for the alternative with the shorter delay. For example, Pigeon P3 showed exclusive preference for the 10-s comparison delay over the 8-s standard delay. This pigeon’s behavior can therefore be described with a step function, but one that switches from exclusive preference of the comparison to exclusive preference of the standard when the comparison delay is 12.8 s. Similarly, Pigeon P4’s choices can be described by a step function that switches between alternatives at a comparison delay of 5 s.

The open circles in Figure 1 show the percentages of trial blocks in which the standard key had a faster latency on the forced trials, calculated according to the method used by Shapiro et al. (2008). Response latencies on the two forced trials of every four-trial block were compared to determine whether the red-key or green-key latency was faster (for a total of 16 comparisons per session). The percentage of blocks in which the standard key had the faster latency was calculated from the last two sessions of each condition. (Latencies were measured in 0.l-s bins, and ties were excluded from the calculations.) According to the sequential choice theory of Shapiro et al., the choice percentages for the standard alternative (filled circles) should tend to match the percentages of forced trials on which the standard alternative had the faster latency (open circles). However, in contrast to the exclusive preference seen in many conditions, there were only a few conditions where the standard latency was always faster than the comparison latency, or vice versa. Overall, the results in Figure 1 show little correspondence between choice percentages and faster latencies.

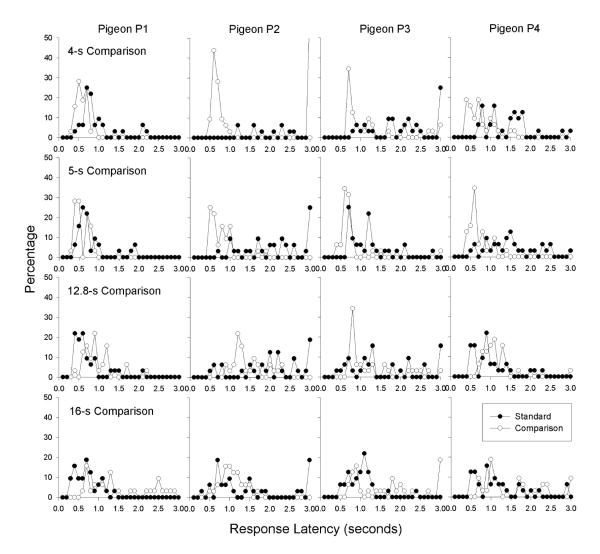
Figure 2 provides some examples of the distributions of response latencies on forced trials for the standard and comparison alternatives. This figure displays frequency distributions from four conditions in Phase 1 (which had fixed delays for the two alternatives). The top two rows are from conditions in which the standard delay of 8 s was longer than the comparison delay (4 s and 5 s), and the bottom two rows are from conditions in which the comparison delay was longer (12.8 s and 16 s). Some of these distributions have sharp peaks and others do not, but overall, response latencies tended to be shorter for whichever alternative had the shorter delay to reinforcement (i.e., the comparison in the top two rows and the standard in the bottom two rows). However, with regard to the sequential choice model, it is important to note the large amount of overlap in the two distributions that can be seen in almost every panel. As has already been shown (Figure 1, left column), the standard choice percentages for all four pigeons were at or near 0% with the 4-s and 5-s comparison delays, and they were at or near 100% with the 12.8-s and 16-s comparison delays. According to the sequential choice model, this exclusive preference should have occurred only if there was no overlap in the latency distributions for the standard and comparison alternatives on the forced trials. That is, all 16 panels in Figure 2 should have looked something like the distributions for Pigeon P2 with the 4-s comparison delay, where there was no overlap between the two distributions. This was not the case in the other 15 panels. These results show that, contrary to the predictions of the sequential choice model, the amount of overlap in latency distributions on forced trials cannot be used to predict the choice percentages on choice trials. The latency distributions from the other conditions of this experiment, though not presented here, were similar to those shown in Figure 2; that is, there was usually substantial overlap in the distributions for the standard and comparison alternatives, both when choice percentages showed exclusive preference and when they did not.

Figure 2.

For each pigeon in Experiment 1, frequency distributions of response latencies on the forced trials of the standard key (filled circles) and the comparison key (open circles) are shown for four of the conditions in Phase 1.

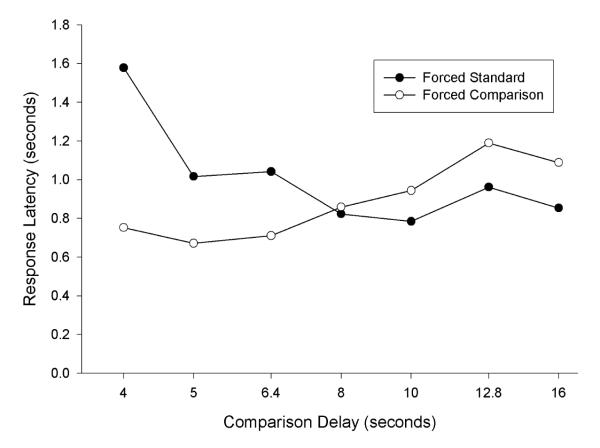
Although the patterns of response latencies did not support the predictions of the sequential choice theory, in several respects the latencies from this experiment were similar to those obtained by Shapiro et al. (2008) with starlings. Shapiro et al. found that the response latencies on forced trials depended on the reinforcement contingencies for both the alternative presented on a trial and for the other alternative (not presented on that trial). The same effect was observed in this experiment. Harmonic means of the response latencies in the last two sessions of each condition were calculated for each pigeon. Harmonic means were used in order to minimize the influence of occasional very long response latencies, because these outliers would have an excessive influence if arithmetic means were used. A three-way repeated-measures ANOVA (phase × comparison delay × alternative) was conducted on the mean latencies from the forced trials. There were no significant main effects or interactions (all Fs < 2.31) except for a significant interaction between delay and which alternative was presented, F(6, 18) = 7.71, p < .001. Figure 3 shows the nature of the delay × alternative interaction by plotting response latencies for the standard and comparison alternatives at each comparison delay. As the mean comparison delay increased from 4 s to 16 s, response latencies tended to increase for the comparison key and to decrease for the standard key (even though the standard delay was the same in all conditions). There were significant simple effects of delay for both the standard alternative, F(6, 18) = 7.13, p < .01, and the comparison alternative, F(6, 18) = 3.80, p < .05. The effects of the comparison delay on response latencies for both alternatives are similar to what Shapiro et al. found.

Figure 3.

Averaged across all pigeons in all phases of Experiment 1, harmonic mean response latencies on forced trials for the standard and comparison alternatives are plotted as a function of the mean comparison delay.

Shapiro et al. (2008) also reported that response latencies were shorter on choice trials than on forced trials, which is predicted by their model. For each condition of the present experiment, harmonic means of choice-trial and forced-trial latencies were compared for whichever alternative was preferred in each condition. (Such comparisons were not possible for the less preferred alternative because there were usually few or no choice trials on which that alternative was chosen.) On average, latencies were slightly shorter on choice trials (M = 0.71 s) than on forced trials (M = 0.77 s), but this difference failed to reach statistical significance, F(1, 3) = 8.04, p = .066.

Overall then, the patterns of response latencies were similar in some ways to what Shapiro et al. (2008) found, but the lack of correspondence between response latencies on forced trials and levels of preference on choice trials poses problems for their sequential choice model.

The results can also be used to evaluate the other five hypotheses about distributed preference described in the Introduction. There was some support for the hypothesis that some instances of distributed preference may be cases in which behavior has not yet reached its asymptotic level. In many conditions of this experiment, a pigeon’s choice percentages eventually reached exclusive preference, but only after 12 or more sessions of 64 trials each. If these conditions had been arbitrarily terminated after fewer conditions, many more instances of apparent distributed preference would have been recorded. However, unless a pigeon showed exclusive preference sooner, every condition in this experiment lasted for a minimum of 12 sessions and until the stability criteria were met. Despite these stability criteria, there were some cases in which the pigeons’ choices did not reach exclusive preference. Of course, it is possible that with much longer exposure to the alternatives, the pigeons eventually might have exhibited exclusive preference in all phases of the experiment, but this possibility seems unlikely.

The hypothesis that distributed preference occurs because there is an evolutionary advantage to the strategy of occasionally sampling all options (Lea, 1979) is difficult to test, because it is not clear how much sampling should occur, and under what conditions. However, the results provide little encouragement for this hypothesis. Every condition of this experiment included 50% forced trials and 50% choice trials. Even when a pigeon chose the better alternative on every choice trial, it was exposed to the lesser alternative at least once in every four-trial block. It therefore seems difficult to maintain that the distributed preference found in some conditions occurred because of the need to sample the lesser alternative. And if one argues that this forced exposure to the lesser alternative was not enough (for instance, because there was no guarantee that choosing the red key on forced trials would produce the same result as on choice trials), this raises another problem for this hypothesis: Exclusive preference was observed in many conditions. Why should the exposure to the lesser alternative on forced trials be enough “sampling” of that alternative in some conditions but not others?

The results were not consistent with the hypothesis that distributed preference will be observed whenever there is overlap in the distributions of delays for the two alternatives (such that the alternative with the longer average delay to reinforcement sometimes delivers a reinforcer after a shorter delay than the other alternative). Perhaps the clearest evidence against this hypothesis was obtained with the mixed delays used in Phase 2. The component delays in these schedules were selected so that there would be overlap between the standard and comparison delays in all conditions. For example, the standard alternative had reinforcer delays of 4 s and 12 s, and the shortest comparison alternative (with a mean of 4 s) had delays of 2 s and 6 s. Because the 6-s component of the comparison was longer than the 4-s component of the standard alternative, on every choice trial there was a 25% chance that the comparison delay would be longer than the standard delay. Similarly, the longest comparison alternative (with a mean of 16 s) had component delays of 8 s and 24 s, so on every choice trial there was a 25% chance that the comparison delay would be shorter than the standard delay. Despite this overlap in the individual delays to reinforcement, the pigeons showed exclusive preference for the alternative with the shorter average delay in most conditions of Phase 2. We can conclude that overlap in the obtained delays to reinforcement is not a sufficient condition for distributed preference to be observed.

For similar reasons, the results from Phase 2 are inconsistent with the assumptions of scalar expectancy theory. This theory assumes that on every trial the animal samples from the memory representations of the two alternatives, and chooses whichever sample has the shorter delay (Gibbon et al., 1988). Because there would be substantial overlap in the memorial distributions for the standard and comparison delays, it follows that non-exclusive preference should have been observed in all of the conditions of with mixed delays. In fact, scalar expectancy theory also predicts that there should have been some instances of non-exclusive preference with the fixed delays used in Phase 1, because the theory assumes the memorial representations of fixed delays are normal distributions, and the distributions for two fixed delays should also have some overlap.

The many examples of exclusive preference found in this experiment are inconsistent with the hypothesis that animals will match their response proportions to the relative values of the two alternatives (e.g., Couvillon & Bitterman, 1991). For example, if a more immediate reinforcer has twice the value of a more delayed reinforcer, this hypothesis predicts that an animal should choose the more immediate reinforcer twice as often, resulting in a choice percentage of 67%. However, the results from Phase 1 are especially clear in showing that when pigeons choose between reinforcers with two different fixed delays, they tend to exhibit exclusive preference for the alternative with the shorter delay; their choice percentages do not match the relative values of the reinforcers.

In summary, the results seem to pose problems for all six of the hypotheses described in the Introduction. However, the following conclusions can be drawn from this experiment: (1) In discrete-trial choice between delayed reinforcers, exclusive preference was observed in many cases, both with fixed delays and with variable delays that featured overlap in the delay distributions for the two alternatives. (2) Examples of distributed preference occurred most often when the mean delays for the standard and comparison were more similar (e.g., 8 s versus 10 s), whereas exclusive preference was usually observed when difference in delays was larger (e.g., 8 s versus 16 s). This suggests that distributed preference may appear in discrete-trial choice situations when the two alternatives are more difficult to discriminate. (3) There were a few cases (with the variable delays in Phase 3) where pigeons showed exclusive preference for the alternative with the longer rather than shorter mean delay. It appears that in these cases the animals adopted a strategy of choosing one alternative consistently, but either because of a response bias (for a particular color or key location) or because of a difficulty in discriminating the two delay distributions, they chose the option with the longer mean delays. Although this performance was certainly not optimal, it can be seen as further evidence for the tendency to display exclusive preference in discrete-trial choice situations.

EXPERIMENT 2

Many of the early experiments on discrete-trial choice that found non-exclusive preference by pigeons and other species involved choices between two probabilistic reinforcers (e.g., Bitterman et al., 1958^; Bullock & Bitterman, 1962^; Graf, et al. 1964). To examine the factors that might lead to either exclusive or distributed preference with probabilistic reinforcers, Experiment 2 used procedures similar to those of Experiment 1, except that the two alternatives varied in their reinforcement probabilities instead of their delays. In Phase 1, the key locations for the two alternatives were fixed, and in Phase 2 they varied randomly over trials. Out of concern that it might take the pigeons longer to reach asymptotic performance with two different reinforcement probabilities than with two delays, each condition lasted for a minimum of 25 sessions unless exclusive preference was reached sooner.

Method

Subjects and Apparatus

The subjects were four male White Carneau pigeons (Palmetto Pigeon Plant, Sumter, South Carolina) maintained at approximately 80% of their free-feeding weights. All had previously participated in a variety of other experiments on choice, so no pretraining was necessary.

The experimental chamber was identical to the one used in Experiment 1, and the same equipment and software were used to conduct this experiment.

Procedure

Experimental sessions were usually conducted six days a week. The experiment included two phases, each consisting of nine conditions with different reinforcement probabilities for the two alternatives. The criteria for terminating a condition were similar to those used in Experiment 1. A condition was terminated immediately if a pigeon chose the alternative with the higher probability of reinforcement on 95% or more of the choice trials for two consecutive sessions. If this did not happen, a condition continued for a minimum of 25 sessions, and ended when (1) the choice percentages from the last 6 sessions did not include a new high or a new low for that condition, and (2) the mean choice percentage from the last 2 sessions was not the highest or lowest 2-session mean for that condition. (In two cases, conditions ended after 15 and 17 sessions rather than the minimum of 25 sessions because of experimenter error.)

Phase 1: Varying probabilities, fixed sides

Each session continued for 160 trials or 60 min, whichever came first. The 160 trials were divided into 40 blocks, with each block including two forced trials followed by two choice trials. At the start of each trial the center key was illuminated with a white light, and the houselight was off. A single key peck on the center key initiated the start of the trial. On choice trials, after a response on the center key, the key light was turned off, and the two side keys were lit, the left key green and the right key red. A peck on either key turned both key lights off and led either to reinforcement or to an ITI. On trials with reinforcement, the hopper light was lit and food was presented for 2.5 s, followed by a 10-s ITI with the white houselights on. On trials without reinforcement, the 10-s ITI began immediately after a peck on one of the side keys. The procedure on forced trials was the same except that only one side key was lit after the center-key response, and a single peck on that key led either to reinforcement or the ITI. Of every two forced trials, there was one for the green key and one for the red key, and the temporal order of the two types of trials varied randomly.

The reinforcement probabilities varied across conditions, but in each condition the probabilities for the green and red keys summed to 1. The order of the reinforcement probabilities for the green key in the nine conditions was .1, .9, .2, .8, .3, .7, .4, .6, and .5. Thus, the experiment began with the two most different reinforcement probabilities (i.e., .1 for the green key and .9 for the red key), the two probabilities became more similar across conditions, and the key with the higher probability was switched in each successive condition. Because the presence or absence of a reinforcer was determined at random according to the probabilities in effect in each condition, it was not possible to predict whether a reinforcer would be delivered for either the green or red key on the choice trials based on whether a reinforcer occurred on the immediately preceding forced trials.

Phase 2: Varying probabilities, random sides

The procedure was the same as in Phase 1, except that the left/right positions of the red and green keys varied randomly on both forced trials and choice trials.

Results and Discussion

The number of sessions per condition needed to satisfy the stability criteria ranged from 2 to 45 sessions. The data from the last two sessions of each condition were used in all analyses.

For each pigeon, the filled circles in Figure 4 show the choice percentages for the green key plotted as a function of the reinforcement probability for that key. The left column shows the results from conditions in which the green key was always on the left (Phase 1). In Phase 2, the randomized key locations had a major effect on choice in many conditions, so the results from this phase are separated into trials with the green key on the left (center column of Figure 4) and trials with the green key on the right (right column). The dashed lines show the step functions that represent exclusive preference for the alternative with the higher probability of reinforcement. As in Experiment 1, a pigeon’s performance will be described as “exclusive preference” if it made 95% or more of its choices for either the red or green key. By this definition, exclusive preference was observed in 30 of 36 cases in Phase 1 (based on 4 pigeons in nine conditions), although in one of these cases the exclusive preference was for the key with the lower probability of reinforcement (Pigeon P6 with a green reinforcement probability of .6). With the results separated by key location in Phase 2, exclusive preference was found in 27 of 36 cases when the green key was on the left, and in 30 of 36 cases when the green key was on the right, although in several of these cases the exclusive preference was for the key with the lower probability of reinforcement. In many of the cases that did not meet this definition of exclusive preference, there was still a strong preference for one alternative: Preference for one of the two alternatives was less than 90% in only 6 of the 108 cases shown in Figure 4.

Figure 4.

The percentage of choice responses for the green key (filled circles) and the percentage of forced-trial response latencies that were faster for the green key (open circles) are shown for each pigeon in Experiment 2. The data from the conditions with random side locations are divided into trials with the green key on the left (center column) and on the right (right column). See text for details about the calculation of the latency percentages.

A close examination of the center and right columns of Figure 4 shows that there were many conditions in which a pigeon’s choice percentages were close to 100% when the green key was on the left and near 0% when the green key was on the right, or vice versa. In other words, these were cases in which the pigeons responded with exclusive or near-exclusive preference for either the left key (Pigeons P5 and P7) or the right key (Pigeon P6). It is interesting to note that with the random key locations in Phase 2, all pigeons showed exclusive preference for the higher reinforcement probability when the two probabilities were most different (e.g., .1 versus .9, or .2 versus .8), but three of the pigeons switched to exclusive preference for either the left or right key when the two reinforcement probabilities became more similar (e.g., .4 versus .6).

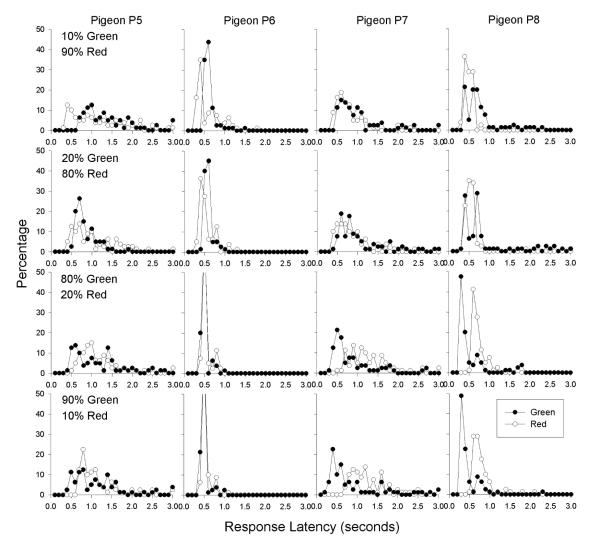
The open circles in Figure 4 show the percentages of trial blocks on which the green key had a faster latency on the forced trials, calculated in the same way as in Experiment 1. As can be seen, there was little correspondence between these percentages and the choice percentages, and in most conditions where exclusive preference was found, the percentages of faster latencies did not exclusively favor one alternative. Figure 5 shows frequency distributions of response latencies from the four conditions in Phase 1 with the most extreme differences in reinforcement probabilities (.1 versus .9, and .2 versus .8). As shown in Figure 4, the pigeons exhibited exclusive preference for the key with the higher reinforcement probability in 15 of these 16 cases. However, all of the panels in Figure 5 show substantial overlap in the latency distributions for the two keys. These latency data are therefore inconsistent with the predictions of the sequential choice model (Shapiro et al., 2008).

Figure 5.

For each pigeon in Experiment 2, frequency distributions of response latencies on the forced trials of the green key (filled circles) and the red key (open circles) are shown for four of the conditions in Phase 1.

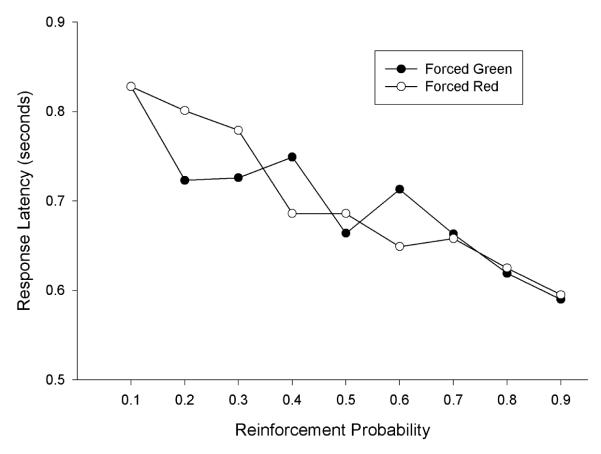
Harmonic means of the response latencies in the last two sessions of each condition were calculated for each pigeon. A three-way repeated-measures ANOVA (phase × reinforcement probability × key) conducted on the mean latencies from the forced trials found a significant main effect of reinforcement probability, F(8, 24) = 7.56, p < .001, but no other significant main effects or interactions (all Fs < 1.83). Figure 6 shows that for both the green and red keys, response latencies on forced trials decreased as their reinforcement probabilities increased.

Figure 6.

Averaged across all pigeons in both phases of Experiment 2, harmonic mean response latencies on forced trials for the green and red keys are plotted as a function of reinforcement probability.

Although the choices in this experiment involved reinforcers that varied in their probabilities rather than their delays, the conclusions about the different hypotheses discussed in the Introduction are similar to those for Experiment 1. As already explained, the overlapping distributions of response latencies on forced trials, compared to the exclusive preference that was often observed on choice trials, are inconsistent with the predictions of the sequential choice model. We cannot completely rule out the hypothesis that with more training, the pigeons might have eventually reached exclusive preference for the alternative with the higher probability of reinforcement in all conditions. However, this possibility seems quite unlikely, because each condition was conducted for a minimum of 25 sessions (unless exclusive preference for the key with the higher probability of reinforcement was reached sooner). The hypothesis that animals have a natural tendency to sample all options occasionally (based on the evolutionary advantage of this strategy) is difficult to reconcile with the fact that exclusive preference for the alternative with the higher probability of reinforcement was observed in some conditions but not others, even though every session included 50% forced trials, which gave the pigeons substantial exposure to both the red and green keys.

The two hypotheses that predict distributed preference when there is overlap between the two alternatives (either in their actual contingencies or in the animal’s memorial representation) must be rephrased slightly for this experiment, because reinforcement probabilities were varied rather than delays. Pecking both the red and green keys led to a high-value consequence (immediate food) on some trials and a low-value consequence on other trials (no food and a 10-s ITI). In that sense, there was overlap in the consequences for the two alternatives in every condition of the experiment (i.e., red-key trials with food had a higher value than green-key trials without food, and vice versa). The exclusive preference observed in many conditions of the experiment, especially in Phase 1, is inconsistent with the predictions of these two hypotheses that overlap in the reinforcement contingencies should result in distributed preference. The results are also inconsistent with the prediction of probability matching. The many examples of exclusive preference, whether for a particular key color or key location, are obviously incompatible with probability matching.

In summary, exclusive or near-exclusive preference was the predominant result in this experiment, although it took a few different forms. With the fixed key locations of Phase 1, exclusive preference for the key with the higher probability of reinforcement was observed in most cases, but there were a few instances of exclusive or near-exclusive preference for the key with the lower probability of reinforcement. With the random key locations of Phase 2, there was exclusive preference for the key color with the higher probability of reinforcement when the two probabilities were very different, but when the two probabilities were more similar, there were many cases of exclusive preference for the left or right key. These results suggest that when the locations of the key colors varied randomly from trial to trial, two factors (color and location) competed for the control of the pigeons’ choices. In a few cases, the result of this competition was distributed preference across both keys and locations. For instance, with a green reinforcement probability of .6, Pigeon P8 chose the green key on 94% of the trials when it was on the left and 62% when it was on the right. However, in the vast majority of cases, one of these two factors dominated choice in each condition, such that the pigeons showed exclusive preference for one key color in some conditions and exclusive preference for one key location in other conditions.

GENERAL DISCUSSION

The results of these two experiments appear to be quite clear in their rejection of the three hypotheses that predict that there will be distributed preference in discrete-trial choice situations whenever there is some type of overlap between the two alternatives. Whether this overlap is in the actual contingencies of reinforcement, in the animal’s supposed memorial representations of the two alternatives (Gibbon et al., 1988), or in response latencies (Shapiro et al., 2008), these hypotheses incorrectly predict distributed preference for many of the conditions of these experiments where exclusive preference was obtained instead. Similarly, the results are incompatible with hypotheses that predict that choice percentages will match the relative values or relative probabilities of the two alternatives (e.g., Couvillon & Bitterman, 1991^; Shapiro, 2000). In Experiment 1, both alternatives presumably had some positive reinforcement value because every trial ended with food (after some delay), yet exclusive preference was observed in most instances. In Experiment 2, both alternatives delivered food on some percentage of the trials, but exclusive preference was observed in many conditions, and there was no indication of probability matching.

In addition, the results do not seem to support the hypothesis that animals have a natural tendency to sample all the alternatives occasionally (Lea, 1979), because half of the trials in every session were forced trials that required the pigeons to sample both alternatives, but on choice trials exclusive preference occurred in some conditions and distributed preference occurred in others. Similarly, the results from previous experiments suggest that, contrary to what one might predict based on Lea’s hypothesis, the presence of forced trials does not always lead to exclusive preference on choice trials, nor does the absence of forced trials always lead to distributed preference. For instance, Young’s (1981) procedure included many forced trials for every choice trial, yet the pigeons showed distributed preference on the choice trials (see also Shapiro et al., 2008). Conversely, in some procedures that included no forced trials (e.g., Graf, et al., 1964^; Meyer, 1960), the animals exhibited exclusive preference for the better alternative (after a learning period in which both alternatives were chosen). Therefore, it seems that the inclusion of forced trials is neither a necessary nor a sufficient condition for exclusive preference to occur.

Based on the present experiments and on previous research, I propose the following hypothesis. In discrete-trial choice situations, pigeons will tend to exhibit exclusive preference for the better alternative, as long as the consequences for the two alternatives are distinctly different (and therefore presumably easy for the animal to discriminate). Exclusive preference will even occur when there is overlap in the reinforcement contingencies (such that on some random subset of the trials, the lesser alternative has the more favorable contingencies), as long as one alternative is, on average, better than the other. Note that in the present experiments, exclusive preference was indeed always found when the alternatives were the most different (e.g., delays of 4 s versus 8 s in Experiment 1, or probabilities of .1 versus .9 in Experiment 2). It can be argued that this is the optimal way to behave, and this hypothesis is by no means a new one. The idea that animals will show exclusive preference for the better alternative is what Bitterman and colleagues referred to as maximizing (e.g, Behrend & Bitterman, ^{1961, 1966}). Herrnstein and Vaughan’s (1980) principle of melioration also implies that behavior will be driven entirely to the better alternative in this type of choice situation, because the better alternative will continue to have higher value no matter how frequently it is chosen. More recently, Gallistel and Gibbon (2000) proposed that in some circumstances animals exhibit opting behavior (exclusive preference for the better alternative) rather than allocating behavior (distributed preference). They suggested that these are two distinctly different choice mechanisms, and that the context and the training conditions determine which mechanism an animal will employ.

Stated in a slightly different way, my hypothesis is that exclusive preference is an animal’s “default option” in discrete-trial choice situations. The obvious challenge for this hypothesis is to account for the many counterexamples in which exclusive preference for the better alternative is not observed. The present experiments and previous research identify several different factors that can lead to non-exclusive preference in discrete-trial choice.

One factor is the similarity of the consequences for the two alternatives. In all three phases of Experiment 1, exclusive preference was observed when the delays were most different, but there were some cases of distributed preference when the delays were more similar. Likewise, in both phases of Experiment 2, there was exclusive preference when the reinforcement probabilities were most different, but there were many examples of distributed preference when the probabilities were more similar. It should be emphasized, however, that in many of the cases where there was not exclusive preference for the shorter delay or the higher probability, there was instead exclusive preference of another type. In both experiments, there were a few cases in which pigeons exhibited exclusive or near-exclusive preference for the less favorable alternative—the key with the longer delay or the lower probability of reinforcement. These might have been due to key color or position bias, or perhaps simply to confusion about which was the better alternative. Furthermore, when key locations varied randomly from trial to trial in Experiment 2, there were many cases where the pigeons showed exclusive preference for either the left or the right key. These instances can be seen as further evidence that pigeons tend to exhibit exclusive preference in discrete-trial choice situations (though not always for what might seem to be the better alternative from the experimenter’s standpoint).

Another possible cause of non-exclusive preference is insufficient training. As already discussed, it seems implausible to argue that every instance of distributed preference in these experiments was the product of insufficient exposure to the choices in a particular condition. Nevertheless, there were several cases in both experiments where the pigeons required more than 12 sessions (in Experiment 1) or 25 sessions (in Experiment 2) to satisfy the stability criteria, but they eventually reached exclusive preference. If these conditions had been arbitrarily terminated after fewer sessions, the results would have provided apparent evidence for distributed preference.

Previous research has identified other factors that can lead to distributed preference by pigeons in discrete-trial situations. In an experiment by Graf et al. (1964), pigeons chose between two keys of different colors. On each trial, one of the two keys was scheduled to deliver a reinforcer, and the reinforcement probabilities for the two keys were 70% and 30%. In conditions with no correction procedure, each trial ended either with or without food (depending on whether the key with food assigned on that trial was chosen or not), and then a new random assignment of the reinforcer was arranged for the next trial. In these conditions, the pigeons showed near-exclusive preference for the key with the 70% reinforcement probability. However, other conditions used a correction procedure: If a pigeon chose the “incorrect” key (the key without food on that trial), the trial was repeated with the same reinforcer assignment until the pigeon chose the other key and obtained the reinforcer. In the correction procedure, the pigeons exhibited approximate probability matching, choosing the 70% key on about 70% of the trials (and these percentages excluded the choices made on correction trials).

An important feature of the correction procedure used by Graf et al. (1964) was that on some trials, the “correct” key was the key with the 30% reinforcement probability, and if a pigeon chose the other key, the trial was repeated until the pigeon chose the key with the lower, 30% reinforcement probability. Therefore, the correction procedure (1) included trials on which the pigeon was required to choose the key with the lower reinforcement probability if it was ever to receive another food delivery, and (2) the stimuli were the same on correction trials and non-correction trials—both keys were lit, both keys were active, and a choice of one key led either to food or no food. (This contrasts with the forced trials used in the present experiments, on which only one key was lit and active.) These studies therefore show that distributed preference may occur in discrete-trial choice situations if the procedure requires the animal to choose the lesser alternative on some trials, and if these trials (i.e., the correction trials) are difficult to discriminate from free-choice trials.

In conclusion, the results of these experiments suggest that in discrete-trial choice situations, pigeons will often display exclusive preference for the better of two alternatives (e.g., the alternative with the shorter mean delay or higher probability of reinforcement), even when there is overlap in the potential consequences for the two alternatives. In other cases, they may show exclusive preference for a particular response location, suggesting that a strong position bias overrides the differences in the reinforcer delays or probabilities. However, distributed preference may occur if the two alternatives have similar consequences ( e.g., similar delays or probabilities) and are presumably difficult to discriminate, or if the procedure, in effect, requires the occasional choice of the lesser alternative, as in a correction procedure (Graf et al., 1964). Based on the examples of exclusive preference found in previous studies with primates and rats (Bitterman et al., 1958; Meyer, 1960), these principles of discrete-trial choice may apply to a wide range of species.