Type I Interferon Receptor is a Primary Regulator of Target-Mediated Drug Disposition of Interferon-β in Mice

Abstract

The purpose of this study is to evaluate the primary mechanism through which interferon (IFN)-β exhibits target-mediated drug disposition (TMDD) and whether the theoretical assumptions of TMDD models are consistent with experimental pharmacokinetic (PK) data. Recombinant murine IFN-β was administered as an intravenous injection at two dose levels (0.5 and 1 million IU/kg) to male wild-type (WT) and type-I IFN-α/β receptor subunit (IFNAR-1) knockout (KO) mice (A129S7/SvEvBrd strain). Sampling was conducted at various times (n = 3/time point), and plasma was analyzed for IFN-β concentrations using a validated enzyme-linked immunosorbent assay. The pharmacodynamic (PD) biomarker was IP-10 mRNA that was isolated from the distal femur bone and quantified using reverse transcription-polymerase chain reaction. An integrated model that includes rapid-binding TMDD and an indirect mechanism of drug action was used to characterize the PK/PD profiles. For an experimental control, PK profiles of recombinant murine erythropoietin (muEPO), another drug that exhibits TMDD, were determined after a single intravenous dose (0.5 μg/kg) in WT and KO animals. The concentration-time profiles for IFN-β differed substantially at initial times for the WT and KO mice at the same dose levels. These differences are characteristic of ligands exhibiting receptor-mediated disposition and were well described by a rapid-binding TMDD model. No differences in muEPO PK were observed in the control study. In summary, the intact IFNAR receptor is a primary regulator of in vivo IFN-β exposure. An integrated PK/PD model was successfully used to assess the receptor-mediated disposition and dynamics of IFN-β.

Interferon (IFN)-β is an endogenous protein currently indicated for multiple sclerosis and is known for its anti-inflammatory, antiproliferative, and immunomodulatory properties (Pestka et al., 1987). Recombinant IFN-β binds with high affinity to the type-I IFN-α/β receptor (IFNAR), and the IFN-β/IFNAR complex may undergo rapid internalization into the cell cytoplasm (Kushnaryov et al., 1985). Pharmacokinetic (PK) studies of IFN-β have shown that its concentration-time profiles are biexponential (Chiang et al., 1993; Salmon et al., 1996). The volume of distribution of IFN-β is relatively low, reflecting plasma or blood space with negligible distribution to tissues, as is expected for large molecules (molecular mass, 19,000 Da). Overall, the concentration-time profiles of IFN-β in dose-ranging studies are predominantly nonlinear in monkeys (Mager et al., 2003) and humans (Buchwalder et al., 2000).

The PK of most protein molecules is generally characterized by rapid clearance from the systemic circulation. Clearance of proteins is governed by processes such as site-specific catabolism, liver metabolism, renal clearance, receptor-mediated endocytosis, or a combination (Sugiyama and Hanano, 1989). Many therapeutic proteins bind with high affinity to their target receptors such that this interaction significantly influences the apparent PK of the molecule; so-called target-mediated drug disposition (TMDD) (Levy, 1994). Drugs exhibiting this phenomenon typically have a decreasing steady-state volume of distribution (V_ss) with increasing dose levels. Proteins and peptides that undergo significant internalization upon binding to its receptor may also exhibit a dose-dependent decrease in clearance (CL). The phenomenon of TMDD is increasingly recognized as a major determinant of in vivo PK profiles of macromolecules, including monoclonal antibodies (Mahmood and Green, 2005; Wang et al., 2008).

Model-based approaches are being used to support the development of macromolecules and to understand the influence of complex nonlinear pharmacological properties (Agoram et al., 2007). A generalized compartmental modeling framework has been proposed to facilitate characterization of drugs exhibiting TMDD (Mager and Jusko, 2001). Mechanism-based TMDD models were developed to describe IFN-β PK in monkeys (Mager et al., 2003) and humans (Mager and Jusko, 2002). In addition to explaining the dose-dependent V_ss and CL of IFN-β, these models predict that receptor-mediated elimination might be a major component of the rapid clearance of this drug. Although model-based analyses suggest that IFN-β exhibits TMDD, experimental data that confirm model assumptions have yet to be reported.

The availability of the IFNAR-1 receptor gene-knockout mouse provides a means for testing the hypothesis that receptor binding influences IFN-β disposition. These mice have been used to assess the role of IFNAR-1 in mediating type-I interferon signaling (Müller et al., 1994; Decker et al., 2005). The purpose of this study is to determine whether IFNAR-1 binding is involved in target-mediated elimination of IFN-β and whether this process significantly contributes to its nonlinear PK properties. We also assess whether the underlying assumptions of a rapid-binding approximation of the general TMDD model (Mager and Krzyzanski, 2005) can be applied to IFN-β. Murine IFN-β was used for this study as human IFN-β has little or no activity in the mouse, which is probably due to the lack of significant binding to the murine IFNAR receptor (Mogensen et al., 1999). In terms of pharmacodynamics, endogenous IFN-β seems to play a role in the regulation of bone homeostasis in addition to its well known immunomodulatory effects (Takayanagi et al., 2002; Abraham et al., 2009). Thus, a secondary goal is to evaluate the time course of IFN-β-induced IP-10 mRNA expression as a biomarker in bone tissue.

Materials and Methods

Animals.

The background strain for this study was the A129SvEvBrd mouse (B&K Universal Ltd., Grimston, Aldbrough, Hull, UK). The WT strain expresses the IFNAR, whereas KO mice lack expression of the IFNAR-1 subunit. Mice were 5 to 6 weeks old and weighed approximately 20 to 25 g. This study was conducted in accordance with an approved protocol by the Institutional Animal Use and Care Committee (University at Buffalo, State University of New York, Amherst, NY).

IFN-β PK/PD.

The PK/PD study was conducted in WT and KO mice. Each strain was anesthetized using 1 to 2% isoflurane inhalation before drug administration. Mice were given a single intravenous bolus injection (penile vein) of 0.5 or 1 million international units (MIU)/kg recombinant mouse IFN-β (PBL InterferonSource, Piscataway, NJ), a nonglycosylated protein derived from Escherichia coli. After dosing, terminal blood samples from the inferior vena cava were collected using heparinized syringes (25-gauge needle) at predosing and 0.166, 0.25, 0.5, 0.75, 1, 1.16, 1.66, 2, 4, 6, and 24 h (n = 3/time point). Collected blood was centrifuged at 3000 rpm for 20 min at 4°C, and supernatant plasma was withdrawn. Plasma samples were stored at −80°C until assay analysis. Distal femur bones were also isolated at the above-mentioned sampling times, which were flash-frozen in liquid nitrogen and stored at −80°C until further processing for IP-10 mRNA.

Murine IFN-β ELISA.

Plasma concentrations of murine IFN-β were measured using a commercially available ELISA kit (PBL InterferonSource) that was validated for mouse plasma. All procedures were followed as per the kit instructions. The lower limit of quantification in mouse plasma was 40 pg/ml. Samples at early time points (≤1 h) were diluted in pooled mouse plasma to ensure a consistent matrix between diluted and undiluted samples for assay purposes.

Mouse Erythropoietin PK.

As a negative control, both WT and KO mice were given an intravenous bolus injection of 0.5 μg/kg recombinant murine erythropoietin (muEPO) (R&D Systems, Minneapolis, MN). Blood was collected and plasma concentrations of muEPO were measured at predose and 0, 0.25, 0.5, 1, 2, 4, and 8 h using an ELISA system (R&D Systems).

RNA Extraction.

Frozen distal femur bones were ground in a chilled mortar and pestle. Adequate precautions were taken to ensure that grinding of samples was carried out in liquid nitrogen to prevent RNA degradation. Further extraction of total RNA was conducted according to the SV Total RNA Isolation System (Promega, Madison, WI). Approximately 100 mg of the ground sample was added to 1 ml of RNA lysis buffer containing guanidine isothiocyanate and β-mercaptoethanol. The spin protocol was then implemented for RNA isolation, which also included an intermediate DNase incubation step. For the final step, isolated and purified total RNA was resuspended in 100 μl of nuclease-free water. Concentrations of total RNA were quantified using a Nanodrop UV-Vis spectrophotometer (Thermo Fisher Scientific, Wilmington, DE), and purity was assessed using the A₂₆₀/A₂₈₀ and A₂₆₀/A₂₃₀ ratios. Extracted total RNA solutions were stored at −80°C.

Quantitative Real-Time Reverse Transcription-Polymerase Chain Reaction.

The quantity of IP-10 mRNA was determined using a two-step RT-PCR. First, equal concentrations of total RNA in each sample were reverse-transcribed to its complementary cDNA using the AffinityScript qPCR cDNA Synthesis kit (Stratagene, La Jolla, CA). No-reverse transcriptase controls were included to detect genomic DNA contamination in the RNA samples. The second step was carried out as per instructions of the RT² qPCR Primer Assay (Superarray Bioscience Corporation, Frederick, MD), with primers optimized to amplify the gene of interest (IP-10) and three housekeeping genes (GAPDH, cyclophilin, and β-actin). These primer assays are designed for use with the SYBR Green method and the RT² SYBR Green qPCR Master Mix (Superarray Bioscience Corporation) was used to prepare the reaction mixtures (final volume, 25 μl). An NAC was included to assess contamination of the reagents used in the RT-PCR reaction mixture.

PK/PD Model.

A preliminary analysis of mean IFN-β concentration-time data obtained from WT and KO mice at each dose level was conducted using noncompartmental methods (WinNonlin Professional version 5.0.1; Pharsight, Mountain View, CA) to detect possible differences in PK between WT and KO animals.

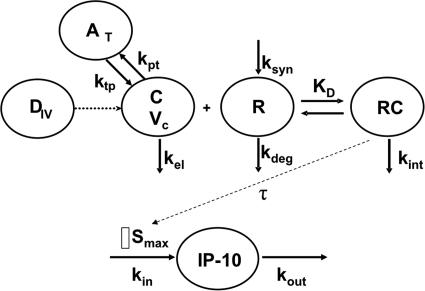
An integrated PK/PD model, consistent with IFN-β pharmacology, was proposed to characterize the data, and the schematic is shown in Fig. 1. Plasma concentration-time profiles of IFN-β were characterized by fitting a rapid-binding TMDD model (Mager and Krzyzanski, 2005) using a naive-pooled approach. In this model, free concentrations of IFN-β in plasma (C) bind to free IFNAR (R_tot) to form the IFNAR/IFN-β complex (RC). The binding process is governed by the equilibrium dissociation constant, K_D. The IFNAR/IFN-β complex may be internalized, and this internalization is governed by a first-order rate constant, k_int. The free receptor turnover is modeled as a first-order degradation rate constant, k_deg, and a zero-order production rate constant, k_syn. The system of differential equations that describe the PK model is as follows:

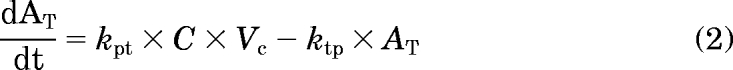where C_tot = C + RC and R_tot = R + RC. The free receptor synthesis rate was calculated from the baseline equation k_syn = k_deg · R_tot,0, where R_tot,0 is the initial concentration of total receptor. The drug concentration in the central compartment is defined by the solution to the following quadratic equation:

Fig. 1.

Mechanism-based pharmacokinetic/pharmacodynamic model for IFN-β disposition and activity. Definitions of abbreviations and model equations are listed under PK/PD Model under Materials and Methods.

Assuming no endogenous IFN-β production (concentrations were below the limit of quantification before dosing), the initial conditions for the above system are defined as follows:

In WT animals, the transient increase in IP-10 mRNA levels from baseline was characterized using an indirect response model for stimulation of biomarker production (Dayneka et al., 1993). The turnover of IP-10 mRNA is governed by a zero-order production rate constant (k_in) and a first-order degradation rate constant (k_out):

The stimulation function is the Hill equation that includes parameters for the maximal stimulation capacity (S_max), effective signal resulting in half-S_max (S₅₀), and the Hill coefficient (γ). A transit compartment, M₁, which accounts for the delay in the PD signal, drives the Hill function. The IP-10 mRNA level was reported as a value normalized to the baseline expression in predosing animals. Assuming steady-state conditions at t = 0, the normalized baseline expression of IP-10 is as follows:

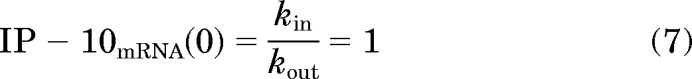To account for the observed time delay in the PD response, the IFNAR receptor occupancy (ρ) was used to drive the stimulation of IP-10 mRNA through a single M₁ that is delayed by a mean transit time, τ. The equations that describe receptor occupancy and the transit compartment are as follows:

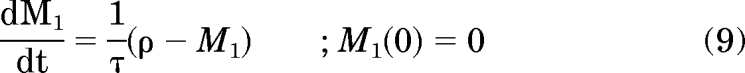Data Analysis.

For the RT-PCR data, the most stable set of housekeeping genes were determined using the GeNorm software (Vandesompele et al., 2002). The ΔΔCt method was used to quantify the fold change in gene expression relative to the housekeeping genes (Pfaffl, 2001).

Model parameters were estimated using nonlinear regression analysis with ADAPT II (D'Argenio and Schumitzky, 1997). The maximum likelihood estimation method in ADAPT II was applied. The variance model was defined as follows:

where σ₁ and σ₂ are the variance model parameters, and Y(θ, t_i) is the ith predicted value from the PK/PD model. Distinct variance models were used for state variables describing PK (IFN-β concentrations) and PD (normalized IP-10 mRNA). Model selection was guided by goodness-of-fit criteria, which included model convergence, Akaike Information Criterion, estimation criterion value for the maximum likelihood method, and visual inspection of fitted profiles and residual plots.

Results

Pharmacokinetics.

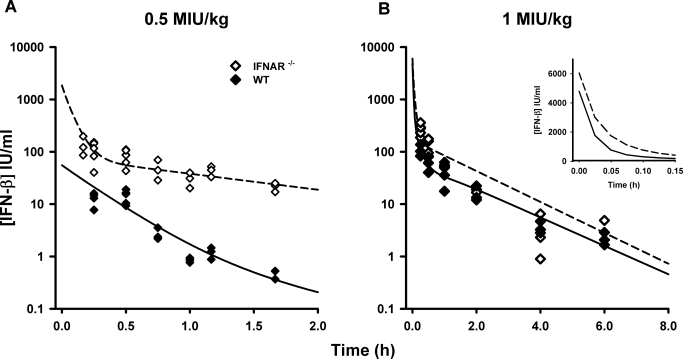
The time course of naive-pooled IFN-β concentrations after intravenous dosing in WT and KO mice is shown in Fig. 2. The concentration-time profiles for the 1 MIU/kg dose exhibit a rapid distribution phase followed by a shallower terminal phase. Although not well characterized for the 0.5 MIU/kg dose, the rapid drop in concentrations is suggestive of a rapid distribution phase. Clear differences are observed between WT and KO animals at early time points for the same dose levels, with KO mice exhibiting greater drug concentrations. Global PK parameters from a noncompartmental analysis of mean data are listed in Table 1. For WT mice, the terminal elimination slope (λ_z) is steeper for the 0.5 MIU/kg dose (1.29 h⁻¹) compared with the 1.0 MIU/kg dose (0.317 h⁻¹). In contrast, λ_z values for the KO mice appear to be dose-independent. Net drug exposure [area under the concentration-time curve extrapolated to infinity (AUC_0-∞)] is dose-proportional in KO mice. However, the AUC_0-∞ increased greater than dose-proportionally in WT mice, suggesting greater systemic clearance of IFN-β at lower dose levels. In addition, the AUC_0-∞ for WT mice is less than that in KO mice at the same dose levels.

Fig. 2.

Concentration-time profiles for murine IFN-β administered intravenously in WT and IFNAR-1 KO mice. Symbols are concentrations from individual mice, and the lines are model-fitted profiles for the 0.5 (A) and 1 MIU/kg (B) doses. Inset panel shows model-predictions for the 1 MIU/kg dose at early time points.

TABLE 1.

Noncompartmental parameter estimates for muIFN-β mean concentration-time profiles in mice

Animal Strain (Dose)	λz	Cmaxa	AUC0-∞	Vss
	h−1	IU/ml	h · IU/ml	ml/kg
WT (0.5 MIU/kg)	1.29	13.5	9.51	25,399
KO (0.5 MIU/kg)	0.930	135	134	3379
WT (1 MIU/kg)	0.317	107	142	10,036
KO (1 MIU/kg)	0.796	269	270	3154

^aMaximal concentration for IFN-β.

The proposed TMDD model (Fig. 1) well captured the concentration-time profiles of IFN-β, and the model fitted profiles are shown in Fig. 2. The parameter estimates for the final model are reported in Table 2. The precision (%S.E.M.) of the parameter estimates is within acceptable limits. The estimate for V_c (46.5 ml/kg) is similar to the reported physiological plasma volume (50 ml/kg) for the mouse (Davies and Morris, 1993). The linear clearance from the central compartment, CL_L = k_el · V_c is 0.457 ml/min for a 20-g mouse. The rapid-binding TMDD model predicts that the initial concentrations (C₀) for the same dose level are different between WT and KO mice. The estimate for K_D in WT mice was 0.0950 nM, whereas it was estimated to be greater in KO mice (4.20 nM). Initial model runs estimated the turnover parameter of IFNAR (k_deg) to be extremely low value, and assuming a constant receptor pool, k_deg was fixed to a null value for the final model run.

TABLE 2.

PK/PD model estimated parameters for IFN-β and IP-10 mRNA

Parameter (Units)	Definition	Estimate	%S.E.M.
Pharmacokinetic model parameter (rapid binding TMDD model)
kel (h−1)	First-order elimination rate constant	29.5	24.2
kpt (h−1)	First-order distribution rate constant from plasma to peripheral sites	40.5	32.5
ktp (h−1)	First-order distribution rate constant from peripheral sites to plasma	1.36	19.7
Vc (ml/kg)	Volume of the central plasma compartment	46.5	14.8
KD_WT (nmol/l)	Equilibrium dissociation constant in WT mice	0.0950	39.4
KD_KO (nmol/l)	Equilibrium dissociation constant in KO mice	4.20	47.4
Rtot,0 (nmol/l)	Total initial IFNAR receptor concentration	29.9	—a
kint (h−1)	First-order rate constant for internalization of IFNAR/IFN-β complex	3.39	11.9
Pharmacodynamic model parameter
kout (h−1)	First-order rate constant of IP-10 mRNA loss	0.202	14.7
Smax	Maximal stimulation capacity constant	115	19.9
S50	Effective signal producing 50% of Smax	0.183	37.5
τ (h)	Mean signal transit time	0.317	45.4
γ (units)	Hill coefficient	5	—a

^a—, fixed value.

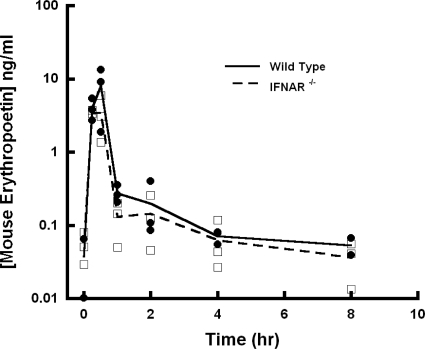
The pharmacokinetics of muEPO in the control study are shown in Fig. 3. For a single intravenous dose of 0.5 μg/kg, WT and KO animals exhibited similar concentration-time profiles.

Fig. 3.

Concentration-time profiles for murine erythropoietin administered intravenously in WT and IFNAR-1 KO mice. Lines are shown that connect mean concentrations at each sampling time point.

Pharmacodynamics.

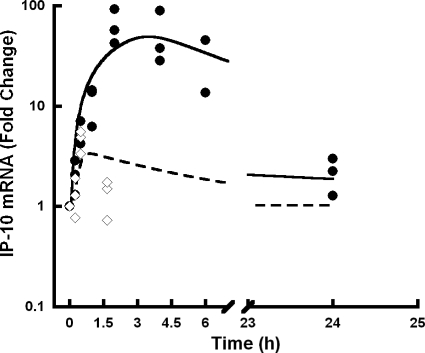
No contaminating DNA was detected using the no-reverse transcriptase and no-amplification controls in the RT-PCR assay. The time course of change from baseline for IP-10 mRNA levels in WT mice is shown in Fig. 4. IP-10 mRNA levels were transiently increased in response to IFN-β administration. Consistent with the indirect mechanism of IFN-β signal transduction (Salmon et al., 1996), there is a slight onset delay in the stimulation of IP-10 mRNA.

Fig. 4.

Normalized expression levels of IP-10 mRNA in WT mice treated with IFN-β relative to control. The lines are the PK/PD model-fitted profiles, and symbols (◊, 0.5 MIU/kg; ●, 1 MIU/kg) are fold change in IP-10 mRNA expression in individual mice.

The model-fitted profiles (Fig. 4) reasonably describe the transient increase in IP-10 mRNA, but with a slight overprediction at 1.5 h for the 0.5 MIU/kg dose. The τ value for signal transduction was estimated to be 0.317 h. The delay in the peak response was dose-dependent, and a single transit compartment was sufficient to fit the model to the data. The peak response of IP-10 mRNA for the highest dose is approximately 2 to 4 h. No increase of IP-10 mRNA was observed in KO mice (data not shown). The Hill coefficient could not be estimated with good precision. However, a fixed value of 5 (as opposed to 1), indicating a steep signal effect gradient, improved model-fitting criteria.

Discussion

The ability to test competing hypotheses is a particularly useful feature of mechanism-based modeling. In the course of developing a model for the exposure-response relationship for IFN-β, it was determined that both nonlinear distribution and elimination processes were operable. Ultimately, a model premised on TMDD theory was derived that successfully captured the time course of drug concentrations and receptor-mediated induction of a specific circulating biomarker (neopterin) in a manner consistent with IFN-β pharmacology (Mager et al., 2003). Following on the principles of TMDD, receptor-binding and endocytosis were sufficient for characterizing the nonlinear disposition and dynamic properties of IFN-β in a parsimonious manner. However, experimental data confirming this hypothesis have not been available and thus is the focus of the present study.

If IFN-β is governed by TMDD, then the lack of an intact IFNAR receptor in KO mice should result in impaired binding of IFN-β, greater initial concentrations, and a reduced total systemic clearance. All of these predictions were observed for muIFN-β in mice, and differences were more pronounced at the 0.5 MIU/kg dose compared with the 1 MIU/kg dose. This was also expected for cases in which initial ligand concentrations are below that of the total receptor. At low concentrations relative to R_tot, a significant proportion of the ligand is rapidly bound to the target, and plasma concentrations of the free ligand decrease rapidly.

A dose-dependent decrease in the apparent volume of distribution from an area/moment analysis is common for TMDD systems (Mager and Jusko, 2001). In addition, drug/receptor complex catabolism can manifest as saturable drug elimination (total clearance decreasing with increasing dose). Although noncompartmental analysis is not valid for nonlinear systems, it is a relatively simple tool that can provide initial insight into system properties. The noncompartmental analysis of IFN-β in WT mice (Table 1) revealed such classical signatures of receptor-mediated disposition. In contrast, the PK of IFN-β in KO mice is dose-independent (Table 1).

The possibility exists that unknown physiological changes might occur in IFNAR KO mice that could affect IFN-β PK. To address this concern, the PK of muEPO was evaluated as a negative control, given that EPO also undergoes receptor-mediated disposition. Busulfan-induced bone marrow ablation in sheep was reported to significantly decrease the clearance of EPO (down 20% of initial values), suggesting that the bone marrow (a major site of erythroid receptors) represents a significant site of drug elimination (Chapel et al., 2001). The magnitude of the decrease in systemic clearance mirrors the extent to which bone marrow ablation decreases the EPO receptor pool (Veng-Pedersen et al., 2004). In our control study, the concentration-time profiles of muEPO were not substantially different between WT and KO mice (Fig. 3), suggesting that the differences in IFN-β PK in WT and KO mice can be directly attributed to the knockout of the IFNAR-1 subunit.

A rapid-binding approximation of the general TMDD model (Mager and Krzyzanski, 2005) was used to formally characterize muIFN-β PK data (Fig. 1). Although nonlinear mixed effects modeling approaches can provide insight into interanimal variability and parameter uncertainty, the necessary destructive sampling scheme limited the analysis to pooled data. The data from both mouse strains were modeled simultaneously, and the final model reasonably captured IFN-β disposition. From the model, the slope (λ_z) of the terminal phase can be calculated as follows (Abraham et al., 2007):

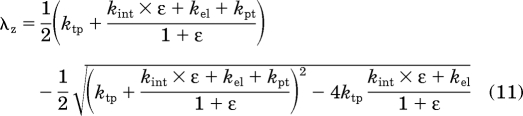where ε = R_tot,0/K_D. Based on eq. 11, the calculated terminal slopes in WT and KO mice are 1.28 and 0.735 h⁻¹. These model-calculated values are similar to the slopes obtained from the noncompartmental analysis (Table 1), with the exception of the 1 MIU/kg dose in WT mice. One hypothesis to explain the discrepancy is that the true terminal phase for this dose level might not be observed, owing to the lower limit of quantification of the ELISA assay. The model estimate for the central compartment (V_c = 46.5 ml/kg) is similar to physiological plasma volume in mice (Davies and Morris, 1993). This lends a physiological basis to the central compartment of the model, and a significant amount of IFN-β is probably confined to this space. A peripheral compartment was required to adequately describe the PK profiles. IFN-β binds to a soluble IFNAR-2a subunit in plasma (de Weerd et al., 2007). Specific binding to soluble IFNAR-2a, along with nonspecific binding and residual partitioning to tissues, might constitute the peripheral compartment. However, additional experiments are required to test this hypothesis.

Initially, R_tot was assumed to be zero for KO mice, and the model well described the PK profiles (data not shown). However, Cohen et al. (1995) showed that IFN-α₂ was able to bind to the IFNAR-2a subunit when expressed alone in NIH 3T3 cells. Human IFN-β also binds to immobilized human IFNAR-2 (Jaks et al., 2007). Hence, it was assumed that IFN-β binds to the IFNAR-2 subunit in KO mice, and the final model included such binding, albeit at a different affinity. The estimate of K_{D_WT} (0.0950 nM) is similar to literature reported values in L₉₂₉ murine fibroblast cells, which range between 0.98 and 0.14 nM (Kushnaryov et al., 1985). The estimated binding affinity of muIFN-β to the IFNAR-2 subunit alone was approximately 50-fold smaller (4.20 nM). Assuming qualitative similarities in binding, this is consistent with experimental evaluations of IFN-α₂ that suggest lower binding affinities to the IFNAR-2c subunit compared with the intact IFNAR receptor (Cohen et al., 1995). IFNAR-2c knockout mice could be used to further evaluate this assumption in future studies.

A classic PD biomarker for IFN-β activity in primates is serum neopterin, which has been incorporated into mechanistic PK/PD models (Mager and Jusko, 2002). However, neopterin is not detected in rodents (Fukushima and Nixon, 1980; Schoedon et al., 1987). The monitoring of PD biomarkers such as neopterin or IP-10 mRNA to assess the activity of IFN-β is important to establish the exposure-response relationship. Administration of IFN-β resulted in a transient stimulation of IP-10 mRNA levels in distal femur bone. Plasma concentrations of IP-10 have been used in mice as a biomarker to monitor IFN-β activity (Petry et al., 2006). Maximal concentrations of IP-10 were achieved approximately 2 h after intravenous dosing of murine IFN-β, with a decrease to nondetectable levels after 12 to 24 h. The messenger levels of IP-10 mimic the temporal aspects of plasma IP-10 concentrations (Fig. 4). Relative expression levels of IP-10 mRNA were well described by a modified indirect response model: stimulation of biomarker production. The IFNAR heterodimer is required for IFN-β signaling, and the ligand/receptor complex was used to generate the stimulatory signal for mRNA induction. A single transit compartment was included to accommodate the slight delay in the onset of response. The structure of the proposed model is consistent with previous models of IFN-β activity in monkeys (Mager et al., 2003) and humans (Mager and Jusko, 2002).

In conclusion, the IFNAR receptor has been shown to have a major role in regulating the PK of IFN-β and is implicated in the nonlinear PK of the drug. A rapid-binding approximation to the general TMDD model successfully captured the PK data in WT and KO mice, implying that the assumptions of this model are reasonable for IFN-β. This study experimentally confirms theoretical model predictions of the nature of IFN-β drug disposition and dynamics.