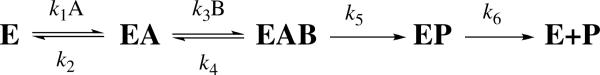Thymidylate Synthase Catalyzed H-transfers: Two Chapters in One Tale

Abstract

Examination of the nature of different bond-activations along the same catalytic path is of general interest in chemistry and biology. In this report we compare the physical nature of two sequential H-transfers in the same enzymatic reaction. Thymidylate synthase (TSase) catalyzes a complex reaction that involves many chemical transformations including two different C-H bond cleavages – a rate-limiting C-H-C hydride transfer and a non-rate-limiting C-H-O proton transfer. Although the large kinetic complexity imposes difficulties in studying the proton transfer catalyzed by TSase, we are able to experimentally extract the intrinsic KIEs on both steps. In contrast with the hydride transfer, the intrinsic KIEs of the proton transfer are temperature-dependent. The results are interpreted within the framework of the Marcus-like model. This interpretation suggests that TSase optimizes the donor-acceptor geometries for the slower and overall rate-limiting hydride transfer, but not for the faster proton transfer.

Introduction

While the last century brought us to a closer understanding of enzyme catalysis, the traditional “lock-and-key” model has been gradually replaced by the views of a more flexible active site. The dynamic nature of enzyme function can be viewed as extended “induced fit”, which includes not only the conformational changes upon substrates binding, but also those along the reaction coordinate. This is addressed today as shifts between different populations of protein conformations that are induced by the change in characteristics of the ligands from the reactant to the product states.^1–5 It is now widely accepted that protein dynamics not only plays an essential role in substrate binding and product release, but is also substantial in promoting the chemical transformations catalyzed by the enzyme.^1–14 Although immense experimental and theoretical effort has been devoted to this field, the relationship between enzyme dynamics and catalysis still remains to be an unsolved question. Important insights to this question come from the recent studies on H-transfers in various enzymatic systems, using temperature dependence of the kinetic isotope effect (KIE).^{11,12,14–19}

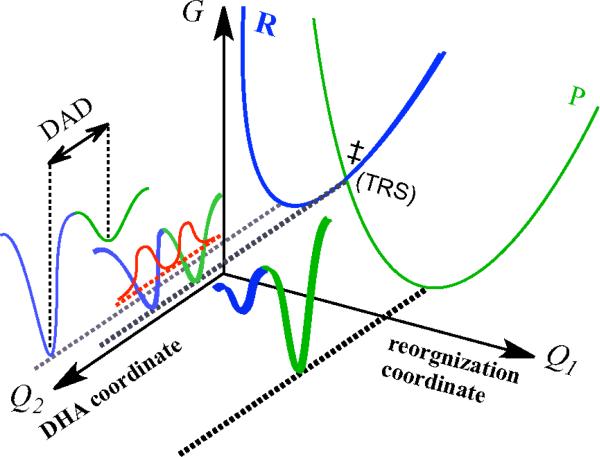
The Marcus-like Model (also addressed as environmentally-coupled tunneling, rate-promoting vibrations, vibrationally-enhanced tunneling, etc).^{11,12,14,16,17,20,21} is often used to correlate the KIE data with protein dynamics for enzyme catalyzed H-transfer reactions. In this model, hydrogen is transferred exclusively by quantum mechanical tunneling^{10,11,14,16,22,23} and the reaction coordinate comprises two designated coordinates (Figure 1). The environmental reorganization coordinate (Q₁) is analogous to the nuclear reorganization coordinate in the Marcus theory (for electron transfer²⁴), while the DHA coordinate (Q₂) represents the dimension along which H-tunneling occurs (where D and A are the donor and the acceptor of H, respectively²⁵). The different forms of Marcus-like model can be summarized by the following equation:

$$k=C\left(\mathrm{T}\right)e^{-{(\Delta G^0+\lambda )}^2∕\left(4\lambda \mathrm{RT}\right)}{\int }_{r_{\min }}^{r_{\max }}{e}^{F(m,r)}{e}^{-E_{F(m,r)}∕k_B\mathrm{T}}dr$$ (1)

where C(T) is the fraction of the reactive enzymatic complexes for the H-transfer step, sometimes addressed as “pre-orgnization”.²⁶ The first exponential corresponds to the environmental reorganization on Q₁, which overcomes the barrier that is determined by the reaction driving force (ΔG⁰) and the reorganization energy (λ) to approach the tunneling ready state (TRS). The TRS is the ensemble of states along the Q₁ coordinate, where H tunnels between the donor and acceptor (the crossing point in Figure 1).²⁷ When the system is at TRS, H tunnels through the DHA barrier on Q₂, as represented by the integral term in Eq.1. In the integral, e^F(m,r) represents the hydrogen wave-function overlap between the reactant and the product states of a double-well potential (i.e., a Franck-Condon term, see Figure 1), which determines the tunneling efficiency at a specific donor acceptor distance (DAD, denoted as r in Eq. 1). The DAD fluctuations that are commonly assumed to be at thermal equilibrium (i.e., Boltzmann distribution, e^{−E_F(m,r) / k_BT}) determine the probability distribution of TRS (r_min<r<r_max). These DAD fluctuations are also addressed as “gating”¹² or “rate-promoting vibrations”^14,17. It is noteworthy that, in Eq. 1, the integral is largely dependent on the mass of the transferring particle, and therefore is the dominant factor for KIEs and their temperature dependence. If the enzyme has evolved to optimize the active site for H-transfer, the TRS is believed to be well defined (i.e. a narrow DAD distribution). In such case, thermal activation of the DAD fluctuations will have minimal effect on the difference in activation energies of the two isotopes, resulting in temperature-independent KIEs. A recent study on formate dehydrogenase with both KIE and time-resolved photon-echo experiments corroborates this suggestion.^28,29

Figure 1.

An illustration of the Marcus-like model (see text). The blue and green curves correspond to the reactant and product states, respectively. The red curve represents the hydrogen wave-function overlap at tunneling ready state (TRS, see text).

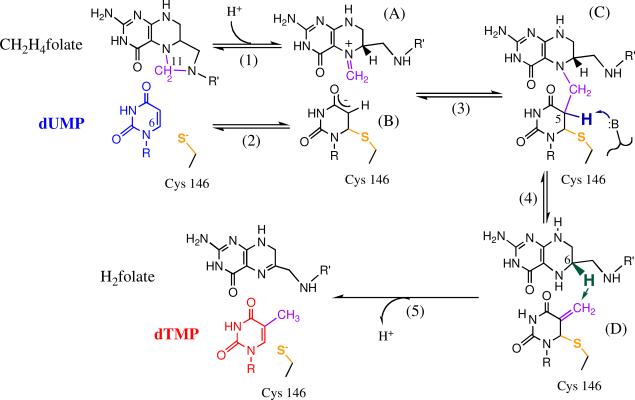
In this work we study thymidylate synthase (TSase, EC 2.1.1.45), which catalyzes the reductive methylation of 2'-deoxyuridine-5'-monophosphate (dUMP) to form 2'-deoxythymidine-5'-monophosphate (dTMP, one of the four DNA bases) using N⁵,N¹⁰-methylene-5,6,7,8-tetrahydrofolate (CH₂H₄folate) as both the methylene and hydride donor (Scheme 1).³⁰ Since TSase is essential for the de novo synthesis of DNA in nearly all organisms including humans, it is a common target for many antibiotic and chemotherapeutic drugs (e.g. Tomudex and 5-fluorouracil). In addition to its important biological functions, the emerging large collection of structural and kinetic data of TSase has suggested an intriguing relationship between catalysis and dynamics,³¹ which has initiated in-depth examinations of the mechanism from both experimentalists and theoreticians.^32–37 The mechanism of TSase comprises a series of bond cleavages and formations including two different C-H bond activations (Scheme 1): a non-rate-limiting proton transfer (step 4) and a rate-limiting hydride transfer^32,38 (step 5). This provides an excellent model system to examine the physical nature of different C-H bond activations in one enzymatic reaction. Sequential H-transfers have been previously studied with two enzymes using noncompetitive KIE experiments. In the case of morphinone reductase (MR), the flavin cofactor on the enzyme permits convenient spectrophotometric measurements of the reaction rates of both the reductive half reaction (a C-H-N hydride transfer) and the oxidative half reaction (concerted N-H-C hydride and O-H-C proton transfers).³⁹ These studies of MR indicated that the first hydride transfer has temperature-dependent KIEs and the second hydride transfer has temperature-independent KIEs. In the case of the light-activated enzyme protochlorophyllide oxidoreductase (POR), the electronically excited-state C-H-C hydride transfer is followed by a ground-state O-H-C proton transfer, and both steps showed temperature-dependent isotope effects at physiological temperatures.⁴⁰

Scheme 1.

Proposed chemical mechanisms of TSase-catalyzed reaction (revised from Ref. 30). R=2'-deoxyribose-5'-phosphate; R'=(p-aminobenzoyl)glutamate.

We have performed the competitive KIE experiments on both the proton and hydride transfers catalyzed by TSase, using specifically labeled C-H bonds of the substrates for that enzymatic reaction. We found that the proton transfer has temperature-dependent KIEs while the hydride transfer has temperature-independent KIEs. The results are discussed below within the framework of Marcus-like Model.

Results and Discussions

The examination on the sequential proton and hydride transfers in the TSase-catalyzed reaction requires different methods to expose the intrinsic KIEs. We have been able to access the temperature dependence of the intrinsic KIEs on both H-transfers, which allows us to compare the nature of these different C-H bond activations.

Intrinsic KIEs on the Non-rate-limiting Proton Transfer

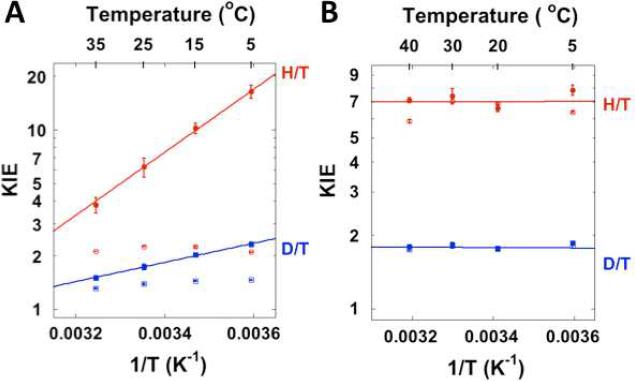
One of the main challenges in enzyme studies is to expose and examine a chemical step that is not rate limiting within the complex catalytic cascade. While the hydride transfer is rate-limiting for both the first and second order rate constants (k_cat and k_cat/K_M, respectively) for dUMP,³² the proton transfer is a reversible non-rate-limiting step and is more difficult to study. A previous study monitored the release of [³H]H₂O and production of [¹⁴C]dTMP using [2-¹⁴C, 5-³H]dUMP as the substrate with a saturating concentration of CH₂H₄folate, which reported a KIE of unity (i.e. no isotope effect) on the proton transfer.⁴¹ We have suggested that the observed KIEs for the fast proton transfer are dependent on the concentration of CH₂H₄folate, due to the sequential binding of dUMP and CH₂H₄folate to the enzyme (Scheme 2).^34,42 Thus, an accurate assessment of the KIEs on the proton transfer requires optimal reaction conditions in which the concentration of CH₂H₄folate is high enough to ensure sufficient conversion of dUMP to dTMP while low enough to ensure that the observed KIEs will not be masked by the forward commitment to catalysis (see below).^11,43 We improved the competitive KIE methods previously developed in our lab (see Experimental Section), and measured observed H/T and D/T KIEs on the proton transfer. Figure 2A shows the observed and intrinsic KIEs on the proton transfer, and 2B the hydride transfer³². The intrinsic KIEs were calculated from the observed KIEs using the Northrop method (see Experimental Section). In contrast with the hydride transfer, the observed KIEs on the proton transfer are much smaller than the intrinsic KIEs, suggesting a “kinetic complexity” that masks the intrinsic KIEs on this step.^11,43

Scheme 2.

A simplified kinetic scheme for of wild-type E. coli TSase (revised from Ref 34). A represents dUMP and B CH₂H₄folate. The only isotopically sensitive step here is represented by the rate constant k₅.

Figure 2.

Arrhenius plots of observed (empty structures) and intrinsic (filled structures) primary KIEs on the proton transfer (A) and the hydride transfer³² (B) catalyzed by E. coli TSase. The KIEs are shown as average values and standard deviations, while the lines are the non-linear fittings of all calculated intrinsic KIEs (see text) to the Arrhenius equation.⁴⁴

Kinetic Complexity on the Non-rate-limiting Proton Transfer

The observed primary KIEs are usually smaller than the intrinsic ones, due to a kinetic complexity that masks the intrinsic KIEs. For the KIE on the second order rate constant (k_cat/K_M or V/K), which is the only KIE measured by the competitive method, this “kinetic complexity” can be described by Eq. 2:⁴³

$$KI{E}_{\mathrm{obs}}=\frac{k_{\mathrm{L}}∕k_{\mathrm{H}}+C_{\mathrm{f}}+C_{\mathrm{r}}\cdot EIE}{1+C_{\mathrm{f}}+C_{\mathrm{r}}}$$ (2)

where k_L/k_H is the intrinsic KIE as the ratio of the light (k_L) vs. heavy (k_H) isotopes for the isotopically sensitive step examined (k₅ in Scheme 2); EIE is the equilibrium isotope effect; and C_f and C_r are the forward and reverse commitments to catalysis, respectively. For the proton transfer catalyzed by TSase, C_r ≈ 0 since the tritium release is irreversible due to the dilution into ~110 M protons in water. Therefore, Eq. 2 can be simplified as Eq. 3:

$$KI{E}_{\mathrm{obs}}=\frac{k_{\mathrm{L}}∕k_{\mathrm{H}}+C_{\mathrm{f}}}{1+C_{\mathrm{f}}}$$ (3)

and for Scheme 2:

$$C_{\mathrm{f}}=\frac{k_5(k_2+k_3\left[\mathrm{B}\right])}{k_2{k}_4}$$ (4)

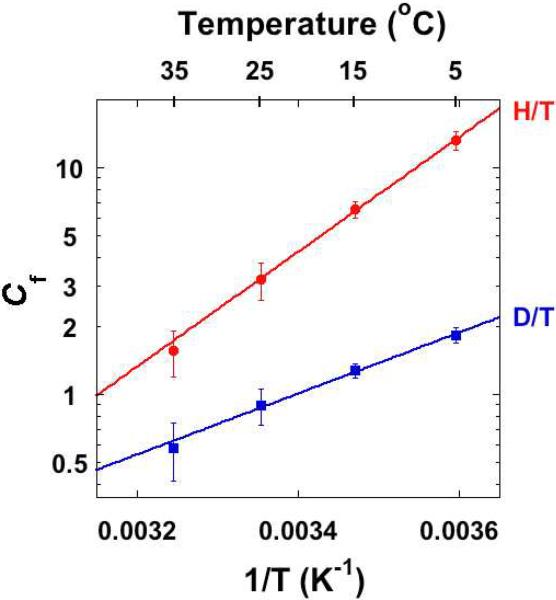
It is apparent form Eqs. 3 and 4 that when the concentration of CH₂H₄folate (B) goes to infinity, C_f will go to infinity and the observed KIE will approach unity (no KIE). At low concentrations of CH₂H₄folate ([B] → 0), on the other hand, C_f will approach the finite value of k₅/k₄, i.e., the ratio between the rate constants of the isotopically sensitive step and the dissociation of CH₂H₄folate from the Michaelis complex (EAB). Empirically, C_f can be calculated from the observed and intrinsic KIEs at each temperature. Figure 3 presents the forward commitment plotted vs. temperature. The linear Arrhenius plots for both H/T and D/T KIEs data suggest that one single kinetic step is responsible for most of the forward commitment for the proton transfer catalyzed by TSase.

Figure 3.

The forward commitment (C_f) of the proton transfer step plotted on the logarithmic scale vs. the reciprocal of the absolute temperature. The data are presented as average values and standard deviations (red: H/T; blue: D/T). The lines are the exponential fittings of all calculated C_f values (see text) to the Arrhenius equation.

Comparison of the Temperature Dependences of Intrinsic KIEs on the Proton and Hydride Transfers

The intrinsic KIEs on both the proton and hydride transfers were fit to the Arrhenius equation to evaluate their temperature dependences:⁴⁴

$$\mathrm{KIE}=\frac{k_{\mathrm{L}}}{k_{\mathrm{H}}}=\frac{A_{\mathrm{L}}}{A_{\mathrm{H}}}\exp \left(-\frac{\Delta E_a}{\mathrm{RT}}\right)$$ (5)

where the subscripts L and H denote a light and a heavy isotope of hydrogen, respectively; k represents the microscopic rate constant of the isotopically sensitive step (step 4 for the proton transfer and step 5 for the hydride transfer in Scheme 1, respectively), and ΔE_a is the difference in the activation energies of that microscopic step between the light and heavy isotopes; R is the gas constant and T is the absolute temperature. Therefore, the isotope effects on both the pre-exponential factors (A_L/A_H) and the activation energy (ΔE_a) can be accessed by fitting the intrinsic KIEs to Eq. 5 (Figure 2). The isotope effects on the Arrhenius parameters of both the proton and hydride transfers are summarized in Table 1. The intrinsic KIEs on the hydride transfer are temperature-independent, and the isotope effects on the pre-exponential factors are well above the semi-classical limits.^11,22,45 In contrast, the KIEs on the proton transfer are temperature-dependent and A_L/A_H's are much lower than the semi-classical limit.

Table 1.

Isotope Effects on Arrhenius Parameters (see text) of E. coli Thymidylate Synthase on the Hydride Transfer and the Proton Transfer.

	Proton Transfer	Hydride Transfer 32	S.C. AL/ATa
AH/AT	8.3×10−6 ±1.0×10−6	6.8 ± 2.8	0.5 – 1.6
AD/AT	2.8×10−2 ±0.1×10−2	1.9 ± 0.3	0.9 – 1.2
Δ Ea H-T b	−8.0 ±0.1	0.02 ± 0.25
Δ Ea D-T b	−2.44 ±0.03	−0.04 ± 0.08

^aSemi-classical limits of isotope effects on the preexponential factor¹¹,²²,⁴⁵

^bThe differences in activation energies in the unit of kcal/mol.

Interpretation of the Results within the Framework of the Marcus-like Model

Several theoretical calculations and simulations have examined the temperature dependence of KIEs in various enzymes.^46–49 Although the details of the calculations and simulations are diverse, they agree on the basic notion that the temperature dependence of KIEs reflects how optimal the donor-acceptor geometry is for the H-transfer, or how well the enzyme “fine-tunes” this step. It is important to recognize that the phenomenological models do not replace or conflict with computer simulations at the molecular level. An excellent review explaining the complimentary nature and the relations between these approaches can be found in ref 50. Here we interpret our results on TSase catalyzed H-transfers within the framework of Marcus-like model.^{11,12,14,16,17,20,21}

As mentioned in the introduction section, the temperature dependence of KIEs is mainly determined by the Franck-Condon term and the DAD fluctuations along the Q₂ coordinate (the integral in Eq. 1, also see Figure 1). In many cases where the enzyme has evolved to optimize the ensemble of TRS geometries via environmental reorganization on Q₁, the integral in Eq. 1 is barely affected by thermal activation of the DAD fluctuations and the KIEs will be mostly temperature-independent. This observation has been reported for various wild-type enzymes with their natural substrates under physiological conditions.^28,32,51,52 If the reorganization is impaired (e.g. by mutation,⁵³ non-physiological conditions⁵¹), however, the enzyme will need to exploit the DAD fluctuation to sample the TRS-like geometries for efficient tunneling, leading to temperature-dependent KIEs.⁵⁴

For an enzymatic reaction that involves two sequential C-H bond activations, it is not intuitive whether the enzyme would have evolved to optimize both steps or to optimize only a single step. One could expect that the non-rate-limiting step has been optimized and thus is a faster step, or the rate-limiting step has been optimized due to its direct effect on the turnover rate. Our studies with TSase exposed the temperature-dependent KIEs on the proton transfer step and the temperature-independent KIEs on the hydride transfer step, which suggests that the rate-limiting hydride transfer is better optimized than the fast proton transfer. This observation is in accordance with the studies of MR,³⁹ where the faster hydride transfer (in the reductive half reaction) has temperature-dependent KIEs while the slower hydride transfer (in the oxidative half reaction, which is concerted with a proton transfer) has temperature-independent KIEs. A reasonable interpretation of these findings would be that the same enzyme activates two C-H bonds using different physical features, such as different degrees of reorganization. The proton abstraction from C5 of dUMP requires little catalytic enhancement, and can be activated in solution by high pH and free thiolates (analogous to the proton transfer, see Experimental Section), whereas a non-enzymatic equivalent of the hydride transfer has never been observed. This suggests that the hydride transfer requires more enzymatic activation than the proton transfer. As the slowest step of the reaction, the hydride transfer directly limits the overall catalytic-efficiency of TSase and thus might be under more direct evolutionary pressure to be optimized. A faster proton transfer, on the other hand, will not further enhance the catalytic turnover. Therefore, the enzyme may have evolved to “fine-tune” only the hydride transfer to better optimize the TRS geometries for that step.

Conclusions

We analyzed and compared the nature of two sequential H-transfers catalyzed by TSase – a non-rate-limiting proton transfer and a rate-limiting hydride transfer. The temperature dependences of intrinsic KIEs on the two H-transfers are dramatically different, which suggests different activation mechanisms. Based on the Marcus-like model and in accordance with the findings of studies using computer simulations,^46–49 our results suggest that TSase has evolved to optimize the active site better for the hydride transfer than the proton transfer. We hope the current findings will invoke theoretical calculations and high-level simulations that may reveal the molecular details of these two C-H activation steps. Since the detailed molecular mechanisms of both H-transfers are still not clear,^35,36 further investigation on these steps will discern the TRS features and may assist in rational drug design.

Experimental Section

Materials and Instruments

[2-¹⁴C] dUMP (specific radioactivity 56 Ci/mol) and [5-³H]-dUMP (specific radioactivity 13.6 Ci/mmol) were from Moravek Biochemicals. Ultima Gold liquid scintillation cocktail were from Packard Bioscience. Liquid scintillation vials were from Fisher Scientific. The wild-type thymidylate synthase (TSase) was expressed and purified following the published procedure.⁵⁵ We used an Agilent Technologies model 1100 HPLC system for all the purifications and analytical separations. All other materials were purchased from Sigma.

Experimental Details

Synthesis of [2-¹⁴C, 5-²H] dUMP (> 99.5% D)

[2-¹⁴C, 5-²H]-dUMP was prepared by adopting the method of Wataya and Hayatsu.^56–58 Briefly, 1 mM [2-¹⁴C] dUMP was incubated in a D₂O solution (> 99.96% D) containing 1 M of _L-cysteine (pD = 8.8) at 37 °C. The complete deuteration (>99.5% D) was achieved after 7 days incubation, verified by ¹H NMR measurements. To ensure that no artifacts were induced during the incubation, a portion of the synthesized [2-¹⁴C, 5-²H]-dUMP was exchanged with H₂O back to [2-¹⁴C] dUMP under the same conditions. The produced [2-¹⁴C] dUMP was used for competitive H/T KIE experiments and replicated the observed H/T KIEs with commercial [2-¹⁴C] dUMP. It is interesting to note that part of this synthesis is analogous to the TSase-catalyzed proton transfer (step 4 in Scheme 1).

Competitive KIE Experiments on Proton Transfer (Step 4 in Scheme 1)

In order to better expose the KIEs of this non-rate-limiting step, we modified the experiment conditions based on the previously developed method.³⁴ The experiments were performed in 100 mM tris(hydroxymethyl)aminomethane (Tris)/HCl buffer (pH 7.5, adjusted at the desired temperature), at 5, 15, 25, and 35 °C. Each reaction mixture (final volume 1 ml) contained 50 mM MgCl₂, 1 mM EDTA, 5 mM formaldehyde, 25 mM DTT, 3 μM CH₂H₄folate, 0.9 Mdpm [5-³H] dUMP, and 0.3 Mdpm [2-¹⁴C] dUMP (for H/T KIE measurement) or [2-¹⁴C, 5-²H] dUMP (for D/T KIE measurement). At each temperature, the experiments were performed following the previously published procedure.³⁴ Two independent control experiments (minus enzymes) were performed to deduct the non-enzymatic effects. All the quenched samples were analyzed by RP HPLC separation and liquid scintillation counting (LSC) to obtain the observed KIEs, as described in previous publications.³² All t_∞ time points were pooled together to provide more accurate average values.

The competitive observed KIEs were determined from three measured values— the fraction conversion (f), the ³H/¹⁴C ratio in the products ([³H]H₂O and [¹⁴C]dTMP) at each time point (R_t), and the ³H/¹⁴C ratio in the products at the infinity time point (R_∞):^11,45

$$\mathrm{KIE}=\frac{\ln (1-f)}{\ln \left(1-f\cdot \frac{R_t}{R_{\infty }}\right)}$$ (6)

The fraction conversion f was calculated by:

$$f=\frac{\left[{}^{14}\mathrm{C}\right]\mathrm{dTMP}}{\left[{}^{14}\mathrm{C}\right]\mathrm{dTMP}+\left[{}^{14}\mathrm{C}\right]\mathrm{dUMP}}$$ (7)

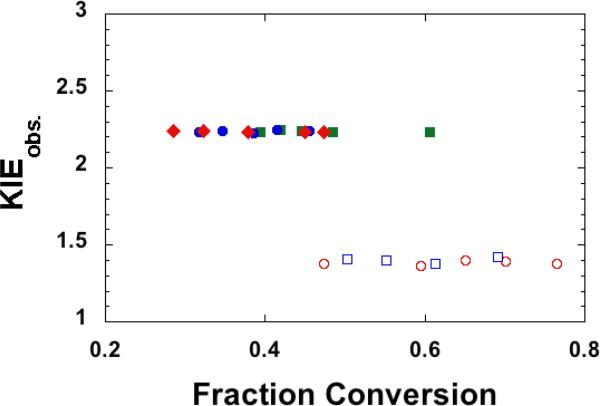
For quality control, Figure 4 presents an example of the observed KIEs (calculated from Eq. 6) as a function of f (calculated form Eq. 7) at 25 °C (the data are from 3 independent H/T experiments and 2 independent D/T experiments, with at least 4 KIE measurements per independent experiment). The KIEs do not show any upward or downward trends as a function of f (most artifacts would result in such trends), suggesting that the results are reliable.

Figure 4.

The observed H/T (filled structures) and D/T (empty structures) KIEs plotted vs. fraction conversion as measured at 25 °C with 3 μM CH₂H₄folate. The different colors and shapes represent different independent experiments.

Intrinsic KIEs on Proton Transfer (Step 4 in Scheme 1)

The intrinsic KIEs were calculated using the Northrop method:^11,43

$$\frac{{}^{\mathrm{T}}{(V∕K)}_{{\mathrm{H}}_{obs}}^{-1}-1}{{}^{\mathrm{T}}{(V∕K)}_{{\mathrm{D}}_{obs}}^{-1}-1}=\frac{k_{\mathrm{T}}∕k_{\mathrm{H}}-1}{{(k_{\mathrm{T}}∕k_{\mathrm{H}})}^{1∕3.34}-1}$$ (8)

where ^T(V /K)_Hobs and ^T(V /K)_Dobs are the observed H/T and D/T KIEs, respectively; k_T/k_H represents the reciprocal of the intrinsic H/T KIE. The intrinsic H/T KIE was solved numerically. All possible combinations of observed H/T and D/T KIEs were analyzed to get the intrinsic KIEs. All intrinsic KIEs were used to fit to the Arrhenius equation (Eq. 5) to evaluate the isotope effects on Arrhenius parameters and temperature dependence of KIEs. This analysis was carried out with KaleidaGraph (Version 4.03) as the least root-mean-square fit exponential regression. The Northrop method assumes ^TK_eq close to unity or that C_r ≈ 0,⁴³ and the validity of these assumptions for TSase has been discussed above and in ref 34.