Temporal Constraints on the Incorporation of Regulatory Mutants in Evolutionary Pathways

Abstract

Understanding the molecular details of the sequence of events in multistep evolutionary pathways can reveal the extent to which natural selection exploits regulatory mutations affecting expression, amino acid replacements affecting the active site, amino acid replacements affecting protein folding or stability, or variations affecting gene copy number. In experimentally exploring the adaptive landscape of the evolution of resistance to β-lactam antibiotics in enteric bacteria, we noted that a regulatory mutation that increases β-lactamase expression by about 2-fold has a very strong tendency to be fixed at or near the end of the evolutionary pathway. This pattern contrasts with previous experiments selecting for the utilization of novel substrates, in which regulatory mutations that increase expression are often fixed early in the process. To understand the basis of the difference, we carried out experiments in which the expression of β-lactamase was under the control of a tunable arabinose promoter. We find that the fitness effect of an increase in gene expression is highly dependent on the catalytic activity of the coding sequence. An increase in expression of an inefficient enzyme has a negligible effect on drug resistance; however, the effect of an increase in expression of an efficient enzyme is very large. The contrast in the temporal incorporation of regulatory mutants between antibiotic resistance and the utilization of novel substrates is related to the nature of the function that relates enzyme activity to fitness. A mathematical model of β-lactam resistance is examined in detail and shown to be consistent with the observed results.

Introduction

Much discussion has focused on the relative role of structural versus regulatory mutations in the evolution of novel phenotypes. Structural changes, whether they alter a protein's function (active site) or its physical structure (e.g., folding, stability, etc.), involve amino acid replacements (e.g., Clark et al. 2003; Hoekstra et al. 2006). In contrast, regulatory mutations include those that alter gene expression in cis or in trans (e.g., Olds and Sibley 2003; Shapiro et al. 2004, 2006; Tishkoff et al. 2007; Brown et al. 2008). Various perspectives are summarized in Carroll (2000, 2005a, 2005b), Wray (2007), Hoekstra and Coyne (2007), and Lynch and Wagner (2008).

In this paper, we take a different tack. We consider the evolution of metabolic capabilities to which both structural and regulatory mutations are likely to contribute. We ask why it is that, in some systems, regulatory mutations are incorporated early in the process; whereas, in other systems, regulatory mutations are incorporated late.

Extensive previous research has observed that regulatory mutations often precede structural ones in enzyme evolution (Mortlock et al. 1965; Wu et al. 1968; Hegeman and Rosenberg 1970; Hall and Hauer 1993; among others). In these situations, existing enzymes often catabolize novel substrates to some extent, but they require constitutive regulatory mutations in order to allow sufficient expression to enable growth. Similarly, cryptic genes for the metabolism of certain substrates reside unexpressed in microbial genomes until mutationally activated by promoter mutations (Hall et al. 1983; Hall 1998). As the initial substitution in an adaptive landscape is predicted to account for ∼30% of the total fitness increase (Orr 2002), these observations suggest that regulatory mutations play a key role in enzyme evolution.

“Regulation first” has some notable exceptions, however. For example, Weinreich et al. (2006) found that structural mutations usually precede regulatory mutations in the evolution of the TEM β-lactamase in Escherichia coli. In the adaptive landscape connecting the wild-type TEM allele of low resistance to a quintuple mutant of high resistance, Weinreich et al. (2006) showed that a particular regulatory mutation denoted g4205a has a 75% chance of being the final mutation fixed (In the absence of other mutations, g4205a yields no increase in resistance on the wild-type genetic background; see Weinreich et al. 2006). Similarly, studies on an evolved β-galactosidase enzyme derived from the E. coli gene ebg have shown that this enzyme requires an initial structural mutation in order to facilitate growth on its substrate (Hartl and Hall 1974; Hall and Hartl 1974; Hall 1990).

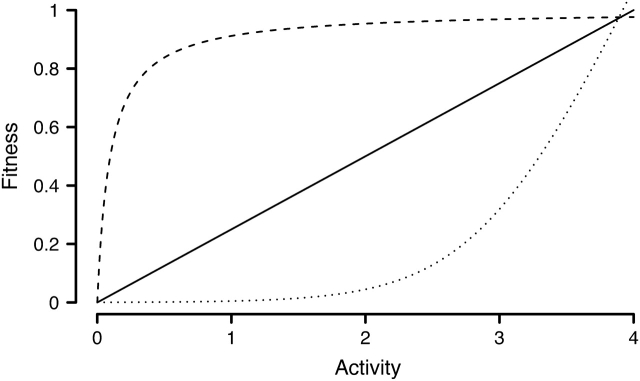
To sharpen the discussion, figure 1 depicts three contrasting functions relating fitness to enzyme activity. The concave function (dashed line) depicts a relationship common for many metabolic enzymes, and the mapping is appropriate when metabolic flux serves as a proxy for fitness (Hartl et al. 1985; Dykhuizen et al. 1987). The convex function (dotted line) is common to enzyme-mediated antibiotic resistance. Although this specific model has been used to successfully predict β-lactam resistance in several bacterial species (Zimmerman and Rosselet 1977; Nikaido and Normark 1987; Lakaye et al. 1999), its implications for the temporal incorporation of structural versus regulatory mutations have not been explored.

FIG. 1.—

Contrasting functions that map enzyme activity onto fitness. The dashed line (top) indicates a concave relationship typical for an enzyme in a metabolic pathway (Hartl et al. 1985). The dotted line (bottom) indicates a convex relationship of the sort predicted for enzyme-mediated antibiotic resistance (Zimmerman and Rosselet 1977). The solid line indicates a linear relationship.

In this paper, we show how temporal constraints on the incorporation of regulatory mutations are associated with the catalytic activity of the genes involved and with the differing relationships between enzyme activity and fitness for metabolic and antibiotic resistance enzymes. By means of studies of resistance to the β-lactam antibiotic cefotaxime in strains of E. coli containing the TEM β-lactamase, we empirically demonstrate the importance of structural mutations incorporated early in the evolutionary pathway of drug resistance. We also show that the temporal ordering of structural versus regulatory mutations in evolution depends on the mapping of enzyme activity onto fitness.

Materials and Methods

Construction of E. coli Strains

The TEM-1 gene from the plasmid pBR322 was isolated via polymerase chain reaction (PCR) and cloned into the pBAD vector with a kanamycin resistance marker using the pBAD TOPO TA expression kit (Invitrogen, Carlsbad, CA). Point mutations (G238S, E104K, and M182T) that had been previously shown to increase resistance to the β-lactam cefotaxime (Weinreich et al. 2006 and citations within) were introduced into this gene via site-directed mutagenesis according to the Quick-change site-directed mutagenesis kit (Stratagene, La Jolla, CA). The entire TEM locus and pBAD promoter were then sequenced to verify the presence of the desired point mutations and the absence of all other substitutions.

In order to ensure that we could modulate the transcript levels in individual cells and not merely the population as a whole, we obtained the K12-derived cell line, BW27783 (Khlebnikov et al. 2001; J. Keasling, University of California, Berkeley), and transformed our pBAD plasmids bearing the TEM alleles into this strain. Previous work had demonstrated that the arabinose operon behaved in individual cells in an “all on” or “all off” fashion (Khlebnikov et al. 2001). The BW27783 cell line has the promoter of its araE gene replaced with a constitutive promoter, eliminating positive feedback of this expression system. Using the BW27783 cell line, arabinose concentrations should correlate to the RNA abundance of the arabinose operon–controlled TEM locus in each cell.

Resistance Assays

We used minimum inhibitory concentration (MIC) assays to measure resistance to the β-lactam antibiotic cefotaxime (Sigma-Aldrich, St Louis, MO). This method is detailed by the Clinical and Laboratory Standards Institute (2007). Briefly, 2-fold dilution series over an appropriate range (0.03125–1,024 ug/ml) of cefotaxime concentrations in Mueller–Hinton broth were prepared in 96-well flat bottom plates. Strains were streaked on fresh Luria Broth (LB) and kanamycin (KAN; 50 ug/ml) plates. Colonies were picked the following day and grown overnight to saturation in LB–KAN media containing the appropriate arabinose concentration. Ninety-six well MIC assay plates were then inoculated with ∼10⁵ cells/ml in each well as determined by cell titer counts on LB–KAN plates. MIC values from wells inoculated with between 10⁴ and 10⁶ cells/liter were insensitive to differences in cell concentration. Wells inoculated with concentrations higher than 10⁶ or lower than 10⁴ cells/ml demonstrated dramatically increased and decreased MIC readings, respectively, and were not used. For each overnight culture of a given strain and arabinose concentration, MIC assays were done in triplicate and the median MIC was determined from these three values.

Transcription Induction Confirmation

Quantitative reverse transcriptase PCRs were used to confirm high levels of TEM allele transcription from pBAD plasmids in the presence of high concentrations of arabinose. Two or three biological replicates for each combination of strains and arabinose concentration were prepared by inoculating 1-ml overnight cultures. After approximately 18 h of growth, the cultures were diluted 10,000 times and grown to log phase (OD₆₀₀ ∼ 0.6). One RNA extraction per biological replicate was performed using the RNeasy kit (Qiagen, Valencia, CA) and treated with Turbo-DNAFree (Ambion, Austin, TX). Adding the same quantity of RNA to each reaction, we created cDNA from total RNA using Random Hexamer Primers and Superscript II (Invitrogen). As previous experiments had shown there to be little variation between cDNA reactions from the same RNA preparation, we prepared only one cDNA reaction per RNA sample. Quantitative PCRs (Q-PCRs) using SYBR green (Qiagen) were used to quantify cDNA concentrations in each RNA sample. At least six Q-PCRs (three experimental and three control) were run in parallel for each RNA sample. Primers for both the TEM alleles and the control tRNA gene trpT (EG30105) were designed to amplify with 95% or greater efficiency, calculated based on the standard curve for each (see Statistical Analysis below). Uninduced and induced cells demonstrated significantly different expression levels. The wild-type and G238S + M182T alleles demonstrated similar mRNA levels at the same arabinose concentrations (supplementary fig. S1, Supplementary Material online).

Protein Purification

In order to quantify the TEM enzymatic concentrations in our cells at different arabinose concentrations, we extracted and purified four of the β-lactamase missense mutants (all combinations of M182T and G238S, see supplementary table S1, Supplementary Material online). Briefly, each allele was moved into a pBAD-based arabinose-inducible overexpression and purification vector (pBAD Directional TOPO expression kit, Invitrogen) carrying a 28-residue C-terminal linker including a 6×His tag. The alleles were constructed with a combination of DNA digestion with the NcoI endonuclease (New England Biolabs) and ligation (EMD Biosciences) or site-directed mutagenesis (Weinreich et al. 2006). All sequences were verified by DNA sequencing of purified plasmids.

Overnight cultures were grown in Terrific Broth containing 0.1% arabinose for each of the missense alleles in E. coli strain LMG194 (Invitrogen). Purified β-lactamase was obtained from 5 ml cultures using His-select iLAP columns (Sigma-Aldrich). Purity of the resulting elutions was verified using sodium dodecyl sulfate–polyacrylamide gel electrophoresis. Pure protein concentrations were between 10 and 1,000 μg/ml as determined by Bradford assays (Quick Start Bradford Protein Assay, Bio-Rad, Hercules, CA). The purified proteins were stored at −80 °C in 40 mM NaPO₄ containing 40% glycerol. Note that neither imidazole nor elution salts were removed from the purified proteins due to problems with protein aggregation and precipitation from the unstable alleles. Neither additive had a significant or systematic effect on kinetic assays performed in this study.

Enzyme Kinetics

Enzyme reaction kinetics were determined using purified protein against nitrocefin (NTF; Oxoid Ltd., Basingstoke, Hampshire, UK; λ = 486 nm, Δϵ = 15,000 M⁻¹ cm⁻¹, concentrations from 10 to 200 μM) at 25 °C in 100 mM NaPO₄, pH 7 buffer containing 2,000 μg/ml bovine serum albumin (Sigma catalog no. A3059-50G) as an enzyme stabilizer (Laraki et al. 1999) on a 96-well spectrophotometer (Spectramax PLUS³⁸⁴ from Molecular Devices). We chose NTF for our activity assays as the change in absorbance associated with NTF hydrolysis is in the visible range. The cefotaxime hydrolysis reaction and the β-lactamase enzyme share absorbance wavelengths in the UV range.

Initial reaction velocities were fit to the complete Michaelis–Menten equation (eq. 1) using nonlinear least squares for high-performance alleles (those with K_M’s less than half the maximum substrate concentration) or to the reduced Michaelis–Menten equation where S << K_M using standard linear regression (eq. 2) where K_M is the Michaelis constant, k_cat is the general rate constant, S is the concentration of substrate, E₀ is the enzyme concentration, and v the reaction rate (Nelson and Cox 2000).

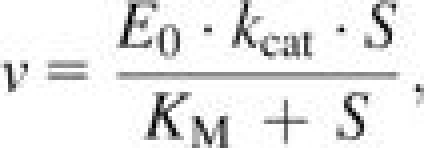(1)

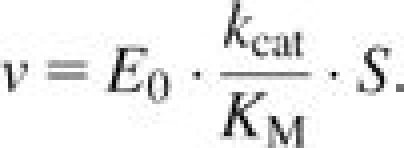(2)

All fits had P values <10⁻³. Presented values are the average of six replicates. Standard errors (SEs) of the mean are less than 4% of the average value (supplementary table S1, Supplementary Material online). Individual k_cat and K_M for each allele against NTF are presented in supplementary table S1 (Supplementary Material online).

Protein Extractions and Enzyme Concentrations

We quantified the enzyme concentration in four of our TEM allele expressing BW27783 cell lines at six of the eight arabinose concentrations used in MIC experiments. For each biological replicate of an allele at a given arabinose concentration, a separate colony was picked into liquid LB–Kan containing the appropriate arabinose concentration and grown for 24 h. Following a method similar to that for MIC assays, overnight liquid cultures were used to inoculate ninety-six well MIC assay plates with 200 μl of MH broth containing arabinose at a cell concentration of ∼10⁵ cells/ml. These cultures were grown without shaking for 24 h. We extracted total soluble protein from the combined volume of eight wells (∼1.5 ml of cell culture) using the B-PER Bacterial Protein Extraction Reagent (Pierce, Rockford, IL) according to the manufacturers’ instructions. We performed three biological replicates for each allele and arabinose concentration tested.

Using the kinetic parameters we calculated for individual β-lactamase alleles toward NTF (supplementary table S1, Supplementary Material online; see above), we used dilute concentrations of protein extractions in saturating concentrations (50 μM) of NTF to determine enzyme concentration in each protein extraction. Under these conditions, the rate of color change of the NTF solution is equal to the maximum rate of enzymatic catalysis, referred to as the V_max. For each protein extraction, we measured V_max by measuring absorbance at 486 nm every 10 s for 5–10 min. Only protein extraction dilutions that yielded linear curves over the entire time course were used to measure V_max (milliΔOD/min). We performed four technical replicates for each protein extraction.

After normalizing by the amount of total soluble protein extract (μg) used (Bradford assay, see above), we substituted our calculated V_max for v in the inverted Michaelis–Menten equation (eq. 1) to calculate the enzyme concentration in each protein extraction. These calculations yielded protein concentrations in the unconventional units of milliΔOD/60 μg total soluble extract. After determining the protein concentration in four technical replicates for each biological replicate, we calculated means and SEs across the three biological replicates (see supplementary fig. S3, Supplementary Material online).

Statistical Analysis

Based on the maximum likelihood approach for reporting MIC values described previously (Weinreich et al. (2006), we report the median MIC of the three replicate assays performed for each allele at each arabinose concentration.

Relative RNA expression levels based on Q-PCRs of cDNA created from total RNA extractions of wild-type and G238S + M182T alleles at 0% and 10⁻²% arabinose were statistically analyzed using the following modified ΔCT approach. Briefly, Q-PCRs produced raw CT values for TEM β-lactamase and trpT tRNA for each cDNA sample. The replicate CT values for the trpT gene for each cDNA sample were averaged. This control CT value was then subtracted from each replicate CT value for β-lactamase to yield ΔCT. A nested analysis of variance revealed much greater variation in ΔCT values among biological replicate than within them. We averaged the replicate ΔCT values obtained from each biological replicate (cDNA preparation). Heteroscedasticity t-tests were used to test for the homogeneity among mean ΔCT values. Analysis of variance calculations and t-tests were carried out in R (version 2.5.0; http://www.R-project.org), and additional t-tests were carried out using in Microsoft Excel 2004 for Mac (version 11.3.7).

Relative RNA expression levels reported in supplementary figure S1 (Supplementary Material online) were calculated as follows. Following typical Q-PCR methodology involving a standard curve, a genomic DNA extraction from cells harboring a TEM-1 containing plasmid (pBR322) was used to create a 10-fold DNA dilution series over six orders of magnitude. CT values from these samples for each primer set were then plotted on a log–log scale against their relative concentrations. Using the best-fit line determined by these points, we used the mean absolute CT value for each cDNA to determine the relative concentration of cDNA of either TEM β-lactamase or trpT for each biological replicate. We normalized the TEM β-lactamase transcription levels by dividing the trpT transcription levels calculated for each cDNA. The calculated normalized relative quantities of TEM β-lactamase were then averaged for each genotype by arabinose combination and plotted as mean relative RNA concentrations in supplementary figure S1 (Supplementary Material online). The error bars in supplementary figure S1 (Supplementary Material online) represent the SE among the normalized relative quantities calculated for each biological replicate.

We constructed a generalized linear model (GLM, function glm() in R, ver. 2.2.1, The R Foundation for Statistical Computing) to analyze our MIC data. We modeled MIC as a function of the presence or absence of the three mutations (G238S, E104K, and M182T) and expression level as determined by inducer concentration. For our GLM analysis, we gave each median MIC value in our data set an ordinal number where 1 corresponded to the lowest expression level (growth in 0% arabinose) and 8 corresponded to the highest expression level (growth in 10⁻¹% arabinose). As our MIC measurements represent quantized values and appeared underdispersed as a Poisson distribution, we used a quasi-Poisson error distribution. To construct the final model, we first ordered the main terms according to decreasing significance in a model with only single terms and no interactions. We then included all interaction terms and removed those that F tests revealed did not significantly contribute to the MIC variance observed. The final model (MIC ∼ G238S + Exp + E104K + M182T + G238S: Exp) included only significant terms.

MIC Predictions

We used a model first developed by Zimmerman and Rosselet (1977) and expanded upon by Nikaido and Normark (1987) to predict MIC values in our experiments (see also Lakaye et al. 1999). Combining Fick's first law of diffusion and the Michaelis–Menten equation, Zimmerman and Rosselet (1977) derive the following equation for MIC:

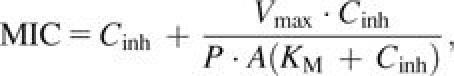(3)

where C_inh is the periplasmic concentration of β-lactam required to inactivate sufficient numbers of PBPs to inhibit growth, V_max is the rate of β-lactamase–mediated hydrolysis of β-lactam, P is the permeability coefficient for the specific β-lactam across the outer bacterial membrane (1.8 × 10⁻⁵ cm s⁻¹ for cefotaxime in E. coli), A is the area of membrane per unit of cells (132 cm² mg⁻¹ for E. coli), and K_M is the Michaelis constant for β-lactamase.

Substituting the relationship of V_max = k_cat × [E] (Nelson and Cox 2000) into equation (3), we rewrite equation (3) as:

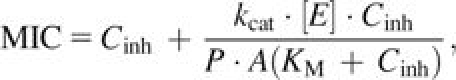(4)

where k_cat is the overall rate constant of the β-lactamase–catalyzed β-lactam hydrolysis and [E] is the periplasmic concentration β-lactamase. We inferred the V_max against cefotaxime (nanomole β-lactam hydrolyzed per second per milligram dry weight) that Nikaido and Normark (1987) calculated for cells expressing TEM β-lactamase (contained on plasmid JF701(R_471a)) based on equation (3). Based on their reported k_cat for JF701-encoded TEM, we calculate [E] in experiments of Nikaido and Normark (1987) to be 0.2508 nmol β-lactam hydrolyzed per milligram dry weight. To obtain a biologically realistic range of relative enzyme concentrations, we used [E] of Nikaido and Normark (1987) to anchor the range of relative expression values over which we used equation (4) to predict MIC for each allele.

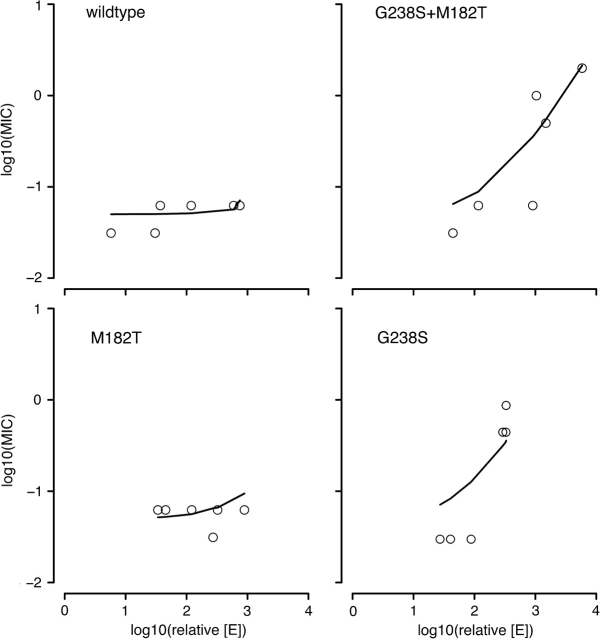
We used the previously reported k_cat and K_M against cefotaxime of four TEM alleles with E at site 104 (Wang et al. 2002) along with equation (4) to predict MIC values for each allele over a range of enzyme concentrations (see fig. 3). The absolute enzyme concentrations we measured for each allele were not readily comparable with the enzyme concentration from Nikaido and Normark (1987; see units of each metric above). Instead, we normalized each value of enzymatic concentration in our experiments by dividing the lowest enzyme concentration we observed (G238S with no arabinose). This procedure yielded an overall enzymatic expression range of nearly four orders of magnitude with each allele spanning only a part of this range (see fig. 3). Setting the lowest observed enzymatic concentration as 1,000-fold lower than the concentration observed by Nikaido and Normark (1987), we predicted MIC values for each allele across its observed relative enzyme concentration (fig. 3; solid lines in each quadrant). For comparison, we then plotted the observed MICs for each allele against their corresponding enzyme concentration (fig. 3; points in each quadrant). Additionally, supplementary figure S4 (Supplementary Material online) depicts MIC prediction for each allele across their entire collective expression range.

FIG. 3.—

Comparison of predicted MIC values (solid lines) and observed data (open circles) for four alleles as a function of relative enzyme concentrations ([E]). Predicted MIC values are based upon the Zimmerman and Rosselet (1977) model, whereas observed data represent laboratory MIC measurements. Relative enzyme concentrations for G238S were adjusted to correct for unusual sensitivity to protein extraction procedures. For MIC predictions for each allele over the entire theoretical range of expression, see supplementary figure S4 (Supplementary Material online).

Results

We constructed all combinations of three TEM β-lactamase mutations associated with increased resistance and placed them under the control of an inducible and titratable promoter derived from the arabinose operon (Materials and Methods). The rationale is that β-lactam resistance is affected by both structural mutations via changes in apparent affinity (k_cat/K_M) and regulatory mutations mediated by changes in promoter sequences altering gene expression and therefore enzyme concentration (Zimmerman and Rosselet 1977). For each of the eight TEM β-lactamase alleles, we measured resistance across a range of expression levels (Materials and Methods). Resistance was assayed as the MIC, the smallest concentration of cefotaxime that completely inhibits growth. For the kinetic parameters of these enzymes toward cefotaxime, we used previously published data (Wang et al. 2002).

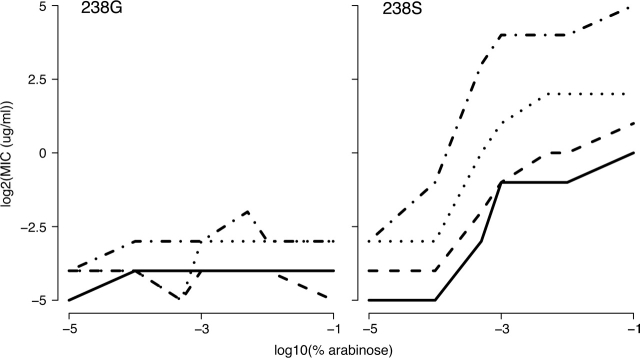
The key discovery was that the effect of increased expression on drug resistance was highly dependent on the TEM structural gene (fig. 2). Most striking, alleles that contain the mutation Gly238Ser (G238S) result in large increases in resistance with increased expression, whereas alleles retaining the ancestral Gly at position 238 show no more than a 2-fold increase in resistance across a more than 100-fold increase in transcription (supplementary fig. S1, Supplementary Material online). Although the sequence-dependent effect of increasing gene expression is most dramatic for the mutation G238S, the mutations Glu104Lys (E104K) and Met182Thr (M182T) also show modest effects (supplementary fig. S2, Supplementary Material online).

FIG. 2.—

Resistance (MIC) versus expression level (arabinose induction) relationships for eight protein-coding alleles. Left panel depicts alleles without glycine at site 238 (solid line = wild type, dashed line = M182T, dotted line = E104K, and dash–dot line = M182T + E104K). Right panel depicts alleles with serine at site 238 (solid line = G238S, dashed line = G238S + M182T, dotted line = G238S + E104K, and dash–dot line = G238S + M182T + E104K). MIC values are log₂ transformed, whereas % arabinose values are log₁₀ transformed.

To quantify the effect of structural mutations on the fitness effects of increased expression, we developed a GLM (Materials and Methods) of antibiotic resistance (MIC) as a function of both coding sequence and expression level. Among the 64 MIC's in our data set, we find significant effects attributable to the independent contribution of each individual mutation (G238S, E104K, and M182T) as well as expression level (F test, P values: G238S = 2.2 × 10⁻¹⁶, E104K = 1.914 × 10⁻¹², M182T = 0.00035, expression level = 1.548 × 10⁻¹⁵). There is, however, a highly significant interaction between expression level and G238S (F test, Expression × G238S P value = 4.776 × 10⁻⁶). Although interactions between regulatory and coding mutations have been noted previously (Stam and Laurie 1996; Weinreich et al. 2006), our experimental design allows a formal statistical confirmation of Expression × G238S epistasis.

To investigate in greater detail how inducer (arabinose) concentration corresponds to expression level, we measured mRNA and protein concentration for a subset of alleles across a range of induction levels. Alleles with different coding mutations had similar mRNA levels at the same level of induction (supplementary fig. S1, Supplementary Material online). However, some alleles result in different steady state enzyme concentrations at the same concentration of inducer (supplementary fig. S3 and table S4, Supplementary Material online). These results are consistent with previous work demonstrating differences in stability among these proteins in vitro (Wang et al. 2002). The ranges in allele-specific protein abundance we observe are also consistent with other observations relating mRNA level to steady state protein abundance (Ghaemmaghami et al. 2003).

Our data on protein abundance support the hypothesis that the structural mutation G238S is the one principally responsible for the temporal phasing of the regulatory mutation g4205a in the evolution of TEM β-lactamase. Correlation analysis between protein abundance and resistance demonstrates that resistance is significantly correlated with relative TEM β-lactamase abundance for alleles containing G238S (G238S and M182T + G238S; Spearman's rank correlation: P = 0.0005641). However, we find no such correlation for the alleles containing a G at site 238 (wild-type and M182T alleles; Spearman's rank correlation: P = 0.287).

As a final step in the analysis, we used known kinetic parameters and our measured protein abundances to test whether a previously described fitness function for TEM β-lactamase (Zimmerman and Rosselet 1977) predicted the observed relationship between structural mutations and expression level. Figure 3 shows that the predicted resistance values (solid lines) do match the observed resistance values (open circles) across the range of protein abundance. This result suggests that the Zimmerman and Rosselet (1977) model is a good predictor of antibiotic resistance. Further exploration of the evolutionary implications of this model might yield additional insights.

Discussion

Our results explain the temporal phasing of the incorporation of the regulatory mutation g4205a in the evolutionary pathway of TEM β-lactamase. The most important constraint is the identity of the residue at amino acid site 238. There is a highly significant epistatic interaction between G238S and expression level. In the presence of wild-type Gly238, the g4205a mutation yields little or no increase in antibiotic resistance, whereas in the presence of G238S, the effect can be large (Weinreich et al. 2006).

Although additional research is needed to understand how structural in β-lactamase mutations affect resistance, crystallographic and modeling studies suggest that mutations with more direct impacts upon the active site have stronger impacts on resistance. Strictly speaking, none of the mutations we examine occur in the active site and none of the wild-type residues at these sites interact with the β-lactam substrate (Matagne et al. 1998). However, crystal structures indicate that a serine residue at site 238 may point into the active site and form a new hydrogen bond with cefotaxime (Matagne et al. 1998). Although more speculative, modeling also suggests that lysine at site 104 may either interact directly with the β-lactam or alter the position of important active site residues (Matagne et al. 1998). With the smallest average effect on resistance (supplementary fig. S2, Supplementary Material online; Weinreich et al. 2006), the M182T substitution is far from the active site and has previously been shown to affect overall enzyme stability (Wang et al. 2002).

Regardless of the exact biophysical mechanisms, G238S has a dramatic effect on resistance because of its impact on the β-lactamase's affinity for its substrate, cefotaxime. The G238S substitution alone increases the overall rate of hydrolysis of cefotaxime by more than 65-fold (wild-type reaction rate constant [k_cat] = 0.636 s⁻¹; G238S reaction rate constant [k_cat] = 41.8 s⁻¹; Wang et al. 2002). This change in reaction rate (k_cat), along with a smaller decrease in the Michaelis constant (K_M), creates a nearly 100-fold higher apparent affinity for cefotaxime (wild type: k_cat/K_M = 2.07 × 10³ s⁻¹ M⁻¹, G238S: k_cat/K_M = 1.78 × 10⁵ s⁻¹ M⁻¹; Wang et al. 2002).

Increased substrate affinity allows for lower concentrations of enzyme to produce the same in vivo activity. The Zimmerman and Rosselet (1977) model of resistance predicts, and our data confirm, that at the same in vivo concentrations of β-lactamase, alleles with G238S have increased resistance, whereas those without it do not (supplementary fig. S4, Supplementary Material online; fig. 3).

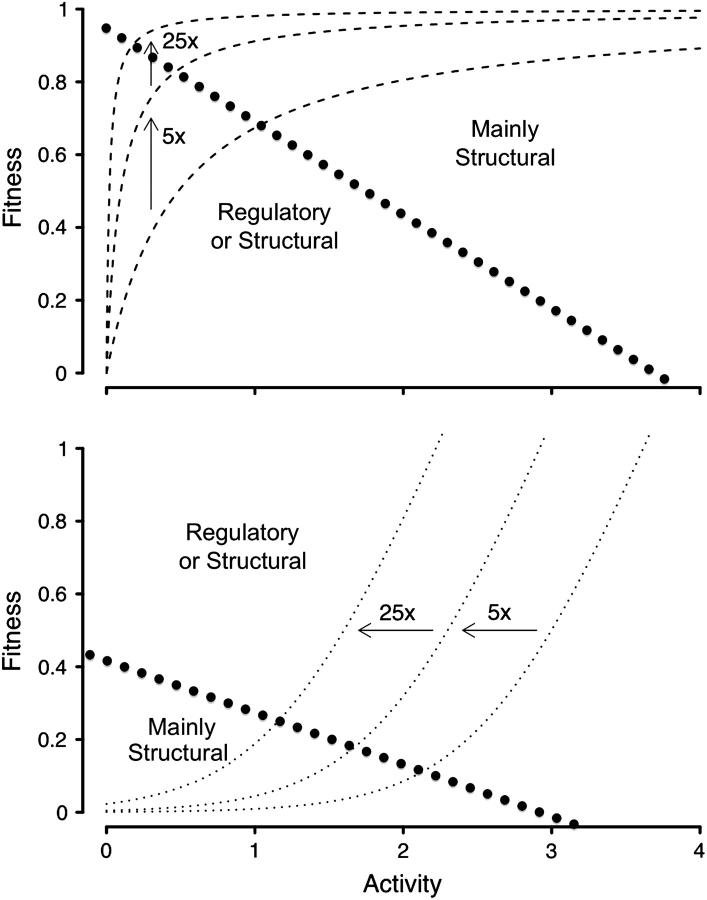
In other words, G238S alters the mapping of enzyme activity onto fitness. The effect is explored in figure 4, which compares the effects of increasing substrate affinity in concave (top) versus convex (bottom) fitness regimes. Each line represents the effect of increasing enzyme concentration for an enzyme with a given set of kinetic parameters. Both sets of curves exhibit fitness plateaus, where increases in enzyme concentration have little or no effect on fitness. In these regions of the curves, structural mutations are likely to be most important because structural mutations can increase fitness by allowing higher activity from the same concentration of enzyme. These kinds of changes can allow jumps from one fitness curve to another. In this way, structural mutations that alter substrate affinity can change the rules of the game. On the other hand, in regions of the curve where fitness increases steeply with activity, regulatory mutations that increase enzyme concentration can be strongly selected.

FIG. 4.—

These curves illustrate the relative importance of regulatory versus structural mutations in enzyme evolution under concave (top) and convex (bottom) fitness mappings. Arrows and labels (e.g., “5x”) indicate jumps between curves corresponding to enzymes with increased substrate affinity.

Figure 4 reconciles the contrasting tempos of when regulatory mutants are likely to be incorporated into evolutionary pathways. In the evolution of flux-limited metabolic pathways illustrated by the concave fitness curves, mutations that increase gene expression are likely to be incorporated early because an increase in expression can have a large effect on fitness. In the evolution of antibiotic resistance, illustrated by the convex fitness curves, mutations that increase gene expression are likely to be incorporated later because increased expression of catalytically inefficient enzymes contributes negligibly to fitness.

Our results suggest that the mapping of activity to fitness determines the relative importance and timing of regulatory and structural mutations in adaptive pathways. Although we focus on well-studied metabolic systems and antibiotic resistance, in principle, the fitness versus activity relationship should dictate the temporal incorporation of mutations during the evolution of a wide variety of enzyme types. Although research continues to focus on the genetic sources of evolutionary novelty, understanding which mutations are likely to create evolutionary novelty may require knowledge of the specific selective forces acting on enzyme activity at any one moment in time.

Supplementary Material

Supplementary tables S1–S4 and figures S1–S4 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).