Incubation Periods of Yellow Fever Virus

Abstract

Yellow fever virus is a global health threat due to its endemicity in parts of Africa and South America where human infections occur in residents and travelers. To understand yellow fever dynamics, it is critical to characterize the incubation periods of the virus in vector mosquitoes and humans. Here, we compare four statistical models of the yellow fever incubation periods fitted with historical data. The extrinsic incubation period in the urban vector Aedes aegypti was best characterized with a temperature-dependent Weibull model with a median of 10 days at 25°C (middle 95% = 2.0–37 days). The intrinsic incubation period, fitted with a log-normal model, had a median of 4.3 days (middle 95% = 2.3–8.6 days). These estimates and their associated statistical models provide a quantitative basis to assist in exposure assessments, model potential outbreaks, and evaluate the effectiveness of public health interventions.

Introduction

Yellow fever is a zoonotic arboviral disease with a long history of outbreaks in human populations.^1,2 Yellow fever virus is endemic to tropical areas of Africa and South America where it is maintained in sylvatic or jungle cycles between non-human primates and tree-dwelling mosquitoes.³ Humans entering areas where sylvatic transmission is occurring may be infected by the same mosquitoes and become infectious, amplifying and transmitting virus to mosquitoes that bite them. Although most human cases are found in or near the edges of jungle areas, infected individuals may also travel to more populated areas, presenting with the disease far from where the infection occurred and potentially, initiating urban outbreaks in areas infested by anthropophilic Aedes aegypti mosquitoes, the most prominent urban vector. This was most recently documented in early 2008 in Paraguay where an infected traveler exposed in an area with sylvatic transmission led to an urban outbreak in the capital city, Asunción.⁴

In the 1930s, an effective vaccine providing long-term protection was developed.⁵ Subsequent immunization and vector-control programs have greatly reduced the frequency and severity of outbreaks, but they have not been able to prevent them altogether.^6,7 Hundreds to thousands of cases are reported annually to the World Health Organization,⁸ but the true number of infections globally is likely many times higher because of asymptomatic or mild infections and underreporting, often exacerbated by the remoteness of the areas where cases tend to occur. Estimates of the global burden of yellow fever adjusted for underreporting reach as high as 200,000 cases and 30,000 deaths per year.⁹

The continued presence and epidemic potential of yellow fever virus make it a global health threat. The growth of international travel, with nearly 9 million persons traveling from Europe and North America to endemic areas annually,¹⁰ has increased the number of travelers potentially exposed to the virus and consequently, increased the risk of introduction into other areas where competent vectors are present.¹ Despite the number of travelers, cases in travelers only occur sporadically,^11–16 most likely because of international health regulations mandating the use of the vaccine. However, increasing concerns regarding the safety of the vaccine may curtail its use and diminish its effectiveness in outbreak prevention.^17–20

Understanding the temporal dynamics of yellow fever infections is critical to assessing transmission risk. Transmission of the virus from human to human requires a competent mosquito to feed on an infected human, survive an extrinsic incubation period in which the virus replicates and disseminates to the salivary glands, and finally, feed on another, susceptible, human. Similarly, disease in humans occurs after an intrinsic incubation period in which the virus replicates and disseminates within the human. Observations related by Hindle²¹ suggest that humans become infectious concurrently with the onset fever. Unfortunately, data on infectiousness in humans are sparse, so we restrict our focus to the timing of the onset of fever rather than infectiousness explicitly.

Characterization of the incubation periods of yellow fever is important for the effective detection, control, and prevention of outbreaks. For example, the intrinsic incubation period can be a critical factor in the differential diagnosis of illness in travelers or rural workers in endemic areas. When cases are detected, the extrinsic incubation period determines the time frame over which people may further be exposed and how quickly an outbreak may grow. These parameters are also critical when simulating outbreak scenarios through mathematical modeling. In the presence of real risk but in the absence of an actual human outbreak, a mathematical model can provide a quantitative basis for making public health decisions aimed at controlling the spread of disease.

Although many researchers and medical texts cite averages and ranges of yellow fever virus incubation periods,^3,22–24 we know of no effort to describe the distributions of these periods statistically. Furthermore, although temperature has long been known to influence the extrinsic incubation period of yellow fever virus in Ae. aegypti,^21,25,26 no analysis has quantified this effect. We aggregate historical data relevant to both incubation periods and fit statistical models to each, including the effect of temperature on the extrinsic incubation period. Because these periods are difficult to measure precisely, we take a time-to-event approach that accounts for this observational uncertainty. We fit and compare four different statistical models of this nature for each incubation period.

Material and Methods

Data.

For the extrinsic incubation period, data were gleaned from sources describing transmission occurring between humans or monkeys and Ae. aegypti mosquitoes. The data were treated as censored: either interval-censored, in the case where the mosquito was known to have become infectious within a known time interval post-exposure, or right-censored, if the mosquito remained non-infectious the last time it was tested. We also recorded the observed average temperature, when available, for each extrinsic incubation-period observation. For laboratory cases with recorded, but highly variable, temperature,^21,25 the average temperature was estimated using the given information. For laboratory studies without temperature data, the average temperature was estimated to be 25°C. For non-laboratory studies without temperature data, the incubation period dates were used to estimate the average temperature using time-of-year and location-specific temperature from the Climate Research Unit climatology dataset (CL 2.0).²⁷

For the intrinsic incubation period, the data used included only cases of transmission to humans by Ae. aegypti. Data on monkey incubation periods were not included, because the course of infection differs significantly from that in humans.²¹ Transmission through direct injection was also excluded, because this is not the natural mode of transmission; it may affect the incubation period because of differences in the initial viral load or the injection technique.²⁸ Observations were treated as uncensored in the case of a controlled single exposure and detailed observation of disease onset or censored, as described above, when exact exposure or onset times were less certain.

Statistical models.

We assumed that the distributions of observed censored incubation periods result from continuous developmental processes. Such processes are naturally modeled with time-to-event or survival models. This approach readily allows for the measurement and prediction of time-dependent hazard, survival, cumulative failure, and cumulative survival. We compared four standard parametric survival models: exponential, gamma, Weibull, and log-normal (Table 1). In the case of the extrinsic incubation period, we incorporated temperature as a linear regression covariate with an assumption of multiplicative hazards. We used a Bayesian approach to allow for the uncertainty in the temperature observations and estimations. Specifically, the observed or estimated average temperature was assumed to be a sample from a normal distribution representing the true, unobserved average temperature distribution. The true average temperature for each observation was assigned a uniform prior between 0°C and 50°C, whereas an uninformative gamma prior was used for its precision. All models were fitted in WinBUGS²⁹ using 100,000 simulations (after a burn-in of 50,000). The relative goodness-of-fit of each model was assessed using the deviance information criterion (DIC).³⁰ Detailed code for all analyses is available in the supplementary material.

Table 1.

Survival distributions

Distribution	Probability density function f(t)	Survival function S(t)*	Parameters	With covariates
Exponential	λe−λt	e−λt	λ = rate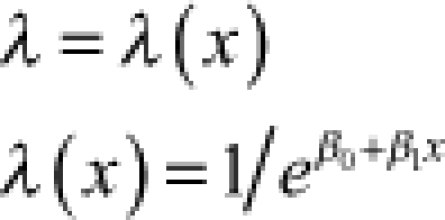
Gamma		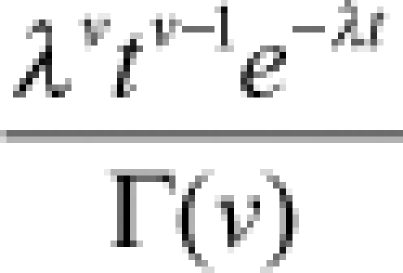	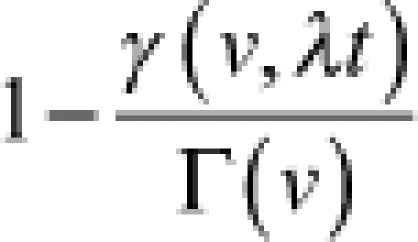λ = rate v = shape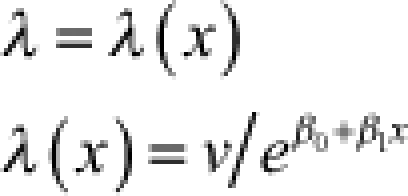
Weibull		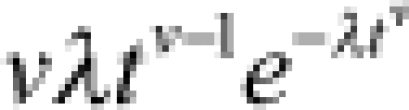	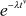λ = rate v = shape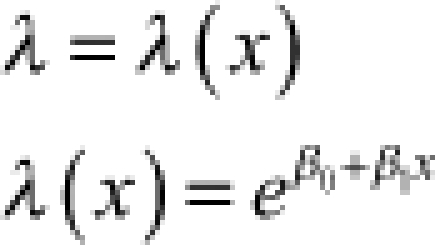
Log-normal		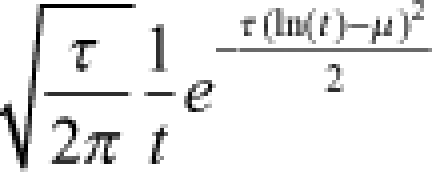	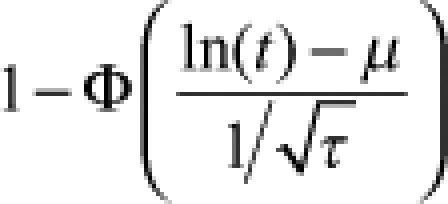μ = mean τ = precision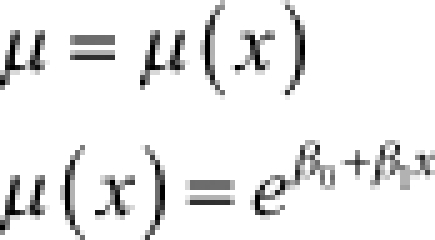

^*Φ is the standard normal cumulative distribution function, and γ is the lower incomplete gamma function.

Results

Data.

For the extrinsic incubation period, we found 164 observations of censored extrinsic incubation periods, 93 interval-censored and 71 right-censored.^{21,25,31–40} For the intrinsic incubation period, we found 87 observations: 19 uncensored, 39 interval-censored, and 29 right-censored. Typical scenarios included transmission from infected mosquitoes to naive humans entering areas with ongoing transmission,^41–43 secondary infections caused by infected people entering disease-free areas where competent vectors were present,^41–43 and experimental human infections aimed at determining the mode of transmission.^{31–35,37,44}

Models.

The mean extrinsic incubation periods ranged from 12 to 16 days at 25°C (Table 2), and the mean intrinsic incubation periods were 4.3–5.6 days (Table 3). All models qualitatively fit the data, and the medians for each model intersected most of the interval- and right-censored data (Figures 1 and 2). Temperature was negatively associated with the extrinsic incubation period in all models: increased temperatures led to shorter incubation periods (Figure 1 and Table 2). As shown in Figures 3 and 4, the gamma, Weibull, and log-normal models had skewed, humped densities. In contrast, the exponential density steadily decreased over time. This is a characteristic of the exponential model, where the single parameter defines a constant transition probability.

Table 2.

Parameter estimates and goodness-of-fit measures for parametric survival models of the extrinsic incubation period of yellow fever

Model	Constant parameter		Dependent parameter		Regression coefficients		Extrinsic incubation period at 25ºC (95% CI*)	DIC
	Notation	Value (95% CI*)	Notation	Value (95% CI*)	β0 (95% CI*)	β1 (95% CI*)
Exponential	–	–	rate (λi)		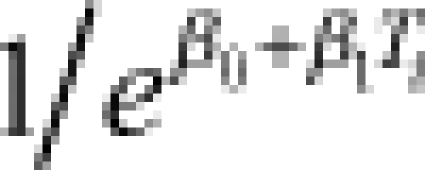4.6 (3.7–5.4)	−0.07 (−0.11 to −0.04)	16 (13–20)	182
Gamma	shape (v)	2.7 (1.5–4.2)	rate (λi)		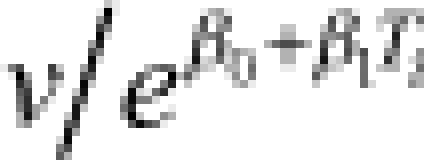4.2 (3.7–4.8)	−0.064 (−0.086 to −0.043)	14 (12–17)	175
Weibull	shape (v)	1.7 (1.3–2.2)	rate (λi)		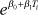−7.6 (−9.9 to −5.4)	0.11 (0.06–0.16)	14 (12–17)	173
Log-normal	precision (τ)	2.2 (1.2–3.6)	mean (μi)		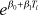1.4 (1.2–1.6)	−0.022 (−0.030 to −0.014)	12 (10–14)	174

^*95% credible interval.

Table 3.

Parameters estimates and goodness-of-fit measures for parametric survival models of the intrinsic incubation period of yellow fever

Model	Parameter 1		Parameter 2		IIP (95% CI)	DIC
	Notation	Mean (95% CI*)	Notation	Mean (95% CI*)
Exponential	rate (λ)	0.18 (0.14–0.23)	–	–	5.6 (4.3–7.3)	298
Gamma	rate (λ)	1.8 (1.1–2.5)	Shape (v)	8.1 (5.4–11.5)	4.6 (4.2–5.1)	243
Weibull	rate (λ)	0.016 (0.005–0.034)	Shape (v)	2.6 (2.1–3.1)	4.6 (4.1–5.1)	242
Log-normal	mean (μ)	1.46 (1.37–1.56)	Precision (τ)	8.0 (5.1–11.5)	4.3 (3.9–4.7)	226

^*95% credible interval.

IIP = intrinsic incubation period.

Figure 1.

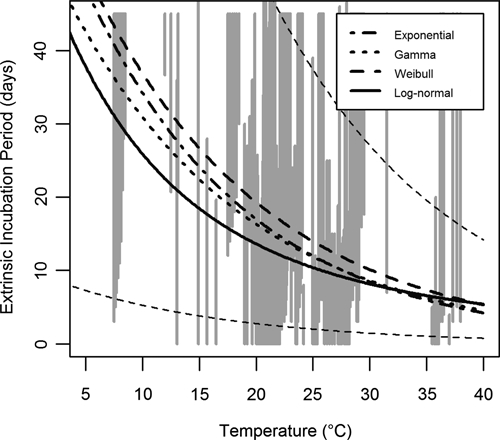
Temperature-dependent extrinsic incubation period models and data. Grey vertical lines indicate censored observations of the extrinsic incubation period in Ae. aegypti mosquitoes. Interval-censored observations indicate the minimum and maximum duration of the period, whereas right-censored observations indicate the minimum duration (and extend to infinity as the maximum is unknown). Observations at identical or very close temperatures were distributed among close temperatures to improve visualization. Thick black lines indicate the median of each tested model: exponential (dash-dot), gamma (dot), Weibull (dash), and log-normal (solid). The thin dashed black lines indicate the middle 95% of the Weibull distribution.

Figure 2.

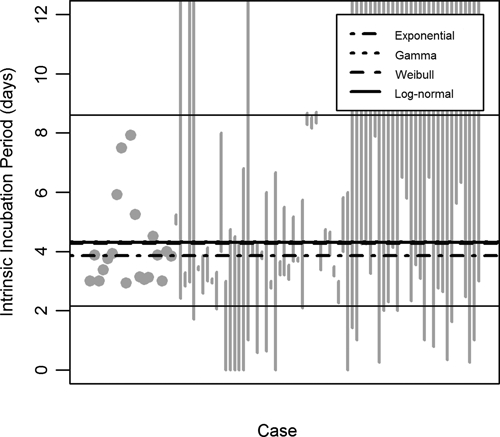
Intrinsic incubation-period models and data. Grey dots and vertical lines represent exact observations and censored data, respectively, of the intrinsic incubation period in humans. The censored data is presented as described in Figure 1. Thick black lines indicate the median of each tested model: exponential (dash-dot), gamma (dot), Weibull (dash), and log-normal (solid). The thin solid black lines indicate the middle 95% of the log-normal distribution.

Figure 3.

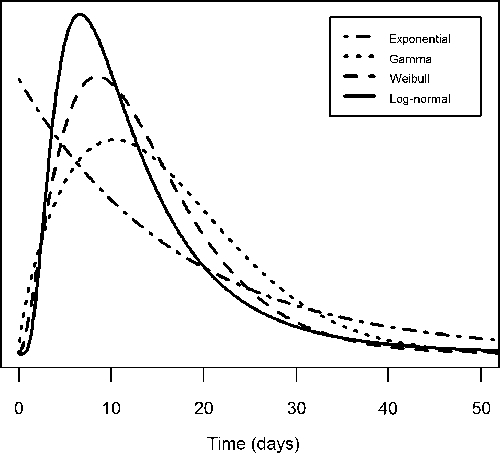
Extrinsic incubation period distribution at 25°C. The curves represent the probability density function of each extrinsic incubation period model at 25°C: exponential (dash-dot), gamma (dot), Weibull (dash), and log-normal (solid).

Figure 4.

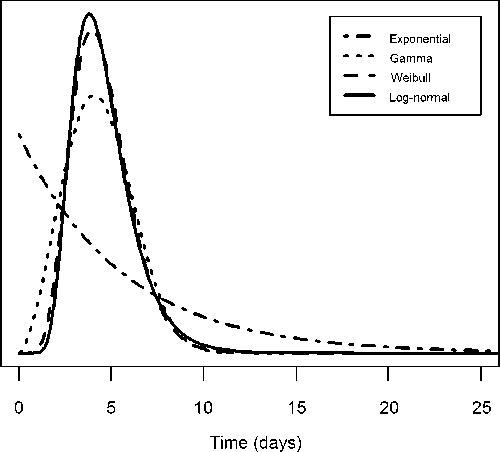
Intrinsic incubation period distribution. The curves represent the probability density function of each intrinsic incubation period model: exponential (dash-dot), gamma (dot), Weibull (dash), and log-normal (solid).

Because all of the models produced reasonable qualitative fits to the data, the DIC was used to differentiate their fits quantitatively. For the extrinsic incubation period, the Weibull model had the lowest DIC value (i.e., the best fit) followed by the log-normal, gamma, and exponential models, respectively (Table 2). For the intrinsic incubation period, the log-normal model had the lowest DIC value followed by the Weibull, gamma, and exponential models (Table 3).

In the Weibull model, the median extrinsic incubation period was 14 days at 25°C (with the middle 95% of the distribution lying between 2.0 and 37 days). As shown in Figure 5, the extrinsic incubation period is highly sensitive to temperature, decreasing at higher temperatures (7.3 days at 35°C) and increasing at lower temperatures (37 days at 10°C). This trend was significant in all models (Table 2, see β₁). The median intrinsic incubation period in the log-normal model was 4.3 days with the middle 95% between 2.2 and 8.6 days (Figure 2).

Figure 5.

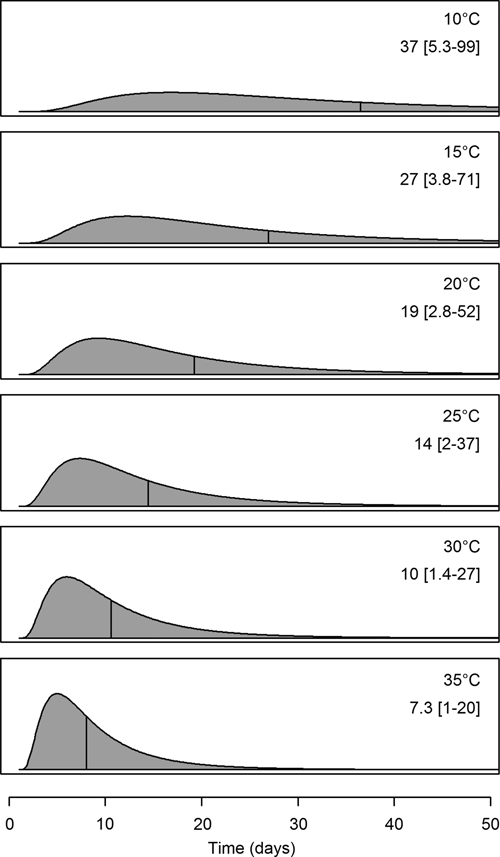
Extrinsic incubation periods at selected temperatures. Each figure shows the log-normal model probability density function at the respective temperatures. The area under each curve is equivalent, and the vertical lines indicate the median incubation period at each temperature. The median and limits of the middle 95% of the distributions are indicated above each curve.

Discussion

The analysis presented here gives a comprehensive description of the distributions of the incubation periods of yellow fever virus in humans and Ae. aegypti mosquitoes and quantifies the effect of temperature on the extrinsic incubation period. The information gleaned from the models presented significantly enhances the understanding of these critical measures of yellow fever activity.

Data relevant to these incubation periods are scarce because of the fact that they were mostly obtained in unrepeatable experiments and through observations made at a time when yellow fever was more common and little was known about its etiology.² Because of the paucity of these data, we were meticulous and cautious in our approach to data collection, using available descriptions to substantiate observations from studies when the mode of exposure was not yet known, and excluding cases where too little information was available. We also estimated the average temperature for some of the observations and accounted for the considerable uncertainty of all the temperature data using a Bayesian approach. Furthermore, we used time-to-event models to allow various forms of time-censored data to be explicitly incorporated.

In this analysis, we defined the intrinsic incubation period as the time from exposure to illness. Although this definition is clinically relevant, it does not inform us about the course of infection in asymptomatic infections nor does it necessarily relate to the probability or timing of the human becoming infectious, a critical component for understanding the possibility of continued transmission. We would have liked to describe this time period as well, but the data on human infectiousness are extremely limited. The only pertinent observations we found were those discussed by Hindle,²¹ who demonstrated that human blood is not infectious during the intrinsic incubation period but that it is infectious during the first 3–4 days of fever. This suggests that the infectious period likely begins at roughly the same time as the onset of fever in symptomatic cases.

We compared four models to describe each period. The single-parameter exponential model implies a constant hazard rate, unlike the other three models. In terms of the intrinsic incubation-period model fitted here, this means that approximately 18% of exposed people become symptomatic each day post-exposure, regardless of if it is the first or tenth day. Although this may be a reasonable model and is often used because of its simplicity, it provided the worst fit of the models used here. The other three models were qualitatively similar, with the log-normal model having the best fit as measured by the DIC. The median intrinsic incubation period for the log-normal model was estimated to be 4.3 days with the middle 95% of symptomatic yellow fever cases having an illness onset between days 2.2 and 8.6 post-exposure. These estimates are similar to a previously published range of 3–6 days.²³ The parametric model, however, gives a more comprehensive picture of the whole distribution, while also allowing further calculations, such as the cumulative probability of becoming ill within the first 3 days post-exposure (15%) or the range over which the middle 50% of cases develop symptoms (3.4–5.5 days).

As expected based on previous work with yellow fever^21,25 and other flaviviruses,^26,45,46 the extrinsic incubation period varied with temperature. The fitting of a parametric model in this case has the same advantages as described above for the intrinsic incubation period with the added benefit of being able to characterize the temperature dependence and thus, predict the period under different temperature conditions. The effect of temperature is of high importance compared with the expected life span of Ae. aegypti mosquitoes. The lowest temperature at which yellow fever infectiousness has been observed to develop in a mosquito is approximately 16.5°C.²¹ Although the model predicts that it may occur at lower temperatures, the estimated life span of a mosquito is 30–50 days under ideal conditions,⁴⁷ and it is shorter at lower temperatures,⁴⁸ making it unlikely for a mosquito to survive a complete incubation period. At higher temperatures, in contrast, the probability of a mosquito surviving the much shorter incubation period is correspondingly greater. Temperatures greater than 35°C, however, also negatively affect Ae. aegypti activity and survival,⁴⁸ and it is, therefore, unlikely that model estimates for temperatures in this range have biological significance.

The analysis presented here has several potential uses including mathematical modeling, which is increasingly used to simulate transmission scenarios or identify vaccination targets.^49,50 Use of appropriate models for incubation periods is vital to constructing reasonable models. Selection of exponential models for incubation periods when other models are more appropriate, for example, can lead to significant underestimation of transmission potential.⁵¹

This incubation-period analysis is also useful in clinical settings and the management of outbreaks. It enables the estimation of past and future transmission risk and may help in diagnosing yellow fever virus infections in individuals who have traveled from endemic areas or who have become ill during an outbreak. More specifically, when a patient presents with yellow fever-compatible symptoms, knowledge of where they were in the previous 2–9 days can eliminate or support a diagnosis, with added weight given to a positive diagnosis when the onset of fever is closest to the median time of 4.3 days. Many diseases may present similarly to yellow fever, and some, such as viral hepatitis, have much longer incubation periods of 2 or more weeks.⁵² When a case of yellow fever is diagnosed, these models provide a tool to estimate when and where exposure may have occurred (if unknown a priori) and where further risk may be present. Furthermore, because the incubation periods regulate the speed of transmission cycles, they are useful in determining the time frame for declaring that an urban outbreak is over and for assessing the success of or need for interventions. The temperature dependence of the extrinsic incubation period in particular is very important because of the influence of geographical and temporal temperature variation on the transmission cycle.