Genome-Wide Conditional Search for Epistatic Disease-Predisposing Variants in Human Association Studies

Abstract

Genome-wide search for new disease variants, based on well-established variants, has a long history in linkage analysis but is less well-known in genetic case-control association studies. We developed a simple yet highly efficient conditional search method that can find new variants, which are associated with a disease only through epistatic interaction with another variant and do not necessarily have a direct association effect. Our approach is analogous to partitioning of χ² in a hierarchical design, which is a well-established statistical technique. Applied to previously published data on age-related macular degeneration, our method found two single-nucleotide polymorphisms with genome-wide significant epistatic interaction that could not be found based only on direct main effects.

Introduction

Even though association studies are traditionally based on direct (main) effects of individual single-nucleotide polymorphisms (SNPs), they have been successful in a number of applications [1,2]. However, variants with low or absent direct main effects cannot generally be discovered by these methods. Here we demonstrate simple yet powerful methods for detecting variants through their epistatic associations with strong loci, even though these variants have low main effects themselves. That is, we aimed to detect disease-causing variants that cannot be found on the basis of their own association with a disease and can only be ‘seen’ via their association with stronger loci. Thus, we propose a conditional search in case-control association studies by initially searching for associated variants based on their direct (main) effects (stage 1), and then by searching the genome again but conditional on genotypes of the previously discovered SNPs (stage 2). Our aim is to combine stages 1 and 2 in a permutation testing framework to obtain a significance level corrected for testing multiple SNPs and working with two stages.

In the context of genetic linkage analysis, several strategies have been distinguished to localize disease susceptibility variants, for example, single-locus search, simultaneous search, and conditional search [3], where simultaneous search methods have previously been proposed [4], and likelihoods at one locus conditional on the phenotype at another locus have been proposed long ago to allow for epistatic interactions between loci [5]. These principles were first applied in human genome-wide linkage searches by subdividing affected sibpairs into two groups depending on the identity-by-descent status at HLA [6] or depending on HLA phenotypes [7], and have since been used widely in linkage mapping [8,9,10]. For family data, one can condition either on genotypes/phenotypes or on IBD statuses at another locus. These two strategies are very different and conditioning on IBD statuses is unique to family data. Di and Thompson [11] discussed how to perform conditional tests based on IBD statuses for extended families.

In genome-wide case-control association studies (GWAS), to allow for the simultaneous effects of multiple susceptibility variants, two-stage approaches have been proposed with the aim to select good candidate variants in stage 1 and then carry out joint analysis in step 2 [12,13]. Another approach consists of analysis in a single step, but the joint effects of multiple SNPs (at different genomic locations) is approximated by the sums of single-locus test statistics [14]. A more recent two-stage strategy compares genotype pattern (diplotype) frequencies in case and control individuals at a number of SNPs that have been picked in a GWAS for their individual main effects [15].

Many of these approaches focus on main effects of single SNPs. In complex traits, it is generally believed that multiple interacting variants contribute to disease susceptibility [16,17]. Multilocus search methods have been proposed [18] and are powerful but, because of the daunting number of SNP combinations, they are not applicable to genome-wide searches. An exhaustive two-locus search for disease-associated variants has been proposed and shown to be feasible [13]. Recently, Bayesian approaches have been described for analyzing all SNPs in human [19,20,21] and animal [22,23] association studies. As an alternative approach, we propose a conditional search, which will allow the detection of disease-associated SNPs with low or absent main effects as long as they act in concert with candidate genes or with variants that exert direct main effects on the occurrence of a disease, where these main effects need not be statistically significant. Our strategy may be called a two-stage or conditional search. We prefer the latter term as previously introduced, for example, in the situation that ‘we have performed a preliminary analysis, for example, a single locus search, and have detected linkage to some loci and would like to continue analysis of the same data to find evidence for linkage to other loci’ [3].

As will be seen below, our methods are applicable to both positive and negative interactions. The latter have been termed antagonistic interactions or negative regulation. In human data, few examples of this type of interaction have been documented [24,25,26]. Also, for example, modifier genes are known to increase or decrease the risk or speed up or delay the time of onset of AIDS [27,28].

Stratification of Data

The idea underlying our approach is simple and has previously been applied in an ad hoc manner [6,7]. Given a SNP (here called test SNP) with known or suspected disease association, we aimed to find a variant (here called target SNP) causing a disease through its association with the test SNP and its own possibly small main effect. We stratified the data using the three genotypes of the test SNP and carried out an association analysis for each of the resulting three subsets of the data. Genotypes at the test and target SNPs form a 3 × 3 contingency table with a total of 8 degrees of freedom (d.f.), 2 d.f. for each of the two main effects and 4 d.f. for the interaction between the two SNPs. Epistatic effects may be detected by a 4-d.f. test for interaction [29] but, as outlined below, here we propose a 6-d.f. test for interaction and main effect at the target SNP.

To see the motivation for our approach, consider a two-locus model previously proposed to show strong epistatic interaction in the absence of main effects at the two loci [30]. We modified this model in the following manner. The test locus has genotypes AA, AB, and BB, with allele frequency p = P(B) = 0.50, while the target locus has genotypes CC, CD, and DD with allele frequency q = P(D) = 0.20, where genotype frequencies are given by the Hardy-Weinberg law. Penetrances at the nine two-locus genotypes are shown in table 1 and are the same as in the original publication [30]. For given sample sizes of cases and controls, n = 20 each, we compute expected numbers of observations at the nine genotypes in case and control individuals. The main (marginal) effect of a locus is then given by the likelihood ratio (LR) χ² obtained from a 2 × 3 table of genotypes, where the two rows correspond to cases and controls and the three columns represent the three genotypes, while the body of the table contains expected numbers of observations. The resulting expected numbers, based on the penetrances in table 1, lead to χ² (2 d.f.) values of 12.78 and 0 for the test and target loci, respectively. Thus, the target locus shows no main effect while the test locus main effect is rather strong, so that a ‘regular’ case-control association analysis has no chance of ever detecting the target locus on its own. However, when the data are subdivided into the three genotypes at the test SNP, the resulting 2 × 3 genotype tables each show strong conditional effects of the target locus. The expected χ² values (2 d.f. each) are 7.20, 10.69, and 15.20 for genotypes AA, AB, and BB, respectively. Thus, this simple device of stratifying the data by test locus genotypes has the potential to exhibit target locus effects that are hidden in the overall picture of things. For an in-depth discussion of purely epistatic inheritance models, see Culverhouse et al. [31].

Table 1.

Penetrances adapted from a modified Frankel and Schork [30] model of two epistatically interacting trait variants with allele frequencies of P(B) = 0.50 and P(D) = 0.20

Test locus	Target locus			Marginal penetrance
	CC	CD	DD
AA	0	0	1	0.04
AB	0	0.5	0	0.16
BB	1	0	0	0.64
Marginal penetrance	0.25	0.25	0.25

Methods

Test Statistics for Data Stratification

Assume that in the data for a given test locus genotype (AA, AB, or BB), we test for association by χ² statistic in a 2 × 3 genotype table with the rows corresponding to cases and controls and the three columns representing the target SNP genotypes CC, CD, and DD. For an overall assessment of the association between target locus and disease, given the test locus genotypes, we aim to combine the three (independent) test statistics in a suitable manner. The two simplest statistics are the sum, T_sum, and the maximum, T_max, of the three χ². Under H₀, T_sum follows a χ² distribution with 6 d.f. The significance level of T_max is given by the p value, p_min, of the largest of the three χ². As three independent data sets are tested, the probability that one or more of them show a χ² exceeding T_max is given by 1 – (1 – p_min)³ (Bonferroni-type correction for multiple testing).

To our knowledge, only one conditional search method, the overall conditional genotype (OGT) method [32,33], has previously been proposed with the aim to find additional genes in the HLA region based on previously detected HLA variants. It applies the same principle of data stratification but, based on marginal genotype frequencies of controls at the target locus, it estimates marginal expected numbers of cases and compares them with observed marginal numbers of genotypes at the target locus. This comparison is then tested with a χ² statistic, here referred to as T_OGT. Its definition is fairly involved and has explicitly been given elsewhere [32].

Partitioning of χ²

Consider a 2 × 9 contingency table, the two rows of which correspond to cases and controls, and the nine columns represent all pairs of genotypes at two SNPs. χ² (8 d.f.) for this table comprises the main association effects of the two SNPs and all interaction effects between the two SNPs. We view the layout of such a 2 × 9 table as a hierarchical design [34]. The data are first stratified by a factor with three levels, AA, AB, and BB (the three genotypes at the test locus), and then further subdivided within each stratum. In analogy to the probability formula P(L₁, L₂) = P(L₁) P(L₂∣L₁), where L₁ refers to the test locus and L₂ to the target locus genotypes, the total χ² for the 2 × 9 table may be partitioned into two components [34], one due to the (main) effects of the test SNP and the other due to main effects at the target locus and its interactions with the test locus. A specific example is shown in table 2 and referred to again in the Application section. This partitioning of χ² is a standard approach in hierarchical designs [34]. It is evident from its construction that the test statistic, T_sum, is identical with the sum of the two χ² due to ‘Target SNP main effect’ and ‘Interaction’ (table 3), which may be obtained as the difference between the total χ² for the 2 × 9 table and the main effect χ² from the marginal 2 × 3 table of the test SNP. Thus, data stratification in genetic analysis has a well-established statistical foundation.

Table 2.

Numbers of genotypes at two SNPs in a genome-wide case-control study of age-related macular degeneration [38]

Test:	AA			AB			BB
Target:	CC	CD	DD	CC	CD	DD	CC	CD	DD
Cases	1	1	4	19	31	8	12	9	11
Controls	3	3	0	14	14	8	30	53	1

Test SNP = SNP_A-1702501, target SNP = rsl957491.

Table 3.

Partitioning of x² for the data in table 2

Source	χ2	d.f.
Test SNP main effect	25.2921	2
Target SNP main effect	12.8013	2
Interaction by subtraction	25.1310	4
Total	63.2244	8

At this point, we are ready to formulate the null hypothesis, H₀, for our test: absence of ‘Target SNP main effect’ and absence of ‘Interaction’.

In case-control studies, tests for epistatic interaction between two SNPs may be formulated within the framework of logistic regression [29,35]. Because of the asymptotic equivalence between χ² tests and logistic regression analysis, our T_sum statistic may also be obtained via logistic regression, which is discussed below.

Power Simulations

In order to see the usefulness of the test statistics considered here (T_sum, T_max, and T_OGT mentioned above) and to compare their power to detect a target SNP, we carried out computer simulations under controlled statistical conditions. Thus, we generated case and control data (n = 200 each, except where noted otherwise) for several common inheritance models and analyzed them with each of the three test statistics, choosing a threshold for significance such that power = 0.05 under the null hypothesis. As mentioned, our interest is in models with weak or absent main effects of the target variant. The different models are generally calibrated to predict a population prevalence of 5%, that is, they represent a fairly common genetic trait. The power simulations reported below refer to stage 2 analysis and do not take into account how test SNPs were obtained at stage 1. That is, genotypes are generated for two SNPs, the test and target SNP. In practice, of course, researchers will generally work with large numbers of SNPs (see Practical Application below), but here we want to compare relative power for different analysis methods rather than absolute power in a genome-wide setting.

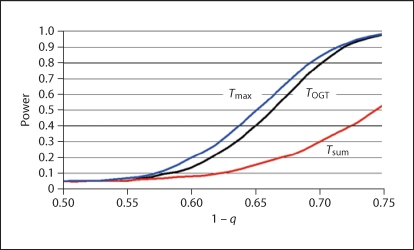
Adapted from the modified Frankel and Schork [30] model demonstrated in table 1, power (y-axis) in figure 1 is shown as a function of 1 – q (x-axis), where q is the allele frequency P(D) at the target SNP. The main effect of the test SNP is zero at q = 0.5 and increases with increasing value of 1 – q. In this model, T_max is most powerful, closely followed by T_OGT, while T_sum is much less powerful. This model is perhaps not very realistic, and we use it mainly to document that our method can easily find a disease susceptibility variant that has no main effect but exerts disease association through its strong epistatic interaction with the test locus.

Fig. 1.

Power (y-axis) as a function of 1 q (q = allele frequency of target locus) of three conditional test statistics adapted from the modified Frankel and Schork [30] model shown in table 1.

Next, we considered a logistic regression model with increasing interaction effects and target SNP main effects, where the latter are at most 1/6 of those at the test SNP. The model equation reads

$$log\left[\phi /\left(1-\phi \right)\right]=c_0+c_1{x}_1+c_2{x}_2+s\left[c_1{x}_3+c_2{x}_4\right]/6+s{c}_1\left(x_1+x_2\right)\left(x_3+x_4\right)/2,$$

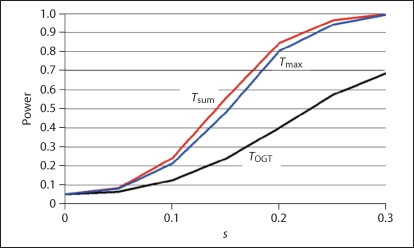
where φ is the conditional probability of being affected given model parameters. The two d.f. of the test SNP genotypes are modeled by two independent dummy variables, x₁ = (−1, 0, +1) and x₂ = (−1, +2, −1), with x₃ and x₄ being the corresponding quantities for the target locus [29,36]. We arbitrarily defined c₁ = 1.2 and c₂ = 0.2, and adjusted c₀ to achieve a population prevalence of 5%. Given these parameter settings, we computed power as a function of s, with s = 0 representing the absence of interaction effects and target locus main effects. As seen in figure 2, the T_sum statistic is most powerful, closely followed by T_max, while T_OGT has considerably less power.

Fig. 2.

Power (y-axis) as a function of a parameter s (x-axis) in a logistic regression model, where s is a measure of target SNP main and interaction effects.

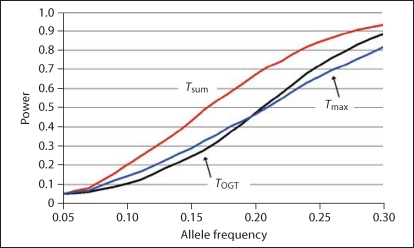
Finally, we adopted the two-locus multiplicative interaction model from figure 1 in Marchini et al. [13], with α = 0.1, θ = 0.5, and n = 500 cases and controls each, where α are baseline odds for a disease and θ represents a genotypic effect. We take the A locus to be our test SNP and compute power (y-axis in fig. 3) as a function of its allele frequency (x-axis), with P(A) = 0.05 as the baseline. The target locus (B locus [13]) with a fixed allele frequency of 0.5 has little main effect. Here again, T_sum has most power, while the other two statistics are clearly less powerful.

Fig. 3.

Power (y-axis) as a function of the allele frequency (x-axis) of the A locus in Marchini et al.'s [13] multiplicative interaction model.

We also investigated the power for a few other genetic models (not shown here) and generally found the T_OGT statistic to be the least powerful for our purpose of finding variants with low or absent main effects. The T_sum statistic often had somewhat more power than T_max.

Practical Application

In practice, the approach proposed here will be carried out in GWAS with possibly large numbers of interdependent SNPs. Also, the fact that test SNPs are ascertained at stage 1 for having marginal association effects may impact significance levels at stage 2 [15]. Thus, we advocate that both stages (finding the test SNP, testing the target SNP) be evaluated in a permutation framework, which will yield proper significance levels, that is, the type 1 error will be controlled for stages 1 and 2 combined. An additional benefit of permutation tests is that they automatically take care of multiple testing in GWAS and of the linkage disequilibrium between SNPs. Software (sumstat program) for these calculations has been made generally available (test statistic code 20, http://linkage.rockefeller.edu/ott/sumstat.html) and computes genome-wide p values corrected for multiple testing.

Application

To demonstrate our approach on a well-known dataset with established results, we applied the T_sum statistic to case-control data on age-related macular degeneration (AMD) [37,38]. Initially, we analyzed the first of these two datasets but did not find any significant SNPs when conditioned on the genotypes of the three most significant SNPs (results not shown). This finding is in agreement with a previous observation of no significant interactions among SNPs in this dataset [19]. Thus, we turned to the second of these two studies, that is, AMD data collected in Hong Kong [38]. After our quality control procedures, this dataset comprised 81,934 SNPs genotyped on 96 case and 127 control individuals. Previous analysis resulted in a significantly disease-associated SNP, rs10490924, whose functional significance had been established experimentally [38].

For our conditional analyses, χ² statistics were computed for the 2 × 3 genotype table of each SNP. After ordering the SNPs by decreasing χ², the best few SNPs were considered test SNPs. For a given test SNP, the T_sum statistic was carried for each of the 81,933 SNPs in the dataset and the largest of these among all SNPs was taken to be our genome-wide test statistic. This whole procedure was repeated in 10,000 randomization samples (sumstat program; labels case and control randomly permuted). The associated empirical significance level, p, was given by the proportion of randomization samples whose largest T_sum statistic was at least as large as the largest observed T_sum.

We selected a small set of test SNPs based on their χ² value. Table 4 shows the four best SNPs with p < 0.30 in the χ² test at stage 1 (the next ranked SNP has p = 0.58). For a conditional analysis as proposed here, there is no need for test SNPs to be significant; here we chose the most significant ones as this seems to be the most plausible approach to pick SNPs with disease involvement. For each of these four SNPs, one analysis was carried out in which the given SNP served as the test SNP and was tested against each of the variants (target SNPs) in the dataset.

Table 4.

The four SNPs with p values less than 0.30 (genotype test) in a genome-wide screen for variants associated with age-related macular degeneration [38]

Rank	SNP	Chrom.	Position	χ2	P
1	rs10490924	10	124204438	50.9622	0.0001
2	rs10504152	8	54292668	31.8137	0.0065
3	SNP_A-1702501	0	0	25.2921	0.1880
4	rs10520462	4	182400252	24.6355	0.2503

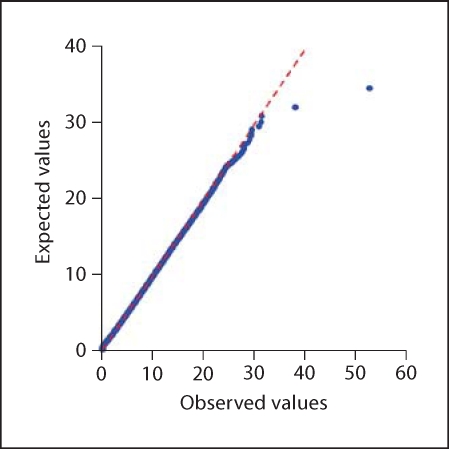
For several of the four test SNPs, highly significant results occurred with rs10490924 as the target SNP. However, this finding simply reflects the known strong main effect of rs10490924 and was disregarded. Two of the test SNPs furnished significant results (table 5): SNP_A-1702501 as the test SNP resulted in T_sum = 37.93 with rs1957491 as the target SNP (p = 0.0557), and rs10520462 as the test SNP resulted in T_sum = 37.42 with rs1599796 as the target SNP (p = 0.0179), where the reported p values are specific for one test SNP and incorporate the whole procedure of finding that test SNP at stage 1 and testing a target SNP at stage 2. The evidence for association with a disease of the two new SNPs, rs1957491 and rs1599796, is not strong but still significant or at least close to it. As the probability plot (carried out with Systat software) in figure 4 shows, despite the modest p value of 0.0557, at least two target SNPs exhibit unusually large values for SNP_A-1702501 as the test SNP. At any rate, the main effects in terms of χ² from the 2 × 3 genotype tables of these two SNPs are low (p = 0.18 and 1.00, respectively). Thus, these SNPs could not have been found by single-locus analysis, but they appear to be associated with a disease through interaction with one of the four strongest SNPs in this analysis. Table 2 shows observed numbers of genotypes at SNPs SNP_A-1702501 (test SNP) and rs1957481 (target SNP). In a genome-wide search, the target SNP main effect of χ² = 12.8013 (2 d.f.) is too small to be detected.

Table 5.

Two SNPs from table 4 serving as test SNPs and their best target SNPs

Test SNP	Target SNP
	name	chrom.	position	Tsum	P	p main
SNP_A-1702501	rs1957491	14	43379465	37.9323	0.0557	0.1809
rs10520462	rs1599796	3	120726624	37.4237	0.0179	1.0000

Fig. 4.

Probability plot (Q-Q plot) for all values of T_sum with SNP_A-1702501 as the test SNP in the AMD dataset [38]; observed values are on the x-axis while expected values, based on the χ² distribution with 6 d.f., are plotted on the y-axis.

It is not the purpose of this paper to discuss AMD genetics and the functional relevance of the two suggestive SNPs found here. However, at least one of them, rs1599796, may well have a real effect. It is located on chromosome 3q13.33 in C3orf1, which has been described as encoding a membrane protein and showing generalized expression in all tissues [39].

Discussion

We made use of the concept of finding new loci anywhere in the genome, well-known in linkage analysis, given previously established disease-associated loci, and extended this approach to human case-control association studies. Of course, instead of conditioning on established loci, researchers may want to condition on candidate variants whether or not they show strong association with a disease. Our approach is analogous to the two-stage strategy proposed by Marchini et al. [13] in that loci detected at stage 1 do not themselves need to be significant, but our approach is different in that, at stage 2, we use a simple conditional test statistic instead of a full logistic regression analysis.

In addition to references already mentioned, several other papers have recommended two-stage procedures. Specifically, Kooperberg and Leblanc [40] focus on gene-gene interactions between SNPs with some marginal effects. Also, gene-environment approaches have been developed [41] that in the first stage select specific environmental effects and, in the second stage, carry out conditional tests similar to the ones proposed here.

Our favored test statistic is the sum, T_sum, over χ² values with 2 d.f. for the three genotypes at a given test locus. Of course, various refinements may be possible here. For example, association tests more powerful than the standard χ² genotype test have been described [42,43] and could be implemented in connection with our approach. Also, an allelic form of these methods would condition on the three genotypes of the test SNP but then compute χ² for 2 × 2 tables of alleles, so that the sum of χ² over the three test SNP genotypes would have 3 d.f. However, the main purpose of our paper has been to demonstrate the usefulness of the principle of conditional search rather than fleshing out specific refinements. Because epistatic effects are likely to be ubiquitous [44], conditional approaches like the one suggested here are expected to be extremely useful in GWAS.

It should be pointed out that ‘Interaction’ is a concept that has been defined and interpreted in different ways. Two important classes are essential and removable interactions, where the latter are robust to changes in scale [45]. Recently, methods have been developed to search for essential interactions on a genome-wide scale [46].

As mentioned above, χ² analyses leading to T_sum may also be carried out with logistic regression analysis. However, in samples of small sizes, like the ones discussed here, logistic regression analysis may fail (the iterative maximum likelihood estimation may not converge). While χ² analyses are also then unreliable when p values are obtained under large-sample assumptions (based on tables of the χ² distribution), permutation tests do not rely on distributional assumptions of the test statistic. In larger samples, the main advantage of logistic regression analysis is that risk factors other than SNP genotypes may be allowed for.

As pointed out by an anonymous reviewer, our approach (and power calculation) assumes that the test SNP is correctly identified in the stage 1 analysis. Of course, it is possible that the test SNP reflects a false-positive result, particularly when its significance is only marginal. However, when both stages 1 and 2 are evaluated in randomization samples (permutation testing) then any uncertainty as to the validity of the test SNP will be reflected in the overall significance level (see Practical Application).

Electronic Resources

Sumstat program: http://www.big.ac.cn/genemapping/ or http://linkage.rockefeller.edu/ott/.

Systat software: http://www.systat.com.

AMD dataset: http://variation.yale.edu/dataDownload.html.