Abstract
Imputation of genotypes for markers untyped in a study sample has become a standard approach to increase genome coverage in genome-wide association studies at practically zero cost. Most methods for imputing missing genotypes extend previously described algorithms for inferring haplotype phase. These algorithms generally fall into three classes based on the underlying model for estimating the conditional distribution of haplotype frequencies: a cluster-based model, a multinomial model, or a population genetics-based model. We compared BEAGLE, PLINK, and MACH, representing the three classes of models, respectively, with specific attention to measures of imputation success and selection of the reference panel for an admixed study sample of African Americans. Based on analysis of chromosome 22 and after calibration to a fixed level of 90% concordance between experimentally determined and imputed genotypes, MACH yielded the largest absolute number of successfully imputed markers and the largest gain in coverage of the variation captured by HapMap reference panels. Following the common practice of performing imputation once, the Yoruba in Ibadan, Nigeria (YRI) reference panel outperformed other HapMap reference panels, including 1) African ancestry from Southwest USA (ASW) data, 2) an unweighted combination of the Northern and Western Europe (CEU) and YRI data into a single reference panel, and 3) a combination of the CEU and YRI data into a single reference panel with weights matching estimates of admixture proportions. For our admixed study sample, the optimal strategy involved imputing twice with the HapMap CEU and YRI reference panels separately and then merging the data sets.
Keywords: admixture, African American, coverage, reference panel
INTRODUCTION
Current genome-wide association studies include a dense set (>100,000) of experimentally genotyped markers across the genome in thousands of individuals using commercially available chips. One way to fill in the gaps between typed markers is to use genotype or haplotype data from an established reference panel to impute genotypes for markers untyped in the study sample. The HapMap project provides one publicly available source of reference panels [The International HapMap Consortium, 2003; The International HapMap Consortium, 2007]. Phase II of the HapMap project consists of genotypes for >3.1 million single nucleotide polymorphisms (SNPs) assayed for 30 trios of Utah residents with ancestry from Northern and Western Europe (CEU), 45 unrelated Han Chinese in Beijing, China (CHB), 45 unrelated Japanese in Tokyo, Japan (JPT), and 30 trios from the Yoruba ethnic group in Ibadan, Nigeria (YRI), yielding a total of 420 founder chromosomes [The International HapMap Consortium, 2003; The International HapMap Consortium, 2007].
In comparison, the HapMap Phase III project consists of genotypes for ~1.5 million SNPs assayed for samples of individuals from seven additional populations (http://www.hapmap.org). The seven new reference panels include: African ancestry in Southwest USA (ASW), Chinese in metropolitan Denver, Colorado (CHD), Gujarati Indians in Houston, Texas (GIH), Luhya in Webuye, Kenya (LWK), Mexican ancestry in Los Angeles, California (MEX), Maasai in Kinyawa, Kenya (MKK), and Toscans in Italy (TSI). These new panels capture more global variation and provide more choices for a single best reference panel with potentially increased coverage. However, SNP density is less for these seven panels than for the original four reference panels, thereby providing less coverage. Given the eleven HapMap reference panels, an open and important question is which choice of reference panel(s) most increases genomic coverage for a given study sample.
If a study sample consists of individuals with well-defined ancestry similar to one of the reference panels, then it is appropriate to use that one reference panel (the “single best” approach). However, if the study sample consists of individuals with ancestry partially similar to more than one of the reference panels, as may occur by admixture, then the choice of reference panel(s) is not as straightforward. Suggested methods for reference panel selection for this latter situation include the “cosmopolitan” and the “weighted mixture” approaches. The “cosmopolitan” approach combines all available reference data (e.g., HapMap data) into a single reference panel [de Bakker et al., 2006]. The “weighted mixture” approach involves the generation of mixtures of the available reference data. Weights can be determined empirically in order to maximize coverage [Pemberton et al., 2008] or imputation accuracy [Huang et al., 2009]. Alternatively, weights can be specified to match estimates of admixture proportions, which may outperform the cosmopolitan approach because greater weight is given to the HapMap reference panels with more similar ancestry to the study sample [Egyud et al., 2009].
Most current methods for imputing missing genotypes are extensions of previously described algorithms for inferring haplotype phase and have been reviewed in detail [Browning, 2008]. We classified several existing programs on the basis of the underlying model for estimating the conditional distribution of haplotype frequencies (Table I). One class is based on localized clusters of haplotypes and includes BEAGLE [Browning and Browning, 2007] and fastPHASE [Scheet and Stephens, 2006]. Both BEAGLE and fastPHASE use a hidden Markov model to cluster haplotypes but BEAGLE is more parsimonious by allowing fewer possible transitions and emissions. fastPHASE fixes the number of clusters in the model whereas BEAGLE dynamically varies the number of clusters at each locus. A second class is based on a multinomial model of haplotype frequencies and includes PLINK [Purcell et al., 2007] and SNPMStat [Lin et al., 2008]. Methods based on the multinomial model estimate haplotype frequencies using an expectation-maximization algorithm but can only consider a window of a few markers at a time because haplotype frequencies become too low for accurate estimation otherwise. A third class is explicitly based on population genetics and includes IMPUTE [Marchini et al., 2007] and MACH [Li et al., 2006; Li et al., 2007]. Whereas cluster models are informally based on population genetic principles, IMPUTE is formally based on population genetic parameters in the coalescent framework [Marchini et al., 2007]. IMPUTE conditions imputation on user-supplied reference haplotypes (i.e., IMPUTE does not infer haplotype phase) and a recombination map. MACH can accept either reference genotypes or reference haplotypes and can either continuously update the recombination map and error rates based on the reference panel and study sample together or condition imputation based on maximum-likelihood estimates generated from only the reference panel.
TABLE I.
Characteristics of six currently used imputation programs
| Feature | IMPUTE | MACH | fastPHASE | BEAGLE | PLINK | SNPMStat |
|---|---|---|---|---|---|---|
| Use phenotype | no | no | no | no | no | yes |
| Requires phased data | yes | no | no | no | no | no |
| Model underlying conditional distribution of haplotypes | population-genetic | population-genetic | cluster-based | cluster-based | multinomial | multinomial |
| Explicitly models population structure | no | no | yes | no | no | no |
| Models admixture | no | no | no | no | no | no |
A recent simulation study focused on imputation accuracy for BEAGLE, fastPHASE, IMPUTE, MACH, and PLINK using 250 kb exemplary regions and the HapMap phase II CEU reference panel [Pei et al., 2008]. Another recent study examined both imputation accuracy and efficacy for BEAGLE, IMPUTE, MACH, and PLINK for genome-wide imputation on a sample of German individuals, also using the HapMap phase II CEU reference panel [Nothnagel et al., 2009]. Two groups have investigated imputation for an admixed study sample; one study was based solely on IMPUTE [Zhao et al., 2008] and the other study was based solely on fastPHASE [Pemberton et al., 2008]. Here, we performed a two-way comparison of the major classes of imputation algorithms and the selection of reference panel(s) specifically for an admixed (African American) study sample.
We had three main objectives in this study: 1) we investigated how well different programs for imputation work for an admixed study sample consisting of African Americans; 2) we investigated how to choose an appropriate reference panel for an admixed study sample; and 3) because each program reports different measures of imputation success, we investigated measures of imputation success and the calibration of these measures across the different programs in order to draw meaningful comparisons.
MATERIALS AND METHODS
STUDY SAMPLE
The Howard University Family Study (HUFS) is a study of African American families and unrelated individuals from the Washington, D.C. metropolitan area [Adeyemo et al., 2009]. In the first phase of recruitment, the HUFS enrolled and examine a randomly ascertained cohort of 350 African American families with members in multiple generations. Families were not ascertained based on any phenotype. In the second phase of recruitment, additional unrelated individuals from the same geographic area were enrolled to facilitate nested case-control study designs. The enrollment procedures (questionnaires, clinical measurements, and lab assays) for unrelated individuals were identical to those for the families. The total number of recruited individuals was 2,028, of which 1,976 remained after data cleaning. Ethical approval was obtained from the Howard University Institutional Review Board and written informed consent was obtained from each participant.
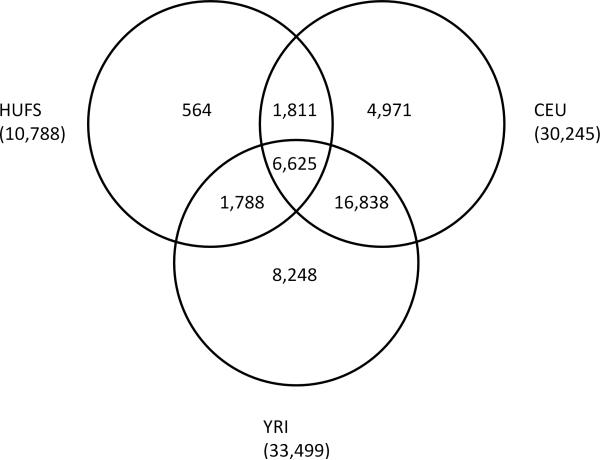
Genome-wide genotyping was performed using the Affymetrix Genome-Wide Human SNP Array 6.0 and genotypes calls were made using the Birdseed algorithm, version 2 [Korn et al., 2008]. We had four genotype inclusion criteria: the individual sample success rate had to be ≥90% (no samples excluded), the SNP success rate had to be ≥95% (41,885 SNPs excluded), the minor allele frequency had to be ≥0.01 (19,154 SNPs excluded), and the p-value for the test of Hardy-Weinberg equilibrium had to be ≥1.0×10-3 (6,317 SNPs excluded). We retained 10,788 SNPs from chromosome 22 (Fig. 1) as the analysis set for this investigation.
Fig. 1.
Distribution of 40,845 SNPs across the study sample and HapMap phase II reference panels for chromosome 22.
REFERENCE PANELS
We retrieved the HapMap release 23a CEU (n = 60 founders) and YRI (n = 60 founders) phase II genotype data for chromosome 22 from http://www.hapmap.org. Quality control filters for inclusion were a minor allele frequency of ≥1%, a genotyping success rate ≥80%, a Hardy-Weinberg equilibrium test p-value ≥1.0×10-3, ≤1 Mendelian inheritance error, and ≤1 duplicate discrepancy. These quality control filters were applied to the two panels separately. After data cleaning, the phase II CEU reference panel consisted of 30,245 SNPs, the phase II YRI panel consisted of 33,499 SNPs, and the combined phase II CEU+YRI reference panel consisted of 40,281 SNPs (Fig. 1).
We also retrieved the HapMap release 2 ASW (n = 49 founders), CEU (n = 112 founders), and YRI (n = 113 founders) phase III genotype data for chromosome 22. There were 12,941 SNPs that passed quality control in all three phase III reference panels.
SOFTWARE
BEAGLE (version 3.0.1)
BEAGLE uses a localized haplotype clustering-based algorithm [Browning and Browning, 2007]. First, it clusters haplotypes at each marker and defines a hidden Markov model to find the most likely haplotype pairs based on the individual's known genotypes. Then, the most likely genotype at untyped loci can be imputed from final haplotype pairs. Due to extensive memory usage, we cut the study sample into three sets of 500 individuals and one set of 476 individuals and we invoked the low memory command line option. By default, the posterior probabilities for the three genotypes at each SNP for each individual are printed in an output file. Software is available at http://www.stat.auckland.ac.nz/~browning/beagle/beagle.html.
MACH (version 1.0.16)
MACH implements a Markov chain Monte Carlo-based algorithm to infer possible pairs of haplotypes for each individual's genotypes (including untyped genotypes) [Li et al., 2006; Li et al., 2007]. Following the authors’ recommendation in the provided documentation, we used a two-stage procedure. First, we inferred haplotype phase for the reference panel using 50 rounds of the Markov chain sampler and allowing at most 200 haplotypes when updating the phase for each individual. Second, we conditioned imputation on the first-stage maximum-likelihood estimates of the crossover map, which specifies the likely locations of haplotype transitions, and the error rate map, which specifies unusual markers based on a combination of discrepancies between the reference panel and study sample data, genotyping error, and recurrent mutation. MACH produces an output file containing the posterior probabilities for two of the three genotypes at each SNP for each individual. Software is available at http://www.sph.umich.edu/csg/abecasis/MACH/download/.
PLINK (version 1.03)
Although the exact algorithm is unpublished, according to the documentation, PLINK appears to directly estimate haplotype frequencies using an expectation-maximization algorithm based on a multinomial model [Purcell et al., 2007]. We used default parameter settings as follows: selecting at most 5 proxy SNPs, searching up to 15 SNPs around the index SNP, searching within 250 kb around the index SNP, genotype missingness of ≤0.2 at proxy SNPs, and a minor allele frequency of ≥0.005 at proxy SNPs. PLINK produces an output file containing the posterior probabilities for the three genotypes at each SNP for each individual. Software is available at http://pngu.mgh.harvard.edu/purcell/plink/.
IMPUTATION ACCURACY
Each program returns the full probability distribution of the imputed genotypes at each SNP for each individual. We generated discrete imputed genotypes by accepting a call if the posterior probability for a genotype reached a pre-specified threshold or recorded the genotype as missing otherwise. For the phase II data, of the 10,788 SNPs experimentally genotyped for chromosome 22, 10,224 SNPs were present in the combined reference panel (Fig. 1). We masked the experimentally determined genotypes for a randomly selected 2% of these SNPs in the study sample, yielding ~200 masked SNPs for each of the three reference panels (phase II CEU, phase II YRI, and phase II CEU+YRI). Similarly, when using the phase III reference data, we masked 200 of the SNPs in the study sample. Due to the fact that both experimentally determined and imputed genotypes are called with some degree of error, we cannot know which call (if either) is correct, so we report concordance rather than accuracy. Concordance was defined as the proportion of genotype calls for which both imputed alleles matched the experimentally determined genotype call for a SNP, averaged over all masked SNPs. The genotype error rate was defined as one minus the concordance.
IMPUTATION YIELD
We first calibrated each of the combinations of program and reference panel by determining the threshold of posterior probability required to achieve a concordance of 90% between imputed and experimentally determined genotypes for typed markers. We then filtered each imputed SNP based on a χ2 test of Hardy-Weinberg equilibrium at a significance level of 0.05. The purpose of this test was to detect genotype-specific imputation failure, and we were intentionally conservative about calling imputation successful because an imputed genotyping error rate of 10% is much higher than the estimated experimental genotyping error rate of 0.5% [The International HapMap Consortium 2003; The International HapMap Consortium, 2007]. We anticipated some level of Hardy-Weinberg disequilibrium due to admixture in the study sample. However, simulation studies have shown that the power of the Hardy-Weinberg test to detect disequilibrium due to admixture is low unless the difference in allele frequencies is large (>0.4) and the minor admixture proportion is high (>0.2) [Deng et al., 2001]. Similarly, simulation studies have shown that the power of the Hardy-Weinberg test to detect disequilibrium due to genotyping errors at typed markers is also low given the estimated error rates for experimental genotyping [Leal, 2005; Cox and Kraft, 2006]. Nevertheless, because the Hardy-Weinberg test has moderate power to detect disequilibrium at an error rate of 10% at untyped markers, we posit that Hardy-Weinberg disequilibrium at untyped markers is most likely due to imputation error.
Imputation efficacy has been defined as the proportion of imputable SNPs for which imputation was deemed successful [Nothnagel et al., 2009]. In keeping with this definition, we defined imputation yield as the absolute number of reference SNPs (i.e., SNPs in the reference panel but not in the study sample) for which imputation was deemed successful. Using the software Haploview [Barrett et al., 2005], available at http://www.broad.mit.edu/mpg/haploview/, we estimated coverage of HapMap variation [Barrett and Cardon, 2006] for a given reference panel based on tag sets consisting of the HUFS study sample with and without successfully imputed SNPs. Briefly, coverage was measured by pairwise correlation between a tag SNP and a potentially captured SNP. A potentially captured SNP was considered covered if r2 ≥ 0.8 between itself and any tag SNP. Coverage was reported as the proportion of the set of potentially captured SNPS covered by the set of tag SNPs.
POPULATION STRUCTURE ANALYSIS
Individual admixture proportions were estimated using a panel of 2,076 ancestry-informative SNPs assuming two clusters and uncorrelated allele frequencies with a 10,000 step burn-in and a 100,000 step chain using STRUCTURE (version 2.2) [Falush et al., 2003]. Ancestry-informative SNPs had the following characteristics 1) a minor allele frequency ≥ 0.01 in both the HapMap phase II CEU and YRI samples, 2) a difference in allele frequencies between the HapMap CEU and YRI samples ≥ 0.6, and 3) an r2 ≤ 0.4 with other SNPs within 1 Mb.
RESULTS
To make fair comparisons about imputation accuracy across BEAGLE, MACH, and PLINK, we needed a summary statistic that we could apply consistently to each program's output. We chose to measure imputation accuracy in terms of genotype concordance, which we defined as the proportion of imputed and experimentally determined genotypes that matched, based on a discrete imputed call being the genotype with a posterior probability exceeding a user-defined threshold. To measure imputation yield, we first calibrated the threshold of posterior probability for each combination of program and reference panel in order to achieve concordance of 0.90, equivalent to an error rate of 10% (the “fixed error rate” approach). Based on this calibration, we assessed the imputation yield and coverage after filtering the imputation results based on a test of Hardy-Weinberg equilibrium to screen for genotype-specific imputation failure. This procedure is analogous to estimating power after controlling the false positive error rate in classical hypothesis testing.
Within the three compared reference panels (i.e., CEU, YRI and unweighted CEU+YRI), imputation yield was highest for BEAGLE using the unweighted phase II CEU+YRI reference panel (Table II). In contrast, imputation yield was highest for MACH using the phase II YRI reference panel. Notably, imputation yield was higher for MACH than for BEAGLE irrespective of the tested reference panel. PLINK failed to achieve an error rate of 10% for all tested reference panels and so yielded no successfully imputed SNPs. Despite the remarkable success of the YRI as a reference panel for this African American sample, it is important to point out that it cannot serve as a reference for those SNPs (n = 6,782) present in the phase II CEU reference panel but not in the phase II YRI reference panel (Fig. 1). Interestingly, when the phase II CEU reference panel was used as the sole reference panel, the lowest error rate that MACH could achieve for this specific set of SNPs was 22.3%; this observation suggests that high quality imputation may not be achievable for SNPs segregating only in an ancestral population making a minor contribution to an admixed population.
TABLE II.
Imputation yield using the fixed error rate approach
| Software | Phase II Reference Panela | Threshold b | Yield |
|---|---|---|---|
| BEAGLE | CEU | 0.967 | 575 |
| YRI | 0.824 | 1,976 | |
| Unweighted CEU+YRI | 0.832 | 3,847 | |
| MACH | CEU | 0.999 | 3,121 |
| YRI | 0.688 | 13,927 | |
| Unweighted CEU+YRI | 0.946 | 10,341 | |
| Weighted CEU+YRI | 0.939 | 9,025 | |
| PLINK | CEU | NA | 0 |
| YRI | NA | 0 | |
| Unweighted CEU+YRI | NA | 0 |
Error rates were fixed at 10% for these analyses.
The phase II CEU and YRI reference panels both consist of 60 founders. The unweighted CEU+YRI panel consists of all 120 CEU and YRI founders in a single reference panel. A weighted CEU+YRI reference panel consisted of 48 randomly chosen YRI founders and 12 randomly chosen CEU founders consistent with observed admixture proportions of ~80% and ~20%, respectively. Results shown for the weighted panel approach are averages of 30 randomly generated panels.
Threshold indicates the minimum posterior probability for imputing discrete genotype calls to achieve concordance between imputed and observed genotypes of 0.90, equivalent to a fixed 10% error rate. NA indicates that the program could not achieve concordance of 0.90 using the reference panel.
We also investigated the weighted mixture approach to reference panel selection using just MACH based on its superior performance from the above analyses. Using STRUCTURE, the HUFS sample showed admixture proportions of 78–81% YRI and 19–22% CEU. Based on these estimates, we generated 30 reference panels, each consisting of 48 randomly chosen phase II YRI founders and 12 randomly chosen phase II CEU founders. On average, the weighted mixture approach yielded slightly fewer SNPs than the unweighted mixture approach (Table II). This result indicated that matching the reference panel to estimates of admixture proportions did not optimize imputation yield.
We further investigated the optimal strategy for imputing missing genotypes for an admixed sample such as the HUFS. Of the 3,121 successfully imputed SNPs using the phase II CEU reference panel, 394 were present only in the phase II CEU reference panel and 2,727 were present in both phase II CEU and YRI reference panels. Similarly, of the 13,927 successfully imputed SNPs using the phase II YRI reference panel, 3,688 were present only in the phase II YRI reference panel and 10,239 were present in both phase II CEU and YRI reference panels. Taken together, we were able to impute 394 SNPs present only in the phase II CEU reference panel, 3,688 SNPs present only in the phase II YRI reference panel, and 10,760 SNPs present in both phase II CEU and YRI reference panels, for a total yield of 14,842 SNPs. This result clearly demonstrates that, at least for our admixed sample of African Americans, the optimal strategy in terms of maximizing imputation yield is to impute missing genotypes separately from the ancestral reference panels and then combine the results.
As would be expected a priori, there were some inconsistencies in the genotypes of the 10,760 SNPs that were successfully imputed using the separate ancestral reference panels (CEU and YRI). Obviously, this issue needs resolution before generated datasets can be merged. The simplest protocol to address this situation is to preferentially accept the imputed genotypes resulting from the reference panel giving the highest concordance, which for our data would lead to a preference of calls based on the phase II YRI reference panel over calls based on the phase II CEU reference panel.
The imputation yield, defined as the nominal number of SNPs imputed successfully, may represent an overestimation of gain because imputation requires high levels of linkage disequilibrium to perform well. To measure the effective gain through imputation accounting for linkage disequilibrium, we estimated the increase in coverage of HapMap variation on chromosome 22 from using the set of tag SNPs on the chip to using the combined set of tag SNPs on the chip and successfully imputed SNPs (Table III). The set of tag SNPs on the chip achieved chromosome coverage of 75% for the phase II CEU reference panel but only 55% for the phase II YRI reference panel. Imputation using BEAGLE, despite yielding several hundred to a few thousand SNPs, increased coverage by only 1–2% regardless of the phase II reference panel. Similarly, imputation using MACH increased coverage of phase II CEU variation by only 1% using the phase II CEU reference panel. In stark contrast, imputation using MACH increased coverage of phase II YRI variation by 21% (from 55% to 76%) using only the phase II YRI reference panel; coverage was increased by 13% (from 62% to 75%) for the combined phase II CEU+YRI variation based on the unweighted phase II CEU+YRI reference panel. The merged set of separately imputed SNPs achieved the best coverage (78%) of the 40,281 phase II CEU+YRI reference SNPs.
TABLE III.
Coverage of HapMap variation for chromosome 22 at the r2 ≥ 0.8 level
| Phase II Reference Panel |
|||
|---|---|---|---|
| Tag Set | CEU | YRI | Unweighted CEU+YRI |
| SNP 6.0 | 75% | 55% | 62% |
| SNP 6.0 + BEAGLE | 75% | 57% | 65% |
| SNP 6.0 + MACH | 76% | 76% | 75% |
| SNP 6.0 + PLINK | 75% | 55% | 62% |
Coverage was measured by pairwise correlation between a tag SNP and a potentially captured SNP. A potentially captured SNP was considered covered if r2 ≥ 0.8 between itself and any tag SNP. Coverage was reported as the proportion of the set of potentially captured SNPS covered by the set of tag SNPs.
Also, we compared the yield and associated error rate obtained from two common approaches (“fixed error rate” and the “best call”) for imputation genotype calling. In the fixed error rate approach, we retained discrete genotype calls after ascertaining the threshold of posterior probability required to achieve pre-specified concordance between imputed and genotyped SNPs. In the “best call” approach, the discrete genotype call corresponded to the genotype with the highest posterior probability, regardless of concordance or the posterior probability [Huang et al., 2009]. The result of our analyses showed that the error rates using the best call approach were uniformly greater than the fixed error rate of 0.10 (Table IV). The fixed error rate approach favored a single best reference panel (Table II) whereas the best call approach favored the unweighted mixture reference panel at the cost of a higher error rate (Table IV).
TABLE IV.
Imputation accuracy and yield using the best call approach
| Phase II Reference Panel | Error Rate | Yield |
|---|---|---|
| CEU | 0.411 | 8,653 |
| YRI | 0.183 | 13,678 |
| Unweighted CEU+YRI | 0.254 | 13,867 |
| Weighted CEU+YRI | 0.261 | 12,803 |
Finally, we investigated the utility of an African American reference panel, the HapMap phase III ASW data. The HapMap phase III ASW, phase III CEU, and phase III YRI reference panels contain different numbers of SNPs. To enable a fair comparison among reference panels controlling for SNP density, we first extracted a common set of 12,941 reference SNPs shared across all three panels. Using this subset of shared SNPs, we determined imputation yield using the fixed error rate approach. The phase III YRI reference panel slightly outperformed the phase III ASW reference panel (Table V). We also estimated the number of SNPs in approximate linkage equilibrium by pruning based on pairwise correlation. This analysis revealed that the number of SNPs in approximate linkage equilibrium was much higher in the phase III YRI reference panel than in the phase III ASW reference panel, but that controlling for an equal number of founders in both reference panels eliminated most of this difference (Table VI). The results imply that, on average, the levels of linkage disequilibrium (and consequently, the average lengths of haplotype blocks) are similar in the phase III ASW and YRI reference panels, whereas linkage disequilibrium is more pronounced in the phase III CEU reference panel. In summary, given equivalent sampling with respect to the numbers of founders and SNP density, we anticipate that YRI and ASW may perform similarly well as reference panels for our African American study sample.
TABLE VI.
Linkage disequilibrium-based SNP pruning for HapMap phase III reference panels
| Phase III Reference Panel | Founders | Retained SNPs |
|---|---|---|
| ASW | 49 | 1,947 |
| CEU | 112 | 1,432 |
| CEU | 49 | 1,138.3 |
| YRI | 113 | 2,886 |
| YRI | 49 | 2,038.2 |
For the CEU and YRI reference panels, 49 founders were randomly sampled from the available founders. Shown are averages from 30 randomly generated data sets.
The number of retained SNPs was determined using the --indep-pairwise function in PLINK, with a window size of 100 SNPs, a step of 25 SNPs, and a maximum r2 threshold of 0.2.
DISCUSSION
In this study, we investigated factors influencing imputation of missing genotypes for admixed populations, specifically African Americans. To achieve this goal, we tested three different programs representing three classes of fundamentally different underlying models for estimating the conditional distribution of haplotype frequencies. We also explored the decision of which populations to include in the imputation reference panel. For African Americans, obvious choices from the HapMap reference panels include the YRI panel (representing the single most closely related founder population with the highest admixture proportion), a mixture of the CEU and YRI panels (representing the presumed two ancestral founder populations), and the ASW panel (representing the single most closely related population). Although none of the programs explicitly account for admixture, the underlying models differ substantially in their ability to capture patterns of haplotype diversity created by admixture. We found that the best imputation results were achieved by running MACH twice, once with the HapMap CEU reference panel and a second time with the YRI reference panel, and then combining the results. In this way, we can capitalize on the higher accuracy of the YRI reference panel while also maintaining access to SNPs present only in the CEU reference panel. Methods to combine imputation results require more investigation. For this paper, we merged the separately generated data sets, giving preference to YRI calls when there were genotypes inconsistencies between the two data sets. Another possibility is to leverage local admixture estimates on a per-individual basis in order to determine which reference panel is the more appropriate choice.
Using MACH, we also found that the HapMap phase III YRI reference panel slightly outperformed the HapMap phase III ASW reference panel. A priori, potential advantages of the ASW reference panel include more representative allele frequencies (the average estimated FST is 0.026 between the ASW reference panel and our study sample compared to 0.0295 between the YRI reference panel and our study sample) and linkage disequilibrium patterns resulting from admixture. On the other hand, potential disadvantages of the ASW reference panel include 2.6-fold less dense SNP sampling and 2.3-fold fewer founders compared to the combined phase II+III YRI data. It is indeed possible that ASW may perform equally to or better than YRI after eliminating these two differences in sampling.
The best use of the full posterior probability distribution for the three genotypes at imputed SNPs when testing association is a matter of ongoing investigation. Three possibilities are to call only those genotypes for which the posterior probability exceeds some threshold (the posterior mode approach), to summarize the distribution by using the posterior mean (the posterior mean approach), and to use the full distribution in the likelihood framework (the full data approach) [Marchini et al., 2007; Guan and Stephens, 2008]. The full data approach makes full use of the uncertainty in the imputed genotype calls whereas the posterior mode and posterior mean approaches are quicker and work best if there is high certainty about the imputed genotype calls at a given SNP [Marchini et al., 2007]. Depending on the downstream application of imputed genotype calls, discrete calls may be useful. We chose to adopt the posterior mode approach and make discrete imputed genotype calls. By setting a suitably stringent threshold, we were able to reduce the effect of genotype uncertainty. Under this approach, it is straightforward to test for Hardy-Weinberg equilibrium as a quality control filter for genotype-specific imputation failure at untyped SNPs. We reiterate the important requirement that replication of significant association for imputed SNPs should always include experimental genotyping in an independent data set [Browning, 2008]. This requirement addresses the possibility that unaccounted for uncertainty in imputed calls may inflate the false positive error rate of association testing.
In addition to issues related to multiple reference populations, there are at least two other major areas for improvement in current imputation algorithms. First, inclusion of phenotype data during imputation is theoretically required for unbiased results [Allison, 2002]. Ignoring phenotype data (or, more generally, dependent variables) during imputation is equivalent to assuming that all sampled individuals are no more related than are individuals randomly sampled from the population [Marchini and Howie, 2008]. However, cases are more related near a disease locus than this assumption implies [Marchini and Howie, 2008]. Incorporating phenotype data into the imputation process results in smaller bias but larger variance of effect size estimates [Epstein and Satten, 2003; Lake et al., 2003; Dai et al., 2006]. The three programs we investigated, BEAGLE, MACH, and PLINK, as well as IMPUTE and fastPHASE, ignore phenotype data. SNPMStat accounts for the phenotype but uses a multinomial model and does not account for long-range linkage disequilibrium [Lin et al., 2008]. Second, BEAGLE and PLINK can infer haplotype phase for certain forms of family data in addition to unrelated individuals. In contrast, fastPHASE, IMPUTE, MACH, and SNPMStat currently assume that all individuals are unrelated and thus ignore pedigree data that could potentially assist haplotype phasing.
Our study sample consisted of admixed individuals for which there are two major ancestral founder populations present in highly unequal admixture proportions. Conclusions drawn from this relatively simple admixture scenario may not apply to more complicated scenarios that include samples with more ancestral founder populations and/or more equally distributed admixture proportions. With this caveat in mind, our results lead to two suggestions. First, given the current MACH implementation, we recommend imputation of missing genotypes separately for each panel for situations requiring multiple reference panels (e.g., admixed populations). We achieved the highest imputation yield and coverage by using the HapMap CEU and YRI reference panels separately and then combining the results, rather than combining multiple reference panels prior to imputation. The optimal method of combining separate sets of imputed SNPs is a question for more investigation. The average extent of European ancestry in African American populations ranges from 3.5% to 22.5% [Parra et al., 1998; Parra et al., 2001], but the admixture proportion in a given individual may range from as low as 1.2% to 77.3% [Xu et al., 2007] and these estimates have been shown to vary by chromosome [Lind et al., 2007]. We therefore think that incorporating local admixture estimates for individuals will be likely necessary for efficient combination of imputed genotypes. Second, we suggest that MACH may be improved by expanding the prior model to explicitly allow for multiple reference populations and gene flow among those populations.
TABLE V.
Imputation yield using HapMap phase III reference panels
| Phase III Reference Panel | Threshold | Yield |
|---|---|---|
| ASW | 0.886 | 2,962 |
| CEU | NA | 0 |
| YRI | 0.872 | 3,201 |
Threshold indicates the minimum posterior probability for imputing discrete genotype calls to achieve concordance between imputed and observed genotypes of 0.90. NA indicates that the program could not achieve concordance of 0.90 using the reference panel.
ACKNOWLEDGEMENTS
The Howard University Family Study was supported by National Institutes of Health grants S06GM008016-320107 to CNR and S06GM008016-380111 to AA. We thank the participants of the study, for which enrollment was carried out at the Howard University General Clinical Research Center, supported by National Institutes of Health grant 2M01RR010284. The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official view of the National Institutes of Health. This research was supported in part by the Intramural Research Program of the Center for Research on Genomics and Global Health, National Human Genome Research Institute, National Institutes of Health (Z01HG200362). Genotyping support was provided by the Coriell Institute for Medical Research.
REFERENCES
- Adeyemo A, Gerry N, Chen G, Herbert A, Doumatey A, Huang H, Zhou J, Lashley K, Chen Y, Christman M, Rotimi C. A genome-wide association study of hypertension and blood pressure in African Americans. PLoS Genet. 2009;5:e1000564. doi: 10.1371/journal.pgen.1000564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison PD. Missing Data. Sage Publications, Inc.; Thousand Oaks, CA: 2002. [Google Scholar]
- Barrett JC, Cardon LR. Evaluating coverage of genome-wide association studies. Nat Genet. 2006;38:659–62. doi: 10.1038/ng1801. [DOI] [PubMed] [Google Scholar]
- Barrett JC, Fry B, Maller J, Daly MJ. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics. 2005;21:263–5. doi: 10.1093/bioinformatics/bth457. [DOI] [PubMed] [Google Scholar]
- Browning SR. Missing data imputation and haplotype phase inference for genome-wide association studies. Hum Genet. 2008;124:439–50. doi: 10.1007/s00439-008-0568-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning SR, Browning BL. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am J Hum Genet. 2007;81:1084–97. doi: 10.1086/521987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DG, Kraft P. Quantification of the power of Hardy-Weinberg equilibrium testing to detect genotyping error. Hum Hered. 2006;61:10–4. doi: 10.1159/000091787. [DOI] [PubMed] [Google Scholar]
- Dai JY, Ruczinski I, LeBlanc M, Kooperberg C. Imputation methods to improve inference in SNP association studies. Genet Epidemiol. 2006;30:690–702. doi: 10.1002/gepi.20180. [DOI] [PubMed] [Google Scholar]
- de Bakker PI, Burtt NP, Graham RR, Guiducci C, Yelensky R, Drake JA, Bersaglieri T, Penney KL, Butler J, Young S, Onofrio RC, Lyon HN, Stram DO, Haiman CA, Freedman ML, Zhu X, Cooper R, Groop L, Kolonel LN, Henderson BE, Daly MJ, Hirschhorn JN, Altshuler D. Transferability of tag SNPs in genetic association studies in multiple populations. Nat Genet. 2006;38:1298–303. doi: 10.1038/ng1899. [DOI] [PubMed] [Google Scholar]
- Deng H-W, Chen W-M, Recker RR. Population admixture: detection by Hardy-Weinberg test and its quantitative effects on linkage-disequilibrium methods for localizing genes underlying complex traits. Genetics. 2001;157:885–97. doi: 10.1093/genetics/157.2.885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egyud MR, Gajdos ZK, Butler JL, Tischfield S, Le Marchand L, Kolonel LN, Haiman CA, Henderson BE, Hirschhorn JN. Use of weighted reference panels based on empirical estimates of ancestry for capturing untyped variation. Hum Genet. 2009;125:295–303. doi: 10.1007/s00439-009-0627-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein MP, Satten GA. Inference on haplotype effects in case-control studies using unphased genotype data. Am J Hum Genet. 2003;73:1316–29. doi: 10.1086/380204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics. 2003;164:1567–87. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan Y, Stephens M. Practical issues in imputation-based association mapping. PLoS Genet. 2008;4:e1000279. doi: 10.1371/journal.pgen.1000279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L, Li Y, Singleton AB, Hardy JA, Abecasis G, Rosenberg NA, Scheet P. Genotype-imputation accuracy across worldwide human populations. Am J Hum Genet. 2009;84:235–50. doi: 10.1016/j.ajhg.2009.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korn JM, Kuruvilla FG, McCarroll SA, Wysoker A, Nemesh J, Cawley S, Hubbell E, Veitch J, Collins PJ, Darvishi K, Lee C, Nizzari MM, Gabriel SB, Purcell S, Daly MJ, Altshuler D. Integrated genotype calling and association analysis of SNPs, common copy number polymorphisms and rare CNVs. Nat Genet. 2008;40:1253–60. doi: 10.1038/ng.237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lake SL, Lyon H, Tantisira K, Silverman EK, Weiss ST, Laird NM, Schaid DJ. Estimation and tests of haplotype-environment interaction when linkage phase is ambiguous. Hum Hered. 2003;55:56–65. doi: 10.1159/000071811. [DOI] [PubMed] [Google Scholar]
- Leal SM. Detection of genotyping errors and pseudo-SNPs via deviations from Hardy-Weinberg equilibrium. Genet Epidemiol. 2005;29:204–14. doi: 10.1002/gepi.20086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Ding J, Abecasis GR. Mach 1.0: Rapid haplotype reconstruction and missing genotype inference. Am J Hum Genet. 2006;79:S2290. [Google Scholar]
- Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR. In silico genotyping for genome-wide association studies. Am J Hum Genet. 2007;81:S2071. [Google Scholar]
- Lin DY, Hu Y, Huang BE. Simple and efficient analysis of disease association with missing genotype data. Am J Hum Genet. 2008;82:444–52. doi: 10.1016/j.ajhg.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lind JM, Hutcheson-Dilks HB, Williams SM, Moore JH, Essex M, Ruiz-Pesini E, Wallace DC, Tishkoff SA, O'Brien SJ, Smith MW. Elevated male European and female African contributions to the genomes of African American individuals. Hum Genet. 2007;120:713–22. doi: 10.1007/s00439-006-0261-7. [DOI] [PubMed] [Google Scholar]
- Marchini J, Howie B. Comparing algorithms for genotype imputation. Am J Hum Genet. 2008;83:535–9. doi: 10.1016/j.ajhg.2008.09.007. author reply 539-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39:906–13. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- Nothnagel M, Ellinghaus D, Schreiber S, Krawczak M, Franke A. A comprehensive evaluation of SNP genotype imputation. Hum Genet. 2009;125:163–71. doi: 10.1007/s00439-008-0606-5. [DOI] [PubMed] [Google Scholar]
- Parra EJ, Kittles RA, Argyropoulos G, Pfaff CL, Hiester K, Bonilla C, Sylvester N, Parrish-Gause D, Garvey WT, Jin L, McKeigue PM, Kamboh MI, Ferrell RE, Pollitzer WS, Shriver MD. Ancestral proportions and admixture dynamics in geographically defined African Americans living in South Carolina. Am J Phys Anthropol. 2001;114:18–29. doi: 10.1002/1096-8644(200101)114:1<18::AID-AJPA1002>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- Parra EJ, Marcini A, Akey J, Martinson J, Batzer MA, Cooper R, Forrester T, Allison DB, Deka R, Ferrell RE, Shriver MD. Estimating African American admixture proportions by use of population-specific alleles. Am J Hum Genet. 1998;63:1839–51. doi: 10.1086/302148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei Y-F, Li J, Zhang L, Papasian CJ, Deng H-W. Analyses and comparison of accuracy of different genotype imputation methods. PLoS ONE. 2008;3:e3551. doi: 10.1371/journal.pone.0003551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pemberton TJ, Jakobsson M, Conrad DF, Coop G, Wall JD, Pritchard JK, Patel PI, Rosenberg NA. Using population mixtures to optimize the utility of genomic databases: linkage disequilibrium and association study design in India. Ann Hum Genet. 2008;72:535–46. doi: 10.1111/j.1469-1809.2008.00457.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–75. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheet P, Stephens M. A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am J Hum Genet. 2006;78:629–44. doi: 10.1086/502802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap Consortium The International HapMap Project. Nature. 2003;426:789–96. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
- The International HapMap Consortium A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–61. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S, Huang W, Wang H, He Y, Wang Y, Wang Y, Qian J, Xiong M, Jin L. Dissecting linkage disequilibrium in African-American genomes: roles of markers and individuals. Mol Biol Evol. 2007;24:2049–58. doi: 10.1093/molbev/msm135. [DOI] [PubMed] [Google Scholar]
- Zhao Z, Timofeev N, Hartley SW, Chui DH, Fucharoen S, Perls TT, Steinberg MH, Baldwin CT, Sebastiani P. Imputation of missing genotypes: an empirical evaluation of IMPUTE. BMC Genet. 2008;9:85. doi: 10.1186/1471-2156-9-85. [DOI] [PMC free article] [PubMed] [Google Scholar]