Limb bone allometry during postnatal ontogeny in non-avian dinosaurs

Abstract

Although the interspecific scaling of tetrapods is well understood, remarkably little work has been done on the ontogenetic scaling within tetrapod species, whether fossil or recent. Here the ontogenetic allometry of the femur, humerus, and tibia was determined for 23 species of non-avian dinosaur by regressing log-transformed length against log-transformed circumference for each bone using reduced major axis bivariate regression. The femora of large theropod species became more robust during ontogeny, whereas growth in the femora of sauropodomorphs and most ornithischians was not significantly different from isometry. Hadrosaur hindlimb elements became significantly more gracile during ontogeny. Scaling constants were higher in all theropods than in any non-theropod taxa. Such clear taxonomically correlated divisions were not evident in the ontogenetic allometry of the tibia and hindlimb bones did not scale uniformly within larger taxonomic groups. For taxa in which the ontogenetic allometry of the humerus was studied, only Riojasaurus incertus exhibited a significant departure from isometry. Using independent contrasts, the regression of femoral allometry against the log of adult body mass was found to have a significant negative correlation but such a relationship could not be established for other limb elements or growth parameters, mainly due to the small sample size. The intraspecific scaling patterns observed in dinosaurs and other amniotes do not support earlier hypotheses that intraspecific scaling differs between endothermic and ectothermic taxa.

Introduction

The biomechanical implications of interspecific limb bone scaling and allometry have been studied extensively in tetrapods, including squamates and crocodilians (Blob, 2000), mammals (McMahon, 1975a,b; Alexander et al. 1979; Biewener, 1983; Bertram & Biewener, 1990) and dinosaurs (Christiansen, 1999; Carrano, 1998, 2001). In general, these studies have sought to determine whether scaling patterns of limb bone length and circumference fit general scaling models such as elastic similarity or geometric similarity (McMahon, 1975a). In marked contrast, intraspecific (ontogenetic) limb bone scaling has been investigated for only a few species, whether living or fossil (Carrier, 1983, 1996; Dodson, 1975; Carrier & Leon, 1990; Blob, 2006). Carrier (1983) and Carrier & Leon (1990) examined intraspecific long bone scaling in jackrabbits (Lepus) and gulls (Larus), respectively, and found them to display positive allometry (increasingly gracile limb bones via length increasing with size faster than circumference) throughout growth in contrast to crocodilians and squamates. The authors proposed that positive intraspecific allometry of limb bones may be an adaptation in endothermic species to compensate for the low mineral content and stiffness of fast-growing juvenile bones. Although a correlation between metabolism and limb bone scaling would have profound implications for paleobiology, the study of Blob (2006) on scaling in two cynodont species is the only study, to our knowledge, that pursues this line of investigation.

Dinosaurs are an obvious clade in which to study the ontogenetic allometry of limb bones. Non-avian dinosaurs exhibit an exceptional range of adult body masses (1–73 000 kg; Mazzetta et al. 2004) as well as disparate postures (bipedal vs. quadrupedal), and locomotor adaptations (cursorial vs. graviportal; Coombs, 1978). Recent work has revealed estimated maximum growth rates ranging from approximately 6 to 1042 kg year⁻¹ in non-avian dinosaurs, with growth rates of some taxa overlapping those of mammals [Erickson et al. 2001; but see Lehman & Woodward (2008) for a different opinion]. This range of locomotory parameters and size makes non-avian dinosaurs an ideal group for examining the correlates of limb bone allometry during ontogeny.

The few studies on intraspecific limb bone allometry and scaling in dinosaur species that have been performed focus on theropods and a single hadrosaurid; none are broadly comparative. Gatesy (1991) investigated intraspecific scaling of hindlimb bones in Allosaurus fragilis using hindlimb length as a proxy for body mass. Bybee et al. (2006) also examined intraspecific scaling in A. fragilis, using femur length as an estimate of body size. Currie (2003) investigated intraspecific allometry of skeletal elements including hindlimb bones in tyrannosaurids, although his regressions included specimens of multiple species, thus conflating intraspecific and interspecific allometric patterns. Dilkes (2001) examined ontogenetic allometry in the limb bones of Maiasaura peeblesorum and found that the proportions of the humerus and tibia became more gracile during ontogeny.

The purpose of this study was to (i) survey intraspecific limb bone allometry across non-avian dinosaur diversity to determine what pattern or patterns of limb bone allometry occurred within this clade of both bipedal and secondarily quadrupedal taxa; (ii) test whether the adult body mass was independent of ontogenetic limb bone allometry; (iii) test whether the estimated maximum growth rate varied independently of ontogenetic limb bone allometry; and (iv) examine the biomechanical implications of dinosaur limb bone allometry during ontogeny.

Scale effects and limb bone allometry during ontogeny

Adult body mass, as defined by somatic rather than sexual maturity (Erickson, 2005), is expected to influence ontogenetic limb bone allometry in an animal that maintains geometric similarity through ontogeny. Body mass scales to the cube of length, whereas cross-sectional areas (which, to a first approximation, determine bone strength) scale with length squared (McMahon, 1975a); species with greater adult body masses should have limb bones exhibiting greater negative allometry, with limb bone circumference increasing relative to limb bone length during ontogeny, to support large adult body masses.

Some rapidly growing tetrapods have bones with relatively low levels of mineralization early in ontogeny (Carrier & Leon, 1990). Poor mineralization in the bones of juveniles causes them to be relatively weaker and less stiff than the bones of adults (Currey & Pond, 1989) and the limb bones in juveniles of some rapidly growing, endothermic taxa are relatively thicker than the limb bones of adults to compensate for the low strength and stiffness of their bone (Carrier & Leon, 1990). Taxa with high growth rates may have bones that become increasingly gracile during ontogeny compared with taxa with slower growth rates. However, these patterns have only been established in two small-bodied taxa and their generality across tetrapod clades remains unknown (Kilbourne, 2007). An examination of scaling patterns in dinosaurs with a range of body sizes and growth rates may reveal patterns that inform this hypothesis. It should be noted that maximum growth rates for dinosaur species were calculated using the developmental mass extrapolation technique (Erickson & Tumanova, 2000; Erickson et al. 2001, 2004), which assumes an isometric relationship between body mass and femoral length.

Materials and methods

Skeletal measurements

The maximum length and circumference measurements for the femur, tibia, and humerus in 23 non-avian dinosaur species (see Table 1 and Fig. 1) were gathered from the literature (Hennig, 1924; Osmolska et al. 1972; Maleev, 1974; Madsen, 1976; Dilkes, 1993; Horner & Currie, 1994; Farlow et al. 1995; Carrano, 1998; Currie & Dong, 2001; Wilhite, 2003; Horner & Padian, 2004; Carr et al. 2005; Lehman, 2007), generously shared by colleagues for this study, or taken directly from specimens using a tape measure and calipers. For Kentrosaurus aethiopicus and Psittacosaurus lujiatunensis, circumference values were calculated from anteroposterior and mediolateral diameter measurements, as no actual circumferences were published (K. aethiopicus) or the limb bones of specimens were not fully prepared (P. lujiatunensis). Raw values of skeletal measurements along with their source are listed in the Supporting Information.

Table 1.

Body mass estimates for the largest individuals for each species used in this study.

		Body mass (kg)
Taxon	Specimen used for mass estimate	Anderson et al. (1985)	Christiansen & Fariña (2004)4/Packard et al. (2009)5	Seebacher (2001)
Theropoda
Allosaurus fragilis1,2	AMNH 630	1778.5	2395.5	952
Tyrannosaurus rex1,2	FMNH PR 2081	5654.1	6205	6650.9
Tarbosaurus bataar	PIN 551-2	1895.5	2164.6
Gorgosaurus libratus1	AMNH 5458	1489	2585.5	2465
Daspletosaurus torosus1	AMNH 5438	1895.5	2626.4
Gallimimus bullatus1	G.I. No. DPS 100/11	284.8	641.4	585.7
Herrerasaurus ischigualastensis1	PVL 2566	194.9	227.4	347.8
Troodon formosus1	MOR 748	34.1	58.9
Sauropodomorpha
Massopondylus carinatus2	QR3054	280	–	–
Riojasaurus incertus1	PVL 3808	1963.5	1932.4	3038.7
Apatosaurus sp.1	–	25 952	18 000	22 407.2
Camarasaurus sp.1	CM 11393	19 069.5
Diplodocus sp.1	USMN 10865	12 447	8135.8	19 654.6
Ornithopoda
Tenontosaurus tilletti1	MOR 682	402	–	249.2
Dryosaurus lettowvorbecki1	BMNH R 12777	103	–	–
Hypacrosaurus stebingeri1	MOR 773	2767.6	–	–
Maiasaura peeblesorum1	MOR 005	1062.6	–	–
Stegosauria
Stegosaurus stenops1	–	–
Kentrosaurus aethiopicus1	bb1/r19	2046.2	1995.5	321.1
Ceratopsia
Pachyrhinosaurus sp.1	–	–	–	–
Centrosaurus apertus1	–	–	–	1833.6
Chasmosaurus mariscalensis1	OMNH 10081	2481	2188.5	1658.7
Psittacosaurus lujiatunensis3		26	–	21.1

Body mass was estimated using the equations in the references in title row. For quadrupedal taxa, estimated adult body mass was calculated only for specimens that possessed both a femur and a humerus. H. stebingeri and P. lujiatunensis were assumed to be bipedal for the calculation of body mass. Sources of measurements are as follows:

¹Literature.

²Personal communication.

³Directly measured by B.M.K. or P.J.M.

⁴Used for estimates for non-avian theropods.

⁵Used for estimates of quadrupedal taxa.

Fig. 1.

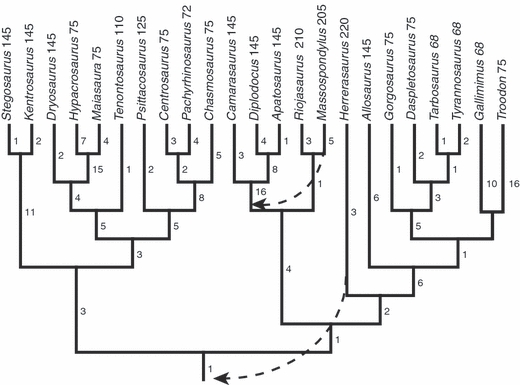
Phylogeny of taxa sampled in this study based on the supertree analysis of dinosaur genera of Lloyd et al. (2008). Arrows indicate permutations of this tree based on recent phylogenetic analyses, including treating Herrerasaurus as a basal saurischian following Langer (2004) and treating prosauropod taxa as paraphyletic following Yates (2003). A version of this tree with all of the branch changes implemented was also used for independent contrasts analysis. Numbers to the right of internodes represent internodal distances calculated from the supertree of Lloyd et al. (2008), whereas numbers next to terminal taxa represent geological age estimates that were used to calculate absolute temporal branch lengths.

To quantify the range of our ontogenetic series, we calculated the size range (SR) for each species sample. To calculate the SR for each limb bone studied for a species we divided the length of the longest bone by the length of the shortest bone as a proxy for our sampling of a taxon’s ontogenetic series. SR is a relevant parameter, as it has a large influence upon the quantification of long bone allometry.

Quantifying allometric growth

To test for the presence of allometry, data were natural log transformed prior to performing bivariate regressions. The regression line can be described by the following function: ln (y) = b (ln (x)) + ln (a). Taking the anti-log of both sides, the equation for the regression line becomes the general allometric equation, y = ax^b, where a is the allometric constant and b is the allometric exponent (Schmidt-Nielsen, 1984). The allometric signal is determined by the exponent b, which corresponds to the slope of the regression line in log-transformed bivariate plots. In the geometric similarity model, all lengths and circumferences maintain a fixed ratio to one another (isometry) and the allometric exponent has a value of 1.0 (Schmidt-Nielsen, 1984). Other scaling models include the static stress and elastic similarity models, in which limb bones change proportions to maintain a constant internal stress or an equal probability of failure by buckling, respectively (McMahon, 1975a). Both of these models predict significant negative allometry, in which limb bones become relatively more robust as the size of the animal increases (static stress similarity exponent: length ∝ circumference^0.5; elastic similarity exponent: length ∝ circumference^0.67) (McMahon, 1975a; LaBarbera, 1986). An allometric pattern is considered to be statistically significant when a value of 1.0 lies outside the 95% confidence intervals (CIs) for the allometric exponent (Jungers et al. 1998). For the purposes of this study, allometry was considered to be positive if b>1.0, whereas allometry was considered negative if b<1.0.

Bivariate regressions to assess allometry were performed using reduced major axis (Model II) regression, using the freeware program RMA 1.17 (PPC) (Bohonak, 2002). We considered Model II to be the most appropriate regression model as it assumes that both variables contain ‘error’ in the form of inaccurate measurements and biological variation (Rayner, 1985). Bivariate regressions were performed between limb length and circumference for each element in each taxon. All regressions were run with 10 000 bootstrap resampling replicates of the data to determine CIs. Within the following text, regression slopes, which are equivalent to the allometric exponent, will be reported as slope followed by the 95% confidence limits in parentheses.

Permutation tests

As a second test for significant departures from isometry, permutation tests (10 000 permutations) were performed between the original log-transformed length and circumference data and the same dataset rotated about its centroid to a slope of exactly 1.0. To accomplish this, we mean-centered the data and calculated the RMA slope. Knowing that the slope of the regression equals the tangent of the angle between the fitted line and the x-axis, we found this angle by taking the inverse tangent of the slope. We then subtracted this angle from the angle corresponding to a slope of 1.0. This difference in angles is the angle through which we rotated the mean-centered data to have a slope of 1.0. Rotation of the dataset was accomplished using the rotation matrices

and

where Q_cc is the rotation matrix for counterclockwise rotation, Q_c is the rotation matrix for clockwise rotation, and θ is the angle of rotation (M. Foote, personal communication). Permutation tests were performed between the original mean-centered data and the rotated data. Departures from isometry indicated by the permutation tests were considered significant if P<0.05.

Estimating life-history traits

A number of methods for estimating body masses of extinct dinosaurs have been proposed, so we employed several methods to derive values for this study. Our first approach was to calculate adult body mass (Table 1) for the largest individual for each growth series from femoral circumference in bipeds or both femoral and humeral circumference in quadrupeds, using the equations developed by Anderson et al. (1985). Estimates of maximum growth rates for each taxon were taken from the literature (Erickson et al. 2001, 2004; Bybee et al. 2006; Lee & Werning, 2008). We chose to use the equations of Anderson et al. (1985) for calculating body mass because these were developed for, and have been broadly applied to, studying dinosaurs. These equations have also been employed in studies of dinosaurian growth rates (Erickson et al. 2001, 2004), which we used for tests of correlation in our study.

Although the equations of Anderson et al. (1985) continue to be frequently employed for extrapolating dinosaur body mass estimates (e.g. Erickson et al. 2001, 2004; Lehman & Woodward, 2008), a number of conceptual and mathematical concerns have been raised regarding their validity. The equations are based on mammals, with an emphasis on bovids, which differ greatly in body plan from dinosaurs. The equation for bipedal dinosaurs is further scaled from historical life reconstructions of three bipedal taxa, which can no longer be considered accurate relative to more recent modeling work. Furthermore, Packard et al. (2009) have shown that non-linear equations provide a better fit to the extant mammal data originally compiled by Anderson et al. (1985) relative to fitting a least-squares linear equation to log-transformed values of these data.

More recent estimates of body mass in dinosaurs tend to rely on graphic or three-dimensional models for individual species (e.g. Farlow et al. 1995; Seebacher, 2001; Henderson, 1999). More specific equations for extrapolating masses for particular lineages of dinosaurs have been developed (e.g. Christiansen & Fariña, 2004) to take into account body plan differences, rather than generalizing across the clade as a whole. A promising development in this field is the use of optical scanning technology to generate accurate models of mounted skeletons that are fleshed out digitally. A benefit of such digital models is that the resulting mass estimates can be bracketed by computing the sensitivity of results with respect to how model parameters such as density, lung and air-sac volume, etc. are set (Hutchinson et al. 2007; Bates et al. 2009). However, none of these methods have been applied consistently across all dinosaurs.

Taking these more recent developments into account, we generated two other ranges of mass estimates for our sample taxa in addition to those determined using Anderson et al. (1985). The first set of data came from Seebacher (2001) who devised a double-graphic integration method to estimate body masses from skeletal lengths for a wide range of taxa, including many of those in our sample (although often from smaller individuals than the largest animals in our sample). We included this method in particular, as it does not rely directly on limb bone measurement and thus avoids the slight potential for autocorrelation that may occur when correlating body mass determined from femoral circumference of the largest individual with allometric scaling determined from length and circumference ratios for a range of individuals. The second set of data used mixed values generated using different mass-estimation methods for those relationships found to be significant in our analyses. Specifically, we employed body mass for theropods calculated using the equations and estimates of Christiansen & Fariña (2004). Body mass estimates for obligate quadrupeds in our sample were recalculated using the corrected non-linear equations of Packard et al. (2009) for fitting the data of Anderson et al. (1985).

In order to determine whether there was a significant correlation between scaling patterns and other life-history parameters, ordinary least squares (Model I) bivariate regressions were separately performed between allometric exponents for the femur, tibia, and humerus and log-transformed adult body mass estimates (logBM) and log-transformed maximum growth rates (logGR) for all taxa. For bivariate regressions involving long bone allometry and another variable calculated from long bone dimensions, we performed Durbin-Watson tests for autocorrelation. Autocorrelation was significant if P<0.05. The two variables derived from long bone dimensions were estimated adult body mass and estimated maximum growth rate. It should be noted that the adult body mass estimates from Seebacher (2001) were not derived from the dimensions of long bones.

Comparative methods

Many of the taxa used here form closely related sub-clades (e.g. tyrannosaurids) and inherited large size from proximate common ancestors, so we supplemented the raw species-level correlation analyses of limb bone allometry and life-history traits with ones using independent contrasts (Felsenstein, 1985). Contrasts were calculated using the PDAP module (Midford et al. 2005) run through the phylogenetic software Mesquite ver. 2.7 (Maddison & Maddison, 2006). Because no comprehensive primary phylogenetic analysis including all of the sampled species is available, we used a recent supertree for Dinosauria (Lloyd et al. 2008) to identify contrasts. Although this supertree resolves recent debates of saurischian relationships according to set algorithmic rules, we chose to examine whether different topologies may affect the outcome of correlations using independent contrasts. In particular, we considered the following topological alternatives: (i) whether Herrerasaurus is a basal theropod (Sereno et al. 1993) or a basal saurischian (Langer, 2004; Langer & Benton, 2006), and (ii) whether Prosauropoda is monophyletic (Upchurch et al. 2004) or polyphyletic (Yates, 2003; Smith & Pol, 2007). The tree was manipulated in Mesquite to reflect these differing topologies to determine whether topological differences affected the outcome of the analyses.

Branch lengths were set in three different ways: all branches set to equal length (unity); branch lengths calibrated to geological ages of specimens with ghost lineages but with a minimum of 1 Myr added to separate sister taxa with equivalent ages loosely following a protocol developed by Laurin (2004); or branch lengths scaled using the number of nodes separating two taxa on the supertree or one of the alternative permutations discussed above as a proxy of patristic distance. We tested (F-statistic) apparent trends in plots of standardized contrasts against their SDs for all combinations of branch lengths and tree topologies for significance, which would indicate when our contrasts were not sufficiently standardized (Garland et al. 1992).

Several recent studies have encountered obstacles when using branch lengths calibrated against absolute age for calculating independent contrasts (e.g. Christiansen & Adolfssen, 2005; Laurin, 2004). This effect is probably due to branch-length heterogeneity, which in fossil examples often reflects uneven preservation potential through time. Our sampling of ontogenetic series was biased toward well-known and historically well-sampled dinosaur faunas. For example, four of the taxa in our sample (Apatosaurus, Diplodocus, Camarasaurus, and Stegosaurus) derive from the Late Jurassic Morrison Formation of the western United States and all were named between 1870 and 1904, reflecting that a protracted history of collecting and scientific publication underlies the ontogenetic samples available to us. Such temporal lumping of taxa within narrow geological time slices results in a tree with extremely long branches representing ghost lineages and very short branches separating coeval terminal taxa. This preservationally driven pattern of stasis interspersed with apparent punctuated events does lead to a near-significant trend between the body mass values and their SDs for most combinations of topology and body mass estimate, and a significant trend is seen in a couple of cases (Table 7.) These trends indicate that the geological branch lengths are not sufficiently standardized in all cases.

Table 7.

Results of correlation analyses for femoral allometric scaling as a function of body mass and growth rate using phylogenetic independent contrasts.

		Adult mass (log10 kg)
Mass estimate	Standard P-value	Significance	Root value	Lower limit	Upper limit	Growth rate (log10 kg/yr)
Femur – geological
Anderson	0.06289	0.00865	0.81241	0.61619	1.00863	0.02856189
Seebacher	0.06013	0.02123	0.80737	0.67041	0.94433
Mixed model	0.06692	0.00935	0.81241	0.61619	1.00863
Femur – internodal
Anderson	0.27409	0.05174	0.91693	0.73450	1.09935	0.13656298
Seebacher	0.47324	0.04253	0.90851	0.72550	1.09152
Mixed model	0.17078	0.03476	0.91693	0.73450	1.09935
Femur – unity
Anderson	0.62530	0.00388	0.94428	0.75573	1.13283	0.15323549
Seebacher	0.80516	0.02466	0.93567	0.73049	1.14085
Mixed model	0.80908	0.03134	0.94428	0.75573	1.13283
Femur – geological (Herrerasaurus basal)
Anderson	0.04105	0.00878	0.81157	0.64557	0.97757	0.02856189
Seebacher	0.52216	0.02174	0.80895	0.69301	0.92488
Mixed model	0.04469	0.00952	0.81157	0.64556	0.97758
Femur – internodal (Herrerasaurus basal)
Anderson	0.42749	0.06572	0.89771	0.72570	1.06972	0.13996415
Seebacher	0.62682	0.05431	0.89176	0.71944	1.06408
Mixed model	0.38003	0.04316	0.89771	0.72570	1.06972
Femur – unity (Herrerasaurus basal)
Anderson	0.74028	0.05448	0.92059	0.73478	1.10640	0.15323549
Seebacher	0.96719	0.03530	0.91718	0.71568	1.11868
Mixed model	0.99893	0.04096	0.92059	0.73478	1.10640
Femur – geological (paraphyletic prosauropods)
Anderson	0.08218	0.00818	0.81136	0.61671	1.00602	0.04843884
Seebacher	0.56855	0.02052	0.81136	0.61671	1.00602
Mixed model	0.08591	0.00898	0.80618	0.66934	0.94302
Femur – internodal (paraphyletic prosauropods)
Anderson	0.36380	0.08898	0.91078	0.73064	1.09091	0.17554175
Seebacher	0.47324	0.04253	0.90851	0.72550	1.09152
Mixed model	0.24509	0.06191	0.91078	0.73064	1.09091
Femur – unity (paraphyletic prosauropods)
Anderson	0.83706	0.04542	0.92123	0.73829	1.10417	0.19724142
Seebacher	0.88375	0.01039	0.91784	0.71219	1.12350
Mixed model	0.92950	0.03850	0.92123	0.73829	1.10417

The first result column provides a significance value (F-test) for the trendline between standardized contrasts for body mass and their SD. Significant trends indicate that body mass contrasts are insufficiently standardized and may bias results. The second result column provides a significance value (F-test) for the negative trend between log-transformed body mass and femoral scaling coefficients. The columns Root Value, Lower Limit, and Upper Limit provide the root scaling coefficient for Dinosauria and its upper and lower bounds (95% confidence interval). Significance values for growth rate are for the negative trend between log-transformed growth rate and femoral scaling coefficients. Trends that deviate significantly from 0 at the 5% level are highlighted in bold.

Several branch-scaling methods have been proposed to overcome such problems, including making all branch lengths uniform and thus forcing traits to change at branching points (e.g. Nudds, 2007; Christiansen, 2002; Christiansen & Adolfssen, 2005) and a variety of methods that rely on the hierarchical position of each node within a tree. Our use of internodal distances from the Dinosauria supertree of Lloyd et al. (2008) followed the uniform branch-length method in considering the distance between any two neighboring branches equal throughout the tree but it accounted for branch lengths implied by phylogeny for which we lacked sufficient specimens. Through its use of non-uniform branch lengths, our internodal distance method deviated from a purely punctuated model of trait change, which would be inappropriate for our sample given the massive phylogenetic and temporal distances separating taxa for which we were able to measure ontogenetic scaling data. As our sampling of different dinosaur growth series improves in the future, however, our branch-scaling method would converge on the uniform branch length method, provided our understanding of dinosaur diversity does not change drastically.

Using the PDTREE software package, we also calculated the root node value (Garland et al. 1992) with CIs to estimate the ancestral scaling coefficients for the femur for Dinosauria under the 27 different combinations of tree topology and branch-scaling models in our study.

Results

Trends in ontogenetic limb bone allometry

Humeral allometry

The humerus was only analyzed for quadrupedal or facultatively bipedal/quadrupedal sauropodomorph and ornithischian dinosaurs (Table 2). With the exception of the positively allometric humerus of the hadrosaurid M. peeblesorum (1.04 [1.01, 1.09]), the ontogenetic allometry of the humerus in ornithischians was never significantly different from isometry and their exponents were all fairly close to 1.0. The humerus of the prosauropod Riojasaurus incertus showed significant negative allometry, with an exponent of 0.64 (0.34, 0.75). Ontogenetic allometry of the humeri of the other sauropodomorphs did not differ significantly from isometry, with values of the allometric exponent never straying far from 1.0.

Table 2.

Results of reduced major axis regressions assessing humeral allometry for each dinosaur species.

Taxon	N	Size range (x)	RMA intercept	RMA slope	Lower Limit (95%)	Upper Limit (95%)	R2	Growth pattern	P
Sauropodomorpha
Riojasaurus incertus	7	1.89	1.809	0.6425	0.3444	0.7516	0.937	R	0.0573
Apatosaurus sp.	18	5.29	0.4805	1.032	0.955	1.123	0.966	I	0.6097
Camarasaurus sp.	32	5.71	0.4777	1.047	0.976	1.122	0.968	I	0.3296
Diplodocus sp.	17	3.43	0.5306	1.053	0.836	1.155	0.933	I	0.5870
Ornithopoda
Maiasaura peeblesorum	41	10.57	0.9462	1.043	1.012	1.085	0.986	G	0.1181
Tenontosaurus tilletti	6	2.84	0.692	1.068	0.878	6.09	0.929	I	0.5745
Stegosauria
Kentrosaurus aethiopicus	14	1.22	−0.07597	1.215	0.88	1.488	0.793	I	0.3894
Ceratopsia
Centrosaurus apertus	6	2.38	1.248	0.9275	0.798	1.502	0.959	I	0.5936

R, I, and G denote growth patterns of negative allometry, isometry, and positive allometry, respectively. Lower and upper limits are the 95% confidence limits for the slope. P-values are the results of permutation tests (with 10 000 permutations). Permutation tests indicate significant departures from isometry if P<0.05. P-values are highlighted in bold in instances where the results of permutation tests disagree with the growth patterns indicated by the range of the slope confidence limits.

For six of the eight sampled taxa, permutation tests of humeral allometry agreed with the results of using slope confidence to determine humeral allometry. In R. incertus and M. peeblesorum, the results of permutation tests disagreed with the results from bootstrapping the confidence limits of the RMA slope (P_{permutation test} = 0.0583 and 0.1181, respectively). For R. incertus and M. peeblesorum, the permutation tests found that the humerus grew isometrically as P>0.05 in both cases.

Femoral allometry

Several clade-specific ontogenetic patterns in the allometry of the femur were apparent across the Dinosauria (Table 3). The allometric exponents in non-avian theropods were all below 1.0, ranging from 0.81 (0.24, 1.18) in Herrerasaurus ischigaulastensis to 0.53 (0.42, 0.97) in Tyrannosaurus rex, with bones growing more robust during ontogeny. Only large theropod dinosaurs exhibited statistically significant negative femoral allometry; the femora of the smaller theropod taxa sampled in this study (Gallimimus bullatus, H. ischigualastensis and Troodon formosus) did not scale significantly different from isometry as gauged by their confidence limits.

Table 3.

Results of reduced major axis regressions assessing femoral allometry for each dinosaur species.

Taxon	N	Size range (x)	RMA intercept	RMA slope	Lower Limit (95%)	Upper Limit (95%)	R2	Growth pattern	P
Theropoda
Allosaurus fragilis	49	4.09	1.611	0.8175	0.7761	0.8532	0.98	R	<0.0001
Tyrannosaurus rex	21	1.87	2.703	0.5341	0.04159	0.9718	0.853	R	0.0582
Tarbosaurus bataar	5	1.73	1.603	0.8176	0.6709	0.9489	0.997	R	0.0395
Gorgosaurus libratus	12	2.30	1.855	0.7666	0.5858	0.8522	0.945	R	0.0996
Daspletosaurus torosus	6	1.55	1.873	0.7465	-0.261	0.9294	0.955	R	0.277
Gallimimus bullatus	5	2.46	2.131	0.8187	0.653	1.271	0.983	I	0.1961
Herrerasaurus ischigualastensis	5	1.72	1.989	0.8081	0.24	1.175	0.828	I	0.4217
Troodon formosus	7	1.92	1.801	0.8632	0.46	1.296	0.796	I	0.7363
Sauropodomorpha
Massospondylus carinatus	16	4.43	2.747	0.8135	0.6412	0.9078	0.905	R	0.0925
Riojasaurus incertus	8	2.01	2.174	0.7437	0.547	1.068	0.826	I	0.1514
Apatosaurus sp.	12	5.48	1.007	0.9709	0.913	1.029	0.993	I	0.5953
Camarasaurus sp.	27	4.83	0.7948	1.000	0.925	1.065	0.969	I	0.9989
Diplodocus sp.	23	3.31	0.8925	1.022	0.931	1.172	0.914	I	0.8215
Ornithopoda
Tenontosaurus tilletti	6	1.99	0.7595	1.035	0.923	1.18	0.978	I	0.7035
Dryosaurus lettowvorbecki	27	2.86	1.003	0.9902	0.93	1.05	0.979	I	0.7387
Hypacrosaurus stebingeri	12	19.04	0.3969	1.094	1.072	1.113	0.999	G	0.0001
Maiasaura peeblesorum	23	8.10	0.9214	1.052	1.025	1.081	0.996	G	0.0134
Stegosauria
Stegosaurus stenops	6	4.27	0.8649	1.043	0.665	1.8	0.973	I	0.8848
Kentrosaurus aethiopicus	37	2.56	1.039	0.9675	0.907	1.04	0.954	I	0.5088
Ceratopsia
Pachyrhinosaurus sp.	8	2.79	0.9107	1.01	0.916	1.229	0.969	I	0.8628
Centrosaurus apertus	4	1.75	0.9067	0.9911	0.962	2.064	0.998	I	0.6887
Chasmosaurus mariscalensis	21	3.10	1.670	0.8651	0.8236	0.9021	0.978	R	0.0009
Psittacosaurus lujiatunensis	5	1.48	0.3927	1.292	0.709	1.779	0.875	I	0.4709

R, I, and G denote growth patterns of negative allometry, isometry, and positive allometry, respectively. Lower and upper limits are the 95% confidence limits for the slope. P-values are the results of permutation tests (with 10 000 permutations). Permutation tests indicate significant departures from isometry if P<0.05. P-values are highlighted in bold in instances where the results of permutation tests disagree with the growth patterns indicated by the range of the slope confidence limits.

With the exception of the negatively allometric femur of the prosauropod Massospondylus carinatus [0.81 (0.64, 0.91)], all sauropodomorph taxa examined in this study exhibited isometry during ontogeny. Excluding M. carinatus, R. incertus was the only sauropodomorph to have an exponent well below a value of 1.0 (0.74) but it was not a statistically significant departure from isometry.

In the majority of ornithischians studied here, femoral allometry did not depart significantly from isometry, with exponents ranging from 0.968 (0.907, 1.04) in K. aethiopicus to 1.29 (0.71, 1.78) in P. lujiatunensis. Chasmosaurus mariscalensis was the only ornithischian possessing significant negative allometry of the femur [0.87 (0.82, 0.90]. In the two hadrosaur taxa, Hypacrosaurus stebingeri and M. peeblesorum, however, femoral scaling was significantly positively allometric with exponents of 1.09 (1.07, 1.11) and 1.05 (1.03,1.08), respectively; the CIs in both species excluded a value of 1.0. Although this indicated that hadrosaurs exhibited increasingly gracile femora during ontogeny, our sampling limited us from determining if this pattern exists outside Hadrosauridae.

For 19 of the 23 sampled taxa, the results of permutation tests of femoral growth agreed with the results of bootstrapping RMA slope confidence limits. The results of permutation tests for femoral allometry in T. rex (P = 0.0582), Gorgosaurus libratus (P = 0.0996), Daspletosaurus torosus (P = 0.277), and M. carinatus (P = 0.0925) disagreed with the pattern of femoral allometry indicated by the RMA slope CI. In the tyrannosaurids T. rex, G. libratus, and D. torosus, and the prosauropod M. carinatus, where P>0.05, the permutation tests identified isometric growth of the femur.

Tibial allometry

Tibial allometry was not as marked in theropods as observed for the femur (Table 4). The exponents for theropods ranged from negatively allometric values (0.42 [-1.03, 1.05] in T. rex) to values close to isometry (0.98 [0.60, 1.62] in H. ischigualastensis) but, of the seven theropods examined, only A. fragilis had a tibia that showed statistically significant ontogenetic allometry. The lack of statistically significant departures from isometry in the tibia of other theropods was probably due to the small SRs and sample sizes of these taxa. For the sauropodomorphs, Apatosaurus sp. was the only taxon to exhibit a significant departure from isometry (1.13 [1.07, 1.19]). In ornithischians, tibial allometry was statistically significant only in Tenontosaurus tilletti (0.77 [0.57, 0.97]), M. peeblesorum (1.09 [1.01, 1.05]), and H. stebingeri (1.12 [1.05, 1.20]). Therefore, an overlap existed in the range of allometric exponent values between saurischians and ornithischians.

Table 4.

Results of reduced major axis regressions assessing tibial allometry for each dinosaur species.

Taxon	N	Size range (x)	RMA intercept	RMA slope	Lower Limit (95%)	Upper Limit (95%)	R2	Growth pattern	P
Theropoda
Allosaurus fragilis	44	2.63	1.638	0.801	0.7419	0.8804	0.942	R	0.0015
Tyrannosaurus rex	8	1.49	4.452	0.4242	−1.029	1.047	0.845	I	0.1149
Tarbosaurus bataar	4	1.48	3.089	0.3911	0.2279	0.5544	0.981	R	0.1987
Gorgosaurus libratus	10	1.95	2.16	0.8348	0.696	1.175	0.838	I	0.3338
Gallimimus bullatus	7	2.42	2.975	0.6771	−0.581	1.017	0.781	I	0.1423
Herrerasaurus ischigualastensis	6	1.60	1.282	0.9795	0.604	1.621	0.806	I	0.89
Troodon formosus	8	1.92	1.77	0.945	0.734	1.08	0.967	I	0.628
Sauropodomorpha
Riojasaurus incertus	7	1.65	1.713	0.6871	0.246	1.166	0.621	I	0.5124
Apatosaurus sp.	14	7.11	0.0250	1.130	1.066	1.189	0.989	G	0.0086
Camarasaurus sp.	15	3.13	−0.0593	1.142	0.969	1.325	0.945	I	0.1867
Diplodocus sp.	20	3.72	0.1244	1.150	0.965	1.306	0.929	I	0.2413
Ornithopoda
Tenontosaurus tilletti	7	2.22	1.562	0.7731	0.5708	0.972	0.944	R	0.0826
Dryosaurus lettowvorbecki	17	3.24	1.317	0.9792	0.899	1.101	0.968	I	0.7879
Hypacrosaurus stebingeri	10	16.06	0.7319	1.118	1.049	1.196	0.993	G	0.0608
Maiasaura peeblesorum	48	9.26	1.089	1.031	1.011	1.052	0.995	G	0.0405
Stegosauria
Stegosaurus stenops	4	5.22	0.1813	1.2	1	3.96	0.951	I	0.7897
Ceratopsia
Centrosaurus apertus	7	2.19	1.1	0.8725	0.733	1.026	0.969	I	0.2662

R, I, and G denote growth patterns of negative allometry, isometry, and positive allometry, respectively. Lower and upper limits are the 95% confidence limits for the slope. P-values are the results of permutation tests (with 10 000 permutations). Permutation tests indicate significant departures from isometry if P<0.05. P-values are highlighted in bold in instances where the results of permutation tests disagree with the growth patterns indicated by the range of the slope confidence limits.

For 14 of the 17 sampled taxa, the permutation test results agreed with growth patterns identified by bootstrapping RMA slope confidence limits. Discrepancies between permutation tests and bootstrapping occurred for Tarbosausus bataar, T. tilletti, and H. stebingeri. Although the RMA regression for tibial growth in T. bataar indicated a significant departure from isometry (0.39 [0.23, 0.55]), the permutation test found that tibial growth did not depart significantly from isometric growth (P = 0.1987). For the ornithischians T. tilletti and H. stebingeri, permutation test results did not achieve significance at the 5% level (P = 0.0899 and 0.0599, respectively), indicating isometric growth of the tibia in these two taxa.

Relationship between life-history traits and allometry

Adult body mass

For our entire sample of Dinosauria, bivariate ordinary least squares regressions were performed between raw (i.e. not phylogenetically corrected) humeral, femoral, and tibial allometric exponents and log-transformed estimates of adult body mass (Tables 5 and 6; Figs S1–S3 in the Supporting Information). Using different estimates of mass, we found no significant relationship between humeral allometry and body mass (Anderson et al.: R² = 0.0033, P = 0.9022; Mixed Model: R² = 0.0016, P = 0.9327; Seebacher: R² = 0.0386, P = 0.6730). None of the slopes for femoral growth were found to be statistically distinguishable from zero (Anderson et al.: R² = 0.0214, P = 0.5384; Mixed Model: R² = 0.0587, P = 0.3033; Seebacher: R² = 0.1564, P = 0.1616). Likewise for tibial allometry, none of the regressions comparing limb bone growth with body mass had slopes significantly different from zero (Anderson et al.: R² = 0.0232, P = 0.5881; Mixed Model: R² = 0.0049, P = 0.8036; Seebacher: R² = 0.1640, P = 0.2166). For both the Anderson et al. (1985) and Mixed Model mass estimates, Durbin-Watson tests for autocorrelation indicated that humeral and tibial allometry were autocorrelated with body mass (P<0.05; Table 5).

Table 5.

Coefficients of determination and significance values for regressions between life-history traits and limb bone allometry using raw data.

	OLS regression				Autocorrelation
	N	R***2	P	Significant?	P	DW
(A) Mass: Anderson et al.
Dinosauria
Humeral	7	0.0033	0.9022	No	0.0009	0.7057
Femoral	20	0.0214	0.5384	No	0.1898	1.5418
Tibial	15	0.0232	0.5881	No	0.018	1.0578
Saurischia
Femoral	13	0.1445	0.2002	No	0.0582	1.2064
Tibial	11	0.0434	0.5389	No	0.0064	0.8414
Ornithischia
Femoral	6	0.4447	0.1018	No	0.4713	1.8762
Non-avian theropods
Femoral	8	0.2146	0.2476	No	0.0004	0.6112
Tibial	7	0.5013	0.750	No	0.6319	1.9581
(B) Mass: mixed model
Dinosauria
Humeral	7	0.0016	0.9327	No	0.001	0.7132
Femoral	20	0.0587	0.3033	No	0.207	1.5625
Tibial	15	0.0049	0.8036	No	0.019	1.0656
Saurischia
Femoral	13	0.0947	0.3063	No	0.0326	1.0988
Tibial	11	0.0167	0.7051	No	0.0057	0.8272
Ornithischia
Femoral	6	0.4320	0.1086	No	0.4626	1.867
Non-avian theropods
Femoral	8	0.1884	0.2826	No	<0.0001	0.4903
Tibial	7	0.4873	0.0811	No	0.4612	1.794
(C) Growth rates
Femoral	9	0.1611	0.2843	No	0.1144	1.3146
Tibial	6	0.1219	0.4975	No	0.4149	1.7913

Sections A and B are regression and Durbin-Watson (DW) test results for ordinary least squares (OLS) regressions of adult body mass and long bone allometry. Section C contains OLS regression and DW test results for regressions of maximum growth rate and long bone allometry. In section A, mass estimates are calculated solely from the equations of Anderson et al. (1985). In section B, mass estimates for non-avian theropods were calculated using the formulas in Christiansen & Fariña (2004), whereas mass estimates for quadrupedal taxa were calculated using formulas from Packard et al. (2009). Mass estimates for bipedal ornithischians in section B were calculated using the equations of Anderson et al. (1985). P-values and DW statistics are also given for DW tests for autocorrelation, as both long bone allometry and mass estimates were determined using long bone circumferences. Autocorrelation is significant if P < 0.05.

Table 6.

Coefficients of determination and significance values for regressions between mass estimates of Seebacher (2001) and limb bone allometry.

	N	R2	P	Significant?
Dinosauria
Humeral	7	0.0386	0.9022	No
Femoral	14	0.1564	0.1616	No
Tibial	11	0.1640	0.2166	No
Saurischia
Femoral	9	0.1541	0.2960	No
Tibial	9	0.1592	0.2874	No
Ornithischia
Femoral	4	0.8312	0.0311	Yes
Non-avian theropods
Femoral	5	0.7410	0.0610	No
Tibial	5	0.5674	0.1415	No

Only in the femora of Ornithischia is long bone allometry significantly related to body mass. However, the relationship is no longer significant after removal of the smallest taxon (Psittacosaurus lujiatunensis) (R² = 0.3515, P = 0.4072).

Plots of independent contrasts of femoral allometric exponents against logBM showed a negatively allometric relationship across non-avian Dinosauria. This correlation was significant in all but four of the 27 combinations of mass estimation method, tree topology, and branch-scaling model, and the four remaining cases all had trends that were near-significant (0.052 < α ≤ 0.065). Three of the four instances in which significance was not achieved had mass estimates determined using Anderson et al. (1985) and two of these (along with a third) had in common a topology in which Herrerasaurus is a basal saurischian rather than a basal theropod. Of the three scaling models, the analyses employing geological ages always achieved significance, whereas the instances with near-significant trends occurred when branches were scaled using one of the other two methods. Thus, we conclude that there is some sensitivity to the three parameters that we considered here but overall our results do support a significant correlation between femoral allometry and adult body mass. However, when lower taxonomic levels (i.e. Ornithischia, Sauropodomorpha, and Theropoda) were considered, the trends were no longer significant, due in part to the small number of possible contrasts. As with the raw species correlations, independent contrasts analyses for humeral and tibial allometric exponents did not show significant correlations with log-transformed body mass under any topology or branch-scaling scheme.

In order to determine if limb bone allometry itself exhibits scale effects at lower taxonomic levels, saurischian, ornithischian, sauropodomorph, and non-avian theropod data were analyzed separately (Tables 5 and 6). Within ornithischians and sauropodomorphs, the number of taxa for which tibial allometry was determined was too small for useful analysis as was the case for humeral allometry. Within Saurischia, femoral exponents were independent of log-transformed estimates of adult body mass regardless of the mass estimate used (Anderson et al.: R² = 0.1445, P = 0.2002; Mixed Model: R² = 0.0947, P = 0.3063; Seebacher: R² = 0.1541, P = 0.2960; Fig. S4 in the Supporting Information). Also for Saurischia, we found tibial allometry to be independent of body mass for all three sets of mass estimates used (Anderson et al.: R² = 0.0434, P = 0.5389; Mixed Model: R² = 0.0167, P = 0.7051; Seebacher: R² = 0.1592, P = 0.2874, Fig. S5 in the Supporting Information). Using the Anderson et al. (1985) and Mixed Model mass estimates, femoral allometry in ornithischians was found not to be a statistically significant function of logBM (Anderson et al.: R² = 0.4447, P = 0.1018; Mixed Model: R² = 0.4320, P = 0.1086; Fig. 2). A regression between the mass estimates of Seebacher (2001) and femoral allometry yielded a slope that was significantly different from zero for ornithischians (R² = 0.8312, P = 0.0311; Fig. 2). However, this result was heavily predicated upon P. lujiatunensis. Removal of this taxon resulted in the regression slope not differing significantly from zero (R² = 0.3515, P = 0.4072). A regression between logBM and long bone allometry was not performed for sauropodomorphs because the small number of species within this group for which we had both long bone allometry and adult body mass estimates would have resulted in a strong phylogenetic influence on the resulting regression. In non-avian theropods a negative relationship existed between logBM and femoral allometry (Fig. 3) but the correlation failed to be significant (Anderson et al.: R² = 0.2146, P = 0.2476; Mixed Model: R² = 0.1884, P = 0.2826; Seebacher: R² = 0.7410, P = 0.0610), a result also found using independent contrasts on all combinations of mass estimation method and branch-scaling model. In non-avian theropods the negative slope of the correlation between logBM and tibial allometric exponents approached, but did not reach, significance at the 5% level (Anderson et al.: P = 0.750; Mixed Model: P = 0.0811; Seebacher: P = 0.1415; Fig. S6 in the Supporting Information) and even less significant trends were observed using independent contrasts. For mass estimates based on long bone dimensions, we performed Durbin-Watson autocorrelation tests and found significant autocorrelation in nearly all of our regressions of body mass and long bone allometry (Table 5). We did not find autocorrelation to be significant for regressions of body mass with ornithischian femoral allometry (Anderson et al.: P = 0.4713; Mixed Model: P = 0.4626) and non-avian theropod tibial allometry (Anderson et al.: P = 0.6319; Mixed Model: P = 0.4612).

Fig. 2.

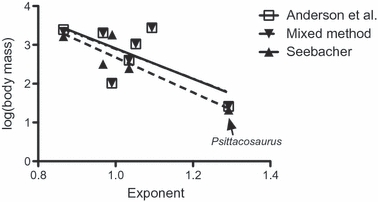
Regression between adult body mass and femoral allometry in Ornithischia. The regression using mass estimates from Anderson et al. (1985) fails to reach significance (R² = 0.4447, P = 0.1018). The regression using mixed methods of mass estimates is also not significant (R² = 0.4320, P = 0.1086). The regression between the mass estimates of Seebacher (2001) and femoral allometry yielded a slope significantly different from zero (R² = 0.8312, P = 0.0311). However, this result is heavily dependent upon Psittacosaurus lujiatunensis. Removal of this taxon results in the slope not significantly differing from zero (R² = 0.3515, P = 0.4072).

Fig. 3.

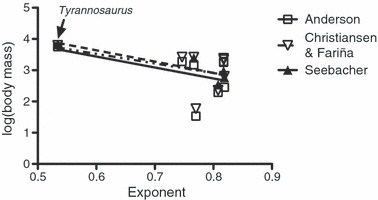
Regression of body mass upon femoral allometry in non-avian theropods. The results using mass estimates from Anderson et al. (1985) are R² = 0.2146 and P = 0.2476. The results using mass estimates from Christiansen & Fariña (2004) are R² = 0.1884 and P = 0.2826. The results using mass estimates from Seebacher (2001) are R² = 0.7410 and P = 0.0610. As these results are heavily dependent on Tyrannosaurus rex, this taxon has been identified in the figure.

Maximum growth rate

Regressions of allometric exponents against logGR were affected by the relatively small number of taxa for which maximum growth estimates were available (Table 5). Raw correlation between femoral scaling exponents and logGR was not significant (R² = 0.1611, P = 0.2843; Fig. S7 in the Supporting Information) but the correlation between these two variables was significant in independent contrasts analyses that employed scale branch lengths to geological ages (P<0.048 for all three topologies), although not when other scaling methods were employed (Table 7). The correlation between tibial allometric exponents and logGR was not significant in either raw or independent contrasts analysis (R² = 0.1219, P = 0.4975; Fig. S8 in the Supporting Information). Growth rates were estimated for only three of the quadrupedal dinosaurs in our sample, so we did not examine the relationship between growth rate and humeral allometry. The small sample size rendered correlation analyses at lower taxonomic levels meaningless. We did not find significant autocorrelation between femoral and tibial allometry and maximum estimated growth rates (P_{Anderson et al.} = 0.1144 and P_{Mixed Model} = 0.4149; Table 5).

Estimation of the root node value for the intraspecific scaling coefficient using independent contrasts (Garland et al. 1999) indicated that femoral scaling did not deviate significantly from isometry ancestrally in dinosaurs (Table 7) in all but five of the various combinations of topology, branch-scaling model, and mass estimation method that we considered. In these five replicates, values indicated negative allometry, with 1.0 excluded from the CI, so it is possible that, as sampling improves, it will be shown that dinosaurs were ancestrally characterized by negative femoral scaling.

Discussion

Limb bone allometry

Confidence limits and permutation tests

Many of the exponents in our sample have wide CIs due to (i) small sample sizes or (ii) small observed SRs in which individual variation could obscure any allometric signal (LaBarbera, 1989). To obtain a clear allometric signal, a 2.5–3.0 SR (i.e. the largest specimen is 2.5–3 times as long as the smallest) is preferable, allowing for a sample as small as N = 8 to yield precise results (M. LaBarbera, personal communication). The effects of sample size and SR can be clearly seen when comparing the CI of A. fragilis (N = 49, SR = 4.09, CI = 0.7836–0.8514) with that of P. lujiatunensis (N = 5, SR = 1.48, CI = 0.451–2.132). Although many taxa in our sample, especially among the ornithischians, do not significantly depart from isometry in femoral, tibial, and humeral scaling exponents, increasing sample sizes and SRs could narrow the CIs and improve the rigor of our tests of significance.

The results of the permutation tests widely agreed with the growth patterns found by bootstrapping slope confidence limits (81% for all RMA regressions; 75, 83, and 82% for humeral, femoral, and tibial RMA regression, respectively). The high percentages of agreement between these two tests of long bone growth indicate that the cases of statistically significant allometric growth that we found in this study are not merely the product of a weak test for departures from isometry (i.e. bootstrapping confidence limits) or small species sample sizes and SRs. However, the numerous observations of isometric growth may be a product of sample size and SR (see previous paragraph). In some instances the results of permutation tests only marginally failed to reach statistical significance when the bootstrapping of slope confidence limits indicated significant departures from isometry (humeral growth: R. incertus, P = 0.0573; femoral growth: T. rex, P = 0.0582; tibial growth: H. stebingeri, P = 0.0608)). In such occurrences, we consider the statistically significant departures from isometric growth inferred from the range of RMA slope confidence limits to be correct and we surmise that the permutation tests would reach significance with only minor increases in sample size and SR. For a given species’ dataset, we found no instances in which the permutation tests found significant departures from isometric growth but for which bootstrapped confidence limits indicated isometric growth. As the permutation test is a more rigorous test than bootstrapping RMA slope confidence limits, we have more confidence in the results of the permutation tests in the instances where they strongly disagree (e.g. P>0.1) with the CI results.

Patterns in limb bone allometry

Despite the challenges posed by small samples, several patterns emerge from our analysis of intraspecific allometry in limb bones of non-avian dinosaurs. Although most taxa analyzed here have femora with a scaling exponent that is indistinguishable from isometry, significant departures toward negative and positive allometries are observed in well-sampled, large-bodied theropods and hadrosaurids, respectively, and all theropods in our sample consistently show negative allometric exponents. These results stand in contrast to an overall negatively allometric (femoral exponent, 0.83; tibial exponent, 0.78; metatarsal III exponent, 0.80) relationship of long bone length and circumference across a broad sample of non-avian dinosaur taxa reported by Carrano (1999) and indicate that intraspecific allometry of bone dimensions differs from interspecific allometric patterns, just as noted by Erickson & Tumanova (2000). Although Carrano (1999) did not test whether the reported scaling deviates significantly from isometry for Dinosauria as a whole, this robust correlation and large sample size support such an interpretation. Carrano (2001) reported femoral, tibial, and humeral allometry within the clades Dinosauria, Saurischia, and Ornithischia, in addition to postural and size-based groupings. He found that the majority of interspecific allometric relationships are significantly negative, especially the allometry between long bone length and medio-lateral diameter in large-bodied taxa, a trend that we only found in theropods in our study of intraspecific allometry.

Estimation of the root node value for intraspecific allometric coefficients using independent contrasts (Garland et al. 1999) indicates that ancestral femoral allometry in dinosaurs did not deviate significantly from isometry (Table 7) and isometric scaling is also reported in Alligator (Dodson, 1975), several squamates (Peterson & Zernicke, 1986, 1987), basal synapsids (Blob, 2006), and a marsupial (Lammers & German, 2002), although the latter observations are based on scaling diameters, rather than circumferences, to bone lengths. Preliminary data gathered by one of us (Kilbourne, 2007) demonstrate isometric scaling of long bones through ontogeny in several mammalian, lizard, and crocodilian species, confirming that isometric limb bone scaling is a widespread pattern for the ontogenetic development of amniotes. Nevertheless, a minority of our independent contrast analyses, especially those that posit Herrerasaurus as closer to the origin of Dinosauria, point to negative scaling as the ancestral condition. Discoveries of growth series of Triassic dinosauromorphs (Nesbitt et al. 2009) may allow for further testing of the possibility that the pattern observed in bipedal theropods may actually have been inherited form the last common ancestor of all dinosaurs.

Scaling patterns for the tibia and humerus appear to vary more appreciably among non-avian dinosaurs. Tibial allometric exponents exhibit a greater range of values than is observed for the femur, although a majority of taxa do not depart significantly from isometry. A plot of tibial on femoral allometric exponents exhibits a general positive trend but with a relatively poor coefficient of determination (R² = 0.5097), indicating that individual hindlimb bones do not change proportion uniformly within taxa (Fig. 4). The correlation between femoral and tibial exponents indicates a general trend in which the femur and tibia of a given species grow with roughly similar allometric exponents. To illustrate this point, the femora and tibiae of hadrosaurids H. stebingeri and M. peeblesorum both grow with positive allometry, whereas the femur and tibia of A. fragilis both grow with negative allometry. However, the low coefficient of determination (∼ 0.5) may be due to differences in the exact values of species’ femoral and tibial allometric exponents, and instances where isometric growth and negatively allometric growth occur within the same limb (e.g. G. libratus). Although the wide CIs, especially for the tibial exponents, dictate caution, Carrano (1999, Table 3 therein) also reported poor correlation between the ratios of raw length to circumference for the femur and tibia in 177 non-avian dinosaur specimens.

Fig. 4.

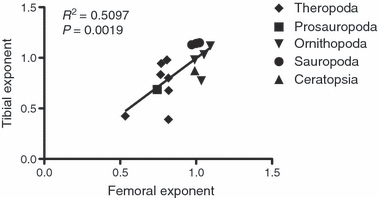
Bivariate plot of tibial allometric exponents against femoral allometric coefficients across Dinosauria.

Apart from the prosauropod Riojasaurus, all of the sampled taxa exhibit humeral allometric exponents that are close to, and statistically indistinguishable from, isometry. Wilhite (2003) and Bonnan (2004) noted isometric growth patterns in sauropod limb bones but it appears that such patterns may also apply broadly to facultative and obligate quadrupeds among the Ornithischia. In addition, in Alligator mississippiensis, a eusuchian archosaur and obligate quadruped, ontogenetic growth of the limb bones is isometric (Dodson, 1975) and the relative proportions of forelimbs and hindlimbs are isometric in relation to one another during ontogeny (Livingston et al. 2009). The different allometric patterns in hadrosaurid humeri and femora hint at possible changes in locomotory behavior through ontogeny in these facultative quadrupeds, such as shifts from quadrupedalism to bipedalism or vice versa (see also Heinrich et al. 1993). Reisz et al. (2005) noted that the humerus of embryonic specimens of the prosauropod Massospondylus had nearly identical humeral and femoral lengths but that humeral length grew with negative allometry with respect to femoral length through the ontogeny of this prosauropod. Although we were unable to collect a statistically meaningful sample of humeral measurements for Massospondylus, the pattern that we observed in Riojasaurus appears to corroborate negative allometry of humeral growth. Reisz et al. (2005) hypothesized that obligate quadrupedality in sauropods evolved by means of a paedomorphic retention of prosauropod limb ratios. Our results indicate that this heterochronic change would be accompanied by a shift from negative allometry to isometry during the growth of the humerus.

Comparisons to previous scaling studies

Many of the scaling exponents are consistent with the exponent values predicted by the scaling models of McMahon (1975a), Kokshenev (2003), and Garcia & da Silva (2004) (Table 8) that have been extensively used in previous studies of interspecific limb bone allometry, although in the hadrosaurids analyzed here, allometric exponents (Tables 3 and 4) are higher than any of the exponents predicted by the standard scaling models. This implies that intraspecific scaling regimes do not necessarily follow any of the proposed similarity models of scaling. To validate whether a scaling model accurately describes empirical scaling relationships, measurements of body mass are needed in addition to long bone length and circumference. At present we cannot test whether any of these models apply to our data in an unbiased manner, however, because the sub-adult and juvenile dinosaur body masses available in the literature were estimated using the developmental mass extrapolation method (Erickson & Tumanova, 2000). This method assumes that body mass scales isometrically to femoral length and thus makes an a-priori assumption of geometric similarity.

Table 8.

Models predicting limb bone allometry.

Model	Predicted exponent	Constraint
Geometric similarity1	1.0	Ratios of linear dimensions kept constant
Elastic similarity1	0.67	Probability of failure by buckling or bending kept constant
Static stress similarity1	0.5	Stress within structure remains constant
‘Bending’ model2	∼ 0.80	Bending loads encountered during locomotion
‘Bending and axial compression’ model3	∼ 0.73	Bending and axial loads encountered in locomotion determine allometry

The predicted exponent corresponds to the allometric exponent in equation l∝d^b, where l is bone length, d is bone diameter or circumference, and b is the allometric exponent predicted by the model. Constraint specifies the theoretical constraint governing the predictions of the model.

¹McMahon (1975a).

²Kokshenev (2003).

³Garcia & da Silva (2004).

Positive long bone allometry and physiology

The departure of ontogenetic long bone allometry from trends seen in interspecific allometry and scaling may be due in part to changes in the material properties of bone during ontogeny, with bones supporting an increase in body mass by becoming stiffer and stronger throughout ontogeny (Currey, 1977; Currey & Pond, 1989; Torzilli et al. 1981, 1982; Carrier, 1983; Carrier & Leon, 1990; Brear & Currey, 1990). To accommodate the evolution of increasing adult body mass (interspecific scaling studies deal with adult individuals of species), limb bones tend to become more robust (Bertram & Biewener, 1990), whereas the material properties of bone are relatively constant across adult members of Tetrapoda (Erickson et al. 2002). Although ontogenetic changes in the material properties of bone are certainly plausible for dinosaurs, we recognize that in the absence of supporting evidence this remains speculative.

Differences in the allometry of hindlimb bones across Dinosauria in our sample are relevant to current ideas on scaling and its correlations to growth patterns and metabolic regimes. Carrier (1983) and Carrier & Leon (1990) found that, in rabbits and gulls, the limb bones become more gracile during ontogeny, whereas the ontogeny of bone proportions in Alligator (Dodson, 1975) and some lizards (Blob, 2006) include isometry or even increasing robustness with growth. Carrier & Leon (1990) proposed that positive allometry is causally related to and reflective of endothermic metabolic regimes, whereas isometry and negative allometry are causally related to and reflective of ectothermic metabolic regimes. Most of the taxa that we sampled exhibit growth that is statistically indistinguishable from isometry but large theropods show negative allometries of hindlimb bones and hadrosaurs show a gradual but significant decrease in robustness. These taxa thus exhibit the expected ‘ectothermic’ and ‘endothermic’ patterns, respectively, as outlined by Carrier & Leon (1990). Although the metabolic regimes of non-avian dinosaurs are the subject of intense debate (Chinsamy & Hillenius, 2004; Padian & Horner, 2004; Gillooly et al. 2006), and are impossible to study directly, a recent analysis of cell size inferred from osteonal lacunae in bones suggests that saurischians, and especially theropods, have smaller cells and cell nuclei than ornithischians (Organ et al. 2007). Smaller cell volumes are thought to promote higher metabolic rates in birds because of their higher surface to volume ratios (Hughes & Hughes, 1995). This paleocytological evidence, coupled with the presence of presumably insulating plumage in a diverse array of non-avian coelurosaurs including tyrannosaurs (Xu et al. 2001), implies that elevated metabolic rates are more likely to be present in theropods than in ornithopods, a conclusion at variance with the inferences of Carrier & Leon (1990) regarding intraspecific scaling and metabolism. We consider that the scaling patterns of Carrier & Leon (1990) may more probably be related to parameters such as body size and/or limb posture, or perhaps may be an artifact of small sample size (Blob, 2006), rather than serving as a predictor of metabolic regimes, a conclusion bolstered by our demonstration of isometric intraspecific allometric patterns in several mammalian taxa (Kilbourne, 2007).

Factors influencing limb bone allometry during ontogeny

Studies of interspecific scaling often interpret changes in scaling patterns as a response to taxonomic shifts in body mass (Bertram & Biewener, 1990; Christiansen, 1999) and cursoriality (Carrano, 1999), two parameters that are obviously interdependent. In light of this, we examined correlations between allometric exponents and log-transformed estimates of adult body mass to determine whether target mass exerts a significant influence on the ontogenetic allometry of weight-bearing limb bones during growth. Correlations on raw species values did not indicate significant relationships, regardless of which mass estimate we used (Table 5). For regressions involving mass estimates based on long bone dimensions, nearly all had significant levels of autocorrelation, which urge caution when interpreting our results. In the regression between ornithischian femoral allometry and logBM, we found a significant negative relationship (R² = 0.8312, P = 0.0311). However, this result was obtained only for mass estimates from Seebacher (2001) and is dependent upon the taxon P. lujiatunensis. A number of significant correlations emerged from analyses using either independent contrasts or following the omission of outliers. Independent contrasts suggest a significant negative trend between logBM and femoral allometric exponents when we applied heterogeneous branch scaling, suggesting that non-avian dinosaur femora become more robust with increasing body size, although poor coefficients of determination indicate a wide variance. The discrepancy between the raw and independent contrasts analyses probably reflects the uneven sampling of clades. Although analyses at lower taxonomic scales do not result in significant trends here, this is probably a result of sample size and may change with the addition of more taxa. If the different patterns of allometry observed in large theropods and iguanodontians are more pervasive, these clades may require separate analyses to tease apart their opposing signals as suggested by Garland et al. (1992).

The raw maximum estimated growth rate did correlate with femoral allometry in dinosaurs (Table 5), which is not surprising given that estimated growth rates are directly related to estimates of body mass at different ages during ontogeny (Erickson & Tumanova, 2000), but this correlation was not robust when analyzed under independent contrasts for two of the three branch-scaling models (Table 7). Estimates of body mass at different stages of ontogeny are based upon femoral lengths; however, regressions for both the femur and tibia are not subject to significant levels of autocorrelation (P_{femoral allometry} = 0.1144, P_{tibial allometry} = 0.4149; Table 5). The correlation for the tibia is affected strongly by the small number of taxa for which growth rates have been calculated and the large impact of single taxa (e.g. T. rex). With the T. rex value removed, a significant negative trend was found with the independent contrasts for the femur. This weak trend indicates that non-avian dinosaurs with higher growth rates tend to scale isometrically or even with positive allometry but is predicated on including Apatosaurus as having the fastest growing taxon along with exclusion of T. rex from the tibial dataset. As noted above, it is very probable that different trends apply to theropods than to most of the remaining taxa and that separate clade level analyses will have to be conducted with broader sampling of dinosaurian growth series. Part of the reasoning of Carrier & Leon (1990) for positive allometry correlating with endothermy was that faster growth rates are associated with less dense and weaker bone structure at early ages, relative to ectotherms (D. Carrier, personal communication). This mechanical disadvantage would be offset by having more robust bone proportions in early ontogeny. Estimates for dinosaurian growth rates are substantially higher than those observed for any ectotherms (Erickson et al. 2001), however, and closer to values observed in therian and placental mammals. In light of this, the weak trends observed between growth rates and limb bone scaling should not be interpreted as endorsing the hypothesis of Carrier & Leon (1990) correlating metabolic regimes/growth rates to scaling.

Another variable that is likely to play a more influential role in limb bone allometry is the degree of cursoriality of a species. Carrano (1999) found that theropods are more cursorial than large bipedal and quadrupedal ornithischians along a gradient of locomotor specialization defined by the second principal component in a dataset of hindlimb measurements, which includes four of the measurements used here (femoral and tibial lengths and circumferences). Carrano (1999) also suggested that juvenile dinosaurs show the same locomotor morphology (and therefore probably the same locomotor habit) as adult dinosaurs. In light of the findings of Carrano (1999), it appears reasonable that the increasing robustness of theropod limb bones during ontogeny may correspond to a higher mechanical demand placed upon the limbs by the more cursorial nature of theropods.

Three important factors with respect to ontogenetic alterations in bone structure are changes in bone material properties, second moment of area, and the cross-sectional area of cortical bone. Although it is currently difficult to estimate the material properties of fossilized bones without extensive destructive sampling, the second moment of area (a bone’s resistance to bending) and the cross-sectional area of cortical bone can be calculated from a cross-section of fossilized bone. Dilkes (2001) found that the second moment of area in the humerus of M. peeblesorum is isometric with respect to humeral length, whereas the tibial second moment of area decreases relative to tibia length. Zelenitsky et al. (2006) found that the second moments of area in the humerus and femur of H. stebingeri are also isometric with regard to humeral and femoral length throughout ontogeny. Dilkes (2001), however, incorrectly stated that the positive allometry of cortical bone width and cross-sectional area with respect to limb bone length would increase bending resistance despite the second moment of area being isometric. Changes in cortical width and cross-sectional area are reflected in the value of the second moment of area, so if the second moment of area is geometrically similar to bone length and circumference during ontogeny, increasing cortical thickness and cross-sectional area will not increase bending resistance significantly.

Concluding remarks

Across Dinosauria, three patterns of allometry are seen in the postnatal ontogenetic growth of long bones: isometric growth, negative allometry (increasing bone robustness), and positive allometry (increasing bone gracility). The majority of non-theropod dinosaur species examined exhibit isometric growth, and isometric growth was found to be ancestral for Dinosauria using ancestral state reconstruction. Non-avian theropods and hadrosaurids possess negatively allometric and positively allometric growth, respectively. Organismal and life-history traits that influence long bone allometry include cursoriality and, to a much lesser degree, maximum growth rate, whereas most relationships, with the exception of the femur, between adult body mass and long bone allometry fail to reach significance. Previously noted large-scale differences in trends in the ontogenetic development of long bones across extant taxa may be the result of growth rates and not metabolic rates as previously hypothesized. Contrary to the previous predictions, the long bones (particularly the femur) of non-avian theropods, which are thought to have higher metabolic rates compared with other dinosaurs, grow more robust during ontogeny.

Few studies have examined the ontogenetic development of the locomotor system or any of its components; however, this unexplored area should be of great interest to both morphologists and physiologists. Our study has examined only one facet of the ontogenetic development of the locomotor system, namely the allometry of limb bones. Many other aspects of the ontogenetic development of the locomotor system remain to be studied, although ideally in extant taxa. Such aspects include ontogenetic changes in muscle force and mechanical advantage, muscle fiber type, peak bone strains, and material and cross-sectional properties of bone, as well as changes in gait kinematics, including duty factor, stride frequency, stride length, and preferred speed, among other variables. Other considerations include precociality/altriciality, migratory behavior, and ontogenetic changes in cursoriality. Examining these ontogenetic changes across widely diverse taxonomic and ecological groups can highlight what roles phylogeny, function, habitat, and behavior play in the development of the locomotor system.

Supporting Information

Additional Supporting Information may be found in the online version of this article:

Fig. S1. Humeral allometry vs. body mass in Dinosauria. Regardless of mass estimate used, the correlation between body mass and humeral growth is not significant (Anderson et al: R² = 0.0033, P = 0.9022; Mixed Model: R² = 0.0016, P = 0.9327; Seebacher: R² = 0.0386, P = 0.6730).

Fig. S2. Femoral allometry vs. body mass in Dinosauria. Regressions between femoral growth and body mass are not significant (Anderson et al: R² = 0.0214, P = 0.5384; Mixed Model: R² = 0.0587, P = 0.3033; Seebacher: R² = 0.1564, P = 0.1616).

Fig. S3. Tibial allometry vs. body mass in Dinosauria. Tibial allometry is independent of body mass (Anderson et al: R² = 0.0232, P = 0.5881; Mixed Model: R² = 0.0049, P = 0.8036; Seebacher: R² = 0.1640, P = 0.2166).

Fig. S4. Femoral allometry vs. body mass in Saurischia. In spite of the positive relationships, none of the regressions are significant (Anderson et al: R² = 0.1445, P = 0.2002; Mixed Model: R² = 0.0947, P = 0.3063; Seebacher: R² = 0.1541, P = 0.2960.

Fig. S5. Tibial allometry vs. body mass in Saurischia. The relationship between tibial growth and body mass is positive, but not significant (Anderson et al: R² = 0.0434, P = 0.5389; Mixed Model: R² = 0.0167, P = 0.7051; Seebacher: R² = 0.1592, P = 0.2874.

Fig. S6. Tibial allometry vs. body mass in non-avian theropods. A negative relationship between these two variables is present, but not significant (Anderson et al: R² = 0.5013, P = 0.750; Mixed Model: R² = 0.4873, P = 0.0811; Seebacher: R² = 0.5674, P = 0.1415).

Fig. S7. The relationship between maximum growth rate and femoral allometry, R² = 0.1611 and P = 0.2843. Included in the plot are Allosaurus, Daspletosaurus, Gorgosaurus, Tyrannosaurus, Massospondylus, Apatosaurus, Psittacosaurus, Tenontosaurus and Maiasaura. Growth rate estimates taken from Erickson et al. (2001, 2004), Lee & Werning (2008), and Lehman & Woodward (2008).

Fig. S8. Maximum growth rate vs. tibial allometry. Taxa included are Tyrannosaurus, Gorgosaurus, Allosaurus, Apatosaurus, Maiasaura, and Tenontosaurus, and R² = 0.1219 and P = 0.4975.

Appendix S1. Femoral measurements and their sources.

Appendix S2. Tibial measurements and their sources.

Appendix S3. Humeral measurements and their sources.

Data S1. Limb bone measurements.

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.