Abstract
The amplitude and time course of synaptic potentials in human motoneurons can be estimated in tonically discharging motor units by measuring stimulus-evoked changes in the rate and probability of motor unit action potentials. However, in spite of the fact that some of these techniques have been used for over thirty years, there is still no consensus on the best way to estimate the characteristics of synaptic potentials or on the accuracy of these estimates. In this review, we compare different techniques for estimating synaptic potentials from human motor unit discharge and also discuss relevant animal models in which estimated synaptic potentials can be compared to those directly measured from intracellular recordings. We also review the experimental evidence on how synaptic noise and intrinsic motoneuron properties influence their responses to synaptic inputs. Finally, we consider to what extent recordings of single motor unit discharge in humans can be used to distinguish the contribution of changes in synaptic inputs versus changes in intrinsic motoneuron properties to altered motoneuron responses following CNS injury.
Keywords: motor unit, motoneuron, synaptic potentials, peri-stimulus time histogram (PSTH), peri-stimulus time frequencygram (PSF)
1. Introduction
Recordings of the discharge of single motor units in human muscles have been used extensively to provide information both about the intrinsic properties of motoneurons and the characteristics of their synaptic inputs. Since each motoneuron drives the muscle fibers comprising the motor unit in a one-to-one fashion, motoneurons are the only CNS cells whose firing patterns can be readily quantified in human subjects. Motoneurons were the first cells in the vertebrate CNS to be extensively studied with intracellular electrodes in experimental animals, and these recordings have provided a wealth of information that helps connect motoneuron properties and the characteristics of their synaptic inputs to synaptic effects on motoneuron discharge (Powers and Binder, 2001). Nonetheless, because there are a number of factors that affect the likelihood of a motoneuron action potential occurring at a given point in time, there is still no consensus on the exact relation between the time course and amplitude of a synaptic input and its effects on motoneuron discharge probability and firing rate (Miles, 1997; Piotrkiewicz et al., 2009; Powers and Binder, 1999; Powers and Türker, 2001; Türker and Powers, 2005). Determining the absolute amplitude and time course of a synaptic input to a human motoneuron may not be particularly important from a functional perspective. However, the ability to determine the relative amplitudes and time courses of synaptic inputs from different sources or from the same source onto different motor units can still yield important information about the normal synaptic control of motor unit discharge. Similarly, the ability to quantitatively compare stimulus-evoked effects on motor unit discharge in patient populations versus unaffected control subjects can potentially provide valuable insight into the pathophysiological mechanisms underlying changes in motoneuron behavior following CNS disease or trauma.
In the following review, we will compare different methods of quantifying the effects of synaptic inputs on human motor unit discharge behavior, and assess the accuracy of these methods based on direct recordings of synaptic potentials and their effects on motoneuron discharge in reduced animal preparations. We will then consider how synaptic noise and intrinsic motoneuron properties influence their responses to synaptic inputs. Finally, we will consider to what extent recordings of single motor unit discharge in humans can be used to distinguish the contribution of changes in synaptic inputs versus changes in intrinsic motoneuron properties to altered motoneuron responses following CNS injury.
2. Quantification of synaptic effects on motor unit discharge
2.1 The Peri-Stimulus Time Histogram (PSTH)
The most common method used to measure the response of a neuron to a synaptic input is the peristimulus time histogram (PSTH), originally introduced by Gerstein and Kiang (Gerstein and Kiang, 1960). Its application to the analysis of human motor unit data began around 1980 (Ashby and Labelle, 1977; Ashby and Zilm, 1982a, 1978; Garnett and Stephens, 1980; Kudina, 1980), and has been fairly widespread ever since. The PSTH is constructed by counting the number of motor unit discharges that occur in different, discrete time bins relative to the stimulus onset. The bin counts (nb) in the PSTH are determined by the mean motoneuron firing rate at a given time relative to stimulus onset (f(t)), the bin width (Δt) and the number of applied stimuli (ns): nb = f(t)* Δt*ns. The PSTH can thus be normalized to reflect either the instantaneous firing rate (f(t); more precisely the spike density) or the probability of spike occurrence in a given time bin (P(t) = nb/ns). Prior to stimulus onset the probability of spike occurrence should be fairly constant and equal to the baseline firing rate times the bin width. The arrival of an excitatory post-synaptic potential (EPSP) leads to an increase in spike probability whereas an inhibitory postsynaptic potential (IPSP) leads to a decrease in spike probability below baseline (e.g., (Fetz and Gustafsson, 1983)). The cumulative sum (CUSUM; (Ellaway, 1978)) is a function derived from the PSTH by subtracting the mean bin count prior to the stimulus from the PSTH, and integrating the remainder. The CUSUM may reveal small synaptic effects that are difficult to detect from the PSTH, and for large EPSPs the time course of the CUSUM is close to that of the PSP itself ((Fetz and Gustafsson, 1983), and see below). If the CUSUM is normalized by the number of applied stimuli, the amplitude of the short-latency peak in the CUSUM reflects the probability of an extra spike occurring given that an EPSP has occurred (also referred to as the firing index), and the minimum of the short-latency trough in the CUSUM reflects a decrease in spike probability below baseline caused by an IPSP.
The interpretation of longer latency changes in the PSTH and CUSUM is complicated by the fact that in the absence of applied stimuli, motor unit discharge is quite rhythmic. This is reflected in a low coefficient of variation (standard deviation/mean) of the interspike interval (typically 0.1 to 0.2; (Kranz and Baumgartner, 1974; Person and Kudina, 1972)), so that the autocorrelogram of motor unit discharge (the probability of a motor unit spike occurring in a given time bin relative to another motor unit spike) shows regular peaks at multiples of the interspike interval. A large enough transient input resets this rhythm, so that spikes are shifted to occur at multiples of the mean interspike interval after the occurrence of a stimulus. Thus, secondary features appear in the PSTH that can reflect the autocorrelogram of the motor unit, rather than direct stimulus effects (Awiszus et al., 1991; Moore et al., 1970; Türker et al., 1997). For example, low strength percutaneous electrical stimulation of a muscle nerve will activates excitatory primary muscle spindle afferents, leading to a brief increase in motor unit firing probability (Ashby and Labelle, 1977; Kudina, 1980). However, the synchronization of motor unit firing to the excitatory stimulus leads to subsequent peaks in the PSTH reflecting the intrinsic rhythmicity of motor unit discharge (Ashby and Labelle, 1977; Kudina, 1980; Türker et al., 1997).
Direct comparisons of the time course of single and complex PSPs and their effects on the discharge patterns of motoneurons have shown that if an increase in the CUSUM returns back to the zero line (average bin count), this may in fact reflect the number of spikes that were phase advanced by the EPSP rather than a genuine inhibition (Türker and Powers, 1999, 2003). Similarly, when a fall in the CUSUM returns back to the zero line, this may reflect that the spikes that have been phase delayed by an IPSP have now fired rather than a genuine excitation (Türker and Powers, 1999, 2003). The PSTH-CUSUM can thus be useful for indicating the sign of the first PSP that is evoked in motoneurons by a stimulus.
The potential complicating effects of motor unit discharge regularity on the interpretation of long-latency synaptic effects are often overlooked, particularly when interpreting multiunit electromyographic (EMG) recordings (Brooke et al., 1999; Okdeh et al., 1999; Sonnenborg et al., 2000). Nonetheless, this complication was recognized early on (Moore et al., 1970), and it was suggested that the autocorrelogram could be used to correct the PSTH so that it only reflects stimulus-induced changes in firing probability (Ashby and Labelle, 1977). One such approach is to modify the calculation of CUSUM, so that instead of subtracting the mean pre-stimulus bin count from every post-stimulus bin, a bin-specific baseline value is subtracted for each bin i depending upon the mean (Mi) and standard deviation (Si) of the interspike intervals preceding spikes in the ith bin (Awiszus et al., 1991). This bin-specific value is calculated by going back in time from the midpoint of the ith bin by Mi and calculating the mean bin count over a period Si in duration centered at Mi prior to the ith bin. For example, for a motor unit discharging at 10 imp/s with a coefficient of variation of 0.1, a peak in the PSTH around time 0 would lead to an echo of increased firing probability centered 100 ms later than the peak. However, because the elevated mean bin count around the peak would be subtracted from the bins around the 100 ms time lag, this delayed peak would not be reflected in the modified CUSUM (mCUSUM). A related correction is based on calculating an expected cumulative spike density in the absence of a stimulus by adding a list of control interspike intervals obtained in the absence of stimulation to the times of spike occurrence relative to stimulus onset (Awiszus, 1993). When this function is subtracted from the cumulative spike density observed in the presence of the stimulus, the difference represents the impulses displaced by the stimulus (displaced impulses function, DIF). Alternatively, the horizontal distance between the control cumulative spike density and the spike density observed in the presence of a stimulus can be used to estimate the change in the interspike interval caused by the stimulus (interspike interval change function, IICF (Awiszus, 1993). Unfortunately, perhaps because of the extra computational effort required, these corrections have not been widely used. Furthermore, since this method has not been tested in reduced animal preparations in which PSP time course can be directly measured, it is not clear whether it can completely eliminate errors due to the motoneuron’s autocorrelation function.
2.2 The Peri-Stimulus Frequencygram (PSF) and Interspike Interval Superposition Plot (IISP)
There are two alternatives to the standard PSTH that are largely free of secondary peaks and troughs reflecting the motor unit’s autocorrelogram. The effects of a stimulus on motor unit discharge can be quantified instead by plotting stimulus-locked changed in instantaneous firing rate (peristimulus frequencygram, PSF; (Türker and Cheng, 1994)) or interspike interval (interspike interval superposition plot, IISP (Awiszus, 1988; Awiszus et al., 1991; Poliakov et al., 1994)). The PSF was originally introduced by Bessou and colleagues (Bessou et al., 1968) to quantify the responses of primary muscle spindle afferents to fusimotor stimulation, and has been used extensively by Türker and colleagues to quantify stimulus-evoked changes in human motor unit discharge (reviewed in (Türker and Powers, 2005)). The PSF is a scatterplot of the instantaneous frequency (reciprocal of the interspike interval) as a function of the delay between the stimulus and the spike terminating the interspike interval. If the frequency values are sorted according to the delay from the stimulus, a moving average can be used to derive a continuous plot of frequency versus delay (Türker and Cheng, 1994; Türker and Powers, 1999). A similar plot can be obtained by plotting the interspike interval as a function of delay instead of its reciprocal. Both response measures provide information that is distinct from the probability of spike occurrence. For example, a large EPSP produces a period of increased spike probability during its rising phase, but a decreased spike probability during its falling phase because spikes that normally would have occurred during this period were phase-advanced by EPSP. Nonetheless, the interspike intervals (and instantaneous frequency values) preceding the few spikes that do occur during this time period can still provide information about ongoing synaptic input, and frequency values are in fact elevated during the falling phase of an EPSP (Türker and Powers, 1999). Similarly, although a large IPSP is associated with a period of decreased firing probability followed by a period of increased firing probability associated with phase-delayed spikes, the frequency values associated with these phase-delayed spikes are lower than the baseline firing rate during the decay phase of the IPSP (Türker and Powers, 1999).
2.3 The Phase-Response Curve (PRC)
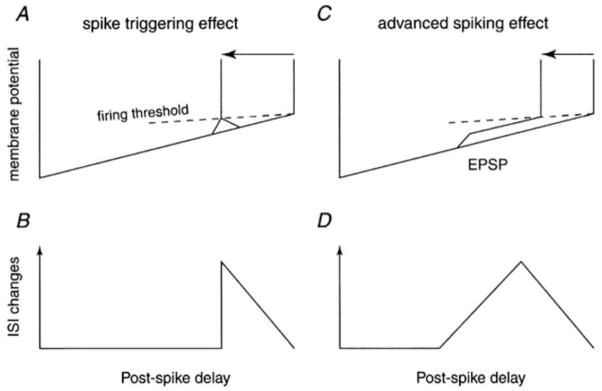
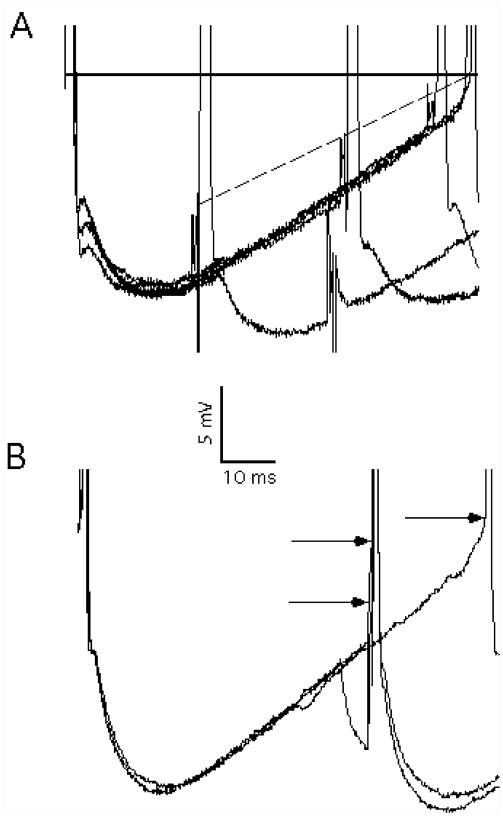
The effects of a synaptic input on spike timing can also be quantified by calculating a phase response curve (PRC: (Gutkin et al., 2005; Reyes and Fetz, 1993)), which plots the percentage change in the interspike interval (ISI) as a function of the relative delay of the stimulus from the last motor unit spike. The mean interspike interval for intervals unaffected by the stimulus is used to normalize both the stimulus-induced change in the ISI and the relative delay of the stimulus. Although the PRC can be derived from the PSTH (Gutkin et al., 2005), the PRC plot is particularly useful for revealing delayed effects of an excitatory stimulus, which may result from activation of intrinsic excitatory currents (see below, and (Reyes and Fetz, 1993)). During tonic discharge, the membrane trajectory between spikes can be roughly approximated by a post-spike drop followed by a linear rise to threshold (Schwindt and Calvin, 1972). If EPSPs can only trigger spikes directly over the portion of the ISI in which the EPSP peak crosses spike threshold, the PRC will equal zero up to the point at which threshold-crossing can first occur, jump to a maximum at this point, and then decline linearly to zero, since EPSPs occurring later in the ISI will cause progressively less shortening (Fig. 1A and B). Reyes and Fetz (Reyes and Fetz, 1993) observed an additional mode of interspike interval shortening in neocortical neurons studied in vitro, in which EPSPs or brief depolarizing pulses occurring early in the ISI were able to shorten the ISI, but the advanced spike occurred at a considerable delay from the time the pulses were applied. This delayed shortening combined with direct threshold crossing for pulses occurring later in ISI produced a PRC that rose from zero up to the point of direct threshold crossing and then declined linearly thereafter (Fig. 1C and D). This effect was quite obvious in the PRC but would only appear in the PSTH as a somewhat smaller trough following the initial peak. The rising portion of the PRC due to delayed spike triggering was most prominent for small inputs, whereas larger inputs produced more direct threshold crossings. Reyes and Fetz (Reyes and Fetz, 1993) attributed the delayed spike triggering to the turning on of a slow regenerative process that may reflect the activation of persistent sodium current.
Figure 1.
Two different effects of EPSPs on spike triggering. A and C, schematic of the interspike interval membrane potential trajectory, showing direct threshold crossing (A) or delayed spike triggering (B; advanced spiking effect). C and D show the corresponding PRC curves. (From Fig. 1 of (Mattei and Schmied, 2002) with permission.)
The PRC described above was obtained in the absence of any synaptic or injected current noise. Although the PRC that would be obtained in the absence of noise can theoretically be obtained by averaging noisy data (Gutkin et al., 2005), the interpretation of the PRC is somewhat more complicated in the presence of synaptic noise if the time course of the synaptic input is not known. Delayed spike triggering could result if synaptic noise riding on top of a slowly decaying phase of an EPSP is sufficient to produce direct threshold crossing. Recent evidence suggests that delayed triggering can occur in human motoneurons and could involve activation of an intrinsic current rather than noise-induced direct threshold crossings. Mattei and Schmied (Mattei and Schmied, 2002) studied the response of extensor carpi radialis motor units to small tendon taps. Since these taps are likely to produce relatively selective, synchronous activation of primary muscle spindle afferents (Lundberg and Winsbury, 1960) that produce monosynaptic EPSPs in motoneurons, the resultant EPSP should be relatively brief in duration, perhaps no more than 20 ms (Ashby and Zilm, 1982a). Mattei and Schmied (Mattei and Schmied, 2002) computed PRCs from the motor units responses to tendon taps and found evidence of delayed spike triggering at latencies up to 50 ms from the arrival of the EPSP, suggesting the activation of an intrinsic current. However, other evidence suggests that tap-induced EPSPs may last up to 50 ms (Türker et al., 1997), so that delayed spike triggering could simply reflect the effects of positive noise excursions superimposed upon a long EPSP.
3. Comparison of direct recordings of synaptic potentials and their effects on motoneuron firing rate and spike probability
3.1 Relation between PSTH and PSP features
Synaptic potentials can be measured directly from intracellular recordings from motoneurons near their resting potential. The same synaptic inputs can then be reapplied when tonic discharge is produced in the motoneuron by injected current, so that the time course and amplitude of the synaptic potential can be compared with its effects on motoneuron discharge rate or probability. Most of such comparisons have used the PSTH as the response measure and have concentrated on the initial effect of the PSP on firing probability. Three different linear models have been proposed to account for the relation between the PSP and PSTH time course: the PSTH can be approximated by a scaled version of the PSP (Moore et al., 1970), the PSP derivative (Fetz and Gustafsson, 1983; Knox, 1974), or a linear combination of the two (Kirkwood and Sears, 1978). Shortly after PSTHs were first used to quantify synaptic effects on human motoneurons, three different intracellular studies of cat motoneurons provided direct comparisons of intracellularly recorded PSPs and their effects on motoneuron discharge (Cope et al., 1987; Fetz and Gustafsson, 1983; Gustafsson and McCrea, 1984). Fetz and Gustafsson (Fetz and Gustafsson, 1983) reported that the time course of the PSTHs produced in motoneurons by electrical stimulation of their own muscle nerve or that of synergists (activating Ia fibers with monosynaptic excitatory connections) often resembled that of the EPSP derivative. However, PSTH peaks associated with small EPSPs in appreciable synaptic noise were generally wider than the EPSP derivative, although not as wide as the EPSP itself. As a result, the addition of a term proportional to the EPSP itself (Kirkwood and Sears, 1978) did not provide a better fit to the PSTH peak. The time course of PSTHs associated with single fiber Ia EPSPs could also be wider than the EPSP derivative, but in these cases as well, the addition of a term proportional to the EPSP itself did not improve the match. In contrast, the two-term linear model often did provide a good fit to PSTHs associated with composite EPSPs evoked by small muscle stretches (Gustafsson and McCrea, 1984), which may have reflected the fact that these EPSPs typically had slower rise times than electrically evoked or single Ia afferent EPSPs.
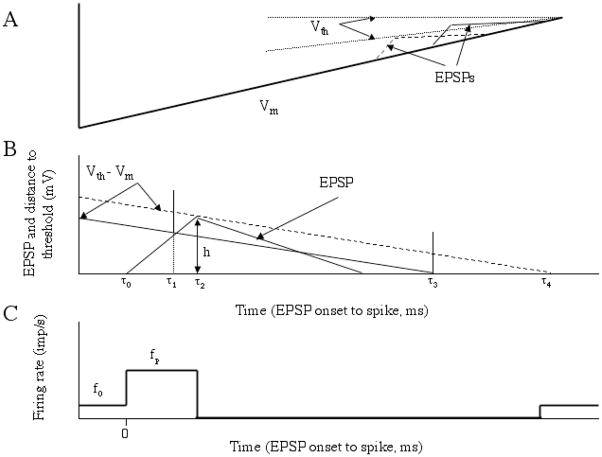
Many of these findings can be accounted for by a threshold-crossing model in which spikes are triggered by EPSPs superimposed upon a motoneuron membrane potential trajectory that rises linearly toward threshold (Fetz and Gustafsson, 1983). Figure 2 illustrates the basic assumptions of this model. The top panel shows an approximation to the membrane potential trajectory between spikes (bold line, Vm), along with two EPSPs occurring at different times during the interspike interval. The dotted lines show two alternatives for the time course of the voltage threshold for spike initiation (Vth) during the interspike interval; either the threshold is constant (horizontal line), or it varies linearly with the membrane potential, so that it is lower earlier in the interspike interval. The middle panel shows an EPSP and the distance to threshold (Vm − Vth, corresponding to the variable threshold alternative) around the time of the EPSP for EPSPs occurring at two different times during the interspike interval. The dashed distance to threshold trajectory corresponds to the EPSP occurring earlier in the interspike interval. At this point in time, the peak amplitude of the EPSP (h) is less than the distance to threshold, so that it has no effect on the interspike interval and the next spike occurs at time τ4 relative to the EPSP onset. In contrast, for the EPSP occurring later in the interspike interval, the distance to threshold (solid line) is less and the EPSP can trigger a spike on its rising phase at time τ1 relative to EPSP onset. In the absence of the EPSP, this spike would have occurred at time τ3. The bottom panel shows the PSTH predicted by the model. Firing rate (or spike probability) is elevated during the rising phase of the EPSP and lowered for period of time after this, since spikes that would have occurred in this time period have been phase advanced by the EPSP. In the absence of noise, the model predicts (Fetz and Gustafsson, 1983) that the firing rate during the PSTH peak (f(τ)) depends upon the background firing rate (f0), the rate at which the membrane potential approaches threshold (v) and the EPSP derivative (de(τ)/dt) as follows: f(τ) = f0 + (f0/v)(de(τ)/dt). If spike threshold is constant, the rate of threshold closure (v) can be obtained by measuring the slope of the membrane potential trajectory. However, comparisons of the model’s predictions with actual PSTHs and measured membrane potential slopes, suggests that the rate of threshold closure is less than the membrane potential slope (Gustafsson and McCrea, 1984), consistent with the variable threshold alternative. The addition of random synaptic noise to the membrane potential trajectories would be expected to widen the PSTH peak, although not as much as the time course of the EPSP itself, as threshold-crossing would still be most likely on the rising EPSP phase and the portion of the falling phase close to the peak.
Figure 2.
A. Approximate membrane potential trajectory between spikes with superimposed EPSPs. Dotted traces indicate to different potential trajectories of spike threshold. B. Two different distance to threshold trajectories referenced to the onset of two different EPSPs. EPSPs occurring earlier in the interspike interval (dashed line) fail to advance spikes, whereas those occurring later do. C. Predicted PSTH. See text for further details. (Adapted from Fig. 11 A – C of (Fetz and Gustafsson, 1983) with permission.)
The model predicts that the peak PSTH firing rate (or other measures of peak height or area) should be linearly related to the rate of rise of the EPSP, and since EPSP amplitude and rate of rise generally co-vary, linear relations between PSTH and EPSP amplitude would also be expected. This is in fact the case for the range of EPSP amplitudes covered in these three studies (< 3.1 mV; (Cope et al., 1987; Fetz and Gustafsson, 1983; Gustafsson and McCrea, 1984)), although significant PSTH peaks are not observed for the smallest single fiber EPSPs (< 0.086 mV; (Cope et al., 1987)). However, other theoretical studies (e.g. (Matthews, 2002, 1999)) suggest that if the effects of a sufficient range of EPSP amplitudes are examined, the relationship between EPSP amplitude and PSP-evoked increase in firing probability should be sigmoidal. A recent reexamination of our study of the effects of large simulated EPSPs and IPSPs on motoneuron firing probability and rate (Türker and Powers, 1999) does show that in many cases the relationship between EPSP amplitude and PSTH peak area becomes sub-linear for the largest EPSP amplitudes (Powers and Türker, in preparation). In addition, when two EPSPs are applied at different times, their amplitudes and derivatives sum linearly, but their effects on firing probability are less than the linear sum of their individual effects (Fetz and Gustafsson, 1983). Nonlinearities are particularly prominent for large IPSPs, since IPSPs of sufficient amplitude completely prevent the occurrence of spikes, and increasing IPSP amplitude cannot further decrease firing rate.
These various observations suggest that a nonlinear model of the PSP-to-PSTH transform is likely to be more accurate. By using injected current waveforms to mimic both synaptic noise and EPSPs and IPSPs of different amplitudes and time courses, Poliakov et al. (Poliakov et al., 1997) were able to develop a nonlinear model that was able to match PSTHs produced by a range of PSPs. The model is a cascade of a dynamic (time-varying) linear filter followed by a static (time-invariant) nonlinearity. The dynamic linear filter is computed by first compiling a spike-triggered average of the noisy injected current preceding motoneuron spikes (average current trajectory, ACT; (Bryant and Segundo, 1976)). The value of the ACT at a particular time before a motoneuron spike (τ) is simply the sum of all the injected noise values that occurred at this relative time divided by the number of motoneuron spikes. ACTs in motoneurons and other cells typically show a relatively narrow peak right before the spike that is preceded by a broad shallow trough (Bryant and Segundo, 1976; Poliakov et al., 1997). The dynamic linear filter (also called the first-order Wiener kernel) is obtained by reversing the ACT in time and multiplying the result by the ratio of the background firing rate to the power of the noise stimulus. The resultant function represents the best linear approximation to the change in firing rate produced by a brief pulse of current with an area of 1 nA-ms. When this function is convolved with the actual current transient producing a simulated PSP, then this is the best linear model of the PSTH associated with that PSP, and in fact this linear model fit the PSTHs for a range of PSPs better than any of the previously proposed linear models. Nonetheless, the linear model tended to underestimate the increase in firing rate produced by the largest EPSPs and overestimate the decrease in firing probability produced by the largest IPSPs. These errors were eliminated by adding a static nonlinearity, which basically added a component to the prediction that was proportional to the square of the first-order kernel. This nonlinear model is also able to predict the reduced spike-triggering efficacy of a second EPSP that closely follows another EPSP. Although this nonlinear model represents an improvement over previous linear models it is not truly general - the shape of the linear filter and the proportionality constant for the static nonlinearity both change with the background firing rate. Also, as discussed below, the noise level also changes the model parameters. Thus, in addition to PSP amplitude and time course, there are a number of other factors that may contribute to the PSTH time course.
3.2 Relation between PSF, IISP and PSP features
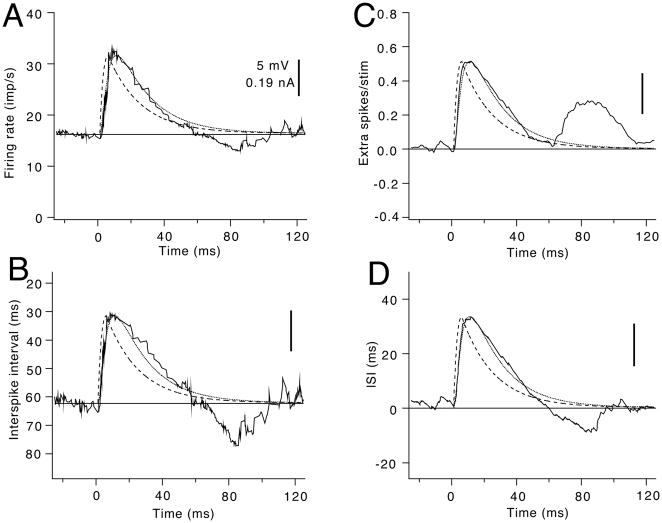
The changes in interspike interval and firing rate produced by PSPs can also be used to provide quantitative estimates of PSP amplitude and time course. Figure 3 illustrates four different measures of the effects of a large excitatory current transient on the discharge of a rat hypoglossal motoneuron. Motoneuron discharge was elicited by superimposing a random injected current waveform with a Gaussian amplitude distribution on a long step of injected current. A train of depolarizing current transients was added to this waveform to mimic periodic activation of a group of excitatory afferents. The dashed line in each panel shows the time course of the injected current transient, whereas the resulting depolarization (simulated EPSP) is indicated by the smooth solid line. The irregular line in Figure 3A shows a running average of the instantaneous frequency values as a function of time from stimulus onset (smoothed PSF), whereas that in Fig. 3B shows a smoothed average of the corresponding interspike intervals (smoothed IISP). Both functions follow the time course of the rising phase of the EPSP quite well, but the smoothed PSF provides a slightly better fit to the falling phase of the EPSP. Both functions also show a clear dip below the EPSP profile at about 60 to 100 ms. As discussed in more detail below, this delayed decrease in firing rate is commonly seen following large excitatory stimuli (Türker and Powers, 1999), and is likely to reflect summation of the conductance underlying the post-spike afterhyperpolarization (AHP). The interspike interval change function (IICF; (Awiszus, 1993)), shown in Fig. 3D, has a very similar profile. The CUSUM of the PSTH (Fig. 3C) also fits the EPSP profile quite well, although there is a large delayed increase in firing probability reflecting an ‘echo’ of the original PSTH peak.
Figure 3.
Comparison of the ability of different output measures to reflect the time course of a large simulated EPSP. In all panels, the time course of the injected current transient is indicated by the dashed line and the resultant simulated EPSP by the smooth solid line. The various response measures are indicted by the irregular solid lines superimposed on the EPSP. A. Smoothed peristimulus frequencygram (PSF). B. Smoothed interspike interval superposition plot (IISP). C. Cumulative sum of the peristimulus histogram (CUSUM). D. Interspike interval change function (IICF). (From Fig. 5.6 of (Powers and Türker, 2001) with permission.)
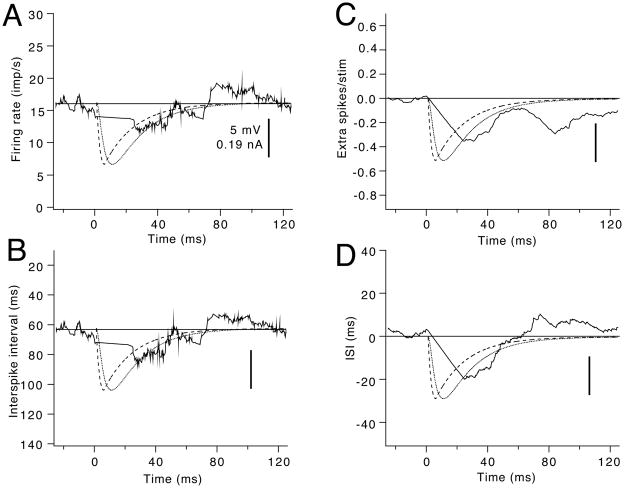
Large IPSPs can completely prevent the occurrence of spikes over much of their initial time course, particular during the peak of hyperpolarization. As a result, none of the response measures fit the IPSP time course very well. This is illustrated in Figure 4, which shows the same four response measures obtained by repeated application of the mirror image of the current transient used in Figure 3. Spikes are delayed from the onset of the IPSP until about 30 ms later, so that the running averages for the PSF (A) and IISP (B) over this period exhibit a straight line connecting the values immediately prior to the IPSP to those about 30 ms later. The smoothed PSF and IISP (Fig. 4A and B) roughly approximate the later portion of the decay phase of the IPSP, whereas the fit of the other two functions (CUSUM; Fig. 4C and IICF; Fig. 4D) is not as good.
Figure 4.
Comparison of the ability of different output measures to reflect the time course of a large simulated IPSP. Same layout as Fig. 3. A. Smoothed PSF. B. Smoothed IISP. C. PSTH CUSUM. D. IICF. (From Fig. 5.7 of (Powers and Türker, 2001) with permission.)
Stimulation of peripheral nerves often excites a mixture of afferent fibers with both excitatory and inhibitory effects on motoneurons. The fibers also can exhibit a range of conduction velocities, and a variable number of synapses between the afferent fiber and the motoneuron. As a result, the resultant PSP can have a number of phases that include both depolarization and hyperpolarization. Due to the contribution of the motoneuron’s autocorrelogram to the PSTH, the PSTH and its CUSUM can not be reliably used to estimate the time course of complex PSPs. However, when used in combination with the PSF, a more accurate estimate of PSP time course is possible (Türker and Powers, 2005, 2003).
Although the PSF can often provide a better indication of PSP time course than the PSTH, estimation of the peak PSP amplitude is more problematic, even for monophasic EPSPs. For individual rat hypoglossal motoneurons, we found that there was a strong linear relationship between the peak amplitude of the simulated EPSP and the peak change in firing rate seen in the smoothed PSF (Türker and Powers, 1999). However, the slope of this relationship in different motoneurons varied over more than a 3-fold range. As illustrated in Figure 4, for large IPSPs, no spikes occur over much of the IPSP time course. Nonetheless, firing rates are lower than the background rate over much of the decay phase of the IPSP, and the peak drop in discharge rate was linearly related to IPSP amplitude in individual motoneurons (Türker and Powers, 1999). As was the case for EPSP, the slope of this relationship was quite different in different motoneurons. From these results and those discussed above (Section 3.1), it is clear that a number of factors other than PSP amplitude and time course can determine its exact effects on motoneuron discharge rate and probability.
As discussed below, the membrane potential trajectory between spikes is relatively stereotyped, reflecting the influence of the post-spike afterhyperpolarization (AHP). Simplified models of this interspike trajectory, like the one shown in Figure 2 (adapted from Fetz and Gustafsson, 1983) have been used to predict PSP effects on motoneuron discharge probability and rate. These models often assume that the increase in conductance due to the AHP has largely decayed over the portion of the interspike interval in which EPSPs or IPSPs can affect spike timing, and that spike threshold is constant. Unfortunately, neither of these assumptions is correct. The peak AHP conductance following a single spike is roughly equal to the resting membrane conductance (Baldissera and Gustafsson, 1974a), so that the total conductance is approximately twice as high shortly after a spike has occurred than it is when the AHP has completely decayed. The peak AHP conductance is likely to be appreciably higher during repetitive discharge due to AHP summation. This will particularly affect the spike-triggering efficacy of large EPSPs, since EPSPs occurring early in the interspike interval that would have been large enough to cross threshold without an increased membrane conductance will be smaller and thus subthreshold due to the increased conductance. In addition, the voltage threshold for spike initiation varies markedly during the interspike interval (Section 4.2).
We have recently used a model based superimposing EPSPs on a 10 mV post-spike hyperpolarization followed by a linear rise to threshold (Türker and Cheng, 1994) to estimate EPSP amplitude in rat hypoglossal motoneurons (Powers and Türker, in preparation). We used injected current transients of different amplitude to produce simulated EPSPs with amplitudes ranging from 0.8 to 13.5 mV. The model tended to overestimate the amplitude of EPSPS < 6 mV and underestimate the amplitude of amplitude of EPSPs > 6 mV. These errors may reflect the influence of interspike threshold variations and conductance variations, respectively.
4. Influence of factors other than PSP amplitude and time course on PSP-evoked changes in motoneuron discharge rate and probability
4.1 Influence of the post-spike afterhyperpolarization (AHP)
Motoneuron spikes are followed by a prominent afterhyperpolarization (AHP) due to a calcium-activated potassium conductance (GKCa (Powers and Binder, 2001)). Depolarization during the action potential leads to calcium entry through specific high-voltage activated calcium channels (Viana et al., 1993) and a build up in local calcium concentration in the vicinity of the calcium-activated potassium channels. The activation of GKCa depends both on the rate of calcium build-up in the vicinity of these channels and the rate constant of calcium activation of the channels. The deactivation of GKCa will depend not only on the rate constants of activation of the channels, but also on the rate at which calcium leaves the vicinity of the channel due to diffusion, binding to intracellular proteins and pumping across the membrane (cf. (Sah, 1996)). The magnitude and duration of the AHP varies according to motor unit type: larger and longer AHPs are recorded in motoneurons innervating low threshold, slow-twitch (type S) motor units than in those innervating higher threshold, fast-twitch (type F) motor units (Kernell, 1983; Zengel et al., 1985). Although the factors underlying this variation are not completely understood, the range of amplitudes and durations are quite large and functionally important (amplitudes of about 1 to 10 mV and durations of 30 – 270 ms (Kernell, 1983; Zengel et al., 1985)). When motoneurons are activated by injected current that is just sufficient to produce regular repetitive discharge, the mean interspike interval is approximately equal to the AHP duration (Kernell, 1965).
The long duration of the AHP suggests that calcium concentration in the vicinity of the channels does not decay to resting levels for 10 to 100 milliseconds following a spike. As a result, during repetitive discharge, calcium may accumulate over several interspike intervals, so that the conductance following a given spike is summed with the residual conductance left from previous spikes, leading to AHP summation. AHP summation may explain some of the long-latency changes in firing rate after a PSP. The smoothed PSF in Fig. 3A shows a drop in firing rate below the background rate at about 60 to 100 ms after the onset of an EPSP. The residual AHP conductance remaining after interspike intervals that are shortened by the EPSP would lead to a larger than average AHP for the following interspike interval and a drop in firing rate. An IPSP that lengthens the interspike interval leads to less AHP summation and a shortened subsequent interval (note the increase in firing rate at about 70 to 120 ms in Fig. 4A).
In addition to these cross-interval effects, the post-spike time course of the AHP conductance is a major determinant of the membrane potential trajectories between spikes. The post-spike increase in the AHP conductance leads to a large hyperpolarization, followed by a gradual depolarization to the next spike as the net excitatory synaptic or injected current drive overcomes the decaying AHP conductance. In fact, threshold-crossing models that incorporate measured AHP conductance time courses are able to reproduce many features of motoneuron firing behavior, including the shape of the interspike membrane potential trajectories (Baldissera and Gustafsson, 1974b, c). Schwindt and Calvin (Schwindt and Calvin, 1972) described these trajectories in cat spinal motoneurons driven by injected current steps of different amplitude over a wide range of firing rates (from around 10 to over 100 imp/s). Recordings of tonically discharging human motor units typically include the lower end of this range (5 – 20 imp/s; (Binder et al., 1996)). Over a small range of injected currents near the threshold for steady repetitive firing, increases in firing rate are associated with a similar post-spike hyperpolarization (‘scoop’) followed by a linear rise to threshold (‘ramp’) whose rate of rise increases with firing rate (Schwindt and Calvin, 1972). Further increases in firing are associated with a decrease in scoop depth and a constant rate of rise for the ramp phase (Schwindt and Calvin, 1972). Models of this interspike membrane potential trajectory have either assumed that changes in firing rate are achieved by differences in the scoop depth followed by a constant ramp (e.g., (Ashby and Zilm, 1982b)) or that rate changes are associated with a variable ramp slope following a constant scoop (e.g., (Miles, 1997; Miles et al., 1989a; Miles et al., 1989b; Nordstrom et al., 1992; Poliakov et al., 1994; Türker and Cheng, 1994)). In addition to errors introduced by variations in membrane conductance and spike threshold during the interspike interval, the accuracy of predictions based on these models will depend in part upon whether the motoneuron is discharging at rates close to its minimum steady firing rate (in which case a constant scoop followed by a variable ramp is appropriate), or at higher rates (in which a variable scoop followed by a constant ramp is more appropriate).
4.2 Influence of spike threshold variations
Spike threshold as measured at the soma is likely to reflect the state of activation and inactivation of sodium channels in the soma and adjacent axon hillock and initial segment. Although the properties of the initial segment sodium current have not been studied directly, they can be inferred from variations in firing level (the somatic voltage at which the rapid upstroke of the action potential begins). Firing level exhibits a delayed dependence upon the value of the somatic membrane potential (Burke and Nelson, 1971; Calvin, 1974) that is thought to reflect subthreshold changes in sodium channel inactivation (Frankenhaeuser and Vallbo, 1964; Schlue et al., 1974; Vallbo, 1964). Experiments on cat motor axons suggest inactivation time constants in the range of 2 – 4 ms (Richter et al. 1974). Sodium inactivation decreases with membrane hyperpolarization making more channels available to respond to depolarization (Hodgkin and Huxley, 1952). The characteristics of sodium inactivation suggest that during repetitive discharge, spike threshold should be reduced when the membrane potential is hyperpolarized following a spike (‘scoop’) and then increase during the ramp phase of depolarization. This type of variation in spike threshold has in fact been reported in both motoneurons (Calvin, 1974; Powers and Binder, 1996) and neocortical neurons (Reyes and Fetz, 1993).
Spike threshold variations can be quite prominent and act to reduce the distance between the membrane potential and spike threshold over most of the interspike interval. Figure 5A shows the effects of superimposing just-threshold, 1 ms current pulses at different delays after the occurrence of spikes in a repetitively firing cat spinal motoneuron (Powers and Binder, 1996). The solid horizontal line represents the spike threshold measured at the end of the unperturbed interspike interval (based on the voltage at which the first derivative of membrane potential exceeds 10 mV/ms, cf. (Brownstone et al., 1992)). If threshold remained constant at this level throughout the interspike interval, the distance to threshold would be almost 15 mV at the point of peak hyperpolarization. The dashed line shows the estimated time course of spike threshold based on the responses to just-threshold current pulses applied at different delays. Near the peak hyperpolarization, the distance to threshold is only about 5 mV. These threshold variations should markedly increase the spike-triggering efficacy of EPSPs, which may explain the overestimates of EPSP amplitude referred to (Section 3.2 and Powers and Türker, in preparation). Figure 5B shows that a 5 ms conditioning hyperpolarizing pulse lowers the spike threshold for a subsequent depolarizing pulse. This example provides further evidence that spike threshold follows membrane potential time course with a relatively short time lag (< 5 ms). This implies that the spike-triggering efficacy of an EPSP will depend on both its amplitude and time course. Fast-rising EPSPs are more likely to cross threshold than slowly-rising EPSPs of the same amplitude, since the fast-rising EPSP can cross threshold before the spike threshold has time to track the depolarization produced by the EPSP itself.
Figure 5.
Interspike variations in spike threshold. A. Superimposed membrane potential trajectories during repetitive discharge with and without the superimposition of 1 ms current pulses at different post-spike delays. The solid horizontal line indicates the spike threshold measured at the end of an unperturbed interspike interval, whereas the dotted line indicates spike threshold at different points during the interspike interval, based on the spike-triggering effects of the current pulses. B. Effects of a conditioning 5 ms hyperpolarizing current pulse on spike threshold. The rightmost arrow indicates spike threshold at the end of an unperturbed interspike interval, whereas the upper left trace indicates spike threshold estimated earlier in the interval. The lower left trace shows the effects of a conditioning hyperpolarizing pulse on spike threshold. (From Fig. 2A, B of (Powers and Binder, 1999) with permission.)
4.3 Influence of background synaptic noise
As mentioned above (Section 3.1), threshold-crossing models predict that background synaptic noise should lead to an increase in the duration of the PSTH peak, since the addition of the noise component implies that the peak depolarization associated with an EPSP can occur over range of times around the peak amplitude measured in the absence of noise (Midroni and Ashby, 1989; Polyakov, 1991). Surprisingly, a study using injected current to mimic small EPSPs and different levels of synaptic noise, showed that the main effect of increasing the level of noise was to reduce the size of the PSTH peak, rather than increase its duration (Poliakov et al., 1996). The reduction in spike-triggering efficacy was proportional to both noise amplitude and the frequency content of the noise – noise filtered with a time constant of 5 ms had no effect on the PSTH peak. The maximum amplitude of high-frequency noise used reduced PSTH peak amplitude by up to 50%. Since these effects were produced by somatically-injected current, they probably underestimate the effects of actual background synaptic noise, since this will also lead to an increase membrane conductance, leading to a decrease in the synaptic current reaching the soma from dendritic synapses (Barrett, 1975).
4.4 Influence of persistent inward currents (PICs)
A variety of motoneurons have been shown to exhibit persistent (i.e, non- or slowly-inactivating) inward currents (PICs) that reflect current flow through voltage-sensitive calcium (Ca) and sodium (Na) channels first activated subthreshold to the spike (reviewed in (Heckman et al., 2008; Heckman et al., 2003; Powers and Binder, 2001). The exact properties and distributions of the channels responsible for the sodium and calcium components of the persistent inward currents (NaPIC and CaPIC, respectively) are not well known and represent a very active area of research. However, the functional properties of the NaPIC and CaPIC are different (Heckman et al., 2008), and thus would be expected to exert different effects on transient synaptic potentials. The NaPIC has fast kinetics, is thought to depend primarily on current flow through channels located near the soma, and slowly inactivates with continued depolarization. In contrast, the CaPIC exhibits much slower activation kinetics, exhibits little or no inactivation, and is thought to depend primarily on current flow from more distally located channels. The fast activation kinetics of the NaPIC component enable it to amplify transient synaptic potentials (e.g., (Manuel et al., 2007; Stuart and Sakmann, 1995)), and may contribute to the delayed interspike interval shortening effects discussed above (Reyes and Fetz, 1993). In contrast, it is possible that the increased conductance associated with the activation of the CaPIC may shunt more distally located synaptic inputs, leading to a decrease in the amplitude of transient synaptic potentials.
4.5 Influence of background discharge rate
All of the factors discussed above are likely to come into play as the background discharge rate of the motoneuron is changed. Higher discharge rates are likely to involve AHP summation, leading to a larger increase in membrane conductance. If synaptic noise is assumed to reflect the largely asynchronous activation of presynaptic inputs, the variance of synaptic noise should increase in parallel with its mean level. Both of these factors would be expected to decrease responsiveness as discharge rate is increased. Moreover, since synaptic inputs are predominantly distributed on the dendrites, increasing voluntary drive will be associated with increased dendritic membrane conductance, acting to shunt currents from reflexively activated inputs, which will again contribute to lower responsiveness with increasing discharge rate. The dependence of interspike variations in spike threshold on background firing rate have not been systematically explored, so it is not clear how threshold variations will influence excitability at different firing rates. The current view on the activation of the persistent inward current mediated by dendritic calcium channels (CaPIC) is that during synaptic activation it is nearly completely activated prior to recruitment (cf. (Gorassini et al., 2002)). If this is indeed the case then the PIC influence of the response of motoneuron to transient synaptic inputs may not change much with changes in background discharge rate. If the PIC is not fully activated at recruitment, then graded activation of the PIC with increasing firing rate can lead to increasing amplification of synaptic inputs (ElBasiouny et al., 2006). However, the effective time constant of the dendritic PIC is thought to be relatively slow (cf. ElBasiouny et al., 2006), so PIC activation may not influence the amplitude of transient synaptic inputs.
A number of researchers have studied the effects of background discharge rate on the size of a PSTH peak produced by a fixed stimulus. Although some studies have found that spike-triggering efficacy is relatively constant over a range of background discharge rates (Ashby and Zilm, 1982a; Miles et al., 1989b), others have found a strong, inverse relationship between spike-triggering efficacy and discharge rate (Jones and Bawa, 1995; Kudina, 1988; Olivier et al., 1995). The inverse relationship may in part reflect the increase in membrane conductance and noise with increasing discharge rate referred to above. However, Türker and Powers (Türker and Powers, 2002) found that when different discharge rates were elicited by superimposing a constant level of noise on different mean levels of injected current that the spike-triggering efficacy of simulated EPSPs also declined with increasing background discharge rate. The relationship was generally not linear, and the largest decline in spike-triggering efficacy took place when comparing the lowest discharge rates (< 12 imp/s) to higher discharge rates. A probable explanation for this result is that the form of the interspike interval trajectory changes from relatively low to higher discharge rates, so that the EPSP is closer to threshold over a higher percentage of interspike intervals when the discharge rate is very low.
A number of researchers have suggested that when human motoneurons are activated physiologically (i.e., by noisy synaptic inputs) their interspike interval trajectories at the lowest discharge rates are significantly different from those of cat motoneurons driven by non-noisy injected currents (Kudina, 1999; Matthews, 1996; Türker, 1995). The presence of appreciable noise allows motoneurons to fire steadily at rates at which the mean interspike interval is longer than the AHP duration (Powers and Binder, 2000). This lower range of firing rates has been called the subprimary range (Kudina, 1999), and during discharge in this range the average membrane potential trajectory is thought to reach a constant distance below threshold toward the end of the interspike interval, so that spikes are triggered by random fluctuations in synaptic noise rather than by a linear rise to threshold (Kudina, 1999; Matthews, 1996; Powers and Binder, 2000; Türker, 1995).
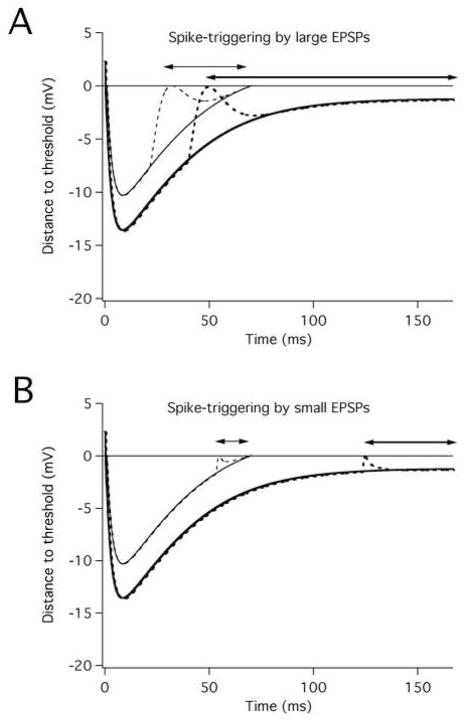
Figure 6 illustrates how the curvilinear interspike membrane potential trajectory characteristic of subprimary range firing can affect the spike-triggering efficacy of different sized EPSPs. The relative spike-triggering efficacy of these EPSPs at different discharge rates depends on the relation between EPSP size and distance to threshold throughout the interspike interval. For the illustrated cases, the large EPSP can trigger spikes over a significantly greater proportion of the interspike interval when the cell is firing at the low discharge rate versus the higher rate (71% versus 54%), whereas the spike-triggering efficacy of the small EPSP is about equal at the two rates (26% versus 22%).
Figure 6.
Effects of membrane potential trajectory shape on spike-triggering efficacy of large and small EPSPs. Each panel shows theoretical membrane potential trajectories for a motoneuron firing at a low (6 imp/s) and higher (14 imp/s) rate. The dashed lines show superimposed large (A) and small (B) EPSPs. The EPSPs have been placed at a point where they would first trigger spikes with a 50% probability in the presence of noise. The lines with double arrows indicate the proportion of the interspike interval over which spikes can be triggered with a 50% or greater probability at the low rate (thick lines) and higher rate (thin lines). (From Fig. 9 of (Türker and Powers, 2002) with permission.)
The analysis of spike-triggering efficacy illustrated in Figure 6 assumes that spike threshold is constant, whereas there is abundant evidence that spike threshold varies during the interspike interval (see above). Matthews (Matthews, 1996) has recently proposed that the interspike interval statistics can be used to estimate the effective distance between membrane potential and threshold throughout the interspike interval during voluntary activation of human motoneurons, and that this distance to threshold estimate can then be used to more accurately assess the amplitude of EPSPs (Matthews, 2002). Our recent analysis of the accuracy of this method (Powers and Türker, unpublished) indicates that the method appears to work relatively well for small and medium-sized EPSPs (peak amplitudes within 2 – 3 noise standard deviations), but not for larger EPSPs. The underlying problem is that the distance to threshold can only be directly estimated over the portion of the interspike interval in which noise is able to trigger spikes; the distance to threshold for the earliest part of the interspike interval must be extrapolated from a curve fit to the estimated distance to threshold for the later part of the interspike interval.
5. Using motor unit discharge to distinguish changes in synaptic input from changes in motoneuron properties
Alterations in the reflexive or voluntary activation of motoneurons resulting from training, injury or disease are likely to involve plasticity at multiple spinal and supraspinal sites (Wolpaw and Tennissen, 2001)), including changes in the intrinsic properties of motoneurons (Halter et al., 1995; Heckman et al., 2005). Changes in the response of a population of motoneurons to a given peripheral input may be difficult to interpret, since an increased excitatory response, for example, could simply reflect an increase in subthreshold depolarization of motoneurons, so that they are closer to threshold (Powers et al., 1988). The use of the PSTH and PSF techniques avoids this particular issue since responses are recorded from motoneurons that are already activated sufficiently to produce tonic, background discharge. Since motoneuron responsiveness can change with background discharge rate (Section 4.5), it is important to match motor unit discharge rate when comparing the responses of different motor units. For example, the susceptibility of different masseter motor units to inhibition was found to depend upon their background discharge rather than their recruitment order (Miles and Türker, 1986). Although high discharge rates may be difficult to achieve in many pathological conditions, motoneuron responses should preferably be studied when motor units are firing above the ‘subprimary’ range’ (Kudina, 1999), since motoneuron responsiveness is likely to vary the greatest over this lower range of firing rates. Even when this condition cannot be met, the PSF can be used to detect changes in the relative excitatory and inhibitory contributions to a reflex response. For example, PSFs evoked in normal subjects by cutaneomuscular stimulation of the medial arch of the foot show an initial phase of excitation, followed by a cessation of discharge, then a period of reduced rate, and a final period of increased firing rate (Norton et al., 2008). In contrast, PSFs obtained in subjects with incomplete spinal cord injuries (SCI) exhibited only a long-lasting increase in firing rate (Norton et al., 2008), suggesting that inhibitory pathways activated by cutaneous stimuli in normal subjects are suppressed following SCI. The total duration of increased firing rate was also much greater in SCI subjects, which could either reflect prolonged synaptic input or the activation of persistent inward currents (PICs).
The relative contribution of alterations in synaptic input versus motoneuron properties is more difficult to disentangle when pathology or training leads to more subtle changes in the time course or amplitude of stimulus-evoked changes in motoneuron firing rate and probability. For example, a recent study by Suresh and colleagues (Suresh et al., 2005) on the response of biceps motor units to tendon taps in stroke patients exhibiting spasticity revealed that the duration of the PSTH peak was shortened in spastic patients compared to control subjects, but the peak amplitude was not changed. The change in PSTH peak duration probably reflects a faster EPSP rising phase, but whether this results from a change in the location of synaptic inputs or changes in motoneuron properties is not clear. Using motor unit discharge recordings to draw inferences about the pathophysiology of a particular motor deficit is likely to require a multi-faceted approach that includes recordings of motor unit discharge during a number of different behaviors and in motor unit responses to many different peripheral and descending inputs. Both animal and computer models are likely to continue to be important tools for interpreting the discharge of human motoneurons. The ability to simulate evoked synaptic inputs and synaptic noise by intracellular current injection and study their effects on discharge is critical to the interpretation of evoked changes in human motor unit discharge (e.g., (Norton et al., 2008; Türker and Powers, 2005, 1999, 2003, 2002). Injected current can also be used to simulate the effects voltage-dependent conductances using the dynamic clamp technique (Manuel et al., 2007, 2006). The combination of these two techniques is likely to shed new light on how synaptic inputs and intrinsic motoneuron properties interact to control motor unit response properties.
Acknowledgments
RKP is supported by NIH grant NS062200. KST is supported by the Marie Curie Chair project of the European Union (GenderReflex; MEX-CT-2006-040317) and Turkish Scientific and Technological Research Organization (TUBITAK - 107S029 - SBAG-3556).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ashby P, Labelle K. Effects of extensor and flexor group I afferent volleys on the excitability of individual soleus motoneurones in man. J Neurol Neurosurg Psychiatry. 1977;40:910–9. doi: 10.1136/jnnp.40.9.910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby P, Zilm D. Characteristics of postsynaptic potentials produced in single human motoneurons by homonymous group 1 volleys. Exp Brain Res. 1982a;47:41–8. doi: 10.1007/BF00235884. [DOI] [PubMed] [Google Scholar]
- Ashby P, Zilm D. Relationship between EPSP shape and cross-correlation profile explored by computer simulation for studies on human motoneurons. Exp Brain Res. 1982b;47:33–40. doi: 10.1007/BF00235883. [DOI] [PubMed] [Google Scholar]
- Ashby P, Zilm D. Synaptic connections to individual tibialis anterior motoneurones in man. J Neurol Neurosurg Psychiatry. 1978;41:684–9. doi: 10.1136/jnnp.41.8.684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Awiszus F. Continuous functions determined by spike trains of a neuron subject to stimulation. Biol Cybern. 1988;58:321–7. doi: 10.1007/BF00363941. [DOI] [PubMed] [Google Scholar]
- Awiszus F. Quantification and statistical verification of neuronal stimulus responses from noisy spike train data. Biol Cybern. 1993;68:267–74. doi: 10.1007/BF00224862. [DOI] [PubMed] [Google Scholar]
- Awiszus F, Feistner H, Schafer SS. On a method to detect long-latency excitation and inhibitions of single hand muscle motoneurons in man. Exp Brain Res. 1991;86:440–6. doi: 10.1007/BF00228970. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Afterhyperpolarization conductance time course in lumbar motoneurones of the cat. Acta Physiol Scand. 1974a;91:512–27. doi: 10.1111/j.1748-1716.1974.tb05707.x. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Firing behaviour of a neuron model based on the afterhyperpolarization conductance time-course and algebraical summation. Adaptation and steady state firing. Acta Physiol Scand. 1974b;92:27–47. doi: 10.1111/j.1748-1716.1974.tb05720.x. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Firing behaviour of a neuron model based on the afterhyperpolarization conductance time-course. First interval firing. Acta Physiol Scand. 1974c;91:528–44. doi: 10.1111/j.1748-1716.1974.tb05708.x. [DOI] [PubMed] [Google Scholar]
- Barrett JN. Motoneuron dendrites: role in synaptic integration. Fed Proc. 1975;34:1398–407. [PubMed] [Google Scholar]
- Bessou P, Laporte Y, Pages B. A method of analysing the responses of spindle primary endings to fusimotor stimulation. J Physiol. 1968;196:37–45. doi: 10.1113/jphysiol.1968.sp008492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binder MD, Heckman CJ, Powers RK. The physiological control of motoneuron activity. In: Rowell LB, Shepherd JT, editors. Handbook of Physiology. Section 12. Exercise: Regulation and Integration of Multiple Systems. Oxford University Press; New York: 1996. pp. 3–53. [Google Scholar]
- Brooke JD, McIlroy WE, Staines WR, Angerilli PA, Peritore GF. Cutaneous reflexes of the human leg during passive movement. J Physiol. 1999;518 ( Pt 2):619–28. doi: 10.1111/j.1469-7793.1999.0619p.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brownstone RM, Jordan LM, Kriellaars DJ, Noga BR, Shefchyk SJ. On the regulation of repetitive firing in lumbar motoneurones during fictive locomotion in the cat. Exp Brain Res. 1992;90:441–55. doi: 10.1007/BF00230927. [DOI] [PubMed] [Google Scholar]
- Bryant HL, Segundo JP. Spike initiation by transmembrane current: a white-noise analysis. J Physiol Lond. 1976;260:279–314. doi: 10.1113/jphysiol.1976.sp011516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke RE, Nelson PG. Accommodation to current ramps in motoneurons of fast and slow twitch motor units. Int J Neurosci. 1971;1:347–56. doi: 10.3109/00207457109146983. [DOI] [PubMed] [Google Scholar]
- Calvin WH. Three modes of repetitive firing and the role of threshold time course between spikes. Brain Res. 1974;69:341–6. doi: 10.1016/0006-8993(74)90012-2. [DOI] [PubMed] [Google Scholar]
- Cope TC, Fetz EE, Matsumura M. Cross-correlation assessment of synaptic strength of single Ia fibre connections with triceps surae motoneurones in cats. J Physiol Lond. 1987;390:161–88. doi: 10.1113/jphysiol.1987.sp016692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elbasiouny SM, Bennett DJ, Mushahwar VK. Simulation of Ca2+ persistent inward currents in spinal motoneurones: mode of activation and integration of synaptic inputs. J Physiol Lond. 2006;570:355–374. doi: 10.1113/jphysiol.2005.099119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellaway PH. Cumulative sum technique and its application to the analysis of peristimulus time histograms. Electroencephalogr Clin Neurophysiol. 1978;45:302–4. doi: 10.1016/0013-4694(78)90017-2. [DOI] [PubMed] [Google Scholar]
- Fetz EE, Gustafsson B. Relation between shapes of post-synaptic potentials and changes in firing probability of cat motoneurones. J Physiol Lond. 1983;341:387–410. doi: 10.1113/jphysiol.1983.sp014812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankenhaeuser B, Vallbo AB. Accomodation in myelinated nerve fibres of Xenopus laevis as computed on the basis of voltage clamp data. Acta Physiol Scand. 1964;63:1–20. doi: 10.1111/j.1748-1716.1965.tb04037.x. [DOI] [PubMed] [Google Scholar]
- Garnett R, Stephens JA. The reflex responses of single motor units in human first dorsal interosseous muscle following cutaneous afferent stimulation. J Physiol. 1980;303:351–64. doi: 10.1113/jphysiol.1980.sp013290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstein GL, Kiang NY. An approach to the quantitative analysis of electrophysiological data from single neurons. Biophys J. 1960;1:15–28. doi: 10.1016/s0006-3495(60)86872-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorassini M, Yang JF, Siu M, Bennett DJ. Intrinsic activation of human motoneurons: possible contribution to motor unit excitation. J Neurophysiol. 2002;87:1850–8. doi: 10.1152/jn.00024.2001. [DOI] [PubMed] [Google Scholar]
- Gustafsson B, McCrea D. Influence of stretch-evoked synaptic potentials on firing probability of cat spinal motoneurones. J Physiol Lond. 1984;347:431–51. doi: 10.1113/jphysiol.1984.sp015074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutkin BS, Ermentrout GB, Reyes AD. Phase-response curves give the responses of neurons to transient inputs. J Neurophysiol. 2005;94:1623–35. doi: 10.1152/jn.00359.2004. [DOI] [PubMed] [Google Scholar]
- Halter JA, Carp JS, Wolpaw JR. Operantly conditioned motoneuron plasticity: Possible role of sodium channels. Journal of Neurophysiology. 1995;73:867–71. doi: 10.1152/jn.1995.73.2.867. [DOI] [PubMed] [Google Scholar]
- Heckman CJ, Gorassini MA, Bennett DJ. Persistent inward currents in motoneuron dendrites: implications for motor output. Muscle Nerve. 2005;31:135–56. doi: 10.1002/mus.20261. [DOI] [PubMed] [Google Scholar]
- Heckman CJ, Johnson M, Mottram C, Schuster J. Persistent Inward Currents in Spinal Motoneurons and Their Influence on Human Motoneuron Firing Patterns. Neuroscientist. 2008 doi: 10.1177/1073858408314986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman CJ, Lee RH, Brownstone RM. Hyperexcitable dendrites in motoneurons and their neuromodulatory control during motor behavior. Trends Neurosci. 2003;26:688–95. doi: 10.1016/j.tins.2003.10.002. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol Lond. 1952;116:500–44. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones KE, Bawa P. Responses of human motoneurons to Ia inputs: effects of background firing rate. Can J Physiol Pharmacol. 1995;73:1224–34. doi: 10.1139/y95-174. [DOI] [PubMed] [Google Scholar]
- Kernell D. Functional properties of spinal motoneurons and gradation of muscle force. Adv Neurol. 1983;39:213–26. [PubMed] [Google Scholar]
- Kernell D. The limits of firing frequency in cat lumbosacral motoneurones possessing different time course of afterhyperpolarization. Acta Physiol Scand. 1965;65:87–100. [Google Scholar]
- Kirkwood PA, Sears TA. The synaptic connexions to intercostal motoneurones as revealed by the average common excitation potential. J Physiol Lond. 1978;275:103–34. doi: 10.1113/jphysiol.1978.sp012180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knox CK. Cross-correlation functions for a neuronal model. Biophys J. 1974;14:567–82. doi: 10.1016/S0006-3495(74)85936-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kranz H, Baumgartner G. Human alpha motoneurone discharge, a statistical analysis. Brain Res. 1974;67:324–9. doi: 10.1016/0006-8993(74)90282-0. [DOI] [PubMed] [Google Scholar]
- Kudina LP. Analysis of firing behaviour of human motoneurones within ‘subprimary range’. J Physiol Paris. 1999;93:115–23. doi: 10.1016/s0928-4257(99)80142-9. [DOI] [PubMed] [Google Scholar]
- Kudina LP. Excitability of firing motoneurones tested by Ia afferent volleys in human triceps surae. Electroencephalogr Clin Neurophysiol. 1988;69:576–80. doi: 10.1016/0013-4694(88)90170-8. [DOI] [PubMed] [Google Scholar]
- Kudina LP. Reflex effects of muscle afferents on antagonist studied on single firing motor units in man. Electroencephalogr Clin Neurophysiol. 1980;50:214–21. doi: 10.1016/0013-4694(80)90148-0. [DOI] [PubMed] [Google Scholar]
- Lundberg A, Winsbury G. Selective adequate activation of large afferents from muscle spindles and Golgi tendon organs. Acta Physiol Scand. 1960;49:155–64. doi: 10.1111/j.1748-1716.1960.tb01939.x. [DOI] [PubMed] [Google Scholar]
- Manuel M, Meunier C, Donnet M, Zytnicki D. Resonant or not, two amplification modes of proprioceptive inputs by persistent inward currents in spinal motoneurons. J Neurosci. 2007;27:12977–88. doi: 10.1523/JNEUROSCI.3299-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manuel M, Meunier C, Donnet M, Zytnicki D. The afterhyperpolarization conductance exerts the same control over the gain and variability of motoneurone firing in anaesthetized cats. J Physiol. 2006;576:873–86. doi: 10.1113/jphysiol.2006.117002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattei B, Schmied A. Delayed and prolonged effects of a near threshold EPSP on the firing time of human alpha-motoneurones. J Physiol. 2002;538:849–65. doi: 10.1113/jphysiol.2001.012701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PB. Measurement of excitability of tonically firing neurones tested in a variable-threshold model motoneurone. J Physiol. 2002;544:315–32. doi: 10.1113/jphysiol.2002.024984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PB. The effect of firing on the excitability of a model motoneurone and its implications for cortical stimulation. J Physiol. 1999;518:867–82. doi: 10.1111/j.1469-7793.1999.0867p.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PBC. Relationship of firing intervals of human motor units to the trajectory of post-spike after-hyperpolarization and synaptic noise. Journal of Physiology - London. 1996;492:597–628. doi: 10.1113/jphysiol.1996.sp021332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Midroni G, Ashby P. How synaptic noise may affect cross-correlations. J Neurosci Methods. 1989;27:1–12. doi: 10.1016/0165-0270(89)90048-4. [DOI] [PubMed] [Google Scholar]
- Miles TS. Estimating post-synaptic potentials in tonically discharging human motoneurons. J Neurosci Methods. 1997;74:167–74. doi: 10.1016/s0165-0270(97)02247-4. [DOI] [PubMed] [Google Scholar]
- Miles TS, Le TH, Türker KS. Biphasic inhibitory responses and their IPSPs evoked by tibial nerve stimulation in human soleus motor neurones. Exp Brain Res. 1989a;77:637–45. doi: 10.1007/BF00249617. [DOI] [PubMed] [Google Scholar]
- Miles TS, Türker KS. Does reflex inhibition of motor units follow the “size principle”? Exp Brain Res. 1986;62:443–5. doi: 10.1007/BF00238864. [DOI] [PubMed] [Google Scholar]
- Miles TS, Türker KS, Le TH. Ia reflexes and EPSPs in human soleus motor neurones. Exp Brain Res. 1989b;77:628–36. doi: 10.1007/BF00249616. [DOI] [PubMed] [Google Scholar]
- Moore GP, Segundo JP, Perkel DH, Levitan H. Statistical signs of synaptic interaction in neurons. Biophys J. 1970;10:876–900. doi: 10.1016/S0006-3495(70)86341-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordstrom MA, Fuglevand AJ, Enoka RM. Estimating the strength of common input to human motoneurons from the cross-correlogram. J Physiol Lond. 1992;453:547–74. doi: 10.1113/jphysiol.1992.sp019244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton JA, Bennett DJ, Knash ME, Murray KC, Gorassini MA. Changes in sensory-evoked synaptic activation of motoneurons after spinal cord injury in man. Brain. 2008;131:1478–91. doi: 10.1093/brain/awn050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okdeh AM, Lyons MF, Cadden SW. The study of jaw reflexes evoked by electrical stimulation of the lip: the importance of stimulus intensity and polarity. J Oral Rehabil. 1999;26:479–87. doi: 10.1046/j.1365-2842.1999.00407.x. [DOI] [PubMed] [Google Scholar]
- Olivier E, Bawa P, Lemon RN. Excitability of human upper limb motoneurones during rhythmic discharge tested with transcranial magnetic stimulation. J Physiol. 1995;485 ( Pt 1):257–69. doi: 10.1113/jphysiol.1995.sp020728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Person RS, Kudina LP. Discharge frequency and discharge pattern of human motor units during voluntary contraction of muscle. Electroencephalogr Clin Neurophysiol. 1972;32:471–83. doi: 10.1016/0013-4694(72)90058-2. [DOI] [PubMed] [Google Scholar]
- Piotrkiewicz M, Kudina L, Jakubiec M. Computer simulation study of the relationship between the profile of excitatory postsynaptic potential and stimulus-correlated motoneuron firing. Biol Cybern. 2009 doi: 10.1007/s00422-009-0293-x. [DOI] [PubMed] [Google Scholar]
- Poliakov AV, Miles TS, Nordstrom MA. A new approach to the estimation of post-synaptic potentials in human motoneurones. J Neurosci Methods. 1994;53:143–9. doi: 10.1016/0165-0270(94)90171-6. [DOI] [PubMed] [Google Scholar]
- Poliakov AV, Powers RK, Binder MD. Functional identification of the input-output transforms of motoneurones in the rat and cat. J Physiol London. 1997;504:401–24. doi: 10.1111/j.1469-7793.1997.401be.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poliakov AV, Powers RK, Sawczuk A, Binder MD. Effects of background noise on the response of rat and cat motoneurones to excitatory current transients. J Physiol Lond. 1996;495:143–57. doi: 10.1113/jphysiol.1996.sp021580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polyakov AV. Synaptic noise and the cross-correlation between motoneuron discharges and stimuli. Neuroreport. 1991;2:489–92. doi: 10.1097/00001756-199108000-00020. [DOI] [PubMed] [Google Scholar]
- Powers RK, Binder MD. Input-output functions of mammalian motoneurons. Rev Physiol Biochem Pharmacol. 2001;143:137–263. doi: 10.1007/BFb0115594. [DOI] [PubMed] [Google Scholar]
- Powers RK, Binder MD. Models of spike encoding and their use in the interpretation of motor unit recordings in man. Prog Brain Res. 1999;123:83–98. doi: 10.1016/s0079-6123(08)62846-0. [DOI] [PubMed] [Google Scholar]
- Powers RK, Binder MD. Relationship between the time course of the afterhyperpolarization and discharge variability in cat spinal motoneurones. J Physiol. 2000;528:131–50. doi: 10.1111/j.1469-7793.2000.t01-1-00131.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers RK, Marder-Meyer J, Rymer WZ. Quantitative relations between hypertonia and stretch reflex threshold in spastic hemiparesis. Ann Neurol. 1988;23:115–24. doi: 10.1002/ana.410230203. [DOI] [PubMed] [Google Scholar]
- Powers RK, Türker KS. Investigating the Synaptic Control of Human Motoneurons: New Techniques, Analyses and Insights from Animal Models. In: Cope TC, editor. Motor Neurobiology of the Spinal Cord. CRC Press; New York: 2001. pp. 108–33. [Google Scholar]
- Powers RKDB, Binder MD. Experimental evaluation of input-output models of motoneuron discharge. Journal of Neurophysiology. 1996;75:367–79. doi: 10.1152/jn.1996.75.1.367. [DOI] [PubMed] [Google Scholar]
- Reyes AD, Fetz EE. Two modes of interspike interval shortening by brief transient depolarizations in cat neocortical neurons. J Neurophysiol. 1993;69:1661–72. doi: 10.1152/jn.1993.69.5.1661. [DOI] [PubMed] [Google Scholar]
- Sah P. Ca2+-activated K+ currents in neurones: Types, physiological roles and modulation. Trends in Neurosciences. 1996;19:150–4. doi: 10.1016/s0166-2236(96)80026-9. [DOI] [PubMed] [Google Scholar]
- Schlue WR, Richter DW, Mauritz KH, Nacimiento AC. Accommodation of cat spinal motoneurones to linearly rising currents before and during long-term changes of membrane potential. Brain Res. 1974;76:213–21. doi: 10.1016/0006-8993(74)90455-7. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Calvin WH. Membrane-potential trajectories between spikes underlying motoneuron firing rates. J Neurophysiol. 1972;35:311–25. doi: 10.1152/jn.1972.35.3.311. [DOI] [PubMed] [Google Scholar]
- Sonnenborg FA, Andersen OK, Arendt-Nielsen L. Modular organization of excitatory and inhibitory reflex receptive fields elicited by electrical stimulation of the foot sole in man. Clin Neurophysiol. 2000;111:2160–9. doi: 10.1016/s1388-2457(00)00472-7. [DOI] [PubMed] [Google Scholar]
- Stuart G, Sakmann B. Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron. 1995;15:1065–76. doi: 10.1016/0896-6273(95)90095-0. [DOI] [PubMed] [Google Scholar]
- Suresh NL, Ellis MD, Moore J, Heckman H, Rymer WZ. Excitatory synaptic potentials in spastic human motoneurons have a short rise-time. Muscle Nerve. 2005;32:99–103. doi: 10.1002/mus.20318. [DOI] [PubMed] [Google Scholar]
- Türker KS. The shape of the membrane potential trajectory in tonically-active human motoneurons. J Electromyogr Kinesiol. 1995;5:3–14. doi: 10.1016/s1050-6411(99)80001-7. [DOI] [PubMed] [Google Scholar]
- Türker KS, Cheng HB. Motor-unit firing frequency can be used for the estimation of synaptic potentials in human motoneurones. J Neurosci Methods. 1994;53:225–34. doi: 10.1016/0165-0270(94)90181-3. [DOI] [PubMed] [Google Scholar]
- Türker KS, Powers RK. Black box revisited: a technique for estimating postsynaptic potentials in neurons. Trends Neurosci. 2005;28:379–86. doi: 10.1016/j.tins.2005.05.007. [DOI] [PubMed] [Google Scholar]
- Türker KS, Powers RK. Effects of large excitatory and inhibitory inputs on motoneuron discharge rate and probability. J Neurophysiol. 1999;82:829–40. doi: 10.1152/jn.1999.82.2.829. [DOI] [PubMed] [Google Scholar]
- Türker KS, Powers RK. Estimation of postsynaptic potentials in rat hypoglossal motoneurones: insights for human work. J Physiol. 2003;551:419–31. doi: 10.1113/jphysiol.2003.044982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Türker KS, Powers RK. The effects of common input characteristics and discharge rate on synchronization in rat hypoglossal motoneurones. J Physiol. 2002;541:245–60. doi: 10.1113/jphysiol.2001.013097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Türker KS, Yang J, Scutter SD. Tendon tap induces a single long-lasting excitatory reflex in the motoneurons of human soleus muscle. Exp Brain Res. 1997;115:169–73. doi: 10.1007/pl00005678. [DOI] [PubMed] [Google Scholar]
- Vallbo AB. Accommodation related to the inactivation of the sodium permeability in single myelinated nerve fibres from Xenopus laevis. Acta Physiol Scand. 1964;61:429–44. [PubMed] [Google Scholar]
- Viana F, Bayliss DA, Berger AJ. Calcium conductances and their role in the firing behavior of neonatal rat hypoglossal motoneurons. J Neurophysiol. 1993;69:2137–49. doi: 10.1152/jn.1993.69.6.2137. [DOI] [PubMed] [Google Scholar]
- Wolpaw JR, Tennissen AM. Activity-dependent spinal cord plasticity in health and disease. Annu Rev Neurosci. 2001;24:807–43. doi: 10.1146/annurev.neuro.24.1.807. [DOI] [PubMed] [Google Scholar]
- Zengel JE, Reid SA, Sypert GW, Munson JB. Membrane electrical properties and prediction of motor-unit type of medial gastrocnemius motoneurons in the cat. J Neurophysiol. 1985;53:1323–44. doi: 10.1152/jn.1985.53.5.1323. [DOI] [PubMed] [Google Scholar]