Providing Positional Information with Active Transport on Dynamic Microtubules

Abstract

Microtubules (MTs) are dynamic protein polymers that change their length by switching between growing and shrinking states in a process termed dynamic instability. It has been suggested that the dynamic properties of MTs are central to the organization of the eukaryotic intracellular space, and that they are involved in the control of cell morphology, but the actual mechanisms are not well understood. Here, we present a theoretical analysis in which we explore the possibility that a system of dynamic MTs and MT end-tracking molecular motors is providing specific positional information inside cells. We compute the MT length distribution for the case of MT-length-dependent switching between growing and shrinking states, and analyze the accumulation of molecular motors at the tips of growing MTs. Using these results, we show that a transport system consisting of dynamic MTs and associated motor proteins can deliver cargo proteins preferentially to specific positions within the cell. Comparing our results with experimental data in the model organism fission yeast, we propose that the suggested mechanisms could play important roles in setting length scales during cellular morphogenesis.

Introduction

Microtubules (MTs) are stiff protein polymers whose polymerization dynamics are characterized by a switching between distinct growth and shrinkage states, a phenomenon that is termed dynamic instability (1,2). MTs are involved in the organization of the eukaryotic intracellular space and the control of cell morphology (3,4). Specifically, MTs are essential components of the mitotic spindle, a structure mediating the redistribution of DNA during cell division. In addition, there is evidence for a role of MTs in steering cell growth in such diverse systems as fission yeast (4), neurons (5,6), fibroblasts (7), and plant root hair cells (8). In these systems, genetic or drug-induced perturbations of MTs affect the directionality of cell growth and correspondingly lead to changes in cell morphology. Similarly, there is experimental evidence that not only the mere presence of MTs, but also the details of MT growth and shrinkage dynamics are important for providing positional information during cell growth. For example, the locomotion rate of NRK fibroblasts is significantly altered by application of low doses of both stabilizing and destabilizing MT drugs that do not lead to a detectable change in the MT level (7). In addition, inhibition of MT dynamics, both by depolymerization and stabilization, causes a wavy growth phenotype in Arabidopsis (9). On a mechanistic level, it is, however, not yet well understood how MT dynamics are linked to cell growth.

In fission yeast (Schizosaccharomyces pombe), which is arguably the best-studied model system for investigating the relationship between MTs and cell morphology (4,8), sites of future cell growth are determined by the localized delivery of a marker protein (Tea1) by dynamic MTs (Fig. 1 A) (10,11). This marker protein is delivered to the tips of growing MTs by a motor protein (Tea2) (Fig. 1 B) (12,13). When MTs undergo a catastrophe (a transition from growth to shrinkage), the motor and its cargo are released (see, for instance, Fig. 1 B in (10)) and locally captured by the membrane (14). Importantly, recent experiments have demonstrated that perturbation of MT dynamics by the application of different doses of an MT destabilizing drug systematically alters the distance at which new growth zones form with respect to the cell center (15). It thus appears that a transport system composed of dynamic MTs and cargo delivered by motor proteins plays an important role in providing positional information for cellular morphogenesis.

Figure 1.

(A) Schematic drawing of a fission yeast cell. (Upper MT) Motor-mediated protein accumulation at the tip of a growing MT. (Lower MT) The MT undergoes a catastrophe and the proteins are locally delivered at the position of catastrophe. (B) Space-time-plot, showing the tip of a growing MT in fission yeast, decorated with the motor protein Tea2-GFP.

In this article, we theoretically investigate how a system of dynamic MTs and associated motor proteins could provide such positional information. We start by analyzing the distribution of MT lengths which results from the process of dynamic instability. In a simple two-state model, dynamic instability is characterized by four parameters: the growth and shrinking velocities, and the catastrophe (switch from growth to shrinkage) and rescue (switch from shrinkage to growth) frequencies (Fig. 2 A). For the simplest case of constant dynamic instability parameters it has been demonstrated that MT lengths are distributed exponentially (16,17). However, there is experimental evidence that in a cellular context, catastrophe and rescue frequencies are not necessarily constant, but can depend on MT length (our own observations in fission yeast (18) and in mitotic Xenopus extracts (19)). Recent computer simulations show that such a spatial dependence of the dynamic instability parameters can in fact be advantageous for MT-related processes during cell division (20–23). Inasmuch as, to our knowledge, no analytical treatment of the effects of spatially varying dynamic instability parameters has been published, we revisit the two-state model to include this possibility.

Figure 2.

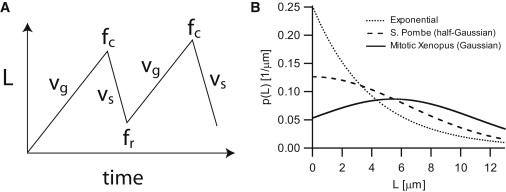
MT length distributions. (A) Schematic drawing of MT length (L) changes, according to the two-state model of dynamic instability. Dynamic instability is commonly characterized by four parameters (63): the growth and shrinkage velocities v_g and v_s, as well as the catastrophe and rescue frequencies f_c and f_r, which are the rates at which microtubules switch from the growing to the shrinking state and vice versa. (B) MT length distributions according to Eq. 2 for different parameter settings. Exponential: f_c = 0.5/min, f_r = 0/min, v_g = 2 μm/min, and v_s = NA. Mitotic Xenopus (Gaussian): f_c(L) = L × 0.19/μm/min, f_r(L) = 2.7/min − L × 0.21/μm/min, v_g = 10 μm/min, and v_s = 15 μm/min. Fission yeast (half-Gaussian): f_c(L) = L × 0.05/μm/min, f_r = 0/min, and v_g = 2 μm/min.

In a separate step, we examine the accumulation of motor proteins at the tips of growing MTs. This is not only necessary to determine the rate of local cargo delivery (see below), but also motivated by the fact that the length-dependence of the MT catastrophe frequency itself could be caused by the accumulation of motor proteins at MT tips (18). Quantifying the MT length-dependence of motor accumulation can thus also serve as a basis for understanding the relation between MT length and catastrophe frequency. The dynamic distribution of motor proteins along MTs has been studied quite extensively. However, previous theoretical work mainly considered the distribution of motors on polymers of fixed length, focusing on traffic jam phenomena, the effects of diffusion of unbound motors in closed compartments, and on effects due to specific arrangements of multiple MTs (see for instance (24–28)). More recently, systems with growing and shrinking polymers have been analyzed as well. In these studies, it was, however, assumed that motors arriving at the end of a polymer either stimulate polymer growth (29,30) or promote shortening of the polymer (31,32,33). Thus, MT growth or shrinkage was directly coupled to motor density. For the purpose of our study, we need to analyze a situation in which motor proteins accumulate at the ends of growing MTs of finite length, where both motors and MT tips move with constant (but independent and different) velocities (see, e.g., (34,35)). In addition, we include the possibility that the kinetics of motor binding/unbinding is different for the MT lattice and the tip. This relatively general case has, to our knowledge, not been addressed before and leads to a model that can be solved analytically.

Finally, using the results obtained by the above analyses we investigate how a transport system, composed of dynamic MTs and molecular motors, could provide positional information during cellular morphogenesis. We formulate a model of localized protein delivery by MTs, which we analyze in the context of the fission yeast system (11,15).

Results

MT length distributions with spatially varying switching frequencies

To investigate how spatially varying dynamic instability parameters affect the steady-state length distribution of MTs, we analyzed the two-state dynamic instability model (16,17) for MT length-dependent catastrophe and rescue frequencies, f_c(L) and f_r(L). For simplicity and by following experimental observations (18,19), however, we assumed that growth and shrinkage velocities v_g and v_s do not depend on MT length, which yielded the following system of coupled differential equations:

$$\begin{array}{c}{\partial }_t{p}_g\left(L,t\right)=-v_g{\partial }_L{p}_g\left(L,t\right)-p_g\left(L,t\right)f_c\left(L\right)+p_s\left(L,t\right)f_r\left(L\right),\\ {\partial }_t{p}_s\left(L,t\right)=+v_s{\partial }_L{p}_s\left(L,t\right)+p_g\left(L,t\right)f_c\left(L\right)-p_s\left(L,t\right)f_r\left(L\right).\end{array}$$ (1)

Here p_g and p_s are the probability distributions of growing and shrinking MTs. By using these equations, we find the following expression for the steady-state distribution of MT lengths (see Appendix A),

$$p\left(L\right)=p\left(0\right)\exp \left(\underset{0}{\overset{L}{\int }}{f}_r\left(L^{\prime }\right)v_s^{-1}-f_c\left(L\prime \right)v_g^{-1}d{L}^{\prime }\right),$$ (2)

where p(L) = p_g(L) + p_s(L) is the probability that an MT has length L. This result is only valid under the assumption that the parameters are such that the MT length distribution is bounded, i.e., p(L) → 0 as L → ∞ (see Appendix A). For constant f_c and f_r, Eq. 2 reduces to the exponential length distribution that was found by Verde et al. (16) (Fig. 2 B):

$$\begin{array}{l}p\left(L\right)=p\left(0\right)\exp \left(-\frac{L}{{\lambda }_{MT}}\right),\\ \text{with}\\ {\lambda }_{MT}=\frac{v_s{v}_g}{f_r{v}_g-f_c{v}_s}.\end{array}$$ (3)

It can be argued that such rather broad exponential length distributions, which peak at zero length, would not be well suited to provide positional information inside cells. However, Eq. 2 shows that if f_c and/or f_r depend on L, there can be a peak in the MT length distribution at L > 0, at the position L, where

$$f_c\left(L\right)v_g^{-1}=f_r\left(L\right)v_s^{-1}.$$ (4)

As a simple general case, we discuss the properties of Eq. 2 for a rescue rate that decreases linearly with L, f_r(L) = f_r⁰ − k_rL, (physically meaningful only for L smaller than $f_r^0/k_r$) and a catastrophe rate that increases linearly with L, f_c(L) = k_cL. In this case, one obtains a Gaussian distribution of MT lengths:

$$\begin{array}{l}p\left(L\right)\sim \exp \left(-\frac{{\left(L-\mu \right)}^2}{2{\sigma }^2}\right)\text{with}\\ \mu =\frac{f_r^0{v}_g}{v_s{k}_c+v_g{k}_r}\text{and}\sigma =\sqrt{\frac{v_g{v}_s}{v_s{k}_c+v_g{k}_r}}.\end{array}$$ (5)

The expression for the peak position μ reflects that both high growth velocities and high rescue rates promote long MTs, whereas rapid shrinkages and many catastrophes promote short MTs. The expression for the width σ says that the distribution is narrow when the excursions that MTs make during growth and shrinkage periods are short; this is achieved through low growth and shrinkage velocities and high switching frequencies. Eq. 5 also shows that—within the limits of biologically realizable parameter values—it is, in principle, possible to obtain an arbitrarily sharp distribution of MT lengths with a freely tunable peak position.

In mitotic Xenopus frog extract (19), it has indeed been found that both f_c and f_r depended linearly on MT length, whereas growth and shrinkage velocities were constant (v_g ≈ 10 μm/min and v_s ≈ 15 μm/min). Revisiting the data from Dogterom et al. (Fig. 10 a and 11 a in (19)) we found that, within the experimentally assessed length regime, the measurements of the switching frequencies could be fitted to linear functions with the following parameters: k_c = 0.19 min⁻¹ μm⁻¹, $f_r^0$ = 2.7 min⁻¹, and k_r = 0.21 min⁻¹ μm⁻¹. Assuming that these linear relations can be extrapolated to L = 0, we show in Fig. 2 B the expected Gaussian length distribution for the experimentally assessed regime of L < 13 μm. For the experimentally observed parameters, both μ and σ result to be ∼5.5 μm. Comparison with Fig. 8 in Dogterom et al. (19) indicates that this model is indeed consistent with the experimentally observed MT length distribution.

In the fission yeast system, the catastrophe frequency was also found to increase linearly with MT length (18). However, in this system, there are no rescues detected—and in this case, Eq. 5 predicts a half-Gaussian distribution, which is peaked at L = 0. This distribution is also plotted in Fig. 2 B for the experimentally observed parameters in fission yeast: k_c = 0.05 min⁻¹ μm⁻¹, f_r = 0 min⁻¹, and v_g = 2 μm/min.

Distribution of motors on a growing MT

To examine the accumulation of motor proteins at the tips of MTs we first have to consider the distribution of motors along the MT. In our theoretical description of the motor distribution on growing MTs, we will follow the conventional nomenclature in the experimental literature, by calling a special region at the growing MT end the tip, whereas the rest of the MT is called the MT lattice (Fig. 3 A). Our model then includes the following ingredients:

• 1.An MT of finite length, growing with constant velocity.
• 2.Binding and unbinding of motors along the whole MT.
• 3.Motor movement on the MT with constant velocity.
• 4.The possibility for motors to bind to and unbind from the MT tip with rates that are different from those on the rest of the MT lattice.

Figure 3.

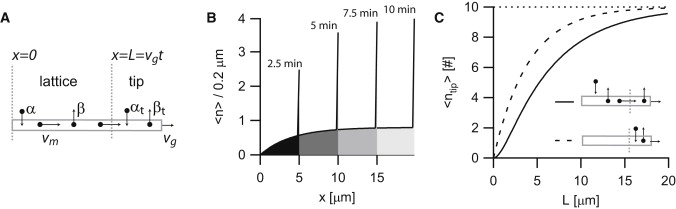
Motor lattice-distribution and tip-accumulation on growing MTs. (A) Schematic drawing of the model, showing binding with rate α, motor motion with velocity v_m, motor dissociation with rate β, and MT growth with velocity v_g. In addition, motors can bind to the MT tip with rate α_t or they can walk into the MT tip via the MT lattice. At the MT tip, motors dissociate with rate β_t. (B) Average number of motors per 0.2 μm of MT lattice on a growing MT, including accumulation at the MT tip (according to Eqs. 9 and 12). Different shaded values correspond to density profiles at different time points. Parameters: α = 4 μm⁻¹ min⁻¹, β = 1/min, v_m = 4 μm/min, v_g = 2 μm/min, α_t = 0/min, and β_t = 2/min. (C) Motor accumulation at MT tip according to Eq. 12. Schematic drawings correspond to panel A. (Dotted line) The value n₀, i.e., the number of motors at infinite length. (Solid curve) Motor proteins bind only to the lattice and walk into the tip: α = 10 μm⁻¹ min⁻¹, β = 0.5/min, v_m = 3 μm/min, v_g = 2μm/min, α_t = 0/min, and β_t = 2/min. (Dashed curve) Motors bind only to the tip: α = 0, β = NA, v_m = 3 μm/min, v_g = 2 μm/min, α_t = 5/min, and β_t = 0.5/min.

We model the density ρ(x,t) of molecular motors on the MT lattice by the equation

$${\partial }_t\rho =\alpha \Theta \left(v_{g}t-x\right)-\beta \rho -v_m{\partial }_x\rho .$$ (6)

In this equation, v_g is the MT elongation velocity and v_m is the motor velocity. The rate constants α and β describe binding to and unbinding from the MT, respectively. To model MT growth, the binding constant α is multiplied with a step function Θ(v_gt − x), which is 1 for 0 < x < v_gt and 0 otherwise. The step function captures the fact that motors can only bind to the currently existing part of the growing MT, which at time t extends until x = v_gt. To begin with, we consider motors walking beyond the current length of the MT (x > v_gt) as being lost. In the next section, we will compute how these motors instead accumulate at the tip. Furthermore, we use the boundary condition j(0,t) = ρ(0,t)v_m = 0, which captures the fact that there can be no flux of motors onto the MT from x < 0. As an initial condition, we use ρ(x,0) = 0, consistent with the fact that the MT has zero length at t = 0.

Before solving Eq. 6, we want to point out some simplifications that this model makes. For instance, it does not contain diffusive terms that can arise through explicit stochastic bidirectional motion but also through stochastic unidirectional motion. By using computer simulations with biologically meaningful parameters, however, we found that fluctuations arising from stochastic unidirectional MT growth and/or motor motion only “smoothen” the motor distribution on short length scales and do not lead to different behavior on the micrometer scales in which we are interested. Moreover, we assume the binding rate α to be temporally and spatially constant (this is a good approximation when the volume of a cell is relatively large and diffusion of unbound motors is relatively fast). In addition, we do not take into account saturation effects that are due to the fact that the motor density has an upper limit (the experimental data of which we are aware suggest that motor densities on the MT lattice are, in vivo, rather low).

Using the method of Laplace transforms, Eq. 6 can be solved analytically and one obtains (see Appendix B)

$$\rho \left(x,t\right)/{\rho }_0=\Theta \left(v_{g}t-x\right)\left(1-\exp \left(\frac{x-L\left(t\right)}{{\lambda }_{gm}}\right)\right)-\Theta \left(v_{m}t-x\right)\left[\exp \left(-\frac{x}{{\lambda }_m}\right)-\exp \left(\frac{x-L\left(t\right)}{{\lambda }_{gm}}\right)\right].$$ (7)

The shape of this distribution is characterized by the following quantities:

$$\begin{array}{l}{\rho }_0=\alpha /\beta ,\\ {\lambda }_m=v_m/\beta ,\\ L\left(t\right)=v_{g}t,\\ {\lambda }_{gm}=\left(v_g-v_m\right)/\beta .\end{array}$$ (8)

Here, ρ₀ is the equilibrium density of motors due to binding and unbinding kinetics. The run-length λ_m is the average distance that motors walk on an MT before dissociation and L(t) is the MT's current length. The parameter λ_gm is a length scale that characterizes the shape of the motor density close to the MT tip for the case that the motors walk slower than the MT grows (see Appendix B).

Within the context of this article, the most relevant case is when the motor velocity is larger than the MT growth velocity (v_m > v_g), as this allows for an accumulation of motors at the MT tip. When motors are walking faster than the velocity at which the MT grows, the expression for the motor density within the physically relevant regime 0 < x < v_gt simplifies to

$$\begin{array}{l}\rho \left(x,t\right)/{\rho }_0=\rho \left(x\right)/{\rho }_0=1-\exp \left(-x/{\lambda }_m\right),\\ 0\le x<v_{g}t.\end{array}$$ (9)

Fig. 3 B shows how the motor density along the MT develops in time. The profile is a result of the fact that the motors which bind close to the nongrowing end (at x = 0) move toward the right; however, there is no influx of motors from the left (x < 0) such that there is depletion of motors at the nongrowing MT end. Interestingly, the motor density at a given position x on the MT does not change with time. The situation v_m > v_g is thus a true adiabatic limit in which the density distribution is always in steady state with respect to the current system size, i.e., MT length (this is not the case if the motors walk slower than the MT grows as discussed in Appendix B).

To our knowledge, there are no quantitative experimental data yet on the distribution of motor proteins on growing MTs. The experiments that come closest were performed in vitro using stabilized (nongrowing) MTs (36). The authors observed a monotonically increasing profile of the kinesin-8 motor protein Kip3 along the MT (see Fig. 3 b in (36)). However, as the MTs used were relatively short (<5 μm) compared with the measured motor run length (∼12 μm), it is difficult to decide whether the experimental data followed the exponential shape that is predicted by our theory.

Motor accumulation at the growing MT tip

To determine the motor accumulation at the growing MT tip, we include in our model a special MT-tip region (Fig. 3 A) in which motors that reach the end of the MT can accumulate (given that motors walk faster than the MT grows). In addition, motors can bind directly to this region with rate α_t and unbind with rate β_t. The equations for the motor density at the MT lattice remain the same as before, and, again neglecting saturation effects, we now add the following equation to compute the number of motors at the MT tip:

$${\partial }_t{n}_{\text{tip}}={\alpha }_t-{\beta }_t{n}_{\text{tip}}\left(t\right)+j\left(t\right).$$ (10)

The first two terms account for the association/dissociation kinetics directly at the tip. One may include the possibility of a limited number of tip-binding sites (saturation effects) by replacing α_t with α_t (1 – n_tip(t)/n_max), yielding

$${\partial }_t{n}_{\text{tip}}={\alpha }_t-{\beta }_t^{\ast }{n}_{\text{tip}}\left(t\right)+j\left(t\right),$$

with

$${\beta }_t^{\ast }=\left({\alpha }_t/n_{\max }+{\beta }_t\right).$$

For simplicity and inasmuch as we are not aware of experimental data on n_max, we assume n_max = ∞ and therefore set ${\beta }_t^{\ast }={\beta }_t$. The third term in Eq. 10 accounts for the flux of motors into the tip, which for v_m > v_g is given by the density of motors at the end of the MT lattice,

$$\rho \left(L=v_{g}t,t\right)=\frac{\alpha }{\beta }\left(1-\exp \left(-v_{g}t/{\lambda }_m\right)\right)$$

(see Eq. 9), multiplied by the relative speed of the motors with respect to the MT tip,

$$j\left(t\right)=\left(v_m-v_g\right)\rho \left(v_{g}t,t\right)=\left(v_m-v_g\right)\frac{\alpha }{\beta }\left(1-\exp \left(-v_{g}t/{\lambda }_m\right)\right).$$ (11)

Note that n_tip is a number, whereas ρ is a line density (number/length). The units of α_t and α are different as well: [α_t] = s⁻¹ and [α] = m⁻¹ s⁻¹.

Using the initial condition n_tip (0) = 0, one obtains an expression for the number of motors at the tip of an MT of length L,

$$n_{\text{tip}}\left(L\right)=n_0\left[1-\psi \exp \left(-L/{\lambda }_m\right)-\left(1-\psi \right)\exp \left(-L/{\lambda }_t\right)\right],$$ (12)

where L = v_gt. The shape of n_tip(L) is characterized by the quantities

$$\begin{array}{l}{n}_0=\frac{1}{{\beta }_t}\left(\frac{\alpha }{\beta }\left(v_m-v_g\right)+{\alpha }_t\right)=\left(j_0+{\alpha }_t\right)/{\beta }_t,\\ {\lambda }_m=v_m/\beta ,\\ {\lambda }_t=v_g/\beta ,\\ \psi ={\left(1+{\alpha }_t/j_0\right)}^{-1}{\left(1-{\lambda }_t/{\lambda }_m\right)}^{-1}\end{array}$$ (13)

where

$$j_0=\frac{\alpha }{\beta }\left(v_m-v_g\right)$$

is the motor influx from the MT lattice into the tip of an infinitely long MT and n₀ is the number of motors at the tip of an infinitely long MT. Furthermore, two length scales emerge:

• 1.The motor run-length λ_m, which governs the influx from the MT lattice.
• 2.The length scale λ_t, which governs the motor dynamics at the tip.

Finally, ψ is a dimensionless quantity that can take any value from −∞ to +∞, which determines the way both length scales contribute to the profile.

Two mechanisms contribute to the MT length-dependence of motor accumulation at the tip (Fig. 3 C). First, the influx of motor proteins from the MT lattice increases as the MT elongates, and leads to an accumulation at the MT tip that is mainly determined by the motor run length λ_m. Second, there is a length-dependence related to the time it takes the motor density to equilibrate at the tip. In the case that motors can only bind to the tip region, this equilibration is solely determined by unbinding from the tip (with rate β_t). Because the MT grows with velocity v_g, this converts into the length-scale λ_t = v_g/β_t.

Localized cargo delivery by a system of MTs and motor proteins

Combining the results obtained above for MT length distributions and the accumulation of motors at growing MT tips, we can now formulate a mathematical model for the spatial distribution of cargo delivery by a transport system composed of dynamic MTs and molecular motors. In the context of the fission yeast system, we assume that MTs have no rescues, f_r = 0, and we assume that the nongrowing minus-ends of the MTs are at the cell center (37), i.e., the distance from the cell center equals MT length L (Fig. 1 A). Under these assumptions, we model the rate r(L) at which proteins are released at a position L as

$$r\left(L\right)\sim n_{\text{tip}}\left(L\right)p_g\left(L\right)f_c\left(L\right).$$ (14)

This equation states that the rate of cargo delivery at position L is proportional to the amount of cargo that sits on the tip of an MT of length L, i.e., n_tip(L), and proportional to the probability that a growing MT has length L, i.e., p_g(L), where p_g(L) ∼ p(L) is the length distribution for growing MT ends (see Appendix A). Furthermore, the rate of delivery is proportional to the probability that an MT of length L releases the cargo by undergoing a catastrophe, i.e., f_c(L). We will assume for simplicity that the transport to the tip is motor-dominated such that the amount of cargo at the MT tip can be approximated by the expression (see Eq. 12)

$$n_{\text{tip}}\left(L\right)\approx n_0\left[1-\exp \left(-L/{\lambda }_m\right)\right].$$

This simplifies the mathematical expressions but does not affect our main conclusions, as those only depend on the fact that n_tip(L) is a monotonically increasing function. As discussed above, the catastrophe rate in fission yeast increases linearly with MT length, and the lengths of growing MTs (consequently) follow a half-Gaussian distribution,

$$p_g\left(L\right)\sim \exp \left(-L^2/2{\sigma }^2\right)$$

with

$$\sigma =\sqrt{v_g/k_c}$$

(Fig. 4 A). The rate of cargo delivery thus reads

$$r\left(L\right)\sim \left(1-\exp \left(-L/{\lambda }_m\right)\right)\exp \left(-L^2/2{\sigma }^2\right)k_{c}L.$$ (15)

Figure 4.

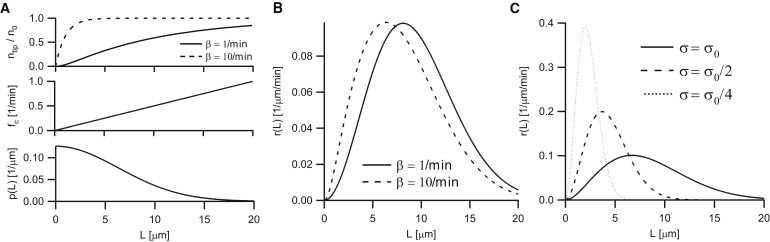
Creating positional information with dynamic MTs and motor accumulation at MT tips in fission yeast (S. pombe). (A) Motor accumulation n_tip/n₀, MT catastrophe rate f_c, and MT length distribution p(L) as used to compute cargo delivery in panel B. (B) Cargo delivery rate by a transport system composed of dynamic MTs and motor proteins, according to Eq. 15, where the MT catastrophe rate linearly increases with MT length as measured in fission yeast. Parameters: k_c = 0.05/μm/min, f_r = 0/min, v_g = 2 μm/min, v_s = NA, v_m = 10 μm/min, and β as indicated. (C) As in panel B, but for MTs of different average length, as determined by the effective parameter $\sigma =\sqrt{v_g/k_c}$ (see Eq. 15). Parameters: f_r = 0/min, v_s = NA, v_m = 10 μm/min, β = 5/min, σ₀ = 6.3 μm, and σ as indicated.

Fig. 4 B shows this function for parameters that were experimentally determined in fission yeast (the lattice unbinding rate β and hence the motor run-length λ_m are not known in this case; we therefore plotted the distribution for two different values of β covering typical values observed experimentally, see Table 1). Although in this case the MT length distribution itself has a peak at L = 0 (see Fig. 4 A), the cargo delivery rate peaks at ∼5–7 μm, which corresponds to the typical cell center to pole distance at the end of interphase. The reason for this peak of cargo delivery is that both the number of motors and the catastrophe rate are low for short MTs. However, the increasing catastrophe rate prevents the occurrence and thereby the cargo delivery from long MTs.

Table 1.

Ranges of experimentally determined parameters in different in vitro and in vivo systems

Microtubule dynamics
vg [μm min−1]	vs [μm min−1]	fc [min−1]	fr [min−1]
2–17	5–30	0.2–5	0–10
Motor protein dynamics
vm [μm min−1]	α [μm−1 min−1]	β [min−1]	αt [min−1]	βt [min−1]
1–90	ND	0.3–10	ND	2–7

Values for microtubule and motor protein dynamics are from the literature (19,35,50–58) (35,36,38,40,59–62). ND, not determined.

In wild-type fission yeast, the growth of long MTs is additionally restricted by the cell pole such that it becomes difficult to validate experimentally whether there really is a drop in cargo delivery at large L. Interestingly, however, Castagnetti et al. (15) measured the spatial distribution of cellular growth zones as potentially induced by MT-mediated cargo delivery in overly long cells. The authors found that the distributions of growth zones were peaked at positions between the cell center and the cell pole. Most importantly, when adding different amounts of an MT destabilizing drug the spatial distribution of growth site formation changed its shape and the peak position shifted: the more drug was added (i.e., the shorter the MT were on average), the closer the peak was to the cell center (see Fig. 5 in (15)).

These findings prompted us to test the effect of a reduced average length of MTs on the distribution of cargo delivery within the framework of our model. As it is not known how the added drug exactly affects MT dynamics, we plotted (Fig. 4 C) the cargo delivery distribution for different $\sigma =\sqrt{v_g/k_c}$, which is the effective parameter governing the average MT length in Eq. 15. As observed in the experiments, the peak distance of cargo delivery decreases for decreasing MT length (Fig. 4 C), and the shapes of the curves in our model are similar to the experimentally observed distributions (see Fig. 5 B in (15)).

For simplicity, we made the assumption that the nongrowing (minus) ends of MTs are strictly at the center of the fission yeast cell. In reality, there is, however, a certain spread (∼1 μm) of the position of the MT minus-ends (36). Taking this into account by convoluting the cargo delivery function with a Gaussian spread of 1 μm produces, in fact, an even better agreement with the data by Castagnetti et al. (15) (our data not shown).

Note that, in general, one may assume that cargo proteins, once released from the MT tip, undergo some three-dimensional diffusive spread before binding to their target receptors. This could be accounted for in our model, for instance by convolution with the propagator of the diffusion equation. The geometry in fission yeast is, however, such that the tips of MTs grow in general close to the cell membrane where the receptor proteins for the cargo reside (14). Concomitantly, the available experimental data suggests that there is hardly any diffusive spread of Tea1 in between release from MTs and binding to the cell boundary (our own observations and Fig. 1 B in (10)).

Discussion

We analyzed a transport system composed of motor proteins that accumulate at the tips of growing MTs, and are released upon MT catastrophes. We find that such a system has the ability to deliver a peak amount of cargo to a tunable distance L from the MT nucleation point even when the MT length distribution itself is peaked at L = 0. This finding demonstrates how a limited number of commonly occurring cellular components (i.e., molecular motors and MTs) can provide positional information within the cell.

To compute the effects of MT length-dependent catastrophe (and rescue) rates (see Eq. 2), we extended the classical two-state dynamic instability model (16), in which it was assumed that all parameters (v_g, v_s, f_c, and f_r) are constant. We find that when f_c(L) and f_r(L) are MT length-dependent, it is possible to obtain peaked MT length distributions. This could be important not only in transport processes but may also facilitate the formation of intracellular structures of a defined size such as the mitotic spindle during cell division (20–23). It will be interesting to see whether quantitative measurements during mitosis will indeed reveal spatially varying dynamic instability parameters in mitotic Xenopus extract (19) as well as in other systems.

We further computed how motor proteins accumulate at the tips of growing MTs. Besides being relevant for the local delivery of cargo proteins, the accumulation of motor proteins could be responsible for the experimentally observed MT length-dependence of the catastrophe frequency itself. Experiments indicate that there are specific motor proteins such as the plus-tip directed kinesin-8 that enhance the frequency at which MTs undergo catastrophes (18, 38). Because the amount of motors at MT tips increases as the MTs grow (see Eq. 12), one would therefore predict that kinesin-8 proteins preferentially enhance the catastrophe frequency of long MTs. Recent experiments have shown that GMPCPP-stabilized MTs are depolymerized by kinesin-8 (Kip3) proteins at a rate that depends on the flux of these proteins to the MT tip, as motor proteins at the MT tip “bump off” each other and in the process remove one or two tubulin dimers (39). However, dynamic MTs have an intrinsic tendency to depolymerize after a catastrophe event, which is different from the slow protein-driven depolymerization observed for GMPCPP-stabilized MTs (36,39,40). The effect of kinesin-8 proteins on dynamic MTs could thus instead be to promote catastrophes preferentially of long MTs (18), possibly by driving depolymerization of a stabilizing structure at the MT tip (2). Quantitative experiments using kinesin-8 proteins together with dynamic MTs will be necessary to determine the exact relation between the amount (or flux) of motor proteins and the probability of a catastrophe to occur.

In this article, we did not examine the distribution of motor proteins along shrinking MTs. The reason is that we mainly aimed to model data from experiments in fission yeast where the rescue rate f_r appears to be zero and the majority of the cargo appears to be delivered upon the moment of a catastrophe (10). In this system, it therefore seems a reasonable approximation that MTs start growth at zero length with zero motors bound. In case of a significant rescue rate, an analysis is in general more complicated because the amount of motors at MT tips will depend on the history of the MT. For instance, an MT that reached length L through growth from length zero will have accumulated a certain number of motors. On the other hand, an MT that starts growth at length L through a rescue event may not have any motors on its tip. How quickly the motor concentration at the tip recovers will in general depend on the equilibration timescale ${\beta }_t^{-1}$. If the equilibration is fast, it may be possible to neglect history effects; otherwise, additional mathematical analyses will be required.

In summary, we presented a theoretical study that shows how MTs and motor proteins can provide positional information inside cells. We show that our model can explain recent experimental findings on cellular morphogenesis in fission yeast, which is a leading model system for investigating the relationship of MTs and cellular growth zone formation. To compare our theory with experiments directly, we explicitly aimed to formulate our models in a way that they only depend on parameters that can be readily measured inside living cells. We hope that this approach will encourage researchers to perform quantitative experiments to test the predictions of our model.

Appendix A

Solution of the two-state dynamic instability model with spatially varying switching frequencies

Within the framework of the two-state model of dynamic instability, the length distribution of microtubules is governed by the system of coupled differential equations (16,17),

$$\begin{array}{l}{\partial }_t{p}_g=-v_g{\partial }_L{p}_g-p_g{f}_c+p_s{f}_r,\\ {\partial }_t{p}_s=+v_s{\partial }_L{p}_s+p_g{f}_c-p_s{f}_r,\end{array}$$

where p_g(L,t) and p_s(L,t) are the probabilities to find a growing or a shrinking MT of length L. The form of these equations implicitly assumes that the growth and shrinkage velocities are constants. Dogterom et al. (19) solved these equations assuming that f_c and f_r are spatially constant. We extend this analysis by allowing for spatially varying f_c(L) and f_r(L). At steady state, this yields

$$\begin{array}{l}0=-v_g{\partial }_L{p}_g\left(L\right)-p_g\left(L\right)f_c\left(L\right)+p_s\left(L\right)f_r\left(L\right),\\ 0=+v_s{\partial }_L{p}_s\left(L\right)+p_g\left(L\right)f_c\left(L\right)-p_s\left(L\right)f_r\left(L\right).\end{array}$$

Adding both equations yields a flux balance for growing and shrinking MTs:

$$v_s{\partial }_L{p}_s\left(L\right)-v_g{\partial }_L{p}_g\left(L\right)=0\iff p_s\left(L\right)-v_g{v}_s^{-1}{p}_g\left(L\right)=const.$$

As we are only interested in bounded solutions, p_s(∞) = p_g(∞) = 0 and the constant on the right side of the equation must be zero. This implies

$$p_s\left(L\right)=v_g{v}_s^{-1}{p}_g\left(L\right),$$

leaving us with one equation,

$$0=-v_g{\partial }_L{p}_g\left(L\right)-p_g\left(L\right)f_c\left(L\right)+v_g{v}_s^{-1}{p}_g\left(L\right)f_r\left(L\right),$$

which can be rearranged to

$$\frac{{\partial }_L{p}_g\left(L\right)}{p_g\left(L\right)}=\frac{f_r\left(L\right)}{v_s}-\frac{f_c\left(L\right)}{v_g}.$$

Integration yields that

$$p_g\left(L\right)=p_g\left(0\right)\exp \left(\underset{0}{\overset{L}{\int }}{f}_r\left(L\prime \right)v_s^{-1}-f_c\left(L\prime \right)v_g^{-1}dL\prime \right).$$

The probability to find an MT with length L is given by the sum of the probabilities to find a growing or a shrinking MT with respective length L: p(L) = p_g(L) + p_s(L). Using

$$p_s\left(L\right)=v_g{v}_s^{-1}{p}_g\left(L\right)$$

yields

$$p=p_g+p_s=p_g\left(1+v_g{v}_s^{-1}\right),$$

and we thus obtain

$$p\left(L\right)=p\left(0\right)\exp \left(\underset{0}{\overset{L}{\int }}{f}_r\left(L\prime \right)v_s^{-1}-f_c\left(L\prime \right)v_g^{-1}dL\prime \right).$$

This equation allows one to compute p(L) by a simple integration. In the case where the experimentally determined f_c(L) and f_c(L) cannot be approximated by analytically integrable functions, one may have to resort to numerical methods to solve the integral. We would like to note that there are already (theoretical) studies that include microscopic details of the catastrophe mechanism and/or more states than the two growing and shrinking states (41,42), as well as effects due to closed systems and/or due to a cell edge and/or due to a limited pool of free tubulin (17,43–47). Including those effects also leads, in general, to nonexponential (peaked) MT length distributions, whose shapes are, however, implicit to the assumptions of each model. Our analysis is different in that we allow for an arbitrary space-dependence of f_c and f_r.

Appendix B

Solution of the motor distribution along a growing MT

To solve Eq. 6,

$${\partial }_t\rho =\alpha H\left(x<v_{g}t\right)-\beta \rho -v_m{\partial }_x\rho ,$$

we used the method of Laplace transforms as described in Kreyszig (48), where the Laplace transform of ρ(x,t) with respect to the variable t is defined as

$$L\left(\rho \left(x,t\right)\right)=\underset{0}{\overset{\infty }{\int }}\rho \left(x,t\right)\exp \left(-st\right)\text{dt}.$$

Using this definition, the Laplace transform of Eq. 6 reads

$$sL\left(\rho \left(x,t\right)\right)-\rho \left(x,0\right)=\frac{\alpha }{s}\exp \left(-\left(xs\right)/v_g\right)-\beta L\left(\rho \right)-v_m{\partial }_{x}L\left(\rho \right).$$

Using the initial condition ρ(x,0) = 0, the above equation becomes a first-order differential equation for L(ρ), which can be solved using standard methods. The general solution reads

$$L\left(\rho \left(x,t\right)\right)=\frac{\alpha }{s}\frac{v_g}{\beta v_g+s\left(v_g-v_m\right)}\exp \left(-\frac{s}{v_g}x\right)+A\left(s\right)\exp \left(-\frac{s+\beta }{v_m}x\right).$$

The free parameter A(s) is determined by the boundary condition

$$\rho \left(x=0,t\right)v_m=0,$$

which for v_m > 0 implies ρ(x = 0,t) = 0, and thus L(ρ)(x = 0,t)) = 0. Inserting the condition L(ρ)(x = 0,t)) = 0 in the above equation yields

$$0=\frac{\alpha }{s}\frac{v_g}{\beta v_g+s{v}_g-s{v}_m}+A\left(s\right),$$

which determines A(s).

Using standard methods for computing inverse Laplace transforms (48), one obtains the expression for ρ(x,t) (i.e., Eq. 7 in the main text):

$$\rho \left(x,t\right)/{\rho }_0=\Theta \left(v_{g}t-x\right)\left(1-\exp \left(\frac{x-L\left(t\right)}{{\lambda }_{gm}}\right)\right)-\Theta \left(v_{m}t-x\right)\left[\exp \left(-\frac{x}{{\lambda }_m}\right)-\exp \left(\frac{x-L\left(t\right)}{{\lambda }_{gm}}\right)\right].$$

Note that, for the special case v_m = 0, the term in Eq. 6 that includes the derivative with respect to x vanishes, such that there is no need to specify a boundary condition; the solution in this case is

$$\rho \left(x,t\right)/{\rho }_0=H\left(x<v_{g}t\right)\left(1-\exp \left(\left(x-L\left(t\right)\right)/{\lambda }_{gm}\right)\right).$$

Density profile for motors that walk slower than the MT grows

In the case that the motors are walking slower than the MT grows (v_m < v_g), the motor density can be written in two parts:

$$\begin{array}{l}\rho \left(x,t\right)/{\rho }_0=1-\exp \left(-\frac{x}{{\lambda }_m}\right),0\le x\le v_{m}t\\ \rho \left(x,t\right)/{\rho }_0=1-\exp \left(\frac{x-L\left(t\right)}{{\lambda }_{gm}}\right),v_{m}t<x<v_{g}t.\end{array}$$

Thus, for values of x smaller than v_mt, the system behaves as discussed above (Eq. 9). However, for v_mt < x < v_gt, the profile is a result of the fact that the corresponding part of the MT only existed for a relatively short time (see Fig. 5, B and C); the system has thus not yet equilibrated with respect to the binding/unbinding kinetics. In addition, the profile at the MT end is affected by the flux of motors. The emerging length scale λ_gm thus depends both on the velocity of MT growth and on the motor velocity (see Eq. 8). In contrast to the case v_m > v_g, the density profile is not in steady state with respect to the current system size for v_mt < x < v_gt: when the MT would stop growing, the density would need some time to relax to the steady state given by Eq. 9.

Figure 5.

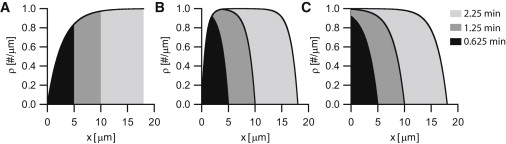
Distribution of motors on growing microtubules. (A–C) Motor densities on growing MTs according to Eq. 7. Shaded areas correspond to different time points (at t = 0, MTs have zero length and there are no motors bound). In all panels: α = 4 μm⁻¹ min⁻¹, β = 4 min⁻¹, and v_g = 8 μm/min. (A) The value v_m = 11 μm/min, assuming that motors reaching the end of the MT do not accumulate but dissociate. (B) The value v_m = 3 μm/min. (C) The v_m = 0 μm/min.