Linking the Acetylcholine Receptor-Channel Agonist-Binding Sites with the Gate

Abstract

The gating isomerization of neuromuscular acetylcholine receptors links the rearrangements of atoms at two transmitter-binding sites with those at a distant gate region in the pore. To explore the mechanism of this reversible process, we estimated the gating rate and equilibrium constants for receptors with point mutations of α-subunit residues located between the binding sites and the membrane domain (N95, A96, Y127, and I49). The maximum energy change caused by a side-chain substitution at αA96 was huge (∼8.6 kcal/mol, the largest value measured so far for any α-subunit amino acid). A Φ-value analysis suggests that αA96 experiences its change in energy (structure) approximately synchronously with residues αY127 and αI49, but after the agonist molecule and other residues in loop A. Double mutant-cycle experiments show that the energy changes at αA96 are strongly coupled with those of αY127 and αI49. We identify a column of mutation-sensitive residues in the α-subunit that may be a pathway for energy transfer through the extracellular domain in the gating isomerization.

Introduction

Nicotinic acetylcholine (ACh) receptors (AChRs) are ion channels that isomerize (gate) between stable conformations, R↔R^∗. The R shape has a low affinity for the transmitter (ACh) and a nonconducting pore, and the R^∗ shape has a high affinity for ACh and a pore that readily conducts monovalent cations. At the nerve-muscle synapse, two transmitter molecules bind to each AChR to increase the R↔R^∗ equilibrium constant and promote the entry of Na⁺ into (and the depolarization of) muscle cells (1–4). We, as well as other investigators, are interested in understanding the mechanisms by which ACh and other agonists increase the R↔R^∗ equilibrium constant and hence the probability that a remote ion channel domain will adopt an ion-conducting conformation. Our approach is to estimate the spatial distribution and timing of energy changes within the protein as determined from isomerization rate constants of mutant AChRs.

Ligand-binding and channel-gating are coupled energetically (Fig. 1) (5). In the absence of an external energy source, and with two equivalent transmitter-binding sites (6), the ratio of the gating equilibrium constants with two versus zero bound agonist molecules [(E₂/E₀) is equal to the square of the ratio of the R/R^∗ equilibrium dissociation constants (K_d/J_d)²]. Although it has been shown in wild-type (wt) AChRs (E₀ << E₂) that the end states and conformational pathway of the R↔R^∗ isomerization are essentially the same whether or not agonists occupy the transmitter-binding sites (7), it has also been demonstrated that many non-binding-site mutations change E₂ by a parallel change in E₀ and do not alter the K_d/J_d ratio.

Figure 1.

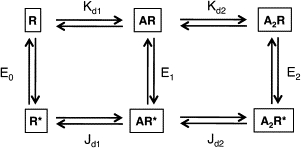
Cyclic activation model for AChRs. Boxed letters are the stable end-states (R, low affinity and closed channel; R^∗, high affinity and open channel; A, the agonist). Arrows indicate the intermediate microstates (horizontal: ligand-binding; vertical: protein isomerization) that are too brief to be detected by our instrument. Equilibrium constants for each step: E, isomerization with zero, one, or two bound agonists; K_d, dissociation constant of R; J_d, dissociation constant of R^∗. For mouse, adult-type AChRs the two binding sites have approximately equal affinities for ACh (K_d = 140 mM and J_d = 20 nM). The energy between any two stable states is independent of the connecting pathway, hence E₂/E₀ = (K_d/J_d)².

In adult mouse AChRs, the gating equilibrium constant is much larger when both binding sites are occupied by ACh (E₂^ACh ≈ 28) (8–10) than when they are not (E₀ ≈ 6.5 × 10⁻⁷) (6). Since energy is proportional to the logarithm of an equilibrium constant, this E₂/E₀ ratio (∼43 million) corresponds to a −10.4 kcal/mol increase in the relative stability of conducting (R^∗) versus nonconducting (R) AChRs, with ACh versus without any agonists at the binding sites. By the same token, between R and R^∗ the equilibrium dissociation constant (for ACh) decreases from ∼140 μM (K_d) to ∼20 nM (J_d). This ∼6600-fold change in affinity corresponds to an increase in ligand-binding energy of 5.2 kcal/mol per transmitter-binding site.

The changes in energy (structure) that comprise the global, gating isomerization of an AChR are neither uniform nor synchronous (11). The increase in agonist affinity involves rearrangements of atoms (water, protein, and perhaps ions) at the transmitter-binding sites that occur at the start, and the change in ionic conductance involves rearrangements of atoms at the gate region of the pore that occur at the end of the channel-opening process (11,12). The transmitter-binding sites and the gate are separated by ∼5 nm (13) and the affinity change may precede the conductance change by ∼1 μs (8,14). A change in the structure of a residue (with respect to its local environment) between R and R^∗ can be manifested as a change in the relative free energies of these end states. That is, if a side-chain substitution changes the gating equilibrium constant (the ratio of the forward/backward isomerization rate constants), then the residue must change its R versus R^∗ relative energy (structure) at some point within the reaction. The extent to which a mutation changes the forward versus the backward rate constant is given by the parameter Φ, which is the position in the reaction when such an energy (structure) change occurs (1-to-0, early-to-late).

A map of the energy changes and Φ-values for adult mouse neuromuscular AChR residues suggests that there are some amino acids in the extracellular domain of the α-subunit that when mutated exhibit a particularly large range of gating equilibrium constants (i.e., have a particularly large energy sensitivity) and change structure relatively early in the gating process (12). Here we examine a hot spot in this population that we speculate is an important element in the pathway for energy transfer between the binding sites and the gate.

In this study we focused on residues αN95 and αA96 (in loop A), αI49 (in loop 2), and αY127 (on β-strand 6) (Fig. 2). This general region of the AChR has previously been examined in some detail. Mutations of loop A residue αD97 mostly increase E₂ (by a parallel increase in E₀) and elicit an early energy change but have little effect on K_d for ACh (15). This position (in all subunits) has been shown to influence channel conductance (16). Loop 2 residues have been shown to be important elements in the isomerization pathway (13,17,18). In the AChR, residues 45–48 have a significant effect on E₂ and change energy early, but after αD97 (17). Mutations of loop 2 residue αE45 have a particularly large effect on E₂. This residue probably does not form a salt bridge with pre-M1 residue R209 (19) (but see Lee and Sine (9)). The β-strand 6-amino-acid residue αY127 has been studied by two groups (20,21). Substitutions of this position have a huge effect on E₂ (by a parallel change in E₀) and a Φ-value similar to that of loop 2, and are coupled energetically with those of residues in the complementary δ/ɛ-subunits. The residues adjacent to αY127 are either at one end of loop 7 (the cys loop; αC128) (22) or bind a structural water whose disposition may be important in the gating isomerization (αS126) (15,23). The next residue in sequence, αK125, is a possible binding site for allosteric modulators (24).

Figure 2.

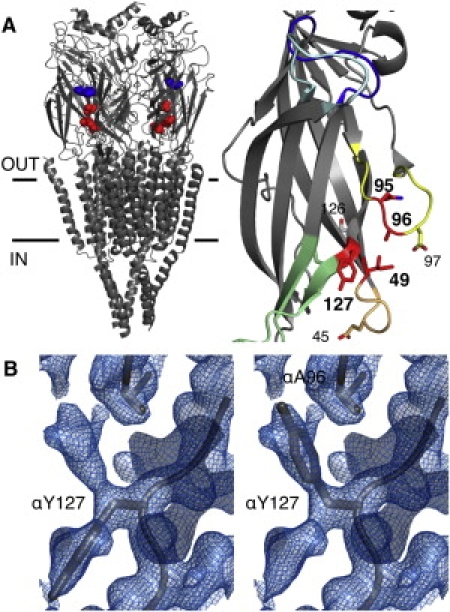
Location and structure of residues. (A) Left: Torpedo AChR structure determined by cyroelectron microscopy (accession number 2BG9.pdb (13)). Shown as spheres in each of the two α-subunits are (blue) αW149 (at the transmitter-binding site) and (red) αI49 (loop 2), αA96 (loop A), and αY127 (β-strand 6). Horizontal lines approximately mark the membrane. The M2 transmembrane helix lines the ion permeation pathway and the M4 helix faces the lipids. Right: Mouse α-subunit extracellular domain fragment (accession number 2QC1.pdb (23)). A bound toxin molecule has been removed for clarity. The highlighted residues (red, bold) are αN95, αA96, αY127, and αI49. Five loops are color-coded: cyan, loop C; blue, loop B; yellow, loop A; tan, loop 2; green, loop 7 (cys loop). (B) Electron density map near the α(A96-Y127) region (from 2QC1.pdb). Left: Residues αA96 and αY127 are shown as sticks according to their position in 2QC1.pdb. Right: The same as the left except that αY127 is shown as an alternate rotamer, approximately filling an unoccupied region of the electron density map near αA96.

Materials and Methods

Mutagenesis and expression

Mutations were made to mouse AChR subunit cDNA using the QuikChange site-directed mutagenesis kit (Stratagene, La Jolla, CA) and verified by nucleotide sequencing. Human embryonic kidney fibroblast cells (HEK 293) were transiently transfected by calcium phosphate precipitation. Cells were treated with ∼0.7 mg total DNA per 35 mm culture dish in the ratio of 2:1:1:1 (α/β/δ/ɛ) for ∼16 h. Electrophysiological recordings were made 24–48 h later.

To make hybrid AChRs with only one of the two α-subunit residues mutated, cells were transfected with both wt and mutant α-subunit (plus wt β-, ɛ-, and δ-subunits) cDNAs. Accordingly, AChRs with zero, one, or two mutated α-subunits were expressed, with each construct having a distinct single-channel kinetic signature (25).

Electrophysiology

Recordings were performed in a cell-attached patch configuration at 22°C. The bath and pipette solutions were Dulbecco's phosphate-buffered saline containing (mmol/L) 134 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄ (pH 7.3). Pipettes were pulled from borosilicate capillaries to a resistance of ∼10 MΩ and coated with Sylgard (Dow Corning, Midland, MI). The pipette potential was held at +70 mV, which corresponds to a membrane potential of approximately −100 mV. Single-channel currents were recorded using a PC-505 amplifier (Warner Instrument Corp., Hamden, CT) with low-pass filtering at 20 kHz. The currents were digitized at 50 kHz using a SCB-68 acquisition board (National Instruments, Austin, TX) and QuB software (www.qub.buffalo.edu).

In some experiments, agonist (500 μM acetylcholine or 20 mM choline) was added only to the pipette solution as indicated. These concentrations are approximately five times the R-conformation equilibrium dissociation constant (K_d) (26).

Determination of rate constants

The isomerization rate constants were estimated with the use of QuB software. Clusters of single-channel R↔R^∗ gating activity were selected by eye. Clusters were idealized using the segmental k-means algorithm with a two-state, C(losed)↔O(pen) model (27). The forward and backward isomerization rate constants were estimated from the interval durations by using a two-state model and a maximum-interval likelihood algorithm after imposing a dead time (and missed event correction) of 50 μs (28). The isomerization equilibrium constant is the ratio of these rate constants, and the corresponding energy change (kcal/mol) is 0.59 times the natural logarithm of the equilibrium constant.

Thermodynamic cycle

The function of AChRs is well described by the thermodynamic cycle shown in Fig. 1. Subsets of the possible stable states of this scheme are apparent under different experimental conditions. For example, by nearly saturating the binding site with agonist we isolate A₂R↔A₂R^∗, and by removing agonist entirely we isolate R↔R^∗. These are the two strategies we used to directly measure the di- and unliganded gating equilibrium constants E₂ and E₀. In wt AChRs, E₂^ACh ≈ 28 (8,9,14,15) and E₂^choline ≈ 0.046 (29). To measure the fold change in E₂ caused by a side-chain substitution, we used either of these agonists depending on whether the mutation increased (choline) or decreased (ACh) E₂.

For some of the point mutations at position αA96 (in both α-subunits), E₂ was so great that it was difficult or impossible to measure gating events directly with choline (that is, the forward isomerization rate constant was >∼10,000 s⁻¹). For these constructs we measured either the gating equilibrium constant using diliganded hybrid AChRs (in which only one α-subunit had the mutation) or unliganded AChRs (E₀). For hybrids, if the contribution of the two mutations is equal and independent, then the fold change of the hybrid is the square root of the fold change of the double mutant. We tested this for the αA96M mutation and found equal and independent contributions from each of the hybrid mutant receptors.

The second approach was to measure E₀. According to the thermodynamic cycle in Fig. 1, mutations that do not affect the R/R^∗ affinity ratio alter E₂ by a parallel change in E₀; that is, the fold change in E₀ is exactly the same as that in E₂. It was necessary to measure E₀ instead of E₂ because the αA96H mutation, for example, increases E₀ by >100,000-fold. From this value we predict that the forward isomerization rate constant for this construct would be ∼5 × 10⁹ s⁻¹ with ACh and ∼1 × 10⁷ s⁻¹ with choline, both of which would result in shut interval durations that are far too brief to be detected by our experimental apparatus.

To gain a more accurate measure of E₀, we increased this value for the construct by adding the energetically independent mutation ɛL269T (in the pore-lining M2 helix), which by itself increases E₂ by 45-fold (Table 1). This is in agreement with the literature value of 41-fold (30). To test the effect of this background mutation on E₀, we measured E₀ for the αA96D mutant with and without the ɛL269T background mutant. The E₀ value for the αA96D mutant alone was 0.01. The measured E₀ value for the αA96D + ɛL269T double-mutant construct was 0.56, which is only 1.2-fold higher than predicted from the E₂ measurement. This result supports the hypothesis that the fold change in E₂ caused by the background mutation was caused by a parallel change in E₀ (ɛL269T does not alter the affinity ratio).

Table 1.

Gating rate and equilibrium constants for AChRs with mutations at positions αN95, αA96, and αI49

Construct	Agonist	f	SE	b	SE	E	Fold-change	n
wt	ACh	48,000	-	1700	-	28.2	1	-
wt	Cho	120	-	2583	-	0.046	1	-
A96C	Cho	5360	370	979	130	5.47	118	3
A96D+ɛL269T	None	3410	100	6150	870	0.56	19,100	3
A96D	None	101	8	9840	1600	0.01	15,800	3
A96E	Cho	8910	1900	456	130	19.5	420	3
A96F+ɛL269T	None	60	5	4160	1100	0.01	497	4
A96F hybrid	Cho	1370	44	1660	290	0.83	17.8	3
A96G	ACh	15,800	970	1110	160	14.2	0.504	3
A96H+ɛL269T	None	5800	570	1710	230	3.38	117,000	4
A96I+ɛL269T	None	1290	180	10,800	1400	0.12	4100	4
A96K	Cho	1650	10	3020	370	0.55	11.8	3
A96L	Cho	6380	770	2770	180	2.31	49.6	3
A96M	Cho	1790	80	5230	480	0.34	7.36	5
A96N+ɛL269T	None	738	100	6250	1200	0.13	4071	3
A96P	Cho	255	1	2920	41	0.09	1.88	3
A96Q hybrid	Cho	2540	420	1490	200	1.71	36.8	3
A96R hybrid	Cho	1790	310	1720	200	1.04	22.3	3
A96S	ACh	8020	1100	3970	750	2.02	0.07	3
A96T	ACh	9630	340	1760	240	5.47	0.19	3
A96V	Cho	5750	1200	629	140	9.15	197	3
A96W+ɛL269T	None	1620	75	4740	310	0.34	11,800	3
A96Y+ɛL269T	None	2800	500	5140	410	0.55	18,800	3
I49A	Cho	293	22	17,700	710	0.02	0.36	3
I49C	Cho	775	58	2920	280	0.27	5.71	3
I49D	Cho	2690	310	3520	860	0.76	16.4	3
I49F	Cho	5180	970	2130	340	2.43	52.3	3
I49H	Cho	1990	240	3130	290	0.64	13.7	4
I49K	Cho	1590	44	4860	50	0.33	7.03	3
I49R	Cho	1240	64	2700	150	0.46	9.86	3
I49Y	Cho	1290	230	3040	340	0.42	9.12	3
N95Q	Cho	220	37	3090	130	0.07	1.54	3
N95W	ACh	287	31	4510	250	0.06	0.0023	3
ɛL269T	Cho	666	170	327	60	2.04	45.0	4

f, forward R→R^∗ isomerization rate constant (s⁻¹); b, backward R←R^∗ isomerization rate constant (s⁻¹); SE, standard error of the mean for n patches; E, isomerization equilibrium constant (=f/b); fold-change, E^mut/E^wt. Agonists: ACh, 0.5 mM acetylcholine; cho, 20 mM choline; none, spontaneous activity only.

We derived two parameters from the rate constants measured for a family of mutations at a particular position. The free-energy change between R and R^∗ caused by the mutations was calculated as (kcal/mol): −0.59ln(E^mutant/E^wt). The first parameter of interest is the range-energy, which is the free-energy difference between the side chains that yield the smallest and largest gating equilibrium constants for that residue. The second parameter of interest is Φ, which is the slope of the rate-equilibrium (R/E) relationship (a log-log plot of forward isomerization rate constant versus the equilibrium constant).

Mutant cycle analysis

The double-mutant cycle analysis approach was used to determine the interaction energies for seven different pairs of residues using 16 different side-chain combinations. A mutant cycle analysis determines the extent to which the energy of a double mutation is not the sum of the energies of the single mutations (31). The coupling free energy is defined as ΔΔG (kcal/mol) = −0.59ln(E^observed/E^predicted), or ΔΔG (kcal/mol) = −0.59ln[(E^{double mutant})(E^wt)/(E^{mutant 1})/(E^{mutant 2})].

R/E plots and mutant cycles are perturbation analyses. Neither method addresses what happens in the unperturbed (wt) condition. The range-energy of an R/E plot gives a lower limit for the energetic sensitivity of a position to mutation, and the coupling-range-energy (from a series of mutant cycles) gives a lower limit for the interaction energy between a residue pair. That is, adding more mutations may increase but cannot decrease these parameters.

Results

αA96

We mutated αA96 to all 19 natural amino acids. Table 1 and Fig. 3 show the isomerization rate and equilibrium constants estimated (by single-channel analysis) for AChRs having side-chain substitutions in both α-subunits. Only three of the mutations (G, T, and S) decreased the diliganded R↔R^∗ equilibrium constant (E₂) compared to wt AChRs activated by ACh. The largest reduction in E₂ was observed for the mutant αA96S (14-fold). Eight mutations (P, M, K, R, L, E, C, and V) increased E₂ by a small to moderate amount, and for these we used the partial-agonist choline to activate the AChRs.

Figure 3.

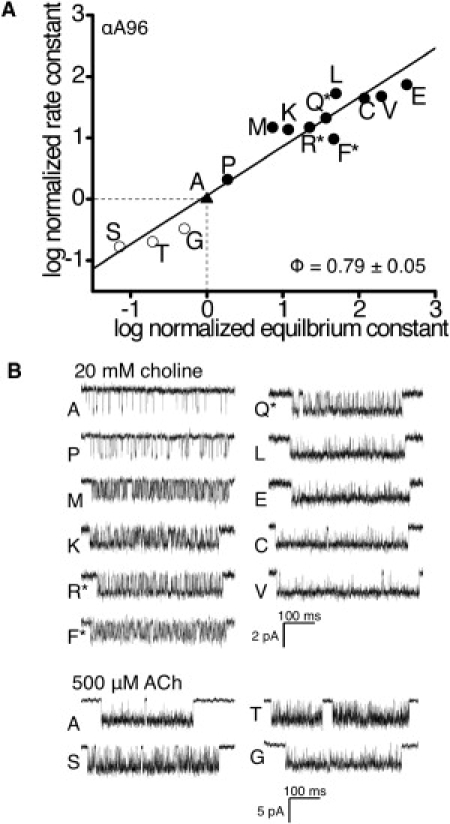
R/E constant analysis of αA96, αN95, αI49. (A) R/E plot for dilganded gating of AChRs with mutations at position αA96. The forward (channel-opening) isomerization rate and the gating equilibrium constants for each mutation were normalized by the wt value (triangle; Table 1). Solid circles: choline-activated; open circles: ACh-activated; ^∗, hybrid AChRs with only one mutant α-subunit. The slope of the line (Φ) is 0.79 ± 05 (SE). (B) Example currents clusters for each αA96 mutant construct (R^∗ is down).

The remaining eight αA96 mutations increased E₂ beyond the range that we could measure using choline, so we applied two alternative approaches. AChRs have two α-subunits. First, we measured E₂ (with choline) in hybrid AChRs that had only one of the two αA96 residues mutated (25). Our expectation was that the energetic consequence of one mutation would be less than that of two, and therefore we would be able to measure E₂ in the hybrids. As a control, we quantified a hybrid E₂-value for αA96M, a mutation whose effects had already been measured for doubly mutated AChRs. We observed only one hybrid αA96M mutant population of clusters, which had an E₂-value that was approximately halfway (on a log scale) between the double mutant and wt constructs (Fig. 4, A–C). This result indicates that each of the two αA96M mutations makes an approximately equal energetic contribution to gating. We next examined three additional, larger gain-of-function hybrid αA96 constructs (F, Q, and R) and again observed only a single hybrid population of currents. The rate and equilibrium constants for these hybrids were added to the R/E plot for αA96 (Fig. 3 A). For all agonist-activated αA96 mutants combined, the slope of the R/E relationship (Φ) was 0.79 ± 0.05.

Figure 4.

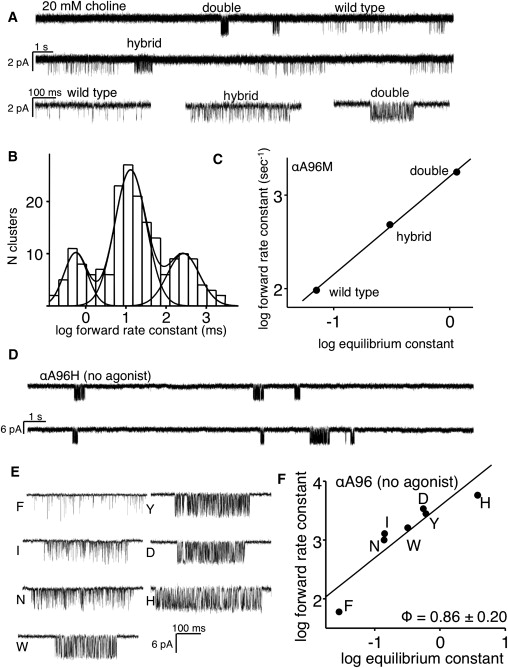
Analysis of large gain-of-function αA96 mutants. (A) Continuous current trace from a cell transfected with αA96M plus wt α-, β-, δ-, and ɛ-subunit cDNAs. Three types of cluster are apparent, generated by wt (αA96+ αA96), double-mutant (αA96M+αA96M), and hybrid (αA96+αA96M) AChRs. (B) Histogram of inverse mean closed interval duration for all clusters in the patch shown in panel A. The three populations are (left to right) double mutant, hybrid, and wt. (C) R/E plot for clusters from the three populations shown in panel A. The gating equilibrium constant of the hybrid population is (on a log scale) about halfway between the wt and double-mutant populations, indicating that the αA96M mutation had approximately equal energetic effects in each subunit. (D) Spontaneous currents from the double αA96H mutant (no agonist in the bath or pipette). Each cluster reflects the gating activity of an individual AChR. The background construct had the mutation ɛL269T (in the M2 helix of the ɛ-subunit). (E) Example spontaneous clusters at higher resolution. (F) R/E plot for unliganded gating of αA96 mutants. The slope of the line (Φ) = 0.86 ± 0.20.

In the second approach used to quantify the large gain-of-function αA96 mutants, we measured their energetic consequences in spontaneously active AChRs (Fig. 4, D–F). If the αA96 mutations do not affect the R versus R^∗ affinity ratio (see below), then the magnitude of the fold change in E₂ should be the same as the magnitude of their effect on the unliganded equilibrium constant (E₀) (Fig. 1) (7). We measured E₀ directly for six different αA96 mutants (N, I, W, D, Y, and H). As a control, we first measured both E₂ and E₀ for the mutant αA96F. Using the value E₀ = 6.5 × 10⁻⁷ for the wt (6), the energy change calculated from the fold-increase in E₀ for this mutant (3.7 kcal/mol) is similar to that calculated from the fold change in E₂, assuming that the two hybrids are equivalent (3.4 kcal/mol). This observation indicates that the increase in E₂ was caused mainly by a parallel increase in E₀, and the R^∗/R affinity ratio for ACh was not altered significantly by this mutation. For all of the tested mutants, the largest fold-increase in E₀ was observed for αA96H (∼117,000-fold; ∼6.9 kcal/mol).

Overall, the range in fold-change of the R↔R^∗ equilibrium constant for the different αA96 side chains (S-to-H) was 1.6 × 10⁶, which corresponds to a range-energy of ∼8.4 kcal/mol (for two α-subunits). To our knowledge, this is the largest energy change observed so far for any α-subunit residue. We plotted the energetic consequence of each αA96 mutation as a function of the size or hydrophobicity of the substituted side chain (see Fig. S1 in the Supporting Material). There was a small tendency for the gating equilibrium to increase with increasing side-chain volume.

We next tested whether the mutation αA96G alters the kinetics or equilibrium constant for ACh binding to R (Fig. S2). We found that the single-site association rate constant (k₊), dissociation (k₋) rate constant, and equilibrium dissociation constant (K_d) were unchanged by the mutation. This result and the above observation that the agonist affinity ratio was not altered by the Phe mutation suggest that none of the αA96 mutants changed the equilibrium dissociation constants for ACh binding to either the R (K_d) or R^∗ (J_d) conformation.

αI49 and αN95

We also measured the energetic consequences (range-energy and Φ) of mutations of two residues near αA96, αN95 (adjacent in sequence), and αI49 (near in structure) (Fig. 5). Two other nearby residues have already been investigated thoroughly (all 19 amino acid substitutions): αY127 (range-energy = 7.4 kcal/mol, Φ = 0.77) (21) and αD97 (range-energy = 3.5 kcal/mol, Φ = 0.93) (15) (see Fig. 2 A, left).

Figure 5.

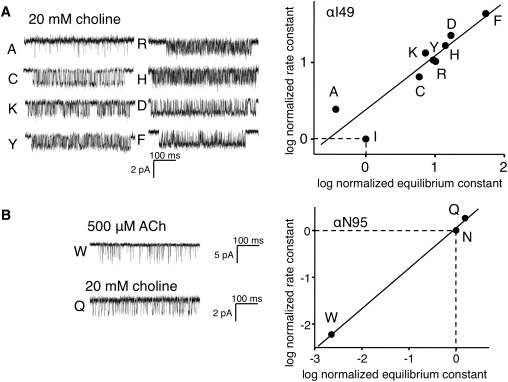
Single-channel currents and R/E plots for position αI49 and αN96. (A) αI49 mutant AChRs. Left: Example single-channel clusters for eight mutants, all activated by choline. Right: R/E plot. All substitutions except Ala increased the diliganded gating equilibrium constant. The slope of the line (Φ) = 0.71 ± 0.13. (B) αN95 mutant AChRs. Left: Example single-channel clusters for the W mutant (activated by ACh) and the Q mutant (activated by choline). Right: R/E plot. The slope of the line (Φ) = 0.86 ± 0.03.

αI49 was mutated to eight different side chains. The range-energy here was 2.9 kcal/mol, which is similar to the value for αD97 but much smaller than that for αA96. The Φ-value for αI49 (0.71 ± 0.13) was not significantly different from that for αA96. αN95 was mutated to W and Q. The Q mutation produced AChRs with nearly wt gating kinetics, but the W mutation greatly reduced E₂. The slope of the R/E plot for αN95 was 0.86 ± 0.03. The range-energy for this position is 1.7 kcal/mol.

In summary, for the group of five neighboring α-subunit residues (95-96-97 (loop A), 127 (β strand 6), and 49 (loop 2)), the Φ-values were similar for 95 and 97 (∼0.9), and for 49, 96, and 127 (∼0.75). Both 96 and 127 experienced very large energy changes in gating.

Mutant cycle analyses

We used mutant cycle analyses to probe the extent to which energy changes consequent to mutation of αA96, αY127, and αI49 are coupled. The results are shown in Table 2 and Fig. S3. For three different 96/127 side-chain pairs, the interaction energies ranged from −3.4 kcal/mol (Cys/Cys) to +2.4 kcal/mol (Tyr/Ala). Thus, the 96/127 side-chain pairs were strongly coupled, by up to 5.8 kcal/mol. Similar experiments for four different 96/49 mutant pairs showed that for these positions the coupling energy ranged from +0.5 kcal/mol (Tyr/Leu) to +6.1 kcal/mol (Cys/Cys). These results indicate that position α96 can interact strongly with both α127 and α49. Of interest, four different 127/49 side-chain pairs (K/D, I/Y, D/K, and C/C) did not show a significant interaction energy.

Table 2.

Coupling energies determined from mutant-cycle analyses

							Fold-change
Construct	Agonist	f	SE	b	SE	E	Observed	Predicted	ΔΔG	n
A96Y+Y127A	Cho	2690	400	3530	850	0.76	16.5	169	1.4	3
A96K+Y127E	Cho	4680	190	5510	480	0.85	18.5	0.118	−3.0	3
A96C+Y127C	Cho	7760	460	793	98	9.79	213	0.589	−3.5	3
I49A+A96L	Cho	1980	290	6360	430	0.31	6.77	18	0.6	5
I49Y+A96L	Cho	8110	1000	925	140	8.77	191	468	0.5	5
I49K+A96D	Cho	3640	15	1230	19	2.97	64.6	65,600	4.1	3
I49C+A96C	ACh	2690	320	3340	410	0.80	0.029	673	5.9	3
I49D+Y127K	ACh	3620	99	8590	1100	0.42	0.015	0.013	−0.1	3
I49Y+Y127I	ACh	3700	270	9460	180	0.39	0.014	0.009	−0.2	4
I49K+Y127D	ACh	321	34	7830	60	0.041	0.001	0.001	−0.0	3
I49C+Y127C	ACh	5570	250	9930	1000	0.56	0.020	0.029	0.2	3
Y93H+A96H	None	203	44	8420	1900	0.024	36,500	48,200	0.1	3
Y93R+A96H	None	124	15	12,200	140	0.010	15,400	8950	−0.32	3
A96N+W149S	None	411	5	9380	800	0.044	66,400	73,300	0.06	3
N95W+Y127F	ACh	12200	1400	2510	22	4.88	0.173	0.132	−0.16	3
I49Y+N95W	ACh	1810	380	4990	590	0.36	0.013	0.021	0.30	5

Column definitions are given in Table 1. Fold-change (observed) is E^mutant-pair/E^wt and fold-change (predicted) is the product of the fold-changes in E measured for each mutant of the pair alone. Rate constants for αY127, αY93, and αW149 mutants can be found in Purohit and Auerbach (21,41). The coupling energy, ΔΔG (kcal/mol), is calculated as described in Materials and Methods. The range-coupling-energy is the difference between the largest and smallest ΔΔG values (kcal/mol): 96-127 (Y/A-C/C) = 4.9; 96-49 (C/C-Y/L) = 5.4; 49-127 (C/C-D/K) = 0.3.

Three observations noted above suggest that the αA96 side chain does not interact energetically with transmitter molecules at the binding site: 1), the rate and the equilibrium constants measured with choline and ACh share the same R/E relationship; 2), the fold increases in E₂ and E₀ are similar for the αA96 mutants (i.e., there is no change in the affinity ratio for the agonist); and 3), the mutation αA96G does not alter the R affinity for ACh. To explore this issue further, we used mutant cycle analyses to test for energetic coupling between αA96 and two binding-site residues: αW149 and αY93 (Table 2 and Fig. S3). The 96/149 interaction energy was only +0.1 kcal/mol (Asn/Ser) and the 96/93 interaction energy was either +0.2 kcal/mol (His/His) or −0.3 kcal/mol (Arg/Arg). These results suggest that αA96 does not interact energetically with these binding-site residues.

Discussion

The main experimental findings in this work were that the αA96 side chain 1), experiences extremely large energy changes in the R↔R^∗ isomerization; 2), is strongly coupled energetically with residues αY127 and αI49 but not directly with the transmitter-binding site; and 3), has a Φ-value that is lower than its loop A neighbors but similar to those for residues in the lower part of the extracellular domain of the α-subunit.

Maps of the energy changes and Φ-values for some important residues in the α-subunit extracellular domain are shown in Fig. 6. αA96 and αY127 comprise a hot spot (two residues with the largest R versus R^∗ energy change and are energetically linked) in a chain of residues between the transmitter-binding site and the M2 transmembrane helix that all can experience a large (≥4 kcal/mol) R versus R^∗ energy change in the gating isomerization. A change in energy reflects a change in structure, and the amino acids that show the largest energy changes form approximately a column in each α-subunit alongside the complementary ɛ/δ-subunit. This result indicates that there is an energetically significant structural change in these regions of the protein between R and R^∗.

Figure 6.

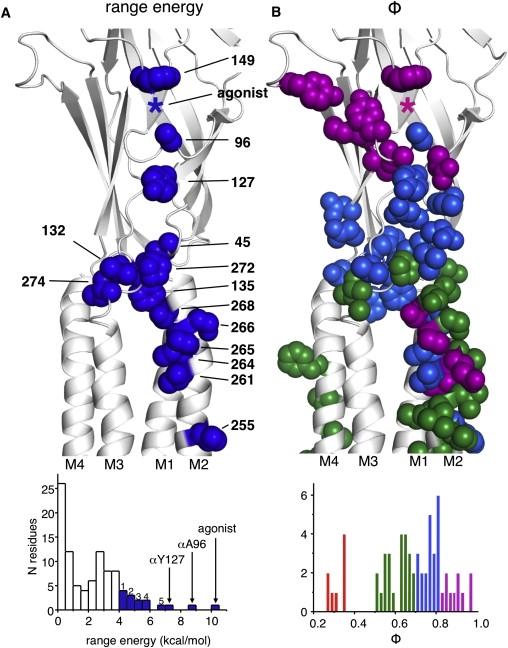
Maps and histograms of range-energy and Φ in the α-subunit extracellular domain. (A) The range-energy is the natural logarithm of the largest/smallest gating equilibrium constant ratio for a family of mutations at each position. Blue spheres: ≥4.0 kcal/mol; ^∗ the approximate position of the agonist. The largest range-energy residues approximately form a column that links the transmitter-binding site (αW149) and the gate region of the pore-lining M2 helix (αV255). Bottom: Histogram of range-energy for all of the residues studied so far in the α-subunit. Residues in the marked bins: 1), W149, V261, S266, and I274; 2), V132, I264, and F135; 3), S268 and P265; 4), V255 and P272; and 5), E45. (B) Φ is the slope of the R/E relationship. Residues in the α-subunit with a range-energy >1.5 kcal/mol are shown as spheres. Color is according to the Φ-value in the histogram (for clarity, residues with Φ < 0.5 are not shown). αA96 and αP272 are surrounded by higher-Φ elements. αA96, αY127, and αE45 have similar Φ-values.

We estimate that the range-energy for position αA96 is 8.4 kcal/mol (S-to-H substitution in both α-subunits). The results indicate that the energy change at this position is entirely attributable to a change in the spontaneous gating equilibrium constant E₀. The αA96 range-energy is larger than the previous point-mutation record (7.4 kcal/mol, a 290,000-fold change in equilibrium constant) for a D-to-F substitution at αY127 (21). These two residues are by far the most energetically sensitive ones that have been identified in the α-subunit in AChR gating. For comparison, the range-energy for two agonist molecules (compared to none) is 10.4 kcal/mol for ACh, 9.4 kcal/mol for carbamylcholine, and 6.6 kcal/mol for choline (6,7,25). That is, an S-to-H substitution at αA96 has nearly the same effect on the channel open probability as does the addition of 1 mM carbamylcholine to a wt AChR.

In addition to having a large range-energy, position αA96 also has the largest side-chain coupling energies between residues in AChR gating reported to date. With the residue pairs tested, position αA96 is coupled energetically with both αY127 and αI49, by ∼5.8 kcal/mol each. This means that the gating equilibrium constant can be nearly 20,000-fold different from what it would be if the energetic consequences of the mutations were independent. This degree of interaction indicates that the gating molecular movements (energy changes) of these three positions are strongly coupled.

We observed that even though 96/127 and 96/49 are coupled, 127/49 are not (four pairs tested). The degree of coupling energy between amino acids depends on the nature of the side-chain substitutions. Because we estimate the coupling energy only by making mutations of both residues, one possible explanation for the lack of coupling between 127/49 is that there is none when position 96 is Ala. Another possibility is that the 96 side chain remains essentially unperturbed by mutations at 127 and 49, in which case the energy would not transfer between these two.

The slope of the R/E plot for a family of mutations (Φ) gives the extent to which the R↔R^∗ reaction has progressed when the perturbed site experiences its energy change. The map of Φ-values (Fig. 6 B) thus provides insight into the intermediate events as a sequence of events (1-to-0, start-to-finish). The Φ-value for αA96 is 0.79 ± 0.05, which indicates that the energy change here occurs fairly early in the channel-opening process. Other nearby loop A amino acids, including αY93, αN95, and αD97 (Φ = 0.86, 0.86, and 0.93, respectively), appear to move even earlier. Additional members of this highest-Φ group include positions in the general vicinity: the agonist itself (0.91), αW149 (0.82 without agonists and 0.86 with ACh), αY190 (0.88 without agonists), αG153 (0.80 without agonists and 0.96 with choline), and αK145 (0.96 with ACh). The mean Φ-value for these eight positions (excluding αA96) is 0.90. We hypothesize that these highest-Φ positions experience their gating energy changes at the onset of the forward isomerization and before the energy change at positions αA96 and αY127.

The Φ-value for αA96 appears to be similar to that for amino acids in the lower part of the extracellular domain. This group includes residues that are close to αA96 in structure and are coupled energetically: αI49 and αY127 (0.71 and 0.77, respectively). Other extracellular domain residues in this group include four loop 2 residues α45–48 (Φ = 0.80 (17,19)), the pre-M1 residue αR209 (0.72 (19)), and five residues in the cys loop (0.77 (32)). The mean Φ-value for these 12 residues is 0.77. The pattern of Φ-values in the α-subunit extracellular domain suggests that αA96 is at a boundary between Φ∼0.90 and Φ∼0.77 blocks of residues. We hypothesize that αA96 gating motions are important for transferring energy across this block boundary. By the same token, the gating motion of αP272 (Φ = 0.62) may be important for transferring energy across the Φ = 0.77 and Φ = 0.64 block boundary.

The electron density map for the toxin-bound α-subunit fragment shows that the αY127 side chain can adopt multiple conformations (23) (Fig. 2 B). In one of these, the tyrosine hydroxyl moiety is in close contact with αA96. Further, the Cα₂ atom of αI49 is also close to αA96. It is possible that in the AChR R↔R^∗ isomerization, residue αY127 flips between these alternative conformations, and this change in position is the basis for the energy transfer with αA96.

It has been proposed that the R↔R^∗ gating in AChRs involves opposing twisting motions of the extracellular and transmembrane domains (33,34) and the closure of loop C over each transmitter-binding site (35,36). Molecular-dynamics simulations of the prokaryote cys-loop receptor GLIC suggest that such a global, quaternary conformational change may involve sequential, tertiary structural rearrangements that propagate between subunits (a so-called domino mechanism (37)). Our experimental observation that residues at the α/δ/ɛ-subunit interfaces experience large energy differences in the gating reaction is consistent with calculations showing that these regions of the protein show substantial structural perturbations within the quaternary twist normal mode (38). The strong energy coupling between positions α96 and α127/α49, the unusual Φ-value for αA96 compared to its neighbors, and the alternative electron densities for position αY127 lead us to further speculate that the above-mentioned perturbation of each subunit interface constitutes a pathway for energy transfer through the extracellular domain in AChR gating, as the diffusion of a structural defect (39,40).

In addition to αA96 and αY127, other significant members of this energy-transfer chain include (range-energy in kcal/mol) the binding-site residue αW149 (4.0 (41)), the agonist (10.4 (6)), loop 2 residue αE45 (6.5 (19)), M2-M3 linker residue αP272 (5.5 (32)), M2 cap amino acids αP268 and αS265 (5.0 and 5.5 (42)), and αM2-13′ residue V255 (5.5 (43)). These nine positions exhibit the largest range-energy values in the extracellular domain of the protein (Fig. 6 A, bottom). They also form a column that spans the regions between the transmitter-binding site and the gate region of the pore. We speculate that after a transmitter molecule occupies its binding site, near-synchronous movements of residues in the immediate vicinity serve to increase the affinity of the protein for the agonist. These movements also perturb loop A, causing a repositioning of αA96, which transfers energy to αY127 and αI49 in loop 2. The detailed mechanisms by which this perturbation spreads through the α-subunit extracellular-transmembrane domain interface and to the M2 gate (in all subunits), and the relationship of these structural rearrangements to larger-scale motions of the protein, remain to be illuminated.