The Human Estrogen Sulfotransferase - a Half-Site Reactive Enzyme

Abstract

The affinity of 17β-estradiol (E₂) for the estrogen receptor is weakened beyond the point of physiological relevance by transfer of the sulfuryl-moiety (-SO₃) from PAPS (3’-phosphoadenosine 5’-phosphosulfate) to the 3’-hydroxyl of E₂. The mechanism of this transfer reaction, catalyzed by estrogen sulfotransferase (EST), is investigated here in detail. The enzyme (a dimer of identical protomers) presents a clear example of half-sites reactivity – only one of the subunits of the dimer produces product during the catalytic cycle. This is the first example of half-sites reactivity in the sulfotransferase family. A burst of product, with an amplitude that corresponds to one-half of the available active sites, reveals that the mechanism is rate-limited by product release. The equilibrium constant governing interconversion of the substrate (E·PAPS·E₂) and product (E·PAP·E₂S) central complexes was determined and is strongly biased toward product (K_{eq int} ~49). Slow product release allows the interconversion of the central complexes to approach equilibrium, with the result that K_{eq int} becomes nearly linearly coupled to K_m, and contributes a factor of ~ 30 to the steady-state affinity of the enzyme for substrate. Typical of its family, estrogen sulfotransferase is partially k_cat-inhibited by its acceptor substrate, E₂. This inhibition does not influence the burst kinetics, and thus occurs after formation of the product central complex – a finding consistent with slow escape of PAP from the non-reactive E·PAP·E₂ complex.

Estrogen sulfotransferase (EC 2.8.2.4) catalyzes transfer of the sulfuryl moiety (-SO₃) from PAPS (3’-phosphoadenosine 5’-phosphosulfate) to the 3’-hydroxyl of 17β-estradiol (E₂), Reaction 1. The remarkably large chemical potential of the phosphoric-sulfuric acid anhydride

$${\mathrm{E}}_2+{\text{PAPS}}^{4-}\rightleftarrows {\mathrm{E}}_2{\mathrm{S}}^{-}+{\text{PAP}}^{4-}+{\mathrm{H}}^{+}$$ (1)

bond found in PAPS $\mathrm{\Delta }{G}_{\mathit{\text{hydrolysis}}}^{o\prime }=-19\text{kcal}/\text{mol}$ (1, 2) facilitates the thermodynamically favorable transfer of the sulfuryl moiety to estradiol (K_eq = 4200 (3)). Initial-rate and ligand-binding studies indicate the catalysis occurs via a random Bi-Bi mechanism (3). Chemical crosslinking and mutagenesis studies have shown that EST, like most cytosolic sulfotransferaes, is a dimer whose monomers are linked by a small interface found in each of the 17 sulfotransferase crystal forms available in the PDB (4–6).

Sulfation of E₂ prevents it from binding to the estrogen receptor (7), and hydrolytic cleavage of the sulfuryl-group from E₂S (catalyzed by sulfatases (8, 9) regenerates the receptor-active form of the hormone. The balance of these activities is expected to determine the receptor-binding potential of the estrogen pool in living cells. Similar sulfation/desulfation cycles regulate numerous other metabolites and processes including steroid hormones (10, 11), signaling peptides (12–15), heparin (16, 17), hemostasis (18–20), lymph circulation (21) and numerous drugs and xenobiotics (22, 23).

The human estrogen sulfotransferase (EST), the focus of the current work, is one of approximately ten human cytosolic sulfotransferases (24, 25), many of which exhibit distinct spatio-temporal distributions in the organism (26). The typically broad substrate specificities of these isoforms are likewise distinct (yet often overlapping) and together they comprise a robust sulfation network whose proper functioning is critical to the well-being of the individual. The cellular levels of EST have been causally linked to the estrogen growth response of cell lines derived from estrogen-dependent breast and endometrial tumors. While present in normal control cells, EST is not detected in most estrogen growth-dependent cancer cell lines (27), and expression of EST at wild-type levels in these otherwise EST-depleted cells abrogates the responses normally associated with E₂ activation, including the E₂ growth response (28, 29).

In the present work, the rates and equilibria of several of the reactions that occur on the surface of EST during its catalytic cycle have been defined. In the process, it was discovered that the enzyme (a dimer of identical subunits) is half-site reactive - that is, only one of subunits produces product during a given catalytic cycle. Furthermore, the mechanism is such that the ratio of the central complexes in the steady-state is linearly coupled to K_m and enhances the affinity of EST for its substrates ~ 30-fold, suggesting that selective stabilization of the central complexes may contribute significantly to substrate selection within the family. Finally, we demonstrate that the partial substrate inhibition that is characteristic of sulfotransferases, becomes operative in the mechanism subsequent to formation of enzyme-bound product – suggesting that inhibition operates by slowing release of product.

Materials and Methods

Materials

The enzymes, reagents and salts, unless specified otherwise, were of the highest grades available from the Sigma-Aldrich Co. Estradiol was purchased from Steraloids Inc. Radiolabelled estradiol ([2,4,6,7-³H]-estradiol (90 Ci/mmol)) was purchased from NEN Life Science Products. [³⁵S]-SO₄ was obtained from ICN Pharmaceuticals. PAPS was purchased from Professor S. Singer (University of Dayton, OH). Factor Xa protease was purchased from Enzyme Research Labs. The Bradford assay mix was obtained from Bio-Rad. Amylose resin was purchased from New England Biolabs Inc. Q Sepharose Fast Flow and Superdex 200 resins were purchased from Amersham Pharmacia Biotech. Poly-(ethylenimine)-cellulose-F thin-layer chromatography sheets (PEI-F TLC) were purchased from EM Science. 10 kDa cutoff Centricon concentrators were obtained from Millipore.

Purification and quantitation of estrogen sulfotransferase

The purification protocol was described previously (3). The > 95% pure enzyme (A₂₈₀ = 1.7) was aliquoted, rapidly frozen in a dry ice/ EtOH bath, and stored at −70 °C in buffer containing 50 mM KPO₄ (pH 6.3) and glycerol (10% v/v). The EST concentration was determined optically at λ_{280 nm} using the following gravimetrically determined extinction coefficient (3): ε₂₈₀* = 1.7 ± 0.1 A₂₈₀ × (mg/ml)⁻¹ cm⁻¹. The gravimetrically determined extinction coefficient was corroborated by determining the extinction coefficient in 6.0 M guanidinium chloride (30): ε₂₈₀* = 1.6 ± 0.08 A₂₈₀ × (mg/ml)⁻¹ cm⁻¹. The gravimetrically determined value was used throughout the manuscript.

[³⁵S]PAPS synthesis

[³⁵S]PAPS was synthesized in a 0.50 ml reaction mixture that contained the following: sulfate activating complex (Rhodobacter sphaeroides), 0.050 U/ml [note: this complex exhibits both ATP sulfurylase and APS kinase activity (31) and U is quoted for conversion of ATP and SO₄ to PAPS]; inorganic pyrophosphatase (baker’s yeast), 0.10 U/ml; pyruvate kinase (rabbit muscle), 0.17 U/ml; [³⁵S]-SO₄ (1.0 mCi, 1491 Ci/mmol); ATP (6.0 mM); PEP (2.0 mM); MgCl₂ (8.0 mM); KCl (100 mM) and Hepes (50 mM, pH 8.0). The reaction was run for 5 hours at 25 (± 2) °C, quenched with EDTA (10 mM final concentration) and protein was removed by filtration (Centricon, 10 kDa). [³⁵S]-PAPS was purified chromatographically by anion exchange HPLC (AX300, SynChropak) using an isocratic eluant (NaPO₄, 0.30 M, pH 6.4). The purified [³⁵S]-PAPS was desalted and concentrated to dryness as described previously (32). The compounds was dissolved in Hepes (50 mM, pH 8.0) and stored at −70°C.

Quenched-flow studies of the EST-catalyzed reaction

Reactions were initiated and quenched using a KinTek quench flow instrument (model RQF-3). The composition of the reaction and quench solutions are defined in figure legends. Following quenching, the samples were centrifuged to remove denatured enzyme, the pH of the supernatant was adjusted to pH 9.0 by addition of 1.0 M Tris (pH 9.0). E₂ was extracted from the aqueous phase twice, using CCl₄, and E₂S was quantitated by liquid scintillation counting (Wallac 1409DSA). Total counts were corrected slightly (< 10 %) by subtracting residual aqueous [³H]-E₂ E2 counts that were determined in control experiments in which EST was omitted.

Simulating the ligand distribution experiment

[E·E₂S] vs [EST] was simulated for half-site and full-site models using Gepasi (3.21) (33). The simulation model allowed enzyme to bind one E₂ per active site, and used a K_d = 26 nM (3). The singly (E·E₂) and doubly (E·E₂·E₂) occupied dimer concentrations were calculated and these values were used to calculate product formed after 0.30 seconds by assuming either that 50% of all of the bound E₂ is converted to product (i.e., the full-site model with K_{eq (int}) = 1.0); or, that 98% of [E·E₂ + (0.50 × E·E₂·E₂)] is converted to product (i.e., the half-site model with K_{eq int} = 49).

Classical trapping of [³⁵S]PAPS

A pulse solution containing EST (1.0 µM) (active sites) and [³⁵S]PAPS (1.5 µM) was mixed with a chase solution of equal volume containing E₂ (3.6 µM) and unlabelled PAPS (2.7 mM). Five seconds later, the reaction was quenched by addition of an equal volume of NaOH to a final concentration of 0.30 M. The quenched solutions were then heated in a boiling water bath for 1.0 min and spun to remove precipitate. The deproteinized supernatant was neutralized by addition of MES (1.0 M, pH 6.3) to a final concentration of 0.50 M. [³⁵S]E₂S and [³⁵S]PAPS were then separated on PEI-F TLC plates using a LiCl (0.9 M) mobile phase, and quantitated as described previously (34). The pulse and chase solutions were equilibrated at 23 (± 2)°C prior to mixing and contained KPO₄ (50 mM, pH 6.3), glycerol (10% v/v), MgCl₂ (7.0 mM) and DTT (1.0 mM).

Pre-steady state trapping of [³⁵S]PAPS

A solution containing EST (1.0 µM, active sites) was mixed rapidly (using a KinTek quench flow) with a solution of equal volume that was identical except that it lacked EST and contained E₂ and [³⁵S]-PAPS (3.6 and 4.5 µM, respectively). The reaction was allowed to proceed for 0.30 seconds before mixing rapidly with an equal volume of chase solution containing 2.3 mM PAPS and 1.8 µM E₂. The reaction was quenched 30 seconds following the addition of chase by addition of NaOH (0.66 M) to a final concentration of 0.33 M. The separation and quantitation of E₂S were the same as described above. Control experiments quenched immediately after the reaction proceeded for 0.3 second were run to determine the amount of E₂S formed at the moment of the chase addition. Solutions were equilibrated at 25 (± 2)°C prior to mixing and contained KPO₄ (50 mM, pH 6.3), glycerol (10% v/v), MgCl₂ (7.0 mM) and DTT (1.0 mM).

Results and Discussion

A presteady-state burst of product formation

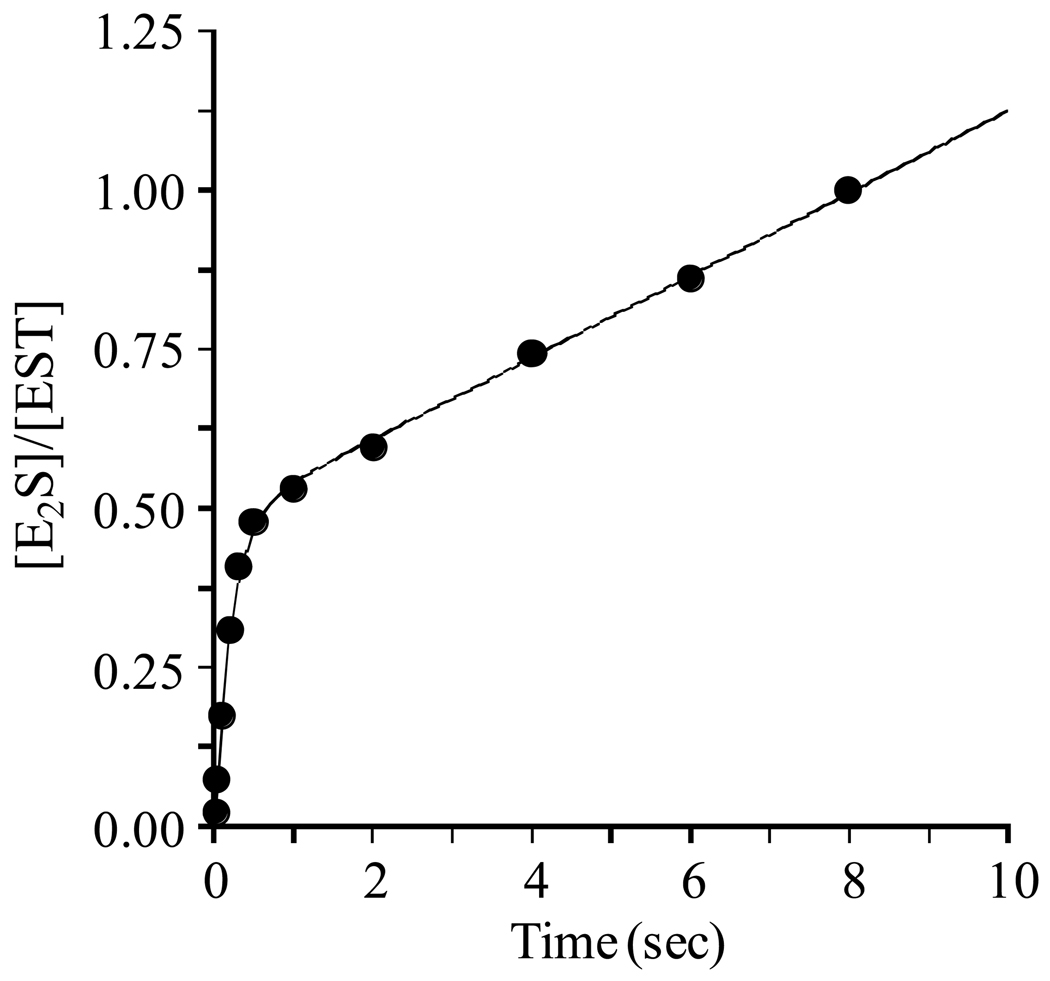
To identify and characterize rate-determining step(s) in the EST mechanism, presteady-state quenched-flow experiments were performed in the forward (E₂S-forming) direction. Enzyme (1.0 µM) saturated with E₂ (3.6 µM, 280 × K_i (34)) was mixed rapidly with an equal volume of a solution containing a saturating concentration of PAPS (18.0 µM, 305 × K_m) and reactions were quenched on a time scale that spanned the presteady- and early steady-state regions of the catalytic cycle (Fig. 1). The burst of product that was observed showed no signs of a lag, and was followed by linear steady-state turnover. Virtually all of the E₂ was converted to E₂S at the endpoint of the reaction (not shown). A burst is indicative of a rate-determining step(s) in the product-release branch of the catalytic cycle. Such a step might occur at the point of delivery of product into solution or be associated with isomerization before or after product release. A striking feature of the burst is that its amplitude corresponds to precisely one-half of an enzyme active site equivalent, suggesting either that EST is a half-sites reactive enzyme or that the ratio of substrate- to product-bound forms of the enzyme during steady-state turnover is approximately one.

Figure 1. A burst of E₂S formation.

E₂S synthesis was initiated by rapidly mixing a solution containing EST (1.0 µM, dimer), [³H]E₂ (3.6 µM, 720 × K_m, SA = 90 Ci/mmol), glycerol (10% v/v), MgCl₂ (7.0 mM), DTT (1.0 mM), and 50 mM KPO₄ (pH 6.3) with a solution of equal volume that was identical except that it lacked EST and E₂, and contained PAPS (18.0 µM, 305 × K_m). Reactions were quenched by rapidly mixing the reacting solutions with an equal volume of HCl (0.66 M). [³H]E₂ was extracted from the quenched mixture using CCl₄ and [³H]E₂S, which remained in the aqueous phase, was counted (see Materials and Methods). All solutions were equilibrated at 25 (± 2) °C prior to mixing. Reactions were performed in triplicate and averaged. The smooth curve represents the best-fit of the averaged data to the equation: A₀ (1–e^−λt) + k_catt.

A general model for an enzymatic burst is given by Equation 2 (35, 36), which sums the exponential and linear phases of the reaction. When Equation 2 is fit to the EST burst data

$$[\text{product}]/[\text{enzyme}]=A_{\mathit{0}}(1-e^{-\lambda t})+k_{\mathit{\text{cat}}}t$$ (2)

using a non-linear least-squares algorithm, the following best-fit parameters are obtained: A_o = 0.52 (± 0.02), λ = 4.2 (± 0.4) s⁻¹, and k_cat = 0.036 (± 0.004) s⁻¹. The progress curve predicted by these parameters is represented by the solid line passing through the data in Figure 1. Equation 2 assumes that both active sites in the dimer are capable of turning over. If, instead, the enzyme is half-sites reactive, the best-fit k_cat increases by a factor of two, to 0.072 (± 0.004) s⁻¹. The value of the amplitude (A_o), 0.52, reiterates the possibility that only half of the EST active sites may be capable of turning over.

Mechanism I is perhaps the simplest mechanism capable of predicting burst of product that is stoichiometric with enzyme. The mechanism assumes that substrate binding is fast relative to E·P formation and aggregates all of the rate constants governing product release into a single net-rate

$$\mathrm{E}·\mathrm{S}\underset{k_{\mathit{2}}}{\overset{k_{\mathit{1}}}{\rightleftarrows }}\mathrm{E}·\mathrm{P}\stackrel{k_{\mathit{3}}}{\to }\mathrm{E}+\mathrm{P}$$ (I)

constant, k₃. Utilizing Mechanism I, product formation is again given by Equation 2, where (35, 36):

$$\begin{array}{c}\hfill \lambda =k_{\mathit{1}}+k_{\mathit{2}}+k_{\mathit{3}}\hfill \\ \hfill {\mathrm{A}}_0={\mathit{k}}_{\mathit{1}}(k_{\mathit{1}}+k_{\mathit{2}})/{(k_{\mathit{1}}+k_{\mathit{2}}+k_{\mathit{3}})}^2\hfill \\ \hfill k_{\mathit{\text{cat}}}=k_{\mathit{1}}{k}_{\mathit{3}}/(k_{\mathit{1}}+k_{\mathit{2}}+k_{\mathit{3}})\hfill \end{array}$$

The best-fit constants (k₁, k₂ and k₃) obtained using this form of Equation 2 depend on whether the values of [E₂S]/[E]_tot are calculated using monomer or dimer concentrations of EST. Normalizing to the monomer tacitly assumes that both subunits of a fully occupied dimer are capable of turning over, and produces best-fit constants that predict an internal equilibrium constant (K_{eq int} = [EP]/[ES] = k₁/k₂) that is near unity: k₁ = 2.2 (± 0.2), k₂ = 1.8 (± 0.2) s⁻¹, and k₃ = 0.071 (± 0.009) s⁻¹; whereas, normalizing to the dimer assumes half-site reactivity and yields a K_{eq int} that strongly favors E·P formation (k₁ = 4.4 (± 0.3), k₂ = ~ 0 s⁻¹, and k₃ = 0.071 (± 0.009) s⁻¹).

Confirming the half-site mechanism

The amplitude of the burst shown in Figure 1 (0.52) represents a stoichiometry ([product-formed]/[saturated-subunits]) obtained under conditions where both of the dimer subunits are saturated. Given this amplitude and condition, we can conclude that for a full-site mechanism (identical subunits) each subunit spends approximately equal time in substrate and product forms during turnover; or, for a half-site mechanism, that the single dimer-subunit that turns over spends the majority of its time in product complexes. These models predict that under conditions where only one of the dimer subunits is bound to substrate, the amplitude for the half-site mechanism will be twice that of the full-site mechanism.

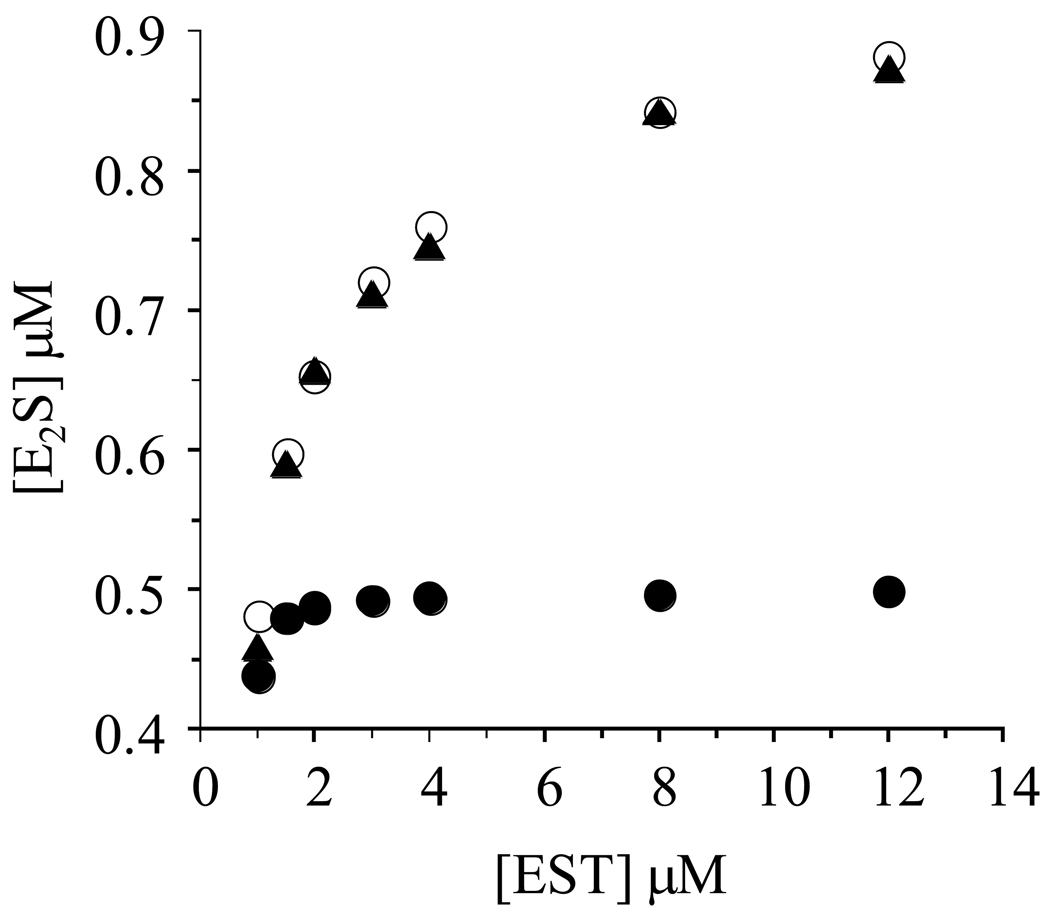
Capitalizing on these differences to identify the operative mechanism, the amplitude was determined at fixed [³H]E₂ and PAPS concentrations (1.0 µM (K_m = 5.0 nM) and 8.0 µM (K_m = 59 nM) respectively) over a range of EST concentrations (1 – 12 µM) chosen such that E₂ remains virtually entirely enzyme-bound throughout the titration (Figure 2). At the lowest EST concentration, both of the dimer subunits are saturated, and either model predicts an amplitude of ~ 0.5. In contrast, at the highest EST concentration (12 µM), the models make very different predictions regarding amplitude: the full-site model continues to predict an amplitude of ~ 0.5, whereas the half-site model predicts an amplitude of 0.88 at 12 µM EST due to the fact that that majority of the dimers will have only one active site occupied (see Simulating the ligand distribution experiment, Materials and Methods). The titration demonstrates that as the EST concentration begins to exceed that of E₂, causing the ligand to redistribute such that the fraction of dimers having only one subunit bound to E₂ increases, the amplitude increases in a well behaved fashion to 0.88, and the data trend suggests a yet larger amplitude at EST concentrations above 12 µM (Figure 2). The simulated amplitudes for the half-site (○) and full-site models (•) strongly favor the half-site mechanism (see Materials and Methods). Thus, EST appears to be a half-site reactive enzyme.

Figure 2. Confirmation of half-sites reactivity.

Reactions were initiated by mixing a solution containing PAPS (16 µM), glycerol (10% v/v), MgCl₂ (7.0 mM), DTT (1.0 mM), and 50 mM KPO₄ (pH 6.3) with an equal volume of an identical solution that did not contain PAPS, but did contain [³H]E₂ (2 µM) and various concentrations of EST (2.0, 3.0, 4.0, 6.0, 8.0, 16.0, 24.0 µM - monomer concentrations). The plotted E₂S concentrations represent the E₂S formed in reactions quenched at 0.30 sec - at this time-point, the burst is essentially complete and steady-state turnover contributes only slightly to overall product formation (see Figure 1). Triangles (▲) represent experimentally determined [E₂S]; open circles (o) represent [E₂S] predicted using a half-site reactivity model in which K_{eq int} ≫ 1.0; closed circles (•) represent [E₂S] predicted using a full-site reactivity model with K_{eq int} ~ 1.0. The simulations are described in Materials and Methods. Quenching and quantitation were as described in the Fig.1 legend (also, see Materials and Methods). Experimental values were determined in triplicate and averaged. All solutions were equilibrated at 25 (± 2) °C prior to mixing.

The internal equilibrium constant (K_{eq int})

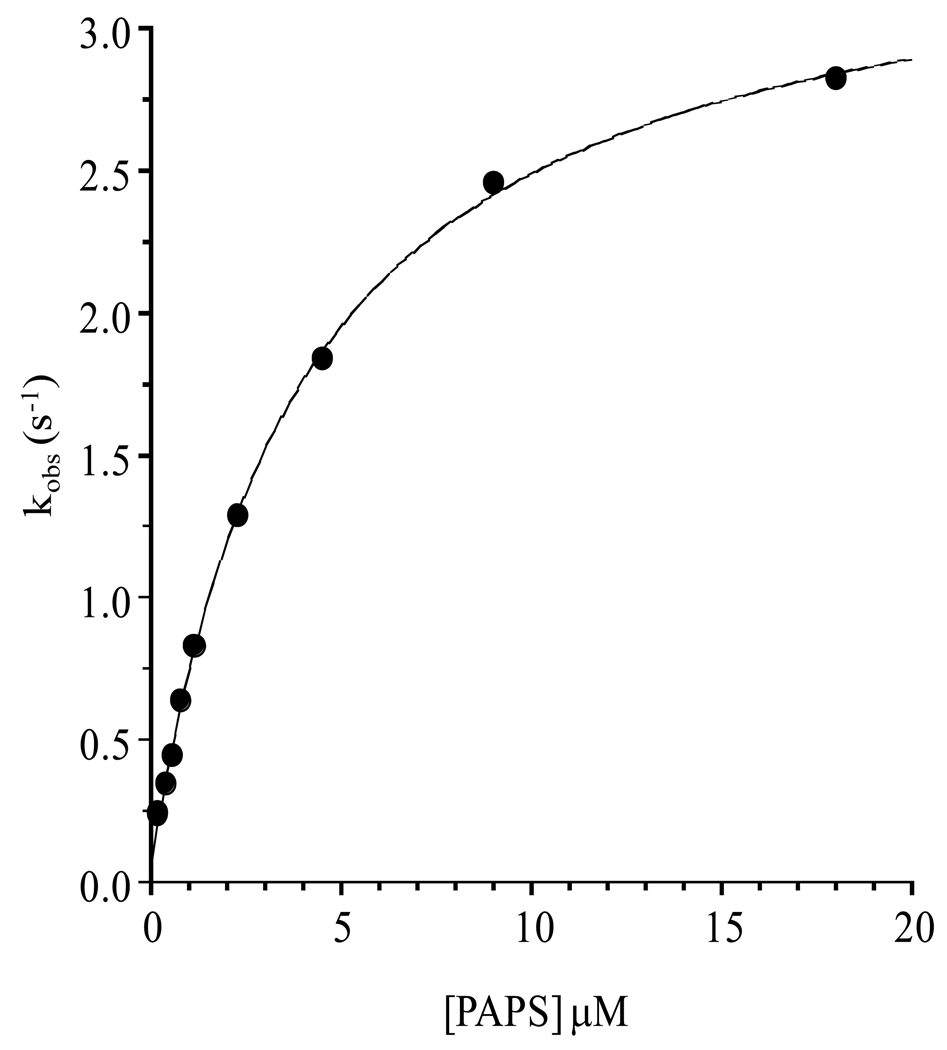
Fitting the burst with a half-site model suggested that the central complex equilibrium constant favors product, and revealed that k₂ (Mechanism I) is too small to determine accurately by that method. It is possible to obtain k₂ from an analysis of the substrate concentration dependence of the rate of E·P formation (35, 36). Toward this end, a plot of k_obs for E·P synthesis as a function of PAPS concentration was constructed (Figure 3). Rates were obtained from linear regression of averaged, duplicate 4-point progress curves taken within the first 15 % of E·P formation – further details are given in the Figure 3 Legend. The data were fit using Mechanism II, in which PAPS (or S) binding to E·E₂ (or E) is at equilibrium. That PAPS binding is near equilibrium is consistent with the absence of a lag preceding the burst, and is supported by the results of the isotope trapping experiment described below.

$$\mathrm{E}+\mathrm{S}\stackrel{K_{\mathit{\text{eq}}}}{\rightleftarrows }\mathrm{E}·\mathrm{S}\underset{k_{\mathit{2}}}{\overset{k_{\mathit{1}}}{\rightleftarrows }}\mathrm{E}·\mathrm{P}$$ (II)

k_obs as a function of [PAPS] for Mechanism II is given by Equation 3 (35, 36):

$$k_{\mathit{\text{obs}}}=\frac{K_{\mathit{\text{eq}}}{k}_1[\mathit{\text{PAPS}}]}{K_{\mathit{\text{eq}}}[\mathit{\text{PAPS}}]+1}+k_2$$ (3)

which, when fit to the data, yields the following best-fit parameters: K_eq = 4.0 (± 0.3) µM, k₁ = 3.4 (± 0.1) s⁻¹, and k₂ = 0.070 (± 0.03) s⁻¹. The progress curve predicted by these parameters is represented by the solid line that passes through the data (Figure 3). Given these constants, one can calculate that the equilibrium constant governing interconversion of the central complexes, Keq _int ~ 49 = 3.4 s⁻¹/0.07 s⁻¹.

Figure 3. k_obs vs [PAPS] for E₂S synthesis.

Reactions were initiated by rapidly mixing a solution containing EST (1.0 µM), [³H]E₂ (3.6 µM, SA = 90 Ci/mmol), glycerol (10% v/v), MgCl₂ (7.0 mM), DTT (1.0 mM), and 50 mM KPO₄ (pH 6.3) with an equal volume of an identical solution that did not contain EST and E₂, but did contain various concentrations of PAPS (0.375, 0.75, 1.125, 1.5, 2.25, 4.5, 9, 18, and 36 µM). Quenching, and quantitation of product are described in the Figure1 Legend (also, see Materials and Methods). All solutions were equilibrated at 25 (± 2) °C prior to mixing. Reaction rates at each PAPS concentration were obtained from least-squares regressions of triplicate, averaged 4-point progress curves taken during the first 15% of product formation. k_obs values were obtained by dividing the reaction rate by the enzyme concentration (0.50 µM). The solid line represents behavior predicted by the best fit of a two-step model that includes PAPS binding and interconversion of the central complexes (see Results and Discussion).

Mechanism II assumes that all product (E·P) is capable of returning to ES, which is tantamount to assuming product is found entirely in ternary complex; alternatively, the concentrations of all complexes that cannot return to substrate (e.g., binary complexes) are treated as if they are negligible. If such non-reactive complexes comprise a substantial fraction of product, the model is in error, the concentration of ternary complex is diminished, and k₂ will increase to achieve the rate of ES formation needed to fit the k_obs vs [PAPS] data. That the majority of E·P is, in fact, in the ternary complex is supported by experiments discusses in the following section (Postioning the rate-determining step).

A classical isotope trapping experiment (37, 38) was performed to assess whether PAPS binding is near equilibrium during turnover. Briefly, EST (1.0 µM) was equilibrated at 25 °C with a saturating concentration of [³⁵S]PAPS (1.5 µM, K_d = 37 nM) and mixed rapidly with a solution of equal volume containing E₂ (3.6 µM, K_m = 5.0 nM) and a 1700-fold excess of unlabelled PAPS (2.7 mM). Experiments, performed in triplicate, revealed that under these conditions only 2.8 (± 0.2) % of the enzyme-bound PAPS (assuming half-sites reactivity) was converted to product. Thus, PAPS departure from the enzyme is fast relative to its conversion to product, and PAPS binding is near equilibrium during turnover.

Postioning the rate-determining step

While the burst reveals a rate-determining step(s) in the product release branch of the catalytic cycle, it does not identify which step(s) causes product to accumulate. If release of the first product from the ternary complex is fast relative to subsequent steps, then either a binary complex or E accumulates - notably, such complexes are incapable of returning to substrate. Alternatively, if release of the first product from the ternary complex is the slow step, the ternary complex accumulates, which, because of its full complement of ligands, can return to substrate. Thus, whether the enzyme-bound product that accumulates during the burst can form substrate is diagnostic for the type of complex and can be used to position the rate-determining step in the mechanism.

The extent to which the product complex can form substrate was assessed using an experiment that quantitates partitioning of this complex in the forward and reverse directions. A solution containing EST (1.0 µM) was mixed rapidly with an equal volume of a solution that was identical except that it lacked EST and contained E₂ (3.6 µM) and [³⁵S]PAPS (4.5 µM). The reaction was allowed to proceed for 0.30 seconds - at which point the burst is nearly complete and the enzyme-bound product forms are reaching their maximum concentration (see Figure 1). At 0.30 sec, the reaction was mixed a second time either with an equal volume of a chase solution containing a large excess (1022-fold) of unlabeled PAPS (2.3 mM) and E₂ (1.8 µM), or a quench solution (NaOH, 0.66 M). The reactions mixed with chase were allowed to continue for 30 sec prior to quenching - during this 30 sec interval the radiolabelled reactants depart from the enzyme either in the forward or reverse direction (as [³⁵S]E₂S or [³⁵S]PAPS, respectively). Departure is considered irreversible due either to vast dilution of labeled PAPS, or to the fact that the measurement is made at the very early stages of the forward reaction. The reactions (performed in triplicate) that were quenched immediately produced 0.44 (± 0.01) µM of [³⁵S]E₂S (i.e., 88 % of a half-site equivalent of EST); whereas, those that were partitioned produced only 0.31 (± 0.02) µM. Hence, partitioning reduced the yield of [³⁵S]E₂S by 30%, indicating that 30% of the E·PAP· [³⁵S]E₂S complex formed during the burst returns to substrate and departs from the enzyme as [³⁵S]PAPS.

Taken together, the 30% return of product to substrate complexes and the shape of the burst (zero-intercept and monophasic) argue strongly that the majority of the product in the burst is in the ternary complex. The return of 30% of the labeled product to substrate confirms that at least this percentage of the product complexes are in the reactive ternary complex at the moment partitioning is initiated. If only 30% were in ternary complex, all of it is trapped, and the remaining 70% is incapable of returning to substrate. In this case, the rate at which the ternary complex returns to substrate must be far greater than the rate at which it partitions forward to the other product forms found in the burst – were this not the case, the 30% would not have been trapped. Such a scenario predicts rapid equilibration of the substrate and product ternary complexes relative to the rate at which other products form, and predicts a biphasic burst – the first phase reports on the equilibration of the ternary complexes, the second on decomposition of the ternary product complex to the other forms found in the burst. The burst shows no signs of multiple phases, it is well fit by a single phase with a zero intercept; thus, the majority of the product is in ternary complex.

The steady-state balance of the central complexes contributes to K_m

K_d for PAPS binding to E·E₂, 4.0 µM (obtained by fitting k_obs vs PAPS), is far greater than K_m for PAPS, 59 nM (3). For mechanism III (which represents the binding of PAPS to E·E₂, followed by

$$\mathrm{E}\underset{k_{\mathit{\text{off}}}}{\overset{[\mathrm{S}]k_{\mathit{\text{on}}}}{\rightleftarrows }}\mathrm{E}·\mathrm{S}\underset{k_{\mathit{2}}}{\overset{k_{\mathit{1}}}{\rightleftarrows }}\mathrm{E}·\mathrm{P}\stackrel{k_{\mathit{3}}}{\to }\mathrm{E}+\mathrm{P}$$ (III)

formation and release of product), K_m is given by Equation 4.

$$K_m=\frac{k_{\mathit{\text{off}}}{k}_2+k_{\mathit{\text{off}}}{k}_3+k_1{k}_3}{k_{\mathit{\text{on}}}(k_1+k_2+k_3)}$$ (4)

Applying the experimental constrains obtained from analysis of the burst (k1 ≫ k₃), k_obs vs [PAPS] (k1 ≫ k₂), and isotope trapping (k_off ≫ k₁) results, Equation 4 reduces to Equation 5.

$$K_m=\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}·\frac{k_2+k_3}{k_1}$$ (5)

Importantly, (k₂ + k₃)/k₁ represents the ratio of [E·S] to [E·P] in the steady state, ([E·S] / [E·P])_ss. This can be seen by applying the steady-state assumption to the rate of formation and disappearance of EP:

$$\frac{\mathit{\text{dEP}}}{\mathit{\text{dt}}}=[\mathit{\text{ES}}]k_1=[\mathit{\text{EP}}](k_2+k_3)=-\frac{\mathit{\text{dEP}}}{\mathit{\text{dt}}}$$ (6)

rearranging,

$${\left(\frac{[\mathit{\text{ES}}]}{[\mathit{\text{EP}}]}\right)}_{ss}=\frac{k_2+k_3}{k_1}$$ (7)

Thus, for the EST mechanism and other similar mechanisms (39), K_m is linked linearly to the steady-state, mass-ratio of the central complexes. Given values for k₁, k₂ and k₃ (4.4 s⁻¹, 0.070 s⁻¹ and 0.072 s⁻¹), ([E·S] / [E·P])_ss is calculated at 0.031, which, when multiplied by K_d for PAPS binding to E·E₂, yields a K_m of 130 nM – a value that is in reasonable agreement with the published value of 59 nM.

This analysis demonstrates that substrate affinity is enhanced ~ 30-fold through a selective balancing of rate constants to achieve a central-complex, mass-ratio that favors product in the steady-state. It is interesting to consider that changes in this ratio across a series of substrates will bias substrate selection. One cannot help but wonder which reactant features might interact with the enzyme to balance the central complexes, and how alterations in such features might be used to control steady-state affinities and ultimately the metabolic disposition of a given sulfotransferase.

Substrate inhibition follows chemistry

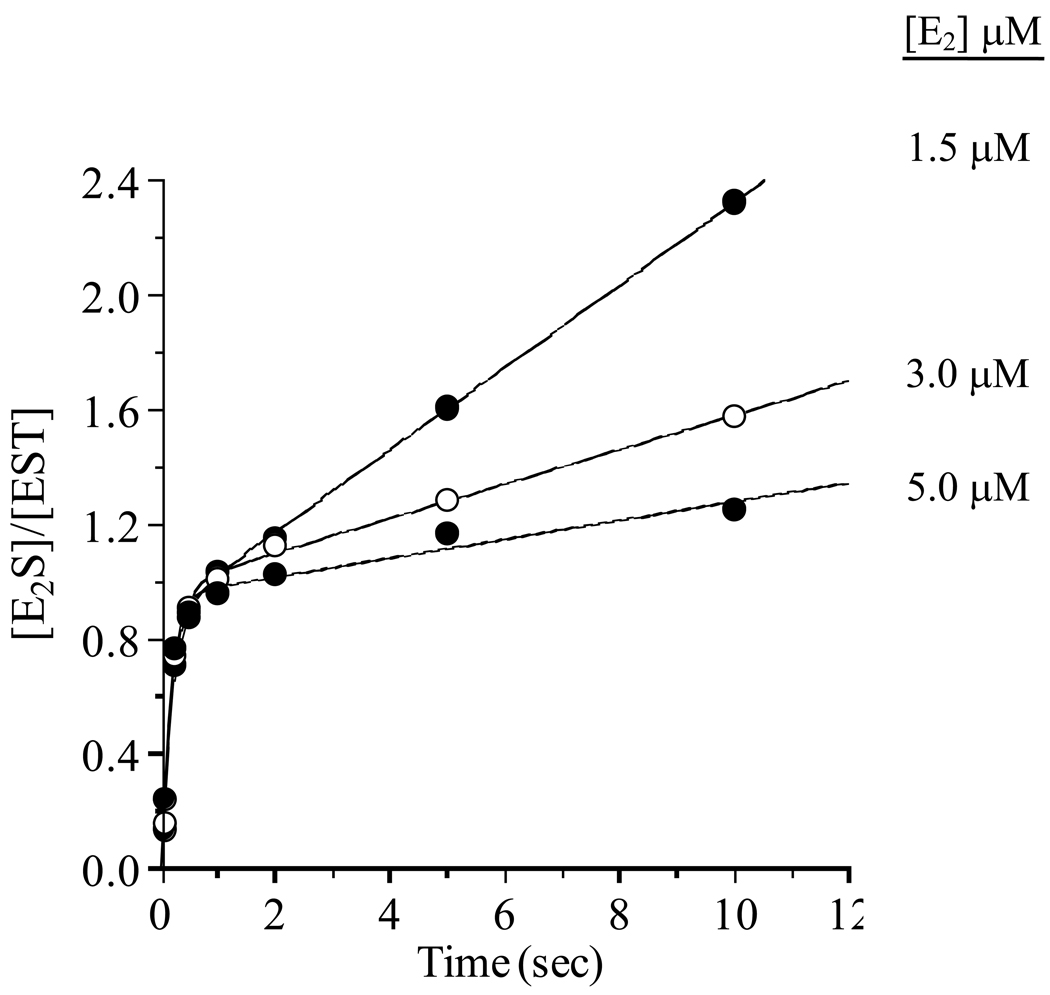
The forward reactions of sulfotransferases are typically inhibited by the non-nucleotidyl (or, acceptor) substrate. In the case of EST, E₂ is a partial k_cat-inhibitor (saturation with inhibitor decreases k_cat ~ 7-fold without altering K_{m (PAPS)} (3)), and the inhibition constant, K_{i (E2)} = 80 nM, is comparable to the levels of estrogen found in breast cystic fluid (40). The product burst provides an opportunity to fine-tune were in the mechanism inhibition occurs. Toward this end, bursts were obtained at a series of inhibiting E₂ concentrations and compared. Remarkably, addition of E₂ to the inhibition pocket has no influence on the burst (Figure 4) - thus, inhibition does not occur until the system reaches the product stages of the catalytic cycle. Notably, the E₂ concentrations needed to observe significant inhibition in the current experiments are higher than expected (3). This discrepancy is likely due to the very different conditions under which these measurements were made. This finding is consistent with a variety of inhibition mechanisms. Previous work suggests that inhibition might occur via binding of E₂ at an allosteric site (3). While such a mechanism remains plausible, the burst results are perhaps explained most simply by a model in which E₂ inhibits by binding to a form of the enzyme that appears only during the product stages - for example, the E·PAP complex, to which E₂ is known to bind - E·PAP·E₂ has been observed crystallographically (41) and, interestingly, the structure gives no indication of an asymmetry that might lead to half-site reactivity. The dead-end inhibition mechanism predicts the onset of inhibition as E₂ binding to E·PAP becomes fast with respect to release of PAP – thus trapping PAP in the dead-end complex. At infinite [E₂], one expects all of the E·PAP generated during turnover to be trapped in the E·PAP·E₂ complex, and that further turnover requires that PAP “escape” directly from the dead-end complex. If PAP could not escape (for example, if release were strictly ordered with PAP releasing last) turnover would be driven to zero at infinite [E₂], and inhibition would be complete rather than partial. The fact that k_cat is non-zero when [E₂] is extrapolated to infinity tells us that PAP does depart from the E·PAP·E₂ complex, and that its departure is rate-limiting at infinite [E₂]; thus, k_cat extrapolated to infinite [E₂] (i.e., 0.18 min⁻¹ (3)) should provide an excellent approximation of the rate constant governing its departure from the E·PAP·E₂ complex.

Figure 4. The effect of E₂ inhibition on the E₂S burst.

Reactions were initiated by rapidly mixing a solution containing PAPS (18.0 µM), MgCl₂ (7.0 mM), DTT (1.0 mM), glycerol (10% v/v), and 50 mM KPO₄ (pH 6.3) with an equal volume of an identical solution that did not contain PAPS, but did contain EST (1.0 µM) and various concentrations of [³H]E₂ (3.0, 6.0, 10.0 µM). Quenching and product quantitation are described in the Figure 1 Legend (also, see Materials and Methods). Measurements were performed in triplicate and averaged. All solutions were equilibrated at 25 (± 2) °C prior to mixing. Solid lines through the data represent the behavior predicted by the best-fit parameters obtained from a non-linear least-squares fit of the parameterized form of Equation 2 to the data, see Results and Discussion.

Conclusions

Estrogen sulfotransferase exhibits half-sites reactivity. The mechanism of EST biases the central-complex equilibrium strongly toward product (K_{eq int} = 49), and releases product slowly enough to allow the interconversion of the central complexes to approach equilibrium. Consequently, the steady-state ratio of the central complexes scales inversely with K_m and results in a ~ 30-fold increase in the affinity of EST for its substrates. Thus, steady-state affinity of the enzyme for substrate is determined by a balance of kinetic factors that begin at the point of binding and reach as far into the mechanism as interactions with the product central complexes. It will be interesting to explore whether such factors contribute to substrate selectivity in the sulfotransferase family.

Consistent with formation of an E·PAPS·E₂ dead-end complex, inhibition of EST by E₂ occurs after formation of the product central complex. Assuming the dead-end mechanism, one is led to conclude that departure of PAP from E·PAP·E₂ is rate-determining in the inhibited system, and that k_cat extrapolated to infinite [E₂] (0.18 min⁻¹) approximates the PAP-release rate constant.

The findings of this work have shed new light on the mechanism of EST (and presumably other members of sulfotransferase family) and raises intriguing questions regarding the molecular basis of half-sites reactivity in this system, and the catalytic and biological necessity for such a mechanism in regulating estrogen metabolism and sulfuryl-transfer in general.

Abbreviations

Hepes

4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid

MES

2-(N-morpholino)ethanesulfonic acid

PEI-F TLC

Poly-(ethylenimine) Cellulose-F Thin Layer Chromatography

PEP

phosphoenolpyruvate

U

unit, micromoles of substrate converted to product per minute at V_max