Summary
Extracting grouping structure or identifying homogenous subgroups of predictors in regression is crucial for high-dimensional data analysis. A low-dimensional structure in particular–grouping, when captured in a regression model, enables to enhance predictive performance and to facilitate a model's interpretability Grouping pursuit extracts homogenous subgroups of predictors most responsible for outcomes of a response. This is the case in gene network analysis, where grouping reveals gene functionalities with regard to progression of a disease. To address challenges in grouping pursuit, we introduce a novel homotopy method for computing an entire solution surface through regularization involving a piecewise linear penalty. This nonconvex and overcomplete penalty permits adaptive grouping and nearly unbiased estimation, which is treated with a novel concept of grouped subdifferentials and difference convex programming for efficient computation. Finally, the proposed method not only achieves high performance as suggested by numerical analysis, but also has the desired optimality with regard to grouping pursuit and prediction as showed by our theoretical results.
Keywords: Gene networks, large p but small n, nonconvex minimization, prediction, supervised clustering
1 Introduction
Essential to high-dimensional data analysis is seeking a certain lower-dimensional structure in knowledge discovery, as in web mining. Extracting one-kind of lower-dimensional structure–grouping, remains largely unexplored in regression. In gene network analysis, a large amount of current genetic knowledge has been organized in terms of networks, for instance, the Kyoto Encyclopedia of Genes and Genomes (KEGG), a collection of manually drawn pathway maps representing the knowledge about molecular interactions and reactions. In situations as such, extracting homogenous subnetworks from a network of dependent predictors, most responsible for predicating outcomes of a response, has been one key challenge of biomedical research. There homogenous subnetworks of genes are usually estimated for understanding a disease's progression. The central issue this article addresses is automatic identification of homogenous subgroups in regression, what we call grouping pursuit.
Now consider a linear model in which response Yi depends on a vector of p predictors:
| (1) |
where β ≡ (β1, …, βp)T is a vector of regression coefficients, xi is independent of εi, and μ(x) is in a generic form, including linear, and nonlinear predictors expressed in terms of linear combinations of known bases. Our objective is to identify all possible homogenous subgroups of predictors, for optimal prediction of the outcome of Y. Here homogeneity means that regression coefficients are of similar (same) values, that is, βj1 ≈ ⋯ ≈ βjK within each group {j1, …, jK} ⊂ {1, …, p}. In (1), grouping pursuit estimates all distinct values of β as well as all corresponding subgroups of homogenous predictors.
Grouping pursuit seeks variance reduction of estimation while retaining roughly the same amount of bias, which is advantageous in high-dimensional analysis. First, it collapses predictors whose sample covariances between the residual and predictors are of similar values, for best predicting outcomes of Y; c.f., Theorem 4. Moreover, it goes beyond the notion of feature selection. This is because it seeks not only a set of redundant predictors, or a single group of zero-coefficient predictors, but also additional homogenous subgroups for further variance reduction. As a result, it yields higher predictive performance. These aspects are confirmed by numerical and theoretical results in Sections 4 and 5. Second, the price to be paid for adaptive grouping pursuit is estimation of tuning parameters, which is small as compared to its potential gain of a simpler model with higher predictive accuracy.
Grouping pursuit considered in here is one kind of supervised clustering. Papers that investigate groping pursuit are those of Tibshirani et al. (2005), where the Fused Lasso is proposed using an L1-penalty with respect to a certain serial order; Bondell and Reich (2008), where the OSCAR penalty involves pairwise L∞-penalties for grouping variables in terms of absolute values, in addition to variable selection. Grouping pursuit dramatically differs from feature selection for grouped predictors. This is in the sense that the former only groups predictors without removing redundancy, whereas the latter removes redundancy by encouraging grouped predictors stay together in selection; see Yuan and Lin (2006), and Zhao, Rocha and Yu (2009).
Our primary objective is achieving high accuracy in both grouping and prediction through a computationally efficient method, which seems to be difficult, if not impossible, with existing methods, especially those through enumeration. To achieve our objective, we employ the regularized least squares method with a piecewise linear nonconvex penalty. The penalty to be introduced in (2) involves one thresholding parameter determining which pairs to be shrunk towards a common group, which works jointly with one regularization parameter for shrinkage towards unknown location. These two tuning parameters combine thresholding with shrinkage for achieving adaptive grouping, which is otherwise not possible with shrinkage alone. The penalty is overcomplete in that the number of individual penalty terms in the penalty may be redundant with regard to certain grouping structures, and is continuous but with three nondifferentiable points, leading to significant computational advantage, in addition to the desired optimality for grouping pursuit (Theorems 3 and Corollary 1).
Computationally, the proposed penalty imposes great challenges in two aspects: (a) potential discontinuities and (b) overcompleteness of the penalty, where an effective treatment does not seem to exist in the literature; see Friedman et al. (2007) about computational challenges for a pathwise coordinate method in this type of situation. To meet the challenges, we design a novel homotopy algorithm to compute the regularization solution surface. The algorithm uses a novel concept of grouped subdifferentials to deal with overcompleteness for tracking the process of grouping, and difference convex (DC) programming to treat discontinuities due to nonconvex minimization. This, together with a model selection routine for estimators that can be discontinuous, permits adaptive grouping pursuit.
Theoretically, we derive a finite-sample probability error bound of our DC estimator, what we call DCE, computed from the homotopy algorithm for grouping pursuit. On this basis, we prove that DCE is consistent with regard to grouping pursuit as well as reconstructing the unbiased least squares estimate under the true grouping, roughly for nearly exponentially many predictors in n as long as , c.f., Theorem 3 for details.
For subnetwork analysis, we apply our proposed method to study predictability of a protein-protein interaction (PPI) network of genes on the time to breast cancer metastasis through gene expression profiles. In Section 5.2, 27 homogenous subnetworks are identified through a Laplacian network weight vector, which surround three tumor suppressor genes TP53, BRACA1 and BRACA2 for metastasis. There 17 disease genes that were identified in the study of Wang et al. (2005) belong to 5 groups containing 1, 1, 1, 1, and 13 disease genes, indicating gene functionalities with regard to breast cancer survivability.
This article is organized in seven sections. Section 2 introduces the proposed method and the homotopy algorithm. Section 3 is devoted to selection of tuning parameter. Section 4 presents a theory concerning optimal properties of DCE in grouping pursuit and prediction, followed by some numerical examples and an application to breast cancer data in Section 5. Section 6 discusses the proposed method. Finally, the appendix contains technical proofs.
2 Grouping pursuit
In (1), let the true coefficient vector be , where K0 is the number of distinct groups, , and denotes a vector of 1's with length . Grouping pursuit, as defined early, estimates true grouping as well as . Without loss of generality, assume that the response and predictors are centered, that is, YT1 = 0 and (x1j, …, xnj)1 = 0; j = 1, …, p.
Ideally, one may enumerate over all possible least squares regressions for identifying the best grouping. However, the total number of all possible groupings, which is the pth Bell number (Rota, 1964), is much larger than that of all possible subsets in feature selection, hence that it is computationally infeasible even for moderate p. For instance, the 10th order Bell number is 115975. To circumvent this difficulty, we develop an automatic nonconvex regularization method to obtain (1) accurate grouping, (2) the least squares estimate based on the true grouping, (3) an efficient homotopy algorithm, and (4) high predictive performance.
Our approach utilizes a penalty involving pairwise comparisons: {βj − βj′ : 1 ≤ j < j′ ≤ p}. When βj − βj′ = 0, Xj and Xj′ are grouped. By transitivity, that is, βj1 − βj2 = 0 and βj2 − βj3 = 0 imply that βj1 = βj2 = βj3, we identify all homogenous groups through p(p − 1)/2 comparisons. Naturally, these comparisons can be conducted through penalized least squares with penalty Σj<j′ |βj − βj′|. However, this convex penalty is not desirable for predictive performance, because it is not adaptive for discriminating large from small pairwise differences. As a result, overpenalizing large differences due to shrinking small differences towards zero impedes predictive performance. We thus introduce its nonconvex counterpart J(β) = Σj<j′ G(βj − βj′) for adaptive grouping pursuit, where G(z) = λ2 if |z| > λ2 and G(z) = |z| otherwise, with λ2 > 0 being the thresholding parameter. For G(z), one locally convex and two locally concave points at z = 0, ±λ2 enable us to achieve computational advantage, as well as to realize sharp statistical properties. First, the piecewise linearity and the two locally concave points of G(z) yield an efficient method (Algorithm 1), and fast finite-step convergence of the surface algorithm (Algorithm 2). Second, they yield a sharp finite-sample error bound in Theorem 3. These aspects are unique for G(z), which may not be shared by other penalties such as SCAD (Fan and Li, 2001); see the discussion after Theorem 2. A function like G(z) was considered in other contexts such as wavelet denoising (Fan, 1997) and a combined L0 and L1 penalty via integer programming (Liu and Wu, 2007).
We now propose our penalized least squares criterion for automatic grouping pursuit:
| (2) |
where λ1 > 0 is the regularization parameter controlling the degree of grouping. For (2), any local/global minimizer can not attain at any of non-smooth locally concave points of J(β).
Lemma 1 Let h(·) be any differentiable function in ℝp and be a local minimizer of f(β) = h(β) + λ1J(β) with J(·) given in (2). Then for j ≠ j′.
2.1 Grouped subdifferentials
We now introduce a novel concept of grouped subdifferentials for a convex function, which constitutes a basis of our homotopy algorithm for tracking the process of grouping.
A subgradient of a convex function f(β) with respect to β at β is any vector b ∈ ℝp satisfying f(β*) ≥ f(β) + bT(β* − β) for any β* with sufficiently small β* − β, and reduces to the derivative at a smooth point. The subdifferential of S(β) at any β is the set of all such b's, which is either a singleton or a non-singleton compact set. Let β̂ be a local minimizer of (2) and ( 1, …,
1, …,  K) be the corresponding grouping, where K is the number of distinct groups. The subgradient of |βj − βj′| with respect to βj at β = β̂ is given by bjj′ = Sign(β̂j − β̂j′) if |β̂j − β̂j′| > 0, and |bjj′| ≤ 1 otherwise. Here bjj′ is a singleton everywhere except at β̂j − β̂j′ = 0.
K) be the corresponding grouping, where K is the number of distinct groups. The subgradient of |βj − βj′| with respect to βj at β = β̂ is given by bjj′ = Sign(β̂j − β̂j′) if |β̂j − β̂j′| > 0, and |bjj′| ≤ 1 otherwise. Here bjj′ is a singleton everywhere except at β̂j − β̂j′ = 0.
To proceed, write β̂ as
, where the index in each group is arranged increasingly, α̂1 < ⋯ < α̂K. Define g(j) ≡ k if β̂j = α̂k; j = 1, …, p, mapping indices from β̂ to α̂. Then grouping ( 1, …,
1, …,  K) partitions index set {1, …, p}, with
K) partitions index set {1, …, p}, with  k ≡ {j : g(j) = k}; k = 1, …, K.
k ≡ {j : g(j) = k}; k = 1, …, K.
Ordinarily, group splitting can be tracked through certain transition conditions for {bjj′ : j ≠ j′}, c.f., Rosset and Zhu (2007). However, {bjj′ : j ≠ j′} are not estimable from data when an overcomplete penalty is used. To overcome this difficulty, we define the grouped subgradient of index j ∈  k at β = β̂ as Bj ≡ Σj′∈
k at β = β̂ as Bj ≡ Σj′∈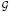 k\{j} bjj′ if |
k\{j} bjj′ if | k| > 1, and Bj ≡ 0 if |
k| > 1, and Bj ≡ 0 if | k| = 1; j = 1, …, p. Note that Σj∈
k| = 1; j = 1, …, p. Note that Σj∈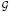 k Bj = 0; k = 1, …, K, because bjj′ = −bj′j; j ≠ j′. Moreover, we define the grouped subgradient of a subset A ⊂
k Bj = 0; k = 1, …, K, because bjj′ = −bj′j; j ≠ j′. Moreover, we define the grouped subgradient of a subset A ⊂  k at β = β̂ as BA ≡ Σj∈A Bj = Σ(j,j′)∈A×(
k at β = β̂ as BA ≡ Σj∈A Bj = Σ(j,j′)∈A×(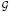 k\A) bjj′. Then
k\A) bjj′. Then
| (3) |
Subsequently, we work with {BA : A ⊂ {1, …, p}} that can be uniquely determined; see Theorem 1.
2.2 Difference convex programming
This section treats non-differentiable nonconvex minimization (2) through DC programming, which is a principle for nonconvex minimization, relying on decomposing an objective function into a difference of two convex functions. The reader may consult An and Tao (1997) for DC programming. Through this DC method, we will design a novel homotopy algorithm for a DC solution of (2) in Section 2.3, which is a solution through DC programming.
First, we decompose S(β) in (2) into a difference of two convex functions and S2(β) = λ1 Σj<j′ G2(βj − βj′), through a DC decomposition of G(·) = G1(·) − G2(·) with G1(z) = |z| and G2(z) = (|z| − λ2)+, where z+ is the positive part of z. This DC decomposition is interpretable in that S2(·) corrects the estimation bias due to use of convex penalty λ1 Σj<j′ |βj − βj′| for a nonconvex problem (2).
Second, we construct a sequence of upper approximations by successively replacing S2(β) at iteration m = 0, 1, …, by its affine minorization based on iteration m − 1, leading to an upper convex approximating function at iteration m:
| (4) |
where ∇ is the subgradient operator, 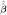 (m−1) (λ1, λ2) is the minimizer of (4) at iteration m − 1, and
(m−1) (λ1, λ2) is the minimizer of (4) at iteration m − 1, and 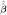 (−1) (λ1, λ2) ≡ 0. The last term in (4) becomes
with ∇G2(z) = Sign(z)I(|z| > λ2) being a subgradient of G2 at z.
(−1) (λ1, λ2) ≡ 0. The last term in (4) becomes
with ∇G2(z) = Sign(z)I(|z| > λ2) being a subgradient of G2 at z.
Third, we utilize the grouped subdifferentials to track the entire solution surface iteratively. One technical difficulty is that 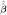 (m) (λ1, λ2) would have jumps in λ1 if
(m) (λ1, λ2) would have jumps in λ1 if 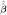 (0) (λ1, λ2) were piecewise linear in λ1 given λ2, in view of (6) and (7) in Theorem 1. This is undesirable for tracking by continuity through homotopy. For grouping pursuit, we therefore replace
(0) (λ1, λ2) were piecewise linear in λ1 given λ2, in view of (6) and (7) in Theorem 1. This is undesirable for tracking by continuity through homotopy. For grouping pursuit, we therefore replace 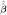 (0) (λ1, λ2) in (4) by
(0) (λ1, λ2) in (4) by 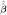 (0) (λ0, λ2), where rough tuning for λ0 suffices because a DC algorithm is not sensitive to an initial value (An and Tao, 1997). This choice leads to a piecewise linear and continuous minimizer β̂(1)(λ) of (4) in λ1 given (λ0, λ2), where λ = (λ0, λ1, λ2)T. Successively replacing
(0) (λ0, λ2), where rough tuning for λ0 suffices because a DC algorithm is not sensitive to an initial value (An and Tao, 1997). This choice leads to a piecewise linear and continuous minimizer β̂(1)(λ) of (4) in λ1 given (λ0, λ2), where λ = (λ0, λ1, λ2)T. Successively replacing 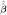 (m−1) (λ1, λ2) in (4) by β̂(m−1) (λ0, λ0, λ2) for m ∈ ℕ, we obtain a modified version of (4):
(m−1) (λ1, λ2) in (4) by β̂(m−1) (λ0, λ0, λ2) for m ∈ ℕ, we obtain a modified version of (4):
| (5) |
which yields its minimizer β̂(m)(λ) and the estimated grouping  (m)(λ). As suggested by Theorems 1 and 2, β̂(m)(λ) converges in finite steps. Most importantly, the iterative scheme yields an estimator having the desired properties of a global minimizer, c.f., Theorem 3.
(m)(λ). As suggested by Theorems 1 and 2, β̂(m)(λ) converges in finite steps. Most importantly, the iterative scheme yields an estimator having the desired properties of a global minimizer, c.f., Theorem 3.
Given grouping  = (
= ( 1, …,
1, …,  K), let Z
K), let Z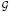 = (z
= (z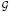 1, …, z
1, …, z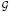 K) be an n × K matrix with z
K) be an n × K matrix with z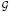 k = X
k = X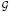 k 1, and X
k 1, and X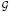 k be the design matrix spanned by the predictors of
k be the design matrix spanned by the predictors of  k; k = 1, …, K.
k; k = 1, …, K.
Theorem 1 Assume that is invertible. Then β̂(m)(λ) defined by (5) is piecewise linear in (Y, λ) and continuous in λ1. In addition,
| (6) |
where , and
| (7) |
Moreover, for with , and k = 1, …, K(m)(λ),
| (8) |
Theorem 1 reveals two important aspects of β̂(m)(λ) from (5). First, α̂(m)(λ) and are continuous and piecewise linear in λ1 and , piecewise constant in λ2 with possible jumps, and piecewise linear in Y with possible jumps. In other words, is continuous in λ1 given (Y, λ0, λ2), but may contain jumps with respect to (Y, λ2). Second, J(·) shrinks β̂(m)(λ) towards the least squares estimate , with the amount of shrinkage controlled by λ1 > 0. This occurs only when a pairwise difference stays below the thresholding value of λ2. As λ2 → 0, the bias due to penalization becomes ignorable, yielding a nearly unbiased estimate for grouping and parameter estimation.
2.3 Algorithms for difference convex solution surface
One efficient computational tool is a homotopy method (Allgower and Georg, 2003; Wu et al., 2009), which utilizes continuity of a solution in λ to compute the entire solution surface simultaneously. To our knowledge, homotopy methods for nonconvex problems have not yet received attention in the literature. This section develops a homotopy method for a regularization solution surface for nonconvex minimization (2) through DC programming. One major computational challenge is that the solution may be piecewise linear with jumps in (Y, λ), which is difficult to treat with homotopy. To overcome this difficulty, we design a DC algorithm to obtain an easily computed solution β̂(λ), which could be local or global. Note that a DC method guarantees a global solution when it is combined with the branch-and-bound method, c.f., Liu, Shen and Wong (2005). However, seeking a global minimizer of (2) is unnecessary, because the DC solution has the desired statistical properties for grouping (Theorem 3), and can be computed more efficiently (Theorem 2).
The main gradients of our DC homotopy algorithm are (1) iterating the entire DC solution surfaces, (2) utilizing the piecewise linear continuity of in for given (λ0, λ2, m), and (3) tracking transition points (joints for a piecewise linear function) through the grouped subdifferentials. This algorithm permits efficient computation of a DC solution for nonconvex minimization (2) with an overcomplete penalty, which is otherwise difficult to treat. To compute β̂(m)(λ), we proceed as follows. First, we fix at one evaluation point of (λ0, λ2), then move along path from λ1 = ∞ towards λ1 = 0 given (λ0, λ2). By Theorem 1, β̂(m)(λ) is piecewise linear and continuous in λ1 given (λ0, λ2). Along this path, we compute transition points at which the derivative of β̂(m)(λ) with respect to λ1 changes. Second, we move to other evaluation points of (λ0, λ2) and repeat the above process.
For given (λ0, λ2), transition in λ1 occurs when either of the following conditions is met:
Merging: Groups and are combined at λ, when ;
Splitting: Group is split into two disjoint sets A1 and A2 with at λ, when , according to (3).
In (A) and (B), at a transition point, two or more groups may be merged, and a single group may be split into two or multiple subgroups.
We now describe the basic idea for computing {β̂(m)(λ) : λ1 > 0} given (λ0, λ2, m). From (6), we track
along the path from λ1 = ∞ towards λ1 = 0 for given (λ0, λ2). Let
be the current transition point. Our algorithm successively identifies the next transition point
along the path. For notational ease, we use ( = (
= ( 1, …,
1, …,  K), Δj) to denote the current
after the current transition; j = 1, …, p. Note that
; j = 1, …, p, remain unchanged before the next transition is reached.
K), Δj) to denote the current
after the current transition; j = 1, …, p. Note that
; j = 1, …, p, remain unchanged before the next transition is reached.
For merging in (A), we compute potential merge points:
| (9) |
1 ≤ k < l ≤ K, where ek is the kth column of Ip. Then
| (10) |
is a potential transition point at which  k′ and
k′ and  l′ are combined into one group. Define
, with ∅ denoting the empty set.
l′ are combined into one group. Define
, with ∅ denoting the empty set.
For splitting in (B), we utilize (3) and the subdifferentials in (8), to compute, for each k = 1, …, K, the largest
and A ⊂  k with |A| < |
k with |A| < | k|/2 such that
k|/2 such that
| (11) |
where
,
, and
. It follows from (8) that
before the next transition occurs, and hence that
for any λ1 ∈ ℝ. Unfortunately, solving (11) through enumeration is infeasible over all subsets A ⊂  k. In Algorithm 1 below, we develop an efficient strategy utilizing piecewise linearity of
in
for computing the potential transition point
, as well as its corresponding grouping, where sk is the solution of (11); k = 1, …, K. This strategy requires roughly O(p2 log p) operations, c.f. Proposition 1.
k. In Algorithm 1 below, we develop an efficient strategy utilizing piecewise linearity of
in
for computing the potential transition point
, as well as its corresponding grouping, where sk is the solution of (11); k = 1, …, K. This strategy requires roughly O(p2 log p) operations, c.f. Proposition 1.
To describe our strategy for solving (11), let
and
be the two subsets of  k of size ℓ corresponding to the ℓ largest and smallest values of
and
, for ℓ = 1, …, |
k of size ℓ corresponding to the ℓ largest and smallest values of
and
, for ℓ = 1, …, | k| and k = 1, …, K, where
if
. Since
, we can refine our search to
for solving (11). Note that
and
by the definition of
's for
. For k = 1, …, K and ℓ = 1, …, [
k| and k = 1, …, K, where
if
. Since
, we can refine our search to
for solving (11). Note that
and
by the definition of
's for
. For k = 1, …, K and ℓ = 1, …, [ k/2], we seek the first zero-crossing λ1 values for
, denoted as
, as λ1 decreases from
. For each k = 1, …, K, we start with ℓ = 1 and compute
k/2], we seek the first zero-crossing λ1 values for
, denoted as
, as λ1 decreases from
. For each k = 1, …, K, we start with ℓ = 1 and compute
| (12) |
For ℓ = 2, …, [ k/2], we observe that elements in
need to be updated as λ1 decreases due to rank changes in
. This occurs at switching points:
k/2], we observe that elements in
need to be updated as λ1 decreases due to rank changes in
. This occurs at switching points:
| (13) |
On this basis, can be computed. First, calculate the largest λ1 ∈ {λ1,A} ∪ {hjj′ : 1 ≤ j < j′ ≤ p} at which or . Second, compute the exact crossing point for through linear interpolation due to the fact that is piecewise linear and continuous in with joints at hjj′, 1 ≤ j < j′ ≤ p.
Algorithm 1 computes the next transition point,  and Δj's.
and Δj's.
Algorithm 1: Computation of next transition point
Given the current grouping  and Δj's with invertible
,
and Δj's with invertible
,
Step 1 (Potential transition for merging) Compute λ1,A as defined in (10) as well as the corresponding grouping.
Step 2 Compute ; k = 1, …, K, as defined in (12), and H ≡ {λ1,A} ∪ {hjj′ : 1 ≤ j < j′ ≤ p} based on (13).
-
Step 3 (Splitting points) Starting with ℓ = 1, and for k = 1, …, K, we
compute the largest λ1 ∈ H such that , and the largest λ1 ∈ H such that , where bisection or Fibonacci search (e.g., Gill, Murray and Wright, 1981) may be applied;
interpolate linearly to obtain satisfying ; set if ;
compute and the corresponding index set;
if sk,ℓ−1 > sk,ℓ and ℓ ≤ [
 k/2] − 1, then go to Step 3 with ℓ replaced by ℓ + 1. Otherwise, set sk,ℓ+1 = ⋯ = sk,[
k/2] − 1, then go to Step 3 with ℓ replaced by ℓ + 1. Otherwise, set sk,ℓ+1 = ⋯ = sk,[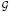 k/2] = 0.
k/2] = 0.
Step 4 (Potential transition for splitting) Compute , as well as the corresponding grouping.
Step 5 (Transition) Compute . If , two groups are merged at . If , a group is split into two at . Update
 and Δj's. If
, no further transition can be obtained.
and Δj's. If
, no further transition can be obtained.
Algorithm 2: Main algorithm
Step 1 (Parameter initialization): Specify the upper bound parameter K*, and evaluation points of (λ0, λ2), where K* ≤ min{n, p}.
Step 2 (Initialization for DC iterations): Given (λ0, λ2), compute β̂(0)(λ0, +∞, λ2), the corresponding
 and Δ's by solving (5) with m = 0. Compute β̂(0)(λ) along the path from λ1 = ∞ to λ1 = 0 until |
and Δ's by solving (5) with m = 0. Compute β̂(0)(λ) along the path from λ1 = ∞ to λ1 = 0 until | (0)(λ)| = K* using Algorithm 1 while holding (λ0, λ2) fixed.
(0)(λ)| = K* using Algorithm 1 while holding (λ0, λ2) fixed.Step 3 (DC iterations): Starting from m = 1, compute β̂(m)(λ0, +∞, λ2), the corresponding
 and Δ's by solving (5); then successively compute β̂(m)(λ) along the path from λ1 = ∞ to λ1 = 0 until |
and Δ's by solving (5); then successively compute β̂(m)(λ) along the path from λ1 = ∞ to λ1 = 0 until | | = K* using Algorithm 1.
| = K* using Algorithm 1.Step 4 (Stopping rule): If S(β̂(m−1)(λ)) − S(β̂(m)(λ)) = 0, then go to Step 3 with m replaced by m + 1. Otherwise, move to next evaluation point of (λ0, λ2) and go to Step 2 until all the evaluation points have been computed.
Denote by m* the termination step of Algorithm 2, which may depend on (λ0, λ2). Our estimate DCE of β is β̂(λ) ≡ β̂(m*)(λ). The corresponding grouping of β̂(λ) is  (λ). In practice, Algorithm 2 is applicable to unstandardized or standardized predictors.
(λ). In practice, Algorithm 2 is applicable to unstandardized or standardized predictors.
Proposition 1 (Computational properties). For Algorithm 1,
is continuous, piecewise linear, and strictly monotone in λ1; k = 1, …, K, ℓ = 1, …, [ k/2]. Moreover, the computational complexities of Algorithms 1 and 2 are no greater than p2 (log p + n) and O(m*n*p2(log p + n)), where n* is the number of transition points.
k/2]. Moreover, the computational complexities of Algorithms 1 and 2 are no greater than p2 (log p + n) and O(m*n*p2(log p + n)), where n* is the number of transition points.
In general, it is difficult to bound n* precisely. However, an application of a heuristic argument similar to that of Rosset and Zhu (2007, Section 3.2, p. 1019) suggests that n* is O(min{n, p}) on average for group combining and splitting.
Theorem 2 (Computation). Assume that is invertible for m ≤ m*. Then the solution of Algorithm 2 is unique, and sequence S(β̂(m)(λ0, λ0, λ2)) decreases strictly in m unless β̂(m)(λ0, λ0, λ2) = β̂(m−1)(λ0, λ0, λ2). In addition, Algorithm 2 terminates in finite steps, i.e., m* < ∞ with
| (14) |
for all λ over the evaluation region of λ and all m ≥ m*.
Two distinctive properties of β̂(m*)(λ) are revealed by (14), leading to fast convergence and a sharp result for consistency of β̂(λ). First, the stopping rule of Algorithm 2, which is reinforced at one fixed λ0, controls the entire surface for all (λ1, λ2) simultaneously, owing to the replacement of 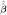 (m−1)(λ0, λ2) by β̂(m−1)(λ0, λ0, λ2) for iteration m in (4). Second, the iteration process terminates finitely with β̂(m*)(λ) satisfying (14), because of the step function of ∇S2(β̂(m−1)(λ)) resulted from the locally concave points z = ±λ2 of G(z). Most critically, (14) is not expected for any penalty that is not piecewise linear with non-differentiable but continuous points.
(m−1)(λ0, λ2) by β̂(m−1)(λ0, λ0, λ2) for iteration m in (4). Second, the iteration process terminates finitely with β̂(m*)(λ) satisfying (14), because of the step function of ∇S2(β̂(m−1)(λ)) resulted from the locally concave points z = ±λ2 of G(z). Most critically, (14) is not expected for any penalty that is not piecewise linear with non-differentiable but continuous points.
3 Estimation of tuning parameters and σ2
Selection of tuning parameters is important for DCE, which involves λ = (λ0, λ1, λ2). In (1), predictive performance of estimator β̂(λ) is measured by MSE(β̂(λ)), defined as , where , μ̂(λ, x) = β̂T(λ)x, and μ0(x) = (β0)Tx.
One critical aspect of tuning is that DCE is a piecewise continuous estimator with jumps in Y. Therefore, any model selection routine may be used for tuning of DCE, which allows for estimators with discontinuities. For instance, cross-validation and the generalized degrees of freedom (GDF, Shen and Huang, 2006) are applicable, but Stein's unbiased risk estimator (Stein, 1981) is not suited because of the requirement of continuity. Then the tuning parameters are estimated by minimizing the model selection criterion.
In practice, σ2 needs to be estimated when it is unknown. In the literature, there have been many proposals for the case of p < n, for instance, σ2 can be estimated by the residual sum squares over (n − p). In general, estimation of σ2 in the case of p > n has not yet received much attention. In our case, we propose a simple estimator , where λ* = (λ0, λ̃1, ∞), λ̃1 is the smallest λ1 reaching the upper bound K(λ0, λ1, ∞) = K*/2, and K* is defined in Step 2 of Algorithm 2. Note that when λ2 = ∞, μ̂i(λ*) is independent of λ0. The quality of estimation depends on the bias of μ̂i(λ*) as well as the variance. By choosing a tight value of K* ≥ K0, one may achieve good performance.
4 Theory
This section derives a finite-sample probability error bound, based on which we prove that β̂(λ) is consistent with regard to grouping pursuit and predictive optimality simultaneously for the same set of values of λ. As a result, the true grouping  0 is reconstructed, as well as the unbiased least squares estimate
given
0 is reconstructed, as well as the unbiased least squares estimate
given  0. Here
with
being invertible.
0. Here
with
being invertible.
Denote by cmin( ) > 0 the smallest eigenvalue of
, where Z
) > 0 the smallest eigenvalue of
, where Z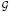 is the design matrix based on grouping
is the design matrix based on grouping  Denote by
, the resolution level that may depend on (p, n), or the level of difficulty of grouping pursuit, with a small value of γmin being difficult. The following result is established for β̂(λ) from Algorithm 2.
Denote by
, the resolution level that may depend on (p, n), or the level of difficulty of grouping pursuit, with a small value of γmin being difficult. The following result is established for β̂(λ) from Algorithm 2.
Theorem 3 (Error bounds for grouping pursuit and consistency). Under the model assumptions of (1) with εi ∼ N(0, σ2), assume that λ0 = λ1, (2K* + 1)λ1/λ2 < min|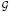 |≤(K*)2 cmin(
|≤(K*)2 cmin( ), where
. Then for any n and p, we have
), where
. Then for any n and p, we have
| (15) |
where
is the cumulative distribution function of N(0, 1), and ‖xj‖ is the L2-norm of xj ∈ 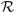 n. Moreover, as p, n → +∞, if
n. Moreover, as p, n → +∞, if
,
,
then P( (λ) ≠ (
(λ) ≠ ( 0) ≤ P(β̂(λ) ≠ β̂(ols)) → 0. In other words,
0) ≤ P(β̂(λ) ≠ β̂(ols)) → 0. In other words,  (λ) =
(λ) =  0 and β̂(λ) = β̂(ols) with probability tending to 1.
0 and β̂(λ) = β̂(ols) with probability tending to 1.
Corollary 1 (Predictive performance) Under the assumption of Theorem 3, , and L(β̂(λ), β0) = Op(K0/n), as p, n → ∞.
Theorem 3 and Corollary 1 say that DCE consistently identifies the true grouping  0 and reconstructs the unbiased least squares estimator β̂(ols) based on
0 and reconstructs the unbiased least squares estimator β̂(ols) based on  0 when p, n → ∞. They also confirm the assertion made in the Introduction for consistency with regard to nearly exponentially many predictors in n. Specifically, consistency occurs when (a)
(Condition (ii)) or
, (b) λ1(2K* + 1) < λ2min|
0 when p, n → ∞. They also confirm the assertion made in the Introduction for consistency with regard to nearly exponentially many predictors in n. Specifically, consistency occurs when (a)
(Condition (ii)) or
, (b) λ1(2K* + 1) < λ2min|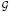 |≤(K*)2 cmin(
|≤(K*)2 cmin( ), (c)
and
(Condition (i)), provided that maxj:1≤j≤p ‖xj‖2/n is bounded. Note that cmin(
), (c)
and
(Condition (i)), provided that maxj:1≤j≤p ‖xj‖2/n is bounded. Note that cmin( 0) may tend to zero as p, n → ∞ even if the number of true groups K0 is independent of (p, n). To understand the conditions (a)-(c), we examine the simplest case in which min|
0) may tend to zero as p, n → ∞ even if the number of true groups K0 is independent of (p, n). To understand the conditions (a)-(c), we examine the simplest case in which min|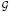 |≤(K*)2 cmin(
|≤(K*)2 cmin( ), K0 and K* are independent of (p, n). Then (a)-(c) reduce to that
, n1/2λ1 → ∞, and λ2 > c1λ1 but
for some constant c1 > 0 and some sequence dn > 0 with n1/2dn → ∞, where the resolution level γmin is required to be not too low in that n1/2γmin → ∞. Interestingly, there is a trade-off between p and the resolution level γmin. Note that p = O(exp(n2δ)) when λ is tuned: λ1 = c2λ2 = c3γmin, given that γmin = O(n−1/2+δ), for some positive constants c2, c3 > 0 and 0 < δ ≤ 1/2. Depending on the value of δ or γmin, p can be nearly exponentially many for high-resolution regression functions with δ = 1/2, whereas p can be ΔO(exp(n2δ)) for low-resolution functions when δ is close to 0. The resolution level for DCE can be as low as nearly O(n−1/2), which, to our knowledge, compares favorably with existing penalties for feature selection.
), K0 and K* are independent of (p, n). Then (a)-(c) reduce to that
, n1/2λ1 → ∞, and λ2 > c1λ1 but
for some constant c1 > 0 and some sequence dn > 0 with n1/2dn → ∞, where the resolution level γmin is required to be not too low in that n1/2γmin → ∞. Interestingly, there is a trade-off between p and the resolution level γmin. Note that p = O(exp(n2δ)) when λ is tuned: λ1 = c2λ2 = c3γmin, given that γmin = O(n−1/2+δ), for some positive constants c2, c3 > 0 and 0 < δ ≤ 1/2. Depending on the value of δ or γmin, p can be nearly exponentially many for high-resolution regression functions with δ = 1/2, whereas p can be ΔO(exp(n2δ)) for low-resolution functions when δ is close to 0. The resolution level for DCE can be as low as nearly O(n−1/2), which, to our knowledge, compares favorably with existing penalties for feature selection.
We now describe characteristics of grouping, in particular—how predictors are grouped. Denote by , the sample covariance between xj and the residual.
Theorem 4 (Grouping). Let
be defined in Theorem 1, where Δj(λ) = Δj′ (λ) if j, j′ ∈  k(λ). Let Ek(λ) ≡ [Δj(λ) − (|
k(λ). Let Ek(λ) ≡ [Δj(λ) − (| k(λ)| − 1), Δj(λ) + (|
k(λ)| − 1), Δj(λ) + (| k(λ)| − 1)] be an interval or a point for any j ∈
k(λ)| − 1)] be an interval or a point for any j ∈  k(λ). Then E1(λ), …, EK(λ)(λ) are disjoint. Finally, j belongs to
k(λ). Then E1(λ), …, EK(λ)(λ) are disjoint. Finally, j belongs to  k(λ) if and only if
; k = 1, …, K(λ).
k(λ) if and only if
; k = 1, …, K(λ).
Theorem 4 says that predictors are grouped according to if their sample covariance values fall into the same intervals, where these disjoint intervals E1(λ), …, EK(λ)(λ) characterize grouping. As λ varies, group splitting or combining may take place when these intervals split or combine.
5 Numerical examples
This section examines effectiveness of the proposed method on three simulated examples and one real application to gene network analysis.
For a fair comparison, we compare DCE with the estimator obtained from its convex counterpart–an ultra-fused version of the fused Lasso based on convex penalty Σj<j′ |βj− βj′|. This allows us to understand the role λ2 plays in grouping. In addition, we examine the Lasso to investigate the connection between grouping pursuit and feature selection, to confirm our intuition in the foregoing discussion. For reference, least squares estimators based on the full model, and the true grouping, are reported as well, in addition to the average number of iterations in Algorithm 2. Finally, we compare DCE with OSCAR using two examples from Bondell and Reich (2008) in Example 3.
5.1 Benchmarks
We perform simulations in several scenarios, including correlated predictors, different noise levels and situations of “small p but large n” and “small n but large p”. Note that a decrease in the value of σ2 implies an increase in the sample size in this case. We therefore fix n = 50 and vary the value of σ2 in Examples 1 and 2 and use different sample sizes in Example 3.
For estimating λ for DCE, we generate an independent tuning set of size n in each example. Specially, the estimated λ, denoted by λ̂, is obtained by minimizing tuning error over the tuning set with respect to λ over the path of λ1 > 0, and λ2 ∈ {0.5, 1, 1.5, 2, 2.5, 3, 5, 10, ∞} in Examples 1-3, where is the largest transition point corresponding to λ2 = ∞. The predictive performance is evaluated by MSE(β̂(λ̂)) as defined in Section 3. The accuracy of grouping is measured by the percentage of matchings between estimated and true pairs of indices (j, j′), for j ≠ j′. Similarly, the tuning parameter of Lasso and the convex counterpart of DCE is estimated over λ1 > 0 based on the same tuning set for a fair comparison. All numerical analyses are conducted in R 2.9.1.
Example 1 (Sparse Grouping)
This example was used previously for feature selection in Zou and Hastie (2005). A random sample of {(xi, Yi) : i = 1, …, n} is obtained with n = 50, where Yi follows (1) with εi ∼ N(0, σ2) and σ2 = 2, 1, .5, and xi is sampled from N(0, Σ40×40) with p = 20, having the diagonal and off-diagonal elements 1 and 0.5. Here .
As suggested in Table 1, DCE outperforms its convex counterpart and the least squares estimate based on estimated grouping across three levels of σ2. This is due primarily to the nonconvex penalty, which corrects the estimation bias due to use of its convex counterpart. This is evident from the fact that the convex counterpart of DCE (m = 0) performs worst than the least square estimates based on the estimated grouping. Furthermore, grouping indeed offers additional improvement in predictive performance in view of the result of the Lasso. Most importantly, DCE reconstructs the least square estimates based on true grouping well, confirming the asymptotic results in Theorem 3 and Corollary 1. The reconstruction is nearly perfectly when σ2 = .5 but is less so when the value of σ2 increases towards 2, indicating that the noise level does impact the accuracy of reconstruction. Overall, grouping identification and reconstruction appear to be accurate, agreeing with the theoretical results.
Table 1.
MSEs as well as estimated standard errors (in parentheses) of grouping pursuit for various methods based on 100 simulation replications in Example 1. Here Full, True, Lasso, Convex, DCE, denote the least squares estimates based on the full model, the true model, the Lasso estimate, our convex counterpart based on iteration m = 0, and our estimate.
| n | σ | Full | True model | Lasso | Our | Ave # Iter | Ave match proportion | ||
|---|---|---|---|---|---|---|---|---|---|
| Grouping | Variable | Convex | DCE | ||||||
| 50 | 2.0 | 1.607 (0.0446) |
0.235 (0.0150) |
0.845 (0.0310) |
1.318 (0.0449) |
1.418 (0.0483) |
0.837 (0.0721) |
4.31 (0.17) |
0.633 |
| 1.0 | 0.402 (0.0111) |
0.059 (0.0037) |
0.211 (0.0077) |
0.330 (0.0112) |
0.362 (0.0128) |
0.070 (0.0050) |
4.08 (0.14) |
0.716 | |
| 0.5 | 0.100 (0.0028) |
0.015 (0.0009) |
0.053 (0.0019) |
0.083 (0.0029) |
0.091 (0.0032) |
0.019 (0.0016) |
3.71 (0.10) |
0.733 | |
| 100 | 2.0 | 0.833 (0.0244) |
0.129 (0.0083) |
0.456 (0.0176) |
0.658 (0.0229) |
0.699 (0.0234) |
0.183 (0.0157) |
4.32 (0.16) |
0.788 |
| 1.0 | 0.208 (0.0061) |
0.032 (0.0021) |
0.114 (0.0044) |
0.164 (0.0058) |
0.175 (0.0059) |
0.040 (0.0035) |
3.94 (0.12) |
0.867 | |
| 0.5 | 0.052 (0.0015) |
0.008 (0.0005) |
0.028 (0.0011) |
0.041 (0.0014) |
0.044 (0.0015) |
0.010 (0.0008) |
3.16 (0.06) |
0.887 | |
| 200 | 2.0 | 0.411 (0.0123) |
0.060 (0.0041) |
0.223 (0.0092) |
0.335 (0.0117) |
0.364 (0.0129) |
0.080 (0.0057) |
4.03 (0.13) |
0.926 |
| 1.0 | 0.103 (0.0031) |
0.015 (0.0010) |
0.056 (0.0023) |
0.084 (0.0029) |
0.091 (0.0032) |
0.020 (0.0014) |
3.33 (0.06) |
0.950 | |
| 0.5 | 0.026 (0.0008) |
0.004 (0.0003) |
0.014 (0.0006) |
0.022 (0.0008) |
0.023 (0.0008) |
0.005 (0.0003) |
2.98 (0.01) |
0.960 | |
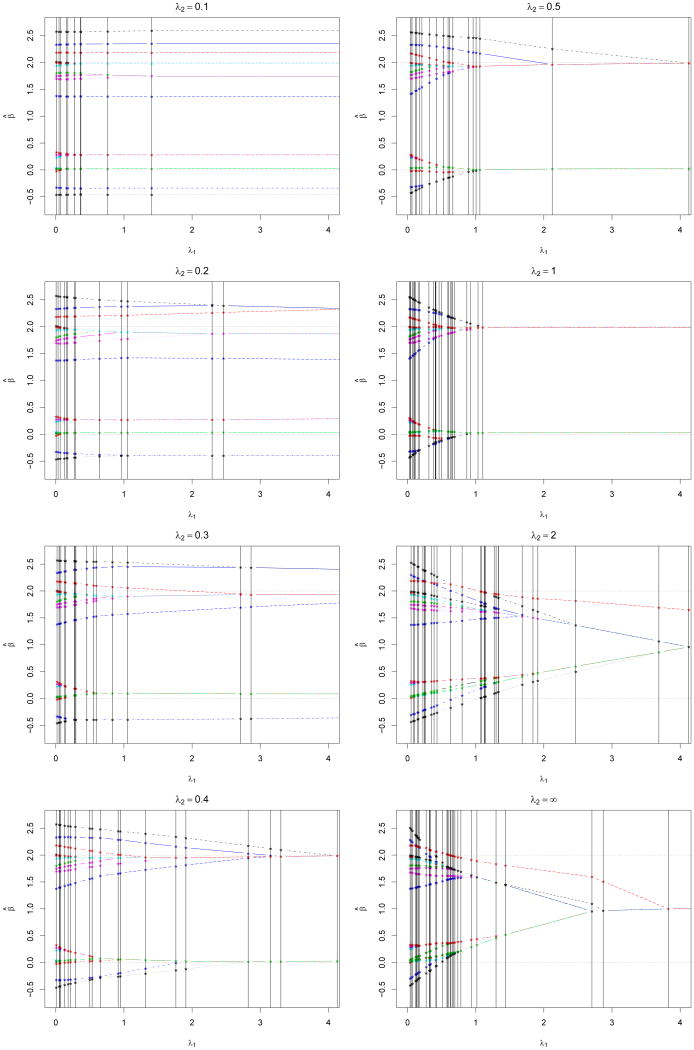
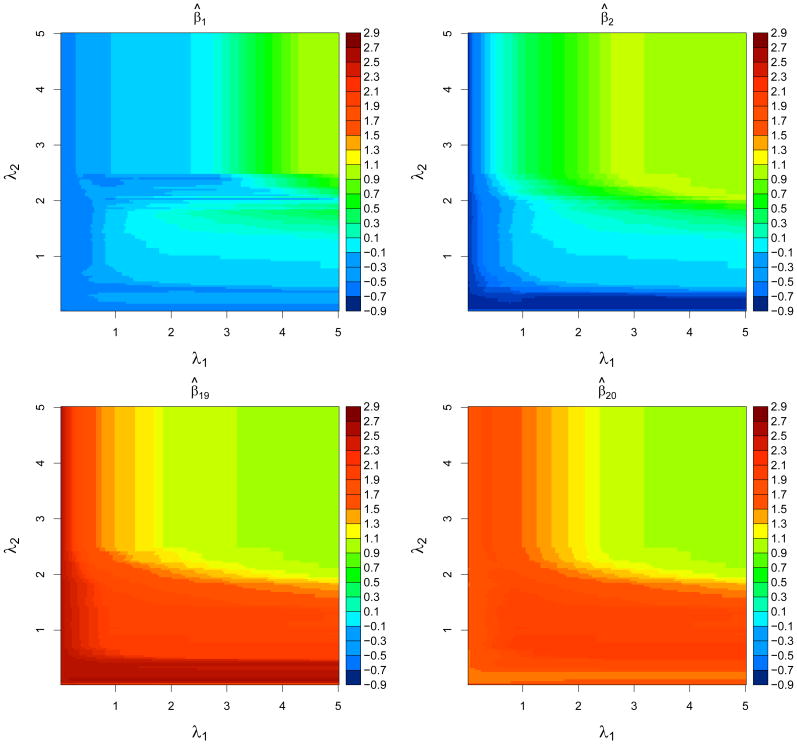
Figure 1 displays the paths in λ1 given various values of λ2 with λ0 = .2. Clearly, β̂(λ) is continuous in λ1 given (λ0, λ2) and has jumps in λ2 given (λ0, λ1), as discussed early. Figure 2 shows four two-dimensional DCE solution surfaces for (β̂1(λ), β̂2(λ), β̂19(λ), β̂20(λ)) with respect to λ. In Figure 2, the four estimates are close to their corresponding least squares estimates when either λ1 or λ2 becomes small. On the other hand, they tend to be close to each other when both λ1 and λ2 become large. Note that some jumps in λ2 are visible for β̂1(λ) around λ = (0.2, 2.5, 2.5).
Figure 1.
Plots of β̂(λ) as a function of λ1 for various λ2 values with λ0 = .2 and σ = 1.2 in Example 1. Different components of β̂(λ) are represented by different types of lines and colors.
Figure 2.
Image plots of regularization solution surfaces of four components β̂1(λ), β̂2(λ), β̂19(λ), and β̂20(λ) as a function of (λ1, λ2) for λ0 = 0.2 and σ = 1.2 in Example 1.
Example 2 (Large p but small n)
A random sample of {(xi, Yi) : i = 1, …, n} with n = 50, is obtained, where Yi follows (2) with εi ∼ N(0, σ2), σ = .41, .58, p = 50, 100, and xi is sampled from N(0, Σ) with the (j, k)th element of Σ being 0.5|j−k|. Here .
In this “large p but small n” example, DCE outperforms its convex counterpart with regard to predictive performance in all the cases, but the amounts of improvement vary. Here, the Lasso performs slightly better in some cases, which is expected because of the large group size of zero-coefficient predictors. Interestingly, the average number of iterations for Algorithm 2 is about 3 as compared to 4 in Example 1. Finally, the matching proportion for grouping is reasonably high.
Example 3 (Small p but large n)
Consider Examples 4 and 5 of Bondell and Reich (2008), which are low-dimensional with relatively large dimensions. Their Example 4 is the same as Example 1 except that n = 100, p = 40, σ2 = 152 and . Their Example 5 has a similar setting, but with n = 50, p = 40, σ2 = 152, and , where xi ∼ N(0, V), and V is a block-diagonal matrix with diagonal blocks , , and Ip−15. In addition, the first 15 components of xi are added to independent noise distributed as N(0, .16) to generate three equally important groups having pairwise correlations being around 0.85.
Overall DCE performs comparably with OSCAR in these noisy situations with σ2 = 152, which performs better but worst, respectively in Examples 4 and 5 of Bondell and Reich (2008). This is mainly due to the fact that DCE does not select variables beyond grouping. This aspect was also evident from Table 2, where DCE performs worse than Lasso in some cases. Most noticeably, DCE performs slightly worse than its convex counterpart when σ is very large. This is expected because an adaptive method tends to perform worse than its non-adaptive counterpart in a noisy situation.
Table 2.
MSEs as well as estimated standard errors (in parentheses) for various methods based on 100 simulation replications in Example 2. Here Full, True, Lasso, Convex, DCE denote the least squares estimates based on the full model, the true model, the Lasso estimate, our convex counterpart based on iteration m = 0, and our estimate.
| p | n | σ | Full | True model | Lasso | Our | Ave # Iter | Ave match proportion | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Grouping | Variable | Convex | DCE | |||||||
| 50 | 50 | 0.58 | 0.327 (0.007) |
0.041 (0.002) |
0.142 (0.004) |
0.227 (0.006) |
0.276 (0.006) |
0.123 (0.010) |
3.01 (0.07) |
0.799 |
| 50 | 100 | 0.41 | 0.089 (0.002) |
0.010 (0.001) |
0.037 (0.001) |
0.056 (0.002) |
0.075 (0.002) |
0.011 (0.001) |
3.12 (0.03) |
0.862 |
| 100 | 50 | 0.58 | 0.325 (0.007) |
0.037 (0.002) |
0.136 (0.004) |
0.311 (0.007) |
0.327 (0.007) |
0.325 (0.007) |
2.17 (0.04) |
0.778 |
| 100 | 100 | 0.41 | 0.165 (0.003) |
0.010 (0.001) |
0.034 (0.001) |
0.073 (0.002) |
0.116 (0.003) |
0.110 (0.003) |
2.06 (0.02) |
0.722 |
5.2 Breast cancer metastasis and gene network
Mapping the pathways giving rise to metastasis is important in breast cancer research. Recent studies suggest that gene expression profiles are useful in identifying gene subnetworks correlated with metastasis. Here we apply our proposed method to understand the functionality of subnetworks of genes for predicting the time to metastasis, which may provide novel hypotheses and confirm the existing theory for pathways involved in tumor progression.
The breast cancer metastasis data (Wang et al., 2005; Chuang et al., 2007) contain gene expression levels of 8141 genes for 286 patients, 107 of whom were detected to develop metastasis within a five year follow-up after surgery. To utilize the present gene network knowledge, we explore the PPI network previously constructed in Chuang et al. (2007).
For breast metastasis, three tumor suppressor genes–TP53, BRACA1 and BRACA2, are known to be crucial in preventing uncontrolled cell proliferation and repairing the chromosomal damage. Certain mutations of these genes increase risk of breast center, c.f., Soussi (2003). In our analysis, we construct a subnetwork of Chuang et al. (2007), consisting of genes TP53, BRCA1 and BRCA2, as well as genes that were regulated by them. This leads to 294 expressed genes for 107 patients who developed metastasis.
For subnetwork analysis, consider a vector of p predictors, each corresponding to one node in an undirected graph together with edges connecting nodes. Also available is a vector of network weights w ≡ (w1, …, wp)T, indicating relative importance of the predictors. The weight vector reflects the biological importance of a “hub” gene. Given predictors ,
| (16) |
where β̃ ≡ (β̃1, …, β̃p)T is a vector of regression coefficients, and x̃i is independent of εi. In (16), we aim to identify all possible homogenous subnetworks of predictors with respect to w. That is, within each group {j1, …, jK} ⊂ {1, …, p}. Model (16) reduces to (1) by letting xi = (w1x̃i1, …, wpx̃ip)T and . Note that existence of a path between nodes j and j′ in the undirected graph indicates if predictors xj and xj′ can be grouped. However, our network is a complete graph in this application.
For data analysis, the 107 patients are divided randomly into two groups with 70 and 37 patients, respectively for model-building and validation. For model building, an estimated MSE based on the generalized degrees of freedom is minimized with regard to a set of grid points over the path of λ1 > 0, and λ2 ∈ {0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, ∞}, where is the largest transition point corresponding to λ2 = ∞, to obtain the optimal tuning parameters based on the data perturbation method, c.f., Shen and Huang (2007). Moreover, we take Yi as the log time to metastasis (in months) and xi to be the expression levels with dimension p = 294, together with a Laplacian weight vector , where dj is the number of directed nodes connecting to node j, c.f., Li and Li (2008).
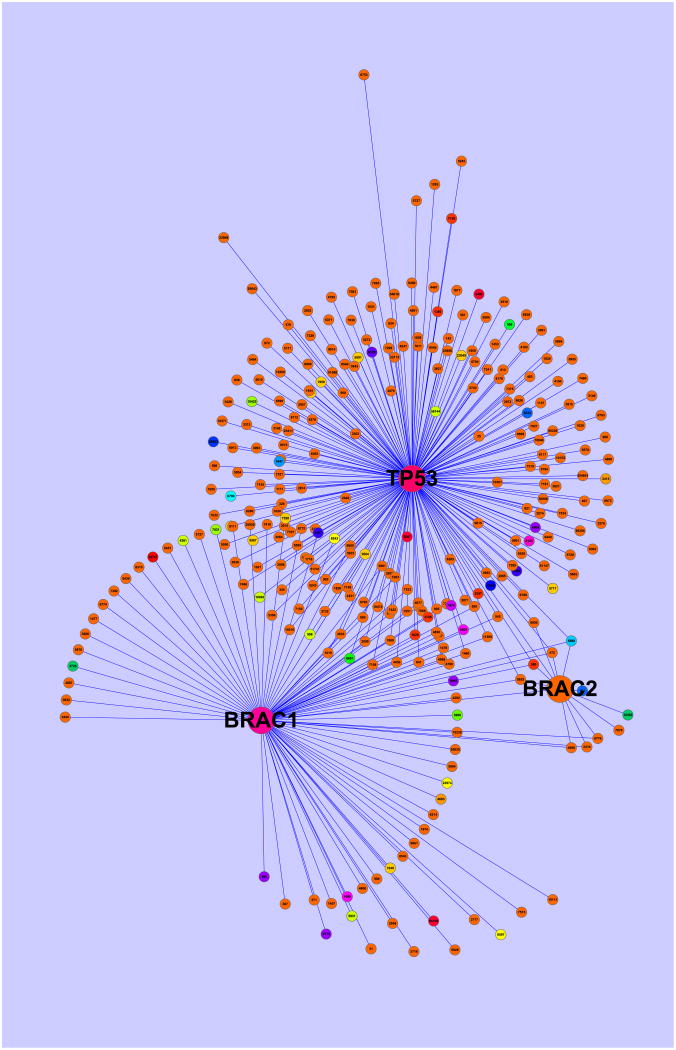
Table 3 summarizes the estimated grouped regression coefficients based on 27 estimated groups with the corresponding subnetworks displayed by different colors in Figure 3. Interestingly TP53 and BRACA1 are similar but they differ from BRACA2, as evident by the corresponding color intensities in Figure 3, indicating the roles that they play in the process of the metastasis. To make a sense of the estimated grouping, we examine the disease genes causing the metastasis, which were identified in Wang et al. (2005). Among the 17 disease genes expressed in our network, 1, 1, 1, 1 and 13 genes belong to the second, 13th, 14th, 17th and 18th groups, respectively. In fact, three disease genes form single groups, and one disease gene belongs to a small group, and 13 of them are in a large group, indicating that genes work in groups according to their functionalities with regard to survivability of breast cancer. In our analysis, the mean squared prediction error is .81 based on the testing data set of 37 observations, which yields the MSE of .3. This is reasonably good relative to the estimated σ2 = .51.
Table 3.
Median MSEs based on 100 simulation replications in Example 3. Here Full, True, Lasso, OSCAR, E-NET, Convex, DCE denote the least squares estimates based on the full model, the true model, the Lasso estimate, the elastic net estimate, the OSCAR estimate, our convex counterpart based on iteration m = 0, and our estimate. Note that the results for OSCAR and E-NET in Examples 4 and 5 of Bondell and Reich (2008) with σ = 15 are taken from Table 1 there.
| Bondell & Reich | σ | Full | True model | Lasso | E-NET | OSCAR | Our | Ave # Iter | Ave match proportion | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | Variable | Conv | DCE | ||||||||
| Ex 4 | 15 | 95.1 | 6.2 | 47.4 | 45.4 | 34.4 | 25.9 | 21.4 | 22.0 | 2 | 0.516 |
| Ex 5 | 15 | 174.8 | 11.6 | 67.4 | 64.7 | 40.7 | 51.8 | 67.6 | 70.0 | 4 | 0.535 |
| 10 | 77.7 | 5.1 | 30.0 | 33.1 | 35.3 | 38.0 | 4 | 0.575 | |||
| 5 | 19.4 | 1.3 | 7.5 | 10.7 | 10.4 | 6.0 | 4.5 | 0.626 | |||
| 1 | 0.86 | 0.05 | 0.30 | 0.47 | 0.43 | 0.06 | 3 | 0.703 | |||
Figure 3.
Plot of the PPI subnetwork for the metastasis data, as described by an undirected graph with 294 nodes and 326 edges. Three regulating genes TP53, BRACA1 and BRACA2 are represented by large nodes. There are 27 estimated groups colored over the color spectrum with dark color corresponding to small estimated group regression coefficients. The plot is produced in Cytoscape.
6 Discussion
This article proposes a novel grouping pursuit method for high-dimensional least squares regression. The proposed method is placed in the framework of likelihood estimation and model selection. It offers a general treatment to a continuous but non-differentiable nonconvex likelihood problem, where the global penalized maximum likelihood estimate is difficult to obtain. Remarkably, our DC treatment yields desired statistical properties expected from the global penalized maximum likelihood estimate. This is mainly because the DC score equation defined through subdifferentials equals to that of the original nonconvex problem, when the termination criterion is met, c.f., Theorem 2. In this process, the continuous but non-differentiable penalty is essential, At present the proposed method is not designed for feature selection. To generalize, one may replace J(β) by in (2). Moreover, estimation of the tuning parameters needs to be further investigated with regard to the accuracy of selection. Further research is therefore necessary.
7 Technical proofs
Proof of Lemma 1
We prove by contradiction. Without loss of generality, assume that is a local minimum of f(β) = h(β) + λ1J(β) attaining at the locally non-smooth concave point λ2 for pair (1, 2) in that . Let , and . Denote by the right derivative of J1(β1) at to be b. By assumption, its left derivative at must be b + λ1. Consider the derivative of h1(β1) at . Note that f1(β1) achieves a local minimum at , implying that its right and left derivatives at are larger than 0 and less than 0. Hence the right and left derivatives of h1(β1) at is larger than −b and smaller than −b − λ1. This contradicts to the fact that h1(β1) is differentiable in β1 for any λ2 > 0. This completes the proof.
Proof of Theorem 1
To prove continuity in λ1, note that the derivative of (5) with respect to β is continuous in λ1 because is independent of λ1. By convexity of (5) in β and uniqueness of β̂(m)(λ), β̂(m)(λ) is continuous in λ1 for each m.
Next we derive an expression for α̂(m)(λ). If K(m)(λ) = 1 and , then the result follows from (5). Now consider the case of K(m)(λ) ≥ 2. For any j = 1, …, p, write as Sign , where j′ ∼ j if j′ and j are in the same group and j′ ≁ j otherwise. Differentiating (5) with respect to β, we obtain
| (17) |
which is an optimality condition (Rockafellar and Wets, 2003). For k = 1, …, K(m)(λ), invoking the sum-to-zero constraint , we have , implying (6). Thus (8) follows from (17).
Proof of Proposition 1
By definition, is piecewise linear and continuous in λ1, and is strictly monotone because and .
Lets gk = | k| − 1. For Algorithm 1, the complexities for Steps 1 and 2 are O(np2). In Step 3, sorting for computing search points is no greater than
for group
k| − 1. For Algorithm 1, the complexities for Steps 1 and 2 are O(np2). In Step 3, sorting for computing search points is no greater than
for group  k. Hence the complexity for Step 3 is O(p2 log p) using the fact that
, because the complexity of search in Step 3 is no great than log p for the bisection (Fibonacci) search. Then the complexity for Algorithm 2 is O(m*n*p2(log p + n)). This completes the proof.
k. Hence the complexity for Step 3 is O(p2 log p) using the fact that
, because the complexity of search in Step 3 is no great than log p for the bisection (Fibonacci) search. Then the complexity for Algorithm 2 is O(m*n*p2(log p + n)). This completes the proof.
Proof of Theorem 2
Uniqueness of the solution follows from strict convexity of S(m)(β) in β for each m under the assumption that is invertible.
Our plan is to prove the result for λ1 = λ0 with λ = (λ0, λ0, λ2)T. Then controlling at this point implies the desirable result for all λ. In what follows, we set λ1 = λ0 unless indicated otherwise. For convergence of Algorithm 2, it follows from (2) and (5) that for m ∈ ℕ, 0 ≤ S(β̂(m)(λ)) = S(m+1)(β̂(m)(λ)) ≤ S(m)(β̂(m)(λ)) ≤ S(m)(β̂(m−1)(λ)) = S(β̂(m−1)(λ)). This implies that limm→∞ S(β̂(m)(λ)) exists, thus leading to convergence. To study the number of steps to termination, note that S(m)(β̂(m−1)(λ)) − S(m)(β̂(m)(λ)) can be written as
which can be simplified, using the following equality from (17), , as , where . By convexity of |z|, , implying S(β̂(m−1)(λ)) − S(β̂(m) (λ)) ≥ S(m) (β̂(m−1) (λ)) −S(m) (β̂(m) (λ)) is bounded below by . That is, is greater than zero unless α̂(m) (λ) = α̂(m−1) (λ).
Finally, finite step convergence follows from strict decreasingness of S(m)(β̂ (λ)) in m and finite possible values of ∇S2(β̂(m−1) (λ)) in (5). For (14), note that when termination, ∇S2(β̂(m−1) (λ)) remains unchanged for m ≥ m*, so does the cost function (5) for m ≥ m*. This implies termination for all λ = (λ0, λ1, λ2)T in (14). This completes the proof.
Proof of Theorem 3
Define event
By (17) with m = m* and (14), for k = 1, …, K, β̂(λ) = β̂(m)(λ) satisfies
| (18) |
for some partition ( 1, …,
1, …,  K) of {1, …, p} with K ≤ min {n, p}, where Δj(β) ≡ Σj′:j′≠j {Sign(βj − βj′) − ∇G2(βj − βj′)}; j = 1, …, p.
K) of {1, …, p} with K ≤ min {n, p}, where Δj(β) ≡ Σj′:j′≠j {Sign(βj − βj′) − ∇G2(βj − βj′)}; j = 1, …, p.
Note that the first event in F, together with the grouped subdifferentials, yields that ; k = 1, …, K0. This, together with the least squares property that , implies that the first equation of (18) is fulfilled with β = β̂(ols). Moreover, the events in F imply the second equation of (18) with β = β̂(ols). Consequently β̂(ols) is a solution of (18) on F.
It remains to show that (18) yields the unique minimizer on F. Define
for ν = 1/2. Given any grouping  with |
with | | ≤ K*, S̃(β) is a function of α
| ≤ K*, S̃(β) is a function of α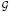 with β = (α11|
with β = (α11|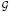 1|, …, αK1|
1|, …, αK1| K|)T. Then
is strictly convex in α
K|)T. Then
is strictly convex in α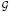 ∈ ℝ|
∈ ℝ|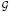 | when
, which occurs when
. To prove that β̂(ols) is the unique minimizer of S̃(β), suppose β̃ is another minimizer of S̃(β) with
| when
, which occurs when
. To prove that β̂(ols) is the unique minimizer of S̃(β), suppose β̃ is another minimizer of S̃(β) with 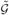 the corresponding grouping and |
the corresponding grouping and |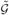 | < K*. Because
and (K*)2 ≤ n, it follows that S̃(β) is strictly convex in α
| < K*. Because
and (K*)2 ≤ n, it follows that S̃(β) is strictly convex in α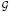 0∨
0∨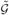 ∈ ℝ|
∈ ℝ|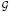 0∨&
0∨&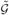 |, implying β̃ = β̂(ols), where
|, implying β̃ = β̂(ols), where  0 ∨
0 ∨ 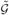 is the coarsest common refinement of
is the coarsest common refinement of  0 and
0 and 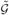 with |
with | 0 ∨
0 ∨ 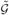 | ≤ min{n, p}.
| ≤ min{n, p}.
To prove that β̂(ols) is the unique minimizer of S(β) on F, we let  * =
* =  0 ∨
0 ∨  with |
with | | ≤ K*. Let
be the estimate corresponding to β̂(ols). By the mean value theorem,
is lower bounded by
| ≤ K*. Let
be the estimate corresponding to β̂(ols). By the mean value theorem,
is lower bounded by
| (19) |
Note that S̃(β) = S(β) over E = {β : ||αk − αl| − λ2| > λ2/2 : 1 ≤ k < l ≤ | |}. Moreover, by construction,
on F, which implies, together with (19), for any β ≠ β̂(ols) ∈ Ec,
is
|}. Moreover, by construction,
on F, which implies, together with (19), for any β ≠ β̂(ols) ∈ Ec,
is
which is lower bounded by , because . This, together with Lemma 1, implies that S(β) has no local minimal in Ec on F, and hence it has the unique local minimal on F. On the other hand, β̂(λ) is a local minimizer of S(β) on F. Consequently, β̂(ols) = β̂(λ) on F.
Note that
with
, and
with
. It follows that P( (λ) ≠
(λ) ≠  0) ≤ P(β̂(λ) ≠ β̂(ols)) ≤ P(Fc), which is upper bounded by
0) ≤ P(β̂(λ) ≠ β̂(ols)) ≤ P(Fc), which is upper bounded by
where and ek is the kth column of Ip. Using an inequality that , we obtain the desired bound.
Proof of Corollary 1
It is a direct consequence of Theorem 3 and the least squares property. The proof is thus omitted.
Proof of Theorem 4
By Theorem 2, β̂(λ) = β̂(m*)(λ). From (3), for any j ∈  k(λ); k = 1, …, K(λ), we have |Bj(λ)| ≤ |
k(λ); k = 1, …, K(λ), we have |Bj(λ)| ≤ | k(λ)| − 1. Note further that for j ∈
k(λ)| − 1. Note further that for j ∈  k(λ), Δj(λ) can be rewritten as Δj(λ) = Σk′:k′≠k {|
k(λ), Δj(λ) can be rewritten as Δj(λ) = Σk′:k′≠k {| k′(λ)|(Sign (α̂k(λ) − α̂k′(λ)) − ∇G2(α̂k(λ̂(0)) − α̂k′(λ̂(0))))}. By (17), |rj(β̂(λ)) − nλ1Δj(λ)| ≤ nλ1|Bj(λ)|, implying
.
k′(λ)|(Sign (α̂k(λ) − α̂k′(λ)) − ∇G2(α̂k(λ̂(0)) − α̂k′(λ̂(0))))}. By (17), |rj(β̂(λ)) − nλ1Δj(λ)| ≤ nλ1|Bj(λ)|, implying
.
For disjointness of Ek(λ)'s, assume, without loss of generality, that α̂1(λ) < ⋯ < α̂K(λ)(λ). For any j ∈  k(λ), j′ ∈
k(λ), j′ ∈  k′(λ), and k < k′, Δj(λ) − Δj′(λ) = (|
k′(λ), and k < k′, Δj(λ) − Δj′(λ) = (| k′(λ)| + |
k′(λ)| + | k′(λ)|)(k′ − k) > (|
k′(λ)|)(k′ − k) > (| k′(λ)| − 1) + (|
k′(λ)| − 1) + (| k(λ)| − 1), implying disjointness.
k(λ)| − 1), implying disjointness.
Table 4.
Estimated group coefficients and group sizes for breast cancer data in Section 5.3.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| α̂k | −0.634 | −0.507 | −0.449 | −0.416 | −0.381 | −0.370 | −0.244 | −0.225 | −0.205 |
| k| k| |
1 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 4 |
| k | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| α̂k | −0.116 | −0.059 | −0.041 | −0.018 | −0.017 | −0.017 | 0.006 | 0.039 | 0.048 |
| k| k| |
1 | 2 | 1 | 1 | 1 | 3 | 1 | 6 | 237 |
| k | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| α̂k | 0.060 | 0.105 | 0.110 | 0.127 | 0.140 | 0.247 | 0.301 | 0.361 | 0.392 |
| k| k| |
2 | 10 | 3 | 5 | 2 | 1 | 1 | 1 | 2 |
Footnotes
Xiaotong Shen is Professor, School of Statistics, University of Minnesota, 224 Church Street S.E., Minneapolis, MN 55455 (E-mail: xshen@stat.umn.edu). His research is supported in part by National Science Foundation Grant DMS-0906616 and National Institute of Health Grant 1R01GM081535. Hsin-Cheng Huang is Research Fellow, Institute of Statistical Science, Academia Sinica, Taipei 115, Taiwan (E-mail: hchuang@stat.sinica.edu.tw). He is supported in part by Grant NSC 97-2118-M-001-001-MY3. The authors thank the editor, the associate editor and three referees for their helpful comments and suggestions.
References
- 1.An HLT, Tao PD. Solving a class of linearly constrained indefinite quadratic problems by D.C. algorithms. J Global Optim. 1997;11:253–85. [Google Scholar]
- 2.Allgower EL, George K. Introduction to Numerical Continuation Methods. SIAM; 2003. [Google Scholar]
- 3.Bondell HD, Reich BJ. Simultaneous regression shrinkage, variable selection, and supervised clustering of predictors with OSCAR. Biometrics. 2008;64:115–23. doi: 10.1111/j.1541-0420.2007.00843.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chuang HY, Lee EJ, et al. Network-based classification of breast cancer metastasis. Molecular Systems Biology. 2007;3:140. doi: 10.1038/msb4100180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Efron B. The estimation of prediction error: covariance penalties and cross-validation. J Amer Statist Assoc. 2004;99:619–32. [Google Scholar]
- 6.Fan J, Li R. Variable selection via nonconcave penalized likelihood and its Oracle properties. J Amer Statist Assoc. 2001;96:1348–60. [Google Scholar]
- 7.Fan J. Comments on “Wavelets in statistics: a review” by A. Antoniadis. J Italian Statist Assoc. 1997;6:131–138. [Google Scholar]
- 8.Friedman J, Haste T, Hofling H, Tibshirani R. Pathwise coordinate optimization. Ann Applied Statist. 2007;1:302–332. [Google Scholar]
- 9.Li C, Li H. Network-constraint regularization and variable selection for analysis of genomic data. Bioinformatics. 2008;24:1175–82. doi: 10.1093/bioinformatics/btn081. [DOI] [PubMed] [Google Scholar]
- 10.Liu S, Shen X, Wong W. Computational developments of ψ-learning. Proc 5th SIAM Intern Conf on Data Mining; Newport, CA. April, 2005; 2005. pp. 1–12. [Google Scholar]
- 11.Liu Y, Wu Y. Variable selection via a combination of the L0 and L1 penalties. J Comput Graph Statist. 2007;16:782–798. [Google Scholar]
- 12.Gill PE, Murray W, Wright MH. Practical Optimization. Academic Press; London: 1981. [Google Scholar]
- 13.Rockafellar RT, Wets RJ. Variational Analysis. Springer-Verlag; 2003. [Google Scholar]
- 14.Rosset S, Zhu J. Piecewise linear regularized solution paths. Ann Statist. 2007;35:1012–30. [Google Scholar]
- 15.Rota GC. The number of partitions of a set. American Mathematical Monthly. 1964;71:498–504. [Google Scholar]
- 16.Shen X, Huang HC. Optimal model assessment, selection and combination. J Amer Statist Assoc. 2006;101:554–68. [Google Scholar]
- 17.Stein C. Estimation of the mean of a multivariate normal distribution. Ann Statist. 1981;9:1135–51. [Google Scholar]
- 18.Soussi T. Focus on the P53 gene and cancer: advances in TP53 mutation research. Human mutation. 2003;21:173–5. doi: 10.1002/humu.10191. [DOI] [PubMed] [Google Scholar]
- 19.Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K. Sparsity and smoothness via the fused lasso. J Royal Statist Soc, Ser B. 2005;67:91–108. [Google Scholar]
- 20.Wang Y, Klijin JG, et al. Gene-expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer. Lancet. 2005;365:671–79. doi: 10.1016/S0140-6736(05)17947-1. [DOI] [PubMed] [Google Scholar]
- 21.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J Royal Statist Soc Ser B. 2006;68:49–67. [Google Scholar]
- 22.Wu S, Shen X, Geyer C. Adaptive regularization through entire solution surface. Biometrika. 2009;96:513–527. doi: 10.1093/biomet/asp038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhao P, Rocha G, Yu B. The composite absolute penalties family for grouped and hierarchical variable selection. Ann Statist. 2009;37:3468–3497. [Google Scholar]
- 24.Zou H, Hastie T. Regularization and variable selection via the elastic net. J Royal Statist Assoc, Ser B. 2005;67:301–20. [Google Scholar]