The Genetic and Environmental Etiology of High Math Performance in 10-Year-Old Twins

Abstract

The genetic and environmental etiology of high math performance (at or above the 85%tile) was examined in a population-based sample of 10-year-old twins (nMZ = 1,279, nDZ = 2,305). Math skills were assessed using a web-based battery of math performance tapping skills related to the UK National Math Curriculum. Probandwise concordance rates and liability threshold models indicated that genetic and shared environmental influences were significant, and that these estimates were generally similar to those obtained across the normal range of ability and did not vary significantly by gender. These results suggest that the genetic and environmental influences at the high end of ability are likely to be continuous with those that affect the entire range of math performance across all children irrespective of gender.

Introduction

As noted throughout this special issue, little is known about etiology of the high extreme of academic and cognitive performance. In fact, to date no study has examined the genetic and environmental etiology of high math performance, an important omission considering that strident nature versus nurture discussions can still be found in the literature. For example, some have argued that exceptionality is driven entirely by higher levels of deliberate practices, or goal-directed work within a particular domain (e.g. Ericsson et al. 1993; Howe et al. 1998; see Winner 2000 for a discussion). According to this argument, exceptionality is not the result of innate ability but the time and effort spent in developing a particular set of skills. Conversely, others have argued for the primacy of innate factors, relying on brain-based differences associated with high performance as evidence (e.g. Geschwind and Galaburda 1987).

In contrast to these either-or approaches, behavioral genetic studies have led to a general acceptance of the importance of both genetic and environmental influences on most measures of complex cognitive behavior, including general cognitive ability (see McGue et al. 1993), reading ability (see Pennington and Smith 1983), and language skills (see Stromswold 2001). Similarly, genetic influences on unselected math performance are substantial and significant, shared environmental influences (environments that make family members similar to one another) are moderate and significant, and nonshared environmental influences (environments that make family members different, including error) are also moderate and significant (see Petrill and Plomin 2007, for a review).

Although understanding the etiology of the entire range of ability is essential, behavioral genetic studies have also focused on the extremes of ability. One important question is whether the genetic and environmental influences at the extremes of ability are continuous or discontinuous with those that operate in unselected ability (see Plomin and Kovas 2005). The Continuity Hypothesis suggests that genetic and environmental influences operate continuously across the distribution of ability and that “disability” is, therefore, the lower tail of ability. This hypothesis is supported to the extent that estimates of genetic and environmental influences are similar in magnitude to those found in the normal range of ability. In contrast, the Discontinuity Hypothesis holds that the extremes of performance are qualitatively different from the individual differences found in the normal range. This hypothesis is supported to the extent that genetic and environmental influences at the extremes are significantly different in magnitude from those estimates found in the normal range.

Most studies examining this issue have concentrated on extreme low performance, and almost all support the Continuity Hypothesis. There are a few possible exceptions related to low language skills in children (higher genetic effects) (Spinath et al. 2004; DeThorne et al. 2005) and young children with mild mental impairment (higher genetic effects) (Spinath et al. 2004). However, in most cases, genetic and environmental influences on extreme low performance are similar in magnitude, in fact, almost identical to the unselected individual differences in general cognitive ability, reading, and language skills (see Plomin and Kovas 2005). In other words, although there are cases where major genetic and environmental events lead to extreme low performance as well as instances where environmental privation may suppress genetic effects (e.g. Turkheimer et al. 2003; Rowe et al. 1999), for most children and adults, cognitive and learning disabilities appear to be the lower tail of normal ability.

In the case of low math performance, evidence for the Continuity Hypothesis has also been found in three published studies. Alarcón et al. (1997) found that the genetic influences on low math skills, as defined as ≤ −1.5 SD on the Wide Range Achievement Test, were $h_{\text{g}}^2=.38$, suggesting that almost 40% of the mean difference between the low math group and the unselected population was due to genetic differences between the two groups. This estimate is similar to the heritability estimates in unselected samples.

More recently, Oliver et al. (2004), using the same sample that was employed in the current study, conducted a comparison of genetic and environmental influences in low versus unselected math performance using a much larger sample of 2,178 pairs of 7-year-old twins from which extremes were selected so that direct comparisons could be made between the extremes and unselected samples. Low math groups were formed at or below the 15th percentile of teacher ratings of UK National Curriculum criteria, yielding 370 pairs of selected twins for analysis. Similar to Alarcón et al. Oliver suggested that the genetic and shared environmental etiology of low math performance was nearly identical to that of the unselected population. Subsequent work on this sample at 10-years using a web-based battery of math measures also suggested continuity between the normal range and low math performance (Kovas et al. 2007). Despite some point estimate differences between individual differences and the low extremes, there were no clear trends and, despite the large sample size, heritability estimates from the individual differences analyses never fell outside the 95% confidence intervals of the estimates from the analyses of extremes.

A handful of studies have examined the high extreme of academic and cognitive performance (Plomin and Thompson 1993). Two twin studies of high cognitive ability in infancy and early childhood yielded results consistent with the Continuity Hypothesis (Petrill et al. 1998; Ronald et al. 2002). Similar results have been reported for high cognitive ability later in life (Saudino et al. 1994; Petrill et al. 2001) as well as high reading performance (Boada et al. 2002). Thus, we expect that expect genetic and environmental influences on high math performance will be consistent with the Continuity Hypothesis.

Another related reason to consider the etiology of high math performance is the widespread belief in the existence and genetic etiology of gender differences related to high mathematics performance (see Hyde and Linn 2006). Meta-analytic studies have suggested that mean gender differences in mathematics are exceptionally small with almost completely overlapping distributions (e.g. Hyde et al. 1990). This has led to the emergence of a ‘gender similarities’ hypothesis, suggesting that mean male and female performance is similar on most psychological variables including mathematics (Hyde 2005; Hyde and Linn 2006). Behavioral genetic studies have examined this issue in another way; by testing whether genetic and/or environmental influences on the variability of performance vary as a function of gender. In general, behavioral genetic studies have found little consistent evidence for differential genetic and environmental influences as a function of gender (Plomin et al. 2001).

Thus, the purpose of the current study is to examine the etiology of high mathematics performance in male and female twins. Given that behavioral genetic studies at the low extreme of performance and the few studies at the high extreme suggest etiological continuity with variation in the rest of the distribution, we hypothesize that genetic and environmental influences will be statistically significant and similar in magnitude to the math skills across the unselected population. With respect to gender differences, in a previous report (Kovas et al. 2007), we found no significant gender differences in etiology of individual differences in the whole range of mathematical ability and at the low end of the distribution. Thus, we also hypothesize that we will find no gender differences at the high end of ability.

Method

Participants

The current study involved 7,168 10-year-old children comprised of 1,279 identical (MZ) pairs, 1,155 same-sex dizygotoc (DZ), and 1,150 opposite-sex DZ twin pairs drawn from the Twins’ Early Development Study (TEDS: Trouton et al. 2002), a longitudinal representative sample of all twins born in England and Wales in 1994, 1995, and 1996. This number refers to all children who took part in the study after the following exclusion criteria, commonly used in the TEDS sample, were applied: no evidence of specific medical syndromes (e.g. Down’s syndrome or other chromosomal anomalies), cystic fibrosis, cerebral palsy, hearing loss, autism spectrum disorder, organic brain damage, extreme outliers for birth weight, gestational age, maternal alcohol consumption during pregnancy, and special care after birth. Additionally, 274 children (137 pairs) for whom English was not the primary language spoken at home were also excluded from the sample. Finally, only the data from children for whom data were available for all of the mathematical tests were analyzed for this study. Thus, the final sample at the point of analysis consisted of 5,348 individuals (2,674 pairs of same- and opposite-sex twins). Zygosity was determined via parental ratings of physical similarity, which has been shown to be 95% accurate in comparison to DNA analysis (see Freeman et al. 2003). As described elsewhere (Harlaar et al. 2005), the TEDS sample is representative of the larger UK population and has remained so over the 10+ years of the study.

Measures

When determining a measurement strategy, it was necessary to assess mathematics in the large TEDS sample within the narrow time frame when twins were 10 year-sold. Given the prohibitive cost of home visits and the fact that over 80% of the TEDS sample had daily access to the internet (determined via pilot study of 100 randomly selected families), we opted for a web-based approach. As described more fully in Kovas et al. (2007), this battery was based on the National Foundation for Educational Research 5–14 Mathematics Series. This measure is linked closely to curriculum requirements in the UK and the English Numeracy Strategy (nferNelson 2001). The seventy-seven age-appropriate items from this battery were drawn from the following three categories:

Understanding number (27 items) requires an understanding of the numerical and algebraic process to be applied when solving problems (such as understanding that multiplication and division are inverse operations). For example, ‘These three numbers are alike in some ways: 9, 36, 81. Click on the two ways in which they are alike’ (Answer: multiples of 9; can be divided by 3). Cronbach’s alpha for these items was α = .88.

Non-numerical processes (19 items) requires understanding of non-numerical mathematical processes and concepts such as rotational or reflective symmetry and other spatial operations. Questions do not have any explicit numerical content. For example “Which is the longest drinking straw? Click on it”. Cronbach’s alpha for these items was α = .78.

Computation and knowledge (31 items) assesses calculation ability and recall of mathematical facts and terms. For example: “Click on each even number”. “All four-sided shapes are called? Click on the answer” (Answer: quadrilateral); or “Type in the answer: 149 + 785 = ?” (Answer: 934). Cronbach’s alpha for these items was α = .93.

Composite (77 items) Test scores were moderately correlated, r = .62 between Understanding Number and computational processes, r = .63 between Understanding Number and Computation and Knowledge, and r = .51 between computational processes and Computation and Knowledge. Principal components factor analysis yielded a general factor (unrotated first principal component) that explained 75% of the total variance (eigen = 2.24). Thus, a composite score was formed by summing performance on all 77 items. Moreover, the correlation was r = .53 (P < .001, N = 1,878) between this web-based composite score and an overall rating of mathematics performance as assessed by their teachers on the National Curriculum Criteria.

As a direct test of the validity of the web-based measures, we conducted a test–retest study in which 30 children (members of 15 twin pairs) who had completed the web-based testing were administered the tests in person using the standard paper and pencil version of the test (nferNelson 2001). Stratified sampling was used to ensure coverage of the full range of ability. The interval between test and retest was 1–3 months with an average of 2.2 months. The total math score from our web-based tests correlated .92 with the total score from the in-person testing for the total sample of 30 children; generalized estimation equations (GEE) that take into account the nested covariance structure also yielded a correlation of .93. For the three subtests reported in this paper the correlations between the web and the paper and pencil scores were .77, .64, and .81 for Understanding Number, Non-numerical Processes, and Computation and Knowledge, respectively.

Procedure

As described more fully in Kovas et al. (2007), the web-based measures were administered by a secure server. After parents logged in with a user name and password for the family, they were asked to examine a demonstration test and complete an online consent form. Each twin then completed the test separately. Adaptive branching was employed so the difficulty of the test was tailored to the ability level of each child. Items were selected from a large pool across different levels of the National Curriculum. Children could only answer the same item once and technical support and other advice was provided to parents and children, if necessary, via a toll-free number. Subsequent analysis suggested that 80% of TEDS children had access to broadband, 10% had access to dial-up, and only 7% had no home access. Of those families who did not have access to the internet at home, 46% completed the battery elsewhere.

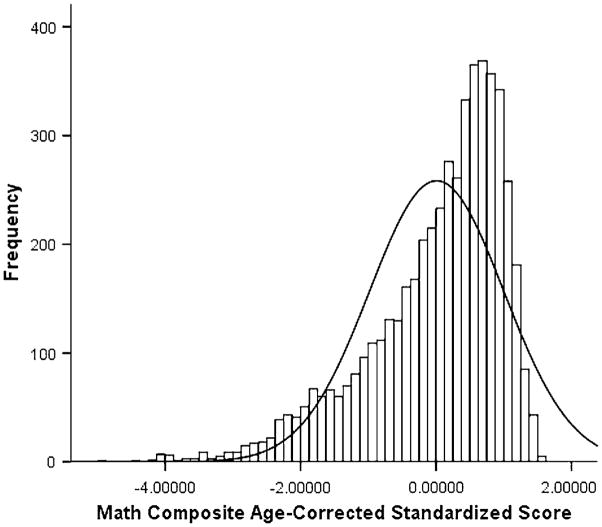
In order to examine high math ability, each math sub-component as well as the composite was first corrected for age using a regression procedure. As presented in Fig. 1, the distribution of test scores for the Math Composite is some-what skewed with ceiling effects. Thus separate groups were then formed at or above the 85%tile for Understanding Number, Non-numerical Processes, Computation and Knowledge and the math composite standardized residuals. This cutoff was selected to not only because of ceiling effects, but also to ensure adequate sample size in the high math group. Table 1 also presents the range of scores and Key Stage 2 level equivalents for each selected group. In all cases, children who were selected into high math groups were performing at least at the level expected for children in the next year of school. In terms of gender, 50% of probands were boys for Understanding Number, 52% were boys for Computation and Knowledge, 52% were boys for Non-numerical Processes, and 54% were boys for the Composite Score. When considering the entire range of ability, as described in Davis et al. (2008) mean gender differences in math performance were statistically significant but accounted for less than .5% of the total variance in math. Finally, in addition to exclusions described in the method section, we also excluded from further analyses all pairs in which one or both twins had missing data; this was done separately for each category.

Fig. 1.

Distribution of math composite

Table 1.

Means, range standard deviations (SD) and scores corresponding to the proband cut-offs for the three mathematics measures

Measure	Total number of items in category	Cut-off (%)	Range of items (min–max) for probands	Mean (SD) for probands	Link to the National Curriculum level and standardization informationa
Understanding number	27	85	25–27	26.18 (.62)	All children perform above their grade-level difficulty, solving items as high as level 5, recommended for children in the following year of education
Non-numerical processes	19	85	16–19	17.49 (.71)	Most children perform above their grade-level difficulty, solving items as high as levels 5 and 6, recommended for children in the following year of education
Computation and knowledge	31	85	30–31	30.66 (.46)	The top items are as difficult as level 5, recommended for children in the following year of education

^aNational Curriculum uses seven levels (level 8 = exceptional performance). Children at Key Stage 2 (7–11 year-olds) are expected to work with levels 2–5, and most children are expected to attain level 4 by the end of the year during which we tested our sample

Results

Probandwise concordance rates

First, we examined probandwise concordance rates, which are defined as the ratio of concordant probands (both twins in a family at or above the 85%tile) divided by the total number of probands (all twins at or above the 85%tile). This statistic indicates how often individuals scoring above the 85th percentile come from the same family. Table 2 presents probandwise concordance rates for MZ males, MZ females, DZ males, DZ females, and DZ opposite-sex pairs. In general, concordance rates are higher in MZ twins (39–59%) compared with DZ twins (30–44%), indicating genetic influences. However, concordance rates for DZ pairs approach MZ probandwise concordance rates in most cases, suggesting shared environmental influences. Finally, concordance rates are roughly equal when comparing MZ males to MZ females and when comparing DZ males, to DZ females, to opposite-sex DZ pairs, indicating similar genetic and environmental influences for males and females and same-sex and opposite-sex DZ pairs.

Table 2.

Probandwise twin concordances and number of affected individuals (probands) for high mathematical ability at 85% cut-offs organized by gender and zygosity for the three measures and the composite

Variable	MZ m	DZ m	MZ f	DZ f	DZ opp
Understanding number	48% n = 120	31% n = 124	49% n = 143	35% n = 119	34% n = 248
Non-numerical processes	42% n = 128	42% n = 130	39% n = 139	40% n = 115	35% n = 239
Computation and knowledge	46% n = 135	30% n = 121	44% n = 131	38% n = 125	31% n = 239
Composite	59% n = 123	40% n = 144	58% n = 135	44% n = 117	37% n = 239

Note: All extremes analyses were calculated on age-, but not sex—regressed scores

Structural equation modeling

Although informative, probandwise concordance rates do not provide inferential statistics for genetic and environmental effects related to high math ability. Therefore, they cannot be used to examine whether genetic and environmental influences are significant in high math groups, whether these estimates vary meaningfully from unselected math ability, and whether these estimates vary by gender. The liability-threshold model (see Sham 1998) is a type of quantitative genetic model that can be used to systematically examine concordance data. This model assumes a normally distributed liability with a mean of zero and a standard deviation of 1. This liability is inferred by comparing the concordance rates within families to the incidence rate across families for groups selected above or below a threshold of a particular trait, in this case, math scores at or above the 85th percentile. To accomplish this, for each math measure, data from the entire twin sample were organized into 2 × 2 contingency tables, where cells represent pairs in which both twins are below the 85th percentile, both twins are at or above the 85th percentile, and two discordant cells where twin one or twin two are at or above the 85th percentile. These data can then be used to quantify genetic and environmental sources of variation in liability in the population.

In order to examine sex-differences we employed a sex-limited extension of the liability threshold model (Neale 1997). The model estimates genetic and environmental effects as described above, but also examines four possibilities with respect to the etiology of individual differences and mean differences in boys and girls. The first possibility examines mean differences, in particular whether thresholds are equal across genders. If thresholds are equal, mean gender differences are not significantly different from zero.

The second possibility examines potential gender differences in the etiology of the variance of high math performance; whether different sets of genetic and environmental factors are responsible for individual differences in mathematics for boys and girls. These qualitative differences are reflected in the genetic correlation (r_g) between DZ opposite-sex twins. In DZ same-sex pairs, the assumption is that on average the twins share 50% of their varying DNA, and the coefficient of genetic relatedness (the genetic correlation between the two children) is therefore .5. If there are qualitative differences, the correlation between opposite-sex DZ pairs will be attenuated relative to same-sex DZ pairs. Such sex-specific effects are not limited to genes on the X chromosome but can also involve different sets of genes on the autosomal chromosomes that affect boys and girls differently, for example, because the genes interact with sex hormones.

The third possibility, not mutually exclusive with the second, is that the same set of genes and environments affect individual differences in high math performance in boys and girls, but that they operate in different proportions. These are known as quantitative differences. If there are quantitative differences, the genetic correlation for DZ opposite-sex pairs will be .5, but the parameter estimates for the A, C, and E components will be significantly different for male–male pairs and female–female pairs.

The fourth possibility is that there are no differences in the etiology of individual differences in high math performance for boys and girls. In this case, DZ opposite-sex (DZos) pairs will have a genetic correlation of .5 and the A, C, and E estimates for male–male and female–female pairs will be the same, and the thresholds on the normal distribution are equal for the two sexes.

These possibilities were tested using the model-fitting program Mx (Neale et al. 2002). In this study a structural equation model was fit to the contingency tables by maximum likelihood to estimate additive genetic (a²) shared environmental (c²) and nonshared environmental (e²) parameters. Mx was also used to provide 95% confidence intervals for these estimates.

Four models were fit to the data. First, we tested the Full Model which allowed for mean differences, qualitative differences, and quantitative differences across gender. This was fit to variance/covariance matrices derived from the raw data. Three nested models were then tested (see Table 3). Model fit was evaluated using three indices. The χ² change statistic, where degrees of freedom equal the number of observed correlations minus the number of estimated parameters, indicates the fit of the full model and also tests the fit of nested models, with a lower value indicating better fit (with degrees of freedom equal to the difference in degrees of freedom between the full and nested models). The other two indices used were Akaike’s information criterion (AIC = χ² − 2df; Akaike 1987) and the root mean square error of approximation (RMSEA), with lower values representing better fitting models.

Table 3.

Liability threshold model fitting analyses

	Model	χ2	df	P	AIC	RMSEA	χ2dif	dfdif	Pdif
Understanding number	Full	3.03	8	.93	−12.97	.000
	Threshold	12.97	9	.16	−5.02	.004	9.94	1	< .05
	Common variance	3.03	9	.96	−14.97	.000	.00	1	> .05
	Scalar	4.45	12	.97	−19.55	.000	1.42	4	> .05
Non-numerical processes	Full	2.50	8	.96	−13.50	.000
	Threshold	17.92	9	.04	−.09	.012	15.42	1	< .05
	Common Variance	2.50	9	.98	−15.50	.000	.00	1	> .05
	Scalar	3.55	12	.99	−20.45	.000	1.05	4	> .05
Computation and knowledge	Full	5.62	8	.69	−10.38	.000
	Threshold	20.25	9	.02	2.25	.018	14.63	1	< .05
	Common variance	5.62	9	.78	−12.38	.000	.00	1	> .05
	Scalar	8.74	12	.73	−15.26	.003	3.12	4	> .05
Composite	Full	6.02	8	.65	−9.98	.000
	Threshold	37.09	9	.00	19.09	.033	31.07	1	< .05
	Common variance	6.02	9	.74	−11.98	.000	.00	1	> .05
	Scalar	8.35	12	.74	−15.48	.000	2.33	4	> .05

The first submodel (Threshold) equated thresholds for males and females to test whether mean differences were significantly different from zero. This model resulted in a significant decrease in model fit for Understanding Number (χ²_dif = 9.94, df_dif = 1, P_dif < .05), Non-numerical Processes (χ²_dif = 15.42, df_dif = 1, P_dif < .05), Computation and Knowledge (χ²_dif = 14.63, df_dif = 1, P_dif < .05), and Math Composite (χ²_dif = 31.07, df_dif = 1, P_dif < .05), suggesting that mean differences between genders. In all cases the mean threshold differences favored males and were less than .18 standard deviation units. Subsequent submodels were fit to the data allowing for threshold (mean) differences between males and female twins.

The remaining submodels examined the statistical significance of qualitative and quantitative gender differences in high math performance. In particular, the second sub-model (Common Variance) set qualitative differences to zero, but allowed for quantitative differences in genetic and environmental effects. This was accomplished by fixing r_g to .5 in opposite-sex DZ pairs, but allowed different A, C, E and variance estimates in boys and girls. This model did not result in a significant decrease in model fit (χ²_dif = .00 for all variables).

The third submodel (Scalar), constrained qualitative differences to zero, constrained A, C, and E to be equal across genders, but allowed for differences in total phenotypic variance between males and females. This model did not result in a significant decrease in model fit for any of the variables, suggesting that qualitative and quantitative differences between genders were not different from zero. Thus, similar to Kovas et al. (2007) study of low math performance, there was no evidence for differences in genetic or environmental estimates in high math performance related to gender. However, there was evidence for different thresholds, suggesting higher mean performance for boys versus girls.

The best-fitting model collapses estimates of genetic (a²), shared environment (c²), and nonshared environment (e²) across gender but allows for mean differences between boys and girls. Parameter estimates for math subtests as well as the Math Composite from this best-fitting model are presented in Table 4. First, genetic effects were significant for high math groups for Understanding Number (a² = .52), Computation and Knowledge (a² = .42) and the Math Composite (a² = .53), but nonsignificant for Non-numerical Processes (a² = .09). Shared environmental effects were significant for Non-numerical Processes (c² = .44) and the Math Composite (c² = .25), but not for Understanding Number (c² = .14) or Computation and Knowledge (c² = .18). Nonshared environment (including error) was significant for all outcomes. For comparison, univariate model fitting results from the unselected sample are also presented in Table 4 (as reported in Kovas et al. 2007). In all cases, differences in genetic and environmental effects were small and nonsignificant between unselected math skills and high math groups, as evidenced by overlapping confidence intervals.

Table 4.

Extremes analyses

Variable	χ2	df	P	AIC	h2(CI)	c2(CI)	e2(CI)
Understanding number
≥85%tile	4.45	12	.974	−19.55	.52(.25–.74)	.14(.00–.35)	.34(.25–.44)
Unselected+	6.66	13	.919	−19.34	.42(.31–.53)	.16(.07–.25)	.42(.38–.46)
Non-numerical processes
≥85%tile	3.55	12	.990	−20.45	.09(.00–.37)	.44(.23–.57)	.47(.36–.56)
Unselected+	9.90	13	.702	−16.10	.32(.20–.44)	.23(.14–.32)	.45(.40–.50)
Computation and knowledge
≥85%tile	8.74	12	.725	−15.26	.42(.14–.69)	.18(.00–.39)	.40(.30–.51)
Unselected+	13.63	13	.401	−12.37	.45(.32–.56)	.07(.00–.17)	.48(.44–.53)
Composite
≥85%tile	8.53	12	.743	−15.48	.53(.31–.75)	.25(.06–.42)	.22(.16–.30)
Unselected+	13.64	13	.399	−12.36	.49(.39–.59)	.19(.10–.27)	.33(.30–.36)

Parameter estimates (and confidence intervals) from the extreme math groups and unselected twins

Note: +, from Kovas et al. (2007)

Note: Parameter estimates were taken from the Scalar Model for all measures from Table 3, which constrained variance components to be equal but allowed for threshold differences between males and females

Discussion

The current study is the first to examine the genetic and environmental etiology of high math performance. Genetic and nonshared environmental influences were significant for Understanding Number and Computation and Knowledge. Shared and nonshared environmental influences were significant for Non-Numeric Processes but genetic influences were not statistically significant. Finally, genetic, shared, and nonshared environmental influences were significant for the Math Composite. Moreover, these results are consistent with and extend the “gender similarities” hypothesis. Not only were mean differences between genders small compared in effect to the variability within gender, but the variability with gender appears to be influenced by the same sets of genetic and environmental influences in the same relative proportions.

Furthermore, estimates in high math groups selected at or above the 85%tile were generally similar in magnitude to genetic, shared environmental, and nonshared environmental influences when examining individual differences across the full range of math skills. These results are consistent with the Continuity Hypothesis. For most children, the genes and environments influencing high math ability represent the upper tail of genetic and environmental effects across the entire range of ability of math skills.

Non-Numeric Processes was the one exception to this general finding in the sense that genetic influences are not significantly different from zero in the high math group but are statistically different from zero in the unselected sample. While it may be the case that Non-Numeric Processes taps into skills that are not influenced by genetics at the high end of ability, it is important to note that the confidence intervals for the two estimates overlap. Thus, the estimates at the high end were not statistically different from estimates across the full range of math performance.

These findings must also be interpreted in light of shortcomings of the current study. First, these quantitative genetic results do not rule out the possibility that there are different genes operating at the high end and in the normal range of math ability even though the magnitude of these genetic effects are similar. The only irrefutable evidence will come when we find the actual genes responsible for the heritability of high math performance and show that they are as much associated with normal variation as they are with the extremes.

Second, because it was not possible to select high math groups above the 85th percentile, we were not able to examine whether discontinuity emerged with more extreme selection. This inability to select more extreme math groups, despite the large sample size of TEDS is due to ceiling effects in the web-based math battery. On the other hand, the content areas measured by the web-based battery are based on skills that are taught in a prescribed manner in the UK national curriculum. It may be the case that, at 10 years of age, the highest levels of math skills as taught in the UK curriculum can be only meaningfully measured up to the 85th percentile.

Third, if being in the same class and having the same teacher increases the similarity between co-twins, the estimate of the shared environment differ depending on whether twins in the study are in the same or different classrooms. However, in another report using the same sample (Kovas et al. 2007) we assessed whether being in the same class and having the same teacher increased similarity between co-twins and affected the genetic findings. Correlational genetic analyses on the same sample were run splitting the data by same versus different teacher. The two groups were equal in size. The correlations were highly similar for the two groups: for example, for the Understanding Number measure, the MZ correlations were .70 and .71 for the same and different teacher, respectively; for DZ twins, the correlations were .45 and .49, respectively.

Despite their shortcomings, these data are wholly inconsistent with the strongly held ideas that innate ability or deliberate practice alone cause high levels of math performance. Instead, these data suggest that genetic and environmental influences operate in a probabilistic manner to influence individual differences in math performance, with some proportion of the population achieving high performance.

The results of the current study also suggest that gender effects are confined to mean differences of very small effect size compared to substantial individual differences of performance within gender groups. Genetic or environmental differences, therefore, do not “make” boys or girls different in math performance. In fact, the differences within boys and girls are far greater than the small mean differences between gender groups.

These findings have important implications for math education. First, the belief that girls are less genetically inclined to achieve in math is simply not supported by the data. Unfortunately, there are significant gender differences in socialization, ranging from teacher and parent factors, math related experiences, gender identification, and test anxiety (see Gallagher and Kaufman 2005) and many of these are fed by the myth of innate differences determining gender differences. The first implication, therefore, is to state clearly that while genetic differences do influence differences in math performance, these genetic differences are not based on gender.

Another important conclusion is that genetic and environmental effects do not operate deterministically. Instead, theories examining gene-environment transactions are necessary (e.g. Scarr and McCartney 1983). Genes do not simply turn on and cause a child to have high performance. At the same time, it cannot be assumed that the skills necessary for high math performance are taught and learned in a genetic vacuum. Using Ericsson et al. (1993) theory as an example, it is clear that individuals with high performance are more likely to engage in activities (deliberate practice) that significantly enhance their abilities. What is not known is whether the probability of engaging in deliberate practice is, in part, a function of genes influencing ability (aptitude), motivation (appetite), or both.

From an educational perspective, the goal of instruction is to provide the proper sequence and intensity of environmental inputs to foster healthy educational outcomes in largest proportion of the population. Going further, the goal of intervention and enrichment is to provide more and/or different environmental stimulation to individuals who are at risk for difficulties or who show particular proficiency in math. If math has both genetic and environmental bases, then understanding gene-environment transactions is essential to understanding why some children fail to benefit fully from enriched environments, why others show high levels of performance despite environmental privation, and why there is substantial variability in response to instruction.