Proximal tibia volumetric bone mineral density is correlated to the magnitude of local acceleration in male long-distance runners

Abstract

The beneficial effect of physical exercise on bone mineral density (BMD) is at least partly explained by the forces exerted directly on the bones. Male runners present generally higher BMD than sedentary individuals. We postulated that the proximal tibia BMD is related to the running distance, as well as to the magnitude of the shocks (while running) in male runners. A prospective study (three yearly measurements) included 81 healthy male subjects: 16 sedentary lean subjects, and 3 groups of runners (5–30 km/wk, n = 19; 30–50 km/wk, n = 29; 50–100 km/wk, n = 17). Several measurements were performed at the proximal tibia level: volumetric BMD (vBMD) and cortical index (CI), i.e., an index of cortical bone thickness and peak accelerations (an index of shocks during heel strike) while running (measured by a three-dimensional accelerometer). A general linear model assessed the prediction of vBMD or CI by 1) simple effects (running distance, peak accelerations, time); and 2) interactions (for instance, if vBMD prediction by peak acceleration depends on running distance). CI and vBMD 1) increase with running distance to reach a plateau over 30 km/wk; and 2) are positively associated with peak accelerations over 30 km/wk. Running may be associated with high peak accelerations to have beneficial effects on BMD. More important strains are needed to be associated with the same increase in BMD during running sessions of short duration than those of long duration. CI and vBMD are associated with the magnitude of the shocks during heel strike in runners.

it is recognized that physical activity has a beneficial effect on bone mineral density (BMD) (3, 5, 22, 28, 29, 32). Sports associated with high strains (i.e., weight lifting, running) exhibit a higher total BMD than those with low strains (i.e., water polo, bicycling) (8, 23, 34). Moreover, a prospective study of 12 mo observed that power athletes (sprinters, jumpers, hurdlers, multievent athletes) gained significantly more bone density at the lumbar site than the other group (middle-distance runners, long-distance runners) (4). Despite the fact that running is not considered to be a typical power sport, it may have a beneficial effect on BMD. For instance, it has been generally reported (9, 21, 24, 25, 33), but not always (7, 13, 15, 17), that male runners have a higher BMD than sedentary individuals. From these results, it appears that, during a running session, bone responds to the amplitude (i.e., strength of the impact) and the number of the shocks (i.e., duration of exercise), but the relative importance of these latter variables is still unknown. On the other hand, it appears that, above a given level, long-distance running may be deleterious for bone health (9, 17, 24), but this issue remains controversial (21).

Human body motion is traditionally captured using standard optic, magnetic, or sonic technologies (1, 26). However, in recent years, advances in the technology of body-worn sensors based on electromechanical sensors (e.g., accelerometer, gyroscope, and electromagnetometer) during the last decade has encouraged investigators to use these sensors for measuring various aspect of human performance (12, 27). The key advantages of using body-wearable sensors are that such technology is inexpensive and does not require a specific environment or installation of any particular infrastructures (26, 35). In the context of this project, we used such technology for measuring the shocks received at tibia. We postulated that the distance of running, as well as the amplitude of the shocks at the tibia level, may have an impact on BMD. In the present study, we measured at the same anatomical site (i.e., proximal tibia level), volumetric BMD (by high-resolution tomodensitometry), as well as peak accelerations, i.e., an index of the shock amplitude (measured using accelerometer strapped on tibia) while running. The amplitude of acceleration measured at the time of impact and in vertical direction was considered as an index of the forces (or the strains) exerted at the bone level. The study was longitudinal and included athletes with a wide range of running distances.

METHODS

Subjects.

Eighty-one male subjects were included into the study. Sixty-six of these subjects were distance runners who were used to running for several years (at least 2 yr). All subjects were healthy and free of disorders that may influence their activity and/or bone metabolism. Moreover, subjects with a recent (<2 yr) joint/skeleton traumatism were excluded from the study. The subjects were divided into three different groups, according to their running habits: 19 were low-distance runners (5–30 km/wk), 29 were middle-distance runners (30–50 km/wk), and 17 were long-distance runners (50–100 km/wk). The weekly running distance was determined with a daily running record during 8 wk. A group of 16 sedentary lean subjects of the same age were also included. The protocol was accepted by the Ethic Committee of the Wallis Medical Association.

The subjects were measured on three occasions (each year during 2 yr, called times 0, 1, and 2). Each measurement consisted of a bone density determination with the tomodensitometry method (Fig. 1), a maximal oxygen uptake (V̇o_2max) measurement, and a submaximal run on a treadmill at the most comfortable speed.

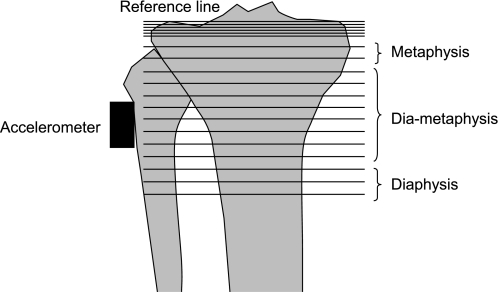
Fig. 1.

Summary of the measurements performed at the proximal tibia level. A total of 19 tomograms were taken from the tibia plateau every millimeter (the first tomogram at the reference line), and 13 tomograms every 5 mm (the last tomogram at distance of 7 cm from the reference line). The densities of the metaphysis, the diametapysis, and the diaphysis were calculated from tomograms 7–8, 9–16, and 17–19, respectively. Moreover, an accelerometer was fixed on the skin at the same site to measure peak acceleration (parallel to the tibia axis) when the heel hits the ground during a running session.

Submaximal exercise measurements.

The subjects were instructed to run on a treadmill for 5 min (Technogym, Runrace, Italy) in the most comfortable speed for long-lasting training sessions. Moreover, the patients were asked to wear their habitual shoes. This speed was chosen to reproduce the peak accelerations exerted in the field during running sessions. During this period, peak accelerations at proximal tibia were measured for 5 min, and the last 4.5 min were taken for calculations.

Acceleration measurements.

The lower as well as upper limb kinematics during running were measured using body-worn sensors, including a light and portable data logger (Physilog, BioAGM, La Tour de Peilz, Switzerland) integrated with two small body-worn sensors strapped using elastic band to the external part of the right knee (close to the tibia plate, Fig. 1) and the lower back. A three-axial accelerometer was included in the sensor module (Analog Devices, ±5 g) and associated with electronic circuits used for signal conditioning and calibration. The signals were digitized (12 bit) at a sampling rate of 40 Hz and stored for offline elaboration on a static memory card (8 Mb). An original algorithm based on wavelet analysis was developed to evaluate the shocks born by tibia during running. First the vertical acceleration signals were filtered, based on subject's speed, using an adaptive multiresolution wavelet transform (Coiflet 5, scales varied 2–7, depending on subject's speed). This process provides an adaptive time-frequency resolution for extracting the signals beyond 0.31 Hz and lower 5 Hz for lower speed or 10 Hz for higher speed. Then an algorithm was developed to estimate the maximum of acceleration (peak acceleration) based on tracking the sign change in filtered vertical acceleration pattern. To remove the artifacts, only the acceleration peaks beyond a relative threshold, which satisfy the interval-timing condition, were chosen.

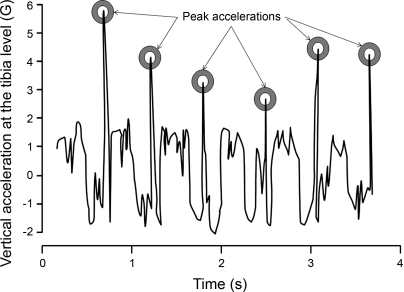
The interval-timing condition was defined according to the subject's speed and the detected peak from lower back accelerometer signal. To identify the relative threshold, the median value of all of the detected peaks beyond a predefined threshold (ranging from 0.1 G for lower speed to 0.3 G for higher speed) was estimated. Then the relative threshold was set at 80% of the median value. To estimate the exact time of shock (i.e., when the heel hits the ground), as well as its true amplitude, the maximum peak of the vertical acceleration in an interval of three samples around the detected peak was identified (Fig. 2). All of the algorithms were developed using Matlab (The MathWorks-Matlab). In addition, to automate the procedures and provide the final report, as well as a graphical interface for verifying the accuracy of detection, a program based on LabVIEW (National Instrument-LabVIEW) was developed. At the middle of the data collection, a damaged accelerometer was replaced, and a calibration procedure was performed to correct the peak acceleration values.

Fig. 2.

An original algorithm was developed to identify the exact time of the shock exerted on the tibia, as well as its intensity. The circles indicated the moments when the ipsilateral heel hits the ground. For each subject, the mean of all peak accelerations recorded throughout the treadmill test was calculated and used for further analyses.

In summary, the program 1) reads all of the subjects' raw data, which were recorded in a predefined folder; 2) runs the algorithm developed in Matlab detecting the peak accelerations; 3) visualizes the results for further verification (Fig. 2); and then 4) recapitulates the results of all subjects in an Excel datasheet to provide the final report. For each subject, the mean of all peak accelerations recorded during the treadmill test was calculated and used for further analyses.

Tomodensitometry.

An appendicular tomodensitograph (Densiscan, Scanco Medical, Bruettisellen/Zurich) measures the geometry and volumetric density of distal bones (radius and tibia). The precision of the method reaches 0.3% (11). For the measurements at the proximal part of the tibia, the leg was placed on a specific support transparent to the X-rays. Attention was paid to place the knee joint about the most proximal region of scanning. A scout view (i.e., a digital X-ray in mediolateral projection) was obtained with scanning every millimeter to define the reference plane with a line tangent to the tibia plateau. The scanning program contained 19 sections: 6 tomograms at a distance of 1 mm between each tomogram from the tibia plateau (defined from the scout view by the reference line) and 13 tomograms every 5 mm (the first tomogram at the reference line). The last tomogram was measured at distance of 7 cm from the reference line (Fig. 1).

The densities of the metaphysis, the diametaphysis, and the diaphysis were calculated from tomograms 7–8, 9–16, and 17–19, respectively.

Cortical index (CI) was calculated as follows:

$$\mathrm{CI}-\left(D-d\right)/D*100$$

Where D is the width of the bone, and d the width of the medullar cavity.

V̇o_2max measurements.

V̇o_2max was determined on a treadmill (Technogym, Runrace, Gambettola, Italy) by using exercise steps of 3 min (increase of 1.8 km/h from 7.2 km/h to exhaustion). O₂ consumption measurements were made during the last 30 s of each step (Quark b2 indirect calorimeter, Cosmed, Rome, Italy).

Statistical analysis.

The associations between the subjects' characteristics (Table 1), running distance groups, and time (as well as the interaction between time and running distance groups) were assessed with an analysis of variance with repeated measurements (split plot design).

Table 1.

Subjects' characteristics

	Time	Sedentary	Runners, 5–30 km/wk	Runners, 30–50 km/wk	Runners, 50–100 km/wk	Group Effect, P Value	Time Effect, P Value
No. of subjects		16	19	29	17
Height, cm	0	181 ± 5	177 ± 5	177 ± 7	174 ± 6	0.012
Age, yr	0	35 ± 6	37 ± 7	36 ± 7	36 ± 7	0.796
Weight, kg	0	77 ± 8	71 ± 7	72 ± 8	66 ± 8	0.002	<0.001
	1	79 ± 8	72 ± 8	73 ± 8	67 ± 8
	2	78 ± 8	72 ± 8	72 ± 9	68 ± 9
Body mass index, kg/m−2	0	23.6 ± 1.9	22.6 ± 1.7	22.9 ± 1.8	21.8 ± 2.1	0.058	<0.001
	1	24.1 ± 2.1	22.8 ± 1.9	23.2 ± 2.1	22.1 ± 2.0
	2	24.0 ± 2.0	22.8 ± 2.0	23.3 ± 2.1	22.3 ± 2.3
V̇o2max, ml O2·kg−1·min−1	0	47 ± 4	59 ± 8	60 ± 6	64 ± 7	<0.001	0.915
	1	49 ± 7	59 ± 8	60 ± 6	63 ± 7
	2	46 ± 6	60 ± 8	60 ± 7	65 ± 9
Most comfortable running speed, km/h	0	9.6 ± 1.3	11.6 ± 0.9	11.3 ± 1.0	12.1 ± 0.8	<0.001	0.010
	1	8.7 ± 1.2	10.9 ± 1.6	11.0 ± 1.2	12.0 ± 1.3
	2	8.9 ± 1.4	11.1 ± 1.2	10.6 ± 1.4	12.3 ± 1.7
Peak acceleration at most comfortable speed, G	0	2.74 ± 0.60	2.91 ± 0.85	2.61 ± 0.80	2.82 ± 0.74	0.333	0.604
	1	2.71 ± 0.58	2.78 ± 0.73	2.65 ± 0.77	2.90 ± 0.51
	2	2.55 ± 0.58	2.90 ± 0.41	2.87 ± 0.62	3.11 ± 0.55

Values are means ± SD. G = 9.81 m/s. V̇o_2max, maximal oxygen consumption. Body weight and body mass index increase with time, whereas most comfortable speed decreases with time. The effect of group (running distance) and time was assessed with an analysis of variance (split-plot design). There are no interactions between time and running distance.

The association of peak acceleration, time, running category, and their two-way interactions with bone density was tested by means of random-intercept linear multilevel regression models. Since time is repeated within subjects, bone density measurements at different times are not independent. Multilevel modeling accounts for correlations among bone densities measured repeatedly within the same subject. Random intercept models make the assumption that the regressions of bone density on time have equal slopes for all subjects, but the intercepts vary randomly among subjects.

Age and weight, which are known to be related to BMD and running distance (for instance, see Refs. 6, 10), were introduced as continuous variables into the regressions to adjust the effect of the independent variables. Scatter plots with Lowess curves showed that the associations between bone density and age or weight were approximately linear at each time point (Lowess: locally weighted scatter plot smoothing) (2).

Acceleration was entered into the models as a continuous variable. Since it cannot be assumed that bone density changes linearly with the categories of running distance or time, the latter two variables were represented by binary dummy variables, where each category was tested against a reference. Reference categories were the sedentary group and time 0, respectively. Each categorical variable being thus represented by a group of dummy variables, several interaction parameters were obtained for each two-way interaction. F-tests were, therefore, applied to test the null hypothesis that all of the parameters involved in a two-way interaction equal zero (30).

The command xtmixed of the STATA package version 11.0 (StataCorp, College Station, TX) was used to fit the regressions.

RESULTS

The subjects' characteristics are illustrated in Table 1. Body weight and height were lower in the long-distance runners (50–100 km/wk), whereas body mass index did not change significantly among the groups. Body weight and body mass index increase significantly with time. Despite an increase in the most comfortable speed in the runners' groups, peak acceleration was not significantly higher. Cross-sectional results of the Densiscan at time 0 (first measurement) are presented in Table 2. BMD and CI are higher in the groups of runners. All bone variables did not change significantly with time. Densiscan-determined BMD was correlated with CI (r = 0.95, P < 0.001).

Table 2.

Results of tomodensimetric variables at the proximal tibial level of different groups of runners

	Time	Sedentary	Runner, 5–30 km/wk	Runner, 30–50 km/wk	Runner, 50–100 km/wk	Group Effect, P Value	Time Effect, P Value
No. of subjects		16	19	29	17
Densities, mg/cm3
Proximal metaphysis	0	310 ± 40	332 ± 35	355 ± 59	351 ± 40	0.024	0.464
	1	311 ± 43	334 ± 39	355 ± 60	344 ± 42
	2	310 ± 42	332 ± 36	356 ± 60	348 ± 40
Proximal diametaphysis	0	543 ± 65	593 ± 71	626 ± 107	634 ± 71	0.011	0.753
	1	541 ± 67	601 ± 71	627 ± 102	629 ± 80
	2	548 ± 74	592 ± 75	629 ± 106	624 ± 86
Proximal diaphysis	0	671 ± 80	731 ± 88	764 ± 123	772 ± 84	0.015	0.925
	1	670 ± 83	739 ± 84	765 ± 116	769 ± 94
	2	676 ± 90	729 ± 92	772 ± 123	766 ± 98
Cortical index, %
Proximal diametaphysis	0	15.9 ± 2.1	17.7 ± 2.2	19.1 ± 4.1	19.5 ± 2.2	0.004	0.602
	1	16.0 ± 2.3	18.2 ± 2.1	19.0 ± 3.8	19.4 ± 2.6
	2	16.2 ± 2.5	17.9 ± 2.3	19.3 ± 4.0	19.2 ± 2.7
Proximal diaphysis	0	15.9 ± 2.1	17.7 ± 2.2	19.1 ± 4.1	19.5 ± 2.2	0.004	0.692
	1	16.0 ± 2.3	18.2 ± 2.1	19.0 ± 3.8	19.4 ± 2.6
	2	16.2 ± 2.5	17.9 ± 2.3	19.3 ± 4.0	19.2 ± 2.7

Values are means ± SD. Cortical index (CI) was calculated as follows: $\mathrm{CI}=\left(D-d\right)/D*100$, where D is the width of the bone, and d is the width of the medullar cavity. The effect of group (running distance) and time was assessed with an analysis of variance (split-plot design). There are no interactions between time and running distance.

Peak acceleration and bone analyses.

Table 3 presents the results of the regression models for the three bone sites. At the diametaphysis and the diaphysis levels, volumetric BMD and CI were significantly predicted by the interaction between the peak accelerations and running-distance groups. In other words, our results provide some evidence for an effect of peak acceleration that varies with running-distance group (Fig. 3). Finally, insufficient evidence is provided for an effect of time on volumetric BMD and CI.

Table 3.

Results of the regression models that predict volumetric BMD and cortical index

		Proximal Diametaphysis		Proximal Diaphysis
	Proximal Metaphysic, BMD, mg/cm3	BMD, mg/cm3	Cortical index, %	BMD, mg/cm3	Cortical index, %
Main effects
Amax	2.0 ± 3.1 (0.520)	−14.3 ± 8.1 (0.076)	−0.65 ± 0.37 (0.079)	−12.3 ± 7.1 (0.083)	−0.77 ± 0.38 (0.039)
0 km/wk (reference)	0	0	0	0	0
5–30 km/wk	32.9 ± 18.3 (0.071)	1.47 ± 38.1 (0.969)	−0.65 ± 1.54 (0.676)	14.6 ± 40.3 (0.716)	−0.52 ± 1.80 (1.000)
30–50 km/wk	53.0 ± 16.8 (0.002)	19.4 ± 35.1 (0.581)	−0.14 ± 1.42 (0.924)	38.3 ± 37.0 (0.301)	0.49 ± 1.66 (0.766)
50–100 km/wk	39.5 ± 18.3 (0.031)	18.6 ± 38.0 (0.624)	−0.01 ± 1.53 (0.994)	41.2 ± 40.4 (0.308)	0.72 ± 1.80 (0.688)
Time 0 (reference)	0	0	0	0	0
Time 1	0.38 ± 4.92 (0.938)	6.58 ± 12.8 (0.607)	0.38 ± 0.59 (0.518)	5.2 ± 11.3 (0.646)	0.56 ± 0.60 (0.351)
Time 2	4.49 ± 5.48 (0.412)	9.38 ± 14.1 (0.506)	0.02 ± 0.65 (0.823)	−0.1 ± 12.5 (0.993)	0.11 ± 0.66 (0.871)
Interaction between time and running distance, overall P value	0.064	0.388	0.658	0.341	0.246
Interaction between time and acceleration, overall P value	0.947	0.700	0.759	0.482	0.449
Interaction between acceleration and running category, overall P value	0.465	0.036	0.023	0.045	0.001
Confounders
Age	−1.69 ± 0.76 (0.025)	−0.83 ± 1.40 (0.557)	0.01 ± 0.05 (0.834)	−0.43 ± 1.64 (0.796)	−0.02 ± 0.07(0.815)
Weight	0.08 ± 0.30 (0.797)	−0.59 ± 0.70 (0.401)	−0.04 ± 0.03 (0.130)	−0.23 ± 0.68 (0.733)	−0.02 ± 0.03 (0.561)

Values are regression coefficients ± SE. P values are shown in parentheses. A_max, peak acceleration when the foot hits the ground (G, G = 9.81 m/s²). BMD, bone mineral density. Time 0 and sedentary individuals are taken as references. CI was calculated as follows: $\mathrm{CI}=\left(D-d\right)/D*100$, where D is the width of the bone, and d is the width of the medullar cavity. Regression coefficients represent the slopes of the prediction equation.

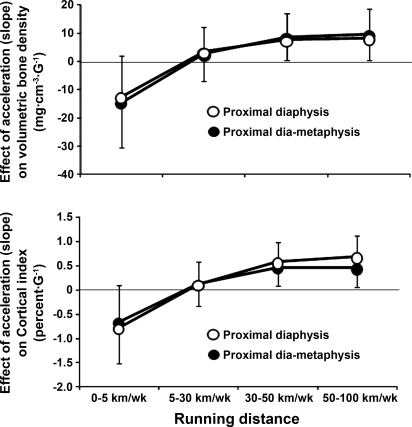
Fig. 3.

Interactions between peak acceleration and running distance group. Vertical axis represents the change in volumetric bone mineral density or cortical index for one unit increase in peak acceleration for each running category. One-half of the coefficient 95% confidence intervals is represented.

Neither time nor peak acceleration or running-distance groups had a significant effect on volumetric BMD at the metaphysis level. At this site, the running groups predict significantly volumetric BMD.

DISCUSSION

This prospective study investigates the effect of running distance and the magnitude of the peak accelerations while running on volumetric BMD in male long-distance runners. A general statistical model allows assessing whether volumetric BMD is predicted by running distance, peak acceleration, and time, as well as the interaction between these variables. This model presents the advantage to identify the relative contribution of time and/or peak accelerations. Moreover, these effects were independent of age and weight.

In accordance with the observations of the previous studies (9, 21, 24, 25, 33), cross-sectional data, collected, for instance, at the first measurement (i.e., time 0), show that volumetric BMD is increased in the runners' groups. As illustrated in Table 2, most of the effect of running on bone is reached at 30–50 km/wk. These results are compatible with the concept that BMD do not increase beyond a given volume of exercise, i.e., over a running distance of ∼30 km/wk (24) or an exercise time of 6 h/wk (20).

Our prospective study was not only designed to analyze the relationship between running distance and volumetric bone density, but, as mentioned above, it was also planed to introduce additional predictive variables (i.e., peak accelerations and time) to better understand BMD regulation in vivo. Interestingly, at the diametaphysis and diaphysis levels, neither the amplitude of peak acceleration nor the running distance appears to predict volumetric BMD (Table 3, main effects). These results appear to be in contradiction with the observed higher volumetric BMD found in runners. However, high volumetric BMD are observed only in subjects who present simultaneously high peak accelerations and running distances over 30 km/wk. In other words, there is an interaction between peak accelerations and running distance. The coefficients, which represent the magnitude of the peak acceleration effect on BMD, for a given group of subject, are similar between the middle-distance (30–50 km/wk) and the long-distance (50–100 km/wk) runners (see Fig. 3, interaction between running distance and peak acceleration). Here also, these results are compatible with the concept that, beyond a given running distance, no additional benefit on BMD is observed (Fig. 3). Conversely, the volumetric BMD of low-distance runners (5–30 km/wk), who obviously run less than the other groups, may experience less beneficial shocks on volumetric BMD. This is compatible with the observed absence of significant correlation between peak accelerations and BMD in this group of runners (Table 3, interaction between running distance and peak acceleration). Despite a lower preferred running speed, sedentary individuals present similar peak accelerations than runners (Table 1). These results are in accordance with the earlier observation that the ground reaction force during running is higher in nonactive subjects than in runners (19). Here also, because sedentary individuals almost do not run, an absence of peak acceleration effect on volumetric BMD is expected. However, peak accelerations tend to negatively predict volumetric BMD and CI in sedentary individuals (Table 3 and Fig. 3). This is probably not a causal-to-effect relationship, because these individuals almost do not experience shocks associated with running. It can be postulated that some very sedentary individuals, who are expected to have low BMD, exhibit at the same time high peak accelerations, because these individuals are known to have higher ground reaction forces (19) (see above). In summary, the magnitude of peak acceleration at the most comfortable running speed does not depend on running distance, but is positively associated with the volumetric BMD only in the runners' group. Moreover, this effect is nonlinear and reaches a plateau after 30 km/wk. In this case, more simple statistics (i.e., linear regression between BMD and peak acceleration, as well as running distance) are not efficient in identifying any relationships and would lead to an erroneous conclusion. Therefore, the subjects have to be stratified after their running distance to find out the relationship between peak acceleration and volumetric bone density.

Earlier studies have already investigated the effect of impact acceleration on BMD. Jamsa et al. (18) have measured the effect of an 12-mo high-impact exercise program on BMD at the proximal femur of middle-aged women. The authors reported that the change in BMD, at the proximal femur, was dependent on the accelerations measured at the iliac crest level. Moreover, these authors have also published (16) other results performed on the same subjects: they found a significant relationship between acceleration slope (i.e., the increase in acceleration with time) and the BMD improvement during the exercise program. These results are in accordance with ours, but the strategy was different: their stratification was performed after the magnitude of acceleration, whereas ours was done after the running distance. These different approaches lead to complementary conclusions. These authors (16) observed an acceleration threshold under which exercise may not have an impact on BMD, whereas we do not observe a real running volume threshold, but an association between both variables that increase progressively with running distance.

Cortical thickness (CI), which is closely related to BMD (r = 0.95 at time 0), is also increased in the groups of runners and may probably explain the high volumetric BMD values. Moreover, similar results of the general statistical model are observed when BMD is replaced by CI (see Table 3). This strongly suggests that the increase in BMD, observed in runners with high peak accelerations, is probably due to a gain in cortical bone thickness. This result is in accordance with the concept that running (14), or exercise in general (31), has a positive effect on cortical thickness. Interestingly, an association between peak acceleration and cortical thickness is already observed in the low-distance runners (5–30 km/wk), suggesting a progressive effect with running distance. These results have a practical importance: more important strains are needed to be associated with the same increase in BMD during running sessions of short duration than those of long duration.

It is important to keep in mind that all of the measurement were performed three times on the same subjects, without any intervention on the training volume (i.e., the runners were told to keep their habitual running distance). This allows us to analyze the effect of time in the “real life” of the runners.

From Table 3, the diaphysis appears to be more sensitive to peak accelerations than the metaphysis. This is probably explained by the fact that the metaphysis is adjacent to the knee joint. For this reason, it cannot be excluded that this site receives important shocks and/or forces from muscles and bone of the thigh (which are not recorded by the accelerometers) that may themselves influence volumetric BMD.

In summary, the present work is the first longitudinal study to investigate simultaneously, in vivo, the association between the magnitude of the shocks, as well as the duration of running on volumetric BMD and cortical thickness at the same site. It can be concluded that the volumetric BMD and cortical thickness at the diaphysis of the proximal tibia are predicted by the peak accelerations recorded while the runner's foot hits the ground, as well as the weekly running distance. This association between bone measurements and peak accelerations appears already in the low-distance runners (5–30 km/wk) and reaches a plateau after 30 km/wk.

GRANTS

This study was financed by a grant of the Swiss Federal Office of Sport.

DISCLOSURES

No conflicts of interest are declared by the author(s).