Genetic integration of molar cusp size variation in baboons

Abstract

Many studies of primate diversity and evolution rely on dental morphology for insight into diet, behavior, and phylogenetic relationships. Consequently, variation in molar cusp size has increasingly become a phenotype of interest. In 2007 we published a quantitative genetic analysis of mandibular molar cusp size variation in baboons. Those results provided more questions than answers, as the pattern of genetic integration did not fit predictions from odontogenesis. To follow up, we expanded our study to include data from the maxillary molar cusps. Here we report on these later analyses, as well as inter-arch comparisons with the mandibular data.

We analyzed variation in two-dimensional maxillary molar cusp size using data collected from a captive pedigreed breeding colony of baboons, Papio hamadryas, housed at the Southwest National Primate Research Center. These analyses show that variation in maxillary molar cusp size is heritable and sexually dimorphic. We also estimated additive genetic correlations between cusps on the same crown, homologous cusps along the tooth row, and maxillary and mandibular cusps. The pattern for maxillary molars yields genetic correlations of one between the paracone-metacone and protocone-hypocone. Bivariate analyses of cuspal homologues on adjacent teeth yield correlations that are high or not significantly different from one. Between dental arcades, the non-occluding cusps consistently yield high genetic correlations, especially the metaconid-paracone and metaconid-metacone. This pattern of genetic correlation does not immediately accord with the pattern of development and/or calcification, however these results do follow predictions that can be made from the evolutionary history of the tribosphenic molar.

A significant amount of research has focused on the shape of teeth, and rightfully so as they yield important information about dietary adaptations, interactions with conspecifics, and phylogenetic relationships (e.g., Swindler, 2002; Irish and Nelson, 2008). Given the advances in molecular genetics, scientists are now able to investigate the genes that are involved and essential to odontogenesis (e.g., Jernvall and Jung, 2000; Thesleff, 2006), and how the interactions between genes may underlie morphological variation (e.g., Salazar-Ciudad and Jernvall, 2002; Salazar-Ciudad, 2006).

One way to approach the critical question of how genes influence population-level variation, and thereby structure evolutionary histories and trajectories, is to estimate genetic correlations – to reveal the pattern of genetic integration that underlies morphological variation (Hlusko, 2004). Quantitative genetics provides a means to achieve this goal. Here, we employ a quantitative genetic approach to reveal the pattern of genetic integration within baboon molar cusp size variation (for a history of quantitative genetics research on the primate dentition see Rizk et al., 2008).

Previously, we published the results of a quantitative genetic analysis of mandibular molar cusp size in baboons (Hlusko et al., 2007). The results from that study were unexpected and prompted more research. This current article follows on that project by reporting the results of the maxillary molar cusp analyses as well as inter-arch analyses. The maxillary data help to provide an interpretive framework for the mandibular results, revealing a pattern of additive genetic correlation that is best interpreted through the longer lens of mammalian dental evolution.

Primate molars derive from a tribosphenic pattern (Simpson, 1936) that first appears in the Early Cretaceous fossil record, approximately 120 million years ago (Luo, 2007). Luo (2007), Rose (2006), and Kielan-Jaworowska et al. (2004) provide extensive overviews of this evolutionary history. Only a brief summary is provided below.

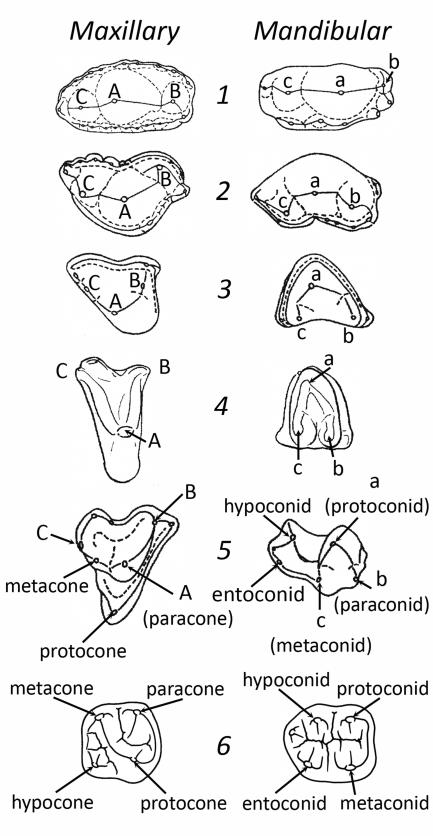
All extant mammals are currently thought to have evolved from the Morganucodonts, small shrew-sized animals recovered from sediments dating to the latest Triassic and Early Jurassic in Europe, Asia, Africa, and North America. Morganucodonts share derived mammalian traits while retaining primitive cynodont features. The mandibular molars have three cusps arranged linearly, with the main cusp in the center. The maxillary molars have three cusps also arranged in a line, with the largest cusp positioned centrally (Figure 1).

Figure 1.

These drawings represent the evolution of the primate molar from a triconodont early mammal ancestor. From top: 1 = Morganucodon; 2, 3, 4 = various “Symmetrodontans” (Kuehneotherium, Spalacotherium, and Spalacolestes, respectively); 5 = Pappotherium (a “tribotherian”/therian of metatherian-eutherian grade); 6 = Homo sapiens. Line drawings modified from Kielan-Jaworowska et al. (2004), Figure 9.1, and Hillson (1996), Figures 2.2 and 2.29.

These early mammals are also characterized by the presence of wear facets on their molars, demonstrating that they had evolved the mammalian characteristic of precise occlusion. These facets occur on the buccal surface of the mandibular molar cusps and on the lingual surface of the maxillary molar cusps (Crompton and Jenkins, 1968).

The “symmetrodontans” lie at or near the base of the therian radiation and are the first to have nearly symmetrical triangular cusp arrangement on both maxillary and mandibular molars (the tritubercular/tuberculosectorial pattern, distinct from the tribosphenic pattern). This triangular configuration is now widely interpreted to have resulted from the rotation, or curving, of the linear cuspal arrangement seen in earlier mammals, such as the Morganucodonts. Through this rotation, the mesial and distal cusps (B/b and C/c) moved more lingually on mandibular molars, or buccally on the maxillary molars, relative to the central cusp (Kielan-Jaworowska et al., 2004: 350). As shown in Figure 1, these cusps are also interpreted to be homologous to the primary cusps of the tribosphenic molars, with A = paracone, a = protoconid, c = metaconid, and the other cusps homologous to those that primates are no longer thought to retain.

A tribosphenic maxillary molar has three main cusps arranged in a triangle with the paracone and metacone along the buccal edge and the protocone oriented lingually. This is also called the trigon. The mandibular tribosphenic molar is a mirror-image, with the paraconid and metaconid on the lingual side and the protoconid on the buccal, forming the trigonid. The lower tribosphenic molar also has a distal basin (the talonid) that occludes with the protocone, the crucial derived feature of the tribosphenic mammalian molar configuration (Simpson, 1936).

Originally, paleontologists interpreted tribosphenic molars to be an evolutionary novelty that evolved once from the linear cuspal arrangement described above. This molar configuration is thought to be a critical innovation that, in part, enabled the therian radiation into herbivorous and omnivorous dietary niches (as these molars are better able to grind as well as shear). Lucas (2004) proposes that this may have been a key innovation for exploiting insects with more heavily tanned cuticles (i.e., adults). New fossil evidence demonstrates that tribosphenic mammals either first evolved in the Southern Hemisphere much earlier than originally thought (i.e., the Early Cretaceous), or evolved convergently in the Northern and Southern Hemispheres (Luo, 2007; Rose, 2006; Kielan-Jaworowska et al., 2004).

Regardless of which evolutionary hypothesis is correct (single origin or parallelism), this cuspal configuration provided the anatomical foundation for the bunodont four- and five-cusped molars now seen in extant cercopithecoids and hominoids. In baboons, the maxillary molars consist of four cusps including the metacone, paracone, protocone, and hypocone, clockwise beginning from the buccal-distal cusp on the right side molars, similar to the human shown in Figure 1 and outlined at the bottom of Figure 3.

Figure 3.

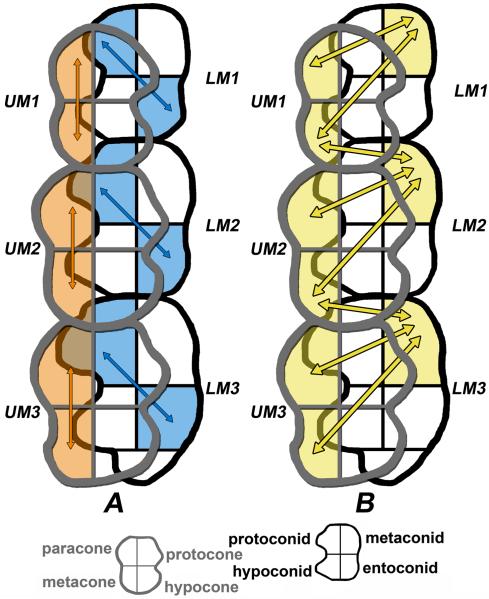
Dorsal view through the skull where mesial is to the top and lingual is to the right. A. This figure shows a view of occluding cusps displaying the most distinct intra-molar cuspal correlations down the left molar row. Orange shading and arrows indicate correlation between maxillary cusps on the same crown. Blue shading and arrows indicate correlation between mandibular cusps on the same crown. Note the significant linear buccal correlation on the maxilla and the diagonal correlation on the mandible. B. This figure shows a view of occluding cusps displaying the most distinct inter-cuspal correlations between the dental arcade on the left side. The yellow shading and arrows indicate the interrelated cusps. Note the significant correlations involving the metaconid, metacone, and paracone.

Variation in the size, shape, and relative positioning of these molar cusps has provided a wealth of information about the phylogenetic relationships and dietary adaptations of primates over the last five decades (e.g., Erdbrink 1965, 1967; Sperber 1974; Corruccini, 1977; Wood and Abbott 1981; Hills et al., 1983; Wood et al., 1983; Wood and Engelman, 1988; Suwa, 1990; Reid et al., 1991; Wood & Xu, 1991; Macho & Moggi-Cecchi, 1992; Macho, 1994; Suwa et al., 1994; Suwa, 1996; Suwa et al., 1996; Uchida, 1996, 1998a, 1998b; Kondo and Yamada, 2003; Bailey, 2004; Bailey et al., 2004; Kondo et al., 2005; Kondo and Townsend, 2006). A review of the methods for assessing cusp size is summarized in Hlusko et al. (2007).

As originally recognized by Darwin (1859), selection can operate only on variation that is heritable (i.e., influenced by genetic effects). Darwin (1859) also recognized that correlation and/or covariation between traits will alter how they can respond to selection, such that selection for one trait may result in concomitant change in another trait which is not actually the target of the selective pressure. Consequently, we need to know how the variation in two traits is influenced by the same gene or suites of genes in order to understand how those traits have evolved through time.

To date, there have been only a few studies investigating the genetics of molar cusp area outside of our own. Biggerstaff (1976) studied basal cusp area in 199 pairs of same-sex twins and concluded that the genetic component to variation in this trait was relatively low. Reports of human genetic disorders suggest a genetic, or at least an epigenetic contribution to molar cusp area variation. For example, human females diagnosed with Turner Syndrome (individuals lacking a second sex chromosome (45, X0) and who are therefore phenotypically female) have relatively smaller distal cusps (Mayhall and Alvesalo, 1992).

In our 2007 study of variation in mandibular molar cusps, we found significant genetic correlations between all cusps on the same crown except for the metaconid-hypoconid pair, which has a genetic correlation of zero. Where most genetic correlations between the cusps indicated incomplete pleiotropy, the protoconid-entoconid has a genetic correlation of one on all three molars. We found this result – opposing diagonal lines of complete versus no genetic correlation – difficult to interpret as it does not accord with patterns predicted from tooth development, mineralization, or lophid coalescence (see Hlusko et al., 2007, for a detailed discussion on the patterns of tooth development, mineralization, and lophid coalescence). These mandibular results begged the question of what the pattern of genetic integration was like in the maxillary molars.

Here we report on this follow-up study, a quantitative genetic analysis of variation in maxillary molar cusp area in a captive pedigreed population of baboons housed at the Southwest National Primate Research Center in San Antonio, Texas.

Efforts to apply an understanding of genetic variance and heritability to the evolution of dental phenotypes are not new. For example, Lande (1976) estimated the level of selection needed to account for the changes in dental size between various species of Eocene oreodonts and Hyopsodus, concluding that the level was quite low and the morphological change may well have resulted from drift (e.g., Lande 1976). And more recently, we have explored additive genetic variance and selection on baboon enamel thickness (Hlusko et al., 2004) and other dental phenotypes (reviewed in Rizk et al., 2008). Evolutionary quantitative genetics research on skeletal phenotypes has expanded over the intervening decades, though this has primarily focus on extant taxa for obvious logistical reasons. For example Marroig and Cheverud (2004) tested the role of selection and drift as the driving forces for New World Monkey cranial diversity, and identified evolutionary trajectories (2005). Analytical methods have also expanded to include correlated characters (e.g., Lande and Arnold, 1983), macroevolutionary patterns (e.g., Turelli et al., 1988), integration and pleiotropy (e.g., Cheverud, 1996), and how we define these (e.g., Roseman et al., 2009).

In the research present here, our four aims were to: 1) test the hypothesis that maxillary molar cusp size variation in this population is influenced by the additive effects of genes as was found for the mandibular molar cusps; 2) test for additive genetic correlations, interpreted as pleiotropy, between cusps on the same molar crown as well as along the tooth row; 3) identify and quantify pleiotropic affects that may exist between dental arcades, i.e., additive genetic correlations between maxillary and mandibular molar cusp size variation; and last, 4) to provide an evolutionary and developmental perspective on the revealed pattern of genetic integration.

DENTAL ABBREVIATIONS

U

Upper (Maxillary)

L

Lower (Mandibular)

M2

Second molar

MATERIALS

Data for 627 individuals were collected from a pedigreed breeding colony of captive baboons, Papio hamadryas, housed at the Southwest National Primate Research Center (SNPRC). Genetic management of the colony began over 30 years ago, making it possible to collect data from non-inbred animals. The female to male sex ratio in the colony is approximately 2:1. Mating within the colony is controlled and therefore all familial relationships are known and all matings are random with respect to dental, skeletal, and developmental phenotypes. Data from approximately 1,000 individuals have been used to construct genetic marker maps, although these maps are not part of the analyses presented here (Rogers et al., 2000; Cox et al., 2006).

Data management and pedigree preparation were conducted using the computer package PEDSYS (Dyke, 1996). Data were collected from animals that are distributed across eleven extended pedigrees, and animals without phenotypic data were used to complete the pedigree structure (n = 1,294). On average there were 44 individuals with data per pedigree, and these animals typically represented the most recent two or three generations of each pedigree. Data collection was carried out in accordance with the protocols of the Guide for the Care and Use of Laboratory Animals (National Research Council, 1996), and are described in detail elsewhere (Hlusko et al., 2002).

Cusp areas were measured from photographs of high resolution plaster dental casts. These casts were photographed (for protocol see Hlusko et al., 2002) and from these photographs, the occlusal view 2-D area of all molar cusps were measured for the right and left UM1, 2, and 3 molars using Image Pro Plus 5.1© software. Data for the left LM1, 2, and 3 molars were collected and reported on previously (Hlusko et al., 2007).

Cusp areas were defined as shown in Figure 2, following Suwa et al. (1994). However, modifications were made to account for the differences between baboon and hominid molar morphology. We defined the boundaries of an individual cusp using the fissure around it. In contrast to the methods described in Suwa et al. (1994) and Wood et al. (1983), buccal enamel shelves between the paracone and the metacone, lingual enamel shelves between the protocone and hypocone, the intercusp enamel areas such as the mesial and distal enamel shelves, and the middle fovea were excluded from area measurements in this study.

Figure 2.

Mesial is to the top and lingual to the center. This figure shows how the cusps were defined for data collection. See text for more details regarding protocol specifics. This figure also shows a schematic for the genetic correlations between cusps on the same molar crown. The solid arrows indicate a genetic correlation that is not significantly different from one. The dotted arrows indicate partial genetic correlations (incomplete pleiotropy). Significance is at p ≤ 0.01. Note the correlation present between the metacone and paracone on all three left maxillary molars. *Correlations using combined data in which right and left sides were averaged when possible, and right or left data were used when only one side was measured. The UM2 hypocone for the combined sample did not return a significant heritability estimate and therefore not analyzed for any genetic correlations.

Cusps were excluded from measurement if the fissures were indistinguishable due to wear. Areas were not measured from broken or unusually worn cusps, or those in which part of the crown was obscured by the gum line.

Sample sizes for the left UMs ranged from 412 to 518; sample sizes for right UMs molars ranged from 396 to 542; and LM sample sizes range from 198 to 498 (Hlusko et al., 2007). We also analyzed combined data in which right and left sides were averaged when possible, and right or left data were used when only one side was measured (sample sizes ranged from 522 to 589).

Four of the authors collected the UM data (C.K., E.Ba., Z.F., E.Br.). Most of the data were collected such that only one researcher measured the same molar (e.g., the same person measured all left first molars) to ensure consistency. N.D. and L.H. collected the LM data. Measurement error was calculated as a percentage of the average measurement for each phenotype. Neither inter-observer nor intra-observer error for any of the molars exceeded 5% (details available upon request). This amount of measurement error accords with the levels reported previously for these types of data (e.g., Bailey, 2004; Bailey et al., 2004; Hlusko et al., 2007).

METHODS

Statistical genetic analyses were performed using a maximum likelihood based variance decomposition approach implemented in the computer package SOLAR (Almasy and Blangero, 1998). For each trait within a pedigree, the phenotypic covariance was modeled as $\Omega =2\Phi {\sigma }_G^2+I{\sigma }_E^2$, where ${\sigma }_G^2$ is the additive genetic variance, ${\sigma }_E^2$ is the environmental variance, Φ is a matrix of kinship coefficients for all relative pairs in a pedigree, and I is an identity matrix. The multiple components of the phenotypic variance are additive, where ${\sigma }_P^2={\sigma }_G^2+{\sigma }_E^2$, therefore we estimated heritability to be the proportion of the residual phenotypic variance due to the additive effects of genes. This relationship can be represented as $h^2={}^{{\sigma }_G^2}/_{{\sigma }_P^2}$. Because h² in our models provides an estimate of the relative importance of additive genetic effects on the residual phenotypic variance, it is also referred to as the “narrow sense” heritability; as opposed to the “broad sense” heritability which also may include, for example, genetic variance attributable to dominance and epistatic effects. We and others (see, e.g., Hill, Goddard, and Visscher, 2008) have observed that additive genetic variance predominates in the determination of normal variation in complex traits like dental crown metrics and is useful for predicting their responsiveness to selection. The proportion of the residual phenotypic variance due to non-additive genetic factors, represented as e², can be calculated directly from the heritability estimate as e² = 1 – h².

It is the residual phenotypic variance for a trait – i.e., that remaining after accounting for the mean effects of selected covariates – which we decompose into its additive genetic and random environmental components. We modeled each of the 2-D area phenotypes as: $y=\mu +{\beta }_1({\stackrel{‒}{x}}_1-x_1)+{\beta }_2({\stackrel{‒}{x}}_2-x_2)+\dots +{\beta }_n({\stackrel{‒}{x}}_n-x_n)+g+e$ ; where μ is the population mean for the trait, x_i are the covariate values, β_i their mean effects coefficients, and g and e, respectively, are the genetic and environmental effects. The effects of age and sex were estimated simultaneously, allowing for estimation of the mean effects of any of these covariates found to significantly influence the cusp area trait. The value of each of these covariate effects was constrained to zero and likelihood ratio tests were utilized to compare the likelihoods of these models to that of the general model in which all covariate effects were estimated. A p-value of ≤ 0.10 indicated a significant mean effect of the covariate for the purposes of these analyses. Covariates found to be significant in the univariate analyses were also included in the bivariate analyses.

The multivariate phenotype is modeled using extensions to univariate genetic analyses that encompass the multivariate state (Hopper and Mathews, 1982; Lange and Boehnke, 1983; Boehnke et al., 1987). We modeled the multivariate phenotype of an individual as a linear function based on the individual’s trait measurement, additive genetic values, random environmental deviations, population trait averages, covariate effects, regression coefficients, and the genetic and environmental correlations between them. The phenotypic covariance using this multivariate extension model is described as Ω = G ⊗ 2Φ+E ⊗ I , where G is the genetic variance-covariance matrix among traits, E is the environmental variance-covariance matrix among traits, and ⊗ is the Kronecker product operator. Using these two variance-covariance matrices we estimated the additive genetic correlation, as well as the shared environmental correlation, between trait pairs. The additive genetic correlation, ρ_G, estimates the additive effects of the same gene or genes on pairs of traits, i.e., pleiotropy. When squared, this genetic correlation provides an estimate of the proportion of the additive genetic variance in each phenotype that is shared; and the product of this correlation and the narrow sense heritability estimate for each trait in a genetically correlated pair is an estimate of the proportion of the residual phenotypic variance that is due to the effects of the same gene or genes. As in the case of the narrow sense heritability, this genetic correlation does not include shared genetic effects due to dominance or other components of the genetic variance. The environmental correlation, ρ_E, is the correlation between trait pairs due to random environmental factors – i.e., non-additive genetic effects, effects of unmeasured covariates, etc.

Similar to the variance-covariance matrix, the genetic and environmental components of the phenotypic correlation matrix are additive. This enables us to use maximum likelihood estimates of the additive genetic correlations to obtain the total phenotypic correlation between two traits. The total phenotypic correlation between two traits, represented as ρ_P, can be calculated as

$${\rho }_P=\sqrt{h_1^2}\sqrt{h_2^2}{\rho }_G+\sqrt{(1-h_1^2)}\sqrt{(1-h_2^2)}{\rho }_E.$$

Likelihood ratio tests were used in order to determine the significance of the maximum likelihood estimates for heritability and other parameters. Two models were used in this test, a general model and a restricted model. In the general model all parameters are estimated. However, in the restricted model the value of the tested parameter is held at a constant value, usually at zero or one. Twice the difference of the maximum likelihoods of a general model and a restricted model is distributed asymptotically (Hopper and Mathews, 1982). For tests of parameters such as heritability, h², a value of zero in a restricted model is at a boundary of the parameter space. For these parameters, this distribution is approximately a ½:½ mixture of χ² and a point mass at zero. It can also be described as a χ² variate for tests of covariates for which zero is not a boundary value. Degrees of freedom are calculated as the difference in the number of estimated parameters in the two models (Boehnke et al., 1987).

Additional tests were performed to compare the likelihood of a model in which the value of the genetic correlation is fixed at 1.00 or zero to that of the unrestricted model in which the value of the genetic correlation is estimated for bivariate models. A significant difference between the likelihoods of the restricted and polygenic models suggests incomplete pleiotropy, in which not all of the additive genetic variance in the two traits is due to the effects of the same gene or genes. For a more detailed discussion of these methods, see Mahaney et al., 1995.

RESULTS

Heritability analyses

Seventeen of the 24 phenotypes are significantly heritable at p ≤ 0.01 and 19 at p ≤ 0.05. Total h² estimates indicate that 12-46% of the phenotypic variance in 2-D cusp size can be attributed to additive genetic effects (Tables 1 and 2).

TABLE 1.

Descriptive statistics and heritability estimates for SNPRC baboon left maxillary molar cusp areas^a

	UM1 hy	UM1 ma	UM1 pa	UM1 pr	UM2 hy	UM2 ma	UM2 pa	UM2 pr	UM3 hy	UM3 ma	UM3 pa	UM3 pr
Mean	13.86	14.48	16.89	13.31	16.79	18.30	23.17	18.05	17.33	15.50	26.98	19.35
Variance	5.47	5.00	6.03	4.74	11.27	10.74	15.10	10.81	7.39	9.85	19.65	9.12
Low value	7.92	3.07	6.66	6.86	9.68	10.11	11.22	10.23	8.07	6.96	18.28	12.86
High value	23.73	21.88	25.42	20.03	30.95	29.07	37.50	38.14	28.39	26.81	40.77	34.70
CV	16.86	15.44	14.54	16.35	19.99	17.91	16.77	18.21	15.69	20.25	16.43	15.61
n	447	437	452	438	412	448	478	504	511	509	518	516
h2 residual	0.105	0.273	0.539	0.000	0.196	0.388	0.346	0.297	0.465	0.353	0.345	0.147
± SE	±0.092	±0.124	±0.118	nc	±0.122	±0.113	±0.110	±0.113	±0.123	±0.101	±0.106	±0.096
P-value	0.067	0.0007	<0.0001	0.500	0.020	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	0.030
Total h2	0.085	0.181	0.378	0.000	0.177	0.292	0.269	0.265	0.340	0.256	0.217	0.115
e 2	0.723	0.482	0.324	0.856	0.729	0.461	0.507	0.626	0.391	0.468	0.412	0.671
c 2	0.192	0.336	0.297	0.144	0.093	0.247	0.225	0.110	0.268	0.276	0.371	0.213
β age	<0.001	0.055	<0.001	<0.001	ns	ns	<0.001	ns	ns	ns	ns	ns
β age2	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns
β sex	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
β age*sex	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns
β age2sex	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns	ns

^aUM1 = first maxillary molar; hy = hypocone area; ma = metacone area; pa = paracone area; pr = protocone area; ns = not significant. Total c² = amount of phenotypic variance attributable to covariates; Total h² = (Residual h²)(1-Total c²); Total e² = [1-(Total c² + Total h²)]; Coefficient of variation (CV) = [standard deviation * 100]/mean; measurements are in mm².

TABLE 2.

Descriptive statistics and heritability estimates for SNPRC baboon right maxillary molar cusp areas^a

	UM1 hy	UM1 ma	UM1 pa	UM1 pr	UM2 hy	UM2 ma	UM2 pa	UM2 pr	UM3 hy	UM3 ma	UM3 pa	UM3 pr
Mean	14.29	14.63	17.17	14.13	18.07	16.81	22.50	18.33	22.95	19.35	16.15	15.48
Variance	4.39	4.46	6.24	4.51	10.70	7.31	15.35	11.45	12.83	10.12	6.47	8.52
Low value	10.25	0.39	0.30	9.70	10.19	9.99	13.80	7.84	14.22	12.25	9.12	8.87
High value	23.13	24.41	31.40	25.94	30.88	27.15	34.78	38.66	34.78	30.37	23.43	25.28
CV	14.66	14.44	14.55	15.02	18.10	16.09	17.41	18.46	15.61	16.44	15.74	18.85
n	464	477	480	459	542	541	538	539	396	396	396	406
h2 residual	0.544	0.318	0.546	0.423	0.396	0.593	0.450	0.232	0.124	0.282	0.090	0.160
± SE	±0.161	±0.112	±0.118	±0.159	±0.118	±0.116	±0.115	±0.088	±0.103	±0.142	±0.107	±0.121
P-value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	0.066	0.005	0.167	0.052
Total h2	0.458	0.231	0.425	0.363	0.331	0.408	0.354	0.207	0.081	0.226	0.073	0.119
e 2	0.384	0.495	0.354	0.495	0.504	0.280	0.433	0.686	0.572	0.575	0.730	0.625
c 2	0.158	0.273	0.220	0.141	0.165	0.311	0.213	0.107	0.348	0.199	0.197	0.257
β age	0.008	ns	ns	<0.001	ns	<0.001	ns	<0.001	<0.001	<0.001	<0.001	ns
β age2	ns	ns	ns	0.008	ns	ns	ns	ns	ns	ns	ns	ns
β sex	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
β age*sex	0.007	ns	ns	0.003	<0.001	<0.001	ns	ns	<0.001	ns	ns	ns
β age2sex	ns	ns	ns	0.075	ns	ns	<0.001	ns	ns	ns	ns	ns

^aUM1 = first maxillary molar; hy = hypocone area; ma = metacone area; pa = paracone area; pr = protocone area; ns = not significant. Total c² = amount of phenotypic variance attributable to covariates; Total h² = (Residual h²)(1-Total c²); Total e² = [1-(Total c² + Total h²)]; Coefficient of variation (CV) = [standard deviation * 100]/mean; measurements are in mm².

Covariate effects account for 9-37% of the total phenotypic variance, with no consistent difference between the left and right sides of the maxillary arcade. Sex is the only consistently significant covariate, indicating that cusp area is sexually dimorphic.

Even though we removed heavily worn specimens from the sample, our heritability analyses do reveal that age has a small but significant contribution to the phenotypic variance for twelve of these phenotypes (Tables 1 and 2). In these analyses, age serves as a proxy for wear since enamel formation stops at eruption. Age/wear does not appear to significantly raise the covariate variance for these twelve cusps relative to the others. Therefore, we interpret this effect to be minimal and not of significant consequence to the overall interpretations.

Bivariate analyses (estimates of genetic correlation)

The heritability analyses provided the foundation for bivariate analyses in which we estimated the proportion of the phenotypic correlation between any two cusps that is due to a genetic correlation – how much of the variation results from the same genetic effects. Only phenotypes that yielded significant (p ≤ 0.05) heritability estimates were used in the bivariate analyses.

Additive genetic correlations between cusps on the same crown

Our first set of bivariate analyses tested for genetic correlations between all possible cusp pairs within the same crown. Figure 2 shows schematically the results presented in Tables 4 and 5, as well as the right and left combined data set (results not shown in tabular form).

TABLE 4.

Bivariate statistical genetic analyses: Maximum-likelihood estimates (MLE) of genetic and environmental correlations for the left maxillary molar cusps^a

			Correlations (MLEs)		Significance of Correlations P(Hypothesis)
	Phenotype pairs	N	ρG (se)	ρ E	ρG =0	∣ ρG ∣=1
UM1	ma-pa	437	0.971 (0.061)	0.531	<0.0001	0.3059
UM2	ma-pr	448	0.275 (0.251)	0.281	0.3081	0.0004
	ma-pa	448	0.782 (0.136)	0.600	0.0023	0.0272
	ma-hy	412	−0.126 (0.458)	0.340	0.7745	0.1286
	pr-pa	478	0.019 (0.324)	0.381	0.9532	0.0014
	pr-hy	412	1	0.634	0.0005	nc
	pa-hy	412	−0.106 (0.468)	0.227	0.8175	0.1000
UM3	ma-pr	509	0.457 (0.234)	0.439	0.1304	0.0080
	ma-pa	509	0.700 (0.141)	0.564	0.0042	0.0004
	ma-hy	509	0.883 (0.078)	0.451	<0.0001	0.0300
	pr-pa	516	1	0.059	0.0015	nc
	pr-hy	511	0.560 (0.197)	0.622	0.0719	0.0087
	pa-hy	511	0.630 (0.150)	0.081	0.0097	<0.0001
Metacone	UM1-UM2	437	0.805 (0.130)	0.380	0.0003	0.0347
	UM1-UM3	437	0.782 (0.136)	0.235	0.0011	0.0165
	UM2-UM3	448	1	0.260	<0.0001	nc
Paracone	UM1-UM2	452	0.841 (0.150)	0.459	0.0001	0.1318
	UM1-UM3	452	0.730 (0.124)	0.491	0.0002	0.0013
	UM2-UM3	478	1	0.366	<0.0001	nc
Protocone	UM2-UM3	504	0.774 (0.286)	0.380	0.0334	0.2033
Hypocone	UM2-UM3	412	0.657 (0.203)	0.301	0.0446	0.0307

^aP(Hypothesis): probability of the hypothesis indicated in the columns below being true given the available pedigreed data; se = standard error; ma = metacone area; pa = paracone area; pr = protocone area; hy=hypocone area; UM1 = first maxillary molar; nc = not calculable.

TABLE 5.

Bivariate statistical genetic analyses: Maximum-likelihood estimates (MLE) of genetic and environmental correlations for the right maxillary molar cusps^a

			Correlations (MLEs)		Significance of Correlations P(Hypothesis)
	Phenotype pairs	N	ρG (se)	ρ E	ρG =0	∣ ρG ∣=1
UM1	ma-pr	459	0.839 (0.086)	0.076	<0.0001	0.0031
	ma-pa	477	0.887 (0.074)	0.734	<0.0001	0.0170
	ma-hy	464	0.845 (0.085)	0.172	0.0001	0.0032
	pr-pa	459	0.642 (0.129)	0.217	0.0028	<0.0001
	pr-hy	459	0.946 (0.037)	0.640	<0.0001	0.0148
	pa-hy	464	0.681 (0.127)	0.158	0.0014	0.0001
UM2	ma-pr	539	0.096 (0.257)	0.358	0.7134	0.0003
	ma-pa	538	0.716 (0.134)	0.555	0.0039	0.0009
	ma-hy	541	0.486 (0.203)	0.352	0.0548	0.0002
	pr-pa	538	−0.017 (0.309)	0.272	0.9540	0.0046
	pr-hy	539	1	0.631	0.0001	nc
	pa-hy	538	0.282 (0.264)	0.211	0.3340	0.0004
Metacone	UM1-UM2	477	0.971 (0.077)	0.438	<0.0001	0.3464
	UM1-UM3	396	0.345 (0.207)	0.520	0.1508	<0.0001
	UM2-UM3	396	0.416 (0.199)	0.269	0.0674	<0.0001
Paracone	UM1-UM2	480	0.780 (0.136)	0.467	0.0005	0.0311
Protocone	UM1-UM2	459	1	0.323	0.0001	nc
Hypocone	UM1-UM2	464	0.819 (0.127)	0.445	0.0012	0.0286

^aP(Hypothesis): probability of the hypothesis indicated in the columns below being true given the available pedigreed data; se = standard error; ma = metacone area; pa = paracone area; pr = protocone area; hy=hypocone area; UM1 = first maxillary molar; nc = not calculable.

For UM1 and UM2 the paracone-metacone and protocone-hypocone consistently show genetic correlations of one or very close to one (p ≤ 0.01). Both the right UM1 and combined UM1 returns evidence of complete or incomplete pleitropy for all pair-wise comparisons. Because only one cusp on the right UM3 yielded a significant heritability, we were not able to run pair-wise analyses for this tooth. For the left UM3 the paracone-protocone pair and metacone-hypocone pair returned genetic correlations of one (p ≤ 0.01). In contrast, when the UM3 combined data was analyzed, the paracone-metacone and the metacone-hypocone pairs were found to have genetic correlations of one. The paracone-hypocone has evidence of incomplete pleitropy.

Additive genetic correlations between homologous cusps along the tooth row

In general, bivariate analyses of cuspal homologues on adjacent teeth yielded correlations that were high or not significantly different from one (Tables 4 and 5), for example the paracones on the first and second molars. Cuspal homologues on non-adjacent teeth yielded genetic correlations that were often lower, for example the metacone on the UM1 versus the UM3. The genetic correlations between hypocones were considerably lower for UM2 and UM3 analyses.

Additive genetic correlations between maxillary and mandibular cusps

Our third set of bivariate analyses tested for genetic correlations across the dental arcades. As was noted above, not all of our heritability estimates for the left UM1 were statistically significant. We have found previously (and in this study; see Table 3) that antimeres have genetic correlations of one or very close to one, indicating that both sides of the dental arcade are influenced by the same gene or set of genes (Hlusko et al., 2004; Hlusko and Mahaney, 2003; Hlusko et al., 2002; Hlusko, 2002). Therefore, we used the right UM1 hypocone and protocone data for the inter-arch analyses in order to have a complete significant data set for the left maxillary dentition (the only side for which we have mandibular data). While all of the available evidence from our previous studies suggests that antimeres can be interpreted as representing the same genetic influences, we do recognize that this is an assumption and therefore the results should be read with the appropriate caution. Results are presented in Table 6, and representatively in Table 7.

TABLE 3.

Bivariate statistical genetic analyses: Maximum-likelihood estimates (MLE) of genetic and environmental correlations between analogous left and right maxillary pairs^a

		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pairs Right-Left	N	ρG (se)	ρ E	ρG =0	∣ ρG ∣=1
UM1 ma v UM1 ma	437	0.937 (0.113)	0.298	<0.0001	0.2745
UM1 pa v UM1 pa	452	0.998 (0.050)	0.225	<0.0001	0.4838
UM2 hy v UM2 hy	412	1	0.185	0.0004	nc
UM2 ma v UM2 ma	448	0.816 (0.096)	0.029	<0.0001	0.0065
UM2 pa v UM2 pa	478	0.978 (0.132)	0.268	<0.0001	0.4329
UM2 pr v UM2 pr	504	0.889 (0.178)	0.222	0.0018	0.2416

^aP(Hypothesis): probability of the hypothesis indicated in the columns below being true given the available pedigreed data; se = standard error; ma = metacone/id area; pr = protocone/id area; pa = paracone area; hy=hypocone/id area; ea = entoconid area; UM1 = first maxillary molar; nc = not calculable.

TABLE 6.

Bivariate statistical genetic analyses: Maximum-likelihood estimates (MLE) of genetic and environmental correlations across the left maxillary and mandibular arches^a

		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pairs Mandible-Maxilla	N	ρG (se)	ρ E	ρG =0	∣ ρG ∣=1
LM1 pr v UM1 pa	338	0.944 (0.095)	−0.259	<0.0001	0.2609
LM1 pr v UM1 ma	338	0.983 (0.116)	−0.074	<0.0001	0.4409
LM1 en v UM1 pa	346	0.783 (0.227)	0.072	0.0016	0.1661
LM1 en v UM1 ma	346	0.877 (0.187)	0.176	0.0038	0.2324
LM1 pr v UM1 pr*	338	0.400 (0.244)	0.240	0.1578	0.0013
LM1 pr v UM1 hy*	338	0.532 (0.200)	0.135	0.0439	0.0012
LM1 ma v UM1 pa	340	0.874 (0.121)	−0.104	<0.0001	0.1144
LM1 ma v UM1 pr*	340	0.298 (0.207)	−0.114	0.1904	<0.0001
LM1 ma v UM1 ma	340	0.983 (0.096)	0.116	<0.0001	0.4291
LM1 ma v UM1 hy*	340	0.356 (0.207)	−0.059	0.1305	<0.0001
LM1 hy v UM1 pa	356	0.519 (0.228)	−0.026	0.0422	0.0091
LM1 hy v UM1 pr*	356	0.616 (0.218)	0.301	0.0353	0.0076
LM1 hy v UM1 ma	356	0.762 (0.203)	−0.055	0.0109	0.0763
LM1 hy v UM1 hy*	356	0.806 (0.121)	0.118	0.0009	0.0094
LM1 en v UM1 pr*	346	0.461 (0.238)	0.027	0.1185	0.0057
LM1 en v UM1 hy*	346	0.594 (0.208)	0.058	0.0506	0.0082
LM2 pr v UM1 ma	437	0.145 (0.310)	0.260	0.6519	0.0005
LM2 pr v UM1 hy*	447	0.768 (0.134)	0.385	0.0040	0.0032
LM2 ma v UM1 ma	437	1	0.023	<0.0001	nc
LM2 ma v UM1 hy*	447	0.410 (0.200)	0.265	0.0894	<0.0001
LM2 pr v UM2 pa	478	0.546 (0.230)	0.002	0.0458	0.0106
LM2 pr v UM2 ma	448	0.434 (nc)	−0.002	0.0709	0.0002
LM2 en v UM2 pa	475	0.780 (0.143)	0.093	0.0003	0.0400
LM2 en v UM2 ma	448	0.766 (0.120)	−0.095	<0.0001	0.0021
LM2 pr v UM2 pr	479	0.860 (0.111)	0.187	0.0002	0.0484
LM2 pr v UM2 hy	412	0.930 (0.123)	0.125	0.0003	0.2699
LM2 ma v UM2 pa	478	0.915 (0.184)	0.151	0.0001	0.3222
LM2 ma v UM2 pr	498	0.504 (0.194)	0.067	0.0242	0.0014
LM2 ma v UM2 ma	448	0.999 (0.083)	−0.179	<0.0001	0.4961
LM2 ma v UM2 hy	412	0.624 (0.207)	−0.020	0.0189	0.0424
LM2 hy v UM2 pa	478	−0.251 (0.241)	0.201	0.2903	0.0030
LM2 hy v UM2 pr	480	0.706 (0.220)	0.199	0.0039	0.0630
LM2 hy v UM2 ma	448	−0.163 (0.210)	0.156	0.4290	<0.0001
LM2 hy v UM2 hy	412	1	0.070	<0.0001	nc
LM2 en v UM2 pr	475	0.504 (0.217)	0.171	0.0375	0.0019
LM2 en v UM2 hy	412	0.991 (0.161)	0.093	0.0003	0.4788
LM3 pr v UM2 ma	405	0.224 (0.212)	0.181	0.3207	<0.0001
LM3 pr v UM2 hy	405	0.717 (0.317)	0.094	0.0397	0.1930
LM3 ma v UM2 ma	406	1	−0.442	<0.0001	nc
LM3 ma v UM2 hy	406	0.242 (0.281)	−0.040	0.4156	0.0150
LM3 pr v UM3 pa	405	0.458 (0.217)	0.186	0.0565	0.0014
LM3 pr v UM3 ma	405	−0.030 (0.243)	0.286	0.9005	0.0001
LM3 en v UM3 pa	382	0.545 (0.191)	0.164	0.0161	0.0018
LM3 en v UM3 ma	382	0.368 (0.228)	0.232	0.1257	0.0008
LM3 hy v UM3 pr	392	0.730 (0.301)	0.220	0.0354	0.1985
LM3 hy v UM3 hy	392	0.372 (0.228)	0.207	0.1435	0.0001
LM3 pr v UM3 pr	405	0.706 (0.374)	0.253	0.0539	0.2461
LM3 pr v UM3 hy	405	0.102 (0.230)	0.327	0.6605	<0.0001
LM3 ma v UM3 pa	406	0.832 (0.133)	0.145	<0.0001	0.0714
LM3 ma v UM3 pr	406	0.571 (0.250)	0.191	0.0371	0.0714
LM3 ma v UM3 ma	406	0.747 (0.253)	−0.012	0.0036	0.1487
LM3 ma v UM3 hy	406	0.372 (0.188)	0.109	0.0671	0.0001
LM3 hy v UM3 pa	392	0.351 (0.243)	0.164	0.1758	0.0010
LM3 hy v UM3 ma	392	−0.254 (0.276)	0.428	0.3449	0.0034
LM3 en v UM3 pr	382	0.671 (0.265)	0.138	0.0247	0.1084
LM3 en v UM3 hy	382	0.548 (0.220)	0.010	0.0196	0.0179

^aP(Hypothesis): probability of the hypothesis indicated in the columns below being true given the available pedigreed data; se = standard error; ma = metacone/id area; pr = protocone/id area; pa = paracone area; hy=hypocone/id area; ea = entoconid area; M1 = first molar; nc = not calculable.

^*Right UM data was used in place of left UM data (refer to results section for further discussion).

Table 7.

Bivariate statistical genetic analyses: Estimates of genetic correlation across the left maxillary and mandibular arches^a

Mandibular cusp	Maxillary cusp	Estimate of Genetic Correlation
		M1	M2	M3	Relationship
metaconid	paracone	1	1	1	NOC
metaconid	metacone	1	1	1	NOC
entoconid	paracone	1	P	ns/0	NOC
entoconid	metacone	1	P	0	NOC
protoconid	paracone	1	ns/P	0	B-B
protoconid	metacone	1	0	0	B-B
hypoconid	metacone	ns/1	0	0	B-B
hypoconid	paracone	0	0	0	B-B
hypoconid	hypocone	P	1	0	OCC
hypoconid	protocone	1	1	ns/1	OCC
protoconid	protocone	0	1	ns/1	OCC
protoconid	hypocone	0	1	0	OCC
metaconid	hypocone	0	ns/1	0	L-L
metaconid	protocone	0	0	ns/1	L-L
entoconid	protocone	ns/0	0	ns/1	L-L
entoconid	hypocone	ns/P	1	ns/P	L-L

^a“0” represents ρ_G = 0; “P” represents 0< ρ_G <1; “1” represents ρ_G = 1; “ns” = not significant at p < 0.01; Score to the right of “/” represents the genetic correlation significant at p <0.05; “NOC” = non-occluding; “B-B” = both cusps are buccal; “L-L” = both cusps are lingual; “OCC” = occluding.

Across all molars the non-occluding cusps have the most consistently high genetic correlations, especially the metaconid-paracone and metaconid-metacone (Figure 3B). The buccal-buccal cusps typically have very high genetic correlations for the M1s, but no genetic correlation on M2s or M3s. The occluding cusp pairs all have genetic correlations of one for the M2s, but less consistent results for the M1 and M3 comparisons. The lingual-lingual cusp pairs typically yielded little to no evidence of a genetic correlation.

An extension of this analysis was to compare occluding cusps that are on different molars, for example the UM1 hypocone and LM2 protoconid (Table 6). Following the pattern of high genetic correlations between non-occluding cusps, the LM2 and LM3 metaconids have a genetic correlation of one with the UM1 and UM2 metacones respectively. The UM1 hypocone and LM2 protoconid pair have a genetic correlation significantly different from zero and one, indicating a partial genetic correlation. All other genetic correlations between occluding cusps between UM1 and LM2 were zero, and for UM2 and LM3 genetic correlations were zero or not statistically significant.

DISCUSSION

Quantitative genetic analyses of morphological variation can sometimes be perceived as mundane given that they often provide us with an answer that we did not actually know, but could be correctly anticipated by most biologists. In one sense our present analysis falls into this category, as we did find that additive genetic effects do significantly influence the variation of molar cusp size in a pedigreed population of baboons. This is not surprising. However, a genetic contribution is essential for selection to operate, and therefore it is important to establish that variation in a trait can respond to selection. It is also not remarkable that the right and left side antimeric phenotypes have a genetic correlation of one, or very close to it, as most biologists predict that the genes influencing the mammalian dentition are identical for the right and left sides of the dental arcade.

With that said, this simple insight is far from where quantitative genetics’ contribution to morphology ends. We can build upon these analyses to gain knowledge of how genetic effects structure morphological variation.

We will first summarize the pattern of genetic integration for mandibular and maxillary molar cusp size variation, then present three hypotheses derived from these results on baboons. These hypotheses may apply to the genetic architecture of primate molars more generally and perhaps even to other mammals with bunodont molars.

The genetic architecture of molar cusp size variation

Our previous quantitative genetic analysis of mandibular molar cusp size yielded a consistent genetic correlation of one between the protoconid-entoconid, incomplete genetic correlations between the other cusp comparisons, and no genetic correlation between the hypoconid-entoconid. The only difference between the LM1, LM2, and LM3 was that the LM1 genetic correlations were all estimated to be one, save for the metaconid-hypoconid and hypoconid-entoconid pairs, which were found to be zero, whereas for LM2 and LM3 the protoconid-entoconid genetic correlation was one, the metaconid-hypoconid correlation was zero, and all others indicated incomplete pleiotropy. As noted in that previous publication, these results do not conform to expectations from the sequence of cusp calcification, patterns of coalescence, or what is known about the genetic development of mouse molars (Hlusko et al., 2007).

Our analysis of maxillary molar cusp size revealed fewer genetic correlations on each crown than did the mandibular molar cusp analyses. Only the paracone-metacone and protocone-hypocone yielded consistently significant genetic correlations for both the right and left UM1 and UM2. While this result does not fit with the coalescence pattern for the mesial and distal lophs that are so characteristic of cercopithecoid molars, this does follow to a certain extent the order of cusp formation/calcification for UMs.

In baboons, the paracone is almost always the first cusp to calcify and there is variation in the relative timing of the metacone and protocone (Swindler et al., 1968; Swindler, 1985; Tarrant & Swindler 1972). The metacone and protocone are known to calcify simultaneously in humans (Rose, 1892, as cited by Butler, 1956), ungulates (Taeker, 1892, as cited by Butler, 1956), cows (Küpfer, 1935; Rose and Barthels, 1896; both as cited by Butler, 1956), macaques (Swindler and Gavan, 1962), and black howlers (Swindler et al., 1968; Tarrant and Swinder 1972). The metacone is also the first cusp added to the paracone during development in dogs (Tims, 1896) and in Ornithorhynchus (Green, 1938). Consequently, it is not unreasonable to hypothesize that the genes determining the relative size of the first cusp may be identical to those that determine the next cusp during development. However, what is confusing from our current study is the apparent disjunction between the second and third cusps in the developmental cascade.

The genetic architecture of the molar field

We propose that the overall mandibular and maxillary patterns of additive genetic correlation reflect the evolutionary origins of the tribosphenic and bunodont molar, and that the pattern of genetic integration can be interpreted to serve a functional demand. Before we elaborate on these two points we will bring into the discussion the additive genetic correlations between the maxillary and mandibular arches, as these inter-arch relationships help to elucidate the intra-arch patterns of genetic integration.

Rather than considering cusps by name only, we can also interpret them through their functional roles and location on the crown. For the purposes of this discussion we divide them into four categories. The first category contains the “occluding cusps”, meaning the cusps that occlude against each other and form the basis of the grinding platforms: protoconid and hypoconid against protocone and hypocone (e.g., the end of Phase I and Phase II of primate chewing, Hiiemae and Kay, 1972). These cusps form a buccal-lingual relationship, as the occluding cusps on the mandibular molars are on the buccal side of the crown and the occluding cusps on the maxillary molars are on the lingual side of the crown.

The second category contains the “non-occluding” cusps: metaconid and entoconid in the mandible with paracone and metacone in the maxilla (these cusps are thought to function as “guides” during mastication, Kay, 1977). These cusps are in a lingual-buccal relationship, as the non-occluding cusps on the mandibular molars are on the lingual side of the crown and the non-occluding cusps on the maxillary molars are on the buccal side of the crown.

The last two categories are defined by position alone. Third category includes the cusps that are all on the buccal side of the molars, both maxillary and mandibular. The fourth category consists of the cusps that are all on the lingual side of the molars. As such, these last two groups do not have a primary functional relationship (although there are some minor wear facets, such as wear facet 5 that results from guidance during Phase I movement, Kay, 1977).

Between the maxillary and mandibular arches we find the highest degree of additive genetic correlation between the “non-occluding” cusps, i.e., the cusps that do not come into direct contact during occlusion (see Table 7). In contrast, the “occluding” cusps, those that come into direct contact during the end of Phase I and Phase II chewing – the buccal mandibular cusps and the lingual maxillary cusps, have a genetic correlation of one on the M2s, but occluding cusp genetic correlations are much lower, if present at all, on the M1s and M3s.

At first glance this inter-arch pattern of genetic integration is the opposite of what would be predicted from previous morphological studies on primates – that the occluding cusps would be the most genetically integrated. For example, in Kay’s (1975) study of phenotypic correlations between occluding and non-occluding elements of cercopithecoid molar crowns, he found that aspects of the molars directly related by occlusion, or function, returned the highest phenotypic correlations, and that functionally unrelated measurements had no significant correlation. It is of particular interest to note that he analyzed data only from the M2s. As such, his results do accord with ours given that the M2 in our study were the only ones to return significant genetic correlations between the occluding (functional) cusps. Therefore, Kay’s (1975) functional correlations may well reflect genetic correlations. Following on our results, we predict that the phenotypic correlations between these functionally related molar features may be lower in the M1s and M3s than was found for the M2s, although phenotypic correlations are, of course, not a perfect reflection of genetic correlations (additive or non-additive).

Taking a broader turn, teeth function on a variety of levels simultaneously. Kay’s (1975) research, and the many other investigations of this sort, focus on the very specific and immediate function of cusp morphology, such as specific crests, wear facets, and slopes. As is widely recognized, molars must also function together as a unit in a dental arcade that includes teeth with other functions, in maxillary and mandibular jaw bones, and in a mouth with soft tissue and various musculature (for a comprehensive overview of this region of the anatomy see Nanci, 2008). Consequently, the genetic integration of the dentition will also be selected upon to serve function at a larger scale – the pattern of the overall dentition.

The pattern of genetic integration we found for cusp size variation in these pedigreed baboons may well result from selective pressure for functional adaptiveness at this larger scale. Our current interpretation is that the additive genetic correlations between the mesiodistally oriented maxillary cusp pairs may serve to maintain a less variable molar row length. We propose that there may be less tolerance for variation in the mesiodistal length of the maxillary molar row given its close anatomical relationship with the rest of the cranium. A high genetic correlation between cusps along the mesiodistal axis may serve to constrain variation. In contrast, the mandibular molars have a diagonal pattern of genetic correlation on that serves to maintain the basic mortar shape to receive the hypocone while enabling some flexibility as the other two or three cusps vary independently. This pattern of integration is presented visually in Figures 3A and B.

While further investigation is needed to explore this possibility, and bearing in mind the need to be cautious of over-interpreting possible “spandrels” (Gould and Lewontin, 1979), the pattern of genetic integration seen in the molar cusps may well reflect a balance between maintaining the basic structure of the molar series within the constraints of the cranium while also enabling a degree of variation. If this pattern of genetic integration is characteristic of other primates, then the buccal cusps of the maxillary molars and the mandibular protoconid and entoconid may well provide the most insight to larger scale phylogenetic and adaptive investigations, as they may reflect the fundamental genetic pattern of molar morphology.

This hypothesis still needs to be investigated via more sophisticated quantitative genetic analyses, such as measures of evolvability and conditional evolvability (e.g., Hansen and Houle, 2008) – analyses that are currently being pursued.

As noted earlier, our results may also reveal remnants of the evolutionary history of the dentition. We refer the reader back to the review of the origins of the tribosphenic molar presented in the introduction of this paper. Following on this evolutionary history, we present three hypotheses that have implications beyond cercopithecoid odontology.

Hypothesis 1: The paracone and metacone are genetically integrated due to their close positional relationships to two of the three main cusps (cusps A and C) in the linear cuspal arrangement of early mammal teeth, prior to the evolution of the tribosphenic molar

This may also be reflected in the pattern of development and mineralization, in that the paracone and metacone are the first cusps to form. It has been previously argued that developmentally later-forming cusps evolved more recently (e.g., Butler, 1956, among many others). A recent study of relative cusp proportions in several species in the genus Homo notes the distinct and taxonomically relevant phenotypic correlation between the size of the paracone and metacone (Quam et al., 2009), as would be predicted from our genetic analysis.

Hypothesis 2: The now non-occluding cusps reflect the primary evolutionary relationship between the maxillary and mandibular molars, due to their original occluding relationship in the triconodont molars of early mammalian molars and reptiles before them

Triconodont molars occluded to form one blade (Lucas, 2004), and early mammals had precise occlusion that resulted in wear facets on the buccal edge of mandibular molar cusps and the lingual edge of maxillary molar cusps (Crompton and Jenkins, 1968). The cusps that remained on the non-wear facet side of baboon molars may still be controlled by the mechanism(s) of genetic integration that determined the earliest molar forms, even as the patterning mechanism(s) evolved to enable the tribosphenic and quadrate molar.

Previous studies have also alluded to a similar interpretation. For example, Reid et al. (1998) found that within Pan troglodytes maxillary and mandibular molars, the non-occluding cusps mineralize faster than do the functional/occluding cusps. As noted for Hypothesis 1, this also bolsters the interpretation that development can mimic evolution, where ontogenetically later forming cusps evolved more recently.

Research in dental developmental genetics may be honing in on this mechanism. Kassai et al. (2005) report that knock-out mice lacking ectodin (a BMP inhibitor) have crests and lophs on the buccal side of the molar crown that are not present in wild type mice (as well as extra teeth in the diastemal region and LM1/LM2 fusion). Eda and Edar mutant mice also show defects in enamel knot function, molar cusp pattern, and number of teeth (Tucker et al., 2000; Kangas et al., 2004), although the resultant phenotypic variation is highly variable and difficult to summarize (Charles et al., 2009). Zhang et al. (2009) report that mice lacking the transcription factor odd-skipped related-2 (Osr2), an important component along the Bmp4-Msx1 pathway, have extra teeth that form along the lingual side of the tooth row (maxillary and mandibular). While none of these developmental studies has reported an affected phenotype that mirrors the patterns of additive genetic correlations interpreted from our baboon results, they suggest that genetic mechanisms do influence morphology along the molar row series, bolstering our interpretation of a larger-scale level of selection.

Hypothesis 3: The metaconid represents the primary cusp on the mandibular molar

This hypothesis is contradictory to the commonly held view within vertebrate evolution that the protoconid is the primary cusp in various mammalian taxa (Tims, 1896; Butler, 1956). However, if patterns of genetic integration reflect evolutionary history, then the metaconid’s strong additive genetic correlation with the size variation of the maxillary molar cusps would argue for the evolutionary primacy of this cusp.

To date, one of the main justifications for the evolutionary primacy of the protoconid has been that it is the first cusp to initiate mineralization. The sequence of cusp calcification is commonly interpreted as a fundamental process that is relatively invariable, particularly for the first cusp. For baboon, macaques, humans, chimpanzees, and gorillas, the sequence for mandibular molar cusps is usually protoconid → metaconid → hypoconid → entoconid (Swindler et al., 1968; Oka and Kraus, 1969; Swindler, 1985; Kraus and Jordan, 1965). However, these reports are typically based on very few specimens given the difficulty of their procurement. But even within these small samples there is evidence of variation. Macaque protoconids and hypoconids initiate calcification very close in time (Swindler and Gavan, 1962) and the second cusp to calcify varies between the metacnoid and hypoconid (Swindler and McCoy, 1965). Berkovitz (1967) reported variation in the primary cusp in the marsupial Setonix brachyurus, in which the metaconid is the first to initiate mineralization on the deciduous second molar and the LM2, but the protoconid is first for the LM1 (this pattern appears to correlate with differences in cusp height). In the maxillary molar the metacone and protocone are known to calcify simultaneously for a number of different mammalian taxa (see references cited above). Additionally, we are restricted to analyses of cusp mineralization given research methodologies, which may not necessary correlate perfectly with cusp development.

We recognize that Hypothesis 3 stands in contradiction to long-held views within mammalian odontology, but argue that it warrants consideration given the pattern of our inter-arch additive genetic correlations and recognition that we may not fully understand population-level variation within the developmental process

Caveat

Before concluding, we want to raise one potential caveat to these analyses. This relates to the difficulty in defining a phenotype that most accurately reflects tooth biology. We have analyzed the 2-D area of cusps, but it is important to keep in mind that cusps are 3-D. Also, the size of a cusp is a combination of the size of the underlying dentine as well as the thickness of the enamel. A number of studies have demonstrated that enamel is thicker on the lateral surface of the functional cusps than it is on other cusps (e.g., Shillingburg and Grace, 1973; Schwartz, 2000). Three dimensional studies have shown an even greater amount of variation in the distribution of enamel than can be explained by function alone (Kono et al., 2002; Suwa and Kono, 2005).

We demonstrated previously that variation in enamel thickness on the buccal surface of the protoconid in these baboons is heritable (h² = 31 – 42% of the phenotypic variance), and genetically independent of sex and tooth size (Hlusko et al., 2004). Therefore, our measured phenotype employed here, 2-D cusp area, may not be a simple or direct representation of the genetic mechanisms responsible for odontogenesis, but rather the amalgamation of several phenotypes (as would be defined by the underlying genetics). It is not immediately obvious how this complication would alter the results presented here, or if it would at all. As we work towards identifying phenotypes that best reflect the underlying genetic architecture, this caveat is relevant to all quantitative genetic analyses; there is a trial-and-error nature to the endeavor.

Summary

We performed a quantitative genetic analysis of variation in 2-D maxillary molar cusp size using data collected from a pedigreed breeding colony of captive baboons, Papio hamadryas. This investigation elucidated the pattern of genetic integration for baboon molar cusp size variation within the maxilla, as well as between the dental arcades. These analyses show that variation in maxillary molar cusp size is both heritable and sexually dimorphic. Total h² estimates indicate that approximately 12-46% of the phenotypic variance in 2-D maxillary cusp size can be attributed to additive genetic effects.

We conducted bivariate analyses testing for additive genetic correlations between cusps on the same crown, homologous cusps along the tooth row, and maxilla and mandible. We found that the paracone- metacone and protocone-hypocone pairs yield the most significant genetic correlation on the UM1 and UM2; the UM3 shares only the paracone- metacone correlation with the UM1 and UM2. In general, bivariate analyses of cuspal homologues on adjacent teeth yield correlations that are high or not significantly different from one. Between the dental arcades the non-occluding cusps have the most consistently high genetic correlations, especially the metaconid-paracone and metaconid-metacone pairs.

Further analyses are needed to determine how pervasive this pattern of genetic integration may be across primates and other mammals. In the meantime, we tentatively propose three hypotheses based on the evolutionary origins of the tribosphenic molar from which bunodont molars derived. We propose that the paracone and metacone are genetically integrated due to their original relationship as two of the three main cusps in the linear cuspal arrangement of early mammal teeth, prior to the evolution of the tribosphenic molar. Second, the non-occluding cusps may reflect the primary evolutionary relationship between the maxillary and mandibular molars, due to their original occluding relationship in the triconodont molars of early mammals and reptiles before them. Lastly, we propose that the metaconid may represent the primary cusp on the mandibular molar.