Comparison of multivariate classifiers and response normalizations for pattern-information fMRI

Abstract

A popular method for investigating whether stimulus information is present in fMRI response patterns is to attempt to “decode” the stimuli from the response patterns with a multivariate classifier. The sensitivity for detecting the information depends on the particular classifier used. However, little is known about the relative performance of different classifiers on fMRI data. Here we compared six multivariate classifiers and investigated how the response-amplitude estimate used (beta or t-value) and different pattern normalizations affect classification performance. The compared classifiers were a pattern-correlation classifier, a k-nearest-neighbors classifier, Fisher’s linear discriminant, Gaussian naïve Bayes, and linear and nonlinear (radial-basis-function-kernel) support vector machines. We compared these classifiers’ accuracy at decoding the category of visual objects from response patterns in human early visual and inferior temporal cortex acquired in an event-related design with BOLD fMRI at 3T using SENSE and isotropic voxels of about 2-mm width. Overall, Fisher’s linear discriminant (with an optimal-shrinkage covariance estimator) and the linear support vector machine performed best. The pattern-correlation classifier often performed similarly as those two classifiers. The nonlinear classifiers never performed better and sometimes significantly worse than the linear classifiers, suggesting overfitting. Defining response patterns by t-values (or in error-standard-deviation units) rather than by beta estimates (in % signal change) to define the patterns appeared advantageous. Cross-validation by a leave-one-stimulus-pair-out method gave higher accuracies than a leave-one-run-out method, suggesting that generalization to independent runs (which more safely ensures independence of the test set) is more challenging than generalization to novel stimuli within the same category. Independent selection of fewer more visually responsive voxels tended to yield better decoding performance for all classifiers. Normalizing mean and standard deviation of the response patterns either across stimuli or across voxels had no significant effect on decoding performance. Overall our results suggest that linear decoders based on t-value patterns may perform best in the present scenario of visual object representations measured for about 60-minutes per subject with 3T fMRI.

Introduction

Pattern-information analysis has become an important method for investigating distributed representations with fMRI (Haxby et al., 2001; Cox and Savoy, 2003; Kriegeskorte, 2004; Kamitani and Tong, 2005; Haynes and Rees, 2005;Kriegeskorte et al., 2006, 2007; for conceptual reviews, see Norman et al., 2006; Haynes and Rees, 2006; Kriegeskorte and Bandettini, 2007; Quian Quiroga and Panzeri, 2009). A popular method of testing for mutual information between experimental stimuli and regional fMRI response patterns is “decoding”: the classification of response patterns so as to determine the stimulus category. Above-chance-level decoding accuracy with any classifier indicates that the response patterns contain information about the stimulus category. However, the sensitivity with which pattern information is detected by decoding depends on the classifier used, and little is known about the relative performance of different classifiers on fMRI data.

How do classifiers differ?

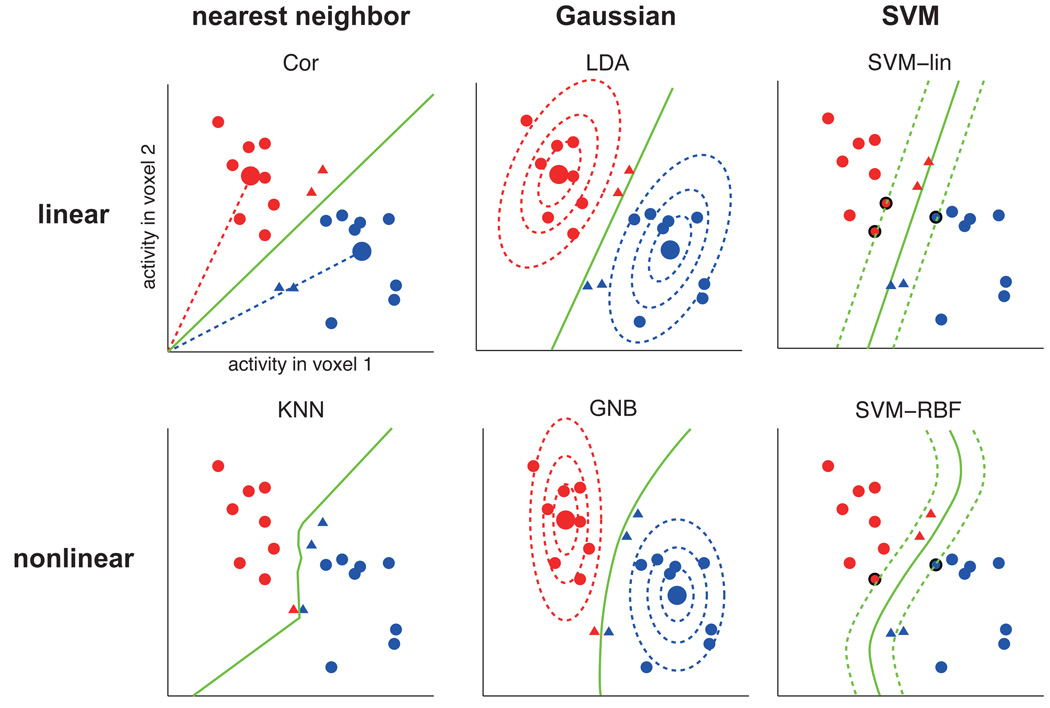
All classifiers have in common that they use a set of training data to define a decision boundary in the space of response patterns, i.e. the space spanned by activity levels of the voxels in the region of interest (ROI). Fig. 1 and Table 1 compare the classifiers in detail. Classifiers differ in the shapes they allow for the decision boundary (e.g. hyperplanes in linear classifiers; more complex nonplanar boundaries in nonlinear classifiers) and in the way the boundary is placed on the basis of the training data (e.g. Fisher’s linear discriminant places the decision hyperplane so as to optimally discriminate of two equal-covariance Gaussians; a linear support vector machine (SVM) places the decision hyperplane so as to maximize the margin to the patterns on either side; Fig. 1). A gentle step-by-step introduction to fMRI pattern-classifier analysis is given in Mur et al. (2009), and a more technical one in Pereira et al. (2009).

Figure 1. Different pattern classifiers use different decision boundaries.

Hypothetical example of classification by different classifiers. Each classifier determines a different decision boundary on the basis of a set of training patterns (red and blue circles). As a result, test patterns in the ambiguous territory between the two clusters (red and blue triangles) will be classified differently by the different classifiers. The color of the triangles indicates which class it is classified as. The large circles, where present, are the class centroids (i.e. class-average patterns). The dotted ellipsoids (for GNB and LDA) are iso-probability-density contours of the fitted Gaussian distributions. For the SVMs, the dotted lines represent the margin around the decision boundary and the bold-edged circles are the support vectors defining the boundary.

Table 1.

Comparison of the six classifiers (as implemented here)

	Cor pattern- correlation classifier	KNN k-nearest- neighbors classifier	LDA Fisher’s linear discriminant analysis	GNB Gaussian naive Bayes	SVM-lin linear support vector machine	SVM-RBF radial-basis- function support vector machine
type	nearest neighbor		Gaussian		SVM
decision boundary	linear	nonlinear	linear	nonlinear (quadratic surface)	linear	nonlinear
pattern distribution model	-	nonparametric	Gaussian (same for each class, correlated voxels)	Gaussian (distinct for each class, independent voxels)	-	-
related distance function	correlation distance	correlation distance	Mahalanobis distance	Mahalanobis distance	Euclidian distance	Euclidian distance
regularization	within-class averaging	training-set cross-validation to select k (defining the size of the neighborhood)	Gaussian assumption, class-pooled, optimal- shrinkage covariance estimate	Gaussian assumption ignoring voxel correlations	training-set cross-validation to select C (defining misclassification penalty)	training-set cross-validation to select C and γ (defining RBF width)

Most of the classifiers commonly applied to fMRI data were originally developed in statistics and machine learning. Their properties are well understood. However, performance in practice will depend on how well the classifier’s implicit assumptions (i.e. its inductive bias; Mitchell, 1997) hold in the domain in which it is applied and on how much data is available. In the present domain, the classifier’s inductive bias needs to be well suited both to the properties of the brain representations investigated and to features of fMRI data including various noise components, the dimensionality of the response patterns (i.e. the number of voxels considered), and the number of available training patterns.

The more flexible the decision boundary fitted to separate the stimulus categories in the training data, the better it will tend to separate the categories in the training data. However, a more flexible boundary is also likely to adapt to the idiosyncrasies of the noise in the training data. This is known as overfitting (e.g. Bishop, 2007; Duda et al., 2000; for the relation to circular analysis, see Kriegeskorte et al., 2009). A highly overfitted decision boundary might perfectly classify the training data, even if the response patterns contain no information about the stimulus category at all. This is why independent test data are needed to assess the performance of a classifier (and to thereby test for stimulus-category information in the response patterns).

The most rigid possible decision boundary is a hyperplane. This is why hyperplane classifiers (i.e. linear classifiers) tend to suffer less from overfitting than nonlinear classifiers, which allow more complex boundaries. However, overfitting concerns not only the shape, but also the placement of the boundary. Though rigid in shape, a hyperplane in a d-dimensional space (e.g. a response pattern space for d voxels) requires d parameters to define its placement (e.g. the intersections of the hyperplane with each of the axes of the space). In fMRI analysis, overfitting can be substantial even with linear classifiers, because the number of voxels in the ROI is often similar to the number of training patterns.

Reducing the set of possible decision boundaries (i.e. the hypothesis space) is one method of reducing overfitting. More generally, overfitting can be reduced by regularization (Krishnapuram et al., 2005, Hastie et al., 2009), i.e. by using prior assumptions to constrain the ways in which the boundary is shaped and shifted so as to discriminate the categories in the training data. Different classifiers utilize different implicit assumptions for this purpose (Fig. 1).

For a given classifier, dimensionality reduction of the response patterns can further reduce overfitting and improve classification performance (Mitchell et al. 2004; Guyon and Elisseeff 2003; De Martino et al. 2008). The simplest variant of dimensionality reduction is perhaps voxel selection. Mitchell et al. (2004) showed that selecting voxels highly responsive to the task was more effective for classification performance than selecting voxels discriminative for classification (higher classification accuracy for training data by a single-voxel classifier). This suggests that strongly responsive voxels had more reliable differences between conditions. Multivariate feature selection procedures have also been applied to fMRI data (e.g. Kriegeskorte et al., 2006; De Martino et al., 2008; Björnsdotter Åberg et al., 2008).

Previous studies comparing classifier performance on fMRI data

Some previous studies have performed comparisons of different classification methods for fMRI data. Cox and Savoy (2003) used SVMs with linear and polynomial kernels for classifying fMRI response patterns into categories of visually presented objects. They employed a block-design experiment, and used percent-signal-change responses in the lower-tier visual areas as input to classifiers. Linear SVM performed better than polynomial SVM, suggesting that the polynomial SVM suffered from overfitting. Consistent with this observation, LaConte et al. (2005) also reported results suggesting that linear SVMs are superior to nonlinear SVMs for decoding block-design fMRI data. Cox and Savoy (2003) also included Fisher’s linear discriminant analysis (LDA). However, the covariance estimates for LDA were based on very few data points (one per experimental block) and the sample covariance estimator was used, so the covariance estimate was singular for most ROI sizes and LDA could not be fairly evaluated for the relevant pattern dimensionalities (larger ROIs).

Mitchell et al. (2004) compared Gaussian naïve Bayes (GNB), SVM, and k-nearest-neighbors (KNN) classifiers. Results for three different data sets suggested that GNB and SVM perform well. KNN was always inferior to GNB and SVM.

Ku et al. (2008) compared four classification methods for high-field (7 Tesla) high-resolution data from monkey inferior temporal cortex: LDA, pattern-correlation classifier (Cor), GNB, and linear SVM. Their results indicated similarly good performance of all linear classifiers (SVM, LDA, and Cor) and worse performance of GNB, which utilizes nonlinear (quadratic) decision boundaries.

This study

In the present study we extend previous findings by systematically comparing six classification methods under different conditions. The six classification methods are

• pattern-correlation classifier (Cor),

• k-nearest-neighbors classification (KNN),

• Fisher’s linear discriminant analysis (LDA),

• Gaussian naïve Bayes (GNB),

• a linear support vector machine (SVM-lin),

• and a nonlinear (radial-basis-function-kernel) support vector machine.

Each method was evaluated for each combination of the following variables:

• brain region (human early visual cortex (EVC) or human inferior temporal cortex (hIT)),

• region-of-interest (ROI) size (different numbers of voxels),

• single-voxel response estimate (beta estimate or t-value),

• pattern normalization (normalization of mean and standard deviation performed either across stimuli or across voxels)

• cross-validation scheme (leave-one-run-out or leave-one-stimulus-pair-out),

• categorical dichotomy (Animate/Inanimate, Face/Body, and Natural/Artificial)

We performed single-trial classification in all cases, i.e. each test pattern to be classified was estimated from the hemodynamic response to a single 300-ms presentation of a visual stimulus. ROIs were defined by selecting voxels according to their responsiveness to the object images in a separate experiment (cf. Mitchell et al. 2004, Kriegeskorte et al. 2008a). Voxel selection and classifier training were always based on data independent of the test data used to assess classifier performance (e.g. Kriegeskorte et al., 2009).

In the literature, some pattern-information studies used beta estimates to define the response patterns (e.g. Haxby 2001; De Martino et al., 2008) and other studies used t-values (e.g. Martínez-Ramón et al., 2006; Kriegeskorte et al., 2008a). A number of studies used raw fMRI responses as input (typically in percent signal change), defining the patterns by single time points or temporal block averages (Cox and Savoy, 2003; Mitchell et al., 2004; Haynes and Rees, 2005; Kamitani and Tong, 2005; LaConte et al., 2005). These latter pattern estimates are equivalent to beta estimates obtained for a design matrix of impulse or rectangular predictors.

Different response-pattern estimates can yield different decoding performance, but have not previously been compared. We therefore compare performance for response patterns defined by either beta estimates or t-values. Beta estimates were obtained in a general-linear-model analysis for the blood-oxygen-level-dependent (BOLD) signal, which was normalized to percent signal change, so the beta estimates are in percent-signal-change units. The t-values were calculated by dividing the beta estimate for each voxel by its standard-error estimate.

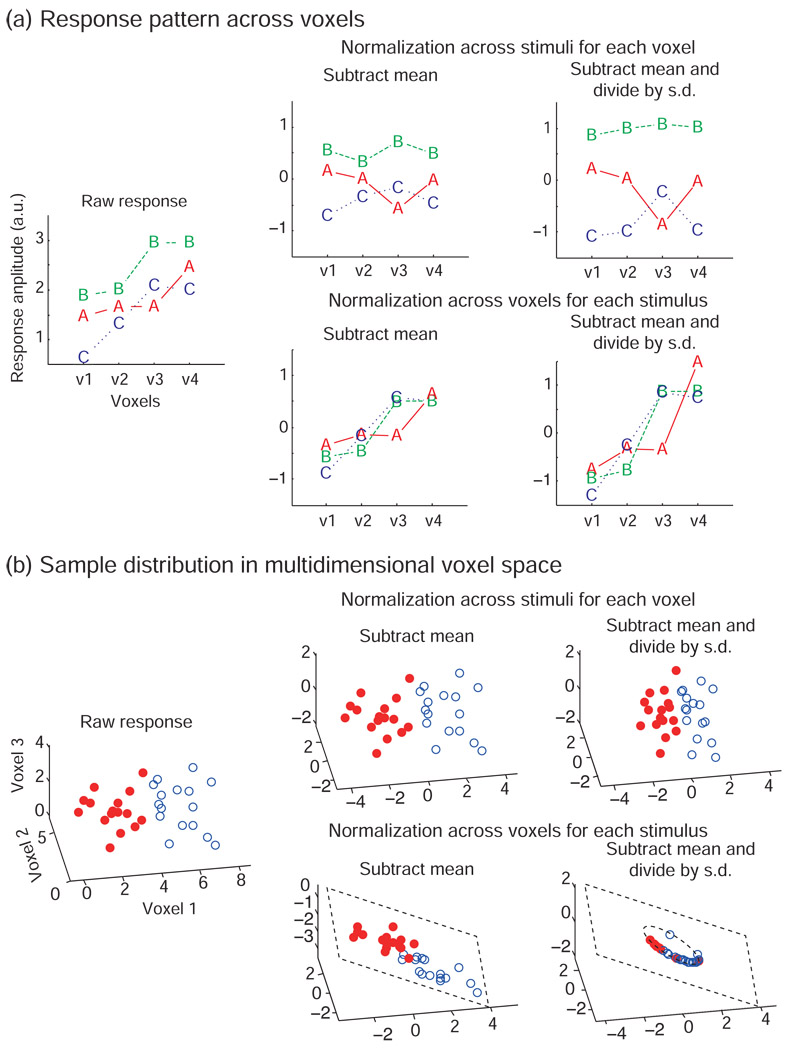
Patterns were normalized either for each stimulus across voxels (as implicit to the popular pattern-correlation classifier of Haxby et al., 2001) or for each voxel across stimuli (as applied, for example, in Ku et al., 2008) by first subtracting the mean and then dividing by the standard deviation (Fig. 2).

Figure 2. Pattern normalization can be performed across voxels or across stimuli.

This figure illustrates how the different normalizations change response patterns. The plotted data are hypothetical. (a) Each panel shows response amplitudes of four voxels (v₁, v₂, v₃, v₄) for each of three stimuli (A, B, and C). The left panel shows the raw response. The upper row shows the normalization across stimuli for each voxel. This normalization changes the response pattern across voxels but preserves relative response differences between stimuli in each voxel. The lower row shows the normalization across voxels in each stimulus. This normalization preserves the shape of the response pattern across voxels for each stimulus but changes relative response differences between stimuli in each voxel. (b) Each panel shows the distributions of the response patterns for two classes (solid red circles and open blue circles) in the voxels’ response space. The left panel shows the raw response-pattern distributions. The upper row shows the normalization across stimuli for each voxel. This normalization shifts and scales the distributions in the response space. Note the shift of the origin of the axes. The lower row shows the normalization across voxels for each stimulus. This normalization projects the points onto a hyperplane by subtracting the mean, and then onto a hypersphere within that hyperplane by dividing by the standard deviation. Note that removing 2 dimensions in this 3-dimensional cartoon example leaves only one dimension (i.e. the circle in the plane) for the patterns to vary along. For high-dimensional response patterns (d dimensions), however, the hypersphere will have similar dimensionality (d-2) as the original space, and the loss of information may be small.

We analyzed fMRI response patterns measured in human subjects in a rapid event-related experiment in which subjects viewed 96 object images from different categories (data from Kriegeskorte et al., 2008a). The analyzed data were taken from two ROIs, in early visual cortex (EVC) and in inferior temporal cortex (hIT). Classification was performed for three different categorical dichotomies: Animate/Inanimate, Face/Body, and Natural/Artificial.

Methods

Stimuli and task

Four human subjects participated in an event-related fMRI experiment, in which they viewed 96 color photos of isolated objects on a gray background. The stimulus duration was 300 ms. Each image was presented once in each experimental run as part of a random sequence. The minimum stimulus onset asynchrony was 4 s. We used a new random sequence for each run (to reduce correlations among temporally overlapping hemodynamic response predictors spanning multiple runs, and obtain more stable amplitude estimates). Six runs were performed for each subject in a single session. The classifier analyses here are based on one such session per subject.

The object categories were hierarchically organized. We used the super-ordinate level category (Animate/Inanimate) and the second-level categories (Face/Body in the Animate category and Natural/Artificial in the Inanimate category) for classification tests. Each pattern estimate corresponded to a particular stimulus image. The number of stimuli (and associated response patterns) for Animate/Inanimate was 96 (48 for each category), for Face/Body it was 48 (24 for each category) and for Natural/Artificial it was also 48 (24 for each category).

Subjects fixated a continually visible fixation cross and performed a color-discrimination task on each trial, reporting a color change of the fixation cross from white to either green or blue, by pressing one of two buttons. The fixation-cross color changes occurred at stimulus onset and lasted for the duration of the stimulus. Green and blue changes occurred according to a random sequence unrelated to the stimulus sequence. More details on the experiment are in Kriegeskorte et al. (2008a).

The fMRI measurements

The fMRI measurements were performed using a 3T GE HDx MRI scanner (Milwaukee, WI) with a receive-only whole-brain surface-coil array (16 elements, NOVA Medical Inc., Wilmington, MA). BOLD fMRI was performed by a single-shot interleaved gradient-recalled echo-planar imaging (EPI) sequence with SENSE (acceleration factor = 2). The EPI matrix size was 128 × 96, the voxel size was 1.95 × 1.95 × 2 mm³, the TE was 30 ms, and the TR was 2 s. Twenty-five 2-mm axial slices (no gap), covering the occipital and temporal lobe, were acquired. Each functional run consisted of 272 volumes (9 min and 4 s).

Data preprocessing and response estimation

The fMRI data sets were adjusted for slice-scan-time differences and corrected for head-motion using the BrainVoyager QX software package (R. Goebel, Maastricht, The Netherlands). All further analysis was conducted in MATLAB (The MathWorks, Natick, MA, USA). The signal values for each voxel were normalized to percent signal change. We performed a single univariate linear model fit to extract an activity-amplitude estimate (beta estimate) for each of the 96 stimuli. Each subject was analyzed separately at this stage.

To estimate the response amplitudes, we first concatenated the runs along the temporal dimension. We used one hemodynamic response predictor for each stimulus. Since each stimulus occurred once in each run, each single-stimulus predictor had one hemodynamic response per run and extended across all runs included. The predictor time courses were computed using the hemodynamic response model of Boynton et al. (1996).

The design matrix also included predictors modeling residual head-motion artefact, trends, and the baseline signal level. For each run, there were six head-motion-parameter predictors, one linear-trend predictor, a 6-predictor Fourier basis for nonlinear trends (sines and cosines of up to 3 cycles per run), and a baseline (confound mean) predictor. The head-motion, trend, and baseline predictors for each run were padded by zeros for the temporal extent of the other runs.

Two regions of interest: EVC and hIT

To define regions of interest (ROIs), we selected the most visually responsive voxels within a manually defined anatomical mask. For the early visual cortex (EVC) ROI, the anatomical mask was an extended cortical region around the occipital pole and calcarine sulcus, excluding the lateral occipital region. For human inferior temporal cortex (hIT), the anatomical mask included all cortical voxels anterior to the EVC mask within our ventral-stream measurement slab, which was near-axial, but tilted to run in parallel with the ventral temporal cortical surface. Visual responsiveness was assessed using the average response (t-value) for the 96 stimuli in a separate experiment. This voxel selection criterion has also been used in Mitchell et al. (2004).

We used three different numbers of voxels for each ROI; 224, 1057, and 5000 for EVC and 316, 1000, and 3162 for hIT. These ROI sizes were chosen to cover a wide range (with logarithmic spacing). Including a large ROI is important because it provides a test of the ability of different methods to handle high-dimensional response spaces, where overfitting may become a problem for some methods.

Two cross-validation procedures for estimating generalization performance

We compared two cross-validation procedures. One is the leave-one-run-out cross-validation. In this procedure, data of one run provided the test samples, and the remaining runs provided the training samples. Each classifier’s discriminant function was fitted using the training samples. Then the classifier’s performance was evaluated using the test samples. The cross-validation had six folds because there were six runs. The mean classification accuracy across the six folds was used as the estimate of the classifier’s performance.

The other cross-validation method used was the leave-one-stimulus-pair-out cross-validation. In this procedure, one stimulus was taken from each class as a test sample and all remaining stimuli were used for classifier training. The responses to each stimulus were estimated using all six runs. We performed 100 cross-validation folds with the left-out pairs of stimuli randomly selected such that each stimulus was in the test set at least once.

In the leave-one-run-out cross-validation, classifiers were trained on responses to all stimuli and tested on responses to all stimuli on independent data (i.e. the left-out run on each fold of cross-validation), thus testing generalization within the same stimuli, but across runs. In the leave-one-stimulus-pair-out cross-validation, classifiers were trained by responses to all stimuli except for one pair (with one stimulus in each of the two categories) and tested by responses to the left-out stimulus pair, thus testing generalization to novel stimuli within the same categories.

Independence of training and test data

In order to estimate decoding performance without bias due to overfitting of the training data, the test data need to be independent of the data used for voxel selection and classifier training (see Kriegeskorte et al., 2009, for a detailed discussion). The ROIs were defined on the basis of a separate experiment. The classifier analyses were performed for these ROIs using data from the event-related experiment, which were split (for each subject) into separate training and test sets for cross-validation. In the leave-one-run-out cross-validation, the linear model analysis was performed for training and test data sets independently and response estimates (beta or t) were estimated from these independent analyses. This procedure was repeated on each fold of the cross-validation. In the leave-one-stimulus-pair-out cross-validation, all runs were used to estimate the response for each stimulus and responses to separate sets of stimuli were used on each fold of cross-validation. As a result, the experimental trials of the test set were in the same scanner runs and temporally intermixed with trials in the training set. The temporal proximity and slight response overlap may have entailed dependencies between training and test sets. We nevertheless include this analysis because it is of methodological interest and does not serve to support particular neuroscientific claims here.

Beta or t-value response-pattern estimates

Patterns of beta estimates (in percent signal change) and t-values were used as input to the classification analyses. For each voxel, the beta estimates for each of the 96 stimuli was obtained by the linear model analysis described above. The t-value was computed by dividing the beta estimate by its standard-error estimate. Because the design contained the same number of stimulus repetitions (in random order) for each condition, the t-values here are essentially proportional to the response expressed in error-standard-deviation units. (Because of slight random differences in pairwise predictor correlations, the factor, by which we multiply the error standard deviation to get the standard error of the beta estimate, is not precisely, but only approximately, equal across the 96 stimuli.) The motivation for using t-values (or responses in error-standard-deviation units) is to suppress the contribution of noisy voxels, which can have high beta estimates due to high noise.

Normalization of response patterns across voxels or across stimuli

In addition to the comparison of beta and t-values, we evaluated the effect of two types of pattern normalization: across stimuli or across voxels. How these normalizations affect the response-pattern ensemble is visualized in Fig. 2 and verbally summarized in Table 2. The normalizations are applied to the 96 pattern estimates (obtained from the univariate linear model using all runs, except the test run in the leave-one-run-out cross-validation).

Table 2.

Effect of different response-pattern normalizations

Geometric intuition for...	Normalization type	Subtract mean	Subtract mean and divide by s.d.
Response response pattern for each stimulus	(1) across stimuli	Pattern shape changed.	Pattern shape changed: Voxels of high variance across stimuli are downscaled.
	(2) across voxels	Pattern shape preserved, but mean-level shifted: spatial- mean response is 0 for all stimuli.	Pattern shape preserved, but shifted and scaled: spatial- mean response and variability across voxels is equal for all stimuli.
Sample sample distribution in voxels’ response space	(1) across stimuli	Distribution is centered on the origin in each dimension.Distribution is shifted in each dimension.	Distribution is centered on the origin and scaled to unit standard-deviation in each dimension.Distribution is shifted and scaled in each dimension.
	(2) across voxels	Distribution is shrunkprojected onto thea hyperplane: tThe dimensionality of the sample distribution is reduced by 1 as samples are projected onto the hyperplane orthogonal to the all-1 vector.	Distribution is shrunkprojected onto thea hypersphere within the hyperplane: tThe dimensionality of the sample distribution is reduced by 2 as samples are projected onto a centered hypersphere within the hyperplane.

In the across-stimuli normalization, we consider the responses to all stimuli for a given voxel. First we subtract the mean value across stimuli from the response to each stimulus in that voxel. Then we divide the resulting values by the standard deviation across stimuli for the voxel. This procedure is repeated for each voxel. The across-stimuli normalization changes the shape of the response pattern for each stimulus across voxels (Fig. 2a, upper row). The sample distribution in the voxels’ response space is shifted, so as to center it on the origin, and then the distribution is scaled to unit standard deviation in each dimension (Fig. 2b, upper row).

In the across-voxels normalization, we consider the responses of all voxels (within the ROI) to a given stimulus. First we subtract the mean value across voxels from the response of each voxel to the stimulus. Then we divide the resulting values by the standard deviation across voxels for that stimulus. This procedure is repeated for each stimulus. The across-voxels normalization does not change the shape of the response pattern to each stimulus; it only shifts and scales each response pattern (Fig. 2a, lower row). In the voxels’ response space, subtracting the mean projects the sample distribution onto a hyperplane (Fig. 2b, lower row). That hyperplane is orthogonal to the all-1 vector and includes the origin. All points on it have coordinates (voxel activities) that sum to zero, reducing dimensionality by 1. Division by the standard deviation across voxels then projects the distribution onto a hypersphere within the hyperplane. The hypersphere is centered on the origin. In total, the dimensionality of the sample distribution is reduced by 2 as samples are projected onto the centered hypersphere within the hyperplane.

Six pattern classifiers

(1) Pattern-correlation classifier

The pattern-correlation classifier (Cor) classifies patterns according to their Pearson correlation coefficient with a category template pattern (Haxby et al., 2001). The template pattern is the average response pattern estimated from the training data for each category. The test pattern is classified as belonging to the category whose template pattern it is most highly correlated with. Haxby et al. (2001) used a pattern-correlation classifier to investigate the representation of categories in the multi-voxel response pattern of the ventral temporal cortex.

(2) Gaussian naïve Bayes

The Gaussian naïve Bayes (GNB) classifier (Mitchell, 1997; Mitchell et al., 2004) models the conditional probability density of the response patterns given a stimulus class as a Gaussian distribution with a diagonal covariance matrix. The conditional probability P(x_j|C_i) of response amplitude x_j in voxel j given that the stimulus is of category C_i is modeled as a univariate Gaussian. The mean and the variance of the Gaussian are estimated from the training patterns. A test pattern x is classified as the class C_i whose posterior probability P(C_i|x) is maximal among all classes. Because the within-class covariance is assumed to be diagonal (i.e. no correlations between voxels across patterns within the same class), the probability density P(x|C_i) of a response pattern x for a stimulus of class C_i obtains as the product of the univariate Gaussian marginals: P(x|C_i=Π_jP(x_j|C_i), where the single-voxel responses x_j form the response pattern x. P(C_i|x) is estimated by the Bayes rule:

$$P(C_i|\mathbf{x})=\frac{P(\mathbf{x}|C_i)\cdot P(C_i)}{{\displaystyle {\sum }_{k}P(\mathbf{x}|C_k)\cdot P(C_k)}}$$ (1)

There are two variants of GNB, which differ with respect to their models of variance. The shared-variance model assumes that the variance of a voxel is identical for all classes. The variance is estimated by the sample variance of the pooled data taken from all classes with the class mean subtracted from each value. In the distinct-variance model, the variance is estimated separately for each class. The shared-variance model yields a linear decision boundary (i.e. a hyperplane). The distinct-variance model yields a quadratic (i.e. nonlinear) decision boundary (Fig. 1). We compared both variants of GNB (comparison not included in the figures). The distinct-variance model gave better performance in most cases, although the difference was not significant. We report the results of GNB using the distinct-variance model.

(3) Fisher’s linear discriminant analysis

Fisher’s linear discriminant analysis (LDA) determines the discriminant dimension in response-pattern space, on which the ratio of between-class over within-class variance of the data is maximized (Duda et al., 2000; Bishop, 2007). After projection of the data on this linear discriminant dimension, a classification threshold is placed at the midpoint between the two class means. This is equivalent to placing a decision hyperplane orthogonal to the discriminant dimension in response pattern space. The resulting classifier is Bayes-optimal (ignoring estimation error) if the distributions corresponding to the two classes are Gaussian and have equal covariance. LDA is closely related to GNB (described above, under (2)) in that both classifiers assume Gaussian within-class distributions. However, GNB relies on a less flexible distributional model in that it assumes zero off-diagonal covariance (i.e. no correlations between voxel pairs across the response patterns within a class). The distinct- variance version of GNB used here is more flexible than LDA in that the two classes can have different variances (i.e. different variabilities within each class for a given voxel). This renders the decision boundary a quadratic surface (i.e. nonlinear) in GNB.

In a two-class classification problem, the normal vector of the hyperplane, w, which points along the discriminant dimension of LDA, is estimated as

$$\mathbf{w}\propto {\mathbf{S}}_{\mathrm{w}}^{-1}({\mathbf{m}}_1-{\mathbf{m}}_2),$$ (2)

where m₁ and m₂ are mean vectors of each class, and S_w is a within-class covariance matrix. When the discriminant value y(x) = w^T (x-m) for a sample x (x is a vector of voxel values, and m is a mean value of all samples) is positive, it is classified as class 1, otherwise it is classified as class 2. In LDA, the covariance structure for each class is assumed to be identical and is often estimated from the training patterns x_n as the sample covariance:

$${\mathbf{S}}_{\mathrm{w}}=\frac{1}{N_1}{\displaystyle \sum _{\mathbf{n}\in {\mathbf{C}}_1}({\mathbf{x}}_{\mathbf{n}}-{\mathbf{m}}_1){({\mathbf{x}}_{\mathbf{n}}-{\mathbf{m}}_1)}^{\mathrm{T}}}+\frac{1}{N_2}{\displaystyle \sum _{\mathbf{n}\in {\mathbf{C}}_2}({\mathbf{x}}_{\mathbf{n}}-{\mathbf{m}}_2){({\mathbf{x}}_{\mathbf{n}}-{\mathbf{m}}_2)}^{\mathrm{T}}.}$$ (3)

When the number of samples is smaller than the dimensionality of the data, the sample covariance is not invertible, and so cannot be used to compute the discriminant weights w. In order to ensure invertibility and improve the stability of the covariance estimate, we use the optimal-shrinkage covariance estimator described in Ledoit and Wolf (2003) (see also Schäfer and Strimmer, 2005; Kriegeskorte et al., 2006), which optimally shrinks the off-diagonal values of the sample covariance toward zero.

(4) k-nearest-neighbors classifier

In the k-nearest-neighbors (KNN) classifier, a test pattern is classified as belonging to the class that is most frequent among the k nearest training patterns (Duda et al., 2000; Bishop, 2007). The parameter k is a positive integer. In the two-class case, k can be set to an odd number to avoid tied classes. KNN is related to the pattern-correlation classifier (described above, under (1)) in that it stores a set of class-related reference patterns and classifies test patterns by determining the nearest reference patterns. However, in the pattern-correlation classifier there is only a single reference pattern for each class: the average of the training patterns for that class and only the nearest reference pattern is considered (as opposed to the k nearest ones). In KNN, each training pattern serves as a separate reference pattern. The nearest patterns are often determined using the Euclidian distance in KNN, but here we used the correlation distance (i.e. 1-r, where r is the Pearson correlation coefficient). This is more consistent with the pattern-correlation classifier. Moreover, we compared both measures for KNN and found significantly better or equivalent performance using the correlation distance (comparison not shown in the figures).

KNN can be motivated as selecting the class of maximum posterior probability based on a nonparametric local probability estimate. We assume that the frequencies of the classes in the training data represent the prior probabilities of the classes (e.g. an equal number of training patterns for each class represents equal prior probability of each class). The posterior probability of class C_i given test pattern x can then be estimated as:

$$p(C_i|\mathbf{x})=\frac{N_i}{N},$$ (4)

where N is the total number of training patterns of any class and N_i is the number of training patterns of class i among the k nearest patterns. In contrast to LDA and GNB, which assume Gaussian distributions, KNN does not assume a particular shape of the distribution. The decision boundaries of KNN are nonlinear (Fig. 1). The parameter k affords a means of adjusting the size of the neighborhood, across which we compute a combined probability-mass estimate, promising some robustness against overfitting despite the nonlinear nature of the method and its attractive ability to model arbitrarily complex distributions given sufficient data. The optimal k was selected by five-fold cross-validation performed on the training data. We searched k = 1, 3, 5, 9, 13, 21, 35, and 57 for Animate/Inanimate classification and k = 1, 3, 5, 7, 9, 13, 21, and 31 for Face/Body and Natural/Artificial classifications.

(5) Linear support vector machine

A linear support vector machine (Fig. 1, SVM-lin) places a decision hyperplane in pattern space to classify test patterns into two classes. In this respect it does not differ from LDA. However, the hyperplane is placed by a different criterion: SVM-lin chooses the hyperplane that has the maximum margin, i.e. the hyperplane that separates the classes with the maximum safety clearance to the closest training patterns on either side (Vapnik, 1995; Cristianini and Shawe-Taylor, 2000; Duda et al. 2000; Bishop, 2007).

For intuition, consider the case of a few training data points and at least as many dimensions, where a hyperplane can perfectly discriminate the training data. We start with some hyperplane that achieves this. Now imagine the plane thickening to form a rigid planar sheet. The sheet shifts and rotates when it hits training data points as it continues to thicken. It keeps thickening until it cannot grow any further without including a training data point. The training data points touching (and jointly fully constraining) the sheet are called the support vectors. The hyperplane chosen by SVM-lin is the central plane within the planar sheet. Note that this method will uniquely define a separating hyperplane in arbitrarily high-dimensional spaces even for just two training data points. In the latter case, the hyperplane will orthogonally bisect the connection between the two training data points.

The general case, where the training data points cannot be perfectly separated is handled by allowing a few misclassifications among the training data points. A parameter C (> 0) defines a penalty for misclassification. C is important for good generalization performance as it controls regularization, which counteracts overfitting of the training data. Here, C was selected by grid search in the range of C = 2⁻⁵ to 2¹⁵ using five-fold cross-validation within the training data. We used the LIBSVM-2.88 package (Chan and Lin, 2005) for the SVM analyses.

(6) Nonlinear radial-basis-function support vector machine

The linear support vector machine (described above) can also be used to create nonlinear decision boundaries: by first redescribing the data using a kernel function so as to define a higher-dimensional alternative space. The kernel function maps the original data space to the higher-dimensional space. A linear SVM can then be used to define a decision hyperplane. The hyperplane in the higher-dimensional space corresponds to a more complex nonlinear decision boundary in the original data space.

We included an SVM with a radial-basis-function kernel (SVM-RBF). For SVM-RBF, the width γ of the radial basis function is a critical parameter, along with the C parameter described above. Here, the optimal C and γ were selected by grid search in the range of C = 2^{− 5} to 2¹⁵ and γ = 2⁻¹⁵ to 2³ respectively, using five-fold cross-validation within the training data.

Differences and commonalities between classifiers

To maintain an overall view, let’s briefly review the main differences and commonalities among the six classifiers (as summarized in Table 1). GNB and LDA are similar in that they assume a Gaussian distribution for the response patterns of each class. However, LDA models within-class correlations between voxels, which GNB assumes to be absent. GNB, here, uses distinct variance estimates for each class, while LDA assumes a distribution of equal shape (only shifted) for each class. As a result, LDA decision boundaries are hyperplanes, whereas GNB decision boundaries are quadratic surfaces. Cor and KNN both classify test patterns by looking for the most similar reference patterns. However, KNN looks for the k most correlated training patterns (and classifies by majority vote), whereas Cor looks for the most correlated class-average training pattern. LDA, Cor, and SVM-lin use linear (i.e. hyperplane) decision boundaries, whereas GNB, KNN, and SVM-RBF use nonlinear decision boundaries. GNB, LDA and KNN can be motivated on the basis of models of the class-conditional response-pattern distributions. The distributional models are Gaussian for GNB and LDA, and nonparametric for KNN. Cor and SVM, in contrast, are motivated by the goal of classification (without implicit or explicit modeling of the distributions).

A classifier with stronger implicit assumptions (i.e. stronger bias) is expected to have better generalization performance as long as the assumptions are approximately correct. In fMRI pattern classification, the number of training patterns is typically small relative to the dimensionality of the response-pattern space (i.e. the number of voxels). This is the case in the present study as well. We therefore expect generalization performance (and thus sensitivity to pattern information) to benefit from strong implicit assumptions even if those assumptions are not precisely correct. Note that violations of the assumptions will reduce sensitivity, not specificity, so the resulting test of pattern information will be valid even if the classifier’s assumptions are violated.

Results

Statistical analysis

Statistical comparison of the performance of different classifiers requires that we account for the dependency between the accuracy estimates resulting from the use of the same data with each classifier (Dietterich, 1998; Nadeau & Bengio, 2003). Here classification performance was compared between classifiers using paired t tests. We first computed the average classification accuracy across cross-validation folds for each stimulus. The difference of these stimulus-specific average performances between methods (i.e. different response estimates, classifiers, and pattern normalizations) were then statistically compared. The statistical analyses were performed separately for each subject. The analysis was performed independently for each cross-validation procedure, ROI location, ROI size, and category dichotomy. Because the levels of these factors were related to each other, they could not be used as independent factors of an ANOVA (Demšar, 2006). For simplicity, we report significant differences (p < 0.05, Bonferroni corrected) observed for at least two of four subjects.

The effect of the type of response estimate (beta and t) on decoding performance

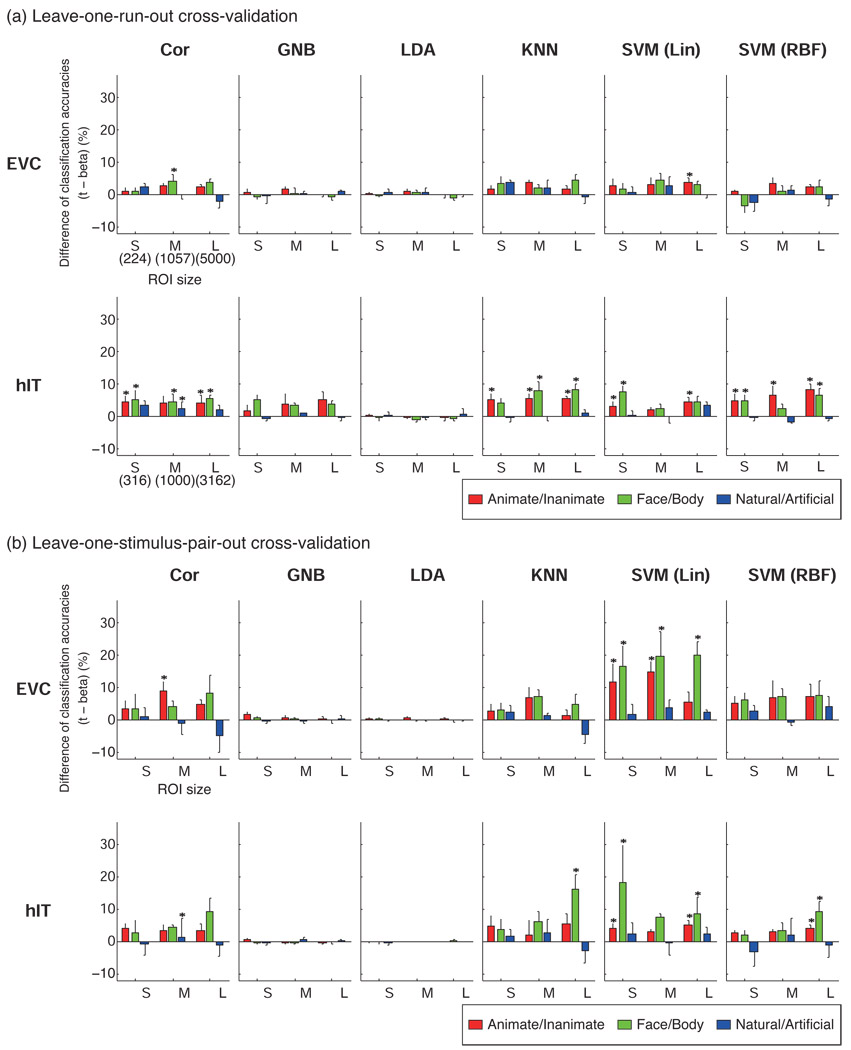
Fig. 3 shows the differences of classification accuracies between the two types of response-pattern estimate (t-values and beta estimates). Significant differences (p < 0.05) that were seen in at least two of four subjects were marked by asterisks in Fig. 3. Classifiers had better performances with t- than beta estimates in most cases. We found no significant negative effect of using t-values.

Figure 3. Defining the response patterns by t-values instead of beta estimates yielded better or equal decoding accuracy.

The bars show the difference of classification accuracy between patterns defined by t-values and patterns defined by beta estimates. Positive values (upward bars) mean that t-values gave better classification accuracy than beta estimates. Error bars show the standard error of the mean across subjects. The statistical analysis (paired t test across stimuli) was performed for each subject separately and an asterisk indicates a significant difference (p < 0.05) in at least two of four subjects. S, M, and L indicate the small, middle and large ROI size, respectively. The numbers of voxels in S, M, L were 224, 1057, 5000 for EVC, and 316, 1000, 3162, for hIT. Significant differences were only seen in favor of t-values. LDA and GNB were not significantly affected by the difference of response estimates because they model and thus correct for the variance along each response dimension (see Discussion for details).

An advantage of t-values was observed for Cor, KNN, and SVMs. GNB and LDA were not sensitive to the difference between t and beta. The latter result is not surprising, because GNB and LDA model each voxel’s variance separately by an entry along the diagonal of the covariance matrix, thus adapting to changes of scale applied separately to each voxel – as in the conversion from beta estimates to t-values. Because t-values gave better performance in most cases, all further results reported will be using t- rather than beta estimates.

The effect of the cross-validation method on decoding performance

The leave-one-run-out cross-validation (Fig. 4, Fig. 6a) produced lower accuracies than the leave-one-stimulus-pair-out cross-validation (Fig. 5, Fig. 6b). In the leave-one-run- out cross-validation, classifiers were trained on a subset of scanner runs (all but one run), using all stimuli, and had to generalize to separate runs (for the same stimuli). In contrast, in the leave-one-stimulus-pair-out cross-validation, classifiers were trained on a subset of stimuli (all except one pair of stimuli), and had to generalize to novel stimuli (measured in the same runs). The results suggest that generalization to new runs was more difficult than generalization to new stimuli within the same class.

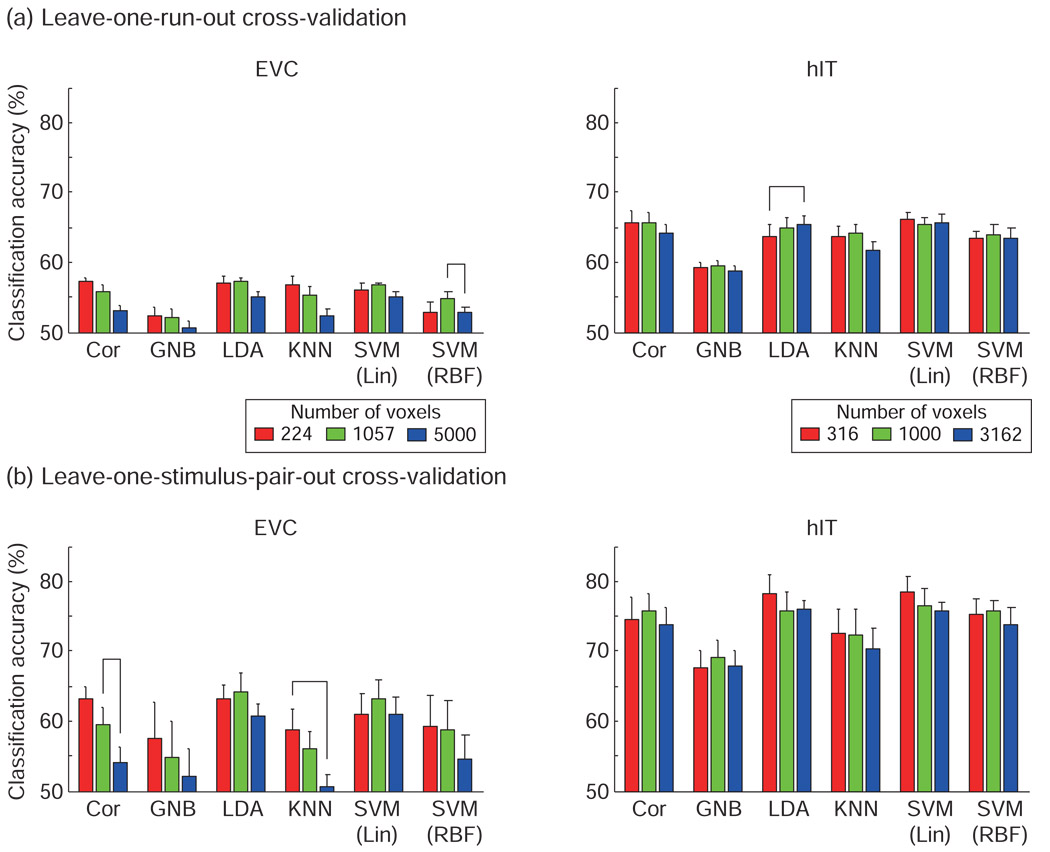
Figure 4. Linear classifiers performed best and not significantly differently (leave-one-run-out cross-validation).

Classification accuracies estimated with leave-one-run-out cross-validation for each classification method for (a) EVC ROI and (b) hIT ROI. The voxels in ROI were selected by visual responsiveness assessed using the average response for the 96 stimuli (t-value) in a separate experiment. Response patterns were defined by t-values. Accuracies are averages across subjects and stimuli. Error bars show the standard error of the mean across subjects. Classifiers were ordered by their mean classification accuracies. Chance-level accuracy was 50% (solid line). The upper dashed line indicates the significance threshold for better-than-chance decoding (indicating the presence of pattern information). For a single-subject accuracy exceeding the significance line, p < 0.05 (not corrected for multiple tests) for a binomial test with 96 trials for Animate/Inanimate, and 48 for Face/Body and Natural/Artificial (H0: chance-level decoding). The horizontal connection lines above the bars indicate significant differences between classifiers (p < 0.05 with Bonferroni correction for the 15 pairwise comparisons of the 6 classifiers) seen in at least two of four subjects (paired t test across stimuli). With this procedure, a horizontal connection indicates a significant difference of decoding accuracy between two classifiers at p<0.036, corrected for the multiple tests across pairs of classifiers, across subjects, and across all scenarios (region, ROI size, category dichotomy, and cross-validation method) of Figs. 4 and 5 combined (see Results for details). LDA and SVM-lin tended to perform best and not significantly differently.

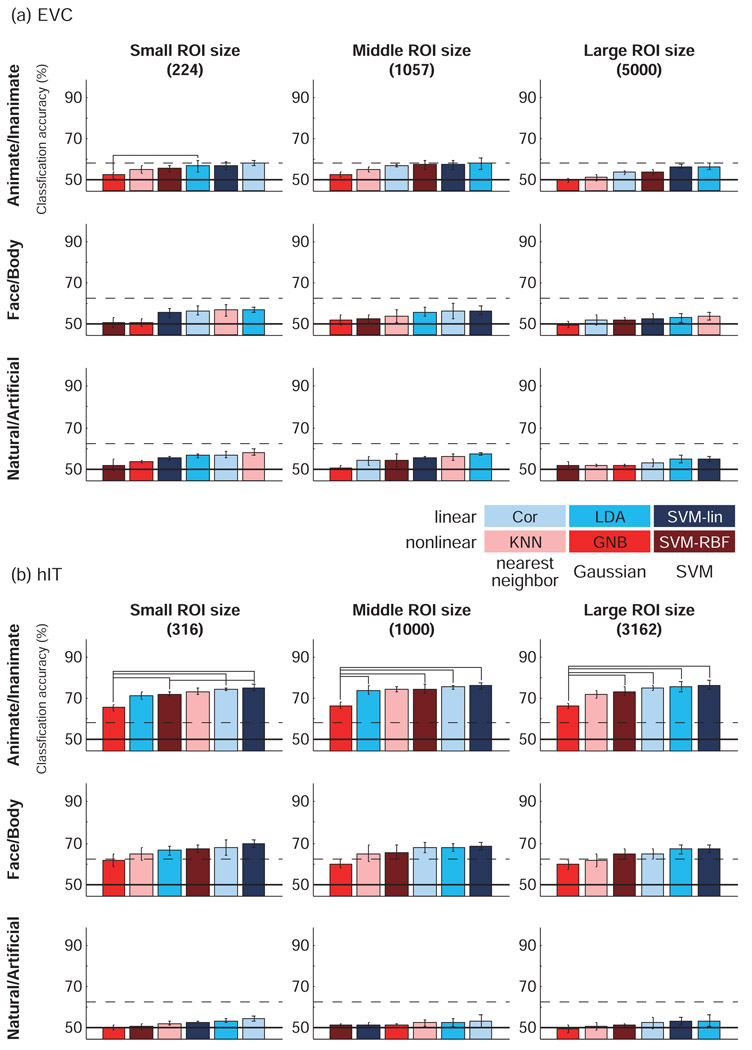
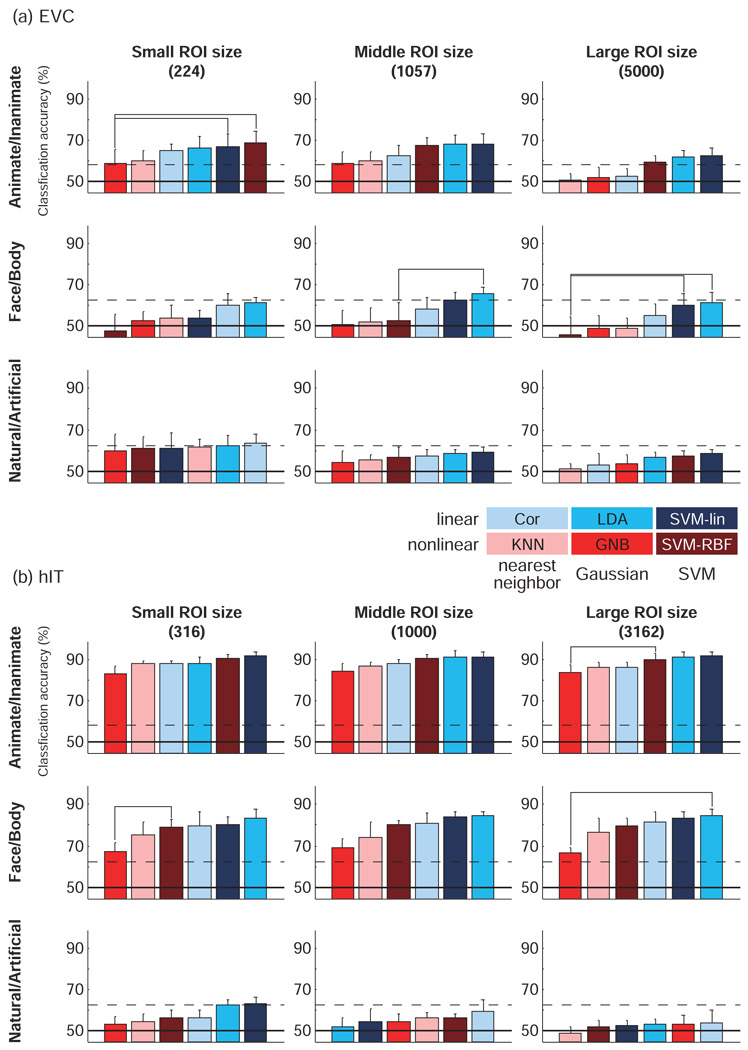
Figure 6. Accuracy was not strongly dependent on ROI size for most classifiers, but dropped for large ROIs in Cor and KNN.

This figure compares decoding accuracies across ROI sizes for each classifier. Classification accuracies were rarely significantly affected by changes of ROI size (horizontal connections between bars). The accuracy of Cor and KNN decreased for larger early visual ROIs, suggesting overfitting. Results are presented separately for each brain region and cross-validation method. Accuracies are averaged across the three category dichotomies (animate/inanimate, face/body, natural/artificial) and across subjects. Error bars show the standard error of the mean across subjects. The horizontal connection lines above the bars indicate significant differences between classifiers (p < 0.05 with Bonferroni correction) seen in at least two of four subjects (paired t test across stimuli).

Figure 5. Linear classifiers performed best and not significantly differently (leave-one-stimulus-pair-out cross-validation).

Classification accuracies estimated with leave-one-stimulus-pair-out cross-validation for each classification method for (a) EVC ROI and (b) hIT ROI. All conventions as in Fig. 4.

The effect of the choice of pattern classifier on decoding performance

Fig. 4 and Fig. 5 show the classification accuracies for each ROI, category definition, and ROI size. The connecting lines between bars indicate significant (p < 0.05) differences between classifier performances (paired t test) in at least two of four subjects. The p values were corrected by the Bonferroni method (p value divided by 15, the number of possible comparisons between six classifiers).

Reporting significant differences seen in at least two of four subjects (marked by connecting lines above the bars in Fig. 4 and Fig. 5) is safe, because it controls the probability of falsely reporting a difference: Under the omnibus null hypothesis that there are no differences between any two classifier accuracies in any subject, the probability of marking any two bars as significantly different is p < ( (0.05/15)⁴ + (0.05/15)³ * (1 − 0.05/15) * 4 + (0.05/15)² * (1 − 0.05/15)² * 6 ) * 15 = 0.00099 for a given panel of Fig. 4. For all 18 panels of Fig. 4, the probability of reporting a difference under the omnibus null hypothesis is p < 0.018. The same goes for Fig. 5, and for Fig. 4 and Fig. 5 together, the probability of a false positive classifier difference is p < 0.036.

In Fig. 4 and Fig. 5, classifiers were ordered by their accuracies. The result most consistently observed across regions, region sizes and cross-validation methods was that GNB performed significantly worse than other classifiers. This may reflect the fact that close-by fMRI voxels tend to be substantially correlated, whereas GNB assumes the absence of correlations between voxels across the patterns of a class. KNN tended to do better than GNB, but was never significantly better than linear classifiers. SVM-RBF performed unreliably, falling among the worst- or the best-performing classifiers in different contexts.

The three linear classifiers (Cor, LDA, and SVM-lin) performed best overall. LDA and SVM-lin were often the best classifier.

The effect of the ROI and its size

For EVC, decoding accuracies did not exceed chance-level performance on average across subjects for any classifier or category dichotomy in the leave-one-run-out cross-validation. However, the animate/inanimate dichotomy could be decoded with significant accuracy with linear classifiers in some subjects in the leave-one-run-out cross-validation and in most subjects in the leave-one-stimulus-pair-out cross-validation.

For hIT, the animate/inanimate and face/body dichotomies could be decoded with significant accuracy with most classifiers (using either cross-validation method). For the natural/artificial dichotomy, significant hIT decoding accuracies were only found using the leave-one-stimulus-pair-out cross-validation and only in some subjects for the best-performing classifiers.

The size of the ROI did not appear to have a big effect on decoding accuracy overall (Fig. 6), despite the fact that the largest ROI was an order of magnitude larger than the smallest ROI (about 22 times larger for EVC and about 10 times larger for hIT). This suggests (a) that our selection of voxels according to their visual responsiveness tended to catch voxels with much discriminative information even for the smallest ROIs, (b) that the additional voxels in the larger ROIs did not add much independent information, and (c) that the most classifiers managed to downweight any noise voxels added in the larger ROIs. Only the nearest-neighbor and nonlinear classifiers (KNN, Cor, SVM-RBF) showed some evidence of a drop in accuracy for the largest ROIs for EVC, suggesting a tendency to overfit the data. A similar trend was observed for GNB. The vulnerability of GNB and KNN to overfitting for high-dimensional patterns was noted in Mitchell (1997).

The effect of pattern normalizations on decoding performance

Pattern normalization provides a simple way to abstract from variability deemed irrelevant, such as the spatial-mean level and the variability of activity across voxels or stimuli. The effect on decoding accuracy of pattern normalization depends on the relative amounts of decodable discriminatory information and noise present in the variability removed by a given normalization.

We used the t-value patterns as the basis for comparing different normalizations. Fig. 7 shows the results averaged across ROI sizes, category definitions, and subjects. Though the figure shows average results, statistical analysis was performed for each of ROI size, category definition, and subject separately.

Figure 7. Normalization of response patterns across stimuli or across voxels had no significant effect on classification accuracy.

Mean classification accuracies for raw patterns of t-values and for normalized patterns. Patterns were initially defined by t-values (red bars). Error bars show the standard error of the mean across subjects. The left-column panels show across-stimuli normalizations: the patterns were normalized by subtracting the mean across stimuli (green bars) and then additionally dividing by the standard deviation across stimuli for each voxel (blue bars). The right-column panels show across-voxels normalizations: the data were normalized by subtracting the mean across voxels (green bars) and then additionally dividing by the standard deviation across voxels for each stimulus (blue bars). Results are shown separately for leave-one-run-out cross-validation (a) and leave-one-stimulus-pair-out cross-validation (b), but averaged across ROIs, ROI sizes, category dichotomies, and subjects. The statistical analysis was performed separately for each ROI, ROI size, category dichotomy, and subject. We found no significant effects of the four different pattern normalizations (paired t tests across stimuli, p < 0.05, Bonferroni-corrected, in at least two of four subjects).

We found no evidence for effects of normalization of t-value patterns on the decoding accuracy of any classifier. Accuracies appeared equal for the original t-value patterns and for the patterns normalized to equalize either the mean or the mean and the variability, either across voxels or across stimuli (see Methods for a detailed description).

Discussion

Linear classifiers performed best

Overall, the linear classifiers performed better than the nonlinear classifiers. This could mean that the true distributions’ Bayes-optimal decision boundaries were approximately linear or that the amount of data available for each subject was insufficient for the nonlinear classifiers to capitalize on their ability to model a nonlinear optimal decision boundary, or a combination of these two possibilities. The amount of data used per subject corresponded to about one hour of fMRI acquisition. It appears that linear classifiers have an appropriate model complexity in this scenario.

The pattern-correlation classifier performed better overall than the more complex nonlinear classifiers. It is attractive for its simplicity and straightforward interpretation in terms of pattern similarity. Moreover, it is rapid to train (time complexity linear in the number of voxels and training patterns), faster than the Fisher discriminant (which requires estimation and inversion of a voxel-by-voxel covariance matrix) and much faster than the linear SVM (which requires within-training-set cross-validation). However, LDA and the linear SVM appeared to perform slightly better than the pattern-correlation classifier.

LDA with optimal-shrinkage covariance estimate: excellent performance and fast to compute

Why does LDA perform well?

The excellent performance of LDA suggests that equal-covariance multinormals provide a reasonable approximate model of the pattern-estimate distributions for the two classes. This is consistent with widespread assumptions in univariate fMRI analysis, namely that the noise is (univariate) normal and homoscedastic (i.e. the same across experimental conditions). In addition, time courses of close-by voxels are known to be correlated (e.g. Kriegeskorte et al., 2008b). The model implicit to LDA would be optimal if each stimulus class were associated with a prototypical response pattern whose estimates are corrupted by homoscedastic Gaussian noise correlated between pairs of voxels. In reality, within-class variability is unlikely to arise only from measurement noise. Instead, each stimulus within a class may elicit a unique response pattern and their distribution may not be multinormal. But a multinormal model may provide a reasonable approximation.

Advantages over linear SVM

LDA appears as an attractive alternative to the linear SVMs because it less computationally costly and conceptually simpler (choosing the discriminant dimension that maximizes the ratio of between- and within-class variance). The lower computational cost makes it suitable for information-based brain mapping with a searchlight (Kriegeskorte et al., 2006) and other computationally intensive multivariate feature selection methods. (The even simpler and faster pattern-correlation classifier is also attractive for these applications.)

In most fMRI scenarios, training will take much less computation for LDA than for a linear SVM because LDA doesn’t require parameter optimization with grid-search and second-level cross-validation within the training data. But when the dimensionality of the data is very large (thousands of ROI voxels), the covariance-matrix estimation and inversion required for LDA become very computationally intensive, and the two classifiers become comparable in computational cost.

Getting a stable and invertible covariance estimate

Our choice of using the optimal-shrinkage covariance estimator (Ledoit and Wolf, 2003) probably contributed to LDA’s good and robust performance. Ledoit and Wolf (2003) showed that the optimal-shrinkage covariance estimator works better than PCA dimension reduction in a stock market analysis. This would explain the discrepancy with a previous study (Mourao-Miranda, 2005), which suggested that SVM performs significantly better than LDA: these authors analyzed whole-brain data and used PCA for dimensionality reduction before LDA.

The optimal-shrinkage covariance estimator is key for two reasons: (a) It stabilizes the covariance estimate, which is expected to improve decoding accuracy and robustness in cases when there are more voxels and/or less training patterns. (b) It ensures that the covariance matrix is invertible, avoiding the singularity problem that disqualified LDA in Cox et al. (2003) for larger ROIs.

The optimal-shrinkage estimate approaches a diagonal covariance matrix as the dimensionality of the data tends to infinity. So in a very high-dimensional case, LDA with the optimal-shrinkage covariance estimate is similar to pooled-variance GNB. However, for the present scenarios, the optimal-shrinkage estimate still had many substantially non-zero off-diagonal elements, even for the largest ROI size. The ability to model voxel correlations, which are known to be substantial in fMRI (e.g. Kriegeskorte et al., 2008b), may explain why LDA outperformed GNB. (Note that we used GNB with class-distinct variances for the comparison here; pooled-variance GNB performed almost identically as distinct-variance GNB in the present case.)

Even using optimal-shrinkage estimation, it is desirable to obtain enough training patterns to get a good covariance estimate. Here we used a condition-rich (Kriegeskorte et al., 2008c) event-related design, providing more pattern estimates for each class than a typical block design. When only few repetitions are available for each class, we can use a single predictor in the design matrix to model the class-mean response amplitude, such that within-class variance is treated as error variance in the initial linear model for response estimation. We can then estimate the covariance matrix from the error time courses of the fitting of the linear hemodynamic response model to each voxel’s time course (Kriegeskorte et al., 2007b; see also Kriegeskorte 2004; Kriegeskorte et al., 2006). We now have as many samples as there are time points for covariance estimation.

The temporal autocorrelation of the errors decreases the effective number of independent time points that determine the covariance estimate. However, using the error time courses exploits whatever temporal complexity fMRI data do provide. The effective number of independent dimensions is larger than for block-average or even single-trial response estimates. Moreover, this approach can handle rapid event-related designs (with overlapping hemodynamic responses to successive events), utilizing a prior model of the shape of the hemodynamic response (e.g. Boynton et al., 1996) for optimal estimation of the average response amplitudes for sets of trials corresponding to experimental conditions.

The orientation and shape of the multinormal distribution of the pattern estimates is accurately characterized by the covariance of the errors (Krzanowski, 1988). The design matrix and condition merely determine the scaling of the covariance of the distribution (e.g. smaller when more data are averaged in estimating a pattern).

Estimating within-class covariance from the errors of the linear-model fit is ideal, when within-class variation is dominated by fMRI measurement noise (which is homoscedastic and characterized by voxel correlations). For the present data set, within-class covariance was also due to different particular images within each category. Nevertheless, covariance estimation from the patterns or from the error time courses yielded equal performance of LDA (comparison not shown, results are for covariance estimation from the single-image response patterns). For experiments with fewer trials and for block designs, it may be preferable to estimate the covariance matrix from the errors. In either case, we expect the optimal-shrinkage estimator to further improve the covariance estimate, and with it classification performance and sensitivity to pattern information.

Linear SVM: excellent performance with error-normalized voxel responses

Linear SVM classification performed excellently and robustly across scenarios. However, the linear SVM was affected by the choice of response-pattern estimate. Using t-values to define the patterns yielded better performance (equivalent to LDA) than using beta estimates. Using t-values means that the response amplitudes are expressed in units of standard errors of the estimates. We could equivalently have expressed the response amplitudes in error standard-deviation units. (Error standard-deviation units are essentially equivalent here, because the t-values just have an additional factor in the denominator, which is very similar across conditions, because every condition had the same amount of data, and differences arise only from predictor correlations resulting from the rapid event-related stimulus sequence, which were small here.) Either method scales each voxel’s responses to an equal noise level.

Linear SVMs are sensitive to the scaling of the input dimensions, because the decision hyperplane is not simply scaled along with the data points, but can reorient as it finds the new maximum-margin configuration (e.g. exploiting stretched dimensions to maximize the margin). It has been suggested previously (Schölkopf and Smola, 2001) that SVMs perform better on inputs scaled to have roughly the same magnitude. The t-values, here, had more similar magnitudes across voxels than the beta values.

Significant improvements with t-value patterns were also observed for SVM-RBF as well as for Cor and KNN. For these methods, a plausible explanation for the improvement is the downweighting of noisy voxels.

LDA and GNB were not significantly affected by the difference between beta- and t-values. This is unsurprising because the decision boundary in these methods is just stretched or squeezed along with the data points (i.e. the patterns) when dimensions are scaled, rendering these methods invariant to differential scaling of dimensions (assuming maximum-likelihood fits of the Gaussians for the moment). LDA and GNB take each voxel’s response variance into account automatically via the diagonal entries of the covariance matrix. (Slight subsignificant differences between these classifiers’ accuracies for beta estimate and t patterns were nevertheless observed, because slightly different standard errors in the same voxel for different conditions (due to weak predictor correlations) apply slightly different scalings to each pattern (i.e. condition) for a given dimension (i.e. voxel). Moreover, the optimal-shrinkage estimator deviates from the maximum-likelihood estimate, shrinking the sample covariance toward a diagonal covariance estimate. Because of these aberrations, LDA here was not precisely invariant to differential scaling of dimensions.)

Advantages of linear SVM over LDA

We may prefer a linear SVM over LDA when we expect the optimal decision boundary to be approximately hyperplanar, but do not expect LDA’s assumption of equal and multinormal pattern distributions to be a good approximation. Although SVM is typically more computationally costly than LDA, the latter method’s covariance estimation and inversion becomes costly as well for large ROIs (thousands of voxels).

Nonlinear classifiers may require more data

Nonlinear classifiers, overall, did not perform as well as their linear counterparts. This is consistent with previous studies comparing linear and nonlinear variants of SVM for fMRI data (Cox and Savoy, 2003; LaConte et al., 2005). SVM-RBF performed acceptably, but significantly worse than SVM-lin, and is more computationally expensive and more difficult to interpret. The low performance of KNN similarly suggested that nonlinear classifiers may not be ideal for fMRI classification unless we have either fewer voxels in the pattern or more data. Dimensionality reduction of the input patterns may also help improve the performance of nonlinear classifiers.

Interpretation of linear decodability as “explicit” coding

In addition to the stability of linear models (conferring greater sensitivity to linearly encoded information), linear classification results are easier to interpret. Linearly decodable information can be thought of as ‘explicit’ in the sense of being amenable to biologically plausible readout in a single step (e.g. by a single unit receiving the pattern as input). Note that this notion of “explicit” coding is much wider than that of single-cell explicit coding (which it includes as a special case: the case where the pattern differences are concentrated in a single unit or in a small subset of units). Linearly decodable information is directly available information, an obviously important property to analyze for when our goal is to characterize the function of a region from a computational perspective.

As an example of pattern information that is not linearly decodable, consider the object-category information in our retinal activity patterns. Object-category information is certainly present in the retina, otherwise we could not categorize visually perceived objects. However, to decode it from retinal data would require a complex nonlinear analysis (the one we usually refer to as object recognition). Because the space of possible nonlinear decoders is very large, we would have no hope of finding a good readout model (and thus to detect the nonlinearly encoded information) even if we had extensive retinal response data. Beyond the statistical challenge, finding the object-category information would also not necessarily help us understand the function of retinal processing. Arguably, knowing what information is linearly decodable provides stronger constraints for computational theory than knowing what information is present (in an arbitrarily complex nonlinear encoding).

Linear decoding results are also inherently easier to characterize in terms of the contributing units. For example, we can simply inspect the map of weights defining the discriminant dimension (e.g. Mourao-Miranda et al., 2005). For nonlinear classifiers, voxel interactions come into play and a map of independent voxel contributions cannot capture the complexity.

Although linear models are statistically stable and key to characterizing the information available for direct readout, our larger goal is to develop computational models of brain-information processing and to constrain these models with brain-activity data (e.g. Kay et al., 2008; Kriegeskorte et al., 2008b,c; Mitchell et al., 2008). These models will necessarily be nonlinear (as the brain itself) and will require much larger amounts of data to constrain them, as might be cumulatively acquired by the community over many years.

Cross-validation: testing generalization to new runs or new stimuli

In the leave-one-run-out cross-validation, training and test set corresponded to separate runs, but responses to the same stimuli were present in both sets. In the leave-one- stimulus-pair-out cross-validation, training and test set corresponded to separate sets of stimuli, but responses from the same run were present in both sets. (The ROI was always defined by a completely separate data set.) Comparing decoding accuracies between the two cross-validation methods suggested that generalization to new runs is more difficult than generalization to new stimuli within the same class. This result is consistent with the notion that run-related changes reflecting scanner state and head motion are substantially larger than activity-pattern effects.

The results of the leave-one-stimulus-pair-out cross-validation should be interpreted with caution, because the training and test data were not entirely independent as they were taken from the same runs and reflect temporally overlapping hemodynamic responses. Because the stimulus sequences were random, the effect of this subtle dependency between training and test data is not obvious here and should not favor correct over incorrect classification. Nevertheless strong conclusions should not rest on analyses where the independence of training and test data is violated. The leave-one-run-out cross-validation therefore appears a safer choice, ensuring that the false-positives rate is controlled at the nominal level.

There are technical and conceptual reasons why accuracies estimated with these methods cannot be directly compared. At the technical level, the leave-one-run-out cross-validation had fewer folds and, on each fold, used slightly less training data (in terms of fMRI volumes), a slightly larger number of the training patterns, and a much larger number of the test patterns than the leave-one-stimulus-pair-out cross-validation. More importantly, however, the two methods test for different types of generalization performance, so this is not just a technical, but a conceptual choice, which affects the interpretation of the results. If generalization to different stimuli within the same category is to be tested, the different stimulus sets should ideally be presented in separate runs.

Selection of fewer more visually responsive voxels improved decoding performance

Selecting fewer voxels tended to improve decoding accuracy in many cases. This is consistent with results reported by Mitchell et al. (2004). More visually responsive voxels may be less noisy. Note that voxels that are more visually responsive on average could, in theory, also be worse discriminators of different stimulus categories. However, our results suggest that more visually responsive voxels also carry more information for distinguishing the categories. The classification accuracies of Cor and KNN degraded for larger ROI sizes. These methods appear susceptible to the inclusion of noisy voxels. The performance of LDA and the SVMs appeared robust to changes of ROI size.

Pattern normalizations had little effect on decoding performance

Normalizing mean and standard deviation of the response patterns either across stimuli or across voxels before training and testing had no significant effect on decoding performance. The popular pattern-correlation classifier (Haxby et al. 2001) implicitly normalizes each pattern by subtracting out the spatial-mean and dividing by the spatial standard deviation. Our pattern normalization across voxels was similar, but applied to the response pattern for each stimulus, whereas in the pattern-correlation classifier it is applied to each category-average pattern. The absence of a significant performance reduction of these pattern normalizations suggests that they do not substantially affect the ratio between the category signal and the noise. This appears plausible if we consider the fact that across-voxel normalizations merely reduce the high dimensionality of the patterns by two dimensions in the voxels’ response space as shown in Fig. 2b. Since the response space has hundreds of dimensions (i.e. ROI voxels), the loss of information will be small, unless the information is concentrated in the dimensions that are removed (e.g. in the spatial-mean activation of the ROI).

Limitations of this study

We systematically varied a number of choices in designing a pattern classifier analysis (classifier, response estimate, pattern-normalization, cross-validation method) and tested these choices in different scenarios (different ROIs, different ROI sizes, different category dichotomies). Results suggested a robust superiority of linear classifiers for fMRI decoding. However, it is important to note that these results were obtained for human visual object representations measured with 3T fMRI (voxels 1.95 × 1.95 × 2 mm³) in four subjects. We used about 1 hour of fMRI data per subject here. Nonlinear methods may work better when more data are available for training or when dimensionality reduction is applied to the patterns. To what extent our findings will generalize to different perceptual, cognitive, and motor regions, to other experimental tasks, and to different fMRI acquisition schemes cannot be predicted.

Conclusion

Overall our results suggest that linear classifiers perform best and that defining the patterns in error-standard-deviation units (or using t-values) improves performance of the pattern-correlation, KNN, and SVM classifiers. With suitable data preprocessing, different methods often perform similarly, although the nonlinear methods GNB and KNN performed significantly worse. In particular, LDA used in conjunction with an optimal-shrinkage covariance estimator is attractive for its simplicity, interpretability, computational speed, and robust good performance. To ensure control of the false-positives rate, both voxel selection and classifier training should be based on data independent from that used for testing (Kriegeskorte et al, 2009). This is ensured by using separate sets of scanner runs.

Pattern-classifier analysis requires many decisions (Pereira et al., 2009). The ideal choices will depend on the stimulus, task, brain region, and the amount of data available. However, any of the six classifiers provides a valid test of pattern information and, across scenarios, we found almost no significant differences in accuracy (and thus sensitivity to pattern information) between the two classifiers performing best here (LDA and linear SVM).