Peaks and Troughs of Three-Dimensional Vestibulo-ocular Reflex in Humans

Abstract

The three-dimensional vestibulo-ocular reflex (3D VOR) ideally generates compensatory ocular rotations not only with a magnitude equal and opposite to the head rotation but also about an axis that is collinear with the head rotation axis. Vestibulo-ocular responses only partially fulfill this ideal behavior. Because animal studies have shown that vestibular stimulation about particular axes may lead to suboptimal compensatory responses, we investigated in healthy subjects the peaks and troughs in 3D VOR stabilization in terms of gain and alignment of the 3D vestibulo-ocular response. Six healthy upright sitting subjects underwent whole body small amplitude sinusoidal and constant acceleration transients delivered by a six-degree-of-freedom motion platform. Subjects were oscillated about the vertical axis and about axes in the horizontal plane varying between roll and pitch at increments of 22.5° in azimuth. Transients were delivered in yaw, roll, and pitch and in the vertical canal planes. Eye movements were recorded in with 3D search coils. Eye coil signals were converted to rotation vectors, from which we calculated gain and misalignment. During horizontal axis stimulation, systematic deviations were found. In the light, misalignment of the 3D VOR had a maximum misalignment at about 45°. These deviations in misalignment can be explained by vector summation of the eye rotation components with a low gain for torsion and high gain for vertical. In the dark and in response to transients, gain of all components had lower values. Misalignment in darkness and for transients had different peaks and troughs than in the light: its minimum was during pitch axis stimulation and its maximum during roll axis stimulation. We show that the relatively large misalignment for roll in darkness is due to a horizontal eye movement component that is only present in darkness. In combination with the relatively low torsion gain, this horizontal component has a relative large effect on the alignment of the eye rotation axis with respect to the head rotation axis.

Electronic supplementary material

The online version of this article (doi:10.1007/s10162-010-0210-y) contains supplementary material, which is available to authorized users.

Introduction

One of the goals of the vestibular system is to stabilize the eye by providing information about changes in angular position of the head. This is mediated by the vestibulo-ocular reflex (VOR) which ideally compensates for a given head rotation with an eye velocity that is equal and opposite to head velocity. Most head movements are not restricted to a single rotation about one particular axis such as yaw, pitch, or roll but are composed of 3D translations and rotations about an axis with different orientation and amplitudes in 3D space (Grossman et al. 1989; Crane and Demer 1997). The contribution and interaction of the different parts of the vestibular system (canals and otoliths) on ocular stabilization has been investigated in many studies (Groen et al. 1999; Schmid-Priscoveanu et al. 2000; Bockisch et al. 2005; for a review, see also Angelaki and Cullen 2008). Although the quality of the VOR response is usually quantified by the gain (ratio between eye and head velocity), alignment of the eye rotation axis with respect to the head rotation axis is also an important determinant. Both errors in gain and alignment compromise the quality of image stabilization during head rotations. Several systematic and non-systematic factors cause that even in normal situations, the eye rotation axis is not always collinear with head rotation axis. Stimulation about an axis in the horizontal plane is such a situation where stimulus and response axis may not align. In monkey, it has been shown that gain and alignment of compensatory eye rotation is directly related to the vector sum of roll and pitch and that misalignment varies with stimulus axis orientation (Crawford and Vilis 1991). This variation in misalignment is caused by the different gain of torsion and vertical eye rotation components.

So far, it is unclear if suboptimal gain and misalignment during head rotations about particular axes is caused by orbital–mechanical properties (Crane et al. 2005, 2006; Demer et al. 2005), orientation selectivity, response dynamics of sensory signals, or by the process of sensory motor transformation.

To find the peaks and troughs in gain and alignment, we tested six upright sitting healthy subjects in the light and in darkness. Subjects were oscillated about the vertical axis and about axes that incremented in steps of 22.5° from the nasal–occipital to the interaural axis. We systematically investigated the gain and misalignment of the VOR in response to 4° peak-to-peak amplitude sinusoidal stimulation at a frequency of 1 Hz. This frequency and amplitude is close to what is normal for activities such as walking where the predominant frequency is 0.8 Hz with mean amplitude of 6° (Grossman et al. 1988; Crane and Demer 1997).

To assess the role of vision in quality of 3D ocular stability, we compared the responses to sinusoidal stimulation in the light to responses in darkness. In addition, we measured compensatory eye movements in response to whole body transient stimulation with constant acceleration of 100°°s⁻² during the first 100 ms of the transient. This technique has the advantage that it measures the VOR during the first 100 ms of the stimulation. In this interval, visual contribution is absent. Although in most previous studies head transients have been used with accelerations up to 2,500°°s⁻² (Tabak et al. 1997a, b; Halmagyi et al. 2001, 2003), we used accelerations and peak velocities in the same amplitude velocity range as our sinusoidal stimuli.

Methods

Subjects

Six subjects participated in the experiment. The subjects’ ages ranged between 22 and 55 years. None of the subjects had a medical history or clinical signs of vestibular, neurological, oculomotor, or cardiovascular abnormalities. All subjects gave their informed consent. The experimental procedure was approved by the Medical Ethics Committee of Erasmus University Medical Centre and adhered to the Declaration of Helsinki for research involving human subjects.

Experimental setup

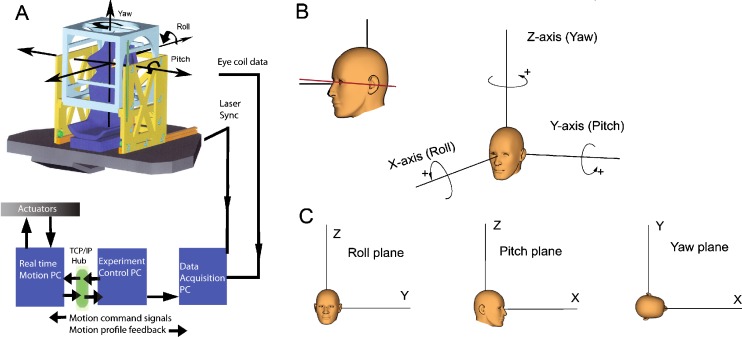
Stimuli were delivered with a motion platform (see Fig. 1A, B) capable of generating angular and translational stimuli at a total of six degrees of freedom (FCS-MOOG, Nieuw-Vennep, The Netherlands). The platform is moved by six electromechanical actuators connected to a personal computer with dedicated control software. It generates accurate movements with six degrees of freedom. Sensors placed in the actuators continuously monitor the platform motion profile. Measured by these sensors, the device has <0.5-mm precision for linear and <0.05° precision for angular movements. Due to the high resonance frequency of the device (>75 Hz), vibrations during stimulation were very small (<0.02°). A comparison between the stimulus signal sent to the platform and the output measured with a search coil fixed in space while oscillating the platform confirmed that the platform produced a perfect sinusoidal stimulus (p < 0.001). During the experiments, platform motion profile was monitored by the sensors in the actuators, reconstructed using inverse dynamics and sent to the data collection computer at a rate of 100 Hz. To precisely synchronize platform and eye movement data, a laser beam was mounted at the back of the platform and projected onto a small photocell at the base of a 0.8-mm pinhole (reaction time, 10 µs). Simultaneously with the eye movement data, the output voltage of the photocell was sampled at a rate of 1 KHz. This way, the photocell signal provided a real-time indicator of zero crossings of the platform motion onset with 1-ms accuracy. During the offline analysis using Matlab (Mathworks, Natick, MA), the reconstructed motion profile of the platform based on the sensor information of the actuators in the platform was precisely aligned with the onset of platform motion as indicated by the drop in voltage of the photo cell.

FIG. 1.

A Schematic drawing of the 6DF motion platform. The boxes represent the computer hardware and the lines indicate the flow of signals to control the movements of the platform and to monitor platform motion and eye movements. B Orientation of the subject’s head when seated on the platform. In the standard orientation, Reid’s line (solid line) makes an angle of 7° with earth horizontal. C Directions of rotations around the cardinal axes according to the right-hand rule. Bottom panels show the yaw, roll, and pitch projection planes used to plot angular eye velocities during sinusoidal stimulation.

Subjects were seated on a chair mounted at the center of the platform (Fig. 1A). The subject’s body was restrained with a four-point seatbelt as used in racing cars. The seatbelts were anchored to the base of the motion platform. A PVC cubic frame that supported the field coils surrounded the chair. The field coil system was adjustable in height such that the subject’s eyes were in the center of the magnetic field. The head was immobilized using an individually molded dental impression bite board which was attached to the cubic frame via a rigid bar. A vacuum pillow folded around the neck and an annulus attached to the chair further ensured fixation of the subject. In addition, we attached two 3D sensors (Analog devices) directly to the bite board, one for angular and one for linear acceleration, to monitor spurious head movements during stimulation.

Eye movement recordings

Eye movements of both eyes were recorded with 3D scleral search coils (Skalar Medical, Delft, The Netherlands) using a standard 25-kHz two-field coil system based on the amplitude detection method of Robinson (model EMP3020, Skalar Medical). The coil signals were passed through an analogue low-pass filter with cutoff frequency of 500 Hz and sampled online and stored to hard disk at a frequency of 1,000 Hz with 16-bit precision (CED system running Spike2 v6, Cambridge Electronic Design, Cambridge). Noise levels of the coil signals during fixation were 0.1° s⁻¹. Coil signals were off-line inspected for slippage by comparing the signals of the left and right eyes. No significant differences were found (p = 0.907). Eye rotations were defined in a head-fixed right-handed coordinate system (see Fig. 1C). In this system, from the subject’s point of view, a leftward rotation about the z-axis (yaw), a downward rotation about the y-axis (pitch), and rightward rotation about the x-axis (roll) are defined as positive. The planes orthogonal to the x, y, and z rotation axes are, respectively, the roll, pitch, and yaw planes (Fig. 1D). Data were also analyzed by projecting them on these three coordinate planes.

Experimental protocol

Prior to the experiments, torsion eye position measurement error due to non-orthogonality between the direction and torsion coil was corrected using the Bruno and Van den Berg (1997) algorithm. At the beginning of the experiment, the horizontal and vertical signals of both coils were individually calibrated by instructing the subject to successively fixate a series of five targets (central target and a target at 10° left, right, up, and down) for 5 s each. Calibration targets were projected onto a translucent screen at 186-cm distance.

We determined head orientation with respect to gravity and its rotation center. Head orientation was as close as possible to the position where subjects felt straight up. In this position, we measured Reid’s line (an imaginary line connecting the external meatus with the lower orbital cantus; Fig. 1C, left panel). In all subjects, Reid’s line varied between 6° and 10° with earth horizontal. The center of rotation was defined as the intersection between the imaginary line going through the external meatus and the horizontal line going from the nose to the back of the head. The x, y, and z offset of this rotation center with respect to the default rotation center of the platform was determined. The offset values were fed into the platform control computer which then adjusted the center of rotation. Thus, all stimuli were about the defined head center of rotation.

Whole body sinusoidal rotations were delivered about the three cardinal axes, the rostral–caudal or vertical axis (yaw), the interaural axis (pitch), and the nasal–occipital axis (roll), and about intermediate horizontal axes between roll and pitch. The orientation of the stimulus axis was incremented in steps of 22.5° azimuth. The frequency of the stimulus was 1 Hz with a total duration of 14 s, including 2 s of fade-in and fade-out. Peak-to-peak amplitude of the sinusoidal rotation was 4° (peak acceleration 80° s⁻²). Sinusoidal stimuli were delivered in light and darkness. In the light, subjects fixated a continuously lit visual target (a red LED, 2-mm diameter) located 177 cm in front of the subject at eye level close to the eye primary position. In the dark condition, the visual target was briefly presented (2 s) when the platform was stationary in between two stimulations. Subjects were instructed to fixate the imaginary location of the space fixed target during sinusoidal stimulation after the target had been switched off just prior to motion onset. In a control experiment where we attached one search coil to the bite board and one coil to the forehead, we found that decoupling of the head relative to the platform was <0.03° (see Electronic supplementary material (ESM) Fig. S2).

All subjects were subjected to short-duration whole body transients in a dark environment where the only visible stimulus available to the subject was a visual target located at 177 cm in front of the subject at eye level. Each transient was repeated six times and delivered in random order and with random timing of motion onset (intervals varied between 2.5 and 3.5 s). The profile of the transients was a constant acceleration of 100° s⁻² during the first 100 ms of the transient, followed by a gradual linear decrease in acceleration. This stimulus resulted in a linear increase in velocity up to 10° s⁻¹ after 100 ms and was precisely reproducible in terms of amplitude and direction. Transients were well tolerated by our subjects. Decoupling of the head from the bite board was <0.03° during the first 100 ms of the transient. Peak velocity of the eye movements in response to these transients was 100 times above the noise level of the coil signals (Houben et al. 2006).

Data analysis

Coil signals were converted into Fick angles and then expressed as rotation vectors (Haustein 1989; Haslwanter and Moore 1995). From the fixation data of the target straight ahead, we determined the misalignment of the coil in the eye relative to the orthogonal primary magnetic field coils. Signals were corrected for this offset misalignment by 3D counter rotation. To express 3D eye movements in the velocity domain, we converted rotation vector data back into angular velocity (ω). Before conversion of rotation vector to angular velocity, we smoothed the data by zero phase with a forward and reverse digital filter with a 20-point Gaussian window (length of 20 ms). The gain of each component and 3D eye velocity gain was calculated by fitting a sinusoid with a frequency equal to the platform frequency through the horizontal, vertical, and torsion angular velocity components. The gain for each component defined as the ratio between eye component peak velocity and platform peak velocity was calculated separately for each eye. Because left and right eye values were not significantly different (p = 0.907), we pooled the left and right eye data.

The misalignment between the 3D eye velocity axis and head velocity axis was calculated using the approach of Aw et al. (1996b). From the scalar product of two vectors, the misalignment was calculated as the instantaneous angle in three dimensions between the inverse of the eye velocity axis and the head velocity axis. Because the calculated values only indicate the misalignment of the eye rotation axis as a cone around the head orientation axis, we also used gaze plane plots to determine the deviation of the eye rotation axis in yaw, roll, and pitch planes (see Fig. 1D).

Because misalignments could be due to changes in horizontal eye position, we calculated the standard deviation around the mean eye position during each 14-s stimulation period. The variability of eye position around the imaginary fixation point during the dark period was too small to have an effect on misalignment.

All transients were individually inspected on the computer screen. When the subject made a blink or saccade during the transient, that trace was manually discarded. This happened on average in one out of six cases. Angular velocity components during the first 100 ms after onset of the movement were averaged in time bins of 20 ms and plotted as function of platform velocity (Tabak et al. 1997b). Because the transients had a constant acceleration during the first 100 ms, the slopes of the linear regression line fitted through the time bins are a direct measure for eye velocity gain (Tabak et al. 1997a, b). Left and right eye gains were not significantly different (p = 0.907) and were averaged.

The 3D angular velocity gain and misalignment for each azimuth orientation were compared to the gain and misalignment predicted from vector summation of the torsion and vertical components during roll and pitch (Crawford and Vilis 1991). From this, it follows that the orientation of the eye rotation axis aligns with the head rotation axis when velocity gains for roll and pitch are equal, but when the two are different, there is deviation between stimulus and eye rotation axis with a maximum at 45° azimuth.

Statistical analysis

Repeated measures analysis of variance was used to test for significant differences in misalignment data during sinusoidal stimulation in the light and in darkness and in response to transient stimulation.

Results

Sinusoidal stimulation

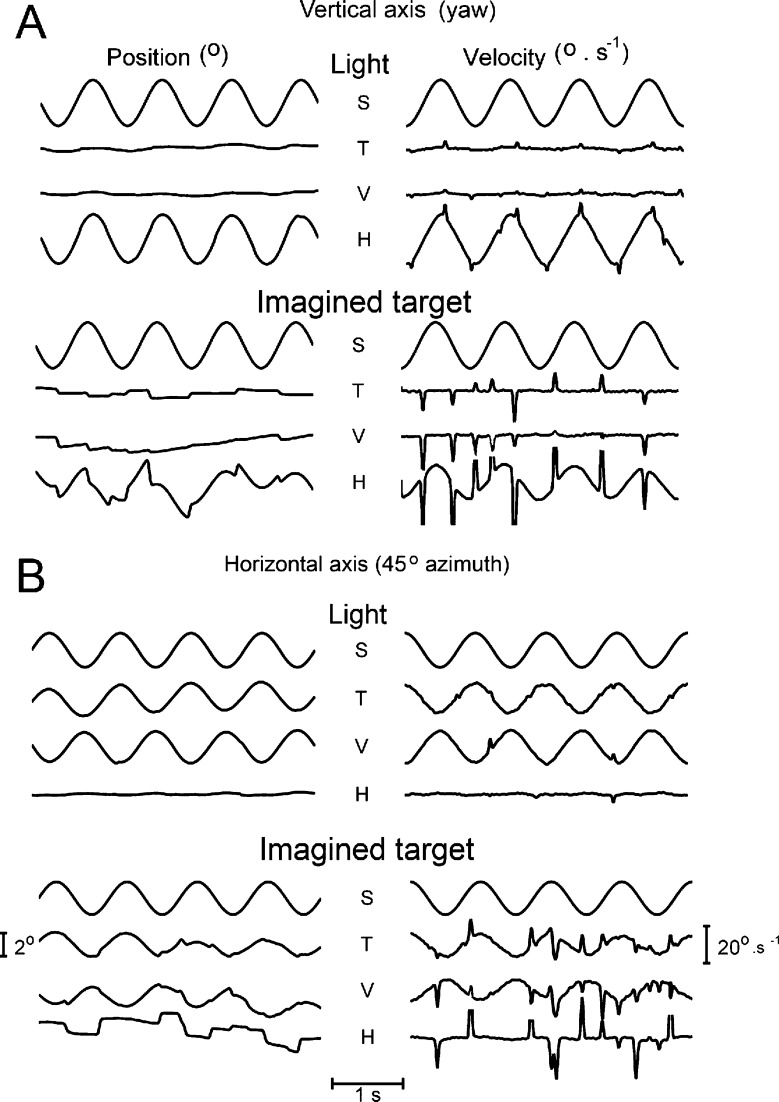
Sinusoidal stimulation about the vertical axis in the light resulted in smooth compensatory eye movements occasionally interrupted by saccades. The mean gain ± one standard deviation (N = 6) was 1.02 ± 0.06 in the light. The responses were restricted to the horizontal eye movement component, with very small vertical and torsion components (gain, <0.05). In darkness, compensatory eye movements were more frequently interrupted by saccades, and in most subjects, there was a small drift of the other components (see Fig. 2A). The standard deviation of the horizontal position change during the 14 s of stimulation was 1.54° in the light and 1.45° in darkness (N = 6). Position changes of the vertical and torsion components were <0.28° in the light. Standard deviations of position changes in darkness of the vertical and torsion components were 0.84° for the vertical and 0.38° for the torsion component.

FIG. 2.

Example of 3D eye movements in response to sinusoidal stimulation about different axes. A Vertical axis in the light (upper panels) and in the dark while the subject imagined a target (lower panels). B Horizontal axis oriented at 45° azimuth. Upper panels, light; lower panels, dark. Left side panels in A and B show the stimulus (S), torsion (T), vertical (V), and horizontal (H) eye position signals. The right side panels show the corresponding angular velocities. Saccadic peak velocities are clipped in the plots. In this and all subsequent figures, eye positions and velocities are expressed in a right-handed, head-fixed coordinate system. In this system clockwise, down and left eye rotations viewed from the perspective of the subject are defined as positive values (see also Fig. 1). Note that for easier comparison, the polarity of the stimulus signal has been inverted.

Compensatory eye movements had different gains of the horizontal, vertical, and torsion components. Gain of the vertical axis VOR in darkness was 0.62° ± 0.16. For horizontal axis stimulation, the relative contribution of each component to the overall gain depended on the orientation of the stimulus axis. When the stimulus axis was in the nasal–occipital direction (roll), torsion was the major component of the response at this orientation. The mean gain of torsion was 0.54 ± 0.16 in the light and 0.37 ± 0.09 in darkness.

Stimulation about an axis in between the nasal–occipital and interaural axis resulted in compensatory eye movements that consisted of a combination of torsion and vertical components. Figure 2B shows examples of eye movements in response to stimulation about an axis oriented at 45° in both the light and in darkness. The torsion component was always smaller than the vertical component, consistent with the differences in gain between pure roll and pitch. We also determined ocular drift that occurred during sinusoidal stimulation in all subjects under light and dark conditions. The standard deviations of, respectively torsion, vertical, and horizontal gaze positions averaged over all six subjects were 0.72°, 0.97°, and 1.02° during roll stimulation and 0.45°, 1.77°, and 1.25° during pitch stimulation in the dark.

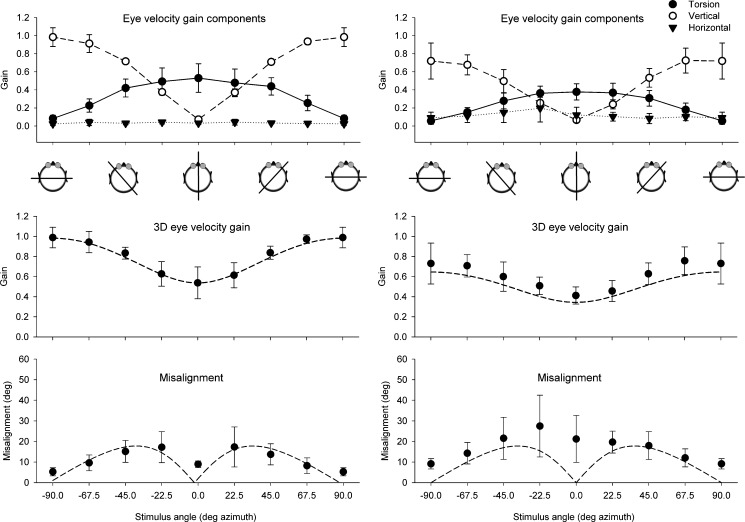
During horizontal axis stimulation, the eye movements were mainly restricted to vertical and/or torsion eye velocities. Figure 3A (top panel) shows the mean gain of the horizontal, vertical, and torsion angular velocity components for all tested stimulation axes in the horizontal plane. The different orientations of the stimulus axis in between pitch and roll resulted in inversely related contributions of vertical and torsion eye movements. Torsion was maximal at 0° azimuth, whereas vertical had its maximum at 90°. The center panel of Fig. 3A shows the 3D eye velocity gain in the light. Gain varied between 0.99 ± 0.12 (pitch) and 0.54 ± 0.16 (roll). The measured data closely correspond to the predicted values calculated from the vector sum of torsion and vertical components (dashed line in center panel of Fig. 3A).

FIG. 3.

Results of horizontal axis sinusoidal stimulation for all tested horizontal stimulus axes averaged over all subjects (N = 6) in the light (A) and in the dark (B). Cartoons underneath the top panels give a top view of the orientation of the stimulus axis with respect to the head. Top panel Mean gain of the horizontal, vertical, and torsion eye velocity components. Center panel Mean 3D eye velocity at each tested stimulus axis orientation. The dashed line represents the vector eye velocity gain response predicted from the vertical and torsion components. Lower panel Misalignment of the response axis with respect to the stimulus axis. The dashed line in the lower panel represents the predicted misalignment calculated from the vector sum of only vertical and torsion eye velocity components in response to pure pitch and pure roll stimulation, respectively. Error bars in all panels indicate one standard deviation.

The misalignment between stimulus and response axis averaged over all subjects is shown in the lower panels of Fig. 3. In the light, misalignment between stimulus and response axis was smallest (5.25°) during pitch and gradually increased toward roll until the orientation of the stimulus axis was oriented at 22.5° azimuth (maximum misalignment, 17.33°) and decreased toward the roll axis. These values for each horizontal stimulus angle correspond closely to what one would predict from linear vector summation of roll and pitch contributions (dashed line in lower panel of Fig. 3A).

In darkness, the maximum gain of both the vertical and torsion components was lower than in the light (vertical, 0.72 ± 0.19; torsion, 0.37 ± 0.09; Fig. 3B). Also, the 3D eye velocity gain values were significantly lower than in the light (Student’s t test, p < 0.0001). Gain was slightly higher than predicted from the vertical and torsion components alone (dashed line in center panel of Fig. 3B). A pronounced difference between sinusoidal stimulation in the light and darkness was a significant (Student’s t test, p < 0.001) change in misalignment of the eye rotation axis with respect to the stimulus axis (Fig. 3A, B, compare lower panels). In the dark, the misalignment was minimal at 90° (pitch) and gradually increased to a peak around the 0° axis (roll). The pattern of misalignment in the dark did not correspond to what one would predict from linear vector summation of only roll and pitch components. In contrast to the light, there was a small but systematic horizontal gain component (0.1 < “gain” <0.23) in the dark condition.

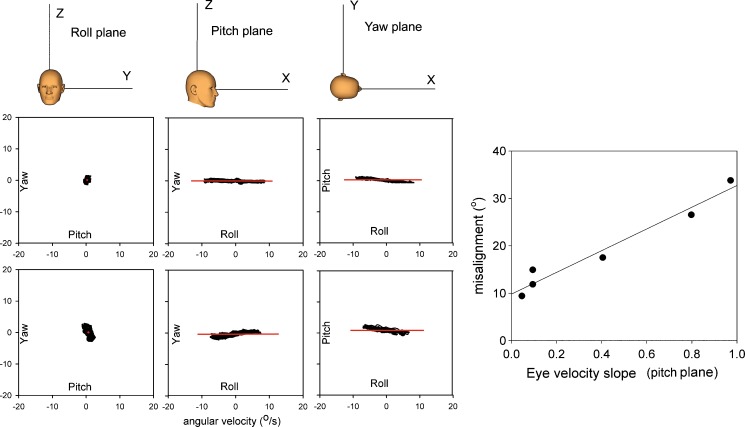
Because the misalignment angle only gives the angle of deviation between head and eye rotation axis, we also plotted the angular velocities projected on the roll, pitch, and yaw planes. An example for stimulation about the x-axis (roll) is given in Fig. 4. The three top panels show that in the light, the angular velocities coincide with the x-axis for each plane. The contributions of yaw and pitch velocities are very small compared to the roll component. In darkness (lower panels), there is considerably more deviation between stimulus and response. There is a small but consistent horizontal velocity component in the dark (left and middle lower panels).

FIG. 4.

Plots of eye velocities projected on the roll, pitch, and yaw plane during sinusoidal stimulation about the roll axis in the light (upper panels) and in darkness (lower panels). The horizontal solid line corresponds to the x-axis shown in the cartoons in the upper panel. Far right panel Correlation between misalignment and the slope of the regression line fitted through eye velocity data obtained during roll stimulation in the dark projected on the pitch plane. Each data point represents one subject.

For each subject, the slope of the regression line fitted through the eye velocity points on the pitch plane was plotted as a function of misalignment. There was a strong correlation between misalignment and slope (r ² = 0.98, intercept 9.8, slope = 22.9).

Transients

Angular rotation head transients about the vertical axis resulted in compensatory horizontal eye movements. The gain of eye versus head velocities in this particular example was 0.76 for rightward and 0.82 for leftward vertical axis (yaw) head transients (Fig. 5, bottom left panel). Mean values between left and right averaged over all six subjects were not significantly different.

FIG. 5.

Top panel Example of eye movements in response to a clockwise transient about the vertical axis (yaw) and horizontal axis stimulation at 45° azimuth. Top row of top panel Eye position and eye velocity of respectively horizontal (H), vertical (V), and torsion (T) components. Lower row of top panel 3D position and angular velocity of stimulus (S) and eye (A) movements. Gray shaded line is one standard deviation. Bottom panels Plots of relationship between instantaneous eye and head velocity during angular VOR whole body impulses in one subject. Left panel Vertical axis (yaw) impulse. Center and right panels Interaural axis (pitch) and nasal–occipital axis (roll), respectively. RW rightward, LW leftward horizontal impulses relative to the head, RD right side down, LW left side down torsion impulses relative to the head. Each black filled circle is one bin (bin width, 20 ms) of mean eye velocity of six repetitions of the impulse. Solid line Linear regression fitted through the 20-ms bins. Note that a RW yaw head impulse leads to a LW eye movement, a head up pitch impulse results in a downward eye rotation, and a LD roll head impulse leads to a RD torsion eye rotation. These eye movements are according to the right-hand rule defined as positive.

Whole body transients about the interaural axis (pitch) resulted in near unity gain for head up and a gain about 0.8 for head down transients. These differences averaged over all subjects (N = 6) between up and down were significant (p < 0.05). Transient stimulation about the nasal–occipital axis (roll) elicited much lower gain of the compensatory eye movement responses, but were symmetrical in both directions. The top right panel in Fig. 5 shows the differences in eye angular velocities evoked by the roll and pitch components of a rotational step about a horizontal axis at 45° azimuth. Torsion components were much smaller than vertical components.

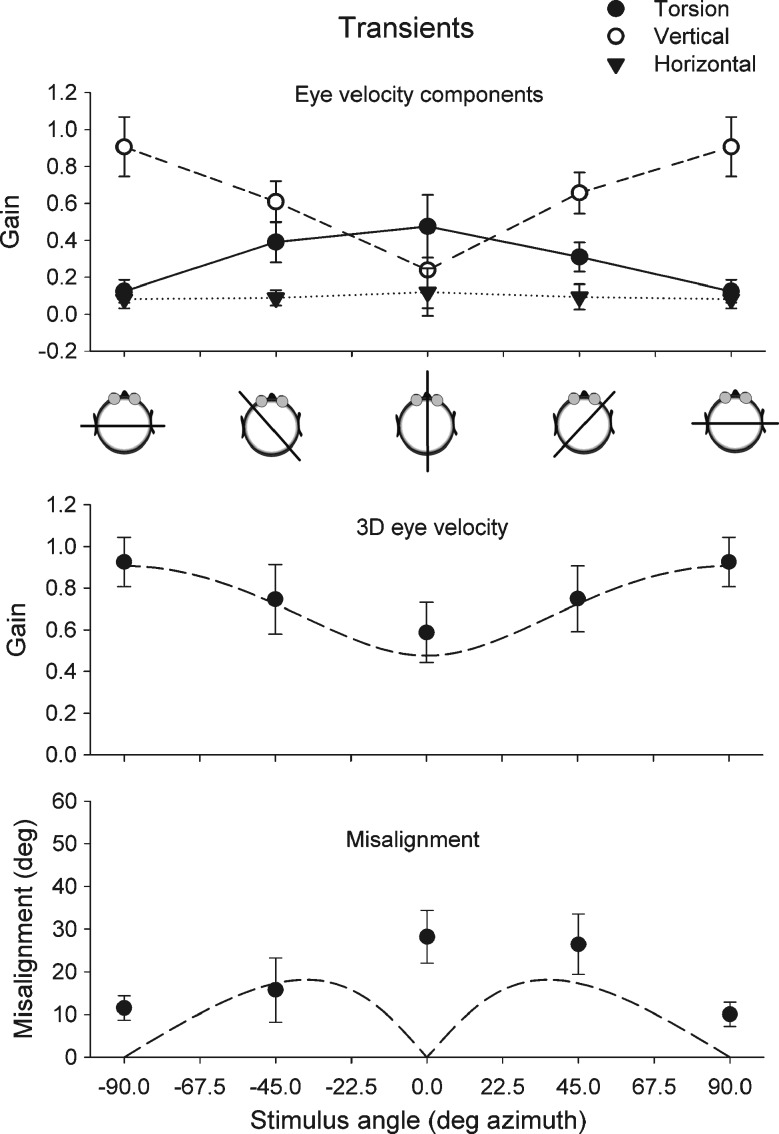
Gain and misalignment in response to transients in the horizontal plane are summarized in Fig. 6. The top panel shows the mean gain of the horizontal, vertical, and torsion eye velocity components. Maximum mean gain for the vertical component alone was 0.85 for pitch (90° azimuth). Maximum gain for torsion was 0.42 for roll (0° azimuth). Vector gains were slightly higher because of the contribution of all three components. Mean 3D eye velocity gain (N = 6) for pitch stimulation was 1.04 ± 0.18 for upward and 0.81 ± 0.14 for downward transients. The mean 3D eye velocity gain in response to roll (N = 6) was 0.65 ± 0.39 for head right side down and 0.52 ± 0.16 for head left side down transients. Similar to sinusoidal stimulation in darkness, misalignment was highest during roll (mean, 28.2 ± 0.18) and had its minimum value during pitch (mean, 11.53° ± 0.51).

FIG. 6.

Results of horizontal axis whole body impulse stimulation for all tested horizontal stimulus axes. Top panel Mean gain of the horizontal, vertical, and torsion eye velocity components. Middle panel Mean gain of 3D eye velocity for each tested stimulus orientation. The dashed line represents the expected vector eye velocity gain predicted from the vertical and torsion components. The lower panel shows the misalignment of the response axis with respect to the stimulus axis. The dashed line in the lower panel represents the predicted misalignment calculated from the vector sum of vertical and torsion eye velocity components. Error bars in all panels indicate one standard deviation. Cartoons underneath the top panel give a top view of the orientation of the stimulus axis with respect to the head.

In conclusion, we find that the gain and misalignment of eye movements in response to whole body transients follow a similar pattern as responses to sinusoidal stimulation in darkness. In both instances, the largest misalignment between 3D head and eye rotation axis occurs during roll stimulation.

To verify that the difference in misalignment between light and dark conditions is related to the absence or presence of a horizontal component, we generated simulated eye movements in response to the same stimulus range as in the real experiment. In the simulation, the maximum gain for vertical eye responses was set at 0.99 and for torsion at 0.54. We simulated two conditions: In condition 1, the gain of the horizontal eye movements was set to zero (similar to what we found in the light). In condition 2, we simulated a horizontal eye rotation component with a gain varying between 0 for pitch to 0.23 for roll. These simulated horizontal, vertical, and torsion eye movement data were analyzed with the same analysis software as the real data. In condition 1, the 3D eye velocity gain exactly matched values predicted from roll and pitch components. Also, predicted (dashed line) and simulated misalignment (open squares) exactly matched in condition 1. The presence of a horizontal component in condition 2 had only a small effect on 3D eye velocity gain. However, it strongly affected misalignment, with a maximum value towards roll. In these simulations, the changes are due to the presence of a horizontal eye rotation component in the dark.

Discussion

In this paper, we show that in humans, the quality of the 3D VOR response varies not only in terms of gain but also in terms of alignment of the eye rotation axis with head rotation axis. Studies in humans on properties of the 3D VOR generally reported on gain and phase characteristics about the cardinal axes, which are yaw, roll, and pitch (Ferman et al. 1987; Tabak and Collewijn 1994; Paige and Seidman 1999; Misslisch and Hess 2000; Roy and Tomlinson 2004). More recently, gain characteristics in the planes of the vertical canals were measured (Cremer et al. 1998; Halmagyi et al. 2001; Migliaccio et al. 2004; Houben et al. 2005). All studies on 3D VOR dynamics report a high gain for horizontal and vertical eye movements compared to torsion. This general property has been described in lateral-eyed animals (rabbits: Van der Steen and Collewijn 1984) and frontal-eyed animals (monkeys: Seidman et al. 1995) and humans (Ferman et al. 1987; Seidman and Leigh 1989; Tweed et al. 1994; Aw et al. 1996b). We show that also for small-amplitude stimulation, the gain of the VOR for stimulation about the cardinal axes is in close agreement with previous studies in humans (Paige 1991; Tabak and Collewijn 1994; Aw et al. 1996a). We found a small but significant higher gain for pitch head up, compared to pitch head down transients (p = 0.05). This is different from earlier reports and possibly related to the fact that our transients were whole body movements in contrast to previous head transient studies that always involved stimulation of the neck (Tabak and Collewijn 1995; Halmagyi et al. 2001).

The second main finding is the systematic variation in misalignment between stimulus and response axis. In the light, misalignment between eye and head rotation axis has minima at roll and pitch and its maxima at ±45° azimuth. This finding is consistent with a coordinate system with a head fixed torsion and pitch axis. In this system, vector summation of near unity response for pitch and a considerably lower response for roll has an effect on misalignment during stimulation about an axis intermediate between roll and pitch. Quantitatively, the misalignment angles in our study are similar to those reported in previous studies in monkeys (Crawford and Vilis 1991; Migliaccio et al. 2004).

Quantitative and qualitative differences exist in misalignment between light and dark conditions. Firstly, there is in the dark and during transient stimulation a twofold increase in misalignment compared to sinusoidal stimulation in the light over the whole range of tested axes.

Because in the dark gain is lower, one possibility is that roll and pitch are not proportionally reduced. However, this is not the case: there was on average a 34% reduction for pitch and a 36% for roll. Differences were not significantly different (p = 0.9). Thus, the larger misalignment is not due to vector summation of different vertical and torsion values.

The second point is the large change in misalignment during roll stimulation in the dark compared to the light. We show that this increase in the dark is due to a horizontal eye movement component. The presence of a horizontal component during roll stimulation in the dark has been reported before (Misslisch and Tweed 2000; Tweed et al. 1994). Misslisch and Tweed (2000) suggested that the horizontal cross-coupling between horizontal and torsional eye movements during head roll occurs because “the brain is so accustomed to eye translation during torsional head motion that is has learned to rotate the eyes horizontall during roll even when there is in fact no translation.” However, this explanation for the presence of a horizontal component is not very satisfactory.

An alternative possibility is a change of eye in head position in the dark. This change can cause an increase in misalignment as eye position in the orbit has an effect on the orientation of the eye velocity axis (Misslisch et al. 1994). However, this explanation is unlikely because we carefully controlled the central fixation of the subject’s eyes by providing a visual fixation target in between stimulus trials. The eyes remained within 1.54° standard deviation around the fixation center. This value is far too small to explain the observed changes in misalignment.

A second possibility is that otolith signals are part of the response (Angelaki and Dickman 2003; Bockisch et al. 2005). The contribution of tilt VOR to the 3D eye velocity response depends on the orientation of the stimulus axis (Merfeld 1995; Merfeld et al. 2005). In particular for stimulation about the roll axis (side down), any contribution from tilt VOR would evoke horizontal eye movements. Because otoliths respond to both linear accelerations and tilt (Angelaki and Dickman 2003), we can estimate the contribution of tilt to the horizontal and vertical components from the responses to linear acceleration. Because in our stimulus conditions (1 Hz, 4° peak-to-peak) the estimated horizontal tilt VOR “gain” is only 0.016, tilt VOR cannot explain our findings. Another possibility is that horizontal eye movements during roll depend on head position. A change in pitch head position alters the anatomical orientation of the semicircular canals with respect to gravity. This could have an effect on response vectors of the three semicircular canals, or it could have an effect on the central integration between canal and otolith signals. In our experiments, we positioned our subjects as close as possible with the head in an upright position with a 7° upward inclination of the frontal pole of Reid’s line (Della Santina et al. 2005). In this position, there is only about 1° deviation from the ideal response vector. Thus, the horizontal eye movements cannot be explained by a change in sensitivity vectors due to different canal plane orientations.

This leaves us with the option that horizontal eye movements in darkness are the result of differences in the central processing of 3D canal signals. Afferent signals from the different canal and otolith sensors are to a large extent processed via specific pathways which have connections with different eye muscles (Ito et al. 1976). Recent work on gravity dependence of roll angular VOR (aVOR) in monkey (Yakushin et al. 2009) supports the special organization of the roll aVOR compared to yaw and pitch aVOR. These differences are not only reflected in the low gain of torsion and poor adaptive capabilities of roll aVOR (Yakushin et al. 2009) but also in the poor alignment of the eyes during roll in the dark. In a control experiment, we confirmed that there is also in human a gravity-dependent effect. We compared two different pitch positions of the head (Reid’s line 10° and 25° up). Pitching the head 15° up resulted in a 5° increase in misalignment (see figure in ESM). This increase in misalignment was paralleled by only a very small decrease in torsion (0.04) and increase in horizontal (0.05) gain. Theoretically, misalignments due to different head orientations may be counteracted by internal neuronal processing (Merfeld et al. 2005). Our data suggest that these compensations are not very effective for stimulation at 1 Hz in the dark, although the effect on vestibular compensation may be frequency-dependent (Groen et al. 1999; Schmid-Priscoveanu et al. 2000; Bockisch et al. 2005; Zupan and Merfeld 2005) This is in line with current ideas that gravito-inertial internal forces play an important role for perceptual representations, whereas head and eye centered reference systems are important for oculomotor stabilization (Angelaki and Cullen 2008).

We agree with the conclusions from Yakushin et al. (2009) that roll aVOR is different from the yaw and pitch aVOR. This is also reflected in the way visual information is integrated with vestibular information. At the subcortical level, visual information has a 3D representation of space, similar to that of the semicircular canals, including representation of torsion (roll; Simpson and Graf 1985; Van der Steen et al. 1994). At the cortical level, the visual system is mainly organized in a 2D system, with little representation of torsion. This organization of the visual system mainly helps to stabilize gaze in yaw and pitch and much less in roll.

Electronic supplementary material

Below is the link to the electronic supplementary material.