Complex Stapes Motions in Human Ears

Abstract

It has been reported that the physiological motion of the stapes in human and several animals in response to acoustic stimulation is mainly piston-like at low frequencies. At higher frequencies, the pattern includes rocking motions around the long and short axes of the footplate in human and animal ears. Measurements of such extended stapes motions are highly sensitive to the exact angulation of the stapes in relation to the measurement devices and to measurement errors. In this study, velocity in a specific direction was measured at multiple points on the footplates of human temporal bones using a Scanning Laser Doppler Vibrometer (SLDV) system, and the elementary components of the stapes motions, which were the piston-like motion and the rocking motions about the short and long axes of the footplate, were calculated from the measurements. The angular position of a laser beam with respect to the stapes and coordinates of the measurement points on the footplate plane were calculated by correlation between the SLDV measurement frame and the footplate-fixed frame, which was obtained from micro-CT images. The ratios of the rocking motions relative to the piston-like motion increased with frequency and reached a maximum around 7 kHz.

A novel method for quantitatively assessing measurements of complex stapes motions and error boundaries of the motion components is presented. In the frequency range of 0.5 to 8 kHz, the magnitudes of the piston-like and two rocking motions were larger than estimated values of the corresponding upper error bounds.

Introduction

Békésy (1960) and Kirikae (1960) described motions of the stapes footplate in human ears as a combination of translational motions along the longitudinal axis of the stapes (piston-like motions) and rotational motions (rocking motions). It has been reported that the human stapes motions are piston-like at low frequencies and include rocking motions along the long and short axes of the footplate at high frequencies (Heiland et al. 1999; Huber et al. 2001; Hato et al. 2003). Studies of rocking motions have been extended to other animals such as cat (Decraemer et al. 2000) and gerbil (Decraemer et al. 2007; Ravicz et al. 2008). Most of the current human cochlear models do not represent the effects of the rocking motions because these motions are believed to produce no net volume displacement on the oval window and have negligible effects on hearing mechanisms (Kolston and Ashmore 1996; Dodson 2001; Lim and Steele 2002). On the measurement side, a previous study by de la Rochefoucauld et al. (2008) reported that motion components other than the piston-like motion did not produce scala-vestibuli pressure in gerbil ears. However, a recent study by Huber et al. (2008) showed that enhancement of the rocking motions of the stapes by mechanical stimulation affected the cochlear response in guinea pigs, as demonstrated by changes in compound action potentials (CAP). It is anticipated that there will be further investigation of the relation between the rocking motions and fluid-flux inside the cochlea, and methods to measure stapes motions, particularly the rocking motions, need to be systemically studied.

Laser Doppler Vibrometer (LDV) systems have been widely used to measure stapes motions, and several methods to measure all or a subset of the 3-D motion components of the stapes have been developed using the LDV system. Hato et al. (2003) measured velocities at five points on the footplate and calculated the piston-like and two rocking motions of the stapes. Eiber et al. (2007) also calculated the piston-like and two rocking motions from 3-D velocity components at a point on the stapes head measured using a 3-D LDV system. In their measurements and resulting calculations, the position and direction of the stapes in the measurement frame were estimated, and location of the measurement points on the stapes and the relative angular position of the laser beam with respect to the stapes were obtained based on the estimation. Inaccuracy in such estimations can cause significant errors in the calculated motion components, especially on small-sized stapes such as that of guinea pigs. In a study by Decraemer et al. (2007), 3-D components of motions at multiple points on the stapes were measured by changing the angular position of the laser beam using goniometers, and six rigid body motion components of the stapes in gerbil ears were calculated. In that study, coordinates of the observation points were read from the xyz-positioning system. A computed tomography (CT) model of the stapes was registered in the position of the stapes during the experiment using these coordinates to fully describe the experimental geometry. However, complicated setups with the goniometers were required for this accurate assessment of the angular position of the laser beam with respect to the stapes.

In our study, velocities at multiple points on the stapes footplate were measured using SLDV. The piston-like and two rocking motions of the stapes were calculated as a response to physiological sound stimuli for six human ears. An accurate way to relate the SLDV measurement frame to the footplate-fixed frame and thus determine coordinates of measurement points and the laser beam direction in the footplate-fixed frame was introduced using micro-CT technology.

Detailed investigation of the quantitative assessment of the effects of measurement errors on the rigid body motion components of the stapes was another goal of this study. In the work by Hato et al. (2003), reverse calculation of velocities at the measurement points from identified rigid body motion components was used to verify consistency of measurement and calculation of the overall stapes motions. However, if contribution of a specific rigid body motion component to the entire stapes motion is relatively small, then good agreement between the original measurement and the reverse calculation does not guarantee accuracy of the rigid body motion component. In this study, the error boundaries of the motion components were examined and compared with the components of the stapes motions obtained from the measurements.

Material and methods

Specimen preparation

Six temporal bones (TBs) from the right side of human cadavers (an average age of approximately 60 years) were used in this study. The human TBs were harvested within 24 h after death and were placed in 0.1% Cialit (sodium-2-ethylmercurimercapto-benzoxazol-5-carbonide) solution, at 4°C. The TBs were inspected using an operating microscope for possible abnormalities. All experiments were performed within 7 days of the explantation. After removal of all connective tissues and muscles, the external ear canal was drilled down to 2 mm from the tympanic annulus. A simple mastoidectomy with posterior tympanotomy, which included removal of the mastoid and a part of the tympanic segment of the facial nerve and surrounding bone, was performed in order to obtain a clear and near-perpendicular view of the stapes footplate. The tympanic membrane (TM), ossicles, stapedius muscle, and tendon were left intact. All temporal bones were periodically moistened with physiological saline solution to prevent drying during preparation.

Velocity measurement

The loudspeaker (ER-2, Etymotic Research, USA) and the microphone probe (ER-7C, Etymotic Research, USA) were placed in an artificial external ear canal near the TM. The artificial external ear canal (AEEC) was attached and sealed acoustically using silicone and bony wax to the bony rim of the former external ear canal, creating an acoustic chamber of about 0.5 ml volume. The distance between the microphone probe and the TM center was maintained at approximately 3 mm.

A multi-frequency sound consisting of harmonic sound waves with 32 different frequencies in the range of 0.5 to 8 kHz was generated by a function generator (HP 33120A, Hewlett Packard, USA) and delivered via the loudspeaker. The frequency steps in the multi-frequency sound were 100 Hz from 0.5 to 2 kHz, 200 Hz from 2 to 3 kHz, 300 or 400 Hz from 3 to 4 kHz, and 500 Hz from 4 to 8 kHz. The sound pressure level (SPL) in the ear canal was measured by the microphone probe in front of the TM, and amplitude of stimulation at each frequency was adjusted by HLV 1.01 software (Polytec GmbH, Germany), such that the SPL had a flat spectrum within 5 dB along the measured frequency range. The final SPL with adjusted amplitudes was in the range of 94 to 105 dB. The magnitude and phase of the velocities at multiple points (150 to 200 points) on the footplate were measured using an OFV-3001 SLDV system (Polytec GmbH, Germany), and the X and Y coordinates of the measurement points in the SLDV measurement frame were recorded by PSV V8.5 software (Polytec GmbH, Germany). A sampling frequency of 25.6 kHz was chosen to prevent aliasing, and the frequency resolution was set at 12.5 Hz.

Frame registration

The XYZ coordinate system of the SLDV measurement frame was set such that the laser beam was along the Z direction and the XY plane was normal to the laser beam, while the xyz coordinate system of the footplate-fixed frame was determined such that the xy plane was best fit to the lateral-side surface of the footplate (the surface to which the stapes crura are attached), and the origin was on the centroid of the surface. The 3-D feature of the stapes obtained from micro-CT images was used for calculation of the footplate-fixed frame. In the footplate-fixed frame, the long axis of the footplate was set as the x axis, the short axis of the footplate as the y axis, and the direction normal to the xy plane as the z axis. The posterior, inferior, and lateral directions were set as positive directions for the x, y, and z axes for the right ear.

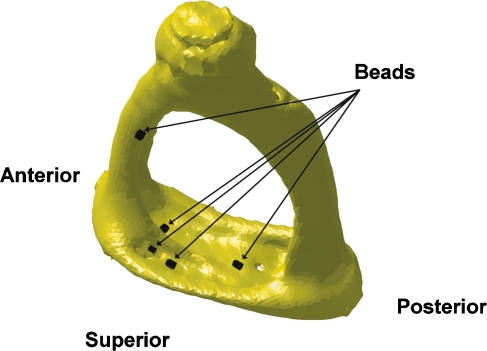
Because an inaccurate estimation of position and direction of the footplate in the SLDV measurement frame may produce significant errors in calculation of the rigid body motion components, an accurate way of obtaining the relation between the SLDV measurement frame and the footplate-fixed frame was developed using micro-CT technology. Five to seven retro-reflective glass beads of 50-micron diameter were placed on the footplate and/or the anterior crus of the stapes. The beads were attached before velocity measurements and were held in position by capillary adhesion during the measurements. After the velocity measurements, while maintaining the SLDV measurement frame, the laser beam was positioned on the beads and the X and Y coordinates of the beads in the SLDV measurement frame were recorded by the PSV V8.5 software. Next, the stapes with glass beads in position was carefully removed from the TBs, and the glass beads were glued onto the stapes. To avoid any displacement of the beads due to the manipulation, a gel-type glue was used, and it was applied from the direction perpendicular to the bony surfaces where the beads were placed. The stapes with glass beads attached was scanned by the micro-CT scanner with a 12-micron resolution to determine their coordinates in the footplate-fixed frame.

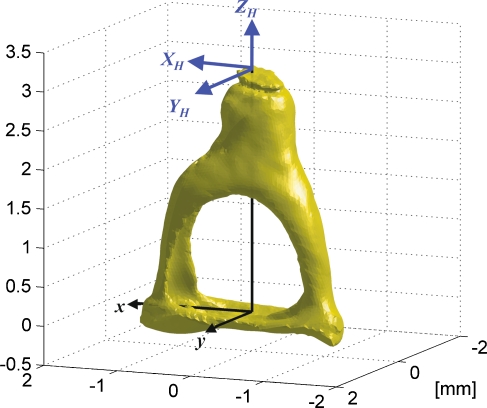
Figure 1 illustrates the 3-D shapes of the stapes and micro-glass beads reconstructed from the micro-CT images. The micro-glass beads were clearly visible and distinguishable from bones in the micro-CT images because they were retro-reflective and had much larger x-ray attenuation than the bones. When the gray-scale level on the image was linearly scaled such that the maximum attenuation and no attenuation corresponded to values of 1,000 and 0, the gray-scale values of the bones were below 500 and the values of the beads were above 980. With coordinate values of the glass beads in the SLDV measurement frame and footplate-fixed frame, the relation between these two frames is given by the following equation (Sim 2007).

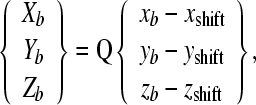1

where

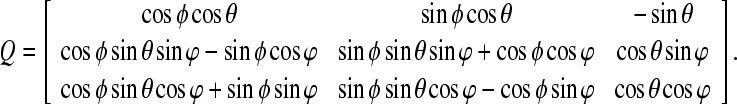X_b, Y_b, and Z_b are coordinates of the glass beads in the SLDV measurement frame, while x_b, y_b, and z_b are the corresponding coordinates in the footplate-fixed frame. x_shift, y_shift, and z_shift indicate the offsets of the origins between the two frames. Three Eulerian angles of φ, θ, and ɸ, which were rotation angles of the footplate-fixed frame with respect to z, y, and x axes in sequence (Type I, Greenwood 1988), and the offsets x_shift, y_shift, and z_shift were calculated by correlation of the coordinate values of the glass beads in both frames. To get three Eulerian angles from five or seven reference points, the Levenberg-Marquardt method, a nonlinear least-square error method provided in Matlab (The MathWorks Inc.), was used. Because the Z coordinate values of the glass beads (Z_b) cannot be detected from the SLDV System, Eq. (1) has two sets of the Eulerian angles as a solution. To avoid an unexpected solution set and “local minimum” in the nonlinear least-square error method, approximate adjusting was performed manually before the numerical calculation.

FIG. 1.

3-D feature of the stapes with micro-glass beads reconstructed from micro-CT images. After velocity measurements, the glass beads were glued to avoid any displacement during the micro-CT scanning.

With the obtained relation between the SLDV measurement frame and the footplate-fixed frame, coordinates X_m and Y_m of a measurement point m in the SLDV measurement frame, which were recorded during the velocity measurement by the PSV V8.5 software, were converted into the corresponding coordinates x_m, y_m, and z_m in the footplate-fixed frame.

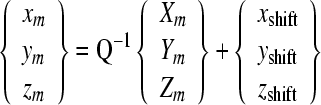2

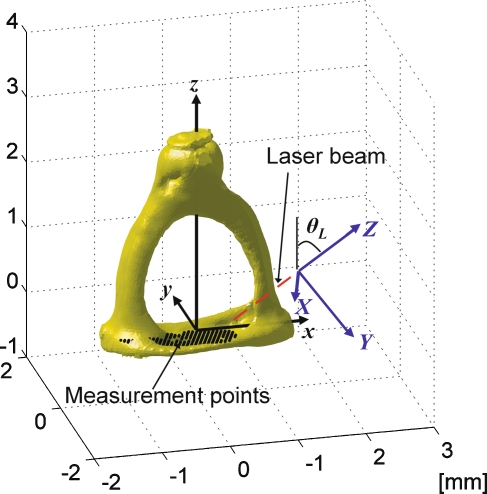
Because the Z coordinate value Z_m of the measurement point could not be measured, Eq. (2) was solved assuming the measurement points were on the xy plane (z_m = 0) of the footplate-fixed frame. Figure 2 illustrates the stapes registered in the footplate-fixed frame and measurement points (black dots on the figure) aligned on the xy plane. With the micro size of the glass beads, the relation between the measurement frame and the footplate-fixed frame could be precisely obtained.

FIG. 2.

The stapes of a human ear and measurement points aligned in the footplate-fixed frame. Coordinates of the measurement points in the footplate-fixed frame were calculated by correlation between the SLDV measurement frame XYZ and footplate-fixed frame xyz, which was obtained from coordinates of the glass beads in both frames. All measurement points were assumed to be on the xy plane of the footplate-fixed frame.

Calculation of the elementary components in the stapes motion

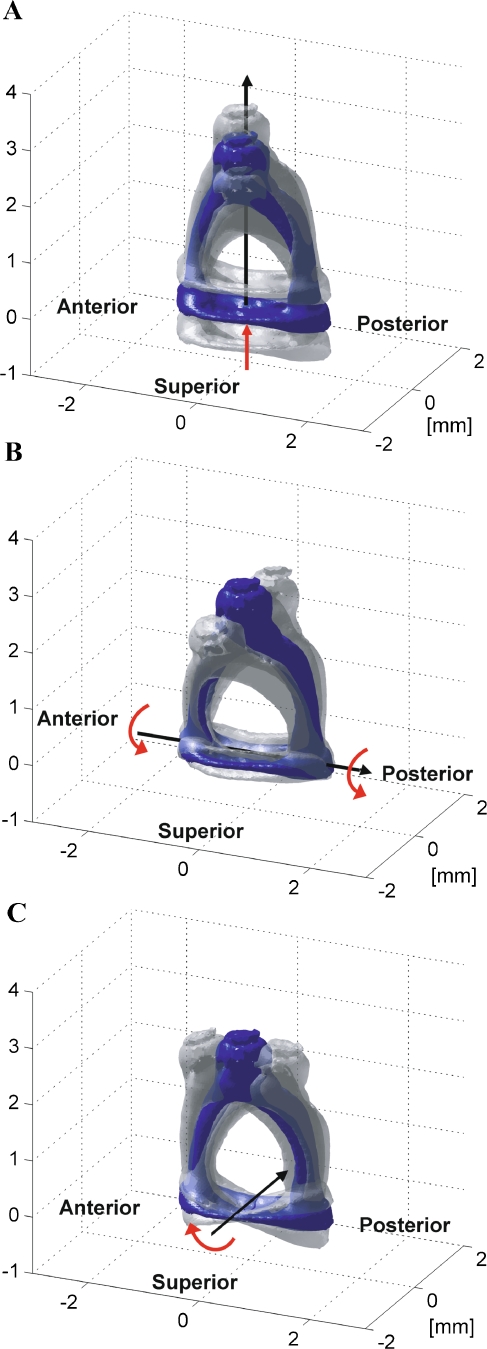
Rigid body motions of the stapes can be described with three translational components and three rotational components about a reference point in a given reference frame. If the annular ring restricts in-plane motions of the stapes footplate considerably, then only three substantial motions of the footplate remain: one translational component in the z direction at the footplate center and two rotational components about the long and short axes of the footplate (Fig. 3). The translational motion of the footplate center in the z direction is usually called a piston-like motion, and the two rotational motions are called rocking motions.

FIG. 3.

Rigid body motion components of the stapes. A Translational motion v_oz of the footplate center (piston-like motion), B rotational motion ω_x around the long axis of the footplate (rocking around the long axis of the footplate), and C rotational motion ω_y around the short axis of the footplate (rocking around the short axis of the footplate).

In previous studies (Békésy 1960; Kirikae 1960; Heiland et al. 1999; Hato et al. 2003), it has been assumed that due to the shape of the annular ligament and the mechanical stress and strain distribution in it, the in-plane motions of the footplate, which resulted from translational displacements in the x and y directions and rotations around the z axis, are much smaller by magnitudes than the piston-like and rocking motions. Though the restriction of the in-plane motion of the footplate has not been proved and there still exists the possibility that the magnitude of the other components are comparable to the piston-like and rocking motions, it is assumed in this study that the piston-like and two rocking motions are the elementary components of the stapes motions.

Denoting the rotational velocity along the x axis as ω_x, the rotational velocity along the y axis as ω_y, and the translational velocity of the footplate center (the origin of the footplate-fixed frame) along the z axis as v_oz, these rigid body motion components are related to the velocity component v_mz of the measured velocity at a point m on the footplate plane (z_m = 0) as follows:

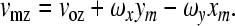3

The velocity at the point has only a z-component because in-plane motions along the footplate plane are assumed to be negligible (ω_z = v_mx = v_my = 0). With an angle θ_L between the laser beam direction and the z axis (shown in Fig. 2), the relation between measured velocities and rigid body motion components of the stapes can be expressed as

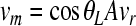4

where v_m is a vector with measured velocities, A is the matrix determined from x and y coordinates of the n measurement points on the footplate, and v_r is a vector with rigid body motion components

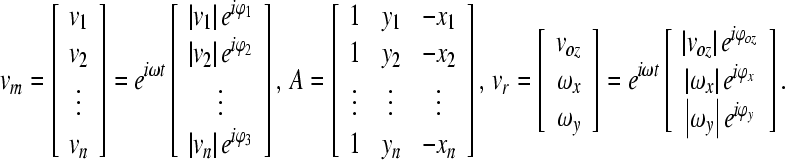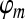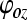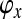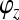Where ω is an angular frequency, is the phase of the velocity of the measured v_m, and , , and indicate the phases of the rigid body motion components v_oz, ω_x, and ω_y. Taking more than three non-colinear measurement points into account, the method of least squares error is used to express v_r by the following relationship

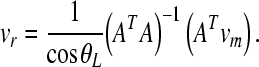5

In the calculation with Eq. (5), the velocities were taken as complex numbers from their magnitude and phase data.

The phases were recorded for both ear canal pressure and velocities of the points on the footplate, and the phase φ_m of the measured velocity v_m was obtained as the relative phases with respect to the phase φ_EC of ear canal pressure P_EC. Consequently, the phases φ_oz, φ_x, and φ_z of the stapes motion components v_oz, ω_x, and ω_y were also calculated with respect to the phase of the ear-canal pressure. The phases of the rotational velocity components were taken in the positive x (posterior), y (inferior), and z (lateral) directions. The distance between the microphone and the TM was much smaller than the wavelengths of the sound waves at the measurement frequencies; therefore, the effects of the phase delay in the ear canal on the measurement data were negligible.

Error analysis

The maximum possible error (MPE) in each rigid body motion component was introduced as an estimation of the maximum possible error of the motion component (Eqs. (A.19–A.21)), and the error ratio (ER) was obtained as a ratio of the MPE to the magnitude of the corresponding rigid body motion component (Eqs. (A.22–A.24)).

In calculation of the MPE, the actual measurement error at a measurement point could not be measured, and a measurement error measure, as defined in Eq. (A.18) was used. This measurement error measure at a measurement point was calculated from the difference between the measured velocity and the recalculated velocity, which was reversely calculated from the rigid body motion components. In calculating the difference, the complex numbers of the two velocities were taken to consider both magnitude and phase. The difference was also weighted by a factor that described the contribution of the measured velocity to calculation of the rigid body motion components. Definitions and details of the mathematical formulations may be found in the “Appendix.”

Results

Motions of the stapes

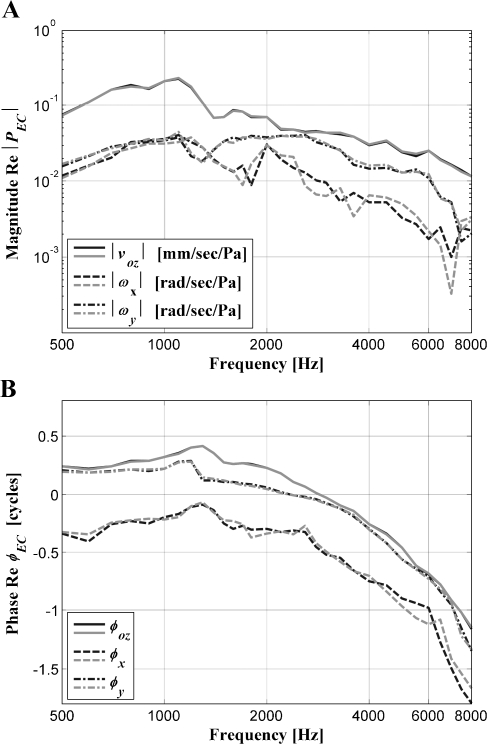
Figure 4 illustrates the piston-like and rocking motions calculated from two separate measurements in a temporal bone. The magnitudes of the motion components were normalized by the magnitude |P_EC| of the ear canal pressure, and the phases of the motion components were calculated for the positive x, y, and z axes relative to the phases φ_EC of the ear canal pressure, as described in the “Calculation of the elementary components in the stapes motions.” The black lines represent the first measurement, while the gray lines represent the second measurements in the temporal bone. In both magnitude (A) and phase (B), the two measurements showed very good (v_oz, ω_y) and good (ω_x) repeatability.

FIG. 4.

Comparison of the two measurements in a temporal bone. A Magnitudes |v_oz|, |ω_x|, and |ω_y| and B phases ϕ_oz, ϕ_x, and ϕ_y of the piston-like and rocking motion components calculated from the two separate measurements (black: first measurement, gray: second measurement) in a temporal bone. The magnitudes were normalized by the magnitude |P_EC| of ear canal pressure, and the phases were calculated relative to the phase ϕ_EC of the ear canal pressure, for the positive x (posterior), y (inferior), and y (lateral) directions.

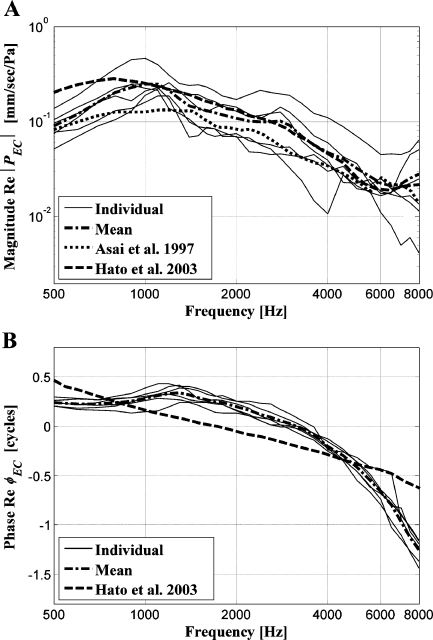
Figure 5 illustrates translational velocities v_oz in the z direction at the center of the footplate normalized by the ear canal pressure as well as their mean values in comparison with the data of Asai et al. (1997) and Hato et al. (2003).

FIG. 5.

Translational velocity (piston-like motion) v_oz in the z direction at the footplate center (piston-like motion) normalized by the ear-canal pressure P_EC in comparison to data from Asai et al. (1997, dotted) and Hato et al. (2003, dashed). A Magnitude |v_oz| and B phase ϕ_oz. The phases were taken from the translational velocity components in the negative z direction (medial direction).

The magnitude of this normalized piston-like motion showed amplitudes between the results from Asai et al. (1997) and Hato et al. (2003) below 2.5 kHz and were similar to Asai et al. (1997) above 2.5 kHz. The averaged magnitude had its peak around 1.0 kHz, and the minimum values were around 6.5 kHz. Variation of the phase of the translational motion in the considered frequency range was less than 2 cycles. The six bone measurements showed considerable individual differences in magnitude.

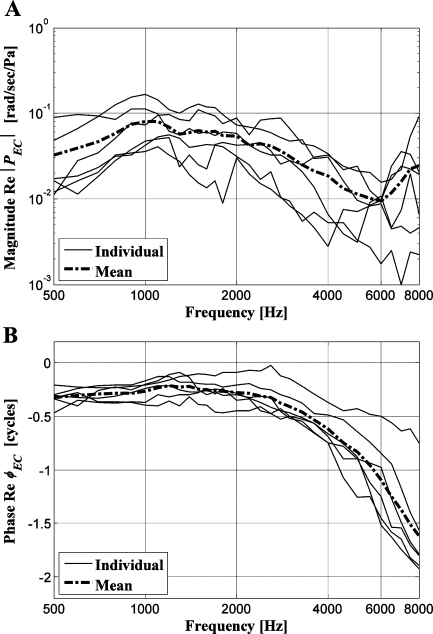
Figure 6 illustrates rotational velocities ω_x along the long axis (x axis) of the footplate normalized by the ear canal pressure (A: magnitude and B: phase).

FIG. 6.

Rotational velocity (rocking motion) ω_x around the long axis normalized by the ear-canal pressure. A Magnitude |ω_x| and B phase ϕ_x. The phases were taken from the rotational velocity components in the positive x direction (posterior direction).

The averaged magnitude had its peak around 1.0 kHz and the minimum values were around 6.0 kHz. At low frequencies around 500 Hz, the phase of the rotational velocity component in the positive x direction showed about a half-cycle difference from the phase of the translational velocity component in the positive z direction at the footplate center (Fig. 6B). The phase of the rotational velocity component in the positive x direction decreased with frequency, showing less than a 2-cycle variation between 0.5 and 8 kHz.

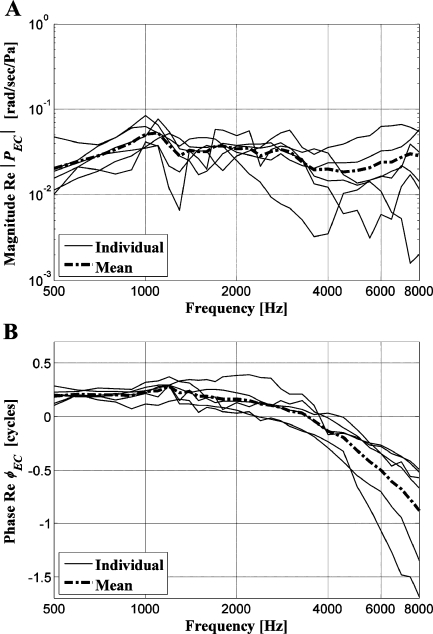
Figure 7 illustrates the rotational velocities ω_y along the short axis of the footplate (y axis), also normalized by the ear-canal pressure (A: magnitude and B: phase).

FIG. 7.

Rotational velocity (rocking motion) ω_y around the short axis normalized by the ear-canal pressure. A Magnitude |ω_y| and B phase ϕ_y. The phases were taken from the rotational velocity components in the positive y direction (inferior direction).

This component also showed considerable individual differences, especially above 2 kHz. In comparison with the individual data, the magnitude of the rotational velocity along the short axis was not proportional to the magnitude of the rotational velocity along the long axis, and a relation between the two magnitudes could not be found. Around 0.5 kHz, the rotational velocity component in the positive y direction was almost in-phase with the translational velocity component in the positive z direction at the footplate center. The phase delay of the rotational velocity along the short axis also tended to increase with frequency. The variation of the phase between 0.5 and 8 kHz was around 1 cycle for the four measurements and more than 1.5 cycles for the other two measurements.

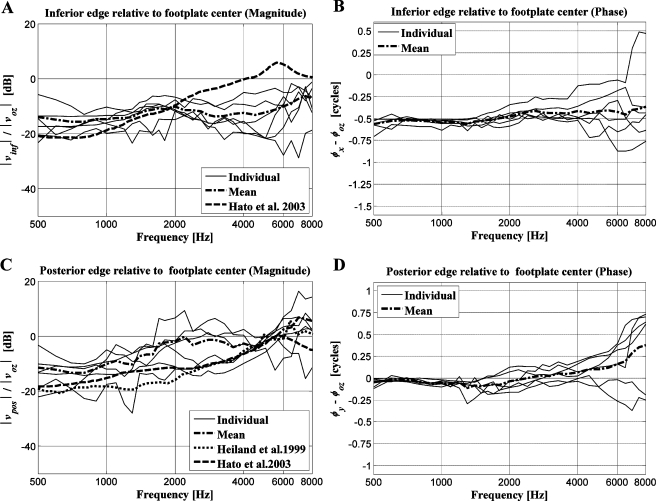
Comparison of the magnitude of the rotational velocities with the magnitude of the translational velocity at the footplate center cannot be directly done. To show the effect of the rotation, the linear velocities at the inferior and posterior edges of the footplate generated by the rotational velocities were calculated (Heiland et al. 1999; Hato et al. 2003). In this article, the edge velocities are defined as the velocities at the edges only due to the rotational velocities ω_x and ω_y. The rotational velocity component ω_x was multiplied by the half length of the footplate short axis (about 0.6 mm) for the inferior-edge velocity v_inf, and the rotational velocity component ω_y was multiplied by the half length of the footplate long axis (about 1.5 mm) for the posterior-edge velocity v_pos. Figure 8 illustrates relative magnitudes (A: inferior-edge velocity and C: posterior-edge velocity) and phases (B: Inferior-edge velocity and D: Posterior-edge velocity) of the edge velocities with respect to the footplate-center velocity in the z direction. The relative phases of the edge velocities were calculated by subtracting the phase of the footplate-center velocity in the positive z direction from the phases of the edge velocities.

FIG. 8.

Relative magnitudes and phases of the edge velocities due to the rocking of the footplate with respect to the footplate-center velocity (piston-like motion) A Relative magnitude and B phase of the inferior-edge velocity v_inf due to the rocking of the footplate along the long axis, and C relative magnitude and D phase of the posterior-edge velocity v_pos due to the rocking of the footplate along the short axis.

The mean ratio of the inferior-edge velocity to the footplate-center velocity began at approximately −14 dB at 0.5 kHz, and reached the maximum of −7 dB around 7.5 kHz. The mean ratio reported by Hato et al. (2003) had the maximum of about 5.5 dB around 5.5 kHz. In contrast, our values for this ratio were larger below 2 kHz and smaller above 2 kHz than the values by Hato et al. The relative phases of the inferior-edge velocities were about −0.5 cycle up to 2 kHz in the averaged value and showed large individual differences above 2 kHz. This means that the rotational motion along the negative x axis (anterior direction) is in-phase with the piston-like motion in the positive z direction (lateral direction) at low frequencies.

The mean ratio of the posterior-edge velocity to the footplate-center velocity tended to increase with frequency, and reached the maximum of 7 dB around 7 kHz. Our values for this ratio were larger than the corresponding values reported by Hato et al. (2003) and Heiland et al. (1999) below 4 kHz. The relative phase of the posterior-edge velocity was around zero (That is, the rotational motion along the inferior direction was in-phase with the piston-like motion in the lateral direction) below 1.5 kHz. Above 1.5 kHz, the relative phase of the posterior-edge velocity tended to increase with frequency for the four measurements, while the relative phase did not increase with frequency for the other two measurements.

Maximum possible error of stapes motion components

Figure 9 illustrates the mean magnitudes of the rigid body motion components normalized by the ear-canal pressure |v_oz|, |ω_x|, and |ω_y| and the corresponding MPE |v_oz|_MPE, |ω_x|_MPE, and |ω_y|_MPE.

FIG. 9.

Mean magnitudes of rigid body motion components (black) and their mean maximum possible errors (MPEs, gray) A Translational velocity at the footplate center and B rotational velocities around the long and short axes of the footplate.

The mean magnitude of the translational velocity at the footplate center normalized to the ear canal sound pressure was much larger than the corresponding maximum possible error across frequency (Fig. 9A). The mean magnitude of the rotational velocity component about the long axis (solid in Fig. 9B) was above the corresponding MPE (dashed in Fig. 9B) up to 5 kHz. The mean magnitude of the rotational velocity component along the short axis (dot-dashed in Fig. 9B) was above the corresponding MPE through the whole measurement frequency range (dotted in Fig. 9B).

Discussion

Rocking motions

In our measurements, there existed rocking motions comparable to the piston-like motion in the frequency range of measurement (Fig. 8). Such rocking motions are presumed to be caused by the stimuli parallel to the footplate, on the stapes head (excitations in the X_H and Y_H in Figure 10, Eiber et al. 2007; Huber et al. 2008).

FIG. 10.

Excitation of the elementary motion components on the stapes head. The excitation in the Z_H direction mainly generates a piston-like motion, while the excitations in the X_H and Y_H directions mainly generate rocking motions about the short and long axes of the footplate.

The excitation in the Z_H direction mainly generates a piston-like motion, while the excitations in the X_H and Y_H directions mainly generate rocking motions about the short and long axes of the footplate. Considering the middle-ear anatomy of the human, stimuli for the rocking motions are expected. The anterior part and posterior parts of the TM in human ears, which are divided by its attachment to the manubrium, have different shapes and sizes. The non-symmetric modes of the TM motions between the anterior and posterior aspects in human ears can cause torsional motions of the malleus (Puria et al. 2007a). Existence of such torsional motions is enhanced by the cross-sectional shape of the malleus handle, which has a circular shape in human (Puria et al. 2007b). The circular cross-section of the human malleus handle has an isotropic strength against forces in all directions, including the torsional stimuli. The torsional motions of the malleus in human ears are expected to be transferred as various stimulations to the stapes through the deformable joint between the malleus and incus. It is known that cat ears also have a non-symmetric TM, a circular cross-sectional shape in the malleus handle, and a deformable joint between the malleus and incus (Puria et al. 2007a). The vibrational modes of the cat stapes have been studied previously (Guinan and Peake 1967; Decraemer and Khanna 1999; Decraemer et al. 2000), and it was demonstrated that complex modes of stapes motion occur, including rocking motions.

Error on the motion components

Considering the magnitudes of the rigid body components reconstructed from measurements and the corresponding maximum possible errors in physiological motions (Fig. 9), the translational velocity component at the footplate's center is valid, but validities of the rotational velocity components are limited. The rotational velocity around the short axis (y axis) has good validity along the whole measurement frequency range (0.5 to 8 kHz), while the rotational velocity around the long axis (x axis) has good validity only below 5 kHz. To get better results for assessing the rocking motion, the signal-to-noise ratio in the LDV measurement should be increased with improved measurement conditions such as reflectivity of the laser beam on the measured surface and performance of the SLDV system. A wider range of measurement area closer to the footplate center and a laser beam direction more perpendicular to the footplate are also desired for better accuracy (see section A.1 in Appendix). However, obtaining such a measurement setup is limited by the surgical access to the stapes. The small measurement area causes large errors on the rotational velocities by making 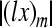and 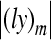in Eq. (A.19–A.20) large. With our surgical access procedure, an angle of approximately 50° to 60° between the laser beam and the footplate plane was obtained. Such limitations in surgical access can be improved by altering the surgical access to expose more area of the footplate.

The footplate position error causes errors in the coordinates of the measurement points and the laser beam direction, and thus errors in the rigid body motion components. In this study, five to seven micro-glass beads of 50-micron diameter were attached to the stapes to obtain a correlation between the SLDV measurement frame and the footplate-fixed frame. Considering the size of the glass bead, the alignment error within the range of ±4.3 degrees is expected with five glass beads. The error range becomes smaller by increasing the number of the glass beads or decreasing the size of the glass beads and placing them as far as possible from each other.

Individual difference

In the magnitudes and phases of all stapes motion components, the measurements showed large standard deviations. The large deviations in the measurements are presumed to be mainly due to large individual differences in middle-ear anatomy (Sim and Puria 2008) as well as the older age of the donors. For the six temporal bones used in this study, the standard deviation of the footplate area was 8.5 % of the averaged values (2.97 ± 0.25 mm²).

Conclusion

For assessing measurements of stapes motion, the maximum possible error was introduced as a reference for error boundaries of the elementary motion components of the stapes. In the measurements of physiological motions with our measurement setup and conditions, the magnitude of the rotational velocity component about the long axis of the footplate was almost the same as the corresponding maximum possible error above 5 kHz. To overcome the small magnitudes of the motion components and get valid results, the measurement conditions such as reflectivity of the laser beam on the measured surface and performance of the SLDV system should be improved.

In this study, micro-CT imaging technology with micro-beads attached to the stapes was introduced to obtain accurate coordinates of the measurement points and laser beam orientation in the footplate-fixed frame.

In the frequency range of 0.5 to 8 kHz, the magnitudes of the rocking motions were comparable to the magnitude of the piston-like motion, although there were large individual differences. Regardless of whether the rocking motions are desirable or not, a considerable amount of these motions exist, at least in human. Therefore, the detailed contribution of the rocking motions to hearing should be investigated in the future.

Appendix: Maximum Possible Error and Error Ratio

Equation (4) can be written as the following form

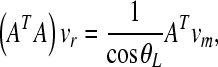A.1

with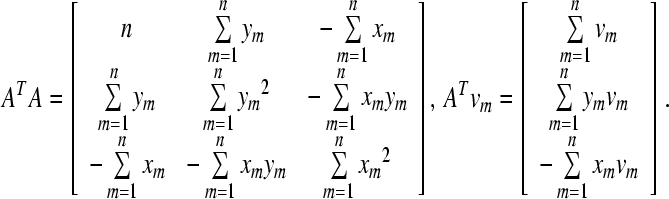

Because in-plane motions of the footplate are assumed to be constrained (“Calculation of the elementary components in the stapes motions”), velocities at points on the footplate plane have only the component in the z direction. The motion of a point on a rigid body can be expressed with translations of a reference point and rotations of the rigid body. Choosing the centroid of the measurement points (x_c, y_c) as the reference point, the velocity components in the z direction v_oz at the origin of the footplate-fixed frame can be described with the velocity component in the z direction v_cz at the centroid of the measurement points and the two rotational velocity components ω_x and ω_y of the stapes.

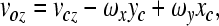A.2

where 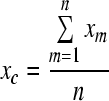and 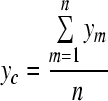, assuming that the measurements points on the footplate plane (xy plane) are equally spaced in the x and y directions. The translational velocity in the z direction at the centroid of the measurement points can be obtained from

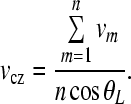A.3

The rotational part of the stapes footplate motions follows as

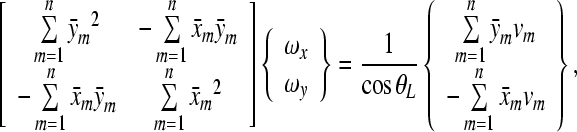A.4

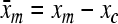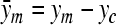where and indicate the distances of measurement points from the centroid. As a consequence from Eq. (A.4) the angular velocities follow as

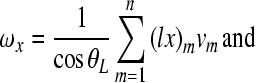A.5

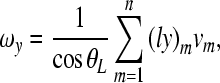A.6

where 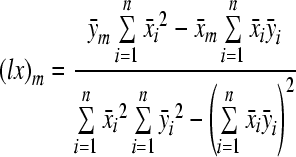and

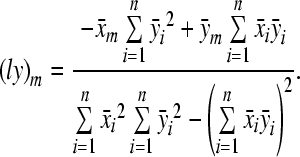In above equations, 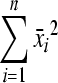and 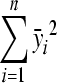are determined by the size of the measurement area, while 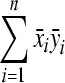is determined by the shape of the measurement area. In the case that the scan area is symmetric with respect to the axes, 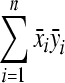becomes zero. The measured velocities v_m contain a true velocity v_m^T and a measurement error v_m^E

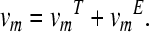A.7

Substituting Eq. (A.3) and (A.7) into Eqs. (A.2), (A.5), and (A.6), the following equations are obtained.

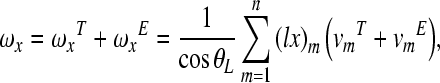A.8

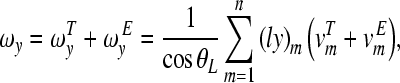A.9

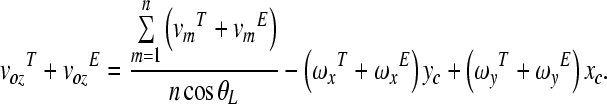A.10

From Eqs. (A.8)–(A.10), it follows,

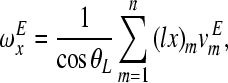A.11

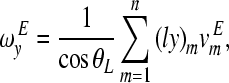A.12

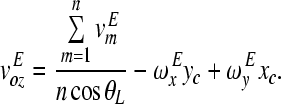A.13

Observing Eqs. (A.11) and (A.12), errors in angular velocities due to measurement errors become smaller with the smaller magnitudes of (lx)_m and (ly)_m. The magnitudes of (lx)_m and (ly)_m can be reduced by increasing the size of the measurement area. In Eq. (A.13), it is shown that error in the piston-like motion (translational components at the footplate center) is related to the location of the scan area. When the scan area is farther from the center of the footplate (that is, the magnitudes of x_c and y_c are larger), errors in angular motions are more reflected into the calculated translational motion of the footplate center. It is also obvious that the smaller θ_L results in smaller errors.

The magnitudes of the velocity component errors in Eqs. (A.11)–(A.13) can be bounded by the following relations

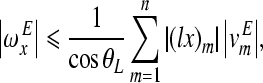A.14

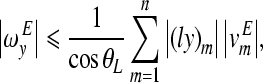A.15

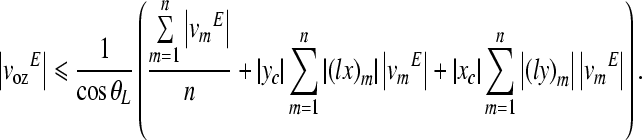A.16

If measurement error at each measurement point could be estimated, then the error boundaries of the rigid body motion components could be obtained by Eqs. (A.14)–(A.16). In actual measurements, the measurement error at each point is not known, and it is difficult to estimate. If we reversely calculate the velocity at a measurement point k from the rigid body motion of the stapes, then we get

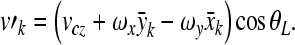A.17

The magnitude of the difference between re-calculated velocity from the rigid body components (Eq. (A.17)) and original measured velocity can be used as a measure of the magnitude of error at the point (Hato et al. 2003). However, in calculation of the rotational velocities, the velocity at each point is weighted by the corresponding distance from the centroid of the scan area (Eqs. (A.5) and (A.6)). Therefore, when the rotational velocity components are large, the difference between recalculated velocity and original measured velocity becomes smaller for the points farther from the centroid and larger for the points closer to the centroid. This results in a reduced measure of the measurement error for the farther points and a magnified measure of the error for the closer points. To get a more reasonable measure of the measurement error, we define ε_k as a measurement error measure at a measurement point k,

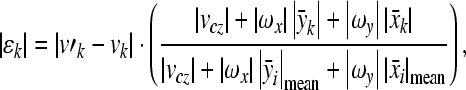A.18

where 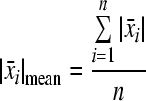and 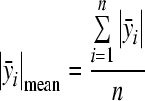are the average distances from the centroid to the measurement points on the stapes footplate in x and y axes. In the definition of the measurement error measure above (Eq. (A.18)), the difference between the measured and recalculated velocities is weighted by a factor that describes the contribution of the velocity at a measurement point k to calculation of the rigid body motion components. Substituting 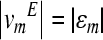into Eqs. (A.14)–(A.16), the following MPEs are derived as

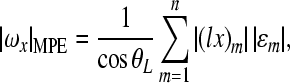A.19

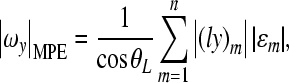A.20

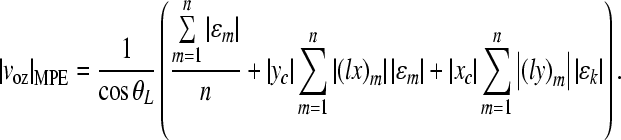A.21

Consequently, the error ratio as the ratio of the MPE to the magnitude of the corresponding calculated motion component is calculated as follows:

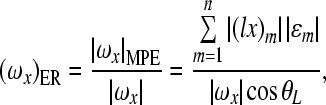A.22

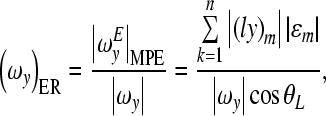A.23

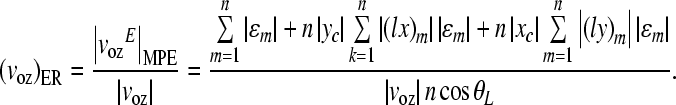A.24