Vestibular Heading Discrimination and Sensitivity to Linear Acceleration in Head and World Coordinates

Abstract

Effective navigation and locomotion depend critically on an observer's ability to judge direction of linear self-motion, i.e., heading. The vestibular cue to heading is the direction of inertial acceleration that accompanies transient linear movements. This cue is transduced by the otolith organs. The otoliths also respond to gravitational acceleration, so vestibular heading discrimination could depend on (1) the direction of movement in head coordinates (i.e., relative to the otoliths), (2) the direction of movement in world coordinates (i.e., relative to gravity), or (3) body orientation (i.e., the direction of gravity relative to the otoliths). To quantify these effects, we measured vestibular and visual discrimination of heading along azimuth and elevation dimensions with observers oriented both upright and side-down relative to gravity. We compared vestibular heading thresholds with corresponding measurements of sensitivity to linear motion along lateral and vertical axes of the head (coarse direction discrimination and amplitude discrimination). Neither heading nor coarse direction thresholds depended on movement direction in world coordinates, demonstrating that the nervous system compensates for gravity. Instead, they depended similarly on movement direction in head coordinates (better performance in the horizontal plane) and on body orientation (better performance in the upright orientation). Heading thresholds were correlated with, but significantly larger than, predictions based on sensitivity in the coarse discrimination task. Simulations of a neuron/anti-neuron pair with idealized cosine-tuning properties show that heading thresholds larger than those predicted from coarse direction discrimination could be accounted for by an amplitude–response nonlinearity in the neural representation of inertial motion.

Introduction

Perceiving the direction of self-motion—the heading—depends on visual and vestibular information (Warren et al., 1988; Crowell and Banks, 1993; Ivanenko et al., 1997; Crowell et al., 1998; Gu et al., 2007; Fetsch et al., 2009). For transient movements, the vestibular cue to translation is linear acceleration, detected by the otolith organs. Here we investigate how human vestibular sensitivity to linear acceleration determines heading perception. Control of locomotion and navigation depends critically on the precision of vestibular heading estimates, so we are particularly interested in measuring that precision and uncovering factors that influence it.

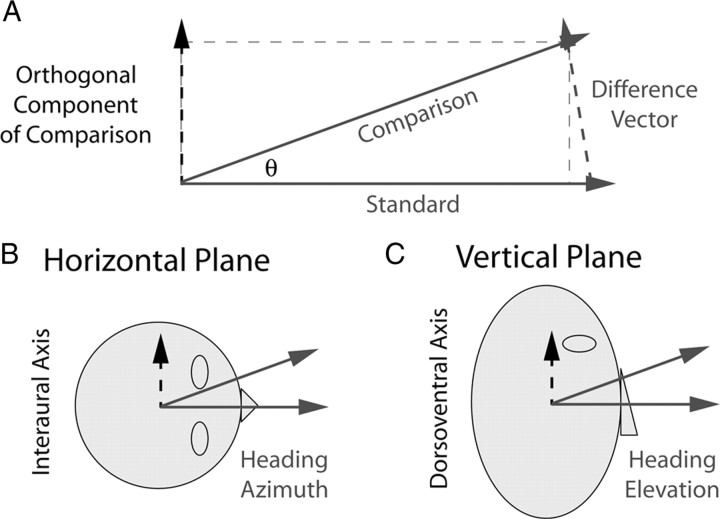
Precision of heading perception is typically assessed in a heading discrimination task (see Fig. 1). Subjects are presented with two consecutive movements and asked to indicate whether the second movement is leftward/rightward (or upward/downward) relative to the first. They can determine this by taking the difference between the two sensed motion vectors and observing the direction of this difference vector (see Fig. 1A). Using this strategy, the precision of heading discrimination should be governed by the precision of the two sensed motion vectors and their difference; we call this the “difference-vector hypothesis.” We test this hypothesis by measuring heading discrimination thresholds for azimuth (see Fig. 1B) and elevation (see Fig. 1C) in one set of experiments and comparing these results with sensitivity to corresponding difference vectors measured in a separate set of experiments.

Figure 1.

Definitions of task parameters. A, Geometry illustrating how heading discrimination may be limited by sensitivity to the difference between the comparison and standard stimulus vectors. Solid gray arrows depict the standard and comparison stimuli presented in the two intervals of the heading discrimination task, and the dashed gray arrow is the difference between them. The dashed black arrow is the orthogonal component of the comparison stimulus, which is identical to the orthogonal component of the difference vector. Heading discrimination may be limited by sensitivity to this orthogonal component (difference-vector hypothesis). According to this hypothesis, discrimination of heading azimuth in the horizontal plane of the head would be limited by sensitivity along the interaural axis (B, dashed arrow), and discrimination of heading elevation would be limited by sensitivity along the dorsoventral axis (C, dashed arrow).

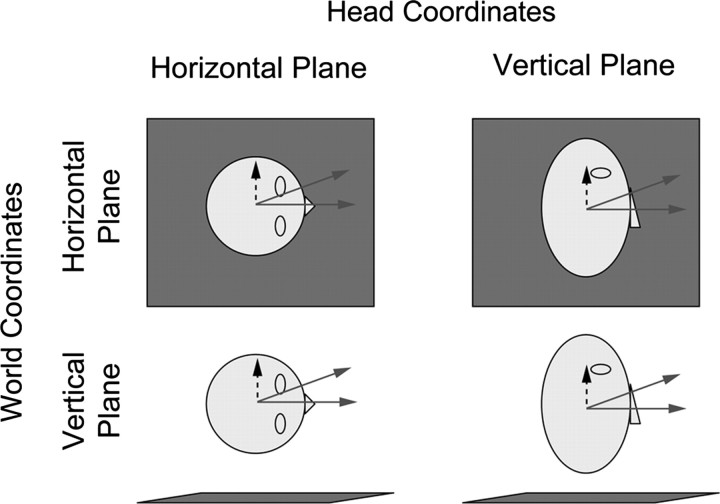
We also investigate how heading estimation depends on movement direction relative to the head and world. During earth-vertical (EV) movements, inertial acceleration acts as an increment on the pedestal of gravitational acceleration (see Fig. 2, bottom), whereas during earth-horizontal (EH) movements, acceleration is perpendicular to gravity, so there is no pedestal (see Fig. 2, top). Thus, one might expect heading sensitivity to depend on movement direction in world coordinates: specifically, less sensitivity for earth-vertical than for earth-horizontal movements. We call this the “gravitational-pedestal hypothesis.” Additionally, one might expect heading sensitivity to depend on movement direction in head coordinates because utricular sensitivity to horizontal plane motion (see Fig. 2, left) is reportedly higher than saccular sensitivity to vertical plane motion (see Fig. 2, right) (Fernández and Goldberg, 1976a). We call this the “head-centric hypothesis.”

Figure 2.

Head and world coordinate combinations. Each panel shows the plane in which discriminations were made. The gray square represents the ground plane, i.e., the plane orthogonal to gravity. When subjects are oriented upright with respect to gravity, head and world coordinates are aligned (top left, bottom right). In side-down orientations, head and world coordinates are dissociated (top right, bottom left). As in Figure 1, the solid arrows illustrate example standard (straight ahead) and comparison (deviant) heading stimuli, whereas the dashed arrows indicate the corresponding axis for coarse direction and amplitude discrimination.

Previous psychophysical studies have reported that perceptual sensitivity depends on movement direction in both head (Benson et al., 1986) and world coordinates (Melvill-Jones and Young, 1978), but these studies did not use a within-subjects design, so it is difficult to assess relative sensitivity across conditions. They also confounded effects of movement direction in head and world coordinates with effects of body orientation. Consequently, the relative influence of these factors remains poorly understood. Our experimental design (see Fig. 2) allows us to distinguish these effects and test the above-mentioned hypotheses. By conducting all experiments in the same subjects using the same apparatus, we ensure that differences in performance across conditions are attributable to factors of interest rather than differences between groups, procedures, or equipment. Our findings support the difference-vector and head-centric hypotheses and not the gravitational-pedestal hypothesis. Furthermore, comparison of vestibular and visual heading discrimination reveals modality-independent effects of body orientation.

Materials and Methods

Equipment

Experiments were conducted using a 6-degree-of-freedom motion platform (Moog 6DOF2000E). Subjects were seated in a padded racing seat mounted on the platform. A five-point harness held their bodies securely in place. A custom-fitted plastic mask secured the head against a cushioned mount, thereby holding head position fixed relative to the chair. In some conditions, the chair was rotated 90° to position the subject in a side-down orientation relative to gravity. Sounds from the platform were masked by playing white noise in the subjects' headphones. Responses were collected using a button box. These experiments were conducted in complete darkness. We describe our results as reflections of vestibular function, but we cannot eliminate the possibility that subjects also used somatosensory cues arising from the chair/harness to do the task.

We also measured heading discrimination based on visual signals. We did so to determine whether body orientation relative to gravity has a general effect that emerges in both vestibular and visual measurements or whether its effect is restricted to the vestibular system. During the visual experiment, subjects viewed the optic flow stimulus on a projection screen (149 × 127 cm) located ∼70 cm in front of the eyes (for details, see Fetsch et al., 2009; Gu et al., 2010). The scene was rendered stereoscopically and viewed through CrystalEyes shutter glasses with a 60 Hz refresh rate for each eye. The field of view through the glasses was ∼70° × 90°.

Experimental procedures

Heading discrimination.

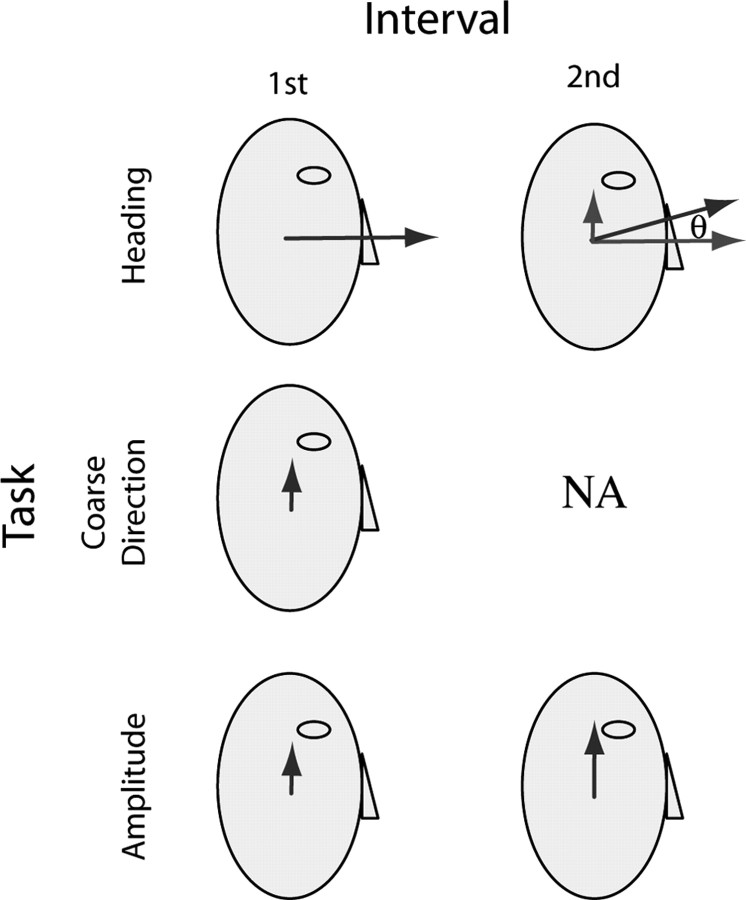
This task measures the azimuth and elevation heading thresholds in degrees (see Fig. 3, top, θ). On each trial, subjects experienced two consecutive forward movements. For azimuth discrimination, they indicated whether the second movement was leftward or rightward relative to the first. For elevation discrimination, they indicated whether the second movement was upward or downward relative to the first. When rolled onto their side, the subjects were specifically instructed to make their judgments relative to their head/body. For azimuth discrimination, subjects were instructed to report “left or right for you, which is now up or down in the world”; for elevation discrimination, the instructions were “up or down for you, which is right or left in the world.”

Figure 3.

Schematic of the three discrimination tasks. Dark gray vectors indicate the acceleration stimulus in each interval for each task. In the heading task (top row), observers indicated whether the acceleration direction in the second interval was up or down relative to the first; the correct response would be “up” in this case. Acceleration amplitude was the same in both intervals, but angle of deviation (θ) of the comparison stimulus (second interval above) relative to straight ahead was varied from trial to trial to find threshold. Light gray arrows show the straight-ahead standard stimulus and the vertical difference vector on which discrimination judgments should depend according to the difference-vector hypothesis (see Fig. 1). The coarse direction task (middle row) was a single-interval task in which observers indicated whether the acceleration was up or down along the vertical (dorsoventral) axis; the correct response would be “up” in this case. Acceleration magnitude was varied to find threshold. In the amplitude task (bottom row), observers indicated whether the acceleration in the second interval was stronger or weaker than the first; the correct response would be “stronger” in this case. Magnitude of the standard acceleration stimulus was fixed and that of the comparison stimulus was varied to find threshold. Although the figure illustrates stimuli in the vertical plane of the head, in which direction judgments were “up” or “down,” experiments were also performed in the horizontal plane, in which direction judgments were “left” or “right”. In the horizontal plane, coarse direction and amplitude tasks presented stimuli along the lateral (interaural), rather than vertical, axis.

Each 1 s translation had a Gaussian speed profile, a displacement of 13 cm, peak velocity of ∼0.3 m/s, and peak acceleration/deceleration of ∼1.13 m/s²; these parameters were identical in the two intervals. In each trial, there was one “standard” straight-ahead movement (along the naso-occipital axis) and a “comparison” movement that deviated from straight ahead in either the horizontal or vertical plane (azimuth and elevation, respectively). The order of presentation of the standard and comparison movements was randomized across trials.

The angle of deviation of the comparison movement was varied according to a staircase procedure (Cornsweet, 1962). The staircase began at the largest deviation angle, ±32°. The deviation angle was reduced to one-half its current value 30% of the time after correct responses and was increased to double its current value 80% of the time after incorrect responses. The minimum comparison angle was ±0.25°. This staircase rule converges to the 73% point of the psychometric function. The comparison angle was positive on 50% of trials and negative on the other 50%. Each subject ran 600 trials in each of four conditions (see Fig. 2): discrimination in the horizontal and vertical planes of the head (azimuth and elevation, respectively) with the body oriented upright and right-ear down. For all experiments, conditions were run in separate blocks of 150 trials each, and the order of blocks was pseudorandom in a given 1 h session.

To determine whether there are general effects of manipulating body orientation that are not specific to vestibular function, an identical heading experiment was conducted on a subset of subjects using visual instead of vestibular self-motion stimuli. Each subject ran 600 trials in each of four conditions (see Fig. 2): azimuth and elevation discrimination while oriented upright and right-ear down. The visual stimulus simulated forward self-translation (i.e., expanding optic flow) through a rigid volume (25/100 cm, near/far clipping planes) of small frontoparallel triangles (1 cm base/height) distributed uniformly in a volume 130 cm wide, 150 cm tall, and 75 cm deep, with a density of 0.01 elements/cm³. From frame to frame, 70% of the triangles moved coherently to simulate self-translation, and 30% were redrawn in a random location (70% motion coherence). We used 70% instead of 100% motion coherence to more closely equate the reliabilities of visual and vestibular heading estimates (Ernst and Banks, 2002; Fetsch et al., 2009).

Coarse direction discrimination.

This task measures sensitivity to direction of acceleration along an axis orthogonal to straight ahead (Fig. 1A–C, dashed black lines). Subjects experienced a single movement (see Fig. 3, middle row) and indicated whether the movement was in the positive or negative direction along that axis. For movements along the interaural (IA) axis, they indicated whether it was leftward or rightward; along the dorsoventral (DV) axis, they indicated upward or downward. Each 1 s translation had a Gaussian speed profile, similar to the heading experiment. Displacement (and thus peak speed and acceleration) was varied from trial to trial according to the staircase procedure described above. Similar to the heading discrimination experiment, each subject ran 600 trials in each of four conditions (Fig. 2): movement along the IA and DV axes with the body oriented upright and right-ear down.

Amplitude discrimination.

In this task, subjects experienced two movements in the same direction and they indicated the greater of the two (Fig. 3, bottom row). The pedestal is the motion that is common to the two intervals. The increment (or decrement) is the motion added to (or subtracted from) the pedestal. The just-noticeable stimulus increment relative to a nonzero pedestal stimulus is called the “increment threshold.” Subjects experienced two consecutive movements in the same direction along either the IA or DV axis and indicated which movement had the greater amplitude. Each 1 s movement had a Gaussian speed profile. The peak acceleration of the standard movement was 0.3 m/s², and the comparison movement was either larger or smaller. Peak acceleration of the comparison was varied according to the same staircase procedure described above. The order of the standard and comparison movements was randomized from trial to trial. Each subject ran 900 trials in each of the four conditions (Fig. 2): movement was along the IA and DV axes with body oriented upright or right-ear down. Importantly, direction of motion was fixed within each block of trials but varied across blocks such that, for each condition, half of the trials measured thresholds for leftward/upward movements and half for rightward/downward movements.

Subjects

Ten subjects (six males) aged 19–34 years with no history of vestibular deficits participated in the experiments. All 10 participated in the vestibular heading discrimination experiment. Seven of them (five males) participated in the coarse direction and amplitude experiments, allowing us to compare performance across tasks for these subjects. Five of the subjects (three males) participated in the visual discrimination experiment. Informed consent was obtained from all participants and all procedures were reviewed and approved by the ethics committee of Washington University.

Analysis

All experiments used a two-alternative, forced-choice procedure (2AFC) and can therefore be analyzed in a similar manner. The percentage of responses for one alternative was plotted as a function of the stimulus variable in question. A cumulative Gaussian was fit to those points using a maximum-likelihood criterion, allowing for a lapse rate of up to 5% (Wichmann and Hill, 2001). Threshold was defined as the standard deviation (σ) of the best-fitting cumulative Gaussian.

By comparing performance within each subject but across the head/world orientation combinations illustrated in Figure 2, we can parse the effects of movement direction in head and world coordinates and of body orientation relative to gravity. We use a 2 × 2 repeated-measures ANOVA that groups the data in three ways (Fig. 2): (1) along the columns, which tests for an effect of movement direction in head coordinates, (2) along the rows, which tests for an effect of movement direction in world coordinates, and (3) along diagonals, which tests for an effect of body orientation relative to gravity. This analysis was used to test the gravitational-pedestal and head-centric hypotheses.

Finally, coarse direction thresholds were used to predict heading thresholds. As illustrated in Figure 1, this was done to test the difference-vector hypothesis, which assumes that the heading task can be reduced to calculating the difference vector between acceleration stimuli in the two intervals and determining the direction of this vector. Note that the length of the difference vector and the orthogonal component are approximately the same for small angles but diverge as the heading angle increases. Nevertheless, it is the component of the difference vector orthogonal to straight ahead that carries information about heading direction; the component parallel to straight ahead carries no information relevant to the task (i.e., it is the same for positive and negative heading angles of equal magnitude). Thus, the amplitude of the difference vector is approximately equal to sin(θ)a, where θ is the angle of the comparison stimulus in the heading task, and a = 1.13 m/s².

To compare thresholds in the heading and coarse direction tasks, it is also necessary to account for the fact that coarse discrimination was measured using a single-interval task, whereas heading discrimination was measured using a two-interval task. In a single-interval task, the value of the 84% point on the psychometric function is equal to the standard deviation of the underlying estimator. In a two-interval task, the 84% point corresponds to $\sqrt{2}$ times the standard deviation of the underlying estimator (Ernst and Banks, 2002). Therefore, the heading threshold predicted from the coarse direction threshold is as follows:

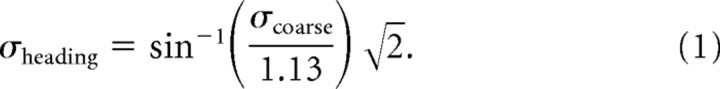Results

Heading discrimination task

The vestibular heading discrimination task (Fig. 3, top) provides a measure of sensitivity to small differences in the direction of inertial acceleration. Data from one subject are shown in Figure 4A, and group data for all observers are displayed in Figure 4B (see also Table 1). The format of these 2 × 2 figures corresponds to the head/world orientation combinations depicted in Figure 2. For a typical subject with head upright, thresholds were lower for azimuth discrimination, i.e., discrimination in the horizontal plane of the head (Fig. 4A, top left), than for elevation discrimination (Fig. 4A, bottom right). With a side-down orientation, both thresholds increased (Fig. 4A, bottom left and top right).

Figure 4.

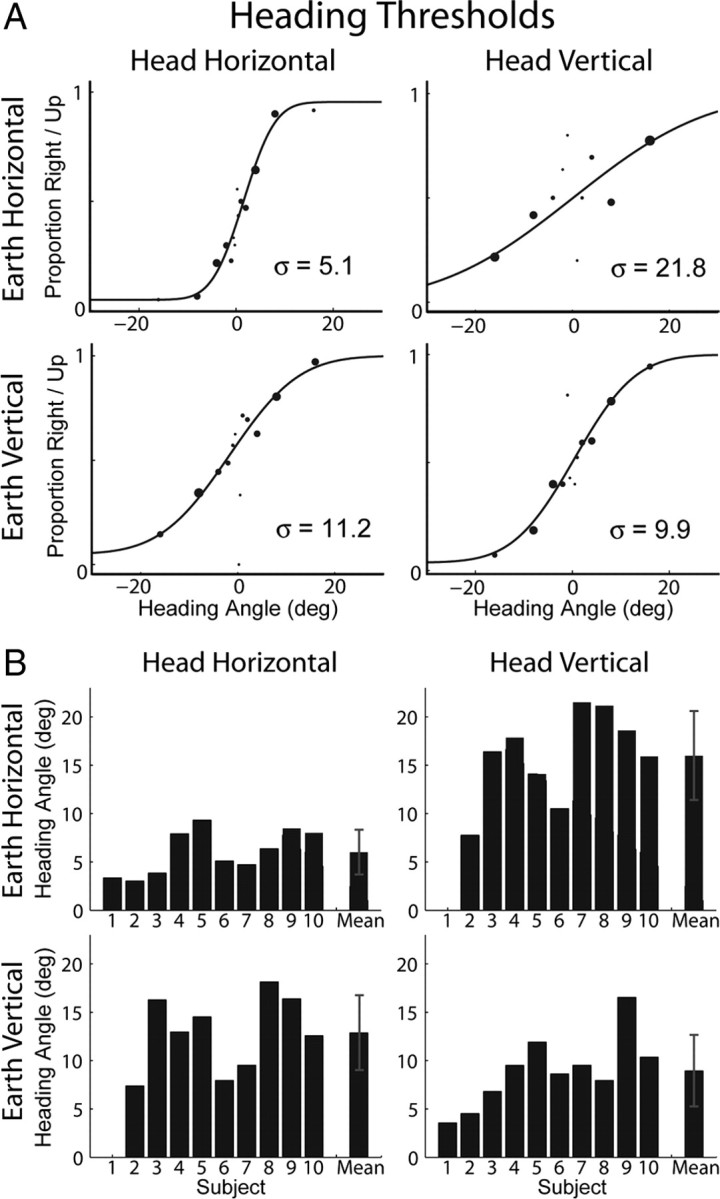
Vestibular heading thresholds. The 2 × 2 panels in A and B show data corresponding to the orientation/direction combinations depicted in Figure 2. A, Example data from an individual subject and psychometric fits to the data. Larger data points indicate more samples at that stimulus magnitude. Threshold is the standard deviation (σ) of the fitted Gaussian function. B, Thresholds for all subjects and the means across subjects. Data were not collected for subject 1 in two conditions. Error bars represent SD.

Table 1.

Mean ± SD thresholds for each condition of each vestibular experiment

	Earth horizontal/head horizontal	Earth horizontal/head vertical	Earth vertical/head horizontal	Earth vertical/head vertical
Vestibular heading
Two-interval	6.01 ± 2.31°	15.97 ± 4.60°	12.86 ± 3.88°	8.93 ± 3.70°
Equivalent one-interval threshold	4.25 ± 1.63°	11.29 ± 3.25°	9.09 ± 2.74°	6.31 ± 2.62°
Coarse discrimination (one-interval)	0.063 ± 0.025 m/s2	0.110 ± 0.029 m/s2	0.093 ± 0.023 m/s2	0.097 ± 0.034 m/s2
Amplitude discrimination
Two-interval	0.126 ± 0.071 m/s2	0.124 ± 0.059 m/s2	0.104 ± 0.054 m/s2	0.117 ± 0.078 m/s2
Equivalent one-interval threshold	0.089 ± 0.05 m/s2	0.088 ± 0.042 m/s2	0.074 ± 0.038 m/s2	0.083 ± 0.055 m/s2

Thresholds correspond to the 84% correct level for each task. Note that heading and amplitude discrimination thresholds were obtained from two-interval tasks (Fig. 3). To facilitate comparison across tasks, these thresholds have also been expressed as equivalent one-interval thresholds (computed by dividing by $\sqrt{2}$). This is because, in a single-interval task, the 84% correct threshold is equal to the SD of the underlying estimator, whereas in a two-interval task, it is $\sqrt{2}$ times the standard deviation of the underlying estimator (Ernst and Banks, 2002).

This pattern of results was quite consistent across subjects. Mean thresholds were lowest for discrimination in the horizontal plane of the head when observers were upright (mean ± SD, 6.01 ± 2.31°) (Fig. 4B, top left), and performance was worst for discrimination in the vertical plane of the head during side-down orientation (mean ± SD, 15.97 ± 4.60°) (Fig. 4B, top right). For mean values for the other two conditions, see Table 1.

Mean thresholds, grouped according to head coordinates, world coordinates, and body orientation, are shown in Table 2(second column). The precision of vestibular heading estimates depended strongly on the direction of movement in head coordinates (F_(1,8) = 16.38, p = 0.004). This means that performance depended on how the inertial acceleration vector is oriented with respect to the head. Thresholds were consistently lower for discrimination in the horizontal than vertical plane of the head (Table 2, second column, first row), suggesting that performance is limited by mechanisms that operate in head coordinates, such as the utricular and saccular otolith organs (Fernández and Goldberg, 1976a).

Table 2.

Mean thresholds and p values associated with ANOVA

	Visual heading	Vestibular heading	Coarse direction	Amplitude
Head coordinates	Horizontal (IA) = 2.7°	Horizontal (IA) = 9.3°	IA = 0.079 m/s2	IA = 0.115 m/s2
	Sagittal (DV) = 3.0°	Sagittal (DV) = 12.3°	DV = 0.104 m/s2	DV = 0.121 m/s2
	p = 0.40	p = 0.004	p value <0.001	p = 0.39
World coordinates	EH = 2.7°	EH = 10.7°	EH = 0.087 m/s2	EH = 0.125 m/s2
	EV = 2.9°	EV = 10.8°	EV = 0.095 m/s2	EV = 0.111 m/s2
	p = 0.60	p = 0.94	p = 0.24	p = 0.021
Body orientation	Upright = 2.6°	Upright = 7.5°	Upright = 0.080 m/s2	Upright = 0.121 m/s2
	Side-down = 3.0°	Side-down = 14.4°	Side-down = 0.102 m/s2	Side-down = 0.114 m/s2
	p = 0.009	p < 0.001	p = 0.009	p = 0.95

Columns indicate the different tasks, and rows indicate the mean comparisons, grouped according to columns (head coordinates), rows (world coordinates), and diagonals (body orientation) in Figs. 2, 4, 5, and 7. Bold indicates p < 0.01. Thresholds correspond to the 84% correct level for each task.

The precision of vestibular heading estimates also depended on body orientation (F_(1,8) = 31.49, p < 0.001). In other words, performance depended on how the gravitational acceleration vector was oriented with respect to the head. Thresholds were consistently lower during upright than side-down orientation regardless of movement direction (Table 2, second column, third row).

However, performance did not depend on movement direction in world coordinates, i.e., how the inertial and gravitational acceleration vectors were oriented relative to one another (F_(1,8) = 0.006, p = 0.94). This last result is contrary to the gravitational-pedestal hypothesis, suggesting that the nervous system compensates for the influence of gravity on vestibular signals initially encoded by the otolith organs. This result is remarkable because it means that humans are not limited in their ability to perceive inertial acceleration by the presence of gravity, a very useful adaptation for the world in which we live.

The means and standard deviations of “visual” heading thresholds—grouped according to head coordinates, world coordinates, and body orientation—are also summarized in Table 2 (first column). In contrast with the vestibular results, there was no effect of movement direction in either head coordinates (F_(1,4) = 0.89, p = 0.40) or world coordinates (F_(1,4) = 0.32, p = 0.60). Similar to the vestibular results, there was a significant effect of body orientation (F_(1,4) = 23.37, p = 0.009) with lower thresholds in the upright orientation compared to side-down. The similarity of this effect for visual and vestibular heading discrimination suggests a nonspecific effect of body orientation on sensory processing for self-motion perception (see Discussion).

Coarse direction discrimination task

The coarse task (Fig. 3, middle) measures directional sensitivity along a particular axis, which is of interest because it provides a way to test the hypothesis that vestibular heading thresholds depend on sensitivity to inertial acceleration along the axis orthogonal to straight ahead, i.e., the difference-vector hypothesis. In agreement with this hypothesis, we observed very similar patterns of results in the coarse direction and heading tasks.

Individual subject data and group data are plotted in Figure 5, A and B, respectively, in a format identical to that used for the heading discrimination results, except that thresholds are expressed in units of meters per square seconds instead of degrees (Tables 1; 2, third column). Coarse direction thresholds averaged 0.063 ± 0.025 m/s² (0.006 G) for inertial motion along the IA axis and 0.097 ± 0.034 m/s² (0.01 G) for inertial motion along the DV axis when the subjects were upright. As in the heading task, there was a significant effect of movement direction relative to the head (F_(1,6) = 41.22, p < 0.001), suggesting that performance is limited by mechanisms operating in head coordinates. Sensitivity also depended significantly on body orientation (F_(1,6) = 14.32, p = 0.009), but there was no effect of movement direction in world coordinates (F_(1,6) = 1.74, p = 0.24), contrary to the gravitational-pedestal hypothesis. This last result is another demonstration that the nervous system compensates for the effect of gravity (see Discussion).

Figure 5.

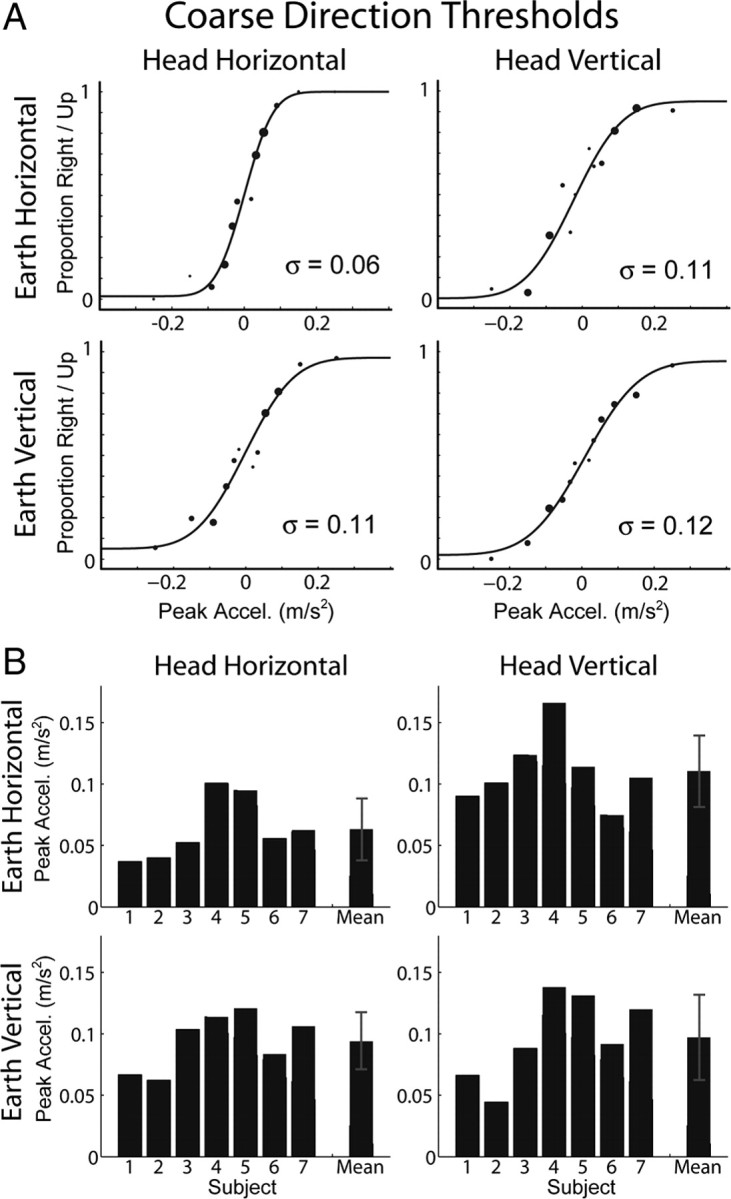
Coarse direction thresholds. The 2 × 2 panels in A and B show data corresponding to the orientation/direction combinations depicted in Figure 2. A, Example data from an individual subject and psychometric fits to the data. Larger data points indicate more samples at that stimulus magnitude. Threshold is the standard deviation (σ) of the fitted Gaussian function. B, Thresholds for all subjects and the means across subjects. Error bars represent SD.

Heading and coarse direction discrimination compared

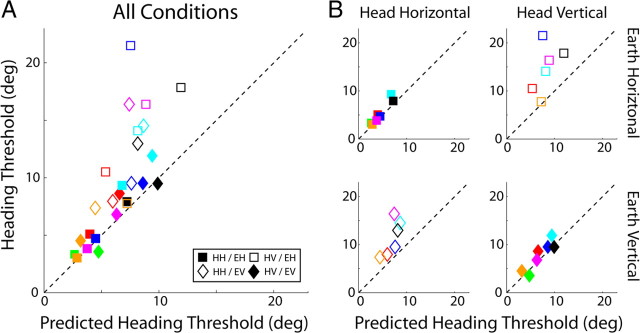
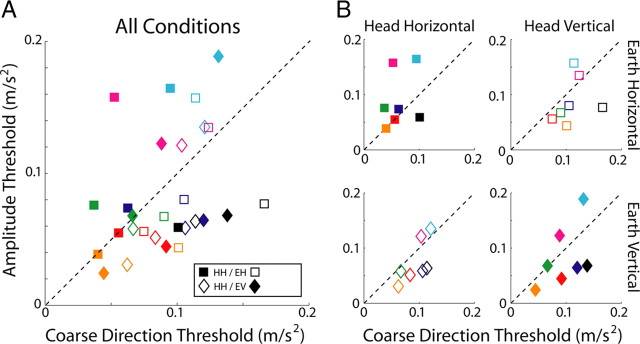
The difference-vector hypothesis (Fig. 1A) predicts that thresholds measured in the heading and coarse direction discrimination tasks will be related because heading discrimination is limited by sensitivity to the component of inertial force that is orthogonal to straight ahead. Coarse direction thresholds provide a measure of this sensitivity, so we should be able to predict heading thresholds according to Equation 1. Figure 6A plots predicted versus observed heading thresholds for the seven subjects who participated in both experiments. Almost all data points lie above the dashed line with unity slope, which means that observed heading thresholds were higher than those predicted from coarse direction thresholds according to the difference-vector hypothesis (p < 0.001, Wilcoxon's signed-rank test). Thus, observers do not seem to use the available sensory information as efficiently as possible when discriminating fine differences in heading direction. Despite this difference, predicted and observed heading thresholds are highly correlated (r = 0.77, p < 0.001) suggesting that performance in both tasks is limited to some extent by a common signal. This correspondence is consistent with the idea that noise along a particular axis scales with linear acceleration magnitude along that axis and does not depend on the sum total linear acceleration magnitude, which was different in the heading and coarse tasks.

Figure 6.

Comparison of predicted and observed heading thresholds. Each subject is a different color. Filled and unfilled symbols represent upright and side-down conditions, respectively. Squares and diamonds represent earth-horizontal and earth-vertical conditions, respectively. A, Comparison across all conditions. Predicted heading thresholds are calculated from coarse direction thresholds using Equation 1. The comparison assumes that heading performance is limited by sensitivity to the orthogonal component, i.e., the difference-vector hypothesis (see Fig. 1). The dashed line has unity slope and shows where points should lie if predicted and observed thresholds matched. HH, Head horizontal; HV, head vertical. B, Same as A but plotted separately for each orientation/direction combination depicted in Figure 2.

To examine this effect more closely, the same data are plotted separately for each of the four stimulus conditions in Figure 6B. For the two upright conditions (top left and bottom right, filled symbols), measured and predicted thresholds are strongly correlated and the slopes of the type II regression lines are close to 1 (head/earth horizontal: r = 0.96, p < 0.001, slope ± SD of 1.34 ± 0.15; head/earth vertical: r = 0.90, p = 0.005, slope ± SD of 1.21 ± 0.22), meaning that observers make efficient use of the available sensory information to judge heading when upright. Said another way, the difference-vector hypothesis predicted the data quite well when the head was upright. In contrast, in the side-down conditions (Fig. 6, open symbols), thresholds were not as well correlated and slopes were much greater than 1 (Fig. 6B, bottom left: r = 0.76, p = 0.08, slope ± SD of 2.84 ± 1.00; top right: r = 0.50, p = 0.31, slope ± SD of 3.83 ± 2.71). Overall, the ratio of observed-to-predicted heading thresholds was significantly higher (p < 0.001, Wilcoxon's rank-sum test) in the side-down condition (1.71 ± 0.46) than in the upright condition (1.14 ± 0.18), suggesting that the mechanisms underlying heading discrimination operate much less efficiently during side-down than upright orientation.

Amplitude discrimination task

Unlike the previous two tasks that measured sensitivity to the “direction” of linear self-motion, the amplitude discrimination task (Fig. 3, bottom) measured observer sensitivity to differences in the “amplitude” of inertial acceleration for fixed directions of movement. This task allows measurement of discrimination relative to a nonzero (0.3 m/s²) inertial acceleration pedestal stimulus, i.e., the increment threshold (see Materials and Methods) (Table 1). Amplitude thresholds are displayed in Figure 7 in the same format as the other tasks. Movement direction was always fixed within a block of trials, but thresholds for leftward versus rightward and upward versus downward movement were not significantly different, so data have been combined across the two opposite directions for each axis of motion. Remarkably, the effects observed in both the heading and coarse direction discrimination experiments are absent here (Table 2, fourth column). There was no significant effect of movement direction in head coordinates (F_(1,6) = 0.85, p = 0.39) and no significant effect of body orientation (F_(1,6) < 0.01, p = 0.95). There was, however, a modest effect of movement direction in world coordinates (F_(1,6) = 9.6, p = 0.021), with slightly lower thresholds for EV than EH motion. EV motion is accompanied by inertial acceleration that is collinear with the constant linear acceleration of gravity, so this surprising result is opposite to that predicted by the gravitational-pedestal hypothesis. In other words, aligning the amplitude discrimination stimuli with the gravity vector improves sensitivity slightly rather than impairing it. This is again evidence that the nervous system compensates for the influence of gravity.

Figure 7.

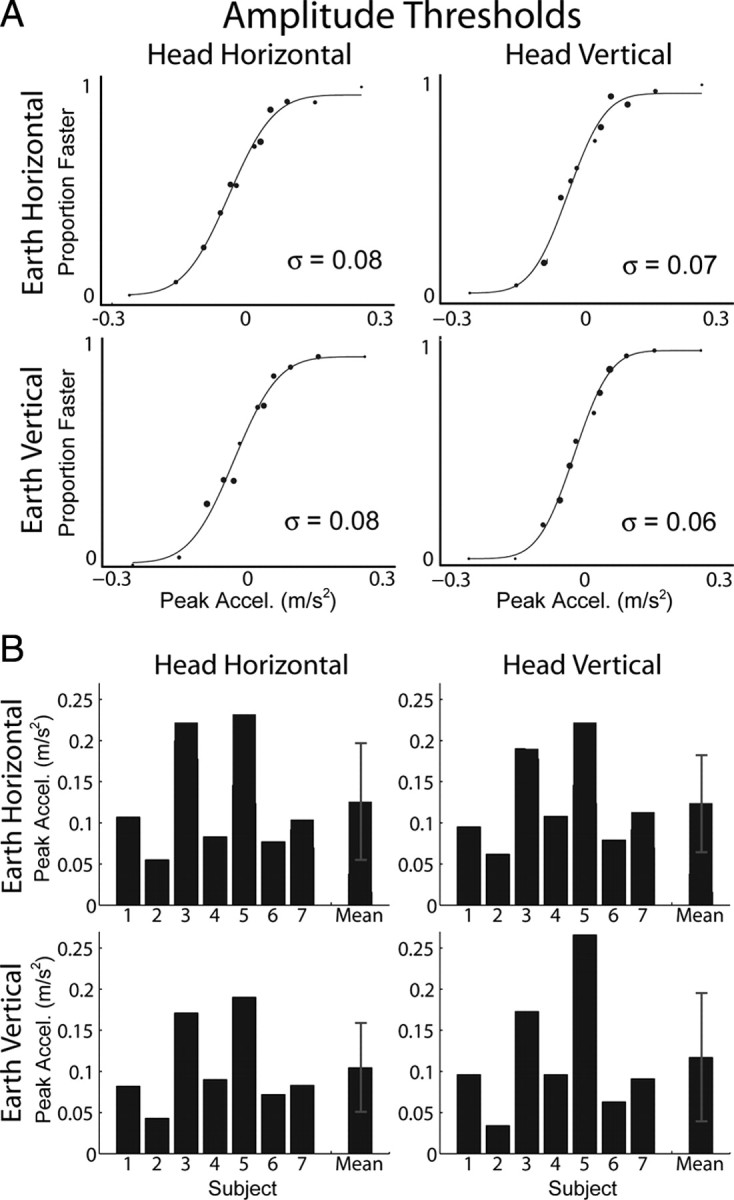
Amplitude thresholds. The 2 × 2 panels in A and B show data corresponding to the orientation/direction combinations depicted in Figure 2. A, Example data from an individual subject and psychometric fits to the data. Larger data points indicate more samples at that stimulus magnitude. Threshold is the SD (σ) of the fitted Gaussian function and represents the acceleration increment (or decrement) relative to the pedestal acceleration (0.3 m/s²) that was just noticeable. B, Thresholds for all subjects and the means across subjects. Error bars represent SD.

Figure 8 compares amplitude and coarse direction thresholds on a subject-by-subject basis. The correlation between amplitude and coarse thresholds is much weaker (Fig. 8A, r = 0.35, p = 0.07) than the corresponding correlation between coarse direction and heading thresholds (Fig. 6A). The correlation is slightly stronger during side-down (Fig. 8A, unfilled symbols, r = 0.50, p = 0.07) than upright (Fig. 8A, filled symbols, r = 0.33, p = 0.24) orientation.

Figure 8.

Comparison of amplitude and direction thresholds. Each subject is a different color. Filled and unfilled symbols represent upright and side-down conditions, respectively. Squares and diamonds represent earth-horizontal and -vertical conditions, respectively. A, Comparison across all conditions. Amplitude discrimination thresholds were measured using a two-interval task and were divided by $\sqrt{2}$ before comparison with coarse direction thresholds measured in a single-interval task (see also Table 1). The dashed line has unity slope and shows where points would lie if coarse direction and amplitude thresholds matched. HH, Head horizontal; HV, head vertical. B, Same as A but plotted separately for each orientation/direction combination depicted in Figure 2.

One can think of these two tasks on a continuum. Coarse discrimination is similar to detecting a signal against a pedestal of zero, whereas amplitude discrimination is similar to detecting a signal against a nonzero pedestal. The effect of pedestals on sensory performance has been well studied in visual contrast discrimination and other sensory discrimination tasks (Mather and Smith, 2002; Solomon, 2009). For example, in visual contrast discrimination—detecting an increase in contrast against a pedestal contrast—one observes that increment threshold is more of less proportional to pedestal contrast when the pedestal is well above threshold (Nachmias and Sansbury, 1974); this is Weber's Law, in which increment threshold is proportional to the pedestal. In our case, amplitude thresholds were not significantly different from coarse direction thresholds (p = 0.27, Wilcoxon's signed-rank test) (Fig. 8A), although the pedestal is higher. There are three possible explanations for the failure to observe an effect of the pedestal. (1) Weber's Law may not apply to vestibular amplitude discrimination. (2) We tested two pedestal values: zero in coarse discrimination and some nonzero values in amplitude discrimination. Perhaps those values straddled the dipper function (a decrease in increment threshold when the pedestal increases from zero to small values) (Nachmias and Sansbury, 1974), and so we did not observe a pedestal effect. (3) The coarse discrimination task does not fit neatly into this framework because it involves discriminating direction rather than discriminating movement against no movement.

Neurometric simulations

Assuming that heading and coarse direction discrimination are mediated by the same populations of neurons, we ran simulations to gain insight into how heading and coarse discrimination performance might be influenced by the tuning properties and noise characteristics of these neurons. We did not intend to represent a particular population at a particular anatomical location (e.g., afferents vs central neurons in brainstem, cerebellum, or cortex). Instead, we used receiver operating characteristic (ROC) analysis (Britten et al., 1992) to estimate heading and coarse discrimination thresholds based on hypothetical neural response properties that are fairly generic.

We simulated responses of an idealized pair of neurons—a so-called “neuron/anti-neuron pair”—with preferred directions along the IA or DV axis. The anti-neuron is identical to the first member of the pair but has the opposite direction preference. Our simulated neurons were cosine tuned to the direction of linear acceleration with response scaled by acceleration magnitude. This is similar to the response characteristics of otolith afferent neurons (Fernández and Goldberg, 1976a,b,c). Note that central vestibular neurons also exhibit approximately cosine tuning to direction of motion (Angelaki and Dickman, 2000; Shaikh et al., 2005; Chen-Huang and Peterson, 2006), but their amplitude response is not yet characterized, a point to which we return below. The mean firing rate of each neuron is given by the following:

where θ is stimulus direction relative to the preferred direction of the neuron in degrees, m is the magnitude of acceleration in meters per square seconds, d₀ is the resting discharge in spikes per seconds, and s is the sensitivity of the neuron in spikes per seconds/meters per square seconds. To compute the ROC curve for a given stimulus, we assumed that the firing rates of the neuron and anti-neuron could be described by two distributions with means given by the tuning curve for each neuron (Eq. 2) and variance determined by one of two noise models: Poisson or Gaussian with fixed variance as described below.

We then sampled the firing rates of the neuron and anti-neuron by taking random draws from these distributions. These random draws were compared with a range of criterion firing rates, and, for each criterion, we plotted the probability that the response of the anti-neuron exceeded criterion [P(null > crit)] versus the probability that the response of the neuron exceeded criterion [P(pref > crit)]. The result is an ROC curve, and the area under this curve indexes the proportion of correct responses by an ideal observer using these neural responses to make decisions in a 2AFC task for a given stimulus intensity. This procedure was repeated to calculate the proportion correct for a range of stimuli. A neurometric function was then fit to these points. For illustrations explaining the neuron/anti-neuron ROC analysis, see Britten et al. (1992, their Fig. 5) or Gu et al. (2007, their Fig. 4).

For simulations of coarse direction discrimination, movement was always in the preferred or null directions of the neuron/anti-neuron pair, and stimulus magnitude was varied (for simulation parameters, see Table 3). For simulations of heading discrimination, stimulus magnitude was held constant, but stimulus direction was varied in fine steps around the point of the cosine-tuning curves in which the slope is steepest (90° away from the peak responses of the neuron and anti-neuron) and sensitivity to fine direction differences is greatest (Purushothaman and Bradley, 2005; Jazayeri and Movshon, 2006; Gu et al., 2007). With Poisson noise, the standard deviation is proportional to the mean firing rate, so the maximal discriminability of a neuron does not occur at the heading that corresponds to the steepest point of the tuning curve because the signal-to-noise ratio (mean/SD) is not lowest at that point; rather, the point of maximal sensitivity occurs at slightly lower firing rates. This effect is small, however, and the outcome of our simulations was essentially unchanged when discrimination occurred around points slightly away from the maximal slope of the tuning curve.

Table 3.

Neurometric simulation parameters

d-zero (resting discharge)	80 spikes/s
s (sensitivity)	30, 45, 60, 75, 90 (spikes/s)/(m/s2)
sigma (Gaussian noise)	9 spikes/s
n (hyperbolic exponent)	2
m50 (hyperbolic inflection)	0.17
θ (heading simulation)	90 ± 20° (orthogonal to preferred direction)
Magnitude (heading simulation)	1.13 m/s2
θ (coarse simulation)	0° (preferred direction)
Magnitude (coarse simulation)	0 ± 0.5 m/s2
Number of samples (each simulation)	1000

Simulations were repeated under various conditions to investigate the influence of neuronal tuning and noise properties. In particular, we first investigated whether heading and coarse discrimination were comparable for the simplest possible model: the amplitude–response function (R as a function of m; Eq. 2) was linear and the noise was Gaussian with fixed variance. We also allowed the noise properties of the neurons to be Poisson (i.e., variance equal to mean), similar to what is observed in cortical neurons (Tolhurst et al., 1983; Celebrini and Newsome, 1994). In addition, we allowed the amplitude–response function to be nonlinear, using a hyperbolic-ratio model:

where n is the exponent, and m₅₀ is the inflection point (for parameters, see Table 3). This function exhibits an expansive nonlinearity at low stimulus magnitudes (<m₅₀) and saturation at high magnitudes. m_nonlinear was used in Equation 2 to implement the nonlinear response. We included the nonlinearity for a couple of reasons. First, all neurons operate within a limited dynamic range of firing rates. Second, given cosine-tuned neurons, a nonlinear amplitude–response function was the only way to obtain substantially different firing rates in the heading and coarse discrimination simulations. This nonlinear amplitude–response function describes how contrast affects the activity of orientation-selective neurons in primary visual cortex (Albrecht and Hamilton, 1982). However, this property has not yet been characterized for central vestibular neurons. Note that the nonlinearity of Equation 2 will cause the amplitude–response function to scale to a lower asymptote for non-optimal directions of motion, similar to contrast–response functions observed in visual cortex in which this characteristic is presumed to reflect a contrast-gain control mechanism (Heeger, 1992).

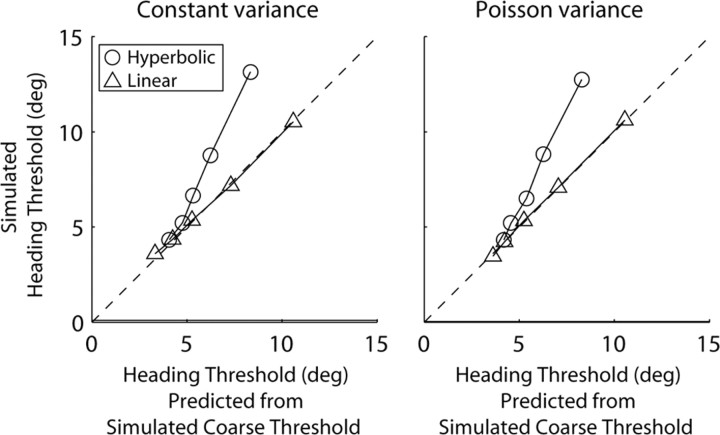
With a linear amplitude–response function and constant Gaussian-distributed noise, heading and coarse discrimination thresholds corresponded closely, as described by Equation 1 (Fig. 9, left, triangles). This is consistent with the intuition, illustrated in Figure 1, that heading discrimination is limited by sensitivity to the orthogonal component of inertial force. The simulation results closely parallel the physical predictions because the cosine-tuning function of our hypothetical neuron (Eq. 2) essentially implements a vector decomposition of inertial acceleration. This in turn mimics the behavior of otolith afferents, which function as one-dimensional accelerometers. Trial-to-trial variability of firing rate has yet to be quantified for vestibular afferents, but it may be the case that regular afferent neurons exhibit constant Gaussian noise properties.

Figure 9.

Output of neurometric simulations. Each point plots output for hypothetical neuron/anti-neuron pairs with different tuning and noise properties. The dashed line has unity slope and shows where points would lie if heading thresholds matched predicted heading thresholds; predictions are calculated from coarse direction thresholds using Equation 1, similar to Figure 6. The panels on the left and right show output for neurons with constant Gaussian distributed noise and Poisson distributed noise, respectively. Triangles show output for linear amplitude response, and circles show output for amplitude response described by the hyperbolic ratio function (Eq. 3). The five points of each type in each panel show output for five different neural sensitivities, i.e., different values of s in Equation 2 (for exact values, see Table 3). High sensitivity yields low thresholds.

To assess whether the noise model of neural activity affects the model predictions, the simulation was also run with Poisson-distributed noise. One might expect Poisson variability to influence heading and coarse neuronal thresholds differently. Coarse neuronal thresholds are calculated by comparing firing-rate distributions around the maximum and minimum firing rates, elicited by motion in the preferred and null directions, respectively. If the noise is Poisson, these distributions will have maximum and minimum variance. In contrast, heading discrimination results from comparing firing-rate distributions with means just greater or less than the baseline firing rate that is elicited by movement directions near the steepest part of the cosine-tuning curve (90° away from the preferred direction). Consequently, the resulting distributions should have approximately equal variance.

Simulation results showed that the close correspondence between heading and coarse discrimination thresholds remained even when Poisson-distributed noise was used in the simulation (Fig. 9, right, triangles). This is because, for low-amplitude movements like those used in the coarse task, the maximum and minimum firing rates of the cosine-tuning curve do not deviate very much from baseline. Provided a much larger-amplitude movement (like the one used in the heading task), the same difference in mean response can be elicited by small directional differences orthogonal to the preferred direction. In other words, heading and coarse neuronal thresholds are influenced similarly by Poisson-distributed noise because they are calculated based on very similar underlying firing-rate distributions.

With the nonlinear amplitude–response function (Eq. 3), we found that heading thresholds were larger than coarse direction thresholds (Fig. 9, circles), similar to what we observed in our experiments (Fig. 6). This occurred in the simulation because the expansive nonlinearity for low magnitudes boosted sensitivity in the coarse task simulation, whereas the saturating nonlinearity at high magnitudes depressed sensitivity in the heading simulation.

These simulations suggest that the modest discrepancy during upright orientation between measured heading thresholds and those predicted from coarse direction discrimination (Fig. 6, filled symbols) might be accounted for by an amplitude–response nonlinearity in the neural representations. Of course, there may be other mechanisms that could account for the disparity between observed and predicted thresholds. We note that the amplitude–response nonlinearity will not account for the larger discrepancies observed in the side-down orientation (Fig. 6, unfilled symbols) unless the parameters of Equation 3 were themselves dependent on orientation relative to gravity.

Discussion

To characterize human vestibular sensitivity to linear self-motion, we used three different tasks (Fig. 3), and, for each task, we tested all four combinations of movement direction in the horizontal and vertical planes of the head and world (Fig. 2). This comprehensive experimental design allowed us to dissociate the effects of movement direction in head and world coordinates and body orientation, something that has not been done previously. We observed a close relationship between conventional measures of vestibular sensitivity (i.e., coarse direction discrimination) and vestibular heading sensitivity, which is directly relevant to control of locomotion and vehicle guidance.

We hypothesized that heading thresholds would depend on sensitivity to the difference between two motion vectors, which we formalized as the difference-vector hypothesis (Fig. 1). Indeed, we found that heading thresholds were predictable from those measured in the coarse direction task (at least in the upright orientation), which supports the difference-vector hypothesis; with side-down orientation, the predictions were less accurate. World-centric direction had little influence on vestibular heading percepts, which argues against the gravitational-pedestal hypothesis. Instead, vestibular direction thresholds depended on movement direction relative to the head, which supports the head-centric hypothesis. Greater sensitivity to head-centric azimuth than elevation persisted in the side-down orientation and did not reverse. In contrast, visual heading sensitivity did not depend on movement direction in either head or world coordinates. As we said previously, it is remarkable that humans are not limited by the presence of gravity in their ability to perceive inertial accelerations, and this is a useful adaptation for the world in which we live.

We also found that both vestibular and visual directional sensitivity was best with the head and body upright, which shows that the nervous system is specialized to operate most efficiently in the most common orientation. Unlike direction discrimination, however, amplitude discrimination did not depend on movement direction in head coordinates or body orientation. We now consider these findings in more detail relative to the existing literature.

Heading and coarse direction discrimination

The finding that vestibular direction thresholds depend on movement direction relative to the head—lower for discrimination along the IA than DV axis—is consistent with previous reports (Benson et al., 1986). Our coarse direction discrimination task is very similar to the one used by Benson and colleagues, but there are some notable methodological differences between our study and theirs: (1) the duration of the movement in their experiment was 3 s instead of 1 s, and (2) translation was always in the earth-horizontal plane (i.e., perpendicular to gravity). Because Benson and colleagues only measured sensitivity in the earth-horizontal plane (two of our four stimulus conditions) (Fig. 2, top row), they could not determine whether differences in sensitivity were caused by movement direction in head coordinates or body orientation.

Benson et al. (1986) reported 67% correct thresholds of 0.06 m/s² for discriminating movement along the IA axis in upright subjects and 0.15 m/s² for DV axis movement in supine (back-down) subjects. For the corresponding conditions in our experiment, we observed 84% correct thresholds of ∼0.06 and 0.1 m/s² for the IA and DV axes, respectively (Table 1), values that are quite similar to those reported by Benson and colleagues. As they suggested, the greater sensitivity along the IA than the DV axis may be a byproduct of the neurophysiology of the otolith organs: utricular afferents, which respond to forces in the horizontal plane of the head, are more sensitive than saccular afferents, which respond to forces in the sagittal plane (Fernández and Goldberg, 1976a).

Neither heading nor coarse direction discrimination thresholds depended on movement direction in world coordinates and were not elevated when the inertial acceleration was collinear with gravity. This finding is surprising given that the otoliths respond equivalently to gravitational and inertial accelerations. Our findings suggest the existence of mechanisms that compensate for the effect of gravity on the peripheral sense organs. Similar effects have been reported previously (Angelaki et al., 1999, 2004; Merfeld et al., 2005; Yakusheva et al., 2007). Indeed, reliable encoding of linear self-motion requires a sensory system that is equally sensitive to a change in linear acceleration regardless of whether this is superimposed on a baseline acceleration of 0 or 9.8 m/s² (i.e., perpendicular or parallel to gravity). In support of this compensation, approximately equal sensitivity to inertial acceleration is observed in the zero-gravity environment of space and on earth (Arrott et al., 1990).

We also found that heading and coarse discrimination thresholds both depended on body orientation relative to gravity with lower thresholds for upright than side-down orientation. This was also observed for visual heading discrimination. Better performance with the head and body upright is not surprising because humans have much more experience estimating movement direction while upright. Because this effect is observed for both visual and vestibular heading discrimination, it may be attributable to body-orientation dependence of multimodal spatial-orientation mechanisms, not modality-specific sensory mechanisms. It is also possible that subjects had elevated thresholds in the side-down condition because directional tasks become more difficult when head/body and world coordinates do not match.

Alternatively, the body-orientation effect could be attributable to cognitive factors. For example, observers may simply be less comfortable physically and therefore less able to concentrate when oriented side-down relative to gravity. This explanation is, however, inconsistent with the results of the amplitude-discrimination experiment in which no effect of body orientation was observed, and it cannot explain the observation that the body-orientation effect is larger for vestibular heading discrimination than for coarse direction discrimination (Table 2, bottom row; Fig. 6B, top right, bottom left).

Another possible explanation for better performance when upright is that observers' ability to resolve gravito-inertial force into separate components may depend on body orientation. Coarse discrimination may rely more directly on linear acceleration signals and may not depend on estimates of the three-dimensional motion trajectory. To evaluate this hypothesis, it would be necessary to explicitly investigate to what extent observers' ability to resolve net linear acceleration into gravitational and inertial components depends on body orientation.

Finally, our finding that visual heading discrimination did not depend on movement direction in either head or world coordinates contradicts the only previous study (D'Avossa and Kersten, 1996) that investigated differences in visual discrimination of heading azimuth and elevation. D'Avossa and Kersten reported that sensitivity was worse for elevation than for azimuth. The discrepancy could be attributable to methodological differences between our study and theirs. We assessed heading discrimination about straight ahead. They assessed sensitivity at much greater eccentricities (up to ±22.5° in azimuth and/or elevation).

Amplitude discrimination

Contrary to heading and coarse direction discrimination, amplitude discrimination did not depend on movement direction in head coordinates or body orientation but had a weak dependence on movement direction in world coordinates: slightly lower thresholds were observed for earth-vertical than earth-horizontal movement directions. This finding is contrary to the gravitational-pedestal hypothesis, which predicts that amplitude thresholds would be higher during earth-vertical than earth-horizontal movements because of the increased pedestal.

Implications for neural population decoding

Under the assumption that heading and coarse direction discrimination result from different “readouts” of the same neuronal population activity (Purushothaman and Bradley, 2005; Jazayeri and Movshon, 2006; Gu et al., 2007), a simple neuron/anti-neuron simulation approximately reproduced the observed relationship between thresholds in the heading and coarse direction tasks (Fig. 9). Notably, the difference between heading and coarse direction thresholds did not depend on the noise model of neuronal spiking but could be reproduced when a hyperbolic-ratio function was applied to the neuron/anti-neuron magnitude response. Whether this is indeed an explanation for the behavioral findings requires characterization of the amplitude-dependent properties of central vestibular neurons, which is not presently available. A worthy goal for future research will be to evaluate whether simple population decoding schemes, based on the directional tuning and amplitude–response properties of neurons at various stages of vestibular processing, can account for the basic features of vestibular perception.