Abstract
Objective:
To evaluate systematic differences in landmark position between cone-beam computed tomography (CBCT)–generated cephalograms and conventional digital cephalograms and to estimate how much variability should be taken into account when both modalities are used within the same longitudinal study.
Materials and Methods:
Landmarks on homologous cone-beam computed tomographic–generated cephalograms and conventional digital cephalograms of 46 patients were digitized, registered, and compared via the Hotelling T2 test.
Results:
There were no systematic differences between modalities in the position of most landmarks. Three landmarks showed statistically significant differences but did not reach clinical significance. A method for error calculation while combining both modalities in the same individual is presented.
Conclusion:
In a longitudinal follow-up for assessment of treatment outcomes and growth of one individual, the error due to the combination of the two modalities might be larger than previously estimated.
Keywords: Cephalogram, Cone-beam CT, Error, Procrustes, Accuracy, CBCT
INTRODUCTION
The advent of cone-beam computed tomography (CBCT) for craniofacial imaging provides volumetric information that allows development of virtual three-dimensional (3-D) models that can be quite valuable in locating impacted teeth, visualizing the temporomandibular joints, and diagnosing asymmetries in complex craniofacial patients.1 Although new applications such as 3-D cephalometrics are developing rapidly, cephalograms are still necessary for comparison to existing databases,2 and while 3-D registration and superimposition of CBCT data is being developed,3 sequential cephalograms provide an easy clinical method for assessing growth and treatment changes. In order to be able to compare the new modalities with our current databases, algorithms have been created to extract information from the CBCT image and to simulate a conventional lateral cephalogram, P-A cephalogram, and panoramic projection. Previous in vitro and in vivo studies comparing both conventional cephalograms and CBCT-extracted cephalograms reported some statistically significant differences that did not reach clinical significance.4–7
The aims of this in vivo study were (1) to evaluate any systematic differences in landmark position between CBCT-generated cephalograms and conventional digital cephalograms, using an optimization method to superimpose sets of landmarks, and (2) to estimate how much variability should be taken into account when combining conventional and synthetic cephalograms within the same longitudinal study.
MATERIALS AND METHODS
Records of consecutive patients who had radiographic examination at a radiology clinic between January 2005 and August 2006 were screened. Those for whom both a digital cephalogram (Planmeca, Helsinki, Finland) and a CBCT of the head (iCAT, Imaging Sciences International, Hatfield, Pa) had been obtained were selected. Initial inclusion criteria for this study were a medium- or full-field of view that allowed visualization of both the cranial base and the face and a patient age between 17 and 46 years. Records of 46 patients were available and included in the sample.
Creation of a Synthetic Cephalogram
CBCT images were converted into DICOM files and were rendered anonymous by an algorithm included in the iCAT software. Images were loaded into Dolphin 3D (version 2.3 beta) (Dolphin Imaging, Chatsworth, Calif). Threshold filters were set for optimal visualization of the soft and hard tissues.
Images were reoriented to align the cranium relative to the tridimensional coordinate system of Dolphin 3D (version 2.3 beta). Orbits were oriented parallel to the horizontal plane in the frontal view. In the sagittal view the cranium was rotated along the long axis so that the key ridges and orbits were aligned. A cranial view was used to confirm the correct head rotation by aligning the intracranial medial structures with the default coordinate system. Once the virtual 3-D models were aligned, synthetic cephalograms were created. The magnification factor was set to 7.5%, the typical magnification for midline structures with a 60-inch distance from radiation source to the midline with conventional cephalometrics, to simulate the magnification in conventional digital cephalograms. The images were enhanced for better visualization by fine tuning of the contrast and brightness options and were saved as JPEG files (Figure 1).
Figure 1.
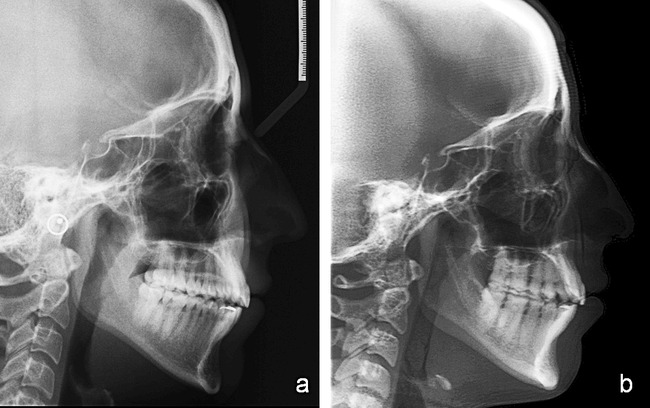
Different aspect of a conventional digital cephalogram (a) and a CBCT-generated cephalogram. (b) Note the difference in contrast and structure superimposition. For the digital cephalogram (JPEG file, 1360 × 2045; 8-bit; Proline, Planmeca, Helsinki, Finland); for the CBCT-generated cephalogram (16 × 22–cm large field of view, primary/axial image type, 1500/5000 window center/width, 400/400 rows/columns; iCAT, Imaging Sciences International).
Cephalogram Tracing
Both conventional and synthetic cephalograms were loaded into Dolphin (version 9.1; Dolphin Imaging) and traced by a single operator. When landmarks were difficult to locate the operator was instructed to change the contrast, gamma, and brightness setting of the image until structures could be visualized. Whenever bilateral structures were not aligned, or when the difference in magnification was obvious between left and right structures, the operator chose the midpoint between the two structures. Cephalograms were verified for anatomic contour and landmark identification by a second operator. Fifteen cephalograms were selected from the sample and were retraced three times, with at least 24 hours in between tracing sessions. Intraclass correlation coefficients were above 0.9 for all landmarks both for x and y coordinates.
Registration Method
The two sets of landmarks belonging to each patient were registered in order to combine landmarks from both modalities into the same coordinate system. The following landmarks were used in the registration process: nasion, orbitale, ethmoid reg, sella ant, sella, articulare, pns, ans, a pt, menton, gnathion, pogonion, b pt, gonion, and porion.
In order to register the landmarks identified on the synthetic cephalogram to the ones belonging to the conventional digital cephalogram, rigid Procrustes registration was employed. Landmark coordinates were exported from Dolphin (version 9.1) into MathLab Software (The MathWorks Inc, Boston, Mass). First, the centers of gravity across all measurements were computed in each set of patient landmarks, both for the conventional and synthetic cephalograms. The centers of gravity of the conventional cephalogram landmarks and the synthetic cephalogram landmarks were superimposed. This process minimizes the translation differences between homologous landmarks while considering all the landmarks in the set. Secondly, an objective function that equals the sum of square distances between the landmark pairs was created. By minimizing this objective function, the best fit relative to the rotation of the two sets of landmarks was obtained.
Measurement
Average difference vector
The residual distances for each patient between homologous landmarks belonging to the two cephalogram modalities were calculated as vectors and will be referred to as “difference vectors” (Figure 2). The average difference at each landmark between synthetic and conventional cephalograms was calculated by averaging difference vectors from all patients. This difference will be referred to as the “average difference vector” (Table 1).
Figure 2.
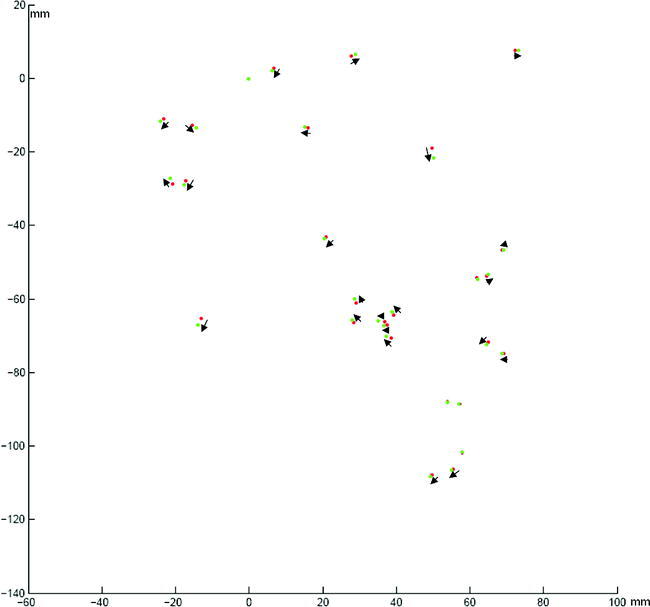
Landmarks located in the CBCT-generated cephalogram (red) have been registered via Procrustes method to the landmarks located on the conventional digital cephalogram (green). Difference vectors are depicted.
Table 1.
Landmarks, Average Difference Vectors (X and Y Components and Module), Significance, False-Discovery Rate Method Correction, and Average Difference Lengths. Statistical Significance Was Established at 0.01 (Measurements are in mm)
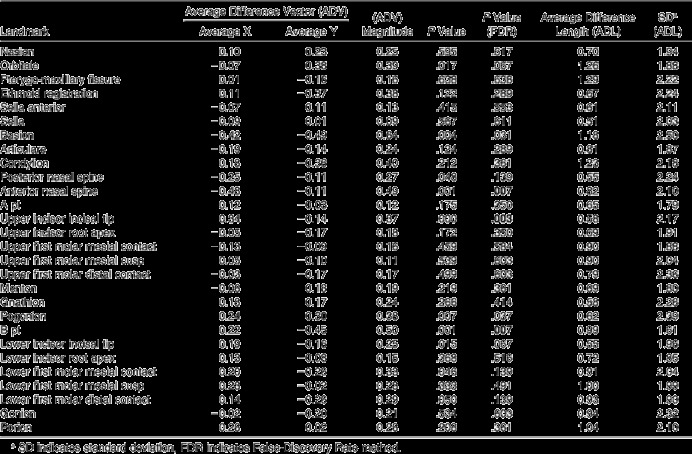
Average difference length
The absolute length of the individual difference vector is referred to as the “difference length.” Based on these length values, we then computed the “average difference length” via standard geometric averaging see (Table 1).
Plotting
In order to visualize the difference vectors around each landmark, these vectors were transposed onto an arbitrarily selected landmark set (Figure 3). In order to visualize the envelope of landmark location probability, we plotted the average difference length (and two standard deviations) around each one of the landmarks (Figure 4).
Figure 3.
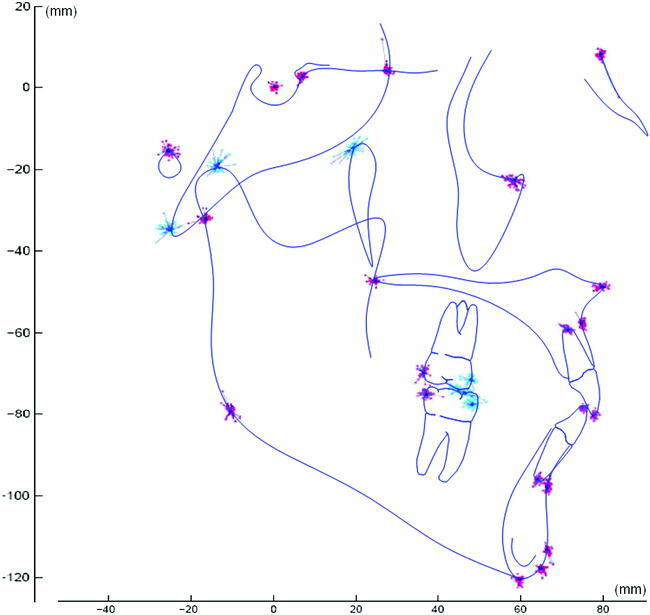
Difference vectors are grouped by landmark on a cephalogram tracing. The envelope of error—or difference between modalities—can be visualized. (Red and purple landmarks were used in the registration process; blue landmarks were only plotted.)
Figure 4.
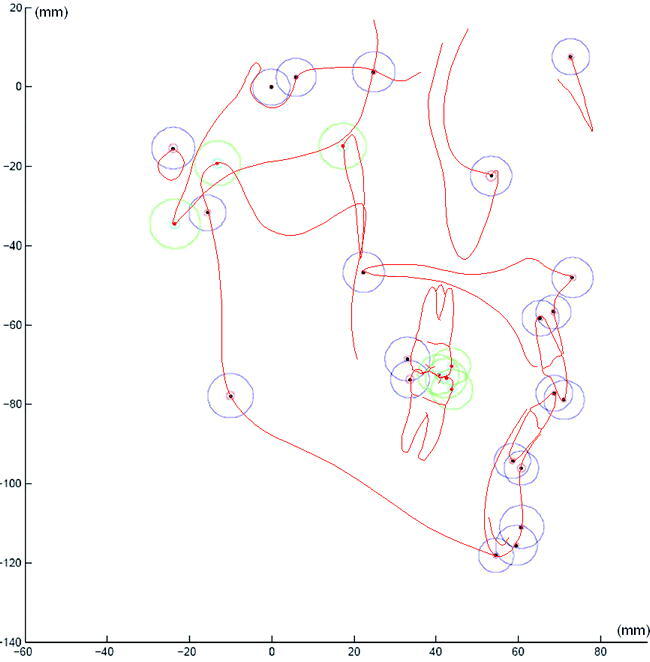
Difference lengths depicted as average plus three standard deviations are plotted on a cephalogram tracing. (Purple landmarks were used in the registration process; green landmarks were only plotted.)
Statistical Analysis
Statistical analyses were performed using SAS (version 9.1; SAS Institute Inc, Cary, NC). The hypothesis of interest was that there was no systematic difference between the two modalities at each landmark. We calculated the Hotelling T2 statistic for the difference vectors between each pair of homologous landmarks in order to formally assess any systematic difference between the two modalities. To account for multiple comparisons across all landmarks, the false-discovery rate method was used.8
If the two modalities were to be used in a longitudinal study, the estimate of the measurement error has to account for the bias and variability derived from the use of two different modalities. Furthermore, to measure a distance on the cephalogram between two different landmarks, the envelope of error for both landmarks has to be considered.
In order to calculate the bias and variability of the measurement errors obtained from the use of the two modalities at each landmark (see Appendix), we used a two-step process. First, we calculated the difference vectors for all subjects and then computed the sample covariance matrix of these difference vectors. Second, we used the Gaussian random vector with a mean of zero and the half of the estimated covariance matrix to characterize measurement errors from both modalities.
To estimate the bias and variability of the distance between any two landmarks obtained from the use of the two modalities, we calculated the difference between the measured location difference vectors obtained from the two modalities and estimated their sample covariance matrix. Then, we can use the Gaussian random vector with a mean of zero and the half of the estimated covariance matrix to characterize measurement errors of location difference vectors between any two landmarks from both modalities.
DISCUSSION
Registration Process
The Procrustes registration process is necessary to avoid an uneven distribution of error (differences) across landmarks. In order to compute the differences between modalities, homologous sets of landmarks have to be combined in the same coordinate system. Most studies simply compare absolute linear or angular measurements between modalities. These methods do not allow for establishment of directionality or discrimination between envelopes of landmark location probability.4–7,9 Combining homologous sets of landmarks through an arbitrary coordinate center introduces bias.
The most frequent arbitrary coordinate center is centered in sella, with a horizontal plane described by a line 6° inferiorly rotated from sella-nasion plane. However, small differences in the locations of the landmarks that compose the coordinate system will have a great impact on the relative locations of landmarks located at a distance from the center of coordinates. The use of this arbitrary coordinate system to describe the relative coordinates of landmarks across modalities could lead to errors. Studies using the sella as the arbitrary coordinate center find their greater differences at mandibular structures or related measurements that are located far away from the coordinate system center.10 In our method, the registration of homologous sets of landmarks and establishment of envelopes of landmark location probability did not depend on a single landmark but rather on a set of landmarks distributed uniformly across the head and face anatomy.
Sources of Variability
Main sources of variability that could affect our results are variability due to landmark identification and variability due to head orientation and alignment of x-ray emitter.
Landmark identification
The variability due to landmark identification displays characteristic patterns described by Baumrind and Frantz.11 The systematic error in landmark identification affects both modalities, and it is likely that the net effect on the difference between modalities is negligible. In terms of landmark identification, general findings in this study are in agreement with in vitro studies by Kumar et al6 and Moshiri et al.9 These studies measured dry skulls, and it is important to note that landmark identification is slightly more complex when soft tissue is present. The general aspect of a CBCT synthetic cephalogram is different from that of a conventional digital cephalogram (Figure 1). Landmark identification was easier in the synthetic cephalograms. Some landmarks that often lack the adequate contrast for an easy identification in conventional digital cephalograms were easily recognized because of the higher difference in contrast in the synthetic cephalograms.
Head orientation and alignment of x-ray emitter
Some of the differences found between homologous landmarks could be related to different head orientation. Malkoc et al12 have found that linear and angular measurements on lateral cephalograms change from 16.1% to 44.7% with 14° of head rotation. Positioning of the patient inside the Planmeca cephalostat depends on the technician's skill, and that introduces another factor for which we cannot control.
The patient's anatomy also affects head positioning in the cephalostat. When the ears are used as a reference, we assume that the patient is relatively symmetric and that his/her ears are at the same level. In asymmetric patients this could create a head positioning error. Once the image is acquired, no corrections can be made to the roll and yaw of the head. Conversely, when a synthetic cephalogram is created the operator can easily manipulate the DICOM three-dimensionally to orient the head until bilateral structures are matching. The operator is able to see through the skull and match the position of para-medial structures. The position of the anatomical structures inside the field of view of the CBCT, in terms of rotation and translation, does not influence the accuracy of the measurements.13 In this study, while creating the synthetic cephalograms, no effort was made to replicate the position of the patient's head obtained in the conventional cephalograms.
Another source of projection errors is the misalignment of the x-ray emitter focal spot, which affects the conventional cephalogram machines. Even though we are certain that our x-ray unit was calibrated periodically, the fact that the cephalograms were obtained over a period of 18 months implies that the alignment of the x-ray source may have not been constant throughout the whole period. In an ex vivo study, Lee et al14 reported that this type of misalignment could cause systematic error in the interpretation of facial asymmetry in PA cephalograms. That could be the case for conventional digital cephalograms too.
Dry Skull and In Vivo Studies
The accuracy and precision of measurements with CBCT have been assessed by several studies.13,15,16 Ludlow et al17 concluded that measuring in both reconstructed panoramic projection and in the 3-D volume through the stack of slices provides accurate measurements of mandibular anatomy. Lascala et al18 reported a slight underestimation in linear measurements compared with direct measurements with a caliper used on skulls.
Our results are in agreement with ex vivo studies that have compared the accuracy and reliability of CBCT-generated cephalograms using skulls. Kumar et al6 concluded that with dry skulls CBCT is comparable to conventional cephalometry in terms of precision and accuracy. In a recent article Moshiri et al9 reported that CBCT-extracted cephalograms were, on average, more accurate than conventional digital lateral cephalograms when compared using direct measurement on skulls as a gold standard. In both studies, linear measurements of the mandible differed between the conventional and the CBCT synthetic cephalograms.
The findings from in vivo studies that assess differences in modalities are more directly comparable to our results. Recent in vivo studies have compared measurements between conventional cephalograms and CBCT-generated cephalograms and have concluded that even though some differences were found, they were not statistically or clinically significant.4,5,7 These studies compared absolute measurements between modalities independently of landmarks' absolute coordinates. Given that there is no systematic error in landmark location between modalities, it is expected that the average differences in measurements reported between modalities would be centered around zero. When applied to an individual, the error in landmark location between modalities (or difference vector) could be much greater than the population average. When the two modalities are utilized in a longitudinal study of the same individual and when linear or angular measurements are computed, the reported error should include the envelope of landmark location probability at both landmarks (and at three landmarks if it is an angular measurement).
With the method presented here, by calculating the envelope of landmark location probability around each landmark we can estimate the mean increase in error while measuring linear distances (Table 2). For instance, according to our method, if both modalities were used to calculate the distance between condylion and gnathion in an individual, the error could be as high as or higher than 2.36 mm (one out of 10 cases would display an error greater than 2.36 mm). This has an obvious impact when one is measuring small changes in mandibular length between time points. With our method, the error in measurement for any combination of two landmarks can be computed, and angular measurements can be analyzed similarly. In longitudinal follow-up for assessment of treatment outcomes and growth of one individual, the error due to combination of the two modalities might be larger than previously estimated.
Table 2.
Difference Between Modalities for Four Linear Measurements. Mean Difference, Standard Deviation (SD), and Percentiles (Measurements are in mm)
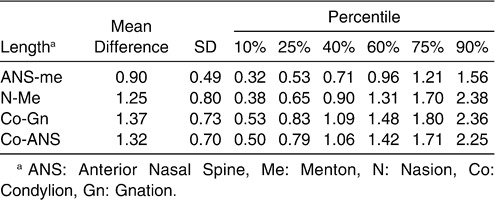
In agreement with previous reports, the average difference in our study is below clinical significance. In longitudinal studies, when both modalities are used in the same individual, we should consider that the error of the method could produce clinically significant differences. This is especially the case when the variables measured display small incremental differences with growth. CBCT-generated cephalograms could be used as a diagnostic tool, but when assessing treatment outcomes at different times for one individual, the variability between modalities makes it advisable to obtain sequential records with the same modality.
RESULTS
The average differences in location between homologous landmarks in both modalities are shown in Table 1 and Figure 2 as the average difference vector and average difference length. In order to compare difference vectors between patients, all sets of difference vectors around each landmark were transposed to an arbitrary center of coordinates and plotted (Figure 3). Most landmarks displayed a circular array of difference vectors. The average difference length and two standard deviations were also transposed to an arbitrary center of coordinates and plotted (Figure 4), which illustrates landmark location probability.
The distribution of the difference vectors was centered around zero for most landmarks, and there was no systematic difference between the two modalities. After adjustment for multiple comparisons via the false-discovery rate method (Table 2), only three landmarks (ANS, MxI and B) showed a statistically significant difference, and even for these landmarks the magnitude of the differences did not reach clinical significance (0.5 mm).
CONCLUSIONS
There is no systematic error when we compare average homologous landmark coordinates in conventional digital cephalograms and CBCT-generated cephalograms.
In longitudinal studies, when both modalities are used in the same individual, the error of the method could produce clinically significant differences.
Acknowledgments
We thank Drs Bob Scholz, Ceib Phillips, and David Hatcher for their help and support. Supported by NIDCR DE017727 and DE018962.
APPENDIX
Statistical Details
To estimate the bias and variability of the measurement errors obtained from the use of the two modalities at each landmark, we employed a two-step process. First, at the l-th landmark we assumed that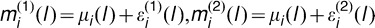 
, where μi(l) denotes the true location of the l-th landmark and where 
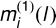and 
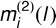represent the measurements obtained from the two modalities, respectively. Assuming that measurement errors 
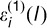and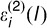 
are independent Gaussian random vectors with mean zero and covariance Σ(l), we can estimate Σ(l) as follows: (1) calculate the difference vectors 
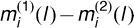for all subjects and then compute the sample covariance matrix 
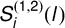of these difference vectors; (2) use 
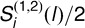as a consistent estimate of Σ(l). Finally, we can use the Gaussian random vector with mean zero and covariance 
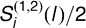to characterize measurement errors from both modalities.
Second, we estimated the bias and variability of the distance between any two landmarks obtained from the use of the two modalities. Specifically, we assumed that
 |
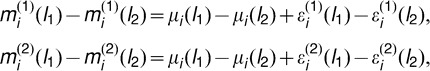where μ(l1) − μ(l2) denotes the true location difference between the l1-th and l2-th landmarks and where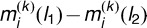 
for k = 1, 2 represents the measured location difference vector obtained from the two modalities. Assume that measurement error difference vectors 
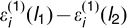and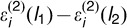 
are independent Gaussian random vectors with mean zero and covariance Σ(l1, l2). Similar to estimating Σ(l), we can use the half of the sample covariance matrix of 
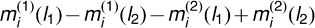, denoted by 
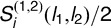, to consistently estimate Σ(l1, l2). Then, we can use the Gaussian random vector with mean zero and covariance 
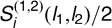to characterize measurement errors of location difference vectors between any two landmarks from both modalities. Finally, we can estimate the bias and variability of the measurement error of the distance between any two landmarks from both modalities.
REFERENCES
- 1.Ludlow J. B, Davies-Ludlow L. E, Brooks S. L. Dosimetry of two extraoral direct digital imaging devices: NewTom cone beam CT and Orthophos Plus DS panoramic unit. Dentomaxillofac Radiol. 2003;32:229–234. doi: 10.1259/dmfr/26310390. [DOI] [PubMed] [Google Scholar]
- 2.Hunter W. S, Baumrind S, Moyers R. E. An inventory of United States and Canadian growth record sets: preliminary report. Am J Orthod Dentofacial Orthop. 1993;103:545–555. doi: 10.1016/0889-5406(93)70095-6. [DOI] [PubMed] [Google Scholar]
- 3.Cevidanes L. H, Styner M. A, Proffit W. R. Image analysis and superimposition of 3-dimensional cone-beam computed tomography models. Am J Orthod Dentofacial Orthop. 2006;129:611–618. doi: 10.1016/j.ajodo.2005.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cattaneo P. M, Bloch C. B, Calmar D, Hjortshoj M, Melsen B. Comparison between conventional and cone-beam computed tomography–generated cephalograms. Am J Orthod Dentofacial Orthop. 2008;134:798–802. doi: 10.1016/j.ajodo.2008.07.008. [DOI] [PubMed] [Google Scholar]
- 5.Kumar V, Ludlow J, Soares Cevidanes L. H, Mol A. In vivo comparison of conventional and cone beam CT synthesized cephalograms. Angle Orthod. 2008;78:873–879. doi: 10.2319/082907-399.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kumar V, Ludlow J. B, Mol A, Cevidanes L. Comparison of conventional and cone beam CT synthesized cephalograms. Dentomaxillofac Radiol. 2007;36:263–269. doi: 10.1259/dmfr/98032356. [DOI] [PubMed] [Google Scholar]
- 7.van Vlijmen O. J, Berge S. J, Swennen G. R, Bronkhorst E. M, Katsaros C, Kuijpers-Jagtman A. M. Comparison of cephalometric radiographs obtained from cone-beam computed tomography scans and conventional radiographs. J Oral Maxillofac Surg. 2009;67:92–97. doi: 10.1016/j.joms.2008.04.025. [DOI] [PubMed] [Google Scholar]
- 8.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Statist Soc Ser. 1995;57:289–300. [Google Scholar]
- 9.Moshiri M, Scarfe W. C, Hilgers M. L, Scheetz J. P, Silveira A. M, Farman A. G. Accuracy of linear measurements from imaging plate and lateral cephalometric images derived from cone-beam computed tomography. Am J Orthod Dentofacial Orthop. 2007;132:550–560. doi: 10.1016/j.ajodo.2006.09.046. [DOI] [PubMed] [Google Scholar]
- 10.Ludlow J. B, Gubler M, Cevidanes L, Mol A. Precision of cephalometric landmark identification: CBCT vs conventional cephalometric views. Am J Orthod Dentofacial Orthop. In press doi: 10.1016/j.ajodo.2008.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baumrind S, Frantz R. C. The reliability of head film measurements. 1. Landmark identification. Am J Orthod. 1971;60:111–127. doi: 10.1016/0002-9416(71)90028-5. [DOI] [PubMed] [Google Scholar]
- 12.Malkoc S, Sari Z, Usumez S, Koyuturk A. E. The effect of head rotation on cephalometric radiographs. Eur J Orthod. 2005;27:315–321. doi: 10.1093/ejo/cjh098. [DOI] [PubMed] [Google Scholar]
- 13.Kobayashi K, Shimoda S, Nakagawa Y, Yamamoto A. Accuracy in measurement of distance using limited cone-beam computerized tomography. Int J Oral Maxillofac Implants. 2004;19:228–231. [PubMed] [Google Scholar]
- 14.Lee K. H, Hwang H. S, Curry S, Boyd R. L, Norris K, Baumrind S. Effect of cephalometer misalignment on calculations of facial asymmetry. Am J Orthod Dentofacial Orthop. 2007;132:15–27. doi: 10.1016/j.ajodo.2005.06.039. [DOI] [PubMed] [Google Scholar]
- 15.Marmulla R, Wortche R, Muhling J, Hassfeld S. Geometric accuracy of the NewTom 9000 cone beam CT. Dentomaxillofac Radiol. 2005;34:28–31. doi: 10.1259/dmfr/31342245. [DOI] [PubMed] [Google Scholar]
- 16.Mischkowski R. A, Pulsfort R, Ritter L, et al. Geometric accuracy of a newly developed cone-beam device for maxillofacial imaging. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007;104:551–559. doi: 10.1016/j.tripleo.2007.02.021. [DOI] [PubMed] [Google Scholar]
- 17.Ludlow J. B, Laster W. S, See M, Bailey L. J, Hershey H. G. Accuracy of measurements of mandibular anatomy in cone beam computed tomography images. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007;103:534–542. doi: 10.1016/j.tripleo.2006.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lascala C. A, Panella J, Marques M. M. Analysis of the accuracy of linear measurements obtained by cone beam computed tomography (CBCT-NewTom) Dentomaxillofac Radiol. 2004;33:291–294. doi: 10.1259/dmfr/25500850. [DOI] [PubMed] [Google Scholar]