Random Partition Models with Regression on Covariates

Abstract

Many recent applications of nonparametric Bayesian inference use random partition models, i.e. probability models for clustering a set of experimental units. We review the popular basic constructions. We then focus on an interesting extension of such models. In many applications covariates are available that could be used to a priori inform the clustering. This leads to random clustering models indexed by covariates, i.e., regression models with the outcome being a partition of the experimental units. We discuss some alternative approaches that have been used in the recent literature to implement such models, with an emphasis on a recently proposed extension of product partition models. Several of the reviewed approaches were not originally intended as covariate-based random partition models, but can be used for such inference.

1 Introduction

We review probability models for random partitions. In particular we are interested in random partition models in the presence of covariates. In other words, we discuss regression models where the outcome is an arrangement of experimental units in clusters.

Let S = {1, …, n} denote a set of experimental units. A partition is a family of subsets S₁, …, S_k with S = S₁ ⋃ … ⋃ S_k, S_j ⋂ S_j′ = Ø. We write ρ_n = {S₁, …, S_k}. The random number of clusters, k, is part of ρ_n. When the sample size n is understood from the context we drop the subindex and write ρ. Sometimes it is technically more convenient to describe a partition by a set of cluster membership indicators s_i with s_i = j if i ∈ S_j, i = 1, …, n. Let s_n = (s₁, …, s_n). Finally, let k_n denote the number of clusters. Again, we drop the index n if the sample size is understood. The number of clusters k is implicitly coded in s_n and ρ_n. We write n_nj = |S_j| for the size of the j-th cluster. Again, we drop the subscript n if the underlying sample size is understood from the context.

A random partition model is a probability model p(ρ_n). Two basic properties are desirable for random partition models. The model should be exchangeable with respect to permutations of the indices of the experimental units. Let π = (π₁, …, π_n) denote a permutation of S, and let s_π = (s_π1, …, s_πn) describe the clusters implied by re-labeling experimental unit i by $h={\pi }_i^{-1}$, i.e., π_h = i. We require

$$p\left(\mathbf{s}\right)=p\left({\mathbf{s}}_{\pi }\right)$$

for all partitions π. A second important property is that the model should scale across sample sizes. We want

$$p\left({\mathbf{s}}_n\right)=\sum _{j=1}^{k_n+1}p({\mathbf{s}}_n,s_{n+1}=j).$$

We refer to these two properties as symmetry and scalability. A probability model on ρ_n that satisfies the two conditions is called an exchangeable product partition function (EPPF) (Pitman, 1996). Exploiting the invariance with respect to relabeling the EPPF can be written as p(n_n1, …, n_nk).

Several probability models p(ρ_n) are used in the recent literature, including product partition models (PPM), species sampling models (SSM) and model based clustering (MBC). The SSM and MBC satisfy the requirements of symmetry and scalability by definition, but not all PPMs do. See, for example, Quintana (2006) for a recent review.

Usually the model is completed with a sampling model for observed data y = (y₁, …, y_n) given ρ_n. A typical sampling model defines independent sampling across clusters and exchangeability within clusters. In the following discussion we assume that this is the case. We do so for the benefit of a more specific discussion, but without loss of generality. We represent exchangeability within clusters as independent sampling given cluster specific parameters ξ_j:

$$p(\mathbf{y}\mid {\rho }_n)=\prod _{j=1}^k\int \prod _{i\in S_j}p(y_i\mid {\xi }_j^{\star })\mathrm{d}p\left({\xi }_j^{\star }\right).$$ (1)

For example, $p(y_i\mid {\xi }_j^{\star })$ could be a normal model $N({\xi }_j^{\star },S)$, and the prior $p\left({\xi }_j^{\star }\right)$ could be a conjugate normal prior. In the following discussion we focus on the prior model p(ρ_n), and assume (1) when a specific sampling model is required. Little changes in the discussion if the sampling model is of a different form.

The most popular choice for p(ρ_n) in the recent Bayesian literature is the special case of the random partition implied by the Dirichlet process (DP) prior (Ferguson, 1973; Antoniak, 1974). DP priors are probability models for unknown distributions G, i.e., the DP is a probability model on probability models. We write G ~ DP(α, G*). The base measure parameter G* defines the prior mean, E(G) = G*. The total mass parameter α is a precision parameter. One of the important properties is the a.s. discrete nature of G. This property can be exploited to define a random partition by considering a sequence of i.i.d. draws, ξ_i ~ G, i = 1, …, n. The discrete nature of G implies positive probabilities for ties among the ξ_i. Let $\{{\xi }_1^{\star },\dots ,{\xi }_k^{\star }\}$ denote the unique values among the ξ_i and define $S_j=\{i:{\xi }_i={\xi }_j^{\star }\}$. The implied probability model on ρ_n = (S₁, …, S_k) is known as the Polya urn scheme. Let [x]_m = x · (x + 1) · … · (x + m − 1) denote the Pochhammer symbol. The Polya urn defines

$$p\left({\rho }_n\right)=\frac{{\alpha }^k\prod _{j=1}^k(n_j-1)!}{{\left[\alpha \right]}_n}.$$ (2)

Model (2) can be written as $p\left({\rho }_n\right)\propto {\Pi }_{j=1}^{k}c\left(S_j\right)$, with c(S_j) = α(n_j − 1)! Models of the form p(ρ_n) ∝ ∏ c(S_j) general c(S_j) are known as PPMs (Hartigan, 1990; Barry and Hartigan, 1993).

Equivalently the Polya urn can be characterized by the predictive probability function (PPF), that is

$$p_j\left({\rho }_n\right)\equiv p(s_{n+1}=j\mid s_1,\dots ,s_n)\propto \{\begin{array}{cc}{n}_j\hfill & j=1,\dots ,k_n\hfill \\ \alpha \hfill & j=k_n+1\hfill \end{array}\phantom{\}}$$ (3)

It is easily verified that the Polya urn defines indeed an EPPF. Models that are characterized by a sequence of PPFs {p_j(ρ_n), j = 1, …, k and n = 1, 2, …} and that satisfy the symmetry and scalability requirements are known as SSMs (Pitman, 1996).

Probability models for random partitions are now routinely used in Bayesian data analysis. In this article we discuss an extension to probability models for random partitions indexed with covariates. An interesting example is reported in Dahl (2008). Proteins are clustered on the basis of 3-dimensional structure. Structure is recorded as a sequence of 7 characteristic angles of the backbone. Let RMSD denote the (root) minimum Euclidean distance between any two proteins, after optimally aligning the two molecules. Dahl (2008) argues that proteins with small RMSD should be a priori more likely to co-cluster than others. In other words the prior probability model on clustering should be indexed with covariates.

Let x_i denote the covariates that are specific to experimental unit i and write x_n = (x₁, …, x_n). We consider models of the form p(ρ_n | x_n). But more generally, the covariates need not be indexed by experimental units. Several of the following models only require that covariates can be grouped by cluster. For example, in Dahl (2008) the covariates are RMSD and are specific to any pair of proteins. Partition models with covariates are useful in many applications, but for a relative lack of standard methods are not currently used extensively.

The rest of this article is organized as follows. In sections 2 through 5 we discuss models for random partitions with covariates based on several alternative approaches, including augmented response vectors, dependent DP models, and hierarchical mixture of experts models. In section 6 we review in more detail an approach based on extending the product partition model.

2 Clustering with Augmented Response Vectors

Probability models p(ρ_n) can systematically be generalized to p(ρ_n | x) by the following device. Assume for a moment that covariates are random, even when they are fixed by design, using a sampling model as in (1), $p(\mathbf{x}\mid {\rho }_n)={\Pi }_j\int {\Pi }_{i\in S_j}p(x_i\mid {\eta }_j^{\star })\mathrm{d}p\left({\eta }_j^{\star }\right)$. The implied conditional distribution p(ρ_n | x) defines a probability model for ρ_n, indexed by covariates, as desired. The approach is particularly convenient when the model is combined with the sampling model (1) for observed data y. This is implemented in combination with the DP model among others, in Müller et al. (1996) or more recently in Shahbaba and Neal (2007) and in Dunson and Park (2008). The combined model becomes

$$p(\mathbf{y}\mid {\rho }_n)p({\rho }_n\mid \mathbf{x})\propto \prod _{j=1}^k\int \prod _{i\in S_j}p(x_i\mid {\eta }_j^{\star })\mathrm{d}p\left({\eta }_j^{\star }\right)\prod _{j=1}^k\int \prod _{i\in S_j}p(y_i\mid {\xi }_j^{\star })\mathrm{d}p\left({\xi }_j^{\star }\right)p\left({\rho }_n\right)=\prod _{j=1}^k\left[\int \prod _{i\in S_j}p(x_i\mid {\eta }_j^{\star })p(y_i\mid {\xi }_j^{\star })\mathrm{d}p\left({\xi }_j^{\star }\right)p\left({\rho }_n\right)\right].$$ (4)

The sampling model p(y | ρ_n) could include additional regression on x, i.e., replace the first factor by p(y | ρ_n, x), without changing anything in the following discussion. If p(ρ_n) is the Polya urn (2) implied by the DP prior, then the model can be rewritten as independent sampling of (y_i, x_i) given latent variables (ξ_i, η_i) that in turn are i.i.d. samples from a random probability measure with DP prior. Let ξ = (ξ₁, …, ξ_n) and similar for η. Conditional on a random measure G consider:

$$p(\mathbf{y}\mid \xi )p(\xi ,\eta \mid \mathbf{x},G)\propto \prod _{i}p(y_i\mid {\xi }_i)p(x_i\mid {\eta }_i)G({\xi }_i,{\eta }_i).$$

The model is completed with a DP prior, G ~ DP (G*, α) with base measure $G^{\star }({\eta }_j^{\star },{\xi }_j^{\star })=p\left({\eta }_j^{\star }\right)p\left({\xi }_j^{\ast }\right)$.

The latent variables (ξ_i, η_i) implicitly code the partition ρ_n by ξ_i1 = ξ_i2 if and only if s_i1 = s_i2. Marginalizing with respect to G is (4) with the Polya urn prior p(ρ_n).

There are two important limitations to this approach. First, the approach requires the specification of a probability model for the covariates x_i, even if these are not random quantities. For long lists of covariates with a mix of different data formats it can be a challenging task to define suitable p(x_i | η_i). Such situations are quite common for many biomedical applications where x_i could be a long list of subject-specific characteristics, including treatment history, age, ethnicity, insurance coverage, health literacy, location, and many more.

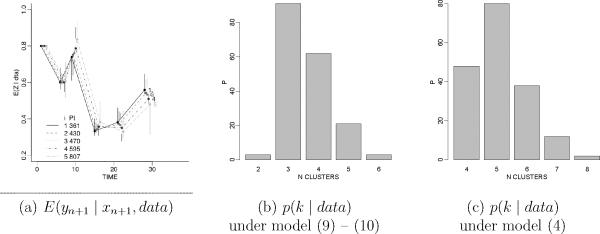
Second, the approach includes a trap. It is usually defined for the special case with x_i ∈ R^p and y_i ∈ R^q as vectors of continous variables. Assume multivariate normal kernels p(x_i | η_i) = N(η_i, T) and sampling model p(y_i | ξ_i) = N(ξ_i, S) and conjugate normal priors $p\left({\eta }_j^{\star }\right)$ and $p\left({\xi }_j^{\star }\right)$. Here S and T are (possibly fixed) hyperparameters. It is tempting to combine factors and write the model as one joint model with augmented response vector $(x_i,y_i)\prime ~N(({\eta }_j^{\star },{\xi }_j^{\star })\prime ,\Sigma )$, where Σ is a (p + q) × (p + q) covariance matrix. However, care needs to be taken to enforce a block diagonal structure with Σ_i1,i2 = 0 for any two indices i₁ ≤ p and i₂ > p. Otherwise the equivalence with (4) is lost and it becomes difficult to understand the implied model. Assume Σ with non-zero off-diagonal elements. Then the cluster-specific sampling model $p(x_i,y_i\mid {\xi }_j^{\star },{\eta }_j^{\star },\Sigma )$ can be factored as $p(y_i\mid {\xi }_j^{\star },\Sigma )\cdot p(x_i\mid y_i,{\eta }_j^{\star },{\xi }_j^{\star },\Sigma )$. In words, the prior for the cluster membership depends on the outcome y_i, or equivalently, the sampling model $p(y_i\mid ,{\xi }_j^{\star },{\eta }_j^{\star },x_i,\Sigma )$ includes an unintended regression on x_i. The same comment is true for the base measure G* and possible hyperpriors. And most importantly, the prior p(ρ_n | x) in (4) includes a normalization constant. Let $p\left(\mathbf{x}\right)={\sum }_{{\rho }_n^{\prime }}{\Pi }_j[\int {\Pi }_{i\in S_j}p(x_i\mid {\xi }_j^{\star })dp\left({\xi }_j^{\star }\right)]$. The marginal p(x) is the proportionality constant in (4). When $p(x_i\mid {\xi }_j^{\star },\varphi )$ and $p(y_i\mid {\eta }_j^{\star },\varphi )$ include a common hyperparameter ϕ, such as the covariance matrix Σ in the normal model, then p(x | ϕ) changes the model in unintended ways. The change is less innocent than what it might seem. See the example in Figure 2 and the corresponding discussion.

Figure 2.

Augmented response vector. Panel (a) shows inference like in Figure 1b, but under a corresponding augmented response vector approach. Panels (b) and (c) show the posterior distribution on the number of clusters k.

3 DDP and Related Models

Dependent Dirichlet process (DDP) models are another class of probability models that can generate covariate-dependent random partitions. DDP models were introduced in MacEachern (1999). Although not usually presented as probability models for covariate dependent random partitions, the special case of DDP models with varying weights can be used to achieve this purpose. Recall the DP model. Let δ(m) denote a point mass at m. A random probability measure (RPM) G has a DP prior, G ~ DP(α, G*) if it can be written as

$$G=\sum _{h=1}^{\infty }{\pi }_h\delta \left(m_h\right)$$ (5)

with m_h ~ G*, i.i.d., and π_h = V_h∏_f<h(1 − V_h) where V_h ~ Be(1, α), i.i.d. (Sethuraman, 1994).

The DDP model was introduced to generalize the DP prior to a probability model for a family of dependent RPMs {G_x, x ∈ X} indexed by x. The marginal model remains a DP prior, G_x ~ DP(·) marginally. Implementations of the DDP vary in the way how the dependence of G_x across x is defined. One variation is to replace the weights π_h in the DP model by covariate-dependent weights π_h(x). This is implemented, for example, in Griffin and Steel (2006).

An alternative implementation of DDP models introduces the desired dependence across x by replacing m_h in (5) with m_xh, and defining a dependent prior p(m_xh, x ∈ X). For example, a Gaussian process prior model. The weights remain unchanged across x. Although this fixed weight implementation is the more popular one, it is not of interest in the current discussion. It does not naturally lead to covariate dependent random partitions.

The varying weights DDP model can be used to define a random partition model p(ρ_n | x) indexed by covariates. This is assuming constant locations m_h, unchanged across the level of x. The approach is simple. Similar to the definition of the Polya urn we consider independent samples ξ_i ~ G_xi with a DDP prior on {G_x, x ∈ X}. The discrete nature of the underlying DP priors implies a positive probability of ties among the ξ_i. We use this to define clusters. Let $\{{\xi }_1^{\star },\dots ,{\xi }_k^{\star }\}$ denote the k ≤ n unique values of ξ_i. We define i ∈ S_j if ${\xi }_i={\xi }_j^{\star }$. The simple form of (3) is lost. But the model still allows straightforward posterior simulation.

A related process is the weighted mixture of DPs (WMDP) proposed in Dunson et al. (2007). The WMDP defines a probability distribution for a family {G_x, x ∈ X} of discrete RPMs. Like the varying weight DDP the construction is such that the random measures G_x share common locations m_h for the point masses, but the weights π_hx vary across locations. The varying weights are defined by multiplying with a kernel that is a function of the covariates. The construction starts with a grid of covariate values $\{x_{\ell }^{\circ },\ell =1,\dots ,L\}$ and associated RPMs $G_{\ell }^{\circ }$. The RPM $G_{\ell }^{\circ }$ characterizes an RPM G_x with covariate $x=x_{\ell }^{\circ }$. For covariate values between the grid points the RPM G_x is defined as a weighted mixture of the $G_{\ell }^{\circ }$ measures.

Let f(x, x′) denote a (fixed) kernel. The WMDP assumes

$$G_x=\sum _{\ell =1}^L\left(\frac{{\gamma }_{\ell }f(x,x_{\ell }^{\circ })}{\sum _{k\prime }{\gamma }_{k\prime }f(x,x_{k\prime }^{\circ })}\right)G_{\ell }^{\circ }\mathrm{and}{G}_{\ell }^{\circ }~\mathrm{DP}(\alpha ,G^{\star }).$$

As usual the construction can be exploited to define a covariate-dependent random partition model. Consider ξ_i ~ G_xi, i = 1, …, n, and let $\{{\xi }_j^{\star },j=1,\dots ,k\}$ denote the k ≤ n unique values of ξ_i. The indicators s_i = j if ${\xi }_i={\xi }_j^{\star }$ define a random partition. The implied model p(ρ_n | x) is a random partition model indexed by covariates, as desired.

A similar construction is the probit stick-breaking process (PSBP) that was recently introduced in Chung and Dunson (2008). They construct a probability model for related RPMs {F_x, x ∈ X} by replacing the weights ρ_h in the DP prior by a probit model.

$${\pi }_h\left(\mathbf{x}\right)=\Phi \left({\eta }_h\left(\mathbf{x}\right)\right)\prod _{\ell <h}\{1-\Phi \left({\eta }_{\ell }\left(\mathbf{x}\right)\right)\}.$$ (6)

Here η_h(x) = α_h−ψ_h|x−Γ_h| is a linear predictor for the probit model and Φ(·) is the standard normal cdf. Chung and Dunson (2008) define the model for a multivariate covariate vector x. They complete the model with independent normal priors for the probit parameters.

4 Hierarchical Mixture of Experts

A widely used method for flexible regression is the hierarchical mixture of experts (HME) model (Jordan and Jacobs, 1994). It is extended to the Bayesian HME in Bishop and Svensén (2003). An implementation for binary outcomes is developed in Wood et al. (2008).

The HME is a flexible regression model for an outcome y_i and covariate x_i. It can be written as

$$p(y_i\mid {\mathbf{x}}_i,\eta ,\xi )=\sum _{j=1}^k{\pi }_j({\mathbf{x}}_i;{\eta }_j)p(y_i\mid {\mathbf{x}}_i,{\xi }_j)$$ (7)

where η parametrizes the weight for the j-th component. Bishop and Svensén (2003) use products of logistic regressions to specify the weights π_j. The parameters ξ parametrize the sampling model for the j-th component, for example a normal linear regression for a continuous outcome, or a probit binary regression for a binary outcome as in Wood et al. (2008). The component models are also known as the experts. Thus the name of the model.

Mixture sampling models like (7) can be used to define random partition models. Partition or clustering schemes induced by such models are known as model based clustering (Dasgupta and Raftery, 1998). The approach is based on writing the mixture model (7) as a hierarchical model with latent indicators s_i:

$$p(y_i=j\mid s_i,\xi )=p(y_i\mid {\mathbf{x}}_i,{\xi }_j)\mathrm{and}p(s_i=j\mid {\mathbf{x}}_i,\eta )={\pi }_j({\mathbf{x}}_i;{\eta }_j).$$

The indicators s_i define the partition and p(ρ_n | x_n) is a multinomial distribution.

The approach is based on the finite parametric model (7). It inherits all advantages and limitations of a parametric approach. An important advantage is parsimony of the parametrization and interpretability of the parameters. An important limitation is the restriction to the specific parametric form of π_j. For example, if the logistic regression for π_j does not include interaction terms, then no amount of data and evidence will be able to introduce such terms in the posterior predictive inference. Another limitation is the fixed number of clusters k. This limitation can easily be addressed by adding a hyperprior p(k). But in either case the number of clusters would not be adaptive to the sample size, as is the case in other random partition models. The same comments apply to any other model with explicitly parameterized weight function, such as the PSBP in (6).

5 Other Approaches

In the previous sections we have reviewed approaches and models that can be used to define covariate-dependent random partitions. A common theme of these approaches is that they were introduced in the literature for different purposes, and just happen to imply covariate-dependent random partition models. The reason for including these approaches in the review is simply the relative lack of literature concerned with covariate-dependent random partition models.

One exception is Dahl (2008). We mentioned the motivating application in the introduction. The desired covariate-based random clustering model is constructed by a smart modification of the Polya urn scheme (3). Let d_i1i2 denote the RMSD between any two proteins i₁ and i₂. Dahl (2008) defines a random partition on the set of proteins. The prior co-clustering probabilities are modified based on d_i1i2. Let d* denote the maximum recorded distance. For each cluster S_j ⊂ {1, …, n} and protein i, Dahl (2008) defines a propensity score $h_i\left(S_j\right)=c_i{\sum }_{f\in S_j}(d^{\star }-d_{if})$. Without loss of generality assume i = n + 1. The scores h_n+1(S_j) are standardized such that ${\sum }_{j=1}^k{h}_{n+1}\left(S_j\right)=n$. Dahl (2008) then modifies (3) to

$$p(s_{n+1}\mid s_1,\dots ,s_n,d_{n+1,i},i=1,\dots ,n)\propto \{\begin{array}{cc}{h}_i\left(S_j\right)\hfill & j=1,\dots ,k_n\hfill \\ \alpha \hfill & j=k_n+1.\hfill \end{array}\phantom{\}}$$ (8)

The standardization of h_i to Σh_n+1 = n serves an important purpose. It leaves the conditional probability of opening a new cluster unchanged. Dahl (2008) recognizes that the modified Polya urn (8) is not necessarily a legitimate PPF anymore, i.e., a predictive probability function that defines a species sampling model (Pitman, 1996). But (8) does define transition probabilities for an ergodic Markov chain. Thus it implicitly defines a joint probability distribution on s that is informed by the relative distances d_i1i2, as desired.

Another interesting recent discussion is Monni and Tadesse (2008). Although they do not define a covariate-based random partition model, we still include the approach in this review since we consider it closely related. The approach can be characterized as a joint probability model for ρ_n and a latent feature corresponding to each cluster. Monni and Tadesse (2008) consider the problem of defining regression models for many response variables y_i, i = 1, …, n on a large set of possible covariates {x_j, j = 1, …, p}. The application is to a regression of comparative genomic hybridization (CGH) on mRNA expression levels, with n = 261 and p = 3291. Their approach is based on a partition ρ_n of S = {1, …, n}. For each partitioning subset S_j ⊂ S they define a subset R_j ⊂ {1, …, p} of regressors. For i ∈ S_j the model includes then a normal linear regression of y_i on {x_f, f ∈ R_j}. The model is completed with a prior p(ρ_n, R₁, …, R_k). The prior is constructed to favor small partitioning subsets. Let n_j = |S_j| and m_j = |R_j. Monni and Tadesse (2008) define

$$p({\rho }_n,R_1,\dots ,R_k)\propto \prod _j{r}^{m_j{n}_j},$$

for some 0 < r < 1 parameter that controls the clustering, with smaller values favoring small clusters and a few active covariates. The model demonstrates the restrictive nature of the Polya urn scheme (2) and the endless possibilities in defining alternative random partition models – in this case jointly with the associated sets R_j. Of course the flexibility comes at a cost. We lose scalability. But this might not be a concern when there is no notion of predictive inference.

6 The PPMx Model

6.1 A Covariate-Dependent Random Partition Model

In Müller et al. (2008) we develop a model for random partitions with covariates that is based on the product partition model (PPM). The PPM is a model for random partitions defined by

$$p\left({\rho }_n\right)\propto \prod _{j=1}^{k}c\left(S_j\right),$$

where c(·) is known as the cohesion function. The Polya urn (2) defines a model that falls within this class by using c(S_j) = α(|S_j − 1)! Compare with the discussion following (2).

In words, the proposed model is an extension of the PPM, defined by augmenting the cohesion function c(S_j) by a factor that favors clusters with similar covariates and discourages clusters with highly dissimilar covariates. Similarity is formalized by a similarity function. The argument of the similarity function are the covariate values recorded in a given cluster. The value is a non-negative number. Specifically, let $x_{S_j}^{\star }=\{x_i,i\in S_j\}$ denote the set of covariate values for experimental units grouped in the j-th cluster. We define a similarity function $g\left(x_{S_j}^{\star }\right)$ with g(·) ≥ 0 such that large values of g indicate high similarity of the x_i, i ∈ S_j. We define an extension of the PPM model to a covariate-dependent random partition model:

$$p({\rho }_n\mid \mathbf{x})\propto \prod _{j}c\left(S_j\right)g\left(x_{S_j}^{\star }\right).$$ (9)

The main component of the proposed model is the similarity function. As a default we propose to define

$$g\left(x_{S_j}^{\star }\right)=\int q(x_i\mid {\eta }_j)\mathrm{d}q\left({\eta }_j\right),$$ (10)

for an auxiliary probability model q(x | η) and a conjugate prior q(η). We refer to model (9) and (10) as PPMx model. A related model for continuous covariates is discussed in Park and Dunson (2009). Their idea is to use a PPM for covariates and then use the posterior random partition as prior for the data model.

Let N(x; m, s²) denote a normal distribution with location m and scale s. For example, for a continuous covariate one could use a normal kernel q(x_i | η_j) = N(x_i; η_j, s²) and q(η) = N(0, τ). The similarity function would then be the marginal n_j-dimensional normal distribution of the set $x_{S_j}^{\star }$, with larger values for more tightly grouped x_i values. We propose similar default models for categorical and count covariates using a multinomial/Dirichlet and a Poisson/gamma model. We argue that under some reasonable assumptions on g(·) the default model (10) is not only a convenient default similarity function. It is the only possible form for a similarity function. The two assumptions are symmetry of g(·) with respect to permutations of the indices of x_i, and $\int g(x_{S_j}^{\star },x)\mathrm{d}x=g\left(x_{S_j}^{\star }\right)$.

For a covariate vector with a mix of different data formats we propose to define a joint similarity function as a product of similarity functions for each covariate or subvector of covariates with common data format.

The proposed model can be considered a special case of (4), with the submodel for x_i defined by the kernel q(x_i | η_j) that appears in (10). But in contrast to approaches that work with an augmented response vector (x_i, y_i) the sampling and prior models are already separated by construction. See the discussion following (4).

The interpretation of the model as a special case of (4) is important for posterior simulation. Exploiting the representation as a special case of a DP mixture one can use any of the many posterior Markov chain Monte Carlo (MCMC) schemes that have been proposed for these models.

6.2 Example: Semiparametric Mixed Effects Model

Wang et al. (2005) describe a clinical trial of carboplatinum, a chemotherapy agent, with additional immunotherapy using γ-interferon and GM-CSF (colony stimulating factor). One of the desired effects of the immunotherapy is to boost monocyte counts. Monocytes are a subpopulation of white blood cells. All patients are administered the same level of γ-interferon and GM-CSF. Carboplatinum dose varies across patients. The data reports monocyte counts for n = 47 patients. For each patient we use 6 repeat measurements over the first cycle of chemotherapy, using the measurements closest to days 1, 6, 9, 15, 21 and 28. Day 1 is the day of the actual chemotherapy. Day 28 is the day just before the second dose of chemotherapy. Let y_ij denote the j-th observation for patient i, and let x_i denote the dose of carboplatinum.

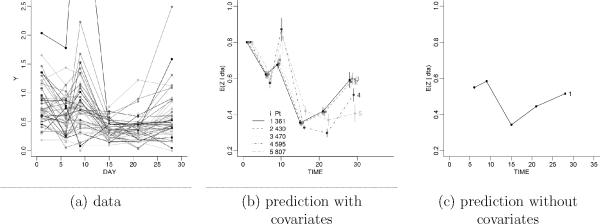
Figure 1a plots the data for the 47 patients. The initial decline is in response to the chemotherapy treatment on day 1. The first immunotherapy leads to the peak around day 9. The second increase reflects the next set of immunotherapy given just before the next chemotherapy dose x_i. We implemented the proposed model for covariate-dependent clustering to define a random partition model with a regression on the chemotherapy dose. Let N(x; m, s) indicate a normal kernel for the random variable x, with moments (m, s), let W (V; ν, S) denote Wishart prior for the random matrix V with scalar parameter ν and matrix variate parameter S, and let Ga(s⁻¹; ν, νs_o) denote a gamma distribution (parametrized to have mean $s_{\circ }^{-1}$ and variance $s_{\circ }^{-2}∕\nu$). Let θ_j = (μ_j, V_j). We used a multivariate normal model p(y_i | θ_j) = N(μ_j, V_j), with a conditionally conjugate prior for θ_j, i.e., $p\left({\theta }_j\right)=N({\mu }_j;m,B)W(V_j^{-1};s,S^{-1})$. The model is completed with conjugate hyperpriors for m, B and S. The similarity function is a normal kernel. We use

$$g\left(x_j^{\star }\right)=\int \prod _{i\in S_j}N(x_i;m_j,s_j)N(m_j;a_0,A_0)\mathrm{Ga}(s_j^{-1};\nu ,\nu S_0)\mathrm{d}{m}_j\mathrm{d}{s}_j.$$

The hyperparameters a₀, A₀, S₀ are fixed.

Figure 1.

Panel (a) shows the data. The figure plots monocyte count versus day of the first cycle chemotherapy for n = 47 patients. Panel (b) shows prediction for $\tilde{y}$ arranged by $\tilde{x}$ from lowest (“1”) to highest (“5”) level of carboplatinum. Panel (c) shows for comparison prediction without covariate-dependent clustering. By construction prediction in (c) is identical for all patients.

Posterior inference in the model provides the desired prediction for a future patient, i = n + 1. Figure 1b shows the prediction arranged by dose level (with increasing doses labeled 1 through 5). For comparison, the right panel of the same figure shows posterior predictive inference in a model using a PPM prior on clustering, without the use of covariates.

For comparison, we also considered an implementation based on (4). For a fair comparison all hyperparameters were left unchanged. In particular, the prior means of the Wishart priors on all precision matrices are block diagonal with zeroes in the elements corresponding to elements of the x and y subvectors. The resulting inference is shown in Figure 2. Under the augmented probability model the number of clusters is sharply reduced. Almost all probability mass is concentrated on only one cluster (not shown). The resulting inference is thus a simple normal linear regression of the mean outcomes on the covariate and misses the complicated structure suggested by the data.

An implementation of the model is provided in an R package that is available at http://odin.mdacc.tmc.edu/~pm/prog.html.

Finally, a few comments about practical implementation issues. The issues are equally relevant for other methods discussed in earlier sections, and for the corresponding random partition models without regression on covariates. We therefore only briefly mention the issues. A full discussion of solution strategies would be beyond the scope of this paper. For any random partition model inference about the actual clusters and cluster-specific parameters is subject to the label switching problem. The posterior distribution remains unchanged under any permutation of the cluster indices, j = 1, …, k. This symmetry makes it meaningless to report posterior summaries for cluster j. Also, apart from the label switching problem posterior distributions in mixture models are notoriously multimodal. This multimodality can lead to very slowly mixing Markov chains in the MCMC implementation. Finally, one needs to be careful with the choice of hyperparameters. In the R package implementation we use default choices based on the empirical moments of the data and covariates. Details can be seen in the default choices for unassigned parameters for the R function ppmx(), which is part of the R package.

7 Conclusion

We have discussed probability models for random clustering. We focused on the problem of defining models that can use covariate information to change a priori clustering probabilities. Such models are suitable for any application where similar experimental units are more likely to co-cluster. Similarity is defined in terms of available baseline covariates. We argued that several recently proposed methods for dependent RPMs and flexible regression can be exploited to define such models. Each of the discussed methods has some merits. The choice of the appropriate method depends on the problem at hand. Clustering with augmented response vector is convenient for continuous covariates x_i and responses y_i, and when simplicity of the implementation is desired. DDP models can accommodate any kind of data format for the covariates x_i. The computational effort is not much beyond the basic DP mixture model, but might require some problem-specific additional programming. HME models are very reasonable when the main focus is prediction and when there is little interest in inference about the random partition.

The main purpose of the review was to establish the context to introduce a new method developed in Müller et al. (2008). The proposed model is discussed in section 6. It is based on an extension of the PPM model by adding an additional factor $g\left(x_j^{\star }\right)$ to the cohesion function. The strengths of the proposal are the conceptually clear way of introducing the desired covariate-dependence, the possibility to include long lists of covariates with a mix of different data formats, and finally the still easy implementation.

The main limitations are (i) the fact that the similarity function can implicitly add a penalty for the cluster size, (ii) the need to elicit parameters for the similarity function, and (iii) the close resemblance to simpler augmented response models.

From a data analysis point of view it is desirable that a cluster size penalty should only be introduced through the cohesion function c(S_j). While mathematically possible, it is undesirable to include an additional cluster size penalty in the similarity function. The same statement in different words, for all equal covariates x_i ≡ x, the model should reduce to the underlying PPM. But this is not the case. It is only approximately true. See Müller et al. (2008) for more discussion.

The elicitation of parameters for the similarity function is a problem and a feature at the same time. On one hand one always wants to limit the amount of required prior elicitation. On the other hand such prior elicitation can prompt the investigator to clearly articulate available prior information. As an opt out it is always possible to use default choices. Alternatively one could extend the model with hyperpriors on these parameters. We recommend against the latter.

In conclusion, we feel that there are important gaps in the literature for random partition models. The current practice is almost entirely dominated by the Polya urn model that is implied by the DP prior. The reason is usually purely technical convenience. The present discussion of covariate-based random partition models identifies one important direction of generalization. Another important research direction is the consideration of alternative underlying models.