Item Selection, Evaluation, and Simple Structure in Personality Data

Abstract

We report an investigation of the genesis and interpretation of simple structure in personality data using two very different self-reported data sets. The first consists of a set of relatively unselected lexical descriptors, whereas the second is based on responses to a carefully constructed instrument. In both data sets, we explore the degree of simple structure by comparing factor solutions to solutions from simulated data constructed to have either strong or weak simple structure. The analysis demonstrates that there is little evidence of simple structure in the unselected items, and a moderate degree among the selected items. In both instruments, however, much of the simple structure that could be observed originated in a strong dimension of positive vs. negative evaluation.

Although there continues to be disagreement about the number of dimensions necessary to account for personality traits (Ashton et al., 2004; Block, 1995; Eysenck, 1992; Goldberg, 1993; Waller, 1999), most researchers would concede that the Five Factor Model (FFM) represents at least a reasonable approximation of the personality space. Discussions of competing models for the multivariate structure of personality space comprise at least two distinct issues: the number of dimensions that are required (e.g., three, five, or seven), and, for any given dimensionality, the descriptive content of the factors that are interpreted (e.g., Eysenck’s Psychoticism, Extraversion, Neuroticism model, or Gough’s, 1987, Internality, Norm-favoring, and Self-realization model). This paper is concerned exclusively with the latter issue. Stipulating some dimensionality for personality space, how do we know which particular dimensions represent the scientifically correct way to parameterize it?

An answer to this question entails both theoretical and empirical considerations. The methodological path from selection of items to represent the personality domain, to a covariance matrix among personality items, to a factor analysis of the dimensions, eventuating in a scientific model of personality, is fraught with statistical and conceptual uncertainties (Maraun, 1996a; Turkheimer, Ford, & Oltmanns, 2008). Although the first generation of factor analysts, in particular Thurstone (1940), was acutely aware of the difficulties of establishing psychological, never mind biological, facts on the basis of factor analysis, the passage of time and proliferation of computational technology has resulted in a routinization of factor analytic procedures that has blurred many of the difficult distinctions that underlay them. Our goal in this paper is to not to assert that any particular set of trait dimensions is correct or incorrect, but rather that such dimensions are underdetermined, and indeed that the question “What are the actual dimensions of human personality?” might itself be ill-posed.

Before elaborating on this somewhat controversial argument, it may be helpful to examine the steps involved in factor analysis of personality items in greater detail. These are:

1. Selection of stimuli for inclusion in the analysis.

2. Selection of an index of similarity among stimuli.

3. Determination of an appropriate dimensionality for the reduced space.

4. Execution of the actual statistical procedure for factoring, e.g., principal components, factor analysis, image analysis, or multidimensional scaling.

5. Choice of a rotation criterion and rotation of the solution.

6. Interpretation of the resulting dimensions.

These steps involve complex considerations of many possibilities, each with profound consequences for the outcome of the analysis, and although in the current paper we need to make decisions about all of them, we will primarily be concerned with Step 5 and its implications for Step 6. Furthermore, our concerns do not involve technical considerations of choices among rotation criteria, but instead the theoretical issue of why we rotate factor solutions in the first place and how we interpret the resulting dimensions.

Rotating factor solutions has become such a universal and easily-accomplished activity that many investigators seem to regard it as a routine transformation of multivariate results that does not require justification, but two facts about factor rotation are important to bear in mind. First, the rotated axes that are chosen are in an important sense indeterminate (Maraun, 1996b). A multidimensional space can be represented mathematically by an infinite number of coordinate systems, which may or may not be at right angles (orthogonal) to each other. The choice among them is based not on their fit to the data – they all fit the data equally well – but on the conformity of the resulting loadings to a criterion of simple structure, which refers to a tendency for the stimuli to have large loadings on one factor and small loadings on the others, or in a graphical representation, the tendency for the stimuli to lie close to the rotated axes. Simple structure is easier to describe than it is to quantify, and many numerical criteria for simple structure have been developed (Yates, 1987). Although any particular criterion of simple structure (e.g., varimax, promax, etc.) can be optimized for any multidimensional data matrix, it is not a given that any particular set of loadings actually has simple structure.

The alternative to the simple structure hypothesis is that stimuli are evenly distributed in the multidimensional space, the most familiar example being the circumplexical structure developed by Guttman (1954). Circumplexical structure is generally viewed as having two components. The first is absence of simple structure, manifested in factor analytic results by items with more than one substantial loading, and graphically by items that are continuously distributed in space, a property sometimes called “interstitiality.” The second component is circularity of structure in space, which in factor analysis implies roughly equal communalities for the items and roughly equal variances of the factors. We will be more concerned with the first property than the second. In any event, if a set of factor loadings is circumplexical or otherwise lacks simple structure, no alarm goes off in the rotation packages commonly employed in the service of factor analysis.

Furthermore, even if something resembling simple structure is evident in a matrix of loadings, it does not necessarily follow that the dimensions identified by the rotated solution are a reflection of the psychological or biological structure of the processes that produced the data in the first place. The justification for simple structure is not mathematical, but ergonomic, relating to human computational preferences rather than actual fit to observed data. In essence, the reason for preferring simple structure is that it in the paper and pencil era it was much easier to calculate the sum of cos(1)+cos(0)+cos(0) than cos(30)+cos(70)+cos(20), but computational preferences are not determinative of causal structure, and in the world of modern computational capacity they barely matter. Moreover, over time in any particular domain of investigation, there is a often a tendency for investigators to eliminate items that do not fit a preferred model of simple structure, so feedback between indeterminate rotational solutions and subsequent selection of items becomes a self-fulfilling mechanism for creating simple structure where it did not originally exist. As an example, consider positive and negative affect. Although these dimensions are often regarded as roughly orthogonal (Tellegen, Watson, & Clark, 1999), with few interstitial variables, if the entire domain of emotions is sampled, a circumplexical structure emerges (Carroll, Yik, Russell, & Barrett, 1999). Likewise, whereas a carefully developed multidimensional personality instrument may conform to simple structure, a representative sampling of trait descriptors might not.

Despite the popularity of rotating dimensional axes to simple structure, there is a rich history of personality theories that eschew orthogonal dimensions in favor of other structures. One such model is the aforementioned circumplex, which was introduced to the personality literature by Leary (1957). Although Leary’s interpersonal circumplex organizes social behavior according to the two broad principles of power and love, with other types of social behavior viewed as blends of these dimensions, no attempt is made to reify the dimensions as essential qualities of the structure. Instead, the emphasis is on the continuous circular structure of traits. There is empirical support for this conceptualization: Wiggins (1987) demonstrated that interpersonal traits conform to a circumplex, and Kiesler (1983) replicated this work with a more comprehensive list of words that varied in evaluativeness.

With the emergence of a replicable five-factor structure of personality, which obviously represents a more complex representation of the trait domain than earlier two-dimensional ones, the question arose as to whether stimuli would still be distributed seamlessly across this high-dimensional configuration. In a series of papers, it was demonstrated that some of the Big Five dimensions appear to form circumplexes, whereas others do not. For example, Peabody and Goldberg (1989) analyzed 57 personality scales and extracted three large and two small factors across seven different samples. After rotating the larger factors to assertiveness, tightness, and evaluation, they split these dimensions into two circumplexes, consisting of positively and negatively evaluated markers of assertiveness and tightness. In other words, they demonstrated that two of the three largest factors conformed primarily to a circular structure rather than orthogonal dimensionality. In contrast, they noted that the two smaller factors (intellect and emotional stability) appeared to display simple structure.

Saucier (1992), working with a different set of stimuli, extracted five dimensions, and noted that factors extraversion, agreeableness, and emotional stability approached an evenly distributed configuration, whereas conscientiousness and culture conformed to simple structure. Hofstee, de Raad, and Goldberg (1992) extracted five factors from a large set of 540 adjectives, and examined the extent to which each of the ten possible pairs of dimensions conformed to simple versus complex structure. Replicating Saucier’s findings, factors extraversion, agreeableness, and emotional stability formed circumplexes, whereas conscientiousness and intellect appeared closer to simple structure. To summarize, it appears that circumplexical structure prevails in at least some domains of the Big Five, particularly between pairs of factors that pertain to interpersonal behavior and affect, whereas simple structure may exist among factors that relate to work and openness to experience.

In considering this literature, two methodological problems cloud the above conclusions. First, in the above studies, interstitiality was usually evaluated graphically by subjectively examining plots of loadings¹. Although subjective evaluations of structures are often useful, we suggest that more objective ways of quantifying simple structure represent a more stringent test of the hypothesis that stimuli align along particular axes. Second, in these studies, simple structure was examined two dimensions at a time. In a high-dimensional domain like personality, however, the structure of the loadings may only be apparent in more than two dimensions, but visualizing multivariate structure in greater than two dimensions is extremely difficult. We suggest that it is more appropriate to evaluate simple structure in the dimensionality that the inventory exhibits.

Another issue in the genesis and quantification of simple structure involves the role of evaluation in responses to personality items. As has been known for some time, evaluative content ranging from good to bad is an important, often the most important, dimension of responses to personality items (Edwards, 1962). Before discussing how evaluation might influence simple structure, however, it may be constructive to briefly consider the various ways in which evaluation has been integrated with models of personality. Perhaps based on Allport’s contention that evaluation is not personality (Allport & Odbert, 1936), the multivariate studies that culminated in the FFM analyzed relatively non-evaluative personality descriptors (John & Srivastava, 1999) and excluded purely evaluative terms (such as bad or evil). Others, however, argued that evaluation represents an important dimension on which individuals differ from one another, and therefore reinstated the highly evaluative terms to the data sets from which the FFM was derived (Waller, 1999).

Multivariate analyses based on both descriptive and evaluative items seem to conform to a seven-factor solution. The first five of these are similar to the FFM, whereas the latter two tap positive and negative valence, respectively (Waller, 1999), suggesting that evaluation represents a trait domain orthogonal to the Big Five. More recent studies, however, have demonstrated that the two evaluative factors are to some extent present within the FFM, and have suggested that it may therefore be unnecessary to measure them separately from the FFM (Durrett & Trull, 2005; Simms, 2007).

The proper role of evaluative content in personality structure is a complex issue that we will not resolve in this paper. Instead, we will be concerned with the empirical hypothesis that evaluative content can introduce simple structure to domains that would not otherwise display it. Consider Figure 1, which is reproduced from Figure 1 in Hofstee et al. (1992), and which was taken by Hofstee et al. as evidence of simple structure in the relation between conscientiousness and openness. The simple structure arising in the dominant dimension running from the lower left to the upper right is entirely defined by evaluation, with negative traits to the left and positive traits to the right. Likewise, in the study by Peabody and Goldberg (1989), evaluation projected the broad traits into two clusters, divided by their goodness and badness. Within these clusters, however, the items were relatively evenly distributed, suggesting that it may be the evaluative content of the items that produces simple structure in personality items. In our analysis, we aim to demonstrate that simple structure decreases after evaluation is isolated from the rest of the structure of the items.

Figure 1.

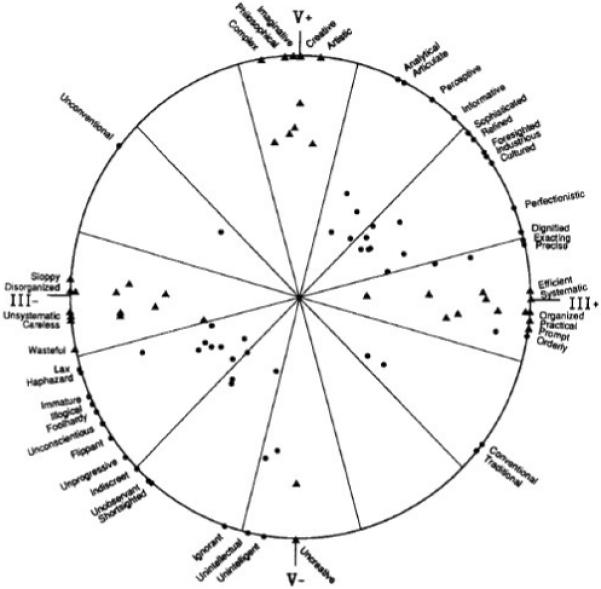
Plot of Conscientiousness and Openness. From “Integration of the Big Five and circumplex approaches to trait structure.” by W. K. B. Hofstee, B. de Raad, and L. R. Goldberg, 1992, Journal of Personality and Social Psychology, 63, p. 153.

We circumvented the two aforementioned methodological problems in evaluating simple structure, and explored the impact of the evaluative variance on simple structure, by examining two very different data sets. The first, a relatively unselected set of lexical self-report descriptors, has been analyzed by Saucier (1997). The second is a set of responses to a carefully constructed personality inventory, the International Personality Item Pool (IPIP) Big Five Factor Markers (BFFM; Goldberg, Johnson, Eber, Hogan, Ashton, Cloninger, & Gough, 2006), collected by Salthouse and colleagues (Salthouse, 2009) as part of a large-scale study of aging and cognition. Our hypothesis is that the latter should conform to simple structure, whereas the former should not. We demonstrate the importance of the evaluative content and its impact on simple structure by contrasting loadings matrices with evaluation spread out across all factors against loading matrices in which evaluation is rotated onto a separate orthogonal dimension. Based on Peabody and Goldberg (1989), we hypothesized that the non-evaluative dimensions among loading matrices in which evaluation is isolated would display a greater degree of complexity.

Method

Measures

Establishing which lexical descriptors should be considered relevant to personality (Step 1 in the sequence above) is not a straightforward task. We started with a subset of 500 personality-related adjectives, originally identified by Saucier (1997). Saucier began with a list of 3,446 adjectives rated as relatively easy to understand. Subsequently, the adjectives were rated for difficulty, leading to a list of 500 terms considered to be reasonably comprehensive and interpretable. These terms were grouped as either stable traits; temporary states and activities; social roles, relationships, and effects; evaluative terms and qualifiers; and anatomical medical, physical, and grooming terms. We selected only the stable traits and temporary states and activities for the current analysis. This resulted in a list of 262 adjectives. We then deleted 67 additional items that were more related to intelligence than personality (e.g., smart, intelligent, and retarded), were highly situational (e.g., humiliated, exhausted, and comfortable), or had very strong evaluative connotations (e.g., violent, alcoholic, and bad). The final list of 195 adjectives is given in Table 1.

Table 1. Unselected Lexical Descriptors with Communality and Percent Descriptive Variance.

Item	Com	Desc
Active	0.20	45
Adventurous	0.22	82
Agreeable	0.29	17
Alert	0.44	43
Alone	0.16	38
Ambitious	0.22	64
Amusing	0.30	87
Angry	0.50	30
Annoyed	0.46	30
Anxious	0.35	46
Argumentative	0.39	49
Arrogant	0.45	49
Artificial	0.28	7
Artistic	0.12	83
Assertive	0.38	87
Attentive	0.19	21
Awkward	0.29	34
Bashful	0.23	57
Believable	0.16	38
Bitter	0.35	23
Bossy	0.39	67
Calm	0.20	5
Caring	0.55	58
Casual	0.05	80
Closed-minded	0.19	11
Compassionate	0.52	58
Competitive	0.22	100
Complaining	0.42	21
Compulsive	0.21	43
Conceited	0.25	68
Concerned	0.29	79
Confident	0.56	50
Conscientious	0.46	48
Considerate	0.55	29
Consistent	0.31	48
Constructive	0.22	55
Controlling	0.38	76
Cooperative	0.29	31
Crabby	0.54	26
Cranky	0.39	31
Creative	0.19	79
Cruel	0.32	25
Curious	0.19	68
Daring	0.28	100
Dedicated	0.32	56
Defensive	0.28	29
Demanding	0.37	81
Dependable	0.37	59
Dependent	0.14	71
Depressed	0.41	39
Devoted	0.25	48
Dishonest	0.11	18
Disobedient	0.19	32
Dominant	0.38	95
Down-to-earth	0.13	38
Eager	0.40	65
Easygoing	0.19	32
Effective	0.44	64
Efficient	0.34	62
Entertaining	0.43	79
Enthusiastic	0.47	57
Ethical	0.25	48
Excited	0.41	83
Expressive	0.44	73
Fair	0.29	34
Faithful	0.22	36
Flexible	0.27	26
Forward	0.31	94
Friendly	0.50	32
Generous	0.32	53
Gentle	0.42	52
Genuine	0.40	40
Good-humored	0.43	28
Good-natured	0.40	30
Gracious	0.30	30
Greedy	0.32	19
Grouchy	0.48	27
Grumpy	0.52	29
Happy	0.40	22
Hard-working	0.19	63
Helpful	0.49	29
Honest	0.35	40
Hostile	0.44	25
Hot-tempered	0.38	45
Humorous	0.29	83
Idealist	0.13	62
Imaginative	0.22	59
Impolite	0.28	18
Impulsive	0.25	96
Inconsiderate	0.36	8
Indecisive	0.28	39
Independent	0.26	69
Insensitive	0.25	20
Intellectual	0.12	75
Irresponsible	0.35	37
Irritable	0.49	33
Jealous	0.26	35
Joyful	0.46	30
Kind	0.57	37
Kind-hearted	0.63	46
Laid-back	0.10	60
Level-headed	0.44	43
Logical	0.31	68
Lonely	0.33	33
Lonesome	0.36	31
Loud	0.31	77
Loving	0.46	52
Loyal	0.33	45
Materialistic	0.12	67
Mature	0.28	32
Modest	0.12	83
Narrow-minded	0.21	10
Natural	0.21	29
Negative	0.46	13
Neighborish	0.25	36
Nervous	0.29	59
Nice	0.29	34
Noisy	0.28	86
Obnoxious	0.38	34
Observant	0.20	50
Obsessive	0.35	40
Open	0.32	53
Open-minded	0.21	38
Opinionated	0.28	86
Organized	0.30	63
Original	0.25	76
Outgoing	0.44	64
Patient	0.25	12
Peaceful	0.28	11
Perceptive	0.20	40
Persistent	0.33	85
Persuasive	0.40	82
Phony	0.23	22
Pleasant	0.43	23
Polite	0.34	29
Practical	0.38	63
Prejudiced	0.17	12
Preoccupied	0.24	29
Private	0.07	100
Productive	0.36	61
Professional	0.21	71
Punctual	0.16	62
Realistic	0.31	68
Reasonable	0.31	16
Relaxed	0.20	15
Reliable	0.41	59
Resourceful	0.34	53
Respectful	0.36	33
Responsible	0.48	56
Rowdy	0.27	81
Sad	0.52	33
Scared	0.43	42
Self-assured	0.53	45
Self-centered	0.32	31
Self-confident	0.56	57
Self-sufficient	0.29	55
Self-supportive	0.15	80
Sensible	0.37	49
Sensitive	0.31	71
Serious	0.17	100
Shallow	0.19	11
Short-tempered	0.39	44
Shy	0.21	62
Social	0.33	45
Soft-spoken	0.12	92
Sophisticated	0.12	83
Stingy	0.22	9
Straight	0.26	58
Strong	0.22	73
Stubborn	0.20	65
Stuck-up	0.30	43
Supportive	0.42	48
Suspicious	0.30	27
Sweet	0.27	56
Temperamental	0.37	38
Tense	0.39	49
Thorough	0.43	65
Thoughtful	0.44	36
Tolerant	0.27	44
Tough	0.21	100
Trusting	0.22	27
Trustworthy	0.40	45
Uncomfortable	0.41	20
Undependable	0.25	36
Understanding	0.43	42
Unfriendly	0.38	8
Unhappy	0.46	17
Unreasonable	0.36	8
Unreliable	0.32	28
Unstable	0.37	16
Upset	0.45	36
Warm	0.54	54
Warm-hearted	0.62	56
Wishy-washy	0.33	33
Witty	0.28	89

Note. Com = Communality; Desc = Percent of communality that is descriptive variance.

We contrasted the lexical analysis with an instrument specifically designed to measure the Big Five. The International Personality Item Pool (IPIP) Big Five Factor Markers (BFFM; Goldberg, 1999; Goldberg et al., 2006) consists of 50 brief items such as Am the life of the party, Like order, and Worry about things, designed to tap the Big Five domain. Starting with about 750 Big Five items translated into English from Dutch, Goldberg added roughly 500 more to create the IPIP. Out of these 1,252 items, the 50 that correlated the highest with the Big Five Factor Markers (Goldberg, 1992) were chosen to describe this domain.

Participants

Lexical Data

The 195 lexical descriptors were mailed to members of a community sample consisting of residents in a medium-sized western city (see Saucier, 1997, for more details). Seven-hundred (400 women) participants returned protocols with no missing responses and were included in the analyses. The average age was 52 (SD = 13). One participant was omitted from the analyses because his or her use of the response scale was obviously in the opposite direction of everyone else’s.

IPIP Big Five Factor Markers

As part of a large-scale study on intelligence and aging (see Salthouse, 2009, for more details), 2640 participants (65 percent women) completed the IPIP BFFM. The average age was 51 (SD = 19), and the average length of education was nearly 16 (SD = 2.70). Participants were recruited through newspaper advertisements, flyers, and referrals from other participants.

Statistical Analysis

The following procedure was applied to both the lexical descriptors and the IPIP BFFM. First, we decided how many factors to extract based on inspection of the Eigenvalues and a scree plot. Second, we conducted an exploratory factor analysis using Mplus 5.2 (Muthen & Muthen, 2007) with maximum likelihood estimation and orthogonal Geomin rotation (Yates, 1987). Third, after interpreting the dimensions, we evaluated whether the configuration conformed to simple structure. This EFA sequence was conducted twice in each dataset, once using the rotation obtained from the Geomin algorithm, and once after rotating evaluation onto a separate dimension.

We rotated evaluation onto a factor by first having a separate set of participants rate how socially desirable each item would be to possess (cf. Edwards, 1962). After confirming that raters tended to agree on the evaluativeness of the items, we averaged them across raters, centered these around the likert-scale midpoint, and computed the factor loadings that would produce the mean evaluation ratings as regression-based factor scoring weights using the formula,

$$Rb=s$$

where R equals the item covariance matrix, b equals the mean evaluation ratings, and s equals the factor structure associated with those evaluation ratings, or regression weights. Subsequently, we fixed an evaluation factor to these regression weights. Finally, we extracted exploratory factors orthogonal to this evaluation dimension.

We employed two indices of simple structure: Cattell’s hyperplane count (1952) and Hofmann’s row-complexity index (1978). The hyperplane count consists of the total number of loadings with an absolute value less than 0.10. The rationale is that in a perfect simple structure solution, most loadings should fall within the so-called hyperplane, that is, lie close to the rotated dimensions. Because a perfect simple structure solution is expected to have k-1 loadings for each item in the hyperplane, where k equals the number of rotated factors, we scaled the hyperplane count by k. For example, a solution having perfect simple structure in a three-dimensional space is expected to have two-thirds of the loadings on each item falling in the hyperplane. By dividing the hyperplane count by 2/3, a perfect simple structure solution would generate an index of 1.0, that is, 100 percent of the loadings would fall within the hyperplane. This way, we are able to compare how closely a solution approaches simple structure across different dimensionalities.

Hofmann’s (1978) complexity index represents the average number of latent variables needed to account for the manifest variables. Whereas a perfect simple structure solution has a complexity of one in that each item would only load on one factor, a solution with evenly distributed items has a complexity greater than 1. For each item, the sum of the squared loadings is squared, and then divided by the sum of the fourth powers of the loadings. A mean is then computed across the items. Let c_i represent the complexity of the ith variable in any rxk loading matrix a, where r represents the number of rows. Then

$$c_i=\frac{{\left(\sum _{j=1}^r{a}^{2}ij\right)}^2}{\sum _{j=1}^r{a}^{4}ij}$$

Hofmann’s complexity index performs well on Thurstone’s classical box problem (1977).

Because there are no well-established guidelines for what values these indices should generate when loadings conform to simple or complex structure, we simulated two extreme types of structures. At one extreme, we simulated data that conformed to perfect simple structure, and at the other, we simulated data that were uniformly distributed in multidimensional space. These simulated data consisted of the same number of rows and columns of the original data sets in order to allow for a fair comparison. Further, we matched the strength of the simulated loadings with the raw data by taking the average of the largest loading in each row of the loading matrix resulting from the raw data. We then simulated data with loadings equal to this average in order to make the simulated data as close as possible to the raw data.

The simulation was conducted in R (Team, 2009), and the code is available upon request from the authors. The procedures are a k-dimensional generalization of an algorithm written for two dimensions by Revelle (2009). First, to simulate a simple structure solution for n persons on v variables represented in k dimensions, k latent factor vectors Θk were simulated by drawing n scores from each of k normal distributions, and then scaled by setting the standard deviation equal to the desired average loading. A vxk matrix Pk consisting values of zero, one and negative one was generated to describe the desired simple structure factor pattern. Third, the respective columns were outer-multiplied, creating a final matrix consisting of n rows and k columns that conform to simple structure. To create a solution with evenly distributed loadings without simple structure, the normally distributed Θk vectors were orthonormalized following Marsaglia’s (1972) equation. These orthonormalized columns were outer-multiplied by the original normal distributions, creating evenly distributed items in a given dimensionality. A small amount of error was added to each solution after the final step in order to enable factor analytic inversion of the matrix.

Results

Lexical descriptors

Exploratory Factor Analysis

The first ten Eigenvalues for the lexical descriptors were 34.70, 13.55, 9.04, 7.31, 5.02, 4.15, 3.17, 2.63, 2.58, and 2.36, and we opted to extract the first four factors and treated the rest as scree. Additionally, we extracted up to seven factors as the scree-plot was somewhat inconclusive, but we only display the four-factor solution here (the higher-dimensional solutions are available upon request from the first author). The four-factor solution accounted for 33 percent of the variance, and provided close fit (Browne & Cudeck, 1993) to the data (RMSEA = 0.044, 90% CI: 0.044-0.045; χ² = 43140.185, df = 18141, p < .001). The ten highest and lowest loadings on each factor are displayed in Table 2. The first dimension was characterized by adjectives such as unfriendly, impolite, self-centered, and arrogant at one end, and by kind-hearted, caring, warm, loving at the other end. We interpreted this dimension as agreeableness, as it appears to tap a willingness to help others versus acting selfishly. The second dimension included loadings such as responsible, thorough, reliable, and logical at one end, and negative loadings consisting of undependable, wishy-washy, unstable, rowdy, and impulsive at the other. We considered this dimension as conscientiousness, as it describes an (in)ability to exert sustained self-control. The third dimension consisted of items such as self-confident, confident, outgoing, enthusiastic, and enthusiastic at one end, and shy, soft-spoken, unhappy, indecisive, and lonely at the other. We interpreted this dimension as surgency because it appears to tap a tendency to assert oneself versus displaying social hesitation and reticence. The fourth dimension was described by items such as self-assured, relaxed, calm, patient, and peaceful at one end, versus angry, grumpy, irritable, annoyed, grouchy, and tense at the other end. Because this dimension consists of items describing a broad range of negative emotions, we interpreted it as neuroticism.

Table 2. Exploratory Factor Analysis of Unselected Lexical Descriptors.

Agreeableness		Conscientiousness		Surgency		Neuroticisism
Item	Loading	Item	Loading	Item	Loading	Item	Loading
Unfriendly	−0.51	Irresponsible	−0.46	Shy	−0.38	Self-assured	−0.40
Inconsiderate	−0.42	Unreliable	−0.42	Bashful	−0.37	Relaxed	−0.38
Insensitive	−0.41	Undependable	−0.40	Soft-spoken	−0.30	Happy	−0.38
Stuck up	−0.37	Wishy-washy	−0.39	Unhappy	−0.29	Calm	−0.37
Impolite	−0.36	Unstable	−0.32	Sad	−0.29	Peaceful	−0.36
Stingy	−0.36	Phony	−0.32	Indecisive	−0.28	Self-confident	−0.34
Self-centered	−0.35	Indecisive	−0.29	Depressed	−0.25	Confident	−0.33
Arrogant	−0.33	Obnoxious	−0.27	Scared	−0.24	Patient	−0.32
Artificial	−0.32	Uncomfortable	−0.27	Lonely	−0.22	Joyful	−0.29
Unreasonable	−0.32	Awkward	−0.26	Uncomfortable	−0.22	Good-natured	−0.26
Helpful	0.64	Logical	0.51	Expressive	0.53	Complaining	0.60
Loving	0.64	Alert	0.51	Excited	0.53	Tense	0.60
Understanding	0.65	Reliable	0.51	Enthusiastic	0.54	Grouchy	0.63
Considerate	0.66	Efficient	0.51	Persuasive	0.54	Irritable	0.64
Warm	0.67	Sensible	0.52	Forward	0.55	Annoyed	0.64
Compassionate	0.72	Realistic	0.53	Assertive	0.55	Sad	0.65
Caring	0.74	Level-headed	0.54	Confident	0.57	Upset	0.65
Kind	0.74	Thorough	0.56	Outgoing	0.57	Grumpy	0.66
Warm-hearted	0.78	Responsible	0.56	Self-confident	0.60	Angry	0.68
Kind-hearted	0.80	Practical	0.57	Entertaining	0.60	Crabby	0.68

Non-Evaluative EFA

To investigate the role that the evaluation dimension played in the multivariate structure of the lexical items, we isolated the evaluative variation onto a single factor by conducting Exploratory Structural Equation Modeling (ESEM; Asparouhov & Muthen, in press) using Mplus 5.2 (Muthen & Muthen, 2007). In order to derive the evaluation factor, we first had participants rate how evaluative each item was (c.f. Edwards, 1962), and because raters tended to agree on the evaluativeness of the items (coefficient alpha = .95), we computed the mean across the evaluation ratings for each item and centered this index around the likert-scale midpoint. Then we computed the factor loadings that would produce the mean evaluation ratings as regression-based factor scoring weights, and fixed a factor to those loadings. Second, we extracted three exploratory factors orthogonal to the evaluative dimension, rendering the exploratory factors non-evaluative (cf. Paulhus, 1981). Thus, this model is essentially a rotation of the original EFA solution in which evaluation is isolated onto a separate factor corresponding as closely as possible to the empirically derived evaluation ratings.

The model fit that data well (RMSEA = .044; 90% CI: .043-.045; χ² = 43180.06, df = 18332, p < .001). The ten highest and lowest loadings on each of the dimensions are displayed in Table 3. The first dimension, which was fixed to the evaluation ratings, consisted of items such as negative, crabby, sad, and angry at one end, and of kind, friendly, happy, and self-assured at the other. The second dimension was characterized by items such as self-confident, self-assured, stuck-up, and unfriendly at the negative end, and by warm-hearted, caring, sensitive, scared, tense, and nervous at the positive end. We interpreted this dimension as sensitivity vs. insensitivity to characterize the positive and negative behavioral consequences of high and low negative affect. Negative loadings on the third dimension included irresponsible, unreliable, laid-back, easygoing, and undependable at one end, and responsible, reliable, logical, serious, and demanding at the other end. Based on previous literature, we labeled this dimension tight vs. loose to capture the positive and negative consequences of exerting self-control (Peabody, 1967). The fourth dimension consisted of items such as soft-spoken, shy, bashful, modest, honest, indecisive, and gentle at one end, and by items such as forward, daring, outgoing, dominant, loud, and rowdy at the other end. We interpreted this dimension as assertiveness vs. unassertiveness, as it replicates previous findings based on non-evaluative lexical descriptors (Peabody, 1967; Saucier, Ostendorf, & Peabody, 2001).

Table 3. Exploratory Structural Equation Modeling of Unselected Lexical Markers.

Evaluation		Sensitive- Insensitive		Tight- Loose		Assertive- Unassertive
Item	Loading	Item	Loading	Item	Loading	Item	Loading
Negative	−0.63	Self-confident	−0.30	Irresponsible	−0.30	Soft-spoken	−0.30
Crabby	−0.63	Self-assured	−0.29	Unreliable	−0.29	Shy	−0.29
Unhappy	−0.61	Confident	−0.25	Undependable	−0.28	Bashful	−0.27
Grumpy	−0.61	Self-supportive	−0.20	Laid-back	−0.21	Modest	−0.21
Sad	−0.6	Competitive	−0.18	Wishy-washy	−0.21	Indecisive	−0.17
Angry	−0.59	Unfriendly	−0.16	Tolerant	−0.21	Honest	−0.16
Grouchy	−0.59	Insensitive	−0.16	Easygoing	−0.21	Gentle	−0.15
Unfriendly	−0.59	Stuck-up	−0.16	Phony	−0.19	Faithful	−0.14
Unreasonable	−0.58	Self-sufficient	−0.15	Good-natured	−0.18	Unhappy	−0.12
Irritable	−0.58	Organized	−0.12	Happy	−0.16	Ethical	−0.12
Self-assured	0.54	Scared	0.42	Sensible	0.43	Witty	0.50
Good-humored	0.56	Gentle	0.44	Level-headed	0.43	Dominant	0.50
Happy	0.56	Loving	0.44	Conscientious	0.43	Expressive	0.52
Joyful	0.56	Warm	0.45	Logical	0.43	Outgoing	0.52
Pleasant	0.58	Kind	0.46	Realistic	0.44	Persuasive	0.52
Friendly	0.58	Sensitive	0.47	Dependable	0.45	Assertive-	0.53
Kind-hearted	0.59	Kind-hearted	0.54	Reliable	0.46	Daring	0.53
Helpful	0.59	Compassionate	0.54	Practical	0.49	Excited	0.54
Kind	0.60	Caring	0.56	Thorough	0.49	Forward	0.54
Considerate	0.62	Warm-hearted	0.58	Responsible	0.50	Entertaining	0.57

Proportion of Evaluative and Descriptive Variance

It is important to note that because evaluation appears to exist to some extent in all personality scales (Durrett & Trull, 2005; Simms, 2007), we treated it as a continuous construct. That is, evaluation does not represent a black or white concept in the sense that some items are completely evaluative whereas others are completely descriptive. Instead, evaluation is continuously distributed among the item pool. To demonstrate this, for each item, we decomposed the communality into evaluative and descriptive variance, as displayed in Table 1. For example, some items, such as unfriendly, are more evaluative than others, such as tough. As a consequence, the former loaded more strongly on the evaluative dimension, whereas the latter contained more descriptive variance.

Assessment of Simple Structure

Next, to examine the extent to which the exploratory factors identified by the Geomin rotation, and the solution in which the exploratory factors were isolated from evaluation conformed to simple structure, we compared their factorial complexity to simulated data sets. Specifically, we applied Cattell’s hyperplane count and Hofmann’s complexity index to the loadings of the evaluative and non-evaluative configurations, as well as to simulated simple and complex structures, to quantify the extent to which the loadings conformed to simple structure (Table 4). We began by investigating the solution that relied on the Geomin rotation. The hyperplane count for a simulated perfect simple structure was 1.00, whereas the hyperplane count for a simulated perfectly uniform structure was 0.42. That is, for a four-dimensional solution with perfect simple structure, you would expect to find 100 percent of the loadings within the hyperplane. For a four-dimensional solution with perfect complex structure, on the other hand, you would expect to find 41 percent of the loadings within the hyperplane. The four-dimensional lexical markers (based on the Geomin rotation) generated a hyperplane count of 0.42, meaning that the items were more or less evenly distributed across the multivariate space. Turning to the Hofmann complexity index, the average number of factors required to account for a variable in a simulated perfect simple structure was 1.04. In contrast, in a simulated perfectly continuous structure, the average number of factors required to account for a variable was 2.05. The lexical markers generated a complexity index of 1.89. Thus, both indices suggested that the Geomin rotated, four-dimensional lexical descriptors were relatively evenly distributed in the multivariate space.

Table 4. Assessment of Simple Structure Among the Unselected Lexical Markers.

	Evaluative Factors		Non-evaluative factors
	Simple structure indices		Simple structure indices
Dimensionality	Hyperplane	Complexity	Hyperplane	Complexity
Three dimensions
Simulated simple structure	-	-	0.98	1.07
Adjective Structure	-	-	0.54	1.64
Simulated sphericity	-	-	0.53	1.72
Four dimensions
Simulated simple structure	1.00	1.04	0.99	1.09
Adjective Structure	0.42	1.89	0.55	1.92
Simulated sphericity	0.42	2.05	0.54	2.05
Five dimensions
Simulated simple structure	1.00	1.05	0.98	1.13
Adjective Structure	0.46	2.10	0.59	2.18
Simulated sphericity	0.44	2.38	0.59	2.34
Six dimensions
Simulated simple structure	1.00	1.06	0.99	1.13
Adjective Structure	0.49	2.27	0.61	2.33
Simulated sphericity	0.46	2.68	0.61	2.67
Seven dimensions
Simulated simple structure	0.99	1.08	0.99	1.16
Adjective Structure	0.55	2.39	0.65	2.47
Simulated sphericity	0.49	3.02	0.64	2.81

We then proceeded to examine the three non-evaluative factors based on the loading matrix in which evaluation had been isolated onto a separate factor. The hyperplane count for a simulated perfect simple structure in three dimensions was 0.98, and 0.53 for a perfectly continuous structure. The hyperplane count for the non-evaluative lexical descriptors was 0.54. The average number of factors to account for a variable was 1.07 for simulated perfect simple structure, and 1.72 for an evenly distributed solution. The average number of factors required to account for a variable in the non-evaluative lexical markers was 1.64.

In order to investigate if the items would align more closely with the factors in a higher-dimensional space, we also examined the degree of simple structure in five, six, and seven-factor solutions. The results revealed that the lack of simple structure was not attributable to the number of extracted factors, as solutions in higher-dimensional spaces still appeared very similar to simulated solutions with items evenly distributed across the multivariate space (Table 4).

An Alternate Rotation

The complex structure of the three nonevaluative solution for the adjectives implies that the rotated dimensions identified by the Geomin rotation procedure were quite arbitrary. To demonstrate this, we compared a cross-loading adjective in the Geomin solution (warm, with a loading of .45 on sensitive vs. insensitive, −.11 on tight vs. loose, and .26 on assertive vs. unassertive) to an adjective that manifested simple structure (sensitive, with a loading of .47 on sensitive vs. insensitive, .02 on tight vs. loose, and −.01 on assertive vs. unassertive). The typical interpretation of complex loadings such as those found for warm (if the item were not summarily eliminated from the pool) would be to say that it is a blend of all three factors, whereas sensitive is purely a reflection of sensitivity. That interpretation would be literally true, but it is not necessary.

We constructed an alternate rotation of the three non-evaluative factors, in which warm was constrained to load freely on one factor, with zero loadings on the other two factors. Under this alternate rotation, the second factor consisted of positive loadings such as warm (as designed), supportive, sensitive, impulsive, outgoing, noisy, and understanding, and negative loadings on realistic, unfriendly, consistent, practical, and organized. This dimension appeared to contrast pragmatism and interpersonal coldness against warmth and sociability. The first factor tapped a construct akin to dominant versus submissive, with positive loadings on dominant, assertive, bossy, entertaining, loud, and hot-tempered, and negative loadings on gentle, shy, bashful, scared, kind-hearted, and compassionate. The third factor included positive loadings such as responsible, conscientious, serious, ethical, genuine, tense, and sad, and negative loadings such as unreliable, happy, rowdy, amusing, and relaxed. This dimension appears to contrast dependability and uptightness against disinhibition and calmness. The alternative rotation had the same fit to the data as the original one.

In the original rotation, warm was a complex blend of all three factors, whereas sensitive was a simple indicator of sensitivity. In the new rotation, warm was by design a perfectly simple indicator of warmth and outgoingness, whereas sensitive became a complex blend of tenderness (loading = −.18), warmth (loading = .39) and dependability (loading = .20). Which rotation is correct? Both and neither: the two rotations fit the data equally well, and neither of them has an exclusive claim to the “real” multivariate structure of the data. The two rotations represent alternate but mathematically equivalent means of parameterizing a three-dimensional item pool that is continuously distributed in three-space. The covariances among the adjectives and the structural model we fit to them are given by the data, but the axes we use to parameterize the multivariate space are up to us.

IPIP BFFM

Exploratory Factor Analysis

To contrast these findings with a set of items designed to tap pre-determined constructs, we conducted the same analyses on the IPIP BFFM. The first ten eigenvalues for this instrument were 7.34, 4.84, 3.72, 3.07, 2.31, 1.51, 1.26, 1.04, 1.01, and 0.95, and we retained the first five factors and considered the rest as scree. This solution accounted for 43 percent of the variance, and provided close fit to the data (RMSEA = 0.047, 90% CI: 0.046-0.048; χ² = 6795.84, df = 985, p < .001). The highest and lowest loadings on each factor are displayed in Table 5. We interpreted the first dimension as extraversion, as it was characterized by items such as Keep in the background, Don’t talk a lot, and Don’t like to draw attention to myself, at one end, and by items such as Am the life of the party, Start conversations, and Feel comfortable around people, at the other end. The second dimension appeared to tap neuroticism, as items such as Am relaxed most of the time, and Seldom feel blue, loaded at one end, and items such as Get upset easily, Have frequent mood swings, Worry about things, and Am easily disturbed loaded at the other end. The third dimension seemed to represent openness, with positive loadings including Am not interested in abstract ideas and Do not have a good imagination, and negative loadings including Have a rich vocabulary, Have excellent ideas, and Spend time reflecting on things, at the other end. The fourth dimension, which we labeled conscientiousness, consisted of positive loadings such as Leave my belongings around, Make a mess of things, and Shirk my duties, and negative loadings such as Get chores done right away, Like order, and Pay attention to details. The fifth dimension contained items such as Feel little concern for others and Insult people, at one end, and Take time out for others, Sympathize with others’ feelings, and Have a soft heart at the other end. We interpreted this dimension as agreeableness. This structure conformed perfectly to the intended scale structure (Goldberg, 1999).

Table 5. Exploratory Factor Analysis of the IPIP BFFM.

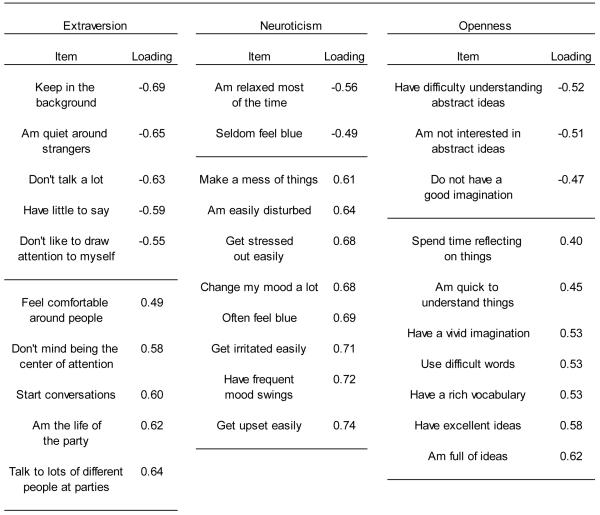
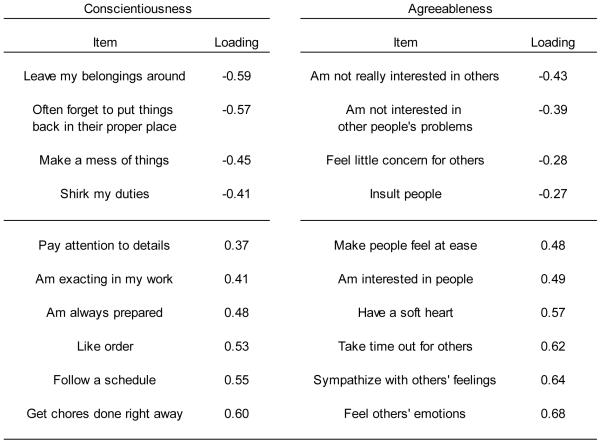
Note. IPIP BFFM = International Personality Item Pool Big Five Factor Markers.

Non-evaluative Exploratory Factor Analysis

We proceeded to isolate the evaluative content onto a separate dimension using the ESEM approach as described above. Participants tended to agree on which items were positive and negative (coefficient alpha = 0.78) and therefore we averaged the ratings into an index, centered them around the midpoint, and derived their corresponding regression weights, as described above. Subsequently, we fixed a factor to those factor loadings, and extracted four non-evaluative factors.

The highest and lowest loadings for each non-evaluative factor are displayed in Table 6. This model fit the data well (RMSEA = .046; 90% CI: .045-.047; χ² = 6838.61, df = 1030, p < .001). The first dimension, which was fixed to evaluation, included loadings such as Often feel blue, Get irritated easily, Make a mess of things, and Am not really interested in others at one end, and by Start conversations, Am relaxed most of the time, and Seldom feel blue at the other end. The second dimension consisted of positive loadings such as Am the life of the party, Don’t mind being the center of attention, Have frequent mood swings, and Change my mood a lot, and negative loadings such as Keep in the background, Am quiet around strangers, Am exacting in my work, and Spend time reflecting on things. We interpreted this dimension as high versus low arousal. At the positive end, the third dimension was characterized by items such as Get upset easily, Am full of ideas, Get stressed out easily, Have excellent ideas, and Spend time reflecting on things, and at the negative end by items such as Am relaxed most of the time, Seldom feel blue, Do not have a good imagination, and Am not interested in abstract ideas. We interpreted this dimension as sensitive versus insensitive. The fourth factor consisted of items such as Leave my belongings around, Make a mess of things, Have a vivid imagination, Have a rich vocabulary, and Shirk my duties, at the positive end, and by items such as Get chores done right away, Follow a schedule, Do not have a good imagination, and Have difficulty understanding abstract ideas at negative end. We interpreted this dimension as tight versus loose. The fifth dimension contained, at the positive end, items such as Feel others’ emotions, Have a soft heart, Am interested in people, Don’t like to draw attention to myself, and Have difficulty understanding abstract ideas, and at the negative end by items such as Am not really interested in other people’s problems, Feel little concern for others, Don’t mind being the center of attention, Insult people, and Have a rich vocabulary. We interpreted this dimension as tender versus tough.

Table 6. Exploratory Structural Equation Modeling of IPIP BFFM.

Note. IPIP BFFM = International Personality Item Pool Big Five Factor Markers.

Assessment of Simple Structure

Next, to examine the extent that the two solutions (with evaluation spread out across the entire loading matrix, and with evaluation isolated on a separate dimension) conformed to simple structure, we compared their complexity to simulated solutions. As with the lexical markers, we applied Cattell’s hyperplane count (the percentage of loadings falling within the hyperplane) and Hofmann’s complexity index (the average number of factors needed to account for a variable) to the loadings of the configuration identified by the Geomin rotation, the configuration with evaluation isolated onto a separate factor, and to simulated simple and complex structures, to quantify the extent to which the loadings conformed to simple structure (Table 7). Starting with the solution in which evaluation was to some extent present among all the factors, the hyperplane count was 1.00 for a simulated five-dimensional solution with perfect simple structure, and 0.37 for a perfectly continuous distribution. The hyperplane count for the BFFM identified by the Geomin rotation was 0.70, indicating that it consisted of a moderate degree of simple structure. Moving on to Hofmann’s complexity index, a simulated perfect simple structure generated 1.01, versus 2.22 for a continuous distribution. The Hofmann index was 1.43 for the BFFM, suggesting that it approached simple structure. Overall, each of these indices indicated that the BFFM was closer to simple structure than a continuous distribution. However, the inventory did not exhibit perfect simple structure, suggesting that even an instrument that is designed to have simple structure has meaningful cross-loadings. Four percent of the secondary Big Five loadings were greater than 0.30, and 76 percent were greater than 0.10.

Table 7. Assessment of Simple Structure Among the IPIP BFFM.

	Evaluative Factors		Non-evaluative factors
	Simple structure indices		Simple structure indices
Dimensionality	Hyperplane	Complexity	Hyperplane	Complexity
Four dimensions
Simulated simple structure	-	-	1.00	1.01
IPIP BFFM structure	-	-	0.53	1.71
Simulated sphericity	-	-	0.51	1.93
Five dimensions
Simulated simple structure	1.00	1.01	1.00	1.02
IPIP BFFM structure	0.70	1.43	0.55	2.00
Simulated sphericity	0.37	2.22	0.54	2.21

Note. IPIP BFFM = International Personality Item Pool Big Five Factor Markers.

Subsequently, we applied the hyperplane count and the complexity index to the four non-evaluative exploratory factors, based on the configuration in which evaluation was isolated onto a separate factor. In a simulated perfect four-dimensional simple structure solution, the hyperplane count was 1.00, and in a simulated evenly distributed four-dimensional solution it was 0.51. The hyperplane count for the non-evaluative BFFM was 0.53. In a perfect simple structure solution, the complexity index was 1.01, and in a continuous distribution it was 1.93. The complexity index for the non-evaluative Big Five was 1.71. In different words, according to both indices the non-evaluative factors appear to resemble a complex rather than simple structure. This remained true in a solution that extracted five non-evaluative factors (Table 7). Thus, it appears that even among the BFFM, which is an inventory designed to have simple structure, nearly all of the simple structure may be attributed to the evaluative dimension.

Discussion

Exploratory factor analysis of an unselected set of lexical descriptors produced a set of four rotated factors that are reasonably familiar from the Five Factor Model. But how necessary are those particular four dimensions as a means of describing personality space? The lexical descriptors were in fact distributed quite evenly throughout the four-dimensional factor space. The relatively small degree of simple structure resulted primarily from the markedly bimodal evaluative content of the items. Furthermore, an alternate rotation of the non-evaluative dimensions, which fit the data equally well, implied that the Geomin rotated factors were but one way of many to conceptualize its multivariate space.

The IPIP BFFM, in contrast, does have simple structure or something reasonably close to it, at least if the items are allowed to retain their evaluative content. Presumably this structure is an indicator of the success of the careful psychometric work that went into the instrument’s construction, but in this regard several important distinctions must be maintained. Any psychometric instrument starts with a large and inchoate set of potential items, which are then winnowed to produce scales with desirable psychometric properties. In a unidimensional context, for example, there is the familiar process of using item-total correlations to select items that share variability with the first principal component, resulting in a reduced set that measures a common latent construct with high internal reliability.

It might seem as though the process of selecting items that conform to a multivariate simple structure like the FFM is no more than the multivariate analog of maximizing coefficient alpha for a unidimensional scale, but that is not the case. The difference is rotational indeterminacy. A unidimensional scale, by definition, can only be identified in one direction, so the process of finding items that vary in that direction is unambiguous. But once the items are arrayed on a plane rather than along a line, which directions of variation are to be selected? An analogy with geographic space might be useful. For measuring location along a linear structure like a straight highway, mile-markers are sufficient and practically necessary. It would make little sense to measure location on a road in terms of a projection on another line that runs at an angle to the direction of the road. But in two-dimensional space, there is no “beginning” and “end” to determine the natural dimensions of the space. We are accustomed to north-south and east-west on a plane, and to latitude and longitude on a sphere, but both are arbitrary conveniences. Geographical features are continuously distributed on the surface of the earth; they do not cluster along the equator and the Greenwich Meridian. Geographical space lacks simple structure, so we are accustomed to the idea that compass directions and polar coordinates are human contrivances, not natural features we might expect to locate in the bedrock.

Simple Structure and Evaluation

One conclusion from this study is that simple structure is highly related to evaluation; specifically, evaluation is a source of simple structure. When the evaluative content was isolated from the descriptive variance, nearly all the simple structure in both the lexical and the BFFM disappeared. Why does this occur? The first reason is that evaluation is by its nature quite bimodal – there are many adjectives with relatively strong positive or negative connotations, but fewer with neutral valences. Consider the results of Peabody and Goldberg (1989), in which evaluation distinguished good from bad items, but within each evaluative cluster, the items were relatively evenly distributed. If evaluation had been removed, the positive and negative clusters would have collapsed on top of each other, thereby decreasing the degree of simple structure. Likewise, our analyses demonstrated that once evaluation was isolated, positively and negatively evaluated items loaded together, and as a consequence, simple structure decreased. It thus appears that evaluative variance polarizes items, and exploring data orthogonal to this dimension creates a model in which items become relatively seamlessly distributed.

The second reason why removing evaluation decreases simple structure is that personality inventories are often designed to have all the positive evaluative variance at one end of the dimension, and all the negative variance at the other. In the BFFM, for example, there are no positively evaluated ways to be low on conscientiousness or agreeableness. So positively evaluated items are high conscientiousness and agreeableness, negatively evaluated items are the reverse, and there is a paucity of evaluatively neutral items that might be low agreeableness and conscientiousness. When the evaluative variance is removed, however, the nonevaluative residuals may correlate in new ways. For example, non-evaluative low conscientiousness may relate to to being laid-back and spontaneous, and non-evaluative low agreeableness may relate to toughness and firmness. Such residuals then fill in the multivariate space in which there previously was only void, making the distribution of items more even.

We have chosen to rotate the configuration in a way that isolates the evaluative variation into a single dimension in order to clarify the role evaluation plays in the construction of simple structure, but we do not take a more general position on the proper role of evaluation in personality, a complex issue that would take us beyond the scope of this paper. On the one hand, there is no doubt that the tendency to describe oneself in generally positive or generally negative terms has meaningful correlations with important aspects of functioning, and thus should not be dismissed entirely from the personality matrix (Block, 1965). On the other hand, some have made the argument that it may be worthwhile to examine covariances among personality items separately from evaluation (e.g., Peabody, 1984; Saucier, 1994). When we describe ourselves or someone else as bossy and controlling, we are not only saying that that the person is authoritative, but also that we disapprove of him or her. If we instead describe that person as assertive and executive, we are again describing the individual as authoritative, but also expressing our approval. Once evaluation is separated from the descriptive variance, items such as bossy, controlling, assertive, and executive tend to cluster together on factors, as the positive and negative aspects of the same trait. If we are interested in whether someone is authoritative – separately from how we may feel about this authoritativeness – then rotating evaluation to a separate dimension may be worthwhile. Isolating evaluation in a separate dimension may offer a reasonable compromise between rotating evaluation into the trait space, as is commonly done today, versus treating evaluation as no more than a response bias that does not belong in the domain of personality.

Non-Evaluative Structure of the BFFM

After isolating the evaluative variance of the BFFM onto a separate dimension, the non-evaluative exploratory factors seem at first glance to be difficult to interpret. For example, non-evaluative extraversion items now clustered with arousability and moodiness, and non-evaluative neuroticism related to openness. Non-evaluative conscientiousness related to closedness, whereas disagreeableness now related to exhibitionism and self-reported intelligence. We suggest that there are two main reasons why these factors seem counterintuitive. First, in the context of a Five Factor instrument like the BFFM, psychologists have become accustomed to the traditional distribution of evaluation across the Big Five, with high agreeableness almost entirely positively evaluated and high neuroticism almost entirely negative. Second, because the BFFM was expressly constructed to be a measure of the traditional, evaluation loaded FFM, it lacks items in crucial regions of the space that might otherwise help identify the nonevaluative factors. The BFFM does not contain any positively evaluative items related to disagreeableness, so the EFA did the best it could with imperfect markers like exhibitionism and self-reported intelligence. The more varied and unselected content of the lexical markers, in contrast, allowed the non-evaluative dimensions to be identified more naturally at both ends of the dimensions.

Although the construct validity of non-evaluative factors is a matter for empirical investigation, we find considerable appeal in separating the descriptive aspects of personality from the relative evaluation of them, and thus including both positively and negatively evaluated exemplars of constructs at the same end of the factors. Most of the constructs we tentatively identified in the de-evaluated BFFM have a history in the personality literature. Regarding extraversion’s tendency to correlate with arousability, a 45 degree rotation of positive and negative affect produces two dimensions that are often interpreted as evaluation and arousal (Carroll et al., 1999). Items that load on the arousal dimension pertain to both positive (e.g., excited) and negative affect (e.g., nervous). Regarding neuroticism’s relation to openness items, some studies have noted that artists, who may be relatively high on openness, tend to also be more neurotic than people in other professions (Rubinstein & Strul, 2007). Erdle, Irwing, and Park (2009) have demonstrated that when the general factor of personality (which is highly related to the evaluative content of the items, Musek, 2007) is controlled, agreeableness and self-esteem are negatively related.

Implications

What are the implications for measurement and classification of personality if these results are taken at face value? We are not arguing that we should abandon the fixed scales that result from factor rotation; rather, we suggest that the complex structure of the multivariate trait space allows for more freedom in how to conceptualize and analyze personality (cf. McCrae & Costa, 1989). We can think of at least three ways this idea has already been recognized the field.

First, rather than committing to pre-determined scales, researchers may impose a theoretically informed rotation on their data that fits a given purpose or context by, for example, using a procrustean instead of varimax rotation, or by relying on confirmatory rather than exploratory factor analysis. Relying on this framework, McCrae, Zonderman, Costa, Bond, and Paunonen (1996) noted that the factor congruences, a measure of factor similarity across samples, was relatively low for extraversion and agreeableness between an American and Japanese sample. However, after applying a Procrustes rotation of the Japanese dimensions to the American dimensions, factor congruence increased substantially. Thus, rather than depending on an algorithm designed to maximize simple structure, which may have indicated that extraversion and agreeableness looked quite different in Japan compared to America, it may sometimes be worthwhile to rotate the axes to an arbitrary position in order to gain theoretical convergence.

Second, rather than examining how a fixed set of personality dimensions relate to outcomes, investigators may simply choose the set of personality dimensions that correlate maximally with a linear combination of the outcomes, for example, by relying on canonical correlation. In one study, Hampson and Goldberg (2006) examined the stability of the FFM dimensions from childhood to adulthood across 40 years. The five latent correlations ranged from .30 to −.02, with an absolute average of .17. A canonical correlation analyses, on the other hand, revealed that two canonical factors correlated .35 and .30 across the same timespan. Thus, instead of relying on fixed scales, which only rendered moderate across-time correlations, a more flexible approach revealed higher trait continuity from childhood to adulthood.

Third, rather than examining how a particular set of personality dimensions relate to a given outcome, researchers could instead correlate all the items with the outcome in order to get a more nuanced picture. This approach has been popular among users of the California Q-Sort (CAQ; 1978), and, we think, has led to interesting findings. For example, relying on this approach, items tapping under-control among adolescent males and over-control among adolescent females related to depression years later (Block, Gjerde, & Block, 1991). Although the latent dimensionality of the CAQ has been thoroughly investigated (Lanning, 1994), it is not certain that relying on those particular factors would have produced as rich results. As demonstrated by these examples, we suggest that embracing the rotational indeterminacy of the personality trait space may lead to new discoveries that would otherwise be hidden by the reliance on fixed coordinate systems.

Summary

Personality data dictate a space in some number of dimensions, with five a good answer for many purposes. A set of axes for multivariate personality space represent a convenient way to navigate it, much like latitude and longitude on an otherwise trackless ocean, but complex structures do not require traveling along pre-ordained routes. Equally valid alternative parameterizations of the same space may take us to different and surprising destinations. Instruments that select items conforming to preconceived notions about where the dimensions are supposed to lie can miss variation occurring interstitial to the fixed factors. Granted that abandoning a fixed dimensional system of parameterizing personality space would make navigation of it more difficult, the payoff in complex characterization of personality may in some instances be worth the price.