Abstract
The present work aims to study the effects of the blood-microstructure on the electrical conduction from two different but correlated properties: Electrical and mechanical (viscosity), and to derive useful parameters for the evaluation of electrical conduction as a function of the blood viscosity. ac-conductivity and dielectric constant of normal and diabetic blood are measured in the frequency range 10 kHz–1 MHz at the room temperature. An empirical relation relating the resistivity and viscosity of the blood has been presented. The results show that a microfluidic device is a viable and simple solution for determination of electrical and rheological behaviors of blood samples.
INTRODUCTION
In recent years the measurement of blood impedance through an alternating current has been suggested as a noninvasive approach to determine some blood disorders.1 Human blood has non-Newtonian fluid dynamic characteristics, the most important of which is the correlation between its microstructure and the electrical and mechanical properties. The intrinsic and extrinsic microcells, molecules, bacteria, protein, hormones, glucose, chemicals, vitamins, and antibodies affect drastically the chemical and physical characters of the viable fluid. For example, Zhouet al.2 showed that deformability of erythrocyte is found to alter the wetting dynamics of red blood cell (RBC) suspensions during their invasion into capillaries. This effect shows the importance of the RBC deformability on microvascular perfusion by directly measuring the flow of blood through a microchannel network with realistic dimensions and architecture similar to real microcirculation.3 This prevents eventually the congenital dyserythropoietic anemia.4 Moreover, Zhou and Chang5 found that blood suspension fails to penetrate a capillary with radius less than 50 μm even if the capillary is perfectly wet table. This is of great significance and consequences in evaluating blood flow occlusion after selective pulmonary artery perfusion.6 Moreover, Basuray and Chang7 demonstrated that the characteristic relaxation frequency of induced nanodipoles by dielectrophoresis is inversely proportional to the charging and discharging time of the diffuse-layer capacitance in microfluids, which affects both the electrical and mechanical properties of the blood.
In general, the electrical properties of human blood have received much of interest some decades ago for many reasons.8, 9, 10 First, they determine the pathways of current flow through the body and, thus, are very important in the analysis of a wide range of biomedical applications, such as functional electrical stimulation and the diagnosis and treatment of various physiological conditions with weak electric currents, radio-frequency hyperthermia, body composition, and electrocardiography.
Second, on a more fundamental level, knowledge of these electrical properties can lead to an understanding of the underlying basic biological processes either on macroscopic level or microscopic one and to correlate between the two extents. Third, biological impedance studies have long been important in electrophysiology and biophysics; one of the first demonstrations of the existence of the cell membrane is based on dielectric studies on cell suspensions.11 To analyze the response of the human blood to electric stimulation, one needs data on the specific conductivities and relative permittivities of the microbodies or micro-organs within that blood. A microscopic description of the response is complicated by the variety of cell shapes, their distribution inside the cytosol, as well as the various properties of the different components of blood. Therefore, a macroscopic approach is always a net result of several microscopic phenomena and is most often used to characterize field distributions not only in blood but also in biological systems as general. In the present work, it will be shown that the macroscopic electric and dielectric measurements of blood properties are due to several microscopic factors: Blood-inhomogeneity (intrinsic internal structure), physiological state of the blood, and the microbody starvation age12 that could play a role for the dielectrophoretic crossover frequency13 (cof) and the cof of the microbodies. It will be seen, in the present work, that this last frequency is correlated with the apparent, macroscopically measured, relaxation time of all the micro particles in the blood.
Moreover, any changes in blood physiology should produce changes in the blood electrical properties.14 This principle has been used to identify or monitor the presence of various illnesses or conditions such as body fluid shift, blood flow, cardiac output, and muscular dystrophy15 by various impedance diagnostic techniques, such as impedance thoracic impedance cardiograph, plethysmography, and rheoencephalography. For a detailed discussion of the applications of bioimpedance methods in medicine and biotechnology, one can see, for example, the work of Morucci et al.16 and Riu et al.17 If the blood flow is interrupted, both micro- and macroeffects will be manifested: Metabolism continues, but in an anaerobic way (macrophenomenon), while on the microlevel osmosis will cause cell swelling and finally tissue damage. As a consequence, the extracellular pathways narrow, which typically leads to an increase in the low frequency impedance (<10 kHz). The time of occurrence of these phenomena is different for different types of blood. Decreased blood flow also accounts for changes in its resistivity.18 In all cases, the conductivity increases with time and changes in the frequency range above 100 Hz are lower and take a longer time to occur. For these reasons, considerable caution must be taken in the interpretation of electrical measurements that are performed on excised blood. The electrical properties of blood also depend on its temperature. The mobility of the ions that transport the current increases with the temperature as the viscosity of the extracellular fluid decreases. A general increase of about 2% occurs in the conductivity of blood19 in the frequency range below 1 GHz up to a temperature of about 40 °C. Above that point, the cell membrane begins to deteriorate and allows the cytosol to leak into the extracellular space. The rapid increase of conductivity with temperature was suggested to be used to monitor the progress of hyperthermia treatment.20
In addition, electrical properties can also depend on the blood components not only the red and white cells but also, with the same importance, the different chemical compounds and biomaterials in vivo or in vitro those present in the blood and affect drastically the electrical properties. For example, plasma contains thousands of different substances, such as proteins, glucose, salts, vitamins, hormones, and antibodies. These substances are not as massive as the RBCs (and white blood cells) but they are, considerably, lighter. Moreover, the presence of some additional and permanent chemical substances in the blood alters the blood properties. Glucose, for example (the diabetes mellitus disorder), affects drastically the electric and dielectric properties of the blood.21 Accordingly, caution must be used in both the design of the measurement procedure and the interpretation of the experimental data.
Moreover, even on a macroscopic level, the electrical properties of blood are complicated. They can depend on the frequency of the applied field (the blood is neither a perfect dielectric nor a perfect conductor), or they can be time- and space-dependent (e.g., changes in blood conductivity during the process of electropermeability). For these reasons, the present contribution aims to give a first step to investigate a microscopic description of the electrical properties of blood by relating both macromeasurements (complex permittivity) with a microphenomenon (dielectrophoretic crossover frequencies) via the relaxation times of the different bodies in the blood. In this work, the term blood means human blood in the standard (normal) conditions without any malady-disorder, and the symbols n and D symbolize the normal and diabetic bloods, respectively. Also, the word sample stands for the blood sample.
EXPERIMENTAL METHODS
At room temperature, the electrical conductivity, σ, and the dielectric constant, , are measured in the frequency range from 10 kHz up to 5 MHz, as it was described by Desouky.21 The samples of heparinized venous blood are collected from 20 patients with diabetes mellitus. The patients are previously diagnosed and are under the supervision of medical professionals. Blood from ten healthy individuals were used as a normal control for this study.21
MODEL AND ANALYSIS
Inhomogeneities of blood
From the electrical point of view, blood is a very inhomogeneous material. The cells, for example, RBCs, themselves are comprised of an insulating membrane enclosing a conductive cytosol. A suspension of cells can be regarded at low frequencies simply as insulating inclusions in a conducting fluid. The insulation is provided by the cell membrane. At higher frequencies in the megahertz range, capacitive coupling across this membrane becomes more important. Beginning in this range, the dispersive properties of the membrane and ultimately the cytosol must also be considered. In blood, the cells are surrounded by an extracellular matrix of different ions, which can be extensive, as in the case of some diseases, for example, diabetes mellitus.21
Interestingly, blood does not contain cells of a single size and function which affects the electrical properties. For example, red cells and white ones have neither the same surface area nor the same mobility in the cytosol and are embedded in a conductive viscous fluid (plasma). The cells are perfused with the cytosol and affected by the external applied electric field on the same time as the conductive cytosol. It is thus difficult to extrapolate from the dielectric properties of a conductive viscous fluid to those of membrane. Moreover, a large discrepancy exists between various data on electrical properties of biological materials found in literature. Why is there such a wide range of values obtained by different researchers? Excised samples carry along with them various amounts of body fluids, and the lack of standardization of measurement techniques presents its own difficulties and probably widens the range of resistivity values. In addition, there are seasonal, aged, and disease-linked changes as well as those that accompany the physiological function of various biologic materials.17
As it is well known,22 blood consists of many components. These include plasma (55%) and components (45%). Of these components, 99% are erythrocytes (red blood cells) and 1% is leucocytes [white blood cells (WBCs)] and thrombocytes (blood platelets). Plasma contains thousands of different substances, such as proteins, glucose, salts, vitamins, hormones, and antibodies.22 These substances are by far lighter than the relatively massive RBCs and WBCs and their inertia at low frequency is negligible, which affects the conduction by linear transport rather than the oscillation motion. However, the presence of these light materials should not be neglected when studying the electrical properties of the blood because they lead to an important drift-scattered motion alongside E. Therefore, in the present work, the blood is considered as insulated cells suspended in a conducting fluid. The cells are classified according to their masses. Let the number of total bodies in the blood be n. These microgerms are arranged so that mass1>mass2>mass3⋯>(mass)n. So, under an external ac-electric field E and at the same environmental conditions, one should expect that the relaxation times of these masses are arranged as τ1>τ2>τ3⋯>τn. At a certain applied frequency, fapp=ωapp∕2π, where ωapp is the applied angular frequency, only certain number of the microbodies having relaxation time τ=1∕2πfapp will respond to the electric field and will form a flux of charges which moves carrying the electric energy alongside E, whereas the other part of bodies either having τ>1∕2πfapp or τ<1∕2πfapp will not match with the applied frequency and will have weak response to the applied electric field. So, they cannot carry the electric energy.
Moreover, these micromasses form electric dipoles, under the application of E, whose inertias are arranged as I1>I2>I3>⋯In. The heavy cells form freely rotated dipoles in the cytosol and, thus, have rotational motion under the application of external field besides minor linear motion, while the lighter cells are considered to have higher drift velocity in a linear motion besides minor rotational motion under the application of E. We will see in the next section that the rotational motion (which is more manifested for m1, m2 rather than mn−1, mn) leads to displacement current while the scattering-drift motion (which is more manifested for mn−1, mn rather than m1, m2) leads to conduction current.
Electrical properties of blood: Mathematical approach
In polar materials, such as blood, the positive and negative charge centers in the molecules do not coincide. An electric dipole moment is said to exist. Owing to the intensity of the electric fields required to move submicrometer particles, the Joule heating can be a problem, often giving rise to electrical forces induced by the variation in the conductivity and permittivity of the suspending medium [electrothermal forces (ETFs)], thus it is necessary that the amplitude of the applied electric field should be kept minimum during the measurements to avoid this ETF. Under this condition, an applied field tends to orient the dipole(s) which produces an opposing field. Moreover, all microbodies respond to the field in different manners: The light substances move abruptly with a certain scattering-drift motion that is nearly linear motion, with scattering on the different ions and charges that exist in their path. Due to their light masses, these particles have small rotational inertia at low frequencies and thus their rotational (oscillation) motion is so feeble that it is neglected in the low frequency range. However, at high frequencies, the high inertia leads to a macroscopic quantity called the infinite value of the dielectric constant, . Under the application of an ac-field, the electric energy is carried by all the particles but not in the same manner.
The linear motion of all the charged particles (dipoles) leads to a constant flux of charges which is referred to as conduction (Ohmic) current, Ic; whereas the rotational motion of the particles occurs with oscillations in order to follow the electric field and leads to a displacement current, Id (instantaneous energy storage within the particle). Thus, the net charge flux (macroscopic total electric current) flowing through the blood is the sum of the all the microcurrents: Both the conduction and the displacement currents. It is worth noting that these two currents are 90° apart in phase because of the difference in the trigonometric functions. This phase difference can be expressed conveniently by writing the time dependence of the applied voltage: V(t)=V0ejωt, where . The flux of the total charge carriers (or simply, current I in coulomb∕s A) is the sum of the conduction current, Ic, and the displacement current, Id, respectively, I=Ic+Id,
| (1) |
Here Rc and Rd are the electric resistance of the conduction and displacement current, respectively. One can write
| (2) |
Here Ici and Idi are the conduction and displacement currents that carried by any particle (i), respectively.
So, the current, I could be written as
| (3) |
where G is the conductance and it equals the inverse of its resistance, R,
The displacement current Id which arises from the rotational motion of all the particles through the cytosol is given by
| (4) |
Thus, the total current that passes through the blood can be represented as
| (5) |
where ω is the angular frequency: ω=2πf, f is the frequency of the applied electric field σci and σdi stand for the electrical conduction-conductivity and displacement-conductivity, respectively, of any particle in the blood. Similarly, εci and εdi represent the conduction-dielectric constant and displacement-dielectric constant, respectively, of any particle i, A and d are the effective area and the effective length, respectively, of the sample between the two electrodes, and ε0 is the reference dielectric constant ε0=8.855×10−12 F∕m.
The blood, then, can be characterized as having complex admittance, Y*, given by
| (6) |
where * indicates a complex-valued quantity. In terms of material properties, one can write a corresponding, complex conductivity,
| (7) |
Describing the blood in terms of its admittance emphasizes its ability to transport current. Alternatively, we could emphasize its ability to restrict the flow of current by considering its impedance, Z*=1∕Y*. Factoring jωε0 in Eq. 5 yields
| (8) |
One can write a complex-valued, relative permittivity as
| (9) |
with
This mathematical approach shows that as a dielectric dispersion is traversed by changing the frequency of measurement, the change in conductivity is directly proportional to the change in permittivity. This follows from the fact that the total energy in the field is constant (for a given voltage) and must either be stored [as reflected in ε′(ω)] or dissipated [as reflected in ε″(ω)] by the system with which it interacts. This allows an additional check upon the validity of the experimental data.
It is also true that the application of the Debye processes cannot be distinguished from a small distribution of relaxation times.23 We may therefore characterize any dielectric dispersion observed in biological materials in terms of two parameters only: The dielectric increment and the relaxation time (τc) or characteristic frequency fc:fc=1∕(2πτc).23 At this frequency, on a microscopic level, knowledge of the net force on the particle (dielectrophoretic) can lead to an understanding of the underlying basic biological processes: The particles (microdipoles) orient their position in order to get the lowest energy position, i.e., they direct themselves in order to have the minimum strength of the dielectrophoretic force. Following the pioneer study of Pohl24 on the subject, dielectrophoresis (DEP) is the net force experienced by a dielectric object in a nonuniform electric field (there is no net force in a homogeneous electric field). This effect exists because the dipole charges ±q induced at characteristic locations are subject to different values of the electric field. The DEP force can produce directed motion of electrically polarizable particles in the convergent field direction to neutralize the external field on the dipole moment and finally the dipoles relax with a relaxation time τc. The vector sum of the net DEP forces results in a net electric force on the charge carriers F=qNJ∕σ, where N is the density of charge carriers at any time t, J is the current density, q is the electronic charge, and σ is the electric conductivity. This force F is a macroscopic quantity.
To get the current density, J, one should consider the conservation of charge law (Kirchhoff’s law): It shows that the charge per second at any condition should be conserved, i.e., the charge per time at very low frequency should equal the charge per time at very high frequency and, also, should equal the charge per time at any time; thus one can write
| (10) |
where N0, N∞, and N are the density of charges at very low, very high frequency and at any frequency f, respectively. τ0, τ∞, and τ are the relaxation time of the particles at very low, very high, and at any frequency, respectively. The complex factor j is necessary because N is out of phase with respect to both N0 and N∞. Equation 6 leads to
| (11) |
Considering that there is no charge leakage, from the boundaries, through the blood flow N0≈N≈N∞, then Eq. 11 gives
| (12) |
which leads to
| (13) |
and
| (14) |
The real part of the relaxation time is given by
| (15) |
while the imaginary relaxation time as
| (16) |
Equation 16 matches exactly with the Debye model despite the present work starts from energy conservation (Kirchhoff’s) law rather than dipole relaxation (Debye model). Moreover, Eq. 16 means that the relaxation time τ is the time necessary for a set of particles having relaxation times in the range τ≈τc±Δτ=1∕2πfc±1∕2πΔfc to respond with the electric field (to try to orient themselves alongside with the applied field). One will see later in Sec. 4C that Δτ is correlated with the width of a Gaussian distribution of relaxation times. The difference between the crossover frequency and the relaxation time is that the former describes the dipole relaxation time reaction under an applied ac-field on microscopic level whereas the latter depict the same time necessary to try to orient the particles alongside with the applied field for a set of dipoles (macroscopic level). This means that under the application of an ac-electric field with very low frequency, the heavy particles (that have high inertia and high relaxation time) will curiously respond faster than the light particles whereas the very high frequency field will stimulate only the light particles.
Thus, our previously mentioned physical model considers the dipoles to be spheres whose rotation in response to the field is opposed by frictional interaction with the surrounding viscous medium. The relevant relaxation time for the orientation of such a sphere is given by25
| (17) |
where X is a molecular friction coefficient which relates the torque exerted on the dipolar molecule by the applied electric field to the molecule’s angular velocity, k is Boltzmann’s constant, and T is the absolute temperature. Assuming the dipole to be equivalent to a rigid sphere of radius R turning in a hydrodynamic fluid of viscosity coefficient η, the Stokes–Einstein relation gives X=(8πηR3) so that the relaxation time could be given as
| (18) |
Now, one applies Eq. 18 for the case of water molecules rotating in bulk water. At 293 K, the distance between adjacent oxygen molecules is 0.28 nm, i.e., R=0.14 nm. The viscosity of water is 10−3 kg m−1 s−1 (i.e., 1 m∕Pa s) so that the value for the relaxation time of water molecules at this temperature that one would derive from Eq. 18 is 8.5 ps, in excellent agreement with the experimentally observed value of 9.3 ps.26 Thus, one will fairly use this model in the next paragraph to interpret the electrical data of normal and diabetic blood.
RESULTS AND DISCUSSION
Electrical conductivity of normal and diabetic blood
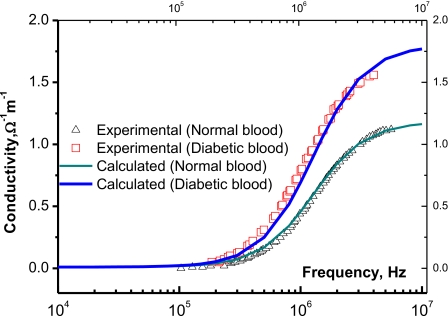
The behavior of the electrical conductivity of both the normal and diabetic bloods is illustrated in Fig. 1. Depending on the frequency, it is clear that the diabetic blood is (13%–43%) more conductive than the normal one. Now, we apply the previously described model to elucidate the experimental data.
Figure 1.
The electrical conductivity of normal and diabetic blood as a function of the applied frequency. Solid lines represent calculated values after Eq. 19 and triangles and squares are experimental data for normal and diabetic bloods, respectively.
First, we consider that n dipoles are suspended inside the cytoplasm, relax under the action of an external ac-field, and obey the Debye model.27 Applying this model on the present data, the conductivity, σ, is given as a function of the applied angular frequency, ω, as
| (19) |
The exact number of particles n is not easy to be defined; however, one can consider the following average quantities: σ0 is the average conductivity of the particles that move linearly leading to drift (dc) conductivity,
| (20) |
Similarly, the part of conductivity which is due to the rotational motion of the particles could be given as σac,
| (21) |
Here, τi is the relaxation time of any particle under the application of an ac-field; the sum over εdi gives the dielectric constant at low frequency (f→0), which gives εs the static dielectric constant; while the sum over εci gives the dielectric constant at high frequency (f→∞), which leads to ε∞ the dielectric constant at very high frequency,
| (22) |
and similarly,
| (23) |
and
| (24) |
Considering these averages, Eq. 19 fits well the experimental data in Fig. 1 with the fitting parameters: First, the normal blood: σ0=1.09×10−2 Ω−1 cm−1, σac=0.91×10−2 Ω−1 cm−1, εs=22 983ε0 F∕m, with ε0=8.855×10−12 F∕m, ε∞=3279.3ε0 F∕m, and τ=1.27×10−7 s. Second, for the diabetic blood: σ0=1.23×10−2 Ω−1 cm−1, σac=1.11×10−2 Ω−1 cm−1, εs=28 115ε0 F∕m, ε∞,=1179.3ε0 F∕m, and τ=1.47×10−7 s. These parameters are not too far from the obtained experimental values and coincide with the published data of Desouky.21
Dielectric constant of normal and diabetic bloods
Similar to the conductivity, we have considered that the dielectric constant of both the normal and diabetic bloods is due to the relaxation of the dipoles with a Debye type. The dielectric constant at any frequency is given as a function of ω as27
| (25) |
Here, one follows the same steps which have been done for the conductivity, i.e., the calculated values (solid line) after Eq. 25 fit well the experimental values (open symbols) as it is shown in Fig. 2. With the mean values given by Eq. 24 and the dielectric mean value ,
| (25′) |
Figure 2.
The dielectric constant of normal and diabetic blood as a function of frequency. Solid lines represent calculated values after Eq. 25 and symbols are experimental data for normal and diabetic bloods, respectively.
In Ref. 28 the authors gave evidence that glucose stimulates the formation of free radicals in diabetes by several bio-oxidation processes.28 So, the increase of free radicals in the diabetic blood augments the density of dipoles and consequently increases the dielectric constant.
Probability of the distribution of relaxation times in the blood
A key feature of the present study is the time elapsed to orient a dipole alongside with an applied ac-electric field. As it is mentioned in Sec. 3A, the blood is considered to be composed of n particles suspended in the plasma. Each of these particles has its own mass m1,m2,m3,…,mn. If one considers that m1>m2>m3⋯>mn, thus, one should expect that under the application of an ac-electric field, the corresponding times necessary to orient the particles alongside with the field are τ1>τ2>⋯>τn, i.e., each particle has its intrinsic relaxation time. These times are considered to be widely distributed through the plasma in a Gaussian manner so that any particle could have a relaxation time under the probability P(τ),29
| (26) |
where the normalization of the probability function is given as
Ts are the standard deviation of the probability which specifies the “width” of the bell curve. One can also consider that Ts encounters the most relaxation times within a narrower width. τc is the most probable relaxation time within the distribution.
Macroscopically, the measured relaxation time τmes is the summation all over the relaxation times, between τ0 (when f→0) and τ∞ (when f→∞), of each particle weighted by its probability, as follows:
| (27) |
Generally, the Gaussian distribution (GD) is widely applied in biosystems in recent times.30 Even so, we have successfully used this distribution in fitting experimental ac-conductivity with a proposed model in semi-insulating materials.31, 32 The interesting application of this distribution is that it significantly correlates the micro- and macroproperties of a biosystem through a comprehensive phenomenon. For example, earlier, Pohl24 defined the cof as follows: It is the frequency at which the induced dipole of a particle exactly vanishes, which is microscopic property. One can correlate this macroscopically; with the most probable relaxation time τc for a set of particles at which the applied electric field is exactly neutralized. Thus, the cof exists if there is only one particle in the GD. In this particular case the GD will turn into a δ-function. Unfortunately, the application of the GD requires definite information about the number of conductive sets which is out the scope of this study. However, one can overcome this problem as follows: If the possible relaxation times are distributed within the range 1.0×10−9 s<τ<1.0×10−3 s.
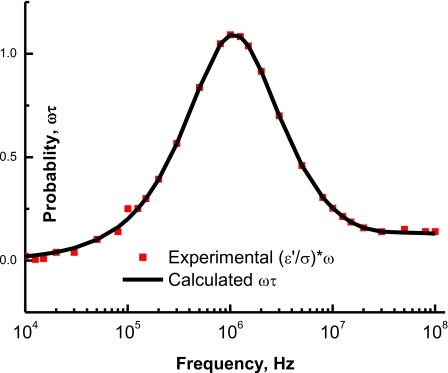
Any particle with its natural relaxation time τ will have a probability ωτ to respond to the applied field if τ>1∕2πf, where f is the applied frequency, there will be weak response; similarly, if τ<1∕2πf, there will be weak response. Only when τ=1∕2πf there will be maximum response. Figure 3 shows the probability, ωτ, as a function of the applied frequency. One can notice that when the intrinsic relaxation time matches with the inverse of applied angular frequency (2π*1.25×106 Hz), the probability will be a maximum which corresponds to maximum transfer of the electric energy.
Figure 3.
Solid squares represent the experimental ω∗(ε′∕σ) which is ωτ, while the solid line represents the calculated probability after the product ωτ: Here τ varies in a logarithmic manner from 10−9 up to 10−3 s. The maximum probability occurs at fc=1.25×106 Hz.
The transfer of energy could be explained as follows: In physical terms, we can conceive the electrical conductivity of the blood as a measure of the ability of its internal charge to transfer the electrical energy from one electrode to another. Similarly, the blood permittivity is a measure of the ability of its dipoles or its charge to store the applied external energy.
As the transfer of energy occurs by oscillations of the particles, the transfer time of the electric energy is related to the conductivity σ and the dielectric constant ε′ for the blood particles as
| (28) |
One can calculate τ from the experimental data of σ and ε′; then calculate the electric loss ε″ as a function of frequency as
| (29) |
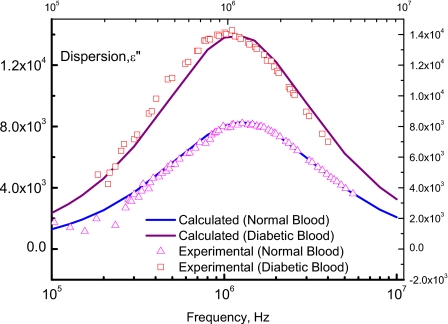
As it is shown in Fig. 4, the frequency dependence of the electric dispersion of the normal and diabetic blood and , respectively, are reported. pass by a maximum at a frequency fmax(n)=1.25 MHz while pass by a maximum at fmax(D)=1.12 MHz.
Figure 4.
The electric dispersion of normal and diabetic blood as a function of frequency. Solid lines represent calculated values after Eq. 30 and triangles and squares are experimental data for normal and diabetic bloods, respectively.
The corresponding relaxation times of the sample in the normal and diabetic bloods, respectively, are τn=1∕2πfmax(n)=1.27×10−7 s and τD=1∕2πfmax(D)=1.42×10−7 s. It is worth noting that τn=1∕2πfmax(n) matches well with the maximum probability occurring at fc=1.25×106 Hz (Fig. 3).
The electrical losses ε″ as a function of angular frequency has been derived after Eqs. 21, 29 as follows:
| (30) |
Taking the average values given by Eqs. 20, 24, 25′, one can calculate the dielectric losses for the normal blood, , and for diabetic one, . The solid lines, which are illustrated in Fig. 4, represent the calculated values after Eq. 30 while the experimental data are shown as open symbols. The best fits of the experimental relaxation times with the calculated values, after Eq. 30, in the normal and diabetic bloods are found to be τn=1.258×10−7 s and τD=1.49×10−7 s, respectively, whereas the net (apparent) values which are calculated from Eq. 28 are τn=1.25×10−7 s and τD=1.40×10−7 s. These values of τn and τD lie in the logic domain and match well with the experimental data of Sozou.33
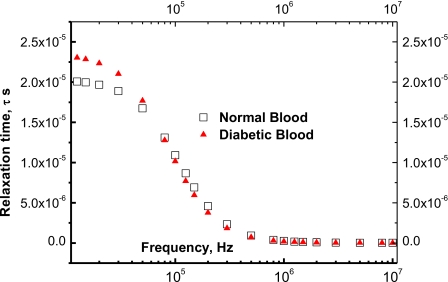
The experimental relaxation time is estimated from dividing the experimental values of the dielectric constant, ε′, by the experimental data of the ac-conductivity, i.e., . Thus, the experimental values of τexpt vary in the range of 2.35×10−5 s>τexpt>2.3×10−8 s. Figure 5 shows the experimental values of the relaxation time (open squares) as a function of the frequency for both the normal and diabetic bloods (solid triangles).
Figure 5.
The relaxation time, τ, of normal and diabetic bloods as a function of frequency. The calculated values after Eq. 30 coincide with the experimental values (squares and triangles are experimental data for normal and diabetic bloods, respectively); but these calculated values are omitted for more clarity.
These curves show that the distribution of the relaxation times extends over the up mentioned range of 2.35×10−5 s>τexpt>2.3×10−8 s. The diabetic blood contains bodies with relaxation times higher than those of normal blood as the presence of glucose enhances the generation of free radicals,28 which increases the number of free charges. This increase raises the values of the dielectric constant34 and consequently, increases the relaxation time.
In the next paragraph, the correlation between the relaxation times of the dipoles in the blood and the viscosity coefficient η is presented. Then, the relation between η and the electrical conductivity σ will be derived.
The blood red cells (and the other relatively massive particles) are polarized when applying an external ac-electric field. So, these RBCs can carry the ac-electric current through the blood. Within the polarization procedure, the normal blood particles relax with a relaxation time τBRC−n and the diabetic ones relax with a relaxation time τBRC−D. These times depend on the internal energy of the particles, i.e., thermal energy, kT and mechanical one. In the absence of an electric field, the particles tend to attain the minimum position of energy which is given when kT equals the total internal (mechanical∕oscillation) energy. On applying an external electric field, however, the previously mentioned minimum (neutrality of energy) will be out of equilibrium and the RBCs are now forced to oscillate according to the new electric force with a certain relaxation time that depends on the applied frequency. Thus, the transfer of energy will maximum when the natural frequency of the RBCs, τ, coincides with the angular frequency of the applied electric field ω, i.e., when τ=1∕ω. The maximum of energy transfer is reflected as two maximum values on the ε″-ω curve (Fig. 4).
Figure 5 shows the experimental values (open symbols) of the relaxation time as a function of the applied frequency. These experimental values are well fitted with Eq. 16 when τ0=2.1×10−5 s, τ∞=1.26×10−7 s, and fc is 1.25×106 Hz. The calculated data are not represented in the figure for more clarity.
Blood viscosity as a function of the ac: Electrical conductivity for normal and diabetic bloods
It is well known34 that the dielectric constant, ε, is a function of the number n of dipoles that relax under the effect of an ac-field. Also, the viscosity coefficient η is a function of n. This number will be divided into two sets of particles: The first contains light-mass particles such as proteins, hormones, micromolecules, free radicals, salts, ions, etc., and denoted L with an average radius RL; the second set contains the relatively heavy mass particles such as erythrocytes, leukocytes, thrombocytes, etc., and denoted H with an average radius RH. Moreover, one will consider that the viscosity coefficient at infinite frequency, η∞, is corresponding to the relaxation time at infinite frequency τ∞ and that the viscosity coefficient at low frequency, η0, corresponds to τ0. Moreover, τ0 and τ∞ are the maximum and minimum relaxation times in the Gaussian distribution. Physically, τ0 represents the relaxation time of the heavy particles and τ∞ stands for the light particles. The limits of the mentioned relaxation times could be given with the aid of Eq. 18 as
| (31) |
If one considers the particles as capacitors of dielectric constant and electric resistivity ρ due to the membrane, the time of charging∕discharging of this capacitor equals to the relaxation time τ: It is related to the resistivity, ρ, and the dielectric constant, , as
| (32) |
The corresponding limit values of the resistivity at high and low frequencies could be given as
| (33) |
ρ∞ is the electric resistivity due to light particles which is rather manifested at higher frequencies and ρs is the electric resistivity due to heavy particles (predominant at low frequency).
Using Eqs. 26, 33, one can write
| (34) |
where Ts is the standard deviation of the distribution,
| (35) |
R(τ) is the radius of any particle inside the blood; the determination of the exact values of these radii is not an easy task and it will be the subject of another study. However, the average values of the resistivity ρ will be considered in this study as
| (36) |
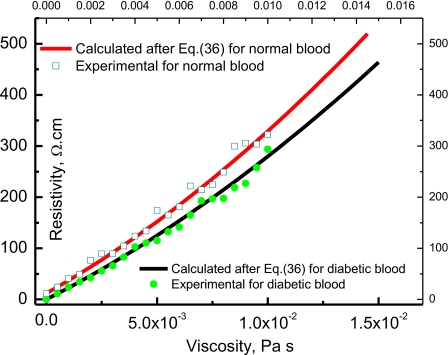
Figure 6 shows the blood resistivity ρ as a function of the normal and diabetic blood viscosity η calculated after Eq. 36 with RL=2 μm and RH=11 μm at T of 300 K, (εs)D=28 513ε0 F∕m and (ε∞)D=3211ε0 F∕m and for the normal blood (εs)n=22 975ε0 F∕m and (ε∞)n=3099ε0 F∕m. These fitting parameters are not too far from the data of Piet Aarts et al.35 On the same figure, the viscosity-electrical conductivity experimental data of Popa et al.36 is plotted as open symbols. From this figure (Fig. 6), one remarks that the blood viscosity is about 7% higher in diabetic than in normal blood. This is in good agreement with the results of Donald McMillan37 and Zingg et al.38 To explain why the diabetic blood is more viscous, Obrosova et al.28 reported that free radicals are produced in diabetes by glucose autoxidation, polyol pathway or∕and nonenzymatic glycation of proteins. Consequently, the increase of free radical density in the diabetic blood increases the density of dipoles and consequently increases both the dielectric constant and the average relaxation time, which leads directly to an increase of the viscosity. Higher dielectric constant for diabetic blood with respect to normal one is reported in Fig. 2. In Fig. 5 one can notice that the relaxation time of diabetic blood, which can respond to the field, is a function of the frequency and is higher than the normal blood.
Figure 6.
Variation of blood electrical resistivity (ρ cm) with the viscosity in Pa s; the continuous lines are calculated after Eq. 36 while closed circles and open squares are experimental values of the conductivity after Popa et al. (Ref. 36).
CONCLUSIONS
It is shown that bioimpedance measurements could provide an important method for the noninvasive investigation of blood internal structure and properties or for monitoring physiological change i.e., “static” or “dynamic” human organism properties. One of the main problems one encounters using bioimpedance measurements is still the reliability of the results. The scatter of the data for the electrical parameters of blood illustrates the problem of measurement reproducibility. This scatter makes it difficult to establish criteria of normality or reference value for particular measurement results. However, in spite of the large differences between reported data on dielectric properties of different samples of blood, we can still find some very useful applications based on the measurements of the differences or changes in the specific conductivity or relative permittivity. As a first step, the presents work shed a light on the importance of the study of the blood internal structure when assessing the blood from its electrical properties. It gives also an important chance to the early diagnosis of the tumor cells in blood.
More future studies are needed to investigate the role participated by each component of the blood in the electrical properties which may open a great chance for both early diagnosis and effective therapy and thus, a microfluidic device could be designed to investigate the electrical and rheological behaviors of blood flow. The electrical measurements under various stimulating frequencies show that the electrical properties of different blood components vary with the flow conditions, and can thus be used as a measure of the rheological behavior. To this extent, the correlation of the apparent viscosity of whole blood and its electrical resistance measured by the device could be performed.
Here, an attempt has been made to predict the role of microfluidic devices in biomedical research. In particular automated detection and automated fluid manipulations will both improve the overall usefulness of such devices. Moreover, automation may also play an important role in the development of creating better in vitro models of in vivo processes. If so, the role of microfluidic devices in laboratory settings will only grow more popular, especially in those areas where high-throughput determinations and biological assays are required.
References
- Carlos Ferrario M., Therapeutic Advances in Cardio vascular Disease 4, 1 (2010). [DOI] [PubMed] [Google Scholar]
- Zhou R., Gordon J., Palmer A. F., and Chang H.-C., Biotechnol. Bioeng. 93, 201 (2006). 10.1002/bit.20672 [DOI] [PubMed] [Google Scholar]
- Yeo L. Y. and Chang H. -C., Mod. Phys. Lett. B 19, 549 (2005). 10.1142/S0217984905008542 [DOI] [Google Scholar]
- Izzo1 P., Spagnuolo1 A., Manicone1 A., Nazzaro P., and Lauta V. M., Journal Clinical Hemorheology and Microcirculation 21, 3 (1999). [PubMed] [Google Scholar]
- Zhou R. and Chang Hsueh-Chia, J. Colloid Interface Sci. 287, 647 (2005). 10.1016/j.jcis.2005.02.023 [DOI] [PubMed] [Google Scholar]
- Marco Grootenboersa J. J. H., Franz Schramela M. N. H., Wim van Bovenb J., Jeroen Hendriksc M. H., van Schilc P. E. Y., De Witd P. E. J., Pasterkampe G., Folkertsf G., and Bart van Putteb P., Lung Cancer 63, 400 (2009). 10.1016/j.lungcan.2008.06.009 [DOI] [PubMed] [Google Scholar]
- Basuray S. and Chang H. -C., Phys. Rev. E 75, 060501 (2007). 10.1103/PhysRevE.75.060501 [DOI] [PubMed] [Google Scholar]
- Trakic A., Akhand M., Wang H., Mason D., Liu F., Wilson S., and Crozier S., Physiol. Meas 31, 13 (2010). 10.1088/0967-3334/31/1/002 [DOI] [PubMed] [Google Scholar]
- Fricke H., J. Gen. Physiol. 6, 375 (1924). 10.1085/jgp.6.4.375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baskurt O. K., Uyuklu M., and Meiselman H. J., Biorheology 46, 3 (2009). [DOI] [PubMed] [Google Scholar]
- Foster K. R. and Schwan H. P., Dielectric Properties of Tissues: Handbook of Biological Effects of Electromagnetic Fields (CRC, New York, 1996). [Google Scholar]
- Gordon J. E., Gagnon Z., and Changa H. -C., Biomicrofluidics 1, 044102 (2007). 10.1063/1.2818767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basuray S. and Chang H. -C., Biomicrofluidics 4, 013205 (2010). 10.1063/1.3294575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olufsen S., Ottesen J. T., and Novak V., J. Appl. Physiol. 99, 1523 (2005). 10.1152/japplphysiol.00177.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nose H., Mack G. W., Shi X. R., and Nadel E. R., J. Appl. Physiol. 65, 318 (1988). [DOI] [PubMed] [Google Scholar]
- Morucci J. P. and Rigaud B., Crit. Rev. Biomed. Eng. 24, 655 (1996). [PubMed] [Google Scholar]
- Riu P. J., Rosell J., Bragos R., and Casas O., Electrical Bioimpedance Methods: Applications to Medicine and Biotechnology (The New York Academy of Sciences, New York, 1999). [Google Scholar]
- Tuqiang X., Chuan Tjin S., Yang Q., and Lee Ng S., IEEE Trans. Instrum. Meas. 47, 1197 (1998). 10.1109/19.746582 [DOI] [Google Scholar]
- Jaspard F. and Nadi M., Physiol. Meas 23, 547 (2002). 10.1088/0967-3334/23/3/306 [DOI] [PubMed] [Google Scholar]
- Sun L., Collins C. M., Smith M. B., and Smith N. B., Proc. Intl. Soc. Mag. Reson. Med., 2004, p. 11.
- Desouky O. S., Romanian J. Biophys. 19, 239 (2009). [Google Scholar]
- Waugh A. and Grant A., Anatomy and Physiology in Health and Illness, 10th edition (Churchill Livingstone Elsevier, Glassgow, UK, 2007), pp. 22. See also: http://anthro.palomar.edu/blood/blood_components.htm [Google Scholar]
- Sheppard R. J. and Grant E. H., Adv. Mol. Relax. Processes 6, 61 (1974). 10.1016/0001-8716(74)80016-7 [DOI] [Google Scholar]
- Pohl H. A., Dielectrophoresis (Cambridge University Press, Cambridge, 1978), pp. 1–50. [Google Scholar]
- Schwarz G. A., J. Phys. Chem. 66, 2636 (1962). 10.1021/j100818a067 [DOI] [Google Scholar]
- Beneduci A., J. Mol. Liq. 38, 55 (2008). 10.1016/j.molliq.2007.07.003 [DOI] [Google Scholar]
- Debye P., Polare Molekeln (S. Hirzel, Leipzig, 1929). [Google Scholar]
- Obrosova I. G., Vanlteysen C., Fathallah L., Cao X., Greene D. A., and Stevens M. J., FASEB J. 16, 123 (2002). [DOI] [PubMed] [Google Scholar]
- Berman S. M., Mathematical Statistics (Intext Educational Publishers, Scranton, PA, 1971). [Google Scholar]
- “Normal distribution,” Encyclopedia of Psychology. FindArticles.com. http://findarticles. Com /p/articles/mi _ g2699 /is_0002/ai_2699000241/Gale, Encyclopedia of Psychology, 2nd ed. Gale Group, 200 (2010).
- Abdalla S., Dongol M., and Ibrahim M. M., Phys. Status Solidi B 144, 745 (1987). 10.1002/pssb.2221440234 [DOI] [Google Scholar]
- Pistoulet B., Roch F. M., and Abdalla S., Phys. Rev. B 30, 5987 (1984). 10.1103/PhysRevB.30.5987 [DOI] [Google Scholar]
- Sozou C., Proc. R. Soc. London, Ser. A 331, 263 (1972). 10.1098/rspa.1972.0176 [DOI] [Google Scholar]
- Sabry A. A., Proceedings of the Physical Society, 1972.
- Piet Aarts A. M. M., Piet Bolhuis A., Kjell Sakariassen S., Robert Heethaar M., and Sixma J. J., Blood 62, 214 (1983). [PubMed] [Google Scholar]
- Popa G. A. M., de Backerb T. L. M. de Jongb M., Struijkc P. C., Morarua L., Changd Z., Goovaertse H. G., Slagera C. J., and Bogersb A. J. J. C., Eur. Surg. Res. 36, 259 (2004). 10.1159/000079910 [DOI] [PubMed] [Google Scholar]
- Donald McMillan E., J. Clin. Invest. 53, 1071 (1974). 10.1172/JCI107644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zingg W., Sulev J. C., Morgan C. D., and Ehrlich R. M., Diabetologia 7, 6 (1971). 10.1007/BF01212063 [DOI] [PubMed] [Google Scholar]