A Study of the Precision and Accuracy of Peak Quantification in Comprehensive Two-Dimensional Liquid Chromatography in Time

Abstract

Simulated chromatographic data were used to determine the precision and accuracy in the estimation of peak volumes (i.e., peak sizes) in comprehensive two-dimensional liquid chromatography in time (LC×LC). Peak volumes were determined both by summing the areas in the second dimension chromatograms determined and by fitting the second dimension areas to a Gaussian peak. The Gaussian method is better at predicting the peak volume than the moments method provided there are at least three second dimension injections above the limit of detection (LOD). However, when only two of the second dimension signals are substantially above baseline, the accuracy and precision of the Gaussian fit method become quite poor because the results from the fitting algorithm become indeterminate. Based on simulations in which the modulation ratio (M_R = 4¹σ/t_s) and sampling phase (φ) were varied, we conclude for well-resolved peaks that the optimum precision in peak volumes in 2D separations will be obtained when the M_R is between two and five, such that there are typically four to ten second dimension peaks recorded over the eight σ width of the first dimension peak. This sampling rate is similar to that suggested by the Murphy-Schure-Foley criterion. This provides an RSD of approximately 2 % for the signal-to-noise ratio used in the present simulations. The precision of the peak volume of experimental data was also assessed, and RSD values were in the range of 4–5 %. We conclude that the poorer precision found in the LC×LC experimental data as compared to LC may be due to experimental imprecision in sampling the effluent from the first dimension column.

1. Introduction

Comprehensive two-dimensional liquid chromatography (LC×LC) in time is under development as a method to increase peak capacity and consequently the average resolution of liquid phase separations [1, 2]. This technique has been used in large part because of its higher resolving power as compared to one-dimensional LC [1, 3]. Typical samples that have been analyzed include those from naturally occurring sources such as blood, urine and plant extracts, as well as man-made items such as drugs and alcoholic beverages [3, 4]. LC×LC can also be useful in metabolomics, proteomics, pharmaceutics, food science and synthetic polymer research [3, 5, 6].

LC×LC techniques can be classified into two categories – heart cutting and comprehensive. Heart-cutting is a technique where a volume of the effluent from the first column is injected onto the second column, and it was once the most popular form of 2D separations [7]. This technique results in two individual chromatograms that must be individually analyzed to provide more information about a particular analyte. When the second dimension separation directly samples the first-dimension effluent over the entire first dimension run time, this technique is considered to be “comprehensive” LC×LC [7]. Unlike a typical LC where one has a detector signal that can be plotted as a virtually continuous function of elution time, comprehensive LC×LC provides a matrix of data that can be illustrated as a contour plot of the detector signal vs. the individual elution time axes [7]. While heart-cutting may provide more information for a single peak that is poorly resolved by the first dimension separation, on-line, comprehensive LC×LC provides more information for multiple overlapped peaks [7]. Furthermore, stop-and-go LC×LC and off-line LC×LC are additional comprehensive LC×LC options that can provide more separation power than on-line LC×LC at the cost of longer total analysis times [2, 8].

Stoll et al. recently demonstrated the ability to successfully reduce the comprehensive LC×LC run time to as little as 15 minutes [9]. To obtain optimum resolution and peak capacity over a reasonable timeframe, the second dimension cycle time must be exceedingly fast. One way of achieving this goal is to use parallel second dimension columns to increase the throughput of second dimension separation [10–12]. Alternatively, Stoll and coworkers used second dimension column temperatures of more than 100 ºC to greatly decrease viscosity and achieve very high linear velocities for analyses of plant leaf tissue extracts, tryptic peptides, wine, coffee, and urine [9, 13–15]. This method employed ultrafast gradients in the second dimension (about 20 s) with a rate of peak capacity production on the order of one peak per second [9]. More recently, they achieved peak capacities of two units per second using 2.7 μm micropellicular phases at high temperature and very high velocities [16].

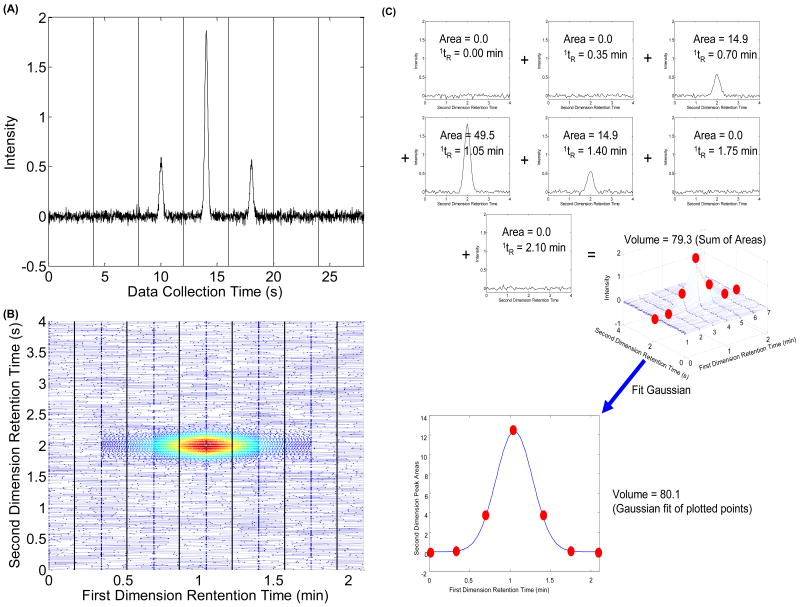
An LC×LC uses a typical LC instrument for the first dimension except that, instead of a detector, there is a switching valve at the end of the column. This switching valve diverts the first dimension effluent into one of two sample loops and the contents of the loop are eventually pumped into the second dimension column. A variety of LC columns have been used in either of the two dimensions including reverse-phase, normal phase, ion-exchange, and size-exclusion columns [17, 18]. The switching valve is programmed to change positions when the run on the second dimension is complete. The second dimension chromatographic run is typically a very short run (20 s) relative to the first dimension run (15–60 min). A major change in the LC×LC design developed by Stoll et al. includes the use of two binary pumps that alternate pumping through the column for the fast second dimension gradient to enable the equilibration of one pump while the second pump delivers the second dimension gradient [14]. A ten-port switching valve regulates the flow from the alternating binary pumps [14]. Eluent pre-heaters and heating jackets around both columns maintain the temperature of the mobile phases in this system and curtail potential band broadening [14]. Flow splitting improves the gradient reproducibility while use of an improved diode array detector allows spectral collection at 80 Hz from 200 nm to 600 nm [9]. A typical signal for a sequence of second dimension chromatograms is shown in Fig. 1A for data taken at a single wavelength [19]. These data contain multiple second dimension chromatograms that are recorded consecutively. A first dimension peak is sampled one or more times and injected onto the second dimension column, depending on the sampling period (i.e., the length of the total second dimension analysis time). Therefore, a peak in a second dimension chromatogram eluting at the same retention time as a peak in the subsequent second dimension chromatogram is likely to be the same analyte, as shown in Fig. 1A [19]. To be even more specific, each second dimension peak area is proportional to the fraction of the first dimension peak that was collected and injected onto the second dimension column. Thus, it is important to recognize that the peaks eluting in these consecutive second dimension chromatograms may be the same component. Keeping this fact in mind, one can rearrange the recorded data into a contour plot as shown in Fig. 1B [19].

Fig. 1.

(A) Simulated sequential second dimension chromatograms for a single component. The vertical lines in this figure denote the point of injection from the first dimension column onto the second dimension column; (B) A contour plot of this same simulated data; (C) Demonstration of how to sum the second dimension chromatogram areas to generate the volume of a LC×LC peak and of the fitting the second dimension peak areas to the Gaussian model to reconstruct the first dimension chromatogram and subsequently to obtain the volume of the two-dimensional peak. The numbers 1–6 in the mesh plot correspond to the sequential ‘slices’ or second dimension chromatograms. This figure corresponds to the ¹σ = 0.20 min (M_R = 2.29), t_R = 1.05 min case shown in Table 2.

Explanations as to how the sizes of two-dimensional peaks (and therefore the relative amount of the compound that gives rise to the peak) are determined are given in detail in the Experimental section [20–22]. However, to be concise, the simplest way to quantify the size of a two-dimensional peak is to sum the areas underneath the corresponding peaks in the second dimension chromatograms as shown in Fig. 1C [21]. Summing the peak areas taken for a single component first-dimension chromatographic peak effectively reconstructs the first dimension peak and subsequently the total amount of sample injected. Since a peak in a 2D separation is a three-dimensional object, the size of such an object is equivalent to a volume. Thus, the size of a peak that is proportional to the amount of analyte injected into the LC×LC will be referred to as a “peak volume” throughout the rest of this work.

Although the use of comprehensive LC×LC separations is increasing, the majority of the reports have been mainly concerned with qualitative issues. There is somewhat more literature in the area of GC×GC peak detection and quantification. For example, the technique of GC×GC-TOF-MS was applied to complex essential oils and provided better resolution than conventional GC and more accurate results in terms of assigning peaks [23]. Quantitative analysis was performed on polychlorinated biphenyls and polyaromatic hydrocarbons by using a new cryogenic modulator [24]. Enantioselective analysis of oxygenated monoterpenes and monoterpene hydrocarbons in Australian tea tree was successfully performed using GC×GC [25]. Fast quantitative enantioselective analysis, i.e., 8.5 minutes, was performed by using a short enantioselective second dimension capillary column in GC×GC analysis of monoterpene compounds in bergamot essential oil [26]. Upon GC×GC-TOF-MS analysis of Pogostemon cablin Benth (Cablin Patchouli) volatile oil in traditional Chinese medicines, 394 components were identified [27]. The first application of quantification using a GC×GC-quadrupole (q) MS took place when European law demanded that fragranced products be analyzed for 24 components that were alleged to be skin allergens [28]. GC×GC-qMS was also applied to Pelargonium graveolens essential oil where 65 components were identified using retention indices and literature mass spectral matching [29]. GC×GC-TOF-MS was used to analyze sterols in doping control samples with acceptable LOD values and adequate specificity based on a library match [30]. GC×GC-TOF-MS was also applied to identification of pesticides in tobacco extracts where pesticide standards were used to isolate matrix interferences and to establish linearity [31]. The ruggedness of retention times using GC×GC was validated in an intralaboratory study where reproducibilities in the retention times were found to be 0.12 % in the first dimension column and 0.74 % in the second dimension column for oxygenated monoterpenes and monoterpene hydrocarbons in Australian tea tree (Melaleuca alternifolia) [32].

Retention time reproducibility is important for some chemometric quantification methods, such as parallel factor analysis (PARAFAC) and trilinear partial least squares (tri-PLS). In conjunction with tri-PLS, six minute GC×GC analyses of cycloalkane and aromatic content of naphtha samples were carried out with adequate quantitative precision [33]. An automated PARAFAC method has been developed for resolving peaks over large sections or even the entire GC×GC-TOF-MS and has been demonstrated on three different GC×GC-TOF-MS data sets that offers valuable identification and quantitative information about the sample [34]. Solid phase micro extraction coupled with GC×GC-TOF-MS has been used to identify and quantify compounds using a PARAFAC graphical user interface in cacao beans [35]. An approach for background removal in GC×GC has been demonstrated by estimating the background level across the chromatographic image and then subtracting from the chromatogram, which is critical for proper quantification [36]. While the quantitative GC×GC literature can lend insights into the issues with quantification in LC×LC, some important differences must be considered, including the type of modulation used (thermal vs. valve) [37] and the nature of the gradient background in LC.

Reports of quantitative analyses by comprehensive LC×LC are not common. Kivilompolo and coworkers have resolved antioxidant phenolic compounds in herbs [38] and in wines and juices [39] with LC×LC-MS. Peak volumes were determined by summing areas [21]; however, an evaluation of precision and accuracy was not performed over a variety of conditions. Mondello and coworkers have reported quantitative results for LC×LC analysis of the compounds present in citrus-fruit essential oils [40], but several aspects of their methodology are ambiguous, namely, their descriptions of two-dimension peak interpolation and their method for peak integration by triangularization [41]. Reichenbach explained that peak interpolation and the triangularization method provides the same result as simply summing the second dimension areas [41].

Some researchers have used chemometric methods, such as PARAFAC, to obtain quantitative results from LC×LC data (similar to the GC×GC studies described above) [42, 43]. A limitation of the PARAFAC method is that the retention times of both the first and second dimension separations must be very reproducible [22], and thus this technique has not been widely applied. In fact, a variety of chemometric techniques has been reviewed for their potential in resolution, identification, and quantification [44]. Van der Klift et al. combined an automated method with analyst intervention to quantify triacylglycerols in corn oil. However, they found that the agreement with a gas chromatographic reference method was fair at best, and cautioned against relying on quantitative results in LC×LC analysis [45]. LC×LC was used in conjunction with a time-of-flight mass spectrometer (TOF-MS) as a detector to analyze atmospheric aerosols [46] and Stevia rebaudiana plant extracts [47]. Calibration curves, limits of detection (LOD) values and precisions were generated based on known standards in these publications. Dugo et al. quantified polyphenols in red wines using LC×LC and compared these results against those in standard LC [48]. Horvath et al. studied the effect of the dilution factor using LC×LC, which could affect quantification in LC×LC [49]. Stoll et al., in a direct comparison of 1D and 2D methods, found that the average precision of peak volumes for the LC×LC separation could be as much as a factor of four worse than the average precision obtained with a LC separation [9]. These authors suggested that the decrease in precision of quantification by LC×LC arises from errors in selecting the start/stop integration points for the multiple second dimension chromatograms

In the present work, we want to understand the fundamental limitations to the precision of quantification in 2D separations. Of specific relevance to our studies, Harynuk et al. used an area summation technique to examine peak volume in simulated GC×GC data [21]. Specifically, their work studied two potential causes of error from GC×GC as opposed to GC. These were (1) errors due to dividing a single large first dimension peak into four or more second dimension peaks and (2) errors related to differences in the phase angle at which the first dimension peak is sampled. Simulated chromatograms with Gaussian peaks were generated in Harynuk et al. analogous to our simulations. Their simulations covered a wide range of modulation ratios at four phase angles. They characterized the accuracy of the peak volume determinations as a function of the number of second dimension peaks summed together. They found that for an M_R = 3.0, four to five second dimension peaks should be summed to obtain accurate peak volumes that were not sensitive to variations in sampling phase [21].

Adcock et al. fit the consecutive second dimension peak areas to a Gaussian function [22], which is essentially the approach used in the present work. However, these authors were mainly concerned with the determination of the first dimension retention time. They found that at least three second dimension injections were needed to properly sample a Gaussian first dimension peak, and when only two injections were obtained this method should not be used. They showed that fitting the second dimension peak areas to a Gaussian provides accurate first dimension retention times, and suggested using the Gaussian fitting method to estimate peak area. The reported work covered a limited range of modulation ratios and phase angles. Column overloading of the second dimension did not affect the accuracy and precision of the results. They attempted to model a Gaussian peak by simply using the three largest peak areas and observed no significant difference in the results when all areas that were above the baseline were included. They concluded that the Gaussian method is a reliable and robust method for determining first dimension retention times, and is a novel means for determining peak volume [22].

We expand upon the important results described above. In Harynuk et al., an optimum modulation ratio (M_R = 3.0) was obtained from a previous publication [50], and they did not use their summation technique to determine a new optimum modulation ratio [21]. In Harynuk et al., their summation technique was documented in tables and was analyzed only in terms of “peak volume,” the two-dimensional peak quantification equivalent to one-dimensional peak areas, while trends in first dimension peak retention time and standard deviation were not evaluated [21]. In Adcock et al., only 0° and 180° phase angles were investigated and their experimental modulation ratios only ranged from three to four [22], which does not allow for the determination of an optimum sampling ratio using the Gaussian method. Neither Harynuk et al. nor Adcock et al. examined the effects of baseline disturbances [21, 22]. These problems are not too serious in GC, but are much more important in gradient LC. Asymmetric phasing also was not thoroughly covered in either work. Finally, the methods of Harynuk et al. and Adcock et al. have not been directly compared [21, 22].

Here, we use simulations of LC×LC chromatograms to investigate the potential causes of the poor precision observed for LC×LC quantification [9]. We hypothesize that the decrease in the precision of LC×LC analyses might be due to the following factors: (1) the decrease in signal-to-noise (S/N) when several smaller peaks in consecutive second dimension chromatograms are summed to obtain the peak volume; (2) errors in baseline estimation and determination of start/stop integration points, especially in the case of the rapid second dimension gradients used in fast LC×LC methods; and (3) errors caused by unavoidable changes in sampling phase (due to retention time shifts) over repeated second dimension injections and; (4) differences in the effective S/N of the total signal at different sampling phases. To investigate these factors, we used simulations to characterize the precision of the peak volume determination as a function of modulation ratio (M_R = 4σ/t_s), sampling phase (φ), and in the presence of background contributions.

We used two methods to estimate LC×LC peak volumes. First, the peak volume was calculated as the zeroth moment of the first dimension peak simply by summing the areas under consecutive second dimension chromatographic peaks [21]; this same method allowed us to also estimate first dimension retention time and peak width [21, 51] . Second, we fit these sequential second dimension peak areas to a Gaussian model to obtain the peak parameters of the first dimension peak, including the amplitude [22]. We postulated that this method might partially compensate for the decrease in precision caused by the errors in determining the area of the second dimension chromatogram peaks occurring in the tails of the first dimension chromatograms. While we acknowledge that a simple Gaussian model is generally inadequate to fit experimental chromatograms, we felt that this approach might yield acceptable results due to the small number of second dimension areas that constitute the first dimension chromatogram (typically two to five areas in experimental work and in our simulations.

2. General Considerations

In the present work we used the modulation ratio, M_R = 4σ/t_s, to represent the effect of changing the sampling frequency on the quantification of the peaks [50]. The value of M_R approximates the number of significant second dimension peaks observed in a given chromatogram. This is similar in nature to the parameter N = 8σ/t_s used by Murphy et al. [7], only differing from it by a factor of two.

The sampling phase represents the time where sampling events begin with respect to the retention time of a particular first dimension peak. We used a modification of the definition proposed by Seeley [20]

$$\phi =2\pi (T-{{}^{1}t}_R)/t_s$$ (1)

where T is the midpoint of the sampling cycle closest to the peak retention time, and ¹t_R is the true retention time of the first dimension peak [20]. Our modification is to include the 2π, rather than representing the phase as a fraction. This is essentially the same method as used by Marriott et al. [21, 22, 50].

The modulation ratio can have a pronounced effect on the appearance and resolution of the first dimension chromatogram [4, 7, 20]. In addition, the sampling phase, φ, has a significant effect on the first dimension chromatogram [4, 20]. According to Seeley, adequate resolution in LC×LC requires a modulation ratio greater than 2.7 [20]. However, according to Murphy et al., in order to preserve first dimension resolution, a modulation ratio of 1.5 is adequate when a peak is in-phase, while a modulation ratio of two is needed when a peak is out-of-phase [7]. However, these works do not address the impact of sampling rate on the precision of quantification.

Davis et al. developed a stochastically-based, empirical model for the effective first dimension peak broadening from undersampling the first dimension chromatogram [53]. The effective peak width of an undersampled first dimension chromatographic peak is expressed by its standard deviation (¹σ_eff) which is the product of the original first dimension peak standard deviation (¹σ) and an average broadening factor (<β>). Davis et al. [4] showed that the effective peak capacity, n’_c,2D, is modified by an average broadening factor <β> such that

$$n_{c,2D}^{\prime }=\frac{n_{c,2D}}{\langle \beta \rangle }$$ (2)

where the Giddings equation for the ideal peak capacity (n_c,2D) is

$$n_{c,2D}={{}^{1}n}_c\times {{}^{2}n}_c$$ (3)

and ¹n_c and ²n_c are the peak capacities of the first and second dimensions, respectively [3, 54–56]. This equation is typically referred to as the “product rule” [53]. Davis et al. determined the average broadening factor based on Monte Carlo simulations and statistical overlap theory of many hundreds of thousands of simulations of complete 2D chromatograms to be

$$\langle \beta \rangle =\sqrt{1+0.21{\left(\frac{t_s}{{}^1\sigma }\right)}^2}$$ (4)

where t_s was the sampling interval in the first dimension, and the quantity t_s/¹σ was between 0.2 and 16 [4, 53]. The salient characteristics of the LC×LC chromatographic simulations include the fact that the sample heights followed a random exponential distribution, and both first dimension and second dimension retention times followed a Poisson random distribution. All peaks in each dimension were assumed to have the same peak width, which differed between the two dimensions. This broadening factor can be used to represent the average loss of peak capacity that occurs due to first dimension undersampling. Blumberg describes the process of sampling from the first dimension as accumulating re-sampling where sampling takes place in two steps: a boxcar accumulator and an ideal snapshot sampler. Blumberg also includes boxcar filters to perform a linear interpolation step between data points [57]. In this work, we calculate moments by summation of the raw second dimension area data points, and thus, the linear interpolation is not necessary [21]. The effective standard deviation of the sampled first dimension chromatograms is therefore calculated as:

$${{}^1\sigma }_{\mathit{eff}}=\sqrt{{{}^1\sigma }^2+\frac{{t_s}^2}{12}}$$ (5)

While in the present work, we are not directly concerned with peak capacity and resolution issues, it is possible that the undersampling that occurs in LC×LC separations could well have a major effect on the precision and accuracy of quantification.

In this work, we have generated a series of simulations wherein the first dimension standard deviation and retention time were varied. While in previous work, effects due to undersampling and variations in the above parameters on the peak width, resolution, and retention time of Gaussian peaks were studied, the effects of these parameters on the accuracy and precision of quantification were not investigated [4, 7, 9, 20]. The goal of the present work was to evaluate and compare the precision and accuracy of peak volumes obtained in LC×LC experiments using area summation and Gaussian fitting methods and to assess in so far as possible the reasons for the poorer precision of LCxLC as compared to LC as seen in Stoll’s work [9].

We make the following assumptions in this paper. First, in both dimensions, all peaks are Gaussian, thus:

$$y=\frac{A}{\sigma \sqrt{2\pi }}{e}^{\frac{-{(t-t_R)}^2}{2{\sigma }^2}}$$ (6)

where A is the peak area (zeroth moment), t_R is the retention time of the peak (first moment), σ² is the variance (second central moment) and t is time. In addition, we assume that the duty cycle of the sampling device is 100 %. Finally, it should be noted that the effects of peak overlap were not considered here. We felt that it was necessary to first study the accuracy and precision of the quantification of a single peak.

We also wanted to test our findings on real LC×LC chromatograms. Thus, we obtained the LC×LC chromatograms of a standard mixture from Stoll et al. [9, 15]. These data were from a comparison of 1D and 2D quantification [9]. Just as was done for the simulations above, peak volumes were calculated both by summing the individual areas of the second dimension chromatograms (i.e., the zeroth moment) [21] and by fitting a Gaussian peak to these second dimension areas [22]. The precision and accuracy of these peak volume estimates were then evaluated. To detect the effects of the chromatographic baselines (background) on our analysis, we added peaks that mimicked the experimental responses to blank chromatograms obtained from Stoll et al. [9].

3. Experimental

All data simulations were run on a Dell^® Optiplex GX270 computer running Windows XP using a Pentium 4 2.8 GHz processor with 1 GB of RAM. Data analysis was performed in the MATLAB^® programming environment, version 7.2.0.232 from Mathworks (Natick, MA, USA). Nonlinear fitting was accomplished using the Optimization Toolbox with the following parameters: 1000 function evaluations maximum, 100 iterations maximum, 10⁻⁸ minimum difference for the function, 10⁻⁴ minimum difference for the variables to be optimized, 10⁻⁶ minimum difference in variables for finite differencing, and 60 seconds maximum time.

An in-house MATLAB program was used to generate sampled Gaussian peaks in the first dimension with known elution times, peak standard deviations, areas and sampling intervals. Only four second sections of the second dimension chromatograms were simulated, as shown in the contour plot in Fig. 1. Five hundred (500) replicate simulations were performed for each set of chromatographic peak parameters used. The area of the i^th second dimension chromatogram was calculated using eqs (7)–(9) [20].

$$A_i=A_{\mathit{Total}}\underset{z_{i,\mathit{start}}}{\overset{z_{i,\mathit{finish}}}{\int }}y(z)dz=A_{\mathit{Total}}\left(\underset{z_{i,\mathit{start}}}{\overset{\infty }{\int }}y(z)dz-\underset{z_{i,\mathit{finish}}}{\overset{\infty }{\int }}y(z)dz\right)$$ (7)

$$A_i=0.5A_{\mathit{Total}}\left(\mathit{erfc}\left(\frac{-z_{i,\mathit{finish}}}{\sqrt{2}}\right)-\mathit{erfc}\left(\frac{-z_{i,\mathit{start}}}{\sqrt{2}}\right)\right)$$ (8)

where y is given by eq. (6), and z is

$$z=\frac{t-t_R}{\sigma }$$ (9)

Here, A_Total is the total area of the first dimension chromatographic peak, A_i is the area of the i^th-sampled section and is therefore the area of the corresponding second dimension peak, and erfc is the complementary error function. In our simulations, the true volume of the peak was constant and set to 80. The above equations were used to generate the first dimension chromatograms according to the desired specifications for the chromatographic peak, i.e., retention time, standard deviation, and sampling interval [20]. Normally distributed noise with a mean of zero and a standard deviation of 0.03 was added to each of the second dimension chromatographic simulations containing a single Gaussian peak. The maximum peak heights in the second dimension using this approach ranged from 0.79 to 2.5, giving S/N values ranging from 26 to 84.

Individual second dimension peak areas were summed to give the total peak volume. In the case of the experimental chromatograms from Stoll et al. [9], the second dimension chromatograms were integrated using an in-house integration program that enabled the user to draw the baseline manually for the second dimension chromatograms, and the resulting areas were summed (the moments method) [21]. The number of samples injected onto the second dimension column from the first dimension effluent encompassed the entire simulated peak, and the number of these fractions was equal in all cases. This integration method will be referred to throughout as the moments method because it provides the zeroth, first and second central moments of the data, i.e., area, mean position, and standard deviation, respectively [51]. These areas were also fit to a Gaussian equation using a nonlinear least-squares solver to estimate the parameters of the parent first dimension chromatographic peak from which they are derived [22]. This technique provides estimates for the peak volume, retention time, and peak standard deviation just like the moments method. The nonlinear least-squares solver provides data-fitting solutions for a nonlinear curve when initial guesses for the solutions, along with upper and lower bounds for the fit parameters are provided. The initial guesses for the nonlinear least-squares solver for these simulations are found in Table 1. Lower bounds of zero were chosen so that solutions would not be negative. The selected upper bounds were chosen to allow for a wide range of solutions but to prevent an unrealistic result. This integration method will be referred to throughout as the Gaussian method [22]. The percent relative standard deviation (% RSD) was calculated for 500 replicates to determine the reproducibility of the first dimension peak parameters using the moments method [21] and the Gaussian method [22].

Table 1.

Summary of initial guesses and bounds used for the Gaussian fitting algorithm

Simulations	Volume	Retention Time	Standard Deviation
a) Parameter Variationsa
Initial guess	86	1.15 min	0.2 min
Lower bound	0	0 min	0 min
Upper bound	286	2.1 min	1.6 min
b) Peaks 1–6b
Initial guess	Volume from moments method	tR from moments method	1σ from moments method
Lower bound	0	0% retention window c	0 min
Upper bound	20000	100% retention window	0.35 min

^aParameter Variations refers to the two simulations where retention time and ¹σ were varied to explore the effect of sampling phase and frequency.

^bPeaks 1–6 refer to the initial guesses for Gaussian fitting used to estimate peak volumes for peaks 1–6 in the experimental LC×LC data from Stoll et al.

^dRetention window refers the range of 1^st dimension times represented in the data to be fit, i.e., if the peak window is from 3.0 5.0 min, 0 % retention window is 3.0 min, 100 % retention window is 5.0 min and 50 % retention window is 4.0 min.

3.1. Effect of Changes in the First Dimension Sampling Phase

For the first set of simulations, eight different first dimension retention times were used ranging from 1.050 to 1.225 min at 0.025 min intervals, as shown in Table 2 and Fig. 1. This results in sampling phases from 0 to −π at 0.143π intervals. Two series of simulations were carried out, with the peak width of the first dimension peak corresponding to a standard deviation of 0.20 min (M_R = 2.29) and 0.12 min (M_R = 1.37) respectively (see Table 2). The sampling interval was 0.35 min, and seven injections from the first dimension column into the second dimension column were simulated, i.e., injections at 0 min, 0.35 min, 0.70 min, 1.05 min, 1.40 min, 1.75 min, and 2.10 min. The second dimension peak conditions were as follows: a retention time of 2 s, a standard deviation of 0.135 s and a sampling interval of 0.0125 s. Five hundred (500) distinct replicates of this data set were generated.

Table 2.

Peak volumes for simulated LC×LC chromatograms to evaluate changes in sampling phase using the moments method.^a

1σ = 0.12 min; MR= 1.37		First Dimension Retention Time (min)
	Slice Position (min)	1.050	1.075	1.100	1.125	1.150	1.175	1.200	1.225
Slice #	Sampling phase (φ)	0	−0.143π	−0.286π	−0.428π	−0.572π	−0.714π	−0.856π	−π
3	Area @ 0.70 min	5.8 (12)b	3.8 (6.9)	2.4 (5.3)	1.5 (3.9)	0.9 (1.7)	0.5 (1.1)	0.3 (0.6)	0.2 (0.4)
4	Area @ 1.05 min	68.4 (130)	67.7 (140)	65.6 (150)	62.3 (170)	57.9 (130)	52.4 (100)	46.3 (85)	39.8 (100)
5	Area @ 1.40 min	5.8 (14)	8.4 (17)	11.9 (19)	16.2 (25)	21.3 (43)	27.0 (71)	33.3 (69)	39.8 (82)
6	Area @ 1.75 min	0.0 (0.2)	0.0 (0.2)	0.0 (0.2)	0.0 (0.2)	0.1 (0.2)	0.1 (0.2)	0.1 (0.2)	0.1 (0.4)
	Sum of All Areasc	80.0	79.9	80.0	80.1	80.0	80.0	80.0	80.0

1σ = 0.20 min; MR = 2.29		First Dimension Retention Time (min)
	Slice Position (min)	1.050	1.075	1.100	1.125	1.150	1.175	1.200	1.225
Slice #	Sampling phase (φ)	0	−0.143π	−0.286π	−0.428π	−0.572π	−0.714π	−0.856π	−π
3	Area @ 0.70 min	14.9 (35)	12.5 (27)	10.2 (18)	8.3 (18)	6.7 (17)	5.3 (15)	4.2 (8.8)	3.2 (7.0)
4	Area @ 1.05 min	49.5 (93)	49.2 (110)	48.3 (110)	46.9 (89)	45.0 (110)	42.5 (80)	39.8 (88)	36.8 (93)
5	Area @ 1.40 min	14.9 (28)	17.6 (26)	20.6 (51)	23.7 (58)	26.9 (60)	30.3 (67)	33.6 (61)	36.8 (93)
6	Area @ 1.75 min	0.0 (0.7)	0.5 (1.0)	0.7 (1.8)	1.0 (1.9)	1.4 (3.0)	1.8 (3.4)	2.4 (4.9)	3.2 (7.8)
	Sum of All Areasc	79.3	80.1	79.9	80.0	80.0	80.1	80.1	80.1

^aSee Fig. 1 to interpret data. All data are the average of the peak areas for 500 runs at the indicated slice position for the indicated first dimension retention time.

^bNumber in parentheses is the signal-to-noise of the peak.

^cThis is the sum of the above peak areas. The true volume is 80.0.

3.2. Effect of Changes in the First Dimension Sampling Frequency

A set of simulations was performed as the first dimension peak width was varied but the elution time was held constant. Nine standard deviations were used from 0.10 to 0.50 min at 0.05 min intervals, corresponding to modulation ratios ranging from 1.14 to 5.71. The first dimension retention time was 1.15 min, and the sampling interval was 0.35 min, giving a constant sampling phase of −0.57π. The second dimension simulation parameters were the same as those used for the previous simulations, and again 500 replicates were simulated. Chromatographic peak areas from the second dimension were then integrated for all seven injections onto the second dimension column because the highest standard deviation, 0.50 min, provided a significant amount of area for all seven injections. The precision and accuracy of the peak volumes as obtained from the moments method and the Gaussian method were assessed as described above.

3.3. Simulations with Experimentally Obtained Baseline Signals

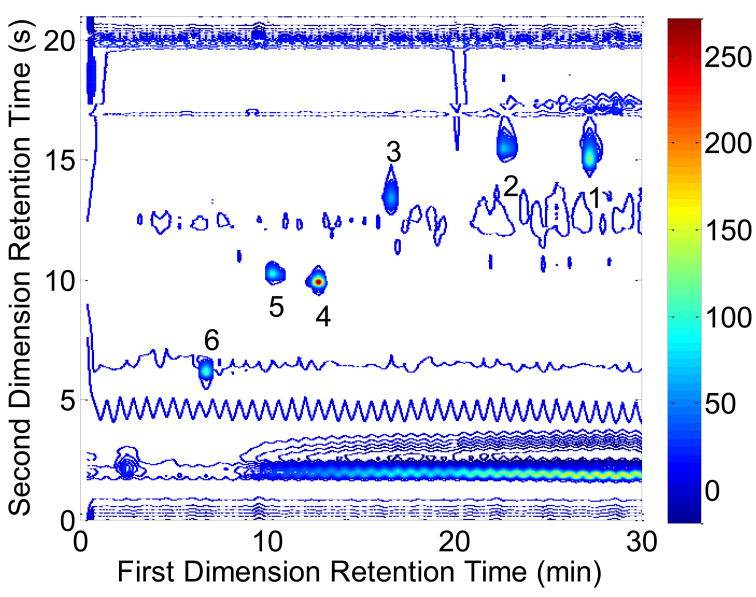
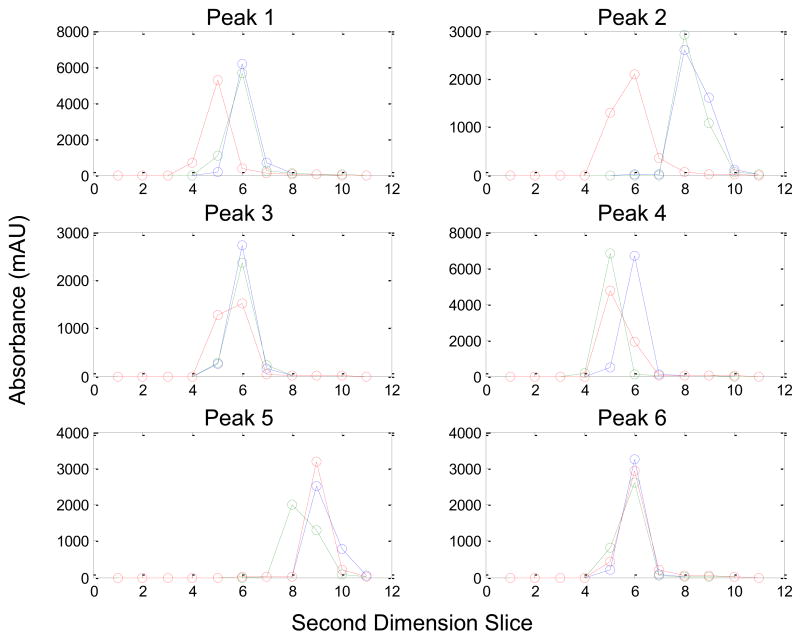
Experimental LC×LC data obtained by Stoll et al. for a series of mixtures containing six compounds (1–6) were analyzed. These standards are indole-3-acetonitrile (1), indole-3-propionic acid (2), indole-3-acetic acid (3), tryptophan (4), 5-hydroxytryptophan (5), and tyrosine (6). The details of this experiment are described by Stoll et al. [9], and an example chromatogram is shown in Fig. 2. These were three replicates of these experimental chromatograms. Prior to integration, the LC×LC chromatogram was divided into sections so that only one peak could be found. For peaks 1–6, the Gaussian method [22] was performed with acceptable value ranges as listed in Table 1b.

Fig. 2.

A contour plot of the LC×LC chromatogram provided by Stoll et al. [9]. Peaks 1 through 6 are the standards identified in the text. The colorbar units are in milliabsorbance units (mAU) measured at a wavelength of 220 nm.

In addition, three sets of simulations were performed where the individual second dimension areas of peaks 1–6 were used as the basis for the generation of second dimension Gaussian peaks. Normally distributed noise with a mean of zero and a standard deviation of 0.03 mAU was added to each of these second dimension chromatographic simulations. These Gaussian peaks were then directly added to blank LC×LC chromatograms. These blank LC×LC chromatograms consisted of water injected onto the same gradient system that was used to separate the indole standards. These peak areas were placed at approximately the same retention times as peaks 1–6 as described in Table 3. The first series of simulated peaks are denoted as 1a–6a. Simulated second dimension Gaussian peaks were added to three replicates of the LC×LC background chromatograms. The areas of these second dimension peaks were obtained from the first replicate of the experimental data for peaks 1–6 and added to all three backgrounds. This analysis was performed to evaluate the effect of the variability of the fast gradient backgrounds on the precision of the peak volume estimates. In the second simulation set, peaks 1b–6b were simulated using second dimension Gaussian peaks with areas corresponding to all three experimental replicates and added to each of the three backgrounds. This simulation was performed to test the reproducibility of peak volumes with shifting retention times. In a third set of simulations, simulated peaks 1c–6c were positioned at randomly generated first dimension retention times with a standard deviation in peak position of 0.35 min, which was the approximate observed variation in first dimension retention times. These simulated peaks were added to the first replicate of blank chromatograms. Fifty simulations were performed and this set demonstrated the effect that variations in the sampling phase has on peak volume quantification. For these peaks, the Gaussian method was performed with the upper and lower bounds as listed in Table 1b.

Table 3.

Summary of second dimension retention times and standard deviations to which second dimension areas for peaks 1–6 were added to blank LC×LC chromatograms (n = 3).

Peak #	2tR (s)	2σ (s)
1a-c	15.25	0.3125
2a-c	15.25	0.2500
3a-c	13.25	0.4688
4a-c	10.25	0.2188
5a-c	10.25	0.2500
6a-c	6.25	0.3125

Peaks 1a–6a, 1b–6b and 1c–6c are simulated Gaussian peaks with areas determined from the experimentally determined first dimension added to real LC×LC blank chromatograms.

4. Results and Discussion

4.1. Effect of Changes in the First Dimension Sampling Phase

4.1.1 Effect of Sampling Phase on Peak Volume Determination

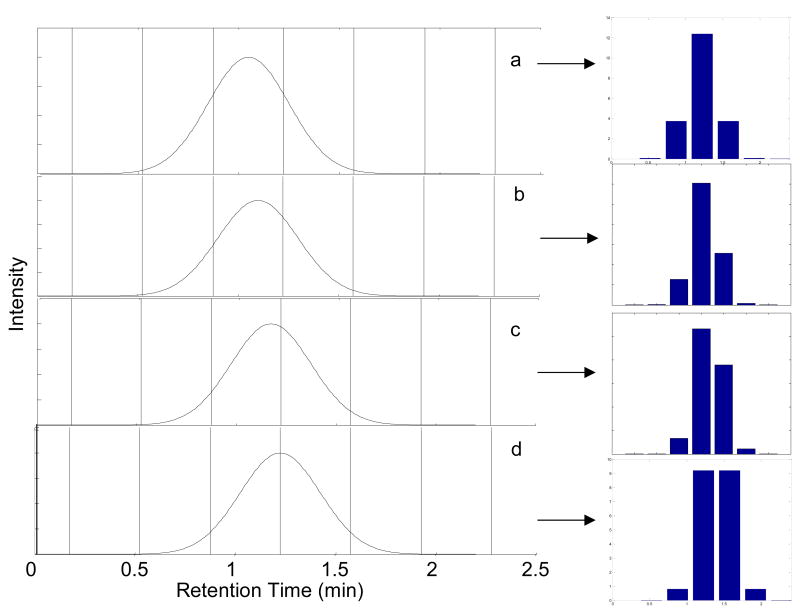
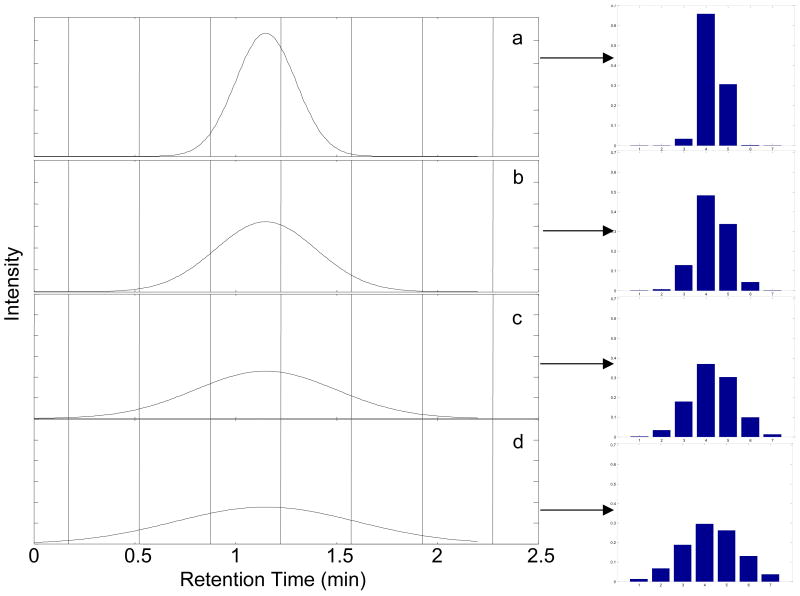
Representative first dimension chromatograms illustrating the effect of sampling phase are shown in Fig. 3. When sampling is exactly in-phase (φ = 0π) a second dimension injection will be is obtained at the center of the peak (Fig. 3a). This results in three consecutive second dimension chromatograms with significant areas, as shown by the bar graph adjacent to Fig. 3a. When sampling is completely out-of-phase (φ = −π), a symmetric pattern of peaks to either side of the peak center is obtained (Fig. 3d). Retention times between 1.050 min and 1.225 min result in an asymmetric distribution of peak areas in the first dimension chromatograms (Fig. 3b and 3c).

Fig. 3.

The effect of first dimension sampling phase on the series of second dimension peak areas. Sampling period is set at 0.35 min for peaks with a first dimension retention times and sampling phases of (a) 1.050 min (φ = 0), (b) 1.100 min (φ = −0.286π), (c) 1.175 min (φ = −0.714π), and (d) 1.225 min (φ = −π). ¹σ = 0.20 min (M_R = 2.29). The vertical lines indicate the start and stop of the accumulation intervals. The bar graphs to the right show the relative amount of analyte injected onto the second dimension column upon sample collection at the indicated vertical lines.

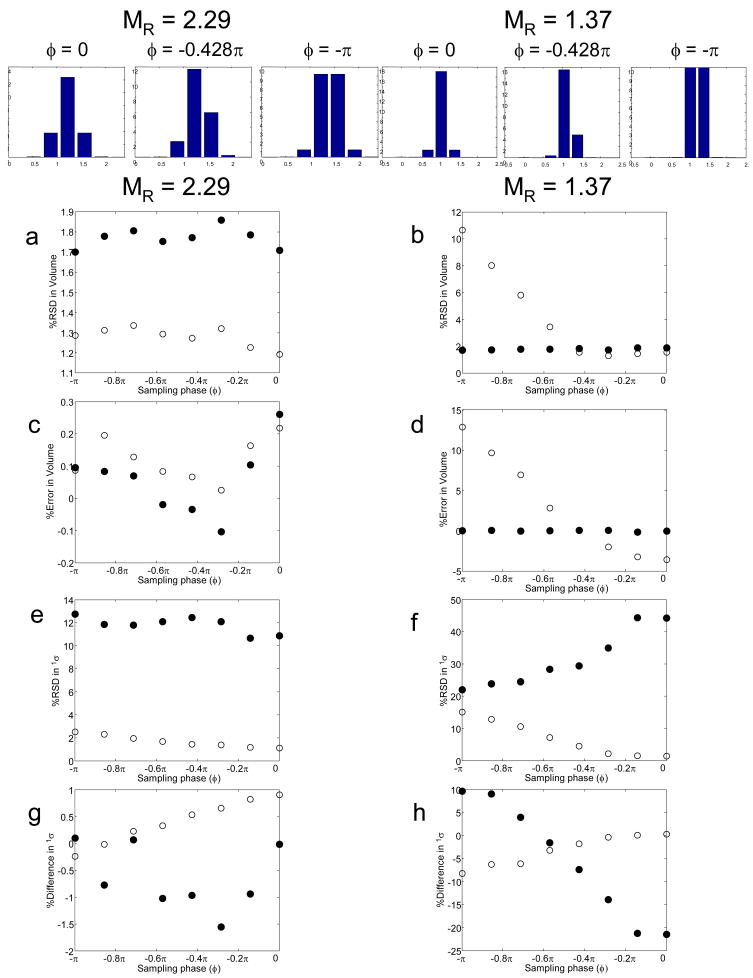
Results for integration of the second dimension chromatographic peaks with ¹σ = 0.12 and 0.20 min are shown in Table 2. These two peak widths correspond to modulation ratios of 1.37 and 2.29, respectively. For the narrower first dimension peak chromatograms, either two or three of the subsequent second dimension chromatograms show significant areas (in bold), while for the broader first dimension peak chromatograms, three or four of the subsequent second dimension chromatograms show significant areas (in bold). The S/N values for the second dimension are given in parentheses. The moments method [21] for both peak widths gives accurate peak volumes in all cases.

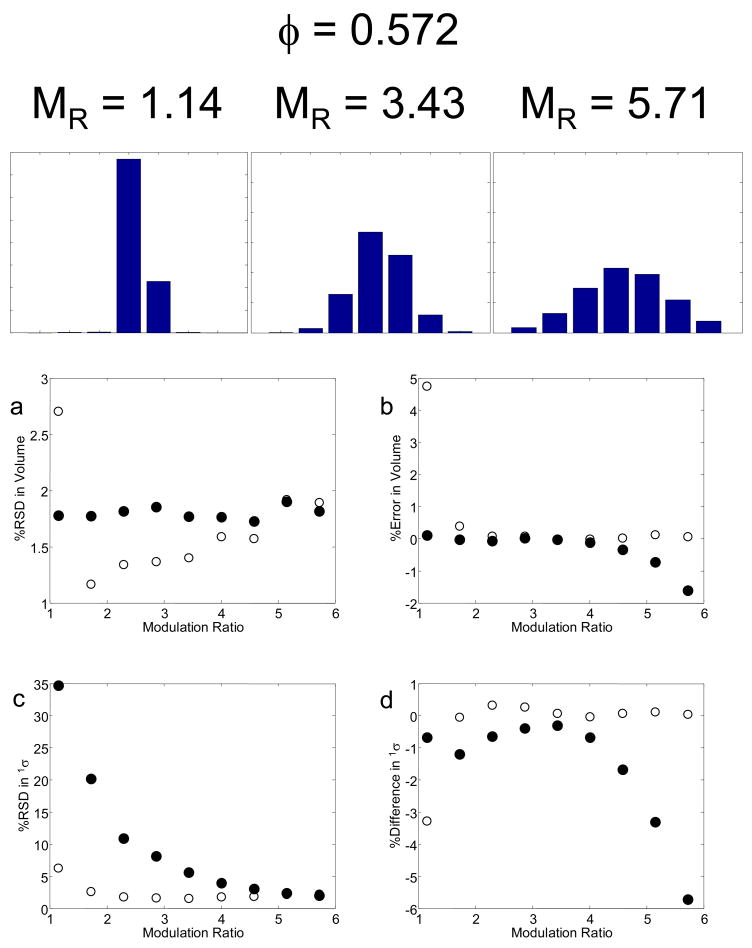
The results from both methods for these simulations are shown in Fig. 4. First, we see that the precision of the moments method at M_R = 2.29 is somewhat better (1.3 %) than the Gaussian fit method (1.7 %), and at this M_R the results from both methods are independent of sampling phase. However, at the lower sampling rate (M_R= 1.37) the moments method gets a bit worse (2.0 %) while the Gaussian fit method becomes much less precise (up to 10% RSD), especially when sampling is fully out of phase. Using a propagation of error equation derived by Eikens and Carr for the calculation of the precision of 0^th moment as a function of the number of data points used in the integration, the % RSD values ranged from 1.4 % to 1.7 % [58]. At the faster sampling rate both methods are rather accurate, typically better than 0.3 %. The moments method remains quite accurate at the slower sampling rate for all sampling phases but the accuracy of the Gaussian method deteriorates quite badly and becomes very sensitive to sampling phase. The behavior of the Gaussian method is expected based on the fact that at the lower value of M_R the parameters from this fitting method become indeterminate, as a minimum of three data are required to determine the three peak parameters (area, ¹t_R and ¹σ.

Fig. 4.

The effect of sampling phase (φ) and M_R on peak metrics as a function of sampling phase variations. Results of the moments and Gaussian fit method are given as filled (●) and open circles (○), respectively: (a) and (b) % RSD in peak volume; (c) and (d) % error in peak volume; (e) and (f) % RSD in ¹σ; (g) and (h) % difference in ¹σ relative to that calculated by eq. 4.

To compare these results against the precision and accuracy obtainable with 1D-LC chromatography, 500 replicates of a peak generated with peak widths corresponding to σ values of 0.12 min and 0.20 min and the same S/N were simulated. The % RSD for the area estimates were 0.70 % and 0.78 %, for M_R values of 1.37 and 2.29, respectively. Relative to the LC×LC results using the moments method, 1D-LC area determination is approximately 2.8 times more precise.

4.1.2 Effect of Sampling Phase on Determination of Retention Times and Peak Widths

Because the Gaussian method [22] and the moments method [21] yield estimates for peak positions (i.e., retention times) and peak widths (i.e., ¹σ values), we evaluated the accuracy and precision of these results as well. The estimated retention times from the Gaussian fit in the vast majority of cases was excellent, with the worst error being an overestimation of 0.8 % (results not shown). The estimated retention time from the moments method in the vast majority of cases was also good with the worst error being an underestimation of 1.0 %. Thus, the use of the Gaussian fit procedure or the moments method to estimate the first dimension retention time could be quite useful. It should be noted that the moments method was overall less precise than the Gaussian method for the retention times, i.e., RSD values of 1.1 % vs. 0.5 %, respectively.

There were large differences in the estimated ¹σ values of the first dimension chromatographic peaks relative to the ¹σ_eff values predicted by eqn. 4 as estimated by the moments method for M_R = 1.37 and shown in Fig. 4h. In the case of these narrower first dimension peaks, inaccurate estimations of ¹σ values occurred ranging from −21.5 % to 9.6 % error, as the sampling phase varied from in-phase (φ = 0) to out-of-phase (φ = −π). This phase dependence was also observed by Blumberg for modulation ratios less than two [57], which will be explained in detail later. For the broader first dimension peaks (M_R = 2.29), ¹σ values were well-estimated, ranging from a −1.6 % to a 0.1 % error as compared to the values predicted by eqn. 4, with a lesser dependence on the sampling phase. Using the Gaussian method, the peak width of the M_R = 1.37 peak was increasingly underestimated as the peak shifted from being in-phase to out-of-phase, i.e., from a 0.3 % error to a −8.2 % error. In the case of the M_R = 2.29 peaks, the errors ranged from 0.9 % to −0.2 %. It should be noted that especially in the case for M_R = 1.37, where the % RSDs for the ¹σ values are quite large, the differences in peak widths are probably insignificant.

4.2. Effect of Changes in the Modulation Ratio

4.2.1 Effect of Modulation Ratio on Peak Volume Determination

Fig. 5 shows the results of simulations when the first dimension peak width parameter (¹σ) and thus M_R was varied at constant sampling interval and phase. This simulation allows the characterization of the effect of sampling frequency. When first dimension peaks are narrow relative to the sampling interval, i.e., ¹σ = 0.15 min (M_R = 1.7, see Fig. 5a), fewer second dimension peaks result, each with a larger S/N. As a result, simulations with ¹σ = 0.15 min (M_R = 1.7) provided a low % RSD value for the peak volume using the moments method as shown in Fig. 6. However, when first dimension peaks are wider, i.e., (¹σ = 0.45 min, M_R = 5.0, see Fig 5d), there is a loss in precision of quantification because more frequent sampling gives rise to a smaller second dimension peaks leading to a lower S/N for each of the second dimension chromatograms. As peak width was increased there was a steady loss in precision using the Gaussian method. The accuracy of the peak volumes was good in all cases over this range. Based on this result and on the results from the previous series of simulations, where it was shown that for an M_R of 2.2 the precision of the volume determination was independent of phase, we conclude for well-resolved peaks that the optimum quantitative precision in 2D separations will be obtained when the modulation ratio to the first dimension standard deviation is approximately two; that is, four samples are taken across the 8σ peak width. According to Blumberg, a change in the sampling phase does not have a significant effect on the broadening until M_R < 2 [53, 57], which we also observe in our simulations.

Fig. 5.

Effect of peak width on sampling the first dimension peak at fixed sampling interval and phase. Conditions: sampling interval 0.35 min, ¹t_R = 1.15 min (φ = −0.572π) for a peak with ¹σ values of (a) 0.15 min (M_R = 1.7), (b) 0.25 min (M_R = 2.9), (c) 0.35 min (M_R = 4.0), and (d) 0.45 min (M_R = 5.1).

Fig. 6.

The effect of M_R on peak metrics. Results of the moments and Gaussian fit method are given as filled (●) and open circles (○), respectively: (a) % RSD in peak volume; (b) % error in peak volume; (c) % RSD in ¹σ; (d) % difference in ¹σ relative to that calculated by eq. 4.

When Gaussian peaks were fitted to the second dimension peak areas at ¹σ = 0.10 min (M_R = 1.1, the average peak volume error was 4.8 % and the % RSD for 500 replicates was 2.7 %. At this low sampling rate, there are only two significant points available for the Gaussian fit. Clearly, the system is ill-defined. Thus, there was an overestimation of the volume in this simulation and a dramatic decrease in precision.

Using the moments method, all simulations resulted in a peak volume % RSD of approximately 1.8 %, and the accuracy varied from +0.1 % to −1.5 % as the peak width increased. The propagation of error as calculated using the Eikens and Carr approach gave % RSD values ranging from 1.4 % to 1.8 % [58]. This is again due to the lower S/N of analyte signal spread over more second dimension chromatograms. This trend includes the simulation where there were only two points (¹σ = 0.10 min) because, in contrast to the Gaussian method, the moments method does not require a minimum number of first dimension data points. Based on the results shown in Figs. 4 and 6, the precision and accuracy of the peak volumes using both the moments and Gaussian methods are comparable if there are at least three data points above the LOD.

To compare results against typical one-dimensional chromatography, 500 replicates of a peak generated with the same ¹σ value ranging 0.10 min to 0.50 min at 0.05 min increments were simulated. As ¹σ increased, the % RSD values increased from 0.67 % to 1.1 %, 1D-LC areas were two to three fold more precise than the LC×LC method based on the moments method, similar to the results obtained in the sampling phase study.

4.2.2 Effect of Sampling Frequency on Measurement of Retention Time and Peak Width

We also evaluated the accuracy and precision of retention times and peak widths. Overall, the estimates of retention time from the Gaussian fit were excellent; the worst error in the retention time of −0.8 % for ¹σ = 0.10 min. The next worse error was +0.3 %. Once again, the use of the Gaussian fit procedure to estimate the first dimension retention time was useful only if there were enough points to define a Gaussian. The highest error in retention time using the moments method was −1.8 % when ¹σ = 0.10 min, while the other estimates ran from only 0.01 % error to −0.9 % error when ¹σ = 0.50 min.

The first dimension peak width parameter (i.e., ¹σ) was computed from the observed second dimension peak areas using both the Gaussian and moments methods and compared to ¹σ_eff computed from eqn. 4. Small differences were observed when the Gaussian method was used except when ¹σ = 0.10 min, (see Figure 6). In this case, an error of −3.3 % was observed. With wider peaks, the difference varied from 0.0 % to 0.3 %. Because there is a larger number of significant samples injected onto the second dimension column when the peaks are wider, the accuracy of the ¹σ estimate improved. The ¹σ = 0.10 min simulation is an extreme case where there are too few significant areas to estimate the standard deviation accurately. Using the moments method, the error in the difference ranged from −0.3 % to −5.7 % as ¹σ increased. For the Gaussian and moments methods, the % RSD decreased from 6.4 % to 2.3 % and from 34.7 % to 2.0 %, respectively, as the M_R value was increased from 1.1 to 5.7. Based on the results shown in Fig. 6, the precision and accuracy of the ¹σ values estimated using both the moments and Gaussian methods are comparable.

4.3 Comprehensive Study of Effect of Sampling Phase and Frequency on Measurement of Peak Parameters

In order to more completely map out the precision and accuracy of the peak volumes as a function of φ and M_R values, we carried out a grid search of the entire range of φ and M_R values. The precisions and accuracies in peak volume, retention time, and peak standard deviation obtained from these simulations are shown in Figs. 7, 8, and 9, respectively. The figures on the left are based on the Gaussian method and those on the right are from the moments method.

Fig. 7.

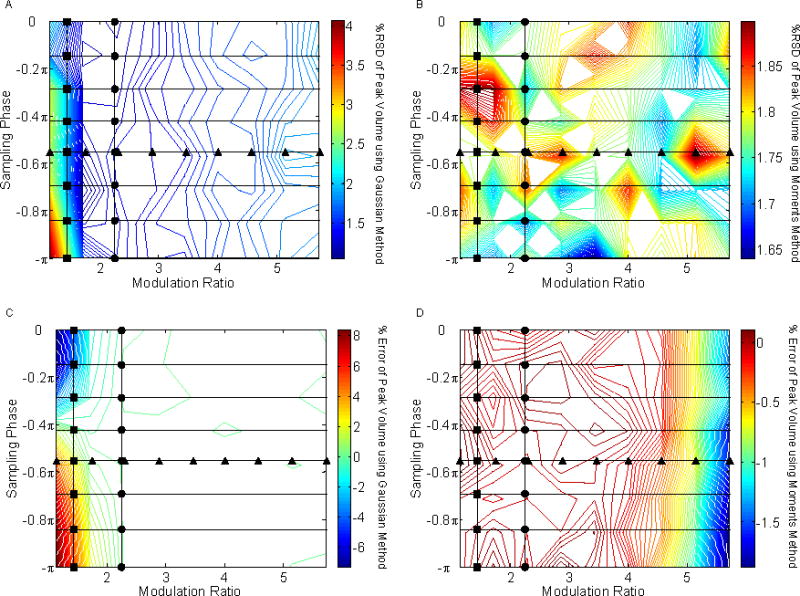
The effect of sampling phase (φ) and modulation ratio (M_R) on the precision and accuracy of peak volume determination.. The circles (●) and triangles (▲) represent the values previously shown in Figs. 4 and 6. (A) %RSD of peak volume using the Gaussian method; (B) %RSD of peak volume using the moments method; (C) % error of peak volume using the Gaussian method; (D) % error of peak volume using the moments method.

Fig. 8.

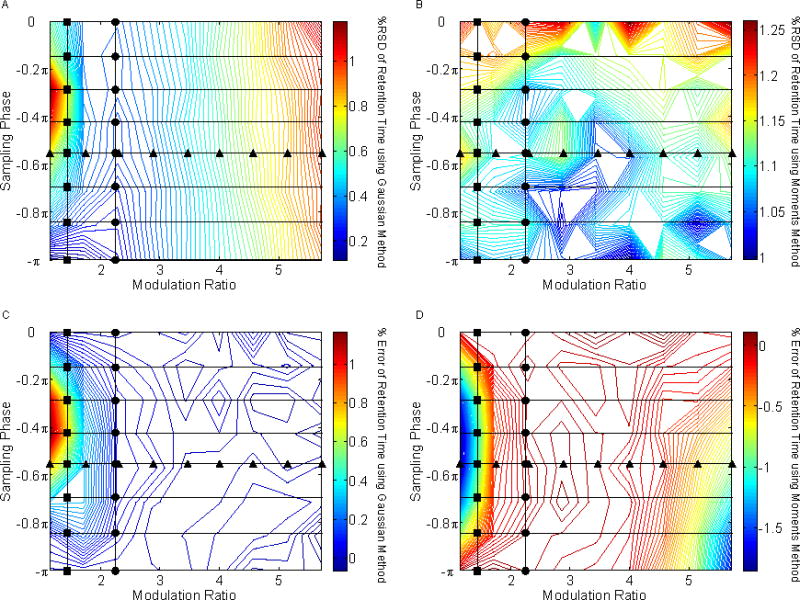
The effect of sampling phase (φ) and modulation ratio (M_R) on the precision and accuracy of peak retention times.. The circles (●) and triangles (▲) represent the values previously shown in Figs. 4 and 6. (A) %RSD of retention time using the Gaussian method; (B) %RSD of retention time using the moments method; (C) % error of retention time using the Gaussian method; (D) % error of retention time using the moments method.

Fig. 9.

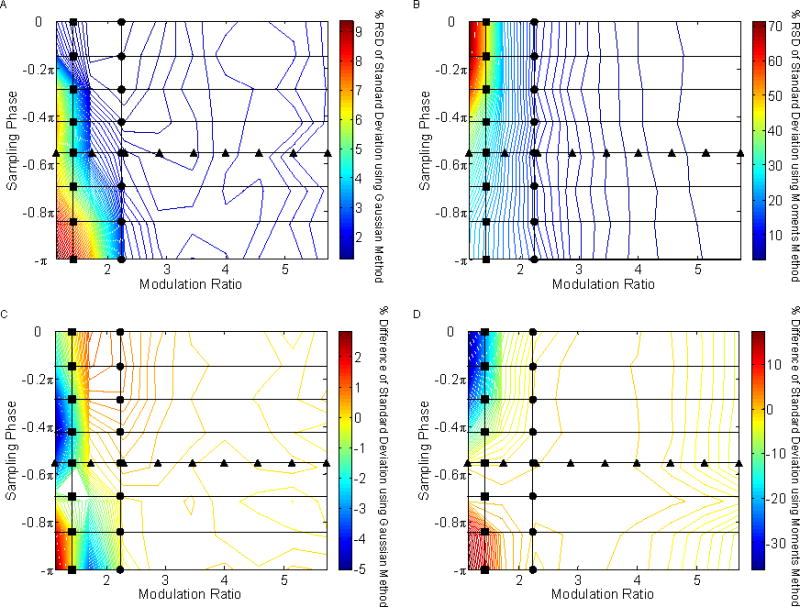
The effect of sampling phase (φ) and modulation ratio (M_R) on the precision and accuracy of peak width determination.. The circles (●) and triangles (▲) represent the values previously shown in Figs. 4 and 6. (A) %RSD of peak volume using the Gaussian method; (B) %RSD of peak volume using the moments method; (C) % error of peak volume using the Gaussian method; (D) % error of peak volume using the moments method.

4.3.1 Effect on the Peak Volume Estimation

The Gaussian method is least precise when sampling is strongly out of phase and very slow (see Fig 7A). Peak volume precision is essentially independent of sampling phase and frequency for the moments method as seen in Fig. 7B. When estimating peak volumes via the Gaussian method, the worst errors are obtained when peaks were undersampled, as seen in Fig. 7C. The moments method gives very good accuracy throughout (see Fig. 7D). We attribute the apparent decrease in % error for high modulation rations to the peak being so wide relative to the data window (i.e., ¹σ value of 0.5 min vs. a 4 min chromatogram) that there are losses in peak recovery in this simulation.

4.3.2 Effect on Retention Time Estimation

When looking at a Gaussian evaluation of retention time precision, the largest %RSD values are obtained for undersampled asymmetric peaks as shown in Fig. 8A. This observation may be explained by low S/N signals in the tails of the first dimension peaks not being detected. Retention time precision is essentially constant when evaluating by the moments method as demonstrated in Fig. 8B. A maximum error in retention time is obtained when using the Gaussian method for undersampled asymmetric peaks as seen in Fig. 8C for the same reason that poor precision in retention time is observed. In Fig. 8D, it can be seen that the retention time is underestimated when using the moments method for the same undersampled asymmetric region as the simulation shown in Fig. 8C.

4.3.3 Effect on Peak Width Estimation

Undersampled, out-of-phase peaks provide poor precisions when peak standard deviations are evaluated via the Gaussian method as seen in Fig. 9A. Sufficient sampling is necessary for the Gaussian method to model a peak adequately. On the other hand, undersampled in-phase peaks provide extremely poor precision when using the moments method as seen in Fig. 9B. It is likely that the low S/N signals in the tails of the first dimension peaks are not being sampled consistently. It is important to note that calculations of the peak standard deviation differences are based against a predicted peak standard deviation formula. In any case, as seen in Figs. 9C and 9D, the maxima and minima % differences against the predicted peak standard deviation are obtained with undersampled first dimension peaks regardless of whether the moments or Gaussian method was used. It is interesting to note, however, that good predictions of the peak width occurred when the M_R > 2 for both fitting methods.

In summary, the Gaussian method provides peak volume precisions that were generally better than those of the moments method except in the cases of out-of-phase sampling and narrow peak widths relative to the sampling interval because in those cases there are only two significant second dimension areas available to fit to a Gaussian peak. A minimum of three sampling points are needed to accurately and precisely fit a Gaussian; however, splitting the first dimension effluent into more than five or six fractions causes some decrease in the precision. Therefore, the Gaussian method is used to best effect with a modulation ratio range from two to five, with changes in sampling phase having little or no effect. For situations where the modulation ratio is less than two or greater than five, the moments method will provide more accurate and precise results for peak volumes.

4.4. Analysis of Sources of Irreproducibility in Experimental Chromatograms

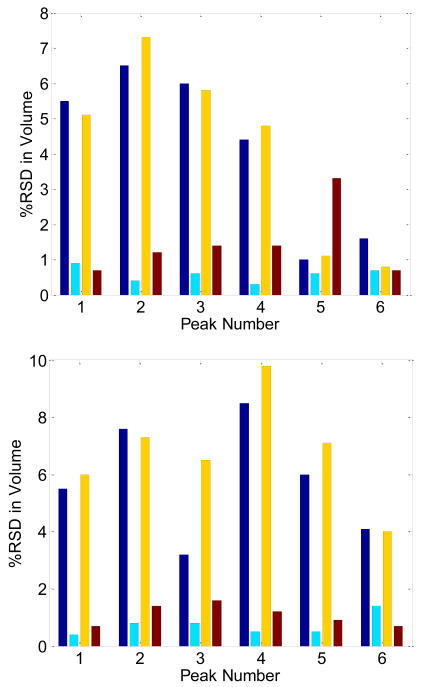
Comparison of the preceding results concerning the %RSD in peak volume with the report of Stoll et al. [9] shows that the precision predicted here is much better than seen by Stoll. There are several reasons why this may be so. The first relates to problems caused by irreproducible baselines. A second is the impact of sampling phase, which can shift between different LC×LC runs due to retention time variations. Both of these effects are considered in Fig. 10.

Fig. 10.

Comparison of Experimental and Simulated Estimates of Peak Volume. The bars represent the % RSD in peak volume for the evaluation of peaks 1–6 in the work of Stoll [9]. Results from the moments method and the Gaussian method are given in the top and bottom panes respectively. The blue bar represents %RSD of quantification of the results of three replicate LCxLC chromatograms from Stoll et al. The cyan bar gives %RSD of quantification of the results from simulated Gaussian peaks in which a single replicate (represented by the six blue profiles shown in Fig. 11) added to three replicate real LC×LC blank chromatograms. The yellow bar represents the %RSD of quantification of simulated Gaussian peaks from the three replicates of shown in Fig. 11 (blue, green and red, respectively) to three LC×LC blank chromatograms. The dark red bar represents the %RSD of quantification for 50 replicate simulated Gaussian peaks positioned at randomly generated first dimension retention times with a standard deviation in peak position of ±0.35 min (±2π), (¹σ_avg = 0.21 min, t_s = 0.35 min), added to the same blank LC×LC chromatogram.

The % RSDs for three replicate LC×LC runs reported by Stoll for their six “standard” peaks are given in Fig. 10 as the dark blue bars (peaks 1–6). These may be compared to the light blue bars which give the %RSDs obtained when the first of the three replicate runs (shown in blue in Fig. 11) was added to three replicate LC×LC runs of a blank (peaks 1a–6a). Thus, the only source of imprecision for peaks 1a–6a is variations in the baseline under the actual peaks. Clearly baseline fluctuations are not the chief problem. This was confirmed by the simulated data for peaks 1b–6b (yellow bars) in which the three replicates of data set a. were added to the three baseline replicates used in data set b. We see only a small increase in %RSD over that observed for the experimental peaks 1–6. Finally, peaks 1c–6c (red bars) illustrate the impact of run-to-run variations in the sampling phase due to retention time variations. This was done by introducing peaks with variable phase to a background chromatogram, and evaluating the %RSD in the estimated peak volumes over 50 randomizations. Clearly sampling phase fluctuations although more important than baseline fluctuations do not account for the poor precision in Stoll’s data.

Fig. 11.

First dimension chromatographic profiles derived from the second dimension peak areas for peaks 1–6. The blue profile is the first replicate, the green profile is the second replicate, and the red profile is the third replicate.

Since we have eliminated the possibility that phase fluctuations and baseline fluctuations do not explain the relatively poor precision of LC×LC analysis, we need to re-examine our assumptions. First, we assumed that all peaks are Gaussian in both dimensions. Chromatographic peaks generally are not perfectly Gaussian but either front or tail. Despite this fact, the moments method should not be affected by peak asymmetry since it works by the simple addition of the second dimension peaks. Next, we assumed that the duty cycle of the sampling device is 100 %. This assumption may be poor because it is possible that the sampling loop collecting the first dimension effluent may be overfilled before being injected into the second dimension column or the timing of this injection into the second dimension column may be inaccurate causing a misrepresentation of the LC×LC contour plot. Confirmation of this conclusion requires further experimental work, which is beyond the scope of the present work. It should be noted that this factor is not relevant to GC×GC experiments where thermal modulation is used, instead of the valve modulation commonly used in LC×LC.

5. Conclusions

The precision of measurement of peak size, retention time and peak width in LC×LC were studied by simulating the process of sampling the first dimension separation for injection onto the second dimension column. The data were analyzed by two independents methods; the second dimension peak areas were used as input into a Gaussian peak fitting algorithm and to the method of moments. The simulations were done over a wide range in modulation ratio (M_R, equivalent to sampling frequency) and sampling phase, φ.

• The Gaussian method is generally better than the moments method in that it provides somewhat better precision and is essentially independent of phasing when M_R is between two and five.

• Both the moments method and the Gaussian method gave good results for estimates of the first dimension retention times, with %RSDs and % errors generally less than 1 %. For either method, the best accuracy and precision were obtained for M_R values ranging from two to five. First dimension peak widths could also be estimated using these methods but with poorer accuracy and precision.

• When we applied our methods of peak size measurement to the experimental data of Stoll et al. [9] agreement between our precison and theirs was acceptable. Stoll et. al. obtained an average precision of 3.9% (by the moments method) over their six “standard” species which were well separated peaks. In this work, the average precision of the moments and Gaussian methods were 4.2 % and 5.8 % respectively. All six standard peaks were well above the limit of quantification (LOQ) with the lowest S/N being 23. These results indicate a precision of LC×LC that is four-fold poorer than in conventional LC.

• Our calculations clearly show that the poorer precision of LC×LC as compared to 1D-LC cannot be attributed to: a) the segmentation of a single 1D peak into multiple second dimension peaks, b) the higher baseline signals encountered in the fast gradient second dimension chromatograms, c) random fluctuations in sampling phase due to variations in first dimension retention time or d) asymmetry in second dimension peaks.