Abstract
As repositories of chemical molecules continue to expand and become more open, it becomes increasingly important to develop tools to search them efficiently and assess the statistical significance of chemical similarity scores. Here we develop a general framework for understanding, modeling, predicting, and approximating the distribution of chemical similarity scores and its extreme values in large databases. The framework can be applied to different chemical representations and similarity measures but is demonstrated here using the most common binary fingerprints with the Tanimoto similarity measure. After introducing several probabilistic models of fingerprints, including the Conditional Gaussian Uniform model, we show that the distribution of Tanimoto scores can be approximated by the distribution of the ratio of two correlated Normal random variables associated with the corresponding unions and intersections. This remains true also when the distribution of similarity scores is conditioned on the size of the query molecules in order to derive more fine-grained results and improve chemical retrieval. The corresponding extreme value distributions for the maximum scores are approximated by Weibull distributions. From these various distributions and their analytical forms, Z-scores, E-values, and p-values are derived to assess the significance of similarity scores. In addition, the framework allows one to predict also the value of standard chemical retrieval metrics, such as Sensitivity and Specificity at fixed thresholds, or ROC (Receiver Operating Characteristic) curves at multiple thresholds, and to detect outliers in the form of atypical molecules. Numerous and diverse experiments carried in part with large sets of molecules from the ChemDB show remarkable agreement between theory and empirical results.
Introduction
As chemical repositories of molecules continue to grow and become more open,1–5 it becomes increasingly important to develop the tools to search them efficiently. In one of the most typical settings, a query molecule is used to search millions of other compounds not only for exact matches, but also frequently for approximate similarity matches. In a drug discovery project, for instance, one may be interested in retrieving all the commercially-available compounds that are “similar” to a given lead, with the aim of finding compounds with better physical, chemical, biological, or pharmacological properties.
The idea of searching for molecular “cousins” is of course not new, and constitutes one of the pillars of bioinformatics where one routinely searches for homologs of nucleotide or amino acid sequences. Search tools such as BLAST6 and its significance “E-scores” have become de facto standards of modern biology, and have driven the exponential expansion of bioinformatics methods in the life sciences.
In chemoinformatics, several approaches have been developed for chemical searches, including different molecular representations and different similarity scores. However, no consensus tool such as BLAST has emerged, for several reasons. Some of the reasons have to do with the cultural differences between the two fields, especially in terms of openness and data sharing. But there are also more technical and fundamental reasons–in particular there has been no systematic derivation of a theory that can account for molecular similarity scores and their distributions and significance levels. As a result, many existing search engines do not return a score with the molecules they retrieve, let alone any measure of significance.
Examples of fundamental questions one would like to address include: What threshold should one use to assess significance in a typical search? For instance, is a Tanimoto score of 0.5 significant or not? And how many molecules with a similarity score above 0.5 should one expect to find? How does the answer to these questions depend on the size of the database being queried, or the type of queries used? A clear answer to these questions is important for developing better standards in chemoinformatics and unifying existing search methods for assessing the significance of a similarity score, and ultimately for better understanding the nature of chemical space.
These questions are addressed here systematically by conducting a detailed empirical and theoretical study of chemical similarity scores and their extreme values. Surprisingly rare previous work related to these questions include an interesting study by Keiser et al.,7 which uses empirical fitting of distributions to extreme chemical similarity scores but does not derive a predictive mathematical theory of chemical scores and their extremes values, and a short preliminary report of some of our own results.8 Here we provide a more general, complete, and self-contained treatment of these questions, including both new theoretical and new simulation results. In particular, we extend previous work by studying several different ways of assessing the significance of chemical similarity scores, by analyzing in detail how the results depend on the parameters of the query molecule as well as the size of the database being searched, by applying the general framework to the analysis and prediction of ROC curves for molecular retrieval, by applying the general framework to the detection of outlier molecules, and by providing a more complete and predictive mathematical theory of the distribution of similarity scores and its extreme values.
The rest of this paper is organized as follows. Section 2 defines the molecular representations and similarity scores that are used throughout the study. Section 3 and 4 develop the probabilistic models required to both approximate empirical distributions of similarity scores and to create random background models against which significance can be assessed. Section 5 presents the main theory for the distribution of chemical similarity scores followed by Section 6 which presents the theory for the distribution of the extreme values of the score distributions. Corresponding experimental results to illustrate and corroborate the theory are described in Section 7 and 8, followed by a Discussion and Conclusions section. To improve readability, the details of the mathematical derivations are given in the Appendix.
Molecular Representations and Similarity Scores
Many different representations and similarity scores have been developed in chemoinformatics. The methods to be described here are broadly applicable but, for exposition purposes, we illustrate the theory using the framework that is most commonly used across many different chemoinformatics platforms, namely binary fingerprint representations with Tanimoto similarity scores. When appropriate, we also briefly describe how the same approach can be extended to other implementations and settings.
Molecular Representations: Fingerprints
Multiple representations have been developed for small molecules, from one dimensional SMILES strings to 3D pharmacophores,9 and different representations can be used for different purposes. To search large databases of compounds by similarity, most modern chemoinformatics systems use a fingerprint vector representation9–15 whereby a molecule is represented by a vector whose components index the presence/absence, or number of occurrences of a particular functional group, feature, or substructure in the molecular bond graph. Because binary fingerprints are used in the great majority of cases, here we present the theory for these fingerprints, but it should be clear that the theory can readily be adapted to fingerprint based on counts. We use 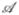 to denote a molecule and A⃗ = (Ai) to denote the corresponding fingerprint. We let A denote the number of 1-bits in the fingerprint A⃗ (A = |A⃗|).
to denote a molecule and A⃗ = (Ai) to denote the corresponding fingerprint. We let A denote the number of 1-bits in the fingerprint A⃗ (A = |A⃗|).
In early chemoinformatics systems, fingerprint vectors were relatively short, containing typically a few dozen components selected from a small set of features, hand-picked by chemists. In most modern systems, however, the major trend is towards the combinatorial construction of extremely long feature vectors with a number of components N that can vary in the 103–106 range, depending on the set of features. Examples of typical features include all possible labeled paths or labeled trees, up to a certain depth. The advantage of these longer, combinatorially-based representations is twofold. First, they do not require expert chemical knowledge, which may be incomplete or unavailable. Second, they can support extremely large numbers of compounds containing both existing and unobserved molecular structures, such as those that are starting to become available in public repositories and commercial catalogs, as well as the recursively enumerable space of virtual molecules.16 The particular nature of the fingerprint components is not essential for the theory to be presented. To illustrate the principles, in the simulations we have used both fingerprints based on labeled paths and fingerprints based on labeled shallow trees with qualitatively similar results. For completeness, the details of the fingerprints used in the simulations are given below in the Data subsection. For brevity and consistency, the examples reported in the Results are derived primarily using fingerprints based on paths.
Fingerprint Compression
In many chemoinformatics systems, the long sparse fingerprint vectors are often compressed to much shorter and denser binary fingerprint vectors. The most widely used method of compression is a lossy compression method based on the application of the logical OR operator to the binary fingerprint vector after modulo wrapping to 512, 1,024, or 2,048 bits.12 Other more efficient lossless methods of compression have recently been developed.15 With the proper and obvious adjustments, our results are applicable to both lossy compressed and uncompressed fingerprints. Because these are widely used, the majority of the simulation examples we report are obtained using modulo-OR compressed binary fingerprints of length N = 1,024. Due to their shorter length, these fingerprints have also the advantage of speeding up Monte Carlo sampling simulations.
Similarity Scores
Several similarity measures have been developed for molecular fingerprints.17,18 Given two molecules 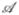 and ℬ, the Tanimoto similarity score is given by
and ℬ, the Tanimoto similarity score is given by
| (1) |
Here (A ∩ B) denotes the size of the intersection, i.e. the number of 1-bits common to A⃗ and B⃗, and A ∪ B denotes the size of the union, i.e. the number of 1-bits in A⃗ or B⃗. Because the Tanimoto similarity is by far the most widely used, the theory and experimental results reported here are based on the Tanimoto similarity. However, we also briefly describe how the same theory can be extended to other measures. Because Tanimoto similarity scores are built from intersections and unions, it will be natural to begin the theoretical analysis by studying the distribution of these intersections and unions, in particular their means, variances, and covariances.
Data
In the simulations, we illustrate the methods using fingerprints that are either randomly generated using one of the stochastic models described in Section 3, or randomly selected from the 5M molecules or so available in the ChemDB database.1 In the case of the actual molecules, we use fingerprints associated with two schemes:15 labeled paths of length up to eight (i.e. 9 atoms and 8 bonds), or labeled circular substructures of depth up to two, with Element (E) and Extended Connectivity (EC) labeling. In the first scheme, referred to as paths throughout the paper, for each chemical we extract all labeled paths of length up to eight starting from each vertex and using depth-first traversal of the edges in the corresponding molecular graph. For this scheme, each vertex is labeled by the element (C,N,O, etc) of the corresponding atom and each edge is labeled by the type (single, double, triple, aromatic, and amide) of the corresponding bond. This scheme is closely related to the scheme used in many existing chemoinformatics systems, including the Daylight system.12 In the second scheme, for each chemical we extract every circular substructure, of depth up to two, from the corresponding molecular graph. Circular substructures (see Hert et al.,19 Bender et al.,20 and Hassan et al.21) are fully explored labeled trees of a particular depth, rooted at a particular vertex. For this scheme, molecular graphs are labeled as follows: each vertex is labeled by the element (C,N,O, etc) and degree (1, 2, 3, etc) of the corresponding atom, and each edge is labeled as above. The degree of a vertex is given by the number of edges incident to that vertex or, equivalently, the number of atoms bonded to the corresponding atom.
Both in the case of randomly generated fingerprints and actual molecular fingerprints, we used both uncompressed fingerprints, corresponding also to lossless compressed fingerprints, as well as lossy compressed fingerprint obtained using the standard modulo-OR-compression algorithm to generate fingerprint vectors of length 1,024. For both the randomly generated fingerprints and actual molecular fingerprints, we run typical simulations using a sample of n = 100 queries against background sets that range from 5,000 to 1 million fingerprints in order to study the effects associated with database size.
Probabilistic Models of Fingerprints
One of the main goals of this work is to derive good statistical models and approximations for the distribution of similarity scores. At the most fundamental level this can be addressed by building probabilistic models of fingerprints. Statistical models of fingerprints are essential for a variety of tasks. For instance, in fingerprint compression, fingerprints can be viewed as “messages” produced by a stochastic source and understanding the statistical regularities of the source is essential for deriving efficient compression algorithms that use short code words for the most frequent events. Here, statistical models are essential in at least two different ways: (1) to model and approximate the distribution of statistical scores; and (2) to assess significance against a random background. Similar observations of course can be made in bioinformatics to, for instance, assess what is the probability of observing a particular sequence or alignment score against a random generative or evolutionary model of protein or DNA sequences. It is worth noting that as a default, we assume that the distribution over the queries is the same as the distribution over the molecules in the database. However, these statistical models can also be used to model particular distributions over the space of queries that may differ from the overall background distribution.
Single-Parameter Bernoulli and Binomial Model
The simplest statistical model for binary fingerprints is a sequence of independent identically distributed Bernoulli trials (coin flips) with probability p of producing a 1-bit, and q = 1 − p of producing a 0-bit. This model can be applied to both long fingerprints with a very low p or to the modulo-OR compressed fingerprints with a higher value of p. The coin flip model corresponds to fingerprint features that are randomly ordered and statistically exchangeable, in fact even independent, and leads to a Binomial model ℬ(N, p), with only two parameters N and p, for the total number of 1-bits in the corresponding fingerprints. The single-parameter Bernouilli model is a weak model of real fingerprints for two reasons. First the probability of the individual components are not identical: some features are more likely to occur than others. Second, the components are not strictly independent. These shortcomings are further addressed in the more complex models described below. Nevertheless, the single-parameter Bernouilli model remains useful because of its simplicity and tractability, and it provides a point of reference or baseline for other models.
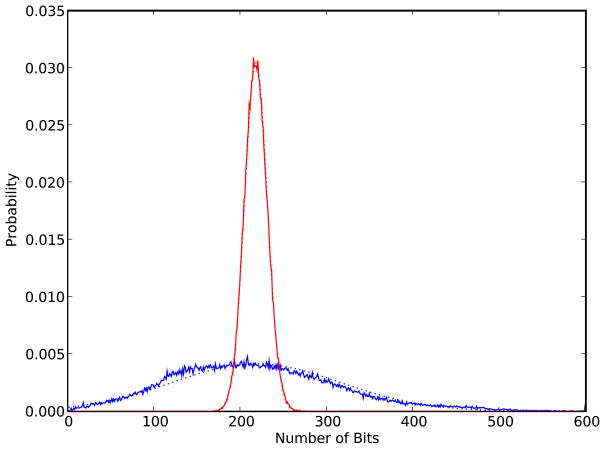
The Bernoulli model can be used to approximate the distribution of fingerprints in an entire database such as ChemDB by setting p to the average fingerprint density in the database. If one then compares the behavior of the number A of 1-bits in the Bernoulli generated fingerprints and in the actual database, one typically observes that the average of A is the same in both cases, by construction of p, but the variance is quite different. The variance A in the Bernoulli generated fingerprints is given by N pq and is always at most equal to the expectation N p, whereas in large databases of compounds one typically observes a larger variance (Figure 1). In general, a better model for A is provided by a Normal distribution 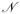 (μ,σ2) where the mean μ = Np and variance σ2 ≠ Npq are fitted empirically to the data.
(μ,σ2) where the mean μ = Np and variance σ2 ≠ Npq are fitted empirically to the data.
Figure 1.
Distributions of the number of 1-bits in fingerprints from the ChemDB (blue solid line) and fingerprints from the matching Single-Parameter Bernoulli model (red solid line) with p ≈ 205/1,024). Both distributions are constructed using a random sample of 100,000 fingerprints. Though both distributions have similar means, the standard deviations differ significantly. The distributions are also fit using two Normal distributions, which approximate the data well (dotted lines).
In some analyses, it is useful to consider fingerprints that contain A 1-bits. These can be modeled using Bernoulli coin flips with p = A/N, although this is at best an approximation since in the resulting fingerprints the number of 1-bits is not constant and varies around the mean value A, introducing some additional variability with respect to the case where A is held fixed (see Conditional Distribution Uniform model below). Finally, a distribution over queries that is different from the overall database distribution can be modeled using two Bernoulli models: one with parameter r for the queries, and one with parameter p (p ≠ r) for the database.
Multiple-Parameter Bernoulli Model
While the coin flip model is useful to derive a number of approximations, it is clear that chemical fingerprints have a more complex structure and their components are not exactly exchangeable since the individual feature probabilities p1,…, pN are not identical and equal to p but vary significantly. In particular, when the fingerprint components are reordered in decreasing frequency order, they typically follow a power-law distribution,15 especially in the uncompressed case. The probability of the j-ranked component is given approximately by pj = Cj−α resulting in a line of slope −α in a log-log plot. Thus the statistical model at the next level of approximation is that of a sequence of non-stationary independent coin flips where the probability pj of each coin flip varies. This Multiple-Parameter Bernoulli model has N parameters: p1, p2, …, and pN. In this case, using the independence, the expectation of the total number A of 1-bits is given by Σi pi and its variance by . In general, this variance is still an underestimate of the variance observed in actual large databases in spite of the larger number of parameters compared to the Single-Parameter Bernoulli Model (not shown). Similarly to the case of the Single-Parameter Bernouilli model, a distribution over queries different from the overall distribution could be modeled using a Multiple-Parameter Bernoulli model with a different set of parameters r1,…,rN.
Conditional Distribution Uniform Model
Both the Single-Parameter and Multiple-Parameter Bernoulli models consider the fingerprint components as independent random variables. The Conditional Distribution Uniform model is an exchangeable model where the components are weakly coupled and thus not independent. To generate a fingerprint vector under this model, one first samples the value A corresponding to the total number of 1-bits in the fingerprint, using a given distribution, typically a Normal distribution (Figure 1). The model then assumes that conditioned on the value of A all fingerprints with A 1-bits are equally probably (uniform distribution). Thus, for example, the Conditional Normal Uniform model has only three parameters: the mean μ, the standard deviation σ2, and N. Compared to the Binomial model, the additional parameter in the Conditional Normal Uniform model allows for a better fit of the variance of A in the data. As we shall see, for the questions to be considered here the Conditional Normal Uniform model performs the best in spite of the fact that it does not model the probability differences between different fingerprint components.
Spin Models
More complex, second order, models are possible but will not be considered here. These models are essentially spin models from statistical physics, and are also known as Markov Random fields or Boltzmann machines.22,23 In these models, one would have to take into account also the correlations between pairs of features which can be superimposed over the Multiple Bernoulli model. In real data, these correlations are often (though not always) weak, but not exchangeable, and thus behave differently from those introduced in the Conditional Distribution Uniform model. The slight improvements in modeling accuracy that may result from spin models come in general at a significant computational cost since these cannot be solved analytically and therefore cannot be used in a straightforward manner to derive the probability distribution of the similarity scores. Study of spin models is left for future work.
Probabilistic Models of Distribution Scores
While in the following sections and the Appendix we show how the distribution of similarity scores can be estimated somehow from “first principles”, i.e. from the corresponding probabilistic model of fingerprints, it is also possible to model or approximate the score distribution directly, for instance by assuming that the scores are approximately normally distributed and obtaining the mean and standard deviation by sampling methods. In a similar way, one can also use a Gamma distribution model to completely avoid negative scores, or a Beta model to insist on bounded scores between 0 and 1, to model the overall distribution of scores. Another intermediary alternative, which is less direct but still avoids modeling the fingerprints themselves, is to model the intersections and unions that are used to derive the Tanimoto scores, and then try to derive the distribution of the scores from those models. For example, one could consider modeling both the intersections and corresponding unions using two different normal distributions and derive the means and standard deviations of these normal distributions by sampling methods. The commonalities, differences, and tradeoffs between these various modeling and approximation approaches to the distribution of chemical similarity scores will become clear in the following sections. The most complex case, where everything is derived from the probabilistic models of fingerprints, is treated in detail in the Appendix.
The Distribution of the Similarity Scores
With these preliminaries in place, we are now set to analyze the distribution of Tanimoto scores under the various probabilistic models.
Main Result
Since the Tanimoto score is the ratio of an intersection over an union, the basic strategy is to first study the distribution of the corresponding intersection and union, their means and variances. Note that the intersection and union, in general, are not two independent random variables, but have a non-zero correlation that must be estimated analytically or through simulations. In turn, from these results one can derive a closed-form approximation for the distribution of the Tanimoto scores and its extreme properties. This analysis can be carried using empirical fingerprint data as well as fingerprints generated by the probabilistic models. Furthermore, the analysis can be conducted by conditioning on the total number of 1-bits contained in the query molecule (A) and the molecules being searched (B), by conditioning on only one of these quantities–typically the number A of 1-bits in the query molecule–and integrating over the other, or with no conditioning at all by integrating over both the fingerprints in the queries and the fingerprints in the database being searched. These forms of conditioning are practically relevant, especially conditioning on A, which will be shown to lead to much better retrieval results.
In all these cases, one in general finds that:
The intersection and union have approximately a Normal distribution with means and variances that can be estimated empirically or computed analytically in the case of the probabilistic models.
The intersection and union have a non-zero (positive) covariance that can be estimated empirically or computed analytically in the case of the probabilistic models.
As a consequence, the distribution of the corresponding Tanimoto scores can be modeled and approximated by the distribution of the ratio of two correlated Normal random variables.
These facts are demonstrated in the Results section using simulations. In Appendix A, mathematical proofs are provided for the probabilistic models of fingerprints together with analytical formula for the means, variances and covariances of the intersections and unions.
Ratio of Two Correlated Normal Random Variables Approximation
Whether one uses the Single Bernoulli/Binomial, Multiple Bernoulli, or Conditional Density Uniform models, or the empirical intersection and union data, in the end, the Tanimoto score distribution can be approximated by the distribution of two correlated Normal random variables approximating the numerator and the denominator. The different models will yield different estimates of the mean, variance, and covariance of the respective Normal distributions.
The density of the ratio of two correlated Normal random variables has been studied in the literature and can be obtained analytically, although its expression is somewhat involved.24–27 The probability density for Z = X/Y, where ![]() , and ρ = Corr(X, Y) ≠ ± 1 is given by the product of two terms
, and ρ = Corr(X, Y) ≠ ± 1 is given by the product of two terms
| (2) |
or
| (3) |
where
| (4) |
| (5) |
and
| (6) |
Thus, anytime one can approximate the intersections and the unions by two correlated Normal random variables, the distribution of the Tanimoto scores can be approximated using Equations 2–6 with X = I and Y = U. This approach can be used, for instance, to derive the mean and standard deviation of the Tanimoto scores under various assumptions including: (1) the Single- and Multiple-Parameter Bernoulli models with p = r (or pi = ri) for the average Tanimoto scores across all queries; (2) the Single- and Multiple-Parameter Bernoulli models with p ≠ r (or pi ≠ ri) for queries modeled by a different Bernoulli model than the one used for the database being searched; (3) the Conditional Distribution Uniform model with A fixed, or A integrated over the database distribution, or a distribution over queries; and (4) the empirically-derived Normal models for the union and intersection averaged over the entire database, or focused on a particular class of molecules.
A Python code implementation for the density of the ratio of two correlated Normal random variables (Equations 2–6) is available from the ChemDB chemoinformatics portal (cdb.ics.uci.edu), under Supplements.
Extensions to Other Measures
While we have described the theory for the Tanimoto similarity scores, the same theory can readily be adapted to most other fingerprint similarity measures.17,18 To see this, it suffice to note that the other measures consist of algebraic expressions built from A ∪ B and A ∩ B, as well as other obvious terms such as A, B, and sometimes N. For example, the Tversky measure28,29 is an important generalization of the Tanimoto measure defined by
| (7) |
where the parameters α and β can be used to tune the search towards sub-structures or super structures of the query molecule. The numerator and denominator in the Tversky measure can again be modeled by two two correlated Normal random variables. The only difference is in the mean and variance of the denominator, and its covariance with the numerator. The new mean, variance, and covariance can be computed empirically. They can also be derived analytically for the simple probabilistic models, as described in Appendix A. Similar considerations apply to all the other measures described in.17,18 Thus the distribution and statistical properties of all the other similarity measures17,18 can readily be derived from the general framework described presented here.
Alternatives and Related Approaches
Because the intersections and unions have always positive values, it is also possible in some cases to approximate their distributions using Gamma distributions. The distribution of Tanimoto scores can then be modeled using the distribution of the ratio of two correlated Gamma distributions, for which some theory exists.30–32 Likewise, in regimes where the finite [0, N] range of the intersections and unions becomes important, the intersection and union can be rescaled by 1/N and the corresponding distributions modeled using Beta distributions. In this case, the distribution of Tanimoto scores can be modeled using the distribution of the ratio of two correlated Beta distributions.33 Finally, as already mentioned, it is also possible to model or approximate a distribution of Tanimoto scores directly using a Normal, Gamma, or Beta distribution (or a mixture of these distributions) without having to first consider the intersections and unions.
It is not possible to give a general prescription as to which approach may work best in a practical application, since this may depend on the details and goals of a particular implementation. However, the theory presented provides a general framework for predicting and modeling the distribution of Tanimoto scores that can be adapted to any particular implementation. And using this distribution, it is possible to derive measures and visualization tools to assess the quality and significance of the molecules being retrieved with a given query and the corresponding rates of false positives and false negatives, as described in the next sections.
Theory: Z-Scores, E-Values, P-Values, Outliers, and ROC Curves
There are various computational approaches for determining the significance of similarity scores. All these approaches derive from the distribution of similarity scores. Significance scores include Z-scores, E-values, and p-values associated with the extreme value distribution34–36 of similarity scores. The distribution of similarity scores can also be used to detect outliers and predict ROC (Receiver Operating Characteristic) curves in chemical retrieval. As we shall see, these significance analyses can be done and yield better results when conditioned on the size of the queries.
Z-Scores
In the Z-score approach, one simply looks at the distance of a score from the mean of the corresponding family of scores, in numbers of standard deviations. Therefore the Z-score is given by
| (8) |
The parameters μ and σ can be determined either empirically from a database of fingerprints, using the statistical models described above. While Z-scores can be useful, their focus is on the global mean and standard deviation of the distribution of the scores, not on the tail of extreme values. Thus we next consider two measures that are more focused on the extreme values.
E-Values
When considering a particular similarity value or selecting a similarity threshold t for a given query, an important consideration is the expected number of hits in the database above that threshold. To use a terminology similar to what is used for BLAST, we refer to this number as the E-value. From the distribution of scores in a database of size D, the E-value corresponding to a Tanimoto threshold t is estimated by
| (9) |
where F(t) is the cumulative distribution of the corresponding similarity scores, which can be approximated using the methods described above.
Extreme Value Distributions and P-Values
The second approach focused on extreme values corresponds to computing p-values. For a given score t, its p-value is the probability of finding a score equal to or greater than t under a random model. Thus in this case, one is interested in modeling the tail of the distribution of the scores, and more precisely the distribution of the maximum score.34–36 This distribution depends on the size of the database being searched since for a given query, and everything else being equal, we can expect the maximum similarity value to increase with the database size.
Consider a query molecule 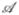 used to search a database containing D molecules, yielding D similarity scores t1,…,tD. The cumulative distribution of the maximum max is given by
used to search a database containing D molecules, yielding D similarity scores t1,…,tD. The cumulative distribution of the maximum max is given by
| (10) |
under the usual assumption that the scores are independent and identically distributed. Here F(t) is the cumulative distribution of a single score. A p-value is obtained by computing the probability
| (11) |
that the maximum score be larger than t under F. The density of the maximum is obtained by differentiation
| (12) |
where f (t) is the density of a single score. In the case of Tanimoto similarity scores, f (t) can be approximated by the ratio of two correlated Normal random variables approach described above, and F(t) is obtained from f (t) by integration. F(t) can also be approximated by25
| (13) |
where is the cumulative distribution of the normalized Normal distribution and
| (14) |
This approximation is good when the denominator of the ratio of two correlated Normal random variables is positive, with its standard deviation much larger than its average. In any case, by combining Equations 2, 12, and 13, we get:
| (15) |
Finally, because the Tanimoto scores are bounded by one, the theory of extreme value distributions shows that the cumulative distribution of the normalized maximum score nD, normalized linearly in the form nD = aDmax + bD using appropriate sequences aD and bD of normalizing constants, converges to a type-III extreme value distribution, or Weibull distribution function, of the form
| (16) |
The linear normalization can be ignored since it is absorbed into the parameters of the Weibull distribution. The advantage of the Weibull formula is its suitability for representing Fmax in a closed form that can be easily and efficiently computed. How to fit in practice the Weibull distribution to the data is described in Appendix B.
Outliers
The framework allows us to detect molecules that are atypical, within their group, in the following sense. From the framework we can predict the typical (average) distribution of Tanimoto scores for a given query size S, or the expected number of hits above any given threshold t, given S. Clearly if we are dealing with an actual query molecule  with a fingerprint containing A = S 1-bits, if the distribution of observed scores for
with a fingerprint containing A = S 1-bits, if the distribution of observed scores for  differs from the typical distribution given A, then the molecule
differs from the typical distribution given A, then the molecule  can be viewed as being atypical within the class of molecules in the database containing A 1-bits in their fingerprints. The difference between the typical distribution of scores for molecules with A 1-bits and the distribution of scores generated by the actual query
can be viewed as being atypical within the class of molecules in the database containing A 1-bits in their fingerprints. The difference between the typical distribution of scores for molecules with A 1-bits and the distribution of scores generated by the actual query  can be measured in many ways, for instance by using the relative entropy or Kullback Leibler divergence between the two distributions.37 Similar considerations can be made using the expected number of scores above a given threshold for molecules with A 1-bits versus the actual number observed for molecule
can be measured in many ways, for instance by using the relative entropy or Kullback Leibler divergence between the two distributions.37 Similar considerations can be made using the expected number of scores above a given threshold for molecules with A 1-bits versus the actual number observed for molecule  .
.
ROC Curves
Finally, the general framework can be used to predict false positive and false negative rates, as well as standard ROC (Receiver Operating Characteristic) curves. For conciseness, let us describe the approach for ROC curves, which plot false positive rates on the x-axis versus true positive rates on the y-axis. Consider a set of molecules (e.g. a set of Estrogen Receptor binding molecules) as a set of positive examples used to search a large database for similar molecules. Empirically, or using the ratio of correlated Normal random variables approach, one can derive a density f and a corresponding cumulative distribution F for the similarity scores of the positive examples, and a density g and a corresponding cumulative distribution G for the similarity scores of the negative examples provided by the overwhelming majority of the molecules in the large database. Thus for a given threshold t on the Tanimoto similarity, the corresponding point on the ROC is easily obtained and given by
| (17) |
In other words, using continuous approximations, the equation of the ROC curve is given by y = 1 − F(G−1(1 − x)). Similarly, other measures such as Specificity or Sensitivity can be estimated at any given threshold.
Now, armed with this theoretical framework we can proceed with simulations to demonstrate how the framework can be applied and assess the quality of the corresponding predictions. The following sections describe experimental results obtained using actual molecules from the ChemDB. A large number of experiments were carried and only a sample of the main results is described here for brevity. Unless otherwise specified, the results reported here are obtained using path fingerprints compressed to 1,024 bits using lossy modulo-OR compression.
Simulation Results: The Distribution of Similarity Scores
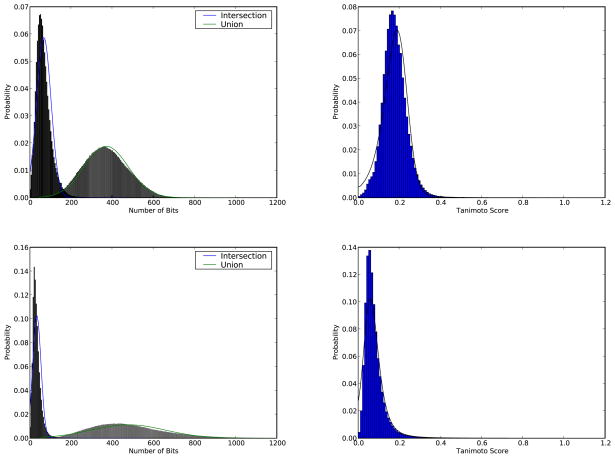
We first examine the quality of the ratio of correlated Normal random variables approximation. Figure 2 shows in the left column the empirical distributions of the sizes of the intersections and unions averaged across the entire database and obtained by Monte Carlo methods, for both lossy compressed fingerprints (upper plots) and uncompressed fingerprints (lower plots) together with their Normal approximations. The positive covariance between the intersections and unions is Cov(I,U) = 3048.5 (with corresponding correlation Corr(I,U) = 0.82) for the lossy compressed fingerprints, and Cov(I,U) = 1253.2 (Corr(I,U) = 0.35) for the uncompressed fingerprints. In the right column, one can see the corresponding histogram of Tanimoto scores and the ratio of correlated Normal random variables approximation. Overall, the ratio of correlated Normal random variables approach approximates the histograms very well in this case, where one is using averaging over all molecules.
Figure 2.
Results obtained with 100 molecules randomly selected from ChemDB used as queries against a sample of 100,000 molecules randomly selected from ChemDB. The two upper figures correspond to fingerprints of length 1,024 with modulo OR lossy compression, while the two lower figures correspond to fingerprints with lossless compression (equivalent to uncompressed fingerprints). The figures in the left column display the histograms of the sizes of the intersections and unions and their direct Normal approximations in blue and green respectively. The figures in the right column display the histograms of the Tanimoto scores (blue bars), while the solid black line shows the corresponding approximation derived using the ratio of correlated Normal random variables approach.
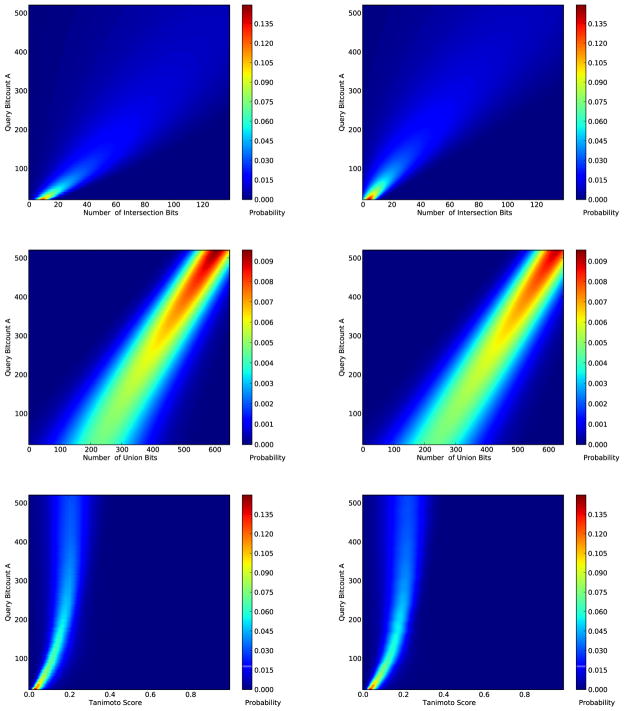
To test whether the ratio of correlated Normal random variables approximation works well at a finer grained level, we repeat a similar experiment but conditioning on the size A of the query molecules. In fact, in this experiment we use an even more stringent theoretical model. Instead of fitting Normal distributions to the intersections and unions (as in Figure 2), we assume that the data is generated by the Conditional Normal Uniform Model with only two parameters that are fit to the mean and variance of B across the entire ChemDB. As described in the Appendix, this gives us analytical formulas for the means and variances of the intersections and unions for each value of A, as well as their covariances. Figure 3 provides heat maps showing the corresponding empirical and predicted distributions of the intersections (first row) and unions (second row) as a function of A. The last row compares the observed Tanimoto score distribution to the predicted Tanimoto score distribution, using the ratio of correlated Normals approach. Overall, there is remarkable agreement between the theoretical predictions and the corresponding empirical observations at all values of A and at all Tanimoto scores, especially considering that the Conditional Normal Uniform model used in these heat maps has only two parameters that are fit to the actual data (the mean and variance of B in ChemDB).
Figure 3.
Empirical (left) and predicted (right) heat maps corresponding to the distribution of the intersections (top), unions (middle), and Tanimoto scores (bottom). The distribution is conditioned on the size of the query molecule, A, shown on the vertical axis. The empirical results are obtained by using for each A 100 molecules randomly selected from the molecules in ChemDB with size A. The theoretical results of the intersection and union distributions use the Conditional Normal Uniform model. At each value of A, the mean and variance of the intersection and union are obtained from Equations 29, 30, 33, and 36 respectively. The theoretical score distribution is a result of the ratio of correlated Normal random variables approximation given by Equations 2–6
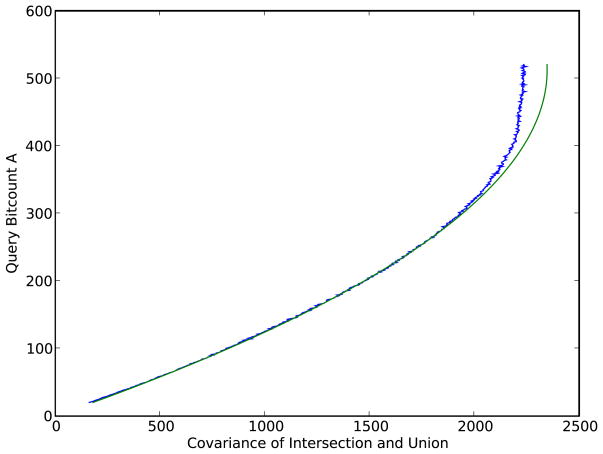
Likewise, Figure 4 shows how for each value of A, the covariance between the union and the intersection is well predicted by the Conditional Normal Uniform model, with a small deviation observed for molecules with a high bit count where the covariance is slightly smaller than predicted by the theory, probably as a result of a decrease in the variability of the size of the union for queries associated with molecules from ChemDB with a large A (the size of the union tends to be close to A since the components in the complement have exceedingly small probabilities).
Figure 4.
The empirical and theoretical covariance Cov(I,U) between the intersection and the union, conditioned on the size A of the query molecule, shown in blue and green respectively. Empirical results are obtained by using, for each A, 100 molecules randomly selected from the molecules in ChemDB with size A. A is shown on the vertical axis for consistency with the previous heat map figures. Theoretical predictions are derived with the Conditional Normal Uniform Model conditioned on A (Equation 39).
In sum, these results show that the distribution of Tanimoto scores can be modeled, predicted, or approximated accurately with the framework proposed here. Among the simplest models, the Conditional Normal Uniform Model performs best. Conditioning on the size A of the query can play an important role, since there are significant variations in the distribution of the scores as A varies.
Z-Scores, E-Values, P-Values, Outliers, and ROC Curves
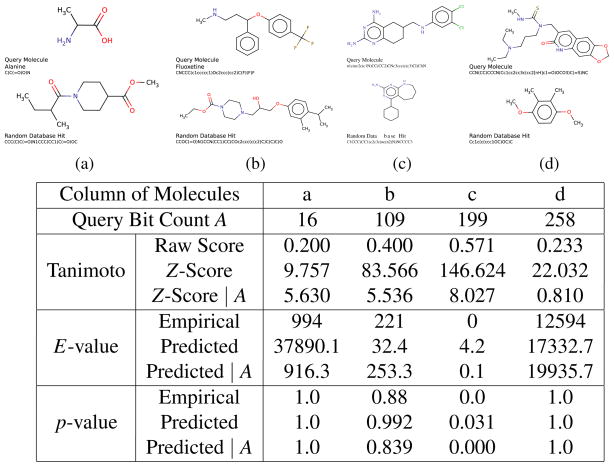
We now turn to the assessment of significance using Z-scores, E-values, extreme value distributions and p-values, and ROC curves. Figure 5 provides four examples, one in each column, of pairs of molecules where the top molecule can be viewed as the query, and the bottom molecule can be viewed as a potential “hit” retrieved while searching a random subset of 100,000 molecules taken from the ChemDB. The four queries have different sizes corresponding to A = 16, 109, 199, and 258. The corresponding four Tanimoto similarity scores are 0.200, 0.400, 0.571, and 0.233. Columns a and d correspond to similar Tanimoto scores, although they should be viewed quite differently due to the disparity in the size A of the corresponding queries, as shown in the following analyses.
Figure 5.
The first row shows four query molecules. The second row considers four corresponding potential “hits” in the corresponding columns. The table shows the size A of the four query molecules followed by the corresponding Tanimoto scores, Z-scores, E-scores, and p-values observed empirically or predicted from the theory with and without conditioning on the size A of the query molecule. Molecules are represented by Daylight-style fingerprints of length 1024 with OR lossy compression.
Z-Scores
The Z-score is the distance of a Tanimoto score from the mean measured in number of standard deviations. As usual, for a given query of size A, the mean and standard deviation can be computed over all molecules, or over molecules of size A only. As expected, Figure 5 shows that the Z-scores computed over all molecules are not very informative and would indicate that all four pairs of molecules have Z-scores above 9 and therefore are significantly very similar. The Z-scores computed by conditioning on A are slightly more informative: while they still return three of the matches corresponding to columns a, b, and c as highly significant (Z-scores above 5) compared to random, they begin to separate these cases from the case of column d which is scored as not being very significant (Z-score of 0.810).
E-Values
As described previously, the E-value for a Tanimoto score t represents the expected number of “hits” above t and can be estimated empirically or predicted from the distribution of the scores and the size D of the database (Equation 9). Figure 5 shows again that theoretical E-values obtained by conditioning on A are more useful and in the range of the E-values observed empirically (here D = 100,000). The empirical E-values, or the predicted E-values conditioned on A, now clearly separate the similarity in column d as being non significant. The empirical and predicted E value show that when the size of the molecular fingerprints is taken into consideration, the E-value in column d is considerably less significant that the E-value in column a, in spite of the fact that the Tanimoto score in d (0.233) is higher than the Tanimoto score in a (0.200). In addition, the E values identify column c as being the only one with really significant similarity (E-value of 0.1).
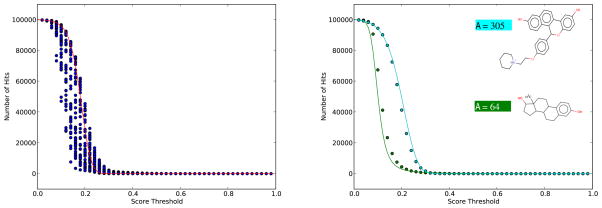
Figure 7 provides further evidence of the utility of E-values and conditioning on A. This Figure is obtained by using 55 Estrogen-Receptor binding molecules38 together with a random sample of 100,000 molecules extracted from the ChemDB. For each one of the 55-Estrogen Receptor ligands and any threshold, the figure essentially plots the number of molecules that have a score above that threshold. Thus, for example, for t = 0 all 100,000 molecules have a score above t, corresponding to 55 superimposed dots on the graph. Likewise, for t = 1 there are 55 superimposed dots with vertical value equal to 0 because no molecule scores higher than 1. Note how the number of hits varies greatly in the threshold interval [0.1, 0.3]. The solid red line represents the predicted E-values obtained using the Conditional Normal Uniform Model and the corresponding ratio of two correlated Normal random variables approximation integrated over all the molecules. The red curve is slightly shifted with respect to the empirical points because the molecules in the Estrogen receptor dataset have an average size of 143 bits, while molecules in ChemDB have an average size of 205 bits. Deviations from the red line are observed in the actual data. The right side of Figure 7 shows how this can be corrected by looking at individual molecules, in this case the molecules with the smallest (A = 64) and largest (A = 305) size among the dataset of Estrogen Receptor ligands. The predicted curves obtained by conditioning on the corresponding values of A are in excellent agreement with the corresponding empirical values.
Figure 7.
Left: 55 Estrogen Receptor ligands are used to query a sample of 100,000 molecules randomly selected from the ChemDB. Horizontal axis represents Tanimoto threshold scores. Vertical axis represents number of scores above the threshold (hits). Each dot represents a query’s number of hits above the corresponding threshold on the horizontal axis. Superimposed dots are indistinguishable (see text). The solid red line represents the predicted E-values based on the ratio of two correlated Normal random variables approximation integrated over all values of A in the sample. Right: Dots associated with the Estrogen Receptor ligand with the largest A (cyan) and the smallest A (green) are isolated. The solid lines show predicted E-values based on the ratio of two correlated Normal random variables conditioned on the size of the two query molecules: A = 305 (cyan) and A = 64 (green).
Extreme Value Distributions and P-values
The p value for a score t is computed from the extreme value distribution and corresponds to the probability of observing a maximum score above t. It is thus given by the complement (Equation 11) of the cumulative distribution of the maximum scores (Equation 10). It can again be measured empirically by Monte Carlo sampling or predicted from the distribution of the scores and its extreme value distribution, in particular using the Weibull form of Equation 16 (see also Appendix B). Figure 5 demonstrates again examples of p-value results for actual molecule searches in ChemDB. Each search yields one binary result of whether or not the maximum score is greater than a threshold. Multiple searches of the query molecule against different samples are thus needed to derive a probability that directly compares to the computed p-value. As in the case of E-values, the figure shows that the p-values obtained by conditioning on A closely approximate the p-values obtained by Monte Carlo simulations. These p-values very clearly identify column c as the only column corresponding to a significant Tanimoto similarity with respect to ChemDB. Unlike the E-value above, the p-value is not effective for separating columns a and d. This is because the p-value is useful for assessing Tanimoto scores that are in the tail of high scores and does not work well on average scores. Additional results showing good agreement between predicted and empirical p-values as well as additional technical details are given in Appendix B (Figure 10 and Figure 12).
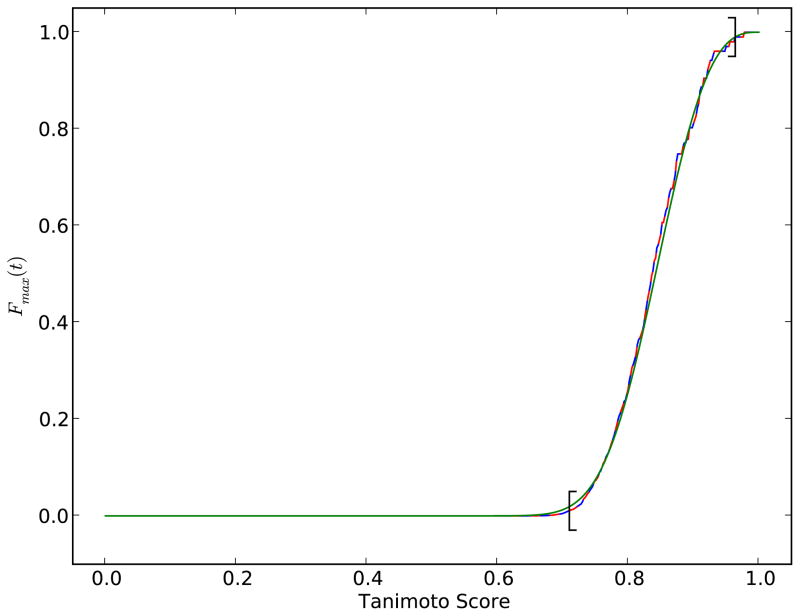
Figure 10.
Plot of Fmax(t), the cumulative distribution of the maximum score, computed on a random sample of 100,000 molecules from the ChemDB in three different ways. The solid blue curve represents the approach of Equation 50. The dashed red line represents that Poisson approach of Equation 53. The green solid line shows the Weibull distribution approach of Equation 54. The left and right brackets on the curve indicate the acceptable boundary within which t1 and t2 ought to be selected (Equations 56 and 57).
Figure 12.
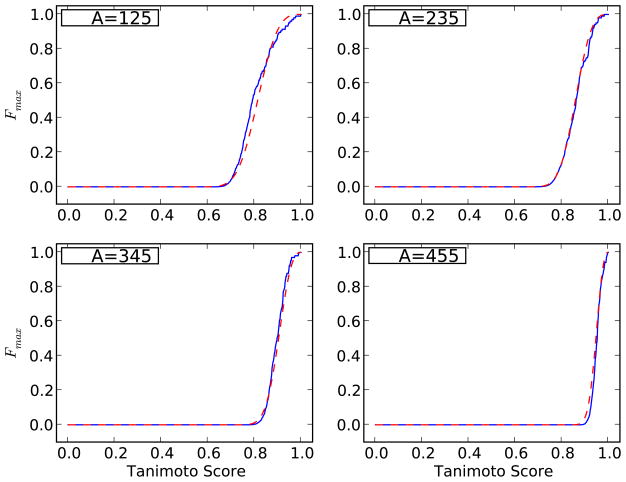
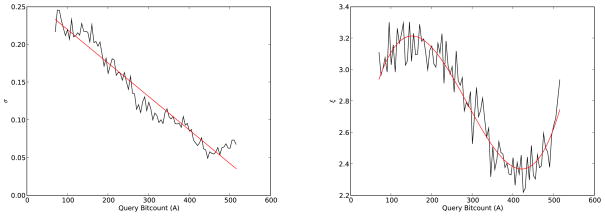
Cumulative extreme value distribution Fmax(t) computed on a random sample of D = 100,000 molecules from the ChemDB, conditioned on different values of A, using 100 query molecules at each value of A. The solid blue curve represents the values obtained using Equation 50 applied with the empirical distribution F(t) of the scores. The dashed red line shows the corresponding Weibull distribution obtained using the polynomial fit for the parameters σ and ξ as a function of A (solid red line in Figure 11).
Outliers
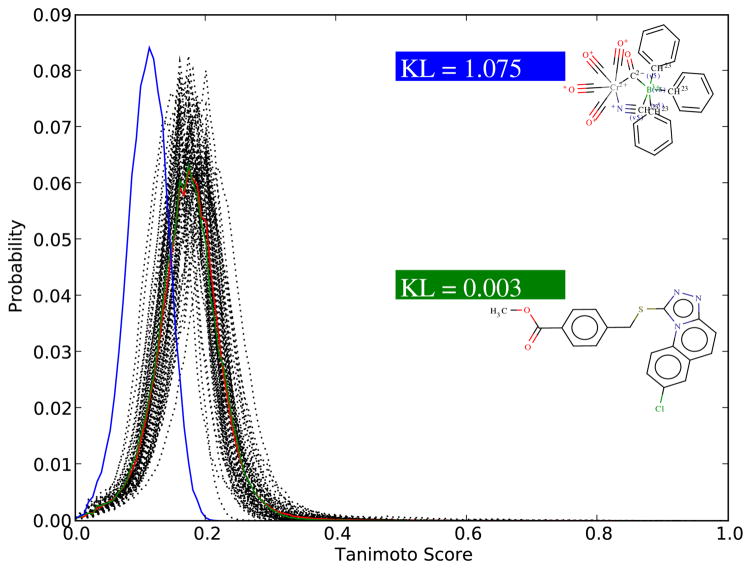
The notion of outliers, like the notion of significance, is relative to a particular background distribution. For instance, we can apply the general framework to easily detect molecules that are outliers, or behave atypically, with respect to the rest of the molecules in a database such as ChemDB. This is illustrated in Figure 6 with an example focusing on molecules satisfying A = 220 showing the distribution of the scores for 100 such molecules. The red curve represents essentially the predicted distribution conditioned on A = 220. The green and blue curve identify two different molecules in this group, with very typical and very atypical behavior, as measured in terms of Kullback-Leibler divergence. The KL divergence is given by and can be used to measure the dissimilarity between any distribution P(t) of scores and the expected distribution M(t). The typical molecule has a KL divergence of 0.003 (green) while the atypical molecule has a KL divergence of 1.075 (blue).
Figure 6.
Empirical score distributions for 100 query molecules satisfying A = 220. Each black curve is associated with one of the molecules and is obtained by scoring the molecule against a random sample of 100,000 molecules from the ChemDB. The red curve corresponds to the mean of the 100 curves and is essentially identical to the predicted distribution of scores conditioned on A = 220. The green curve corresponds to a molecule in the group that is typical and the blue curve to a molecule that is atypical. The difference between the distributions is measured here in terms of Kullback-Leibler (KL) divergence or relative entropy.
ROC Curves
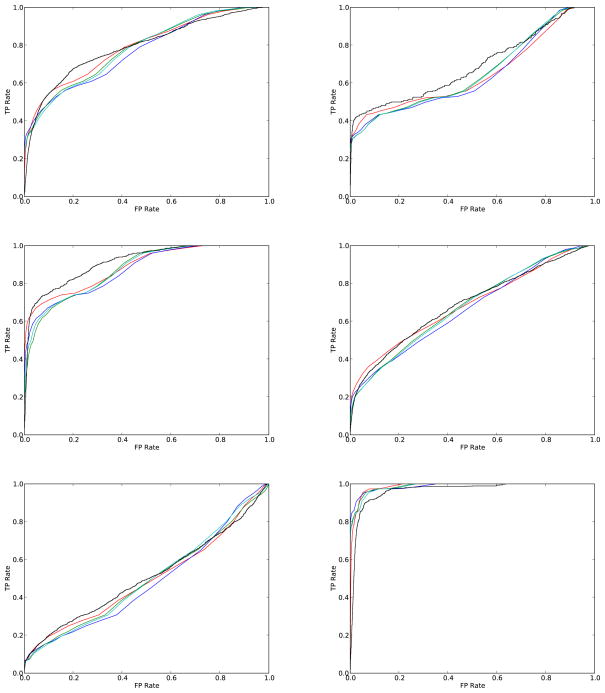
Figure 8 compares empirical and predicted ROC curves for six diverse data sets of molecules taken from the literature: (1) 55 Estrogen Receptor ligands;38 (2) 17 Neuraminidase inhibitors;38 (3) 24 p38 MAP Kinase inhibitors;38 (4) 40 Gelatinase A and general MMP ligands;38 (5) 36 Androgen Receptor ligands;39 and (6) 28 steroids with Corticosteroid Binding Globulin (CBG) Receptor affinity40 against a random background of 100,000 molecules selected from the ChemDB and used as negative examples. The distribution of positive scores is obtained empirically by deriving all the pairwise scores in each dataset. The distribution of negative scores is obtained in each case by all the pairwise scores between molecules in the corresponding positive sets and the 100,000 molecules in the negative set. The distribution of negative scores is modeled here as a ratio of two correlated Normal random variables, or as a single Normal, Gamma, or Beta (after rescaling) distribution. In all cases, the predicted ROC curves approximate the empirical ROC curves well. Thus in short, the framework presented here allows one to predict both True and False, Positive and Negative, rates at all possible thresholds quite accurately and estimate retrieval measures such as Specificity, Sensitivity, Precision, and Recall at a given threshold, or estimate ROC curves over then entire set of possible score thresholds.
Figure 8.
ROC curves for six data sets of active molecules (from left to right and top to bottom): (1) 55 Estrogen receptor ligands; (2) 17 Neuraminidase inhibitors; (3) 24 p38 MAP Kinase inhibitors; (4) 40 Gelatinase A and general MMP ligands; (5) 36 Androgen receptor ligands; and (6) 28 steroids with Corticosteroid Binding Globulin (CBG) receptor affinity. Empirical ROC curves are in black. Various approximations of the negative molecule scores distribution are used to get the theoretical curves, including a ratio of two correlated Normal random variables distribution (red), a single Normal distribution (blue), a single Gamma distribution (green), and a single Beta distribution (cyan), using a random sample of 100,000 molecules from the ChemDB.
Discussion and Conclusions
This paper develops the statistical theory for modeling, predicting, approximating, and understanding the distributions of chemical similarity scores and their extreme values. The framework allows one to answer the questions raised in the Introduction and yields simple guidelines to determine the significance of chemical similarity scores by computing Z-scores, E-values, and p-values. To demonstrate the advantages of Z-scores, E-values, and p-values, consider for example a Tanimoto score of 0.5. The significance of this score depends on many considerations including the size of the database, the kinds of molecules represented in the database, and the molecular representations used. For instance, the significance of a 0.5 score varies when it is obtained in a database containing 1,024 modulo-OR-compressed path fingerprints versus one containing circular substructure finger-prints with lossless compression. This makes the 0.5 Tanimoto score very specific to the particular implementation. In contrast, the Z-score, E-value, and p-value corresponding to a Tanimoto score of 0.5 take into account the global distribution of the scores and are more intrinsic and comparable across different implementations and experiments.
The parameters describing the score distributions can be derived from various models of finger-prints or they can be learned empirically. The detailed derivation in Appendix A demonstrates how the models can be conditioned on the size of the query molecule (A) and/or database molecule (B) providing multiple sets of parameters specific to those sizes. Parameters learned from empirical data can also be conditioned on molecule size, by sampling correspondingly from molecule finger-prints containing A and/or B 1-bits. Conditioning the parameters on both A and B greatly increases the number of parameters. For instance, in a typical implementation using 1,024 modulo-OR-compressed path fingerprints, the value of A and B could span the 1–500 range, requiring a number of parameters in the 5002 range. A large number of parameters may increase the look-up time thus adding complexity to the search. The results presented here show that conditioning on the query molecule size A alone offers a good tradeoff because of the manageable parameter size (~ 500) and considerably improved retrieval results compared to no conditioning at all. Furthermore, using probabilistic models such as the Conditional Normal Uniform model, the number of parameters can be further reduced to a very small number (~ 2), although it may still be desirable to precompute and store the parameters of the score distributions at each possible value of A. Likewise, in order to condition the parameters of the Weibull extreme value distribution on A, Appendix B demonstrates a simple approach where the parameters can be computed economically by simple polynomial functions of A. For several applications, it is also possible to condition the distribution of scores or extreme values on groups of related molecules, for instance molecules known to have the same biological function or bind to the same receptor. In this case, theoretical distributions such as the distribution of the ratio of two correlated Normal random variables or the Weibull distribution for extreme values must be fitted to empirical data.7
This work has been in part inspired by analogies with the field of bioinformatics and the problem of searching large databases of nucleotide or amino acid sequences using standard tools such as BLAST. However, in considering future applications of the theory to chemoinformatics, it is important also to take into consideration some of the differences between the two fields, including differences in culture with respect to data sharing, openness, and standardization. In addition, BLAST was originally created to detect homology due to evolution. While natural evolution is different from the process that has led to the small molecules found in chemoinformatics databases today, we do not believe that this alone results in a fundamental difference, especially in light of the fact that increasing numbers of synthetic biological sequences are being bioengineered. Perhaps more significant is the fact that simple die toss models are better in general at modeling biological sequences, than simple coin flips are at modeling small molecule fingerprints. This is due to the sequential nature of biological sequences and the non-sequential nature of molecular fingerprints. For instance, a small die toss perturbation of a biological sequence results in another sequence, whereas a coin flip perturbation of a fingerprint does not correspond, in general, to a valid fingerprint. However, even such a difference, appears to be more quantitative than qualitative and implies that different probabilistic models may be used in different domains.
As far as other domains are concerned, it is worth noting that the greneral methods presented here are not limited to chemoinformatics, but could be applied to other areas of information retrieval, particularly to text retrieval which is formally very similar to chemical retrieval. Text retrieval methods often represent documents precisely by binary fingerprints, similar to molecular fingerprints, using the well-known “bag of words” approach. In this approach, each document is viewed as a bag of words, and the components of the corresponding fingerprint index the presence or absence of each word from the vocabulary in the document. In addition, similarity between documents is often computed from the corresponding fingerprints using precisely the same Jaccard-Tanimoto similarity measure.
In the short term, however, it is likely that users of chemoinformatics search engines, as well as users of Google and other text search engines, will continue to inspect the top hits returned by a search manually and rely on the raw Jaccard-Tanimoto scores or the corresponding Z-scores, E-values, and p-values to assist them with their inspections. It is in high-throughput data mining applications with large number of queries applied to one or multiple databases, possibly orders of magnitude larger than the ones available today, and when manual inspection becomes impossible, that the framework developed here may find its most fruitful applications.
Acknowledgments
Work supported by NIH Biomedical Informatics Training grant LM-07443-01 and NSF grants EIA-0321390 and IIS-0513376 to PB. We would like also to acknowledge the OpenBabel project and OpenEye Scientific Software for their free software academic license, as well as additional support from the Camille and Henry Dreyfus Foundation, and thank Dr. R. Benz for useful discussions.
Appendix A: Probabilistic Models of Fingerprints
In this Appendix, we show how the probabilistic models can be treated analytically and how the means, standard deviations, and covariances of the intersections and unions can be computed.
A1. Single-Parameter Bernoulli Model
For this model, we assume that the fingerprints B⃗ in the database are generated by N coin flips with a constant probability p of producing a 1-bit. The distribution of the number of 1-bits in the database fingerprints is then given by a a Binomial distribution ℬ(N, p), which can be approximated by a Normal distribution 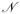 (N p, N pq) for N large. Likewise, we can assume that the query fingerprints are produced by coin flips with constant probability r of producing a 1-bit. The case where r ≠ p can be treated at no extra cost. Consider a fingerprint query A⃗, with A 1-bits with Binomial distribution ℬ(N, r), which can be approximated by
(N p, N pq) for N large. Likewise, we can assume that the query fingerprints are produced by coin flips with constant probability r of producing a 1-bit. The case where r ≠ p can be treated at no extra cost. Consider a fingerprint query A⃗, with A 1-bits with Binomial distribution ℬ(N, r), which can be approximated by 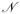 (Nr, Nrs) (s = 1 − r) for N large. Let I⃗ = (Ii) and U⃗ = (Ui) denote the intersection and union fingerprints. Then the intersection size I = A ∩ B = Σi Ii = Σi(Ai ∩ Bi) is a random variable with Binomial distribution ℬ(N, pr), which can be approximated by a Normal distribution
(Nr, Nrs) (s = 1 − r) for N large. Let I⃗ = (Ii) and U⃗ = (Ui) denote the intersection and union fingerprints. Then the intersection size I = A ∩ B = Σi Ii = Σi(Ai ∩ Bi) is a random variable with Binomial distribution ℬ(N, pr), which can be approximated by a Normal distribution 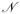 (N pr, N pr(1 − pr)) for N large, as well as a Poisson distribution
(N pr, N pr(1 − pr)) for N large, as well as a Poisson distribution 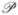 (N pr) when N is large and pr is very small. Similarly, the union size U = A ∪ B = Σi Ui = Σi(Ai ∪ Bi) is a random variable with Binomial distribution ℬ(N, 1 − qs) = ℬ(N, p + r − pr), which can be approximated by a Normal distribution for N large
(N pr) when N is large and pr is very small. Similarly, the union size U = A ∪ B = Σi Ui = Σi(Ai ∪ Bi) is a random variable with Binomial distribution ℬ(N, 1 − qs) = ℬ(N, p + r − pr), which can be approximated by a Normal distribution for N large 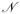 (N(1 − qs), N(1 − qs)qs), and a Poisson distribution
(N(1 − qs), N(1 − qs)qs), and a Poisson distribution 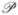 (N(p + r − pr)) when N is large and p +r − pr is small.
(N(p + r − pr)) when N is large and p +r − pr is small.
Under the Binomial model, we can get an exact expression for the distribution of the Tanimoto scores. The Tanimoto score T = I/U can only take rational values t between 0 and 1. Assuming that n and m are irreducible, with 0 ≤ n ≤ m and t = n/m, the probability P(T = t) is given exactly by
| (18) |
where K is the largest integer such that Km ≤ N, i.e. . Clearly if t is not rational, this probability is 0. Thus, from this distribution we can derive all the properties of the score distribution, including its mean and variance, under the assumptions of the Binomial model.
To further simplify matters, by approximating the numerator I and denominator U by Normal distributions as described above, we can view the Tanimoto score as the ratio of two correlated Normal random variables. Thus we next need to compute the covariance between I and U. Noticing that the components Ii and Uj are independent for i ≠ j, we have
| (19) |
A direct calculation gives
| (20) |
so that
| (21) |
Thus we can approximate the distribution of the Tanimoto scores under the simple Bernoulli model by studying the ratio of two correlated Normal random variables approximating the numerator I and denominator U, with means, variances, and covariances as described above.
In Figure 1, the distributions of the number of 1-bits in actual fingerprints contained in the ChemDB and fingerprints generated by the Single-Parameter Bernoulli model, with p chosen to fit the average, are compared. Though both distributions have the same mean by construction, the variance of the ChemDB distribution is significantly larger. Both distributions are also well approximated by Normal distributions with 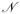 (μ = 218, σ2 = 9552) for the empirical distribution, and
(μ = 218, σ2 = 9552) for the empirical distribution, and 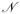 (μ = 218, σ2 = 172) for the Binomial model. The additional width parameter of the Normal model helps to capture the diverse sizes of molecules represented in the empirical fingerprints and can be used effectively in a Conditional Normal Uniform model.
(μ = 218, σ2 = 172) for the Binomial model. The additional width parameter of the Normal model helps to capture the diverse sizes of molecules represented in the empirical fingerprints and can be used effectively in a Conditional Normal Uniform model.
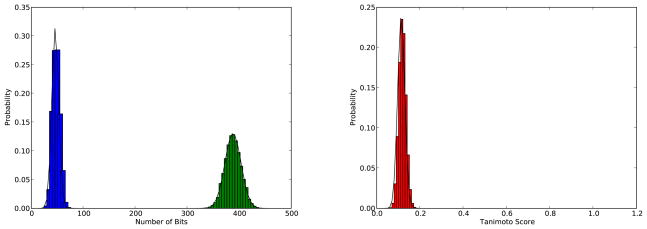
Figure 9 shows the distributions of the intersections and unions of fingerprints generated using a Single-Parameter Bernoulli model with p fit to approximate the mean of the fingerprints in ChemDB (p ≈ 205/1,024) for both the queries and the database. Normal approximations to these distributions are superimposed on the two histograms. Figure 9 also shows the empirical distribution of the scores together with the corresponding ratio of correlated Normal random variables approximation.
Figure 9.
Results obtained using 100 query fingerprints to search 100,000 fingerprints. All finger-prints have length N = 1,024 and are generated using a Single-Parameter Bernoulli model with p = 205/1,024 to fit the average values in the actual ChemDB fingerprints. Left: histograms for the size of the intersections (blue) and the unions (green), together with their Normal approximations (solid black lines). Right: histogram for the corresponding Tanimoto scores (red), together with the corresponding ratio of correlated Normal random variables approximation (solid black line).
A2. Multiple-Parameter Bernoulli Model
The analysis above for the Single-Parameter Bernoulli model can easily be extended to the Multiple-Parameter Bernoulli model by using similar expressions for the mean, variance, covariance of the individual variables Ii and Ui and combining them using the linearity of the expectation and the independence of components associated with different indices. In this case, we let p1, p2,… pN be the vector of probabilities for the database and r1,r2,…rN the vector of probabilities for the queries. The mean and variance of I are given by Σi piri and Σi piri(1 − piri) respectively. Thus I can be approximated by a Normal distribution 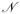 (Σi piri,Σi piri(1 − piri)). Likewise, the mean and variance of U are given by Σi(1 − qisi) and Σi(1 − qisi)qisi respectively. Thus U can be approximated by a Normal distribution
(Σi piri,Σi piri(1 − piri)). Likewise, the mean and variance of U are given by Σi(1 − qisi) and Σi(1 − qisi)qisi respectively. Thus U can be approximated by a Normal distribution 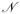 (Σi(1 − qisi),Σi(1 − qisi)qisi). Finally, for the individual covariance terms we have Cov(Ii,Ui) = piri(1 − pi −ri + piri) and Cov(Ii,Uj) = 0 for i ≠ j. Therefore the full covariance is given by the sum Cov(I,U) = Σi piri(1 − pi − ri + piri). Thus one can effectively proceed with the ratio of two correlated Normal random variables approximation, as for the Single-Parameter Bernoulli model.
(Σi(1 − qisi),Σi(1 − qisi)qisi). Finally, for the individual covariance terms we have Cov(Ii,Ui) = piri(1 − pi −ri + piri) and Cov(Ii,Uj) = 0 for i ≠ j. Therefore the full covariance is given by the sum Cov(I,U) = Σi piri(1 − pi − ri + piri). Thus one can effectively proceed with the ratio of two correlated Normal random variables approximation, as for the Single-Parameter Bernoulli model.
In spite of its many parameters, the Multiple-Parameter Bernoulli model suffers from some of the same weaknesses as the Single-Parameter Bernoulli model compared to empirical fingerprints (result not shown). In particular, when using the empirical probabilities pi, the model can easily fit the average of A but tends to underestimate the variance of A, where A is the number of 1-bits in the empirical fingerprints.
A3. Conditional Distribution Uniform Model
With the Conditional Distribution Uniform we can first fit a distribution, typically a Normal, to the size A of the fingerprints in the database or the set of queries. This in general provides a better fit than what can be obtained using the Bernoulli models. Second, this model allows exact conditioning on the size A of the queries or of the molecules being searched. In the Single-Parameter Bernoulli approach, conditioning on A is not implemented exactly but approximated by using p = A/N. Finally, once A is fixed, the uniform portion of the model ensures exchangeability without independence of the components.
Conditioning on A and B
In the Conditional Distribution Uniform model it is easy to see that for fixed A and B the intersection I = A ∩ B has a hypergeometric distribution with probabilities given by
| (22) |
for A + B − N ≤ k ≤ min(A, B), and 0 otherwise.
To study the Tanimoto scores directly, we have the conditional density
| (23) |
and conditional cumulative distribution
| (24) |
Therefore, the probability distribution for the similarity T can be derived from the hypergeometric distribution of I, given A, B and N. In particular, we have the conditional distribution
| (25) |
where the sum is over the distribution P(B). This approach is thus consistent with the Conditional Distribution model which depends on the model for P(B). To model this distribution, we can use the Binomial model . But it is often preferable, as previously discussed, to use a more flexible Normal model with
| (26) |
where the mean and standard deviation are fitted to the empirical values. The unconditional distribution of Tanimoto scores is given by a second integration over the distribution P(A) of queries
| (27) |
For the Conditional Distribution Uniform model, we can derive the means, variances, and covariances of the intersections and unions at all levels of conditioning. First, conditioned on A and B the mean of this hypergeometric distribution is E(I|A,B) = AB/N. The variance is given by Var(I|A,B) = A(B/N)(1 − B/N)(N − A)/(N − 1). The union can be studied from the intersection by writing U = A + B − I, so that P(U = k|A,B) = P(I = A + B − k|A, B). So conditioned on A and B, the expectation of U is given by E(U) = A + B − E(I) using the linearity of the expectation. Likewise, Var(U|A,B) = Var(I|A,B), i.e. the variance of U is equal to the variance of I. In the same way, we can also estimate the covariance by writing Cov(I,U) = E(IU) − E(I)E(U) and writing U = A + B − I yields
| (28) |
Conditioning on A only (or B only)
We can now condition over A only (or B only, mutatis mutandis), i.e. integrating over B. For this we assume that B has a distribution with mean μB and variance . This distribution could be Normal but does not have to be so. Only the mean and variance of this distribution are used in the following calculations, and similarly for the distribution of A. Integrating over B, the mean of the intersection and the union are given by
| (29) |
and
| (30) |
To compute the corresponding variances, we write
| (31) |
here by B⃗ we wish to denote all the fingerprints in the database, and B = |B⃗| is the bit counting function. By expanding the square and integrating first over molecules satisfying B = |(B⃗)|, and then over B, we get
| (32) |
These integrals can easily be calculated and yield
| (33) |
This is an example of the law of total variance or variance decomposition formula
| (34) |
which will be used again in the following calculations without further mention. The same decomposition for the union yields
| (35) |
and finally
| (36) |
Similarly, to calculate the covariance, we have
| (37) |
which gives
| (38) |
After integration over B, we finally get
| (39) |
No Conditioning
If now we integrate with respect to the query molecules A, the means are given by
| (40) |
and
| (41) |
To compute the variances, we apply again the law of total variance to obtain:
| (42) |
which yields
| (43) |
Likewise, for the union
| (44) |
which yields
| (45) |
And finally for the covariance we have
| (46) |
which can again be expanded as
| (47) |
from which
| (48) |
which yields
| (49) |
When the queries come from the database itself with the same distribution, we can simplify the last set of formulae for the mean, variance, and covariance using μA = μB and σA = σB.
In short, we have derived general analytical formulas for the means, variances, and covariances of the intersections and unions of fingerprints under the Conditional Distribution Uniform Model, with various degrees of conditioning. These formulas can be used directly to derive corresponding ration of correlated Normal random variables approximations to the corresponding Tanimoto score distributions.
Appendix B: Extreme Value Distribution
This Appendix describes a complementary approach to the Extreme Value Distribution (EVD) of the similarity scores using a Poisson distribution. It also describes how the parameters of the Weibull approximation to the EVD (Equation 16) can be fit to the data.
B1. Extreme Value Distribution Using the Poisson Distribution
As described in the main text, the cumulative distribution of the maximum score, max, in a database of size D is given by
| (50) |
F(t) is the cumulative distribution of the similarity scores which can be obtained empirically through Monte Carlo experiments, or analytically using, for instance, the ratio of correlated Normal random variables approach. For a large enough Tanimoto threshold t, it is reasonable to assume that obtaining a score above t is a rare event which thus ought to follow a Poisson distribution. In other words, the probability of obtaining k similarity scores above t with a database of size D should be approximately given by the Poisson distribution
| (51) |
with parameter λt,D dependent on the threshold t and the size D of the database being searched. Note that λ could also depend on the A of the query. λ is size also the expectation of the corresponding Poisson distribution, thus λt,D is the expected number of scores above threshold t, which is also called the E-value, and can be computed by Equation 9
| (52) |
The cumulative distribution Fmax(t) corresponds to the probability of having no scores above the threshold t and therefore is given by Pt,D(0):
| (53) |
Equations 50 and 53 give indistinguishable results for Fmax (Figure 10), which can be expected also by looking at the Taylor expansion of e−[1−F(t)].
B2. Fitting the Weibull Distribution Function
As previously described, the probability of max can be represented by a type-III extreme value distribution, or Weibull distribution function, of the form
| (54) |
where μ is the location parameter, σ is the scale parameter and ξ is the shape parameter. μ is set to one because the Tanimoto score, t, is bounded by one. Parameters σ and ξ depend on underlying cumulative distribution of scores, F(t), and the size of the database, D. Substituting Fmax(t) from Equation 50 in Equation 54 and solving for the parameters we get the Equation defined over F(t) > 0, t ≠ 1
| (55) |
To solve for σ and ξ, we substitute two values of t (t1 ≠ t2) in the equation to get the following solutions:
| (56) |
| (57) |
Equations 56 and 57 show very explicitly how the parameters can be calculated for a specific database size(D) and Tanimoto cumulative distribution(F(t)). F(t) can be computed either empirically, by sampling Tanimoto scores from random fingerprints in the database, or theoretically, by using the derivations presented in this work. In principle, one could use arbitrary values of t1 and t2 in Equations 56 and 57. However, it is clear that values too close to t1 = 0 and t1 = 1 do not work and one must be careful to select values of t1 and t2 corresponding to the region where Fmax(t) = F(t)D is not flat (Figure 10). In practice, values of t1 and t2 such that F(t1)D and F(t2)D are in the interval [0.01,0.99] give consistent results and allow for a good fit by the Weibull distribution. Figure 10 shows the fit of Fmax by the Weibull distribution and the corresponding [0.01,0.99] interval. When fitting the Weibull parameters, one can condition F(t) in Equations 56 and 57 on A. This results in a family of parameters ξ(A) and σ(A)) for each value A. These of values can be tabulated or one can try to fit them using a simple regression model. Figure 11 shows how the parameter can be fit with simple polynomial curves and Figure 12 shows Fmax as well as the Weibull distribution for different values of A. For each A, the parameters are calculated using the polynomial functions demonstrated in Figure 11.
Figure 11.
Polynomial fitting of the parameters σ (left) and ξ (right) of the Weibull distribution (Equation 54) using a first and third degree polynomial respectively (in red) as a function of the size A of the query. The empirical values (black) are obtained using a random sample of D=100,000 molecules from the ChemDB. The range of A used for fitting is [70,520]. The polynomials are σ = −0.00044423A + 0.26429116 and ξ = 0.00000009A3 − 0.00007387A2 + 0.01643368A +2.12103400.
References
- 1.Chen J, Swamidass SJ, Dou Y, Bruand J, Baldi P. ChemDB: a public database of small molecules and related chemoinformatics resources. Bioinformatics. 2005;21:4133–4139. doi: 10.1093/bioinformatics/bti683. [DOI] [PubMed] [Google Scholar]
- 2.Irwin JJ, Shoichet BK. ZINC–A Free Database of Commercially Available Compounds for Virtual Screening. J Chem Inf Comput Sci. 2005;45:177–182. doi: 10.1021/ci049714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen J, Linstead E, Swamidass SJ, Wang D, Baldi P. ChemDB Update–Full Text Search and Virtual Chemical Space. Bioinformatics. 2007;23:2348–2351. doi: 10.1093/bioinformatics/btm341. [DOI] [PubMed] [Google Scholar]
- 4.Wheeler D, Barrett T, Benson D, Bryant S, Canese K, Chetvernin V, Church D, DiCuccio M, Edgar R, Federhen S, et al. Database resources of the national center for biotechnology information. Nucleic Acids Res. 2006;35:D5–D12. doi: 10.1093/nar/gkl1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang Y, Xiao J, Suzek T, Zhang J, Wang J, Bryant S. PubChem: a public information system for analyzing bioactivities of small molecules. Nucleic Acids Res. 2009;37:W623–W633. doi: 10.1093/nar/gkp456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Altschul S, Madden T, Shaffer A, Zhang J, Zhang Z, Miller W, Lipman D. Gapped Blast and PSI-Blast: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Keiser M, Roth B, Armbruster B, Ernsberger P, Irwin J, Shoichet B. Relating protein pharmacology by ligand chemistry. Nat Biotechnol. 2007;25(2):197–206. doi: 10.1038/nbt1284. [DOI] [PubMed] [Google Scholar]
- 8.Baldi P, Benz RW. BLASTing Small Molecules - Statistics and Extreme Statistics of Chemical Similarity Scores. Bioinformatics. 2008;24:i357–i365. doi: 10.1093/bioinformatics/btn187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leach AR, Gillet VJ. An Introduction to Chemoinformatics. Springer; Dordrecht, The Netherlands: 2005. [Google Scholar]
- 10.Fligner MA, Verducci JS, Blower PE. A Modification of the Jaccard/Tanimoto Similarity Index for Diverse Selection of Chemical Compounds Using Binary Strings. Technometrics. 2002;44:110–119. [Google Scholar]
- 11.Flower DR. On the Properties of Bit String-Based Measures of Chemical Similarity. J Chem Inf Comput Sci. 1998;38:379–386. [Google Scholar]
- 12.James CA, Weininger D, Delany J. [accessed January 5, 2010];Daylight Theory Manual. Available through: http://www.daylight.com/dayhtml/doc/theory/
- 13.Xue L, Godden JF, Stahura FL, Bajorath J. Profile scaling increases the similarity search performance of molecular fingerprints containing numerical descriptors and structural keys. J Chem Inf Comput Sci. 2003;43:1218–1225. doi: 10.1021/ci030287u. [DOI] [PubMed] [Google Scholar]
- 14.Xue L, Stahura FL, Bajorath J. Similarity search profiling reveals effects of fingerprint scaling in virtual screening. J Chem Inf Comput Sci. 2004;44:2032–2039. doi: 10.1021/ci0400819. [DOI] [PubMed] [Google Scholar]
- 15.Baldi P, Benz RW, Hirschberg D, Swamidass S. Lossless Compression of Chemical Fingerprints Using Integer Entropy Codes Improves Storage and Retrieval. J Chem Inf Model. 2007;47:2098–2109. doi: 10.1021/ci700200n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bohacek RS, McMartin C, Guida WC. The art and practice of structure-based drug design: a molecular modelling perspective. Med Res Rev. 1996;16:3–50. doi: 10.1002/(SICI)1098-1128(199601)16:1<3::AID-MED1>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 17.Holliday JD, Hu CY, Willett P. Grouping of coefficients for the calculation of intermolecular similarity and dissimilarity using 2D fragment bit-strings. Comb Chem High Throughput Screening. 2002;5:155–166. doi: 10.2174/1386207024607338. [DOI] [PubMed] [Google Scholar]
- 18.Swamidass S, Baldi P. Bounds and Algorithms for Exact Searches of Chemical Fingerprints in Linear and Sub-Linear Time. J Chem Inf Model. 2007;47:302–317. doi: 10.1021/ci600358f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hert J, Willett P, Wilton DJ, Acklin P, Azzaoui K, Jacoby E, Schuffenhauer A. Comparison of topological descriptors for similarity-based virtual screening using multiple bioactive reference structures. Org Biomol Chem. 2004;2:3256–3266. doi: 10.1039/B409865J. [DOI] [PubMed] [Google Scholar]
- 20.Bender A, Mussa H, Glen R, Reiling S. Similarity Searching of Chemical Databases Using Atom Environment Descriptors (MOLPRINT 2D): Evaluation of Performance. J Chem Inf Model. 2004;44:1708–1718. doi: 10.1021/ci0498719. [DOI] [PubMed] [Google Scholar]
- 21.Hassan M, Brown RD, Varma-O’Brien S, Rogers D. Cheminformatics analysis and learning in a data pipelining environment. Mol Diversity. 2006;10:283–299. doi: 10.1007/s11030-006-9041-5. [DOI] [PubMed] [Google Scholar]
- 22.Ackley DH, Hinton GE, Sejnowski TJ. A learning algorithm for Boltzmann machines. Cogn Sci. 1985;9:147–169. [Google Scholar]
- 23.Frey B. Graphical Models for Machine Learning and Digital Communication. MIT Press; Cambridge, MA: 1998. [Google Scholar]
- 24.Marsaglia G. Ratios of Normal Variables and Ratios of Sums of Uniform Variables. J Am Stat Assoc. 1965;60:193–204. [Google Scholar]
- 25.Hinkley DV. On the Ratio of Two Correlated Normal Random Variables. Biometrika. 1969;56:635–639. [Google Scholar]
- 26.Cedilnik A, Kosmelj K, Blejec A. The Distribution of the Ratio of Jointly Normal Variables. Metodoloski Zveki. 2004;1:99–108. [Google Scholar]
- 27.Pham-Gia T, Turkkan N, Marchand E. Density of the Ratio of Two Normal Random Variables and Applications. Commun Stat Theory Methods. 2006;35:1569–1591. [Google Scholar]
- 28.Tversky A. Features of similarity. Psychol Rev. 1977;84:327–352. [Google Scholar]
- 29.Rouvray D. Definition and role of similarity concepts in the chemical and physical sciences. J Chem Inf Comput Sci. 1992;32:580–586. [Google Scholar]
- 30.Lee RY, Holland BS, Flueck JA. Distribution of a Ratio of Correlated Gamma Random Variables. SIAM J Appl Math. 1979;36:304–320. [Google Scholar]
- 31.Iubbs JD, Smith OE. A note on the ratio of positively correlated gamma variables. Commun Stat Theory Methods. 1985;14:13–23. [Google Scholar]
- 32.Loaiciga HA, Leipnik RB. Correlated gamma variables in the analysis of microbial densities in water. Adv Water Resour. 2005;28:329–335. [Google Scholar]
- 33.Nagar DKM, Orozco-Castaneda J, Gupta AK. Product and Quotient of Correlated Beta Variables. Appl Math Lett. 2009;22:105–109. [Google Scholar]
- 34.Galambos J. The Asymptotic Theory of Extreme Order Statistics. John Wiley; New York: 1978. [Google Scholar]
- 35.Leadbetter MR, Lindgren G, Rootzen H. Extremems and Related Properties of Random Sequences and Series. Springer-Verlag; New York: 1983. [Google Scholar]
- 36.Coles S. An Introduction to Statistical Modeling of Extreme Values. Springer-Verlag; London: 2001. [Google Scholar]
- 37.Cover TM, Thomas JA. Elements of Information Theory. John Wiley; New York: 1991. [Google Scholar]
- 38.Stahl M, Rarey M. Detailed Analysis of Scoring Funtions for Virtual Screening. J Med Chem. 2001;44:1035–1042. doi: 10.1021/jm0003992. [DOI] [PubMed] [Google Scholar]
- 39.Oprea T, Davis A, Teague S, Leeson P. Is There a Difference between Leads and Drugs? A Historical Perspective. J Chem Inf Comput Sci. 2001;41:1308–1315. doi: 10.1021/ci010366a. [DOI] [PubMed] [Google Scholar]
- 40.Coats E. The CoMFA steroids as a benchmark dataset for development of 3D QSAR methods. Perspect Drug Discov. 1998;12–14:199–213. [Google Scholar]